1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 69, № 3, 2023

Акустический журнал, 2023, T. 69, № 3, стр. 277-283

Дисперсионные и энергетические характеристики изгибных волн в пластине, лежащей на двухпараметрическом упругом основании

В. И. Ерофеев a, *, Е. Е. Лисенкова a, **

a Институт проблем машиностроения РАН – филиал ФГБНУ “Федеральный исследовательский центр Институт прикладной физики Российской академии наук”
603024 Нижний Новгород, ул. Белинского 85, Россия

* E-mail: erof.vi@yandex.ru
** E-mail: eelissen@yandex.ru

Поступила в редакцию 28.05.2022
После доработки 23.10.2022
Принята к публикации 22.12.2022

Полный текст (PDF)

Аннотация

Рассматривается распространение изгибных волн в пластине, лежащей на двухпараметрическом упругом основании. В отличие от классической модели Кирхгофа, используемая здесь для исследования математическая модель учитывает не только кинетическую и потенциальную энергии изгибных колебаний, но и кинетическую энергию, обусловленную инерцией вращения элементов пластины при изгибе. Проводится анализ дисперсионного уравнения, фазовой скорости, скорости переноса энергии и энергетических характеристик волн, распространяющихся в пластине, в зависимости от соотношения коэффициентов, определяющих жесткости упругого основания на сдвиг и сжатие. Найдены условия, при которых возможно существование в пластине волн, фазовая и групповая скорости которых имеют противоположные направления (часто называемых “обратными” волнами). Показано, что такие волны существенно изменяют характер поведения потока энергии. Кроме того, найдены соотношения, связывающие кинематические и средние значения энергетических характеристик волн.

Ключевые слова: тонкая упругая пластина, обобщенное упругое основание, обратная волна, скорость переноса энергии, вектор плотности потока энергии, тензор плотности потока волнового импульса

ВВЕДЕНИЕ

Пластина на упругом основании широко используется как расчетная модель, описывающая различные элементы объектов авиации, судостроения, машиностроения, строительства и т.д.

Непрерывное увеличение скорости, времени работы и удельной мощности машин и механизмов, забота о снижении веса конструкции при улучшении ее надежности в работе, а также широкое внедрение в современную технику новых композиционных материалов – все это приводит к повышению требований к модели и точности расчетов. Современные тенденции исследования колебаний пластин на упругом основании идут по пути усложнения модели, которые в подавляющем большинстве случаев выполняются численными методами. Например, если ранее для проведения анализа изгибных волн выбиралась пластина модели Кирхгофа [1], то в последнее время все чаще используется модель Тимошенко [1–3]. Это касается и упругого основания, для описания которого используются более сложные модели [4–6], чем линейная модель Винклера [7].

Как известно [8–16], в пластинах и тонких слоях существует особый тип волн, характеризующихся противоположным направлением фазовой и групповой скорости. Такие волны часто называют “обратными”, в отличие от обычных, “прямых” волн, у которых направления фазовой и групповой скоростей совпадают. При изучении “обратных” акустических волн в пластинах было установлено, что они весьма чувствительны к параметрам пластины [12, 17–19].

Данная работа посвящена нахождению параметров как пластины, так и упругого основания, при которых могут существовать “обратные” изгибные волны.

УРАВНЕНИЯ ДИНАМИКИ ПЛАСТИНЫ

Рассмотрим изгибные колебания пластины, лежащей на упругом основании, свойства которого характеризуются двумя коэффициентами постели: на растяжение k1 и на сдвиг k2. Коэффициент k1 имеет размерность Н/м3, а коэффициент сдвига k2, который учитывает совместную работу соседних областей, имеет размерность Н/м. Такую модель упругого основания называют обобщенной, двухпараметрической, невинклеровой или моделью Пастернака [20–24]. Вырожденный случай (k2 = 0) соответствует классической модели основания Винклера. Использование модели Пастернака позволяет не только сохранить простоту математического аппарата, которая присуща винклеровой модели, но и получить более достоверные результаты.

Для лагранжиана малых колебаний пластины с учетом инерции вращения ее элементов при изгибе будем иметь выражение [25]

(1)
$\begin{gathered} \lambda = \frac{1}{2}\left\{ {\rho {{h}_{*}}u_{t}^{2} + \frac{{\rho h_{*}^{3}}}{{12}}\left( {u_{{xt}}^{2} + u_{{yt}}^{2}} \right) - } \right. \\ - \,\,\frac{{h_{*}^{3}}}{6}\left( {\frac{{\Lambda + 2\mu }}{2}{{{\left( {{{u}_{{xx}}} + {{u}_{{yy}}}} \right)}}^{2}} + } \right. \\ \left. {\left. { + \,\,2\mu \left( {u_{{xy}}^{2} - {{u}_{{xx}}}{{u}_{{yy}}}} \right)} \right) - {{k}_{1}}{{u}^{2}} - {{k}_{2}}\left( {u_{x}^{2} + u_{y}^{2}} \right)} \right\}. \\ \end{gathered} $

Здесь $\rho {{h}_{*}}$ – поверхностная плотность, $\Lambda $, $\mu $ – константы Ляме, ${{h}_{*}}$ – толщина, u(x, y, t) – поперечное смещение пластины, ${{k}_{1}}$ и ${{k}_{2}}$– коэффициент “постели” на сжатие и коэффициент “сдвига” основания пластины, соответственно, индексами t и x, y обозначаются частные производные функции смещения по времени и пространственным координатам.

Подставляя (1) в уравнение Эйлера–Остроградского [1], получим уравнение изгибных колебаний пластины

(2)
$\begin{gathered} \rho {{h}_{*}}{{\partial }_{{tt}}}u - \frac{{\rho h_{*}^{3}}}{{12}}{{\partial }_{{tt}}}\Delta u + \frac{{\left( {\Lambda + 2\mu } \right)h_{*}^{3}}}{{12}}\Delta \Delta u - \\ - \,\,{{k}_{2}}\Delta u + {{k}_{1}}u = 0. \\ \left( {{{\partial }_{{tt}}} = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}},\,\,\,\,\Delta = {{\partial }_{{xx}}} + {{\partial }_{{yy}}}} \right), \\ \end{gathered} $
решение которого можно представить в виде суперпозиции плоских волн
$u\left( {x,y,t} \right) = A\exp \left[ {i\left( {{{\omega }}t - {{k}_{x}}x - {{k}_{y}}y} \right)} \right],$
где $A$, $\omega $, ${{k}_{x}}$, ${{k}_{y}}$ – комплексные постоянные.

УРАВНЕНИЯ ПЕРЕНОСА ЭНЕРГИИ И ВОЛНОВОГО ИМПУЛЬСА

Особенностью распределенных упругих систем является возможность переноса с конечной скоростью энергии и волнового импульса. Для получения соответствующих уравнений переноса умножим уравнение динамики (1) на частные производные функции поперечного смещения u(x, y, t) пластины ut, ux, uy и приведем полученные соотношения к дивергентному виду. В результате будем иметь

(3)
$\frac{{\partial h}}{{\partial t}} + div{\mathbf{S}} = 0,\,\,\,\,\frac{{\partial {\mathbf{p}}}}{{\partial t}} + div{\mathbf{T}} = 0.$

Здесь

$\begin{gathered} h = \frac{1}{2}\left\{ {\rho {{h}_{*}}u_{t}^{2} + \frac{{\rho h_{*}^{3}}}{{12}}\left( {u_{{xt}}^{2} + u_{{yt}}^{2}} \right) + } \right. \\ + \,\,\frac{{h_{*}^{3}}}{6}\left( {\frac{{\Lambda + 2\mu }}{2}{{{\left( {{{u}_{{xx}}} + {{u}_{{yy}}}} \right)}}^{2}} + } \right. \\ \left. {\left. { + \,\,2\mu {{{\left( {u_{{xy}}^{2} - {{u}_{{xx}}}{{u}_{{yy}}}} \right)}}^{{^{{}}}}}} \right) + {{k}_{1}}{{u}^{2}} + {{k}_{2}}{{{\left( {u_{x}^{2} + u_{y}^{2}} \right)}}^{{^{{^{{^{{}}}}}}}}}} \right\} \\ \end{gathered} $
– плотность энергии, ${\mathbf{S}} = \left\{ {{{S}_{x}},{{S}_{y}}} \right\}$ – вектор плотности потока энергии, часто называемый вектором Умова–Пойнтинга [26, 27], с компонентами:
$\begin{gathered} S_{x}^{{}} = {{u}_{t}}\left( {\frac{{h_{*}^{3}\left( {\Lambda + 2\mu } \right)}}{{12}}\left( {{{u}_{{xxx}}} + {{u}_{{xyy}}}} \right) - \frac{{\rho h_{*}^{3}}}{{12}}{{u}_{{xtt}}} - {{k}_{2}}{{u}_{x}}} \right) - \\ - \,\,\frac{{h_{*}^{3}\left( {\Lambda + 2\mu } \right)}}{{12}}{{u}_{{xt}}}{{u}_{{xx}}} - \\ - \,\,\frac{{h_{*}^{3}\Lambda }}{{12}}{{u}_{{xt}}}{{u}_{{yy}}} - \frac{{h_{*}^{3}\mu }}{6}{{u}_{{yt}}}{{u}_{{xy}}},\,\,\,\,\left( {x \leftrightarrow y} \right) \\ \end{gathered} $
${\mathbf{p}} = \left\{ {{{p}_{x}},{{p}_{y}}} \right\}$ – вектор плотности волнового импульса с координатами:
$p_{x}^{{}} = - \rho {{h}_{*}}{{u}_{t}}{{u}_{x}} - \frac{{\rho h_{*}^{3}}}{{12}}{{u}_{{xt}}}{{u}_{{xx}}} - \frac{{\rho h_{*}^{3}}}{{12}}{{u}_{{yt}}}{{u}_{{xy}}},$
${\mathbf{T}}$ – тензор плотности потока волнового импульса с компонентами

$\begin{gathered} T_{{xx}}^{{}} = \left\{ {\rho {{h}_{*}}u_{t}^{2} + } \right.\frac{{\rho h_{*}^{3}}}{{12}}\left( {u_{{xt}}^{2} + u_{{yt}}^{2} + 2{{u}_{x}}{{u}_{{xtt}}}} \right) + \\ + \,\,\frac{{h_{*}^{3}\left( {\Lambda + 2\mu } \right)}}{{12}}\left( {u_{{xx}}^{2} - u_{{yy}}^{2} - 2{{u}_{x}}\left( {{{u}_{{xxx}}} + {{u}_{{xyy}}}} \right)} \right) - \\ {{\left. { - \,\,{{k}_{1}}{{u}^{2}} + {{k}_{2}}\left( {u_{x}^{2} - u_{y}^{2}} \right)} \right\}} \mathord{\left/ {\vphantom {{\left. { - \,\,{{k}_{1}}{{u}^{2}} + {{k}_{2}}\left( {u_{x}^{2} - u_{y}^{2}} \right)} \right\}} 2}} \right. \kern-0em} 2}, \\ \end{gathered} $
$\begin{gathered} T_{{xy}}^{{}} = {{u}_{y}}\left( {\frac{{\rho h_{*}^{3}}}{{12}}{{u}_{{xtt}}} - \frac{{h_{*}^{3}\left( {\Lambda + 2\mu } \right)}}{{12}}\left( {{{u}_{{xxx}}} + {{u}_{{xyy}}}} \right) + {{k}_{2}}{{u}_{x}}} \right) + \\ + \,\,\frac{{h_{*}^{3}\left( {\Lambda + 2\mu } \right)}}{{12}}{{u}_{{xy}}}\left( {{{u}_{{xx}}} + {{u}_{{yy}}}} \right),\,\,\,\left( {x \leftrightarrow y} \right). \\ \end{gathered} $

Вычисляя средние значения этих величин за период волны 2πω–1, получим:

(4)
$\begin{gathered} \left\langle h \right\rangle = \frac{1}{2}\rho {{h}_{*}}\left( {1 + \frac{{h_{*}^{2}}}{{12}}\left( {k_{x}^{2} + k_{y}^{2}} \right)} \right){{\omega }^{2}}AA*, \\ \left\langle {S_{x}^{{}}} \right\rangle = \\ = \frac{1}{2}\left( {\frac{{h_{*}^{3}\left( {\Lambda + 2\mu } \right)}}{6}\left( {k_{x}^{2} + k_{y}^{2}} \right) - \frac{{\rho h_{*}^{3}}}{{12}}{{\omega }^{2}} + {{k}_{2}}} \right)\omega {{k}_{x}}AA*, \\ \left\langle {{{p}_{x}}} \right\rangle = \frac{1}{2}\rho {{h}_{*}}\left( {1 + \frac{{h_{*}^{2}}}{{12}}\left( {k_{x}^{2} + k_{y}^{2}} \right)} \right)\omega {{k}_{x}}AA*, \\ \left\langle {T_{{xy}}^{{}}} \right\rangle = \\ = \frac{1}{2}\left( {\frac{{h_{*}^{3}\left( {\Lambda + 2\mu } \right)}}{6}\left( {k_{x}^{2} + k_{y}^{2}} \right) - \frac{{\rho h_{*}^{3}}}{{12}}{{\omega }^{2}} + {{k}_{2}}} \right){{k}_{x}}{{k}_{y}}AA*, \\ \left( {x \leftrightarrow y} \right). \\ \end{gathered} $

Верхний индекс * означает комплексное сопряжение.

На кинематические характеристики волны –частоту ω, компоненты волнового вектора κ ={kx, ky} и параметры распределенной системы – уравнениями динамики накладывается связь, которую принято называть дисперсионным уравнением [28].

АНАЛИЗ ДИСПЕРСИОННЫХ ЗАВИСИМОСТЕЙ

На основе уравнения динамики пластины (2) получим, что частота ω и компоненты волнового вектора kx, ky связаны посредством дисперсионного соотношения

(5)
$\begin{gathered} {{\omega }}\, = \, \pm {{\left( {\frac{{h_{*}^{3}\left( {\Lambda \, + \,2\mu } \right)}}{{12}}{{{\left( {k_{x}^{2}\, + \,k_{y}^{2}} \right)}}^{2}}\, + \,\,{{k}_{2}}\left( {k_{x}^{2}\, + \,k_{y}^{2}} \right)\, + \,{{k}_{1}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\, \times \\ \times \,\,{{\left( {\rho {{h}_{*}} + \frac{{\rho h_{*}^{3}}}{{12}}\left( {k_{x}^{2} + k_{y}^{2}} \right)} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $

Определяя наименьшую частоту возбуждаемых в пластине волн, будем иметь

${{{{\omega }}}_{{{\text{RP}}}}} = \frac{2}{{\sqrt \rho {{h}_{*}}}}{{\left( {6\left( {\Lambda + 2\mu } \right)\left( {\sqrt {1 - \frac{{{{k}_{2}}}}{{{{h}_{*}}\left( {\Lambda + 2\mu } \right)}} + \frac{{{{k}_{1}}{{h}_{*}}}}{{12\left( {\Lambda + 2\mu } \right)}}} + \frac{{{{k}_{2}}}}{{2{{h}_{*}}\left( {\Lambda + 2\mu } \right)}} - 1} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$
при $\frac{{{{k}_{2}}}}{{{{k}_{1}}h_{*}^{2}}} < \frac{1}{{12}}$. Низкочастотное поле с частотой ω < ωRP не распространяется, а экспоненциально спадает по мере проникновения в систему. Сравнивая с частотой
${\begin{gathered} {{{{\omega }}}_{{{\text{RV}}}}} = \\ = 2{{\left( {6\left( {\Lambda \, + \,2\mu } \right)\left( {\sqrt {1\, + \,{{{{k}_{1}}h_{*}^{{}}} \mathord{\left/ {\vphantom {{{{k}_{1}}h_{*}^{{}}} {12\left( {\Lambda \, + \,2\mu } \right)}}} \right. \kern-0em} {12\left( {\Lambda \, + \,2\mu } \right)}}} - 1} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \\ \end{gathered} \mathord{\left/ {\vphantom {\begin{gathered} {{{{\omega }}}_{{{\text{RV}}}}} = \\ = 2{{\left( {6\left( {\Lambda \, + \,2\mu } \right)\left( {\sqrt {1\, + \,{{{{k}_{1}}h_{*}^{{}}} \mathord{\left/ {\vphantom {{{{k}_{1}}h_{*}^{{}}} {12\left( {\Lambda \, + \,2\mu } \right)}}} \right. \kern-0em} {12\left( {\Lambda \, + \,2\mu } \right)}}} - 1} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \\ \end{gathered} {\sqrt \rho {{h}_{*}}}}} \right. \kern-0em} {\sqrt \rho {{h}_{*}}}}$
для винклеровского основания, можно утверждать, что ωRV < ωRP . Следовательно, область непропускания для пластины с учетом инерции вращения ее элементов при изгибе, лежащей на винклеровском основании ýже, чем для упругого основания модели Пастернака.

На рис. 1 представлены дисперсионные кривые (зависимость частоты ω от волнового числа κ – модуля волнового вектора κ волны) при различных значениях коэффициента сдвига основания пластины. Видно, что существует участок дисперсионной кривой, на котором тангенс угла наклона касательной отрицателен. Следовательно, для рассматриваемой модели имеется область частот $\left( {{{{{\omega }}}_{{{\text{RP}}}}},\sqrt {{{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {\rho {{h}_{*}}}}} \right. \kern-0em} {\rho {{h}_{*}}}}} } \right)$, где справедлив “эффект обратной волны” [29–31]. Для таких волн (как было сказано выше) имеет место противоположная направленность фазовой и групповой скоростей. На возможность этой ситуации впервые было указано Лэмбом [32], который построил ряд моделей сред, обладающих данным свойством.

Рис. 1.

Зависимость безразмерной частоты от безразмерного волнового числа при различных значениях приведенного коэффициента сдвига (${{\tilde {k}}_{2}} = {{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} {{{k}_{1}}h_{*}^{2}}}} \right. \kern-0em} {{{k}_{1}}h_{*}^{2}}}$) упругого основания: 1 – ${{\tilde {k}}_{2}} = 0$; 2 – ${{\tilde {k}}_{2}} = 0.01$; 3 – ${{\tilde {k}}_{2}} = 0.04$; 4 – ${{\tilde {k}}_{2}} = 0.2$.

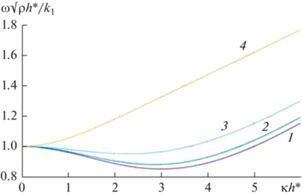
Ширина частотной области существования “обратных” волн зависит от отношения величин коэффициентов постели на сдвиг и на сжатие. При k2 = 0, что соответствует модели основания Винклера, частотная область наличия “обратных” волн шире, чем для модели основания Пастернака $\left( {{{{{\omega }}}_{{{\text{RP}}}}},\sqrt {{{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {\rho {{h}_{*}}}}} \right. \kern-0em} {\rho {{h}_{*}}}}} } \right) \subset \left( {{{{{\omega }}}_{{{\text{RV}}}}},\sqrt {{{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {\rho {{h}_{*}}}}} \right. \kern-0em} {\rho {{h}_{*}}}}} } \right)$. Увеличение коэффициента упругого основания пластины на сдвиг приводит к уменьшению частотной области, где имеют место быть “обратные” волны, а при ${{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} {{{k}_{1}}h_{*}^{2}}}} \right. \kern-0em} {{{k}_{1}}h_{*}^{2}}} > {1 \mathord{\left/ {\vphantom {1 {12}}} \right. \kern-0em} {12}}$ делает невозможным их существование. Следует также отметить, что в пластине модели Кирхгофа поперечные волны являются “прямыми” (направления фазовой и групповой скоростей совпадают) [33].

Определяя фазовую скорость волн как vph = = ωκ/κ2, в безразмерных переменных

$\begin{gathered} a = \sqrt {\frac{{\Lambda + 2\mu }}{{{{k}_{1}}{{h}_{*}}}}} ,\,\,\,\,{{{\tilde {k}}}_{2}} = \frac{{{{k}_{2}}}}{{{{k}_{1}}h_{*}^{2}}},\,\,\,\,{{\tilde {\omega }}} = {{\omega }}\sqrt {{{\rho {{h}_{*}}} \mathord{\left/ {\vphantom {{\rho {{h}_{*}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}} , \\ {{{\tilde {k}}}_{x}} = {{k}_{x}}{{h}_{*}},\,\,\,\,{{{\tilde {k}}}_{y}} = {{k}_{y}}{{h}_{*}},\,\,\,\,{{{\tilde {v}}}_{{{\text{ph}}}}} = \left| {{{{\mathbf{v}}}_{{{\text{ph}}}}}} \right|\sqrt {\frac{\rho }{{{{k}_{1}}{{h}_{*}}}}} , \\ \end{gathered} $
получим выражение для модуля фазовой скорости

${{\tilde {v}}_{{{\text{ph}}}}} = \tilde {\omega }{{\left( {\frac{6}{{{{a}^{2}}}}\left( {\frac{{{{{\tilde {\omega }}}^{2}}}}{{12}}\, - \,{{{\tilde {k}}}_{2}} \pm \sqrt {{{{\left( {\frac{{{{{\tilde {\omega }}}^{2}}}}{{12}}\, - \,{{{\tilde {k}}}_{2}}} \right)}}^{2}} - \frac{{{{a}^{2}}}}{3}\left( {1 - {{{\tilde {\omega }}}^{2}}} \right)} } \right)} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$

Знак “–” соответствует интервалу частот ${{\tilde {\omega }}} \in \left[ {{{{{\omega }}}_{{{\text{RP}}}}}\sqrt {{{\rho {{h}_{*}}} \mathord{\left/ {\vphantom {{\rho {{h}_{*}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}} ;\;1} \right]$, знак “+” – интервалу $\left[ {{{\omega }_{{{\text{RP}}}}}\sqrt {{{\rho {{h}_{*}}} \mathord{\left/ {\vphantom {{\rho {{h}_{*}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}} ;\; + \infty } \right)$. На рис. 2 представлены зависимости модуля фазовой скорости от частоты при различных значениях коэффициента сдвига. Расчетные графики построены для безразмерных переменных при a = 0.2.

Рис. 2.

Частотные зависимости фазовой скорости при различных значениях коэффициента сдвига упругого основания: 1 – ${{\tilde {k}}_{2}} = 0$; 2 – ${{\tilde {k}}_{2}} = 0.01$; 3 – ${{\tilde {k}}_{2}} = 0.04$; 4 – ${{\tilde {k}}_{2}} = 0.2$.

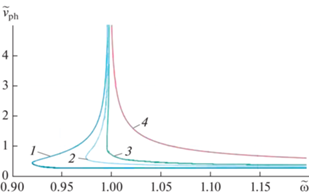
Фазовая скорость в безразмерных переменных имеет горизонтальную асимптоту ${{\tilde {v}}_{{{\text{ph}}}}} = a$ (при ${{\tilde {\omega }}} \to \infty $) и вертикальную асимптоту $\tilde {\omega } = 1$ (рис. 2). Частотная область $\left( {{{{{\omega }}}_{{{\text{RP}}}}}\sqrt {{{\rho {{h}_{*}}} \mathord{\left/ {\vphantom {{\rho {{h}_{*}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}} ;\;1} \right)$ является областью существования “обратных”, а $\left( {{{{{\omega }}}_{{{\text{RP}}}}}\sqrt {{{\rho {{h}_{*}}} \mathord{\left/ {\vphantom {{\rho {{h}_{*}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}} ;\; + \infty } \right)$ – “прямых” волн.

Определяя минимальную фазовую скорость волн, получим

$\tilde {v}_{{{\text{ph}}}}^{{\min }} = {{\left( {{{\left( {\sqrt {1 + 12{{a}^{2}} - 12{{{\tilde {k}}}_{2}}} - 1 + 6{{{\tilde {k}}}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {\sqrt {1 + 12{{a}^{2}} - 12{{{\tilde {k}}}_{2}}} - 1 + 6{{{\tilde {k}}}_{2}}} \right)} 6}} \right. \kern-0em} 6}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Эта скорость является одной из важных среди критических скоростей, которые рассматриваются в литературе. Так, например, как было показано в работах [34, 35], при равномерном движении объекта со скоростью, превышающей минимальную фазовую скорость излучаемой волны, его поперечные колебания, вследствие аномального эффекта Доплера [36, 37], могут быть неустойчивыми. В связи с этим при исследовании колебаний упругой системы, несущей высокоскоростную движущуюся нагрузку, определение минимальной фазовой скорости становится первоочередной задачей [35, 38–40].

Заметим, что скорость V переноса волновой энергии определяется как S/h [28]. Можно убедиться, что для квазигармонических волн среднее за период значение V равно dω/dκ = gradκω, что совпадает с известным приближенным выражением для групповой скорости [28].

Зависимость составляющей Vx скорости переноса волновой энергии (групповой скорости) от частоты при ky = 0 и различных значениях коэффициента сдвига основания пластины в безразмерных переменных (${{\tilde {V}}_{x}} = {{V}_{x}}\sqrt {\rho {{{\left( {{{k}_{1}}{{h}_{*}}} \right)}}^{{ - 1}}}} $) представлено на рис. 3.

Рис. 3.

Частотные зависимости групповой скорости при различных значениях коэффициента сдвига упругого основания: 1 – ${{\tilde {k}}_{2}} = 0$; 2 – ${{\tilde {k}}_{2}} = 0.01$; 3 – ${{\tilde {k}}_{2}} = 0.04$; 4 – ${{\tilde {k}}_{2}} = 0.2$.

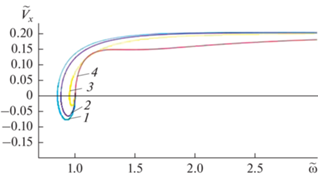
Для частоты ωRP, где “обратные” волны переходят в “прямые”, групповая скорость обращается в нуль, а следовательно, энергия на этой частоте не переносится.

При высоких частотах значение скоростей V и vph близко к скорости продольной волны в безграничной среде. Следует ожидать, что путем введения поправочного коэффициента в модели (1)–(2) можно добиться более точного описания дисперсионных свойств реальной пластины, в частности, в пределе при ω → ∞ фазовая скорость будет близка к скорости сдвиговой волны.

Сравнивая фазовую и групповую скорости (при ky = 0, рис. 4), следует также выделить две области волновых чисел. Для первой области – фазовая скорость больше групповой, для второй – фазовая меньше групповой скорости. Следовательно, в первой области имеем нормальную дисперсию волн, во второй – аномальную. Имеется волновое число (а соответственно, и частота), перенос энергии колебаний при котором осуществляется с максимальной скоростью.

Рис. 4.

Зависимость фазовой (1) и групповой (2) скоростей от волнового числа для приведенного коэффициента сдвига упругого основания ${{\tilde {k}}_{2}} = 0.01$.

АНАЛИЗ ЭНЕРГЕТИЧЕСКИХ СООТНОШЕНИЙ

Представляет интерес оценить локальный поток энергии, переносимый волнами в пластине, изгибные колебания которой описываются уравнением (2). Следует отметить, что впервые, по-видимому, изучение плотностей потоков энергии “обратных” волн в упругой полосе в зависимости от поперечной координаты слоя было проведено в работе [41], где для нормальных волн обнаружены локальные потоки энергии встречного направления. В [42] при исследовании продольных колебаний бесконечной пластины постоянной ширины было установлено, что на частоте возникновения “обратной” волны происходит принципиальная перестройка поля вектора потока энергии. В случае, когда у дисперсионной кривой нет участка, соответствующего “обратной” волне, плотность потока энергии остается знакопостоянной. Хотя в составной модели, как показано в работе [43], локальные потоки энергии могут носить знакопеременный характер не только для обратных, но и для прямых волн, которые не связаны с обратными волнами одной дисперсионной кривой.

На рис. 5 изображены зависимости плотности потока энергии ${{\tilde {S}}_{x}} = \left\langle {{{S}_{x}}} \right\rangle \sqrt \rho {{\left( {\sqrt {k_{1}^{3}{{h}_{*}}} AA{\text{*}}} \right)}^{{ - 1}}}$ от волнового числа при различных значениях приведенного коэффициента сдвига упругого основания (для случая ky = 0).

Рис. 5.

Плотность потока энергии в зависимости от волнового числа при 1 – ${{\tilde {k}}_{2}} = 0$; 2 – ${{\tilde {k}}_{2}} = 0.01$; 3 – ${{\tilde {k}}_{2}} = 0.04$; 4 – ${{\tilde {k}}_{2}} = 0.2$.

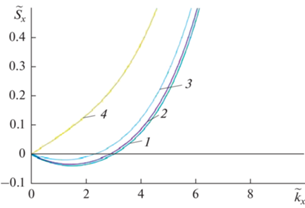
Видно, что поведение плотностей потоков энергии носит знакопеременный характер, если ${{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} {{{k}_{1}}h_{*}^{2}}}} \right. \kern-0em} {{{k}_{1}}h_{*}^{2}}} < {1 \mathord{\left/ {\vphantom {1 {12}}} \right. \kern-0em} {12}}$; в противном случае, а именно, при ${{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} {{{k}_{1}}h_{*}^{2}}}} \right. \kern-0em} {{{k}_{1}}h_{*}^{2}}} > {1 \mathord{\left/ {\vphantom {1 {12}}} \right. \kern-0em} {12}}$ изменение знака плотности потока энергии не наблюдается.

Из (4) и (5) следует, что для средних значений локальных энергетических характеристик справедливы следующие соотношения:

– скалярное произведение фазовой скорости на вектор плотности волнового импульса равно плотности волновой энергии:

$\left\langle h \right\rangle = {{{\mathbf{v}}}_{{{\text{ph}}}}}\left\langle {\mathbf{p}} \right\rangle ;$
– произведение вектор-столбца групповой скорости V = (Vx,Vy)T на вектор-строку плотности волнового импульса равно тензору плотности потока волнового импульса:

$\left( {\begin{array}{*{20}{c}} {{{V}_{x}}} \\ {{{V}_{y}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\left\langle {{{p}_{x}}} \right\rangle }&{\left\langle {{{p}_{y}}} \right\rangle } \end{array}} \right) = \left\| {\begin{array}{*{20}{c}} {\left\langle {{{T}_{{xx}}}} \right\rangle }&{\left\langle {{{T}_{{xy}}}} \right\rangle } \\ {\left\langle {{{T}_{{yx}}}} \right\rangle }&{\left\langle {{{T}_{{yy}}}} \right\rangle } \end{array}} \right\|.$

Отношение модулей средних значений плотности потока энергии к плотности волнового импульса равно произведению модулей фазовой и групповой скоростей волн:

$\frac{{\left| {\left\langle {\mathbf{S}} \right\rangle } \right|}}{{\left| {\left\langle {\mathbf{p}} \right\rangle } \right|}} = \left| {{{{\mathbf{v}}}_{{{\text{ph}}}}}} \right|\left| {\mathbf{V}} \right|.$

Отношение плотности энергии к частоте равно отношению модуля вектора плотности волнового импульса к волновому числу.

$\frac{{\left\langle h \right\rangle }}{{{\omega }}} = \frac{{\left| {\left\langle {\mathbf{p}} \right\rangle } \right|}}{\kappa }.$

ВЫВОДЫ

Таким образом, для пластины, лежащей на упругом основании, учет инерции вращения ее элементов при изгибе приводит к наличию частотной области существования “обратных” волн, т.е. волн, у которых фазовая и групповая скорости противоположно направлены.

При наличии двух коэффициентов постели (на сдвиг k2 и на сжатие k1), характерных для модели Пастернака, ширина этой области зависит от их соотношения. С уменьшением значения коэффициента сдвига упругого основания k2 → 0 частотная область существования “обратных” волн увеличивается. Пороговое значение, при котором невозможно их существование, определяется равенством ${{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} {{{k}_{1}}h_{*}^{2}}}} \right. \kern-0em} {{{k}_{1}}h_{*}^{2}}} = {1 \mathord{\left/ {\vphantom {1 {12}}} \right. \kern-0em} {12}}$.

На частоте возникновения “обратной” волны скорость переноса волновой энергии обращается в нуль и происходит принципиальная перестройка поля вектора плотности потока энергии.

Плотность волновой энергии связана с плотностью переносимого квазигармонической волной импульса посредством фазовой скорости.

Компоненты тензора плотности потока волнового импульса и плотности переносимого волной импульса связаны посредством групповой скорости.

Работа выполнялась в рамках государственного задания ИПФ РАН на проведение фундаментальных научных исследований на 2021–2023 гг. по теме № 0030-2021-0025.

Список литературы

  1. Вибрации в технике. Т. 1. Колебания линейных систем / Под ред. Болотина В.В. М.: Машиностроение, 1999. 504 с.

  2. Уфлянд Я.С. Распространение волн при поперечных колебаниях стержней и пластин // Прикладная математика и механика. 1948. Т. 12. № 3. С. 287–300.

  3. Mindlin R.D. Influence of rotator inertia and shear on flexural motions of isotropic, elastic plates // Trans. ASME. J. Appl. Mech. 1951. V. 18. № 1. P. 31–38.

  4. Пастернак П.Л. Основы нового метода расчета фундаментов на упругом основании при помощи двух коэффициентов постели. М.: Госстройиздат, 1954. 56 с.

  5. Козин В.М., Жесткая В.Д., Погорелова А.В., Чижиумов С.Д., Джабраилов М.Р., Морозов В.С., Кустов А.Н. Прикладные задачи динамики ледяного покрова. М.: Изд-во Академии естествознания, 2008. URL: https://www.monographies.ru/ru/ book/view?id=14.

  6. Иванченко И.И. Динамика транспортных сооружений: высокоскоростные подвижные, сейсмические и ударные нагрузки. М.: Наука, 2011. 574 с.

  7. Winkler E. Die Lehre von der Elastizität und Festigkeit. Prague, 1867.

  8. Meitzler A.H. Backward-wave transmission of stress pulses in elastic cylinders and plates // J. Acoust. Soc. Am. 1965. V. 38. № 5. P. 835–842.

  9. Викторов И.А. Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике. М.: Наука, 1966. 168 с.

  10. Меркулов Л.Г., Рохлин С.И. Дифракция волн Лэмба в пластине на полубесконечном разрезе // Дефектоскопия. 1969. № 4. С. 24–36.

  11. Бурлий П.В., Кучеров И.Я. Обратные упругие волны в пластинах // Письма в ЖЭТФ. 1977. Т. 26. № 9. С. 644–647.

  12. Бурлий П.В., Ильин П.П., Кучеров И.Я. Обратные упругие волны в изотропных пластинах // Журн. техн. физ. 1981. Т. 51. № 10. С. 2196–2198.

  13. Бурлий П.В., Ильин П.П., Кучеров И.Я. О возможности существования поперечных обратных волн в пластинах // Письма в ЖТФ. 1982. Т. 8. № 9. С. 568–571.

  14. Абрамова О.П., Сторожев В.И., Шпак В.А. Дисперсия нормальных волн в ортотропном слое с закрепленными границами // Акуст. журн. 1996. Т. 42. № 1. С. 5–9.

  15. Бурлий П.В., Ильин П.П., Кучеров И.Я. Обратные поперечные акустические волны в пластинах кубических кристаллов // Акуст. журн. 1997. Т. 43. № 3. С. 310–314.

  16. Toda K., Motegi K. Propagation characteristics of leaky Lamb waves in a liquid-loaded double-layered substrate consisting of a thin piezoelectric ceramic plate and thin glass plate // J. Acoust. Soc. Am. 1999. V. 105. № 6. P. 3290–3294. https://doi.org/10.1121/1.424657

  17. Бырдин В.М., Дюдин Б.В., Лепендин ЛЛ. Обратная симметричная волна Лэмба первого порядка // Письма в ЖТФ. 1978. Т. 4. Вып. 13. С. 781–785.

  18. Rokhlin S. Interaction of Lamb waves with elongated delaminations in thin sheets // Int. Advances in Nondest. Test. 1979. V. 6. P. 263–285.

  19. Кучеров И.Я., Маляренко Е.В. Потоки энергии обратных и прямых нормальных поперечных акустических волн в пьезоэлектрических пластинах // Акуст. журн. 1998. Т. 44. № 4. С. 492–497.

  20. Ерофеев В.И., Лисенкова Е.Е., Царев И.С. Динамическое поведение балки, лежащей на обобщенном упругом основании, с движущейся нагрузкой // Прикладная математика и механика. 2021. Т. 85. № 2. С. 193–209. https://doi.org/10.31857/S0032823521020041

  21. Большаков А.А. Прямоугольная пластина на двухпараметрическом упругом основании: аналитическое решение // Вестник Самарского университета. Естественнонаучная серия. 2011. Т. 17. № 8. С. 128–133.

  22. Высоковский Д.А., Русакова Е.Б. Устойчивость плиты Э. Рейсснера на упругом невинклировом основании // Инженерный вестник Дона. 2017. № 2(45). С. 10. URL: ivdon.ru/ru/magazine/archive/n2y2017/4250

  23. Козел А.Г., Старовойтов Э.И. Изгиб упругой трехслойной круговой пластины на основании Пастернака // Механика композиционных материалов и конструкций. 2018. Т. 24. № 3. С. 392–406. https://doi.org/10.33113/mkmk.ras.2018.24.03.392_406.06

  24. Feng Q., Fu Sh., Wang Ch., Liu W.W. Analitical solution for fracture problem of stope roof based on Pasternak foundation model // Soil Mechanics and Foundation Engineering. 2019. V. 56. № 2. P. 142–150.

  25. Весницкий А.И. Волны в системах с движущимися границами и нагрузками. М.: Физматлит, 2001. 320 с.

  26. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. II. Теория поля. М.: Физматлит, 2003. 536 с.

  27. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VIII. Электродинамика сплошных сред. М.: Физматлит, 2005. 656 с.

  28. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука, 1984. 432 с.

  29. Tolstoy I., Usdin E. Wave propagation in elastic plates: low and high mode dispersion // J. Acoust. Soc. Am. 1957. V. 29. № 1. P. 37–42.

  30. Гринченко В.Т., Мелешко В.В. Гармонические колебания и волны в упругих телах. Киев: Наукова думка, 1981. 284 с.

  31. Шевченко В.В. Прямые и обратные волны: три определения, их взаимосвязь и условия применимости // Успехи физ. наук. 2007. Т. 177. № 3. С. 301–306.

  32. Lamb H. On group velocity // Proc. Lond. Math. Soc. Ser. 2. 1904. V. 1. № 849. P. 473–479.

  33. Ляпунов В.Т., Никифоров А.С. Виброизоляция в судовых конструкциях. Л.: Судостроение, 1975. 232 с.

  34. Метрикин А.В. Неустойчивость поперечных колебаний объекта, равномерно движущегося вдоль упругой направляющей как следствие аномального эффекта Доплера // Акуст. журн. 1994. Т. 40. № 1. С. 99–103.

  35. Бутова С.В., Герасимов С.И., Ерофеев В.И., Камчатный В.Г. Устойчивость движения высокоскоростных объектов по направляющим ракетного трека // Проблемы машиностроения и надежности машин. 2015. № 1. С. 3–8.

  36. Гинзбург В.Л. Теоретическая физика и астрофизика. Доп. главы. М.: Наука, 1975. 414 с.

  37. Гапонов-Грехов А.В., Долина И.С., Островский Л.А. Аномальный эффект Доплера и радиационная неустойчивость движения осциллятора в гидродинамике // Доклады АН СССР. 1983. Т. 268. № 4. С. 827–831.

  38. Метрикин А.В., Веричев С.Н., Вострухов А.В. Фундаментальные задачи высокоскоростного наземного транспорта. Saarbrucken, Germany. LAP Lambert Academic Publishing, 2014. 208 с.

  39. Руденко О.В., Гусев В.А. Движущийся объект: спектры сигналов пассивной, активной локации и переходное излучение // Акуст. журн. 2020. Т. 66. № 6. С. 599–609. https://doi.org/10.31857/S032079192006009X

  40. Руденко О.В., Маков Ю.Н. Звуковой удар: от физики нелинейных волн до акустической экологии (обзор) // Акуст. журн. 2021. Т. 67. № 1. С. 3–30. https://doi.org/10.31857/S0320791921010032

  41. Veshev V.A., Kouzov D.P., Mirolybova N.A. On opposite directions of the energy’s flux of normal wave propagation in thin-wall waveguide // Анализ и синтез нелинейных механических колебательных систем: Тр. XXIV летней школы-семинара. СПб: Изд-во ИПМаш РАН. 1997. С. 71–78.

  42. Коузов Д.П., Миролюбова Н.А. Локальные потоки энергии вынужденных колебаний тонкой упругой полосы // Вычислительная механика сплошных сред. 2012. Т. 5. № 4. С. 397–404. https://doi.org/10.7242/1999-6691/2012.5.4.47

  43. Вешев В.А., Коузов Д.П., Миролюбова Н.А. Потоки энергии и дисперсия нормальных волн изгибного типа в балке крестообразного профиля // Акуст. журн. 1999. Т. 45. № 3. С. 331–336.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал