Астрономический журнал, 2020, T. 97, № 3, стр. 206-224
3D моделирование анизотропной теплопроводности во внешних слоях замагниченных нейтронных звезд
И. А. Кондратьев 1, 2, *, С. Г. Моисеенко 1, **, Г. С. Бисноватый-Коган 1, 3, 4, ***, М. В. Глушихина 1, ****
1 Институт космических исследований РАН
Москва, Россия
2 Национальный исследовательский университет “Высшая школа экономики”, Факультет физики
Москва, Россия
3 Московский инженерно-физический институт, Национальный исследовательский ядерный институт
Москва, Россия
4 Московский физико-технический институт (Государственный университет)
Долгопрудный, Россия
* E-mail: mrkondratyev95@gmail.com
** E-mail: moiseenko@iki.rssi.ru
*** E-mail: gkogan@iki.rssi.ru
**** E-mail: m.glushikhina@iki.rssi.ru
Поступила в редакцию 21.09.2019
После доработки 22.10.2019
Принята к публикации 22.10.2019
Аннотация
В статье представлены результаты трехмерного численного моделирования распространения тепла во внешних слоях замагниченных нейтронных звезд. Определение структуры магнитного поля на поверхности нейтронной звезды является важной задачей современной астрофизики. При наличии сильных магнитных полей среда становится анизотропной, и законы распространения тепла изменяются. Тензорный коэффициент теплопроводности для замагниченной вырожденной плазмы был получен в работах Бисноватого-Когана и Глушихиной путем решения уравнения Больцмана методом Чепмена-Энскога. В данной работе распределение температуры на поверхности замагниченной нейтронной звезды получено для магнитных полей дипольного и квадрупольного типа, а также их суперпозиции. Для численного решения задачи о стационарном распределении температуры во внешних слоях замагниченной нейтронной звезды на трехмерный случай был обобщен метод опорных операторов. Задача решалась на сетке, состоящей из тетраэдров.
1. ВВЕДЕНИЕ
На поверхности нейтронных звезд (НЗ) магнитные поля могут составлять $ \sim {\kern 1pt} {{10}^{{12 - 13}}}$ Гс и более. Один из способов оценки величины магнитного поля на поверхности НЗ основан на наблюдении их теплового излучения в мягком рентгеновском диапазоне [1–4]. Периодические изменения спектра таких объектов говорят о неоднородном распределении поверхностной температуры, связанном с влиянием поля [5]. Неоднородное распределение температуры на поверхности НЗ определяется анизотропной теплопроводностью вырожденного вещества при наличии сильного магнитного поля. В оболочках НЗ, состоящих из плазмы вырожденных (становящихся ультрарелятивистскими при плотности $\rho \gg {{10}^{6}}$ г/см3) электронов и невырожденных нерелятивистских ядер, подавляется теплопроводность поперек силовых линий магнитного поля. Давление определяется электронами, ядра находятся в состоянии кулоновского кристалла, при этом тепло переносится электронами с участием лучистой теплопроводности во внешних слоях НЗ. Степень подавления теплового потока перпендикулярно магнитному полю определяется параметром магнетизации $\omega \tau $, где $\tau $ – среднее время между электрон-ядерными соударениями, $\omega = eB{\text{/}}m_{e}^{*}c$ – гирочастота релятивистского вырожденного электрона, $m_{e}^{ * } = {{m}_{e}}\sqrt {1 + p_{{fe}}^{2}{\text{/}}{{m}_{e}}{{c}^{2}}} $ – эффективная масса релятивистского электрона, где ${{p}_{{fe}}} = \hbar {{(3{{\pi }^{2}}{{n}_{e}})}^{{1/3}}}$ – его импульс Ферми, $e$ – заряд электрона, $c$ – скорость света, $\hbar $ – редуцированная постоянная Планка. Тензор теплопроводности для плазмы в магнитном поле с вырожденными электронами получен в работах Бисноватого-Когана и Глушихиной [6] методом Чепмена-Энскога для решения уравнения Больцмана, при этом степень подавления теплового потока поперек поля оказывается сильнее, чем в работах [7, 8], где отношение потоков тепла вдоль и поперек поля $\tfrac{{{{F}_{\parallel }}}}{{{{F}_{ \bot }}}} = 1 + {{(\omega \tau )}^{2}}$.
В данной работе получено стационарное распределение температуры в оболочках нейтронных звезд. Решается трехмерное уравнение теплопроводности в коре НЗ для плотностей $\rho = {{10}^{{10}}}{\kern 1pt} - {\kern 1pt} 2 \times {{10}^{{14}}}$ г/см3, с использованием построенного нами соотношения “${{T}_{s}} - {{T}_{b}}$” для внешней замагниченной оболочки НЗ с учетом обновленного тензора теплопроводности из [6], связывающего температуру ${{T}_{b}}$ при $\rho = {{10}^{{10}}}$ г/см3 с температурой ${{T}_{s}}$ на поверхности НЗ, аналогично [9] (расчет без магнитного поля) и [10] (расчет при наличии магнитного поля, см. также обзор [11] и ссылки в нем).
В двумерном рассмотрении задача о нахождении стационарного распределения температуры в коре и на поверхности НЗ при наличии дипольных полей разных конфигураций решалась в работе [12], а также с рассмотрением тороидального магнитного поля в [13, 14] (см. также работы по магнито-тепловой эволюции [15–17]).
Данная статья состоит из следующих частей. Во второй части приводятся описание теплопроводности электронов в магнитном поле, структура магнитного поля в коре НЗ и находится распределение плотности. В третьей части представлена одномерная плоскопараллельная модель замагниченной оболочки НЗ от плотности $\rho = {{10}^{{10}}}$ г/см3 до поверхности фотосферы ($\rho \sim 1$ г/см3), с учетом коэффициентов теплопроводности [6] и росселандовых непрозрачностей плазмы в магнитном поле для учета процессов радиационного переноса в приближении лучистой теплопроводности. По выходным параметрам этой модели находится граничное условие для задачи трехмерного моделирования теплопроводности в коре НЗ. В четвертой части работы приведены результаты 3D моделирования стационарного процесса распространения тепла в оболочке НЗ при плотностях $\rho = {{10}^{{10}}}{\kern 1pt} - {\kern 1pt} 2 \times {{10}^{{14}}}$ г/см3. В пятой части суммируются результаты расчетов. В приложении представлено описание используемого численного метода, дана формулировка краевой задачи в операторном виде, а также алгоритм самосогласованного решения задачи.
2. ФИЗИЧЕСКАЯ КАРТИНА
2.1. Теплопроводность в магнитном поле
В работе используется приближение, в котором тензор теплопроводности $\hat {\kappa }$ определяет потоки тепла в отсутствие вектора диффузии ${{{\mathbf{d}}}_{{\mathbf{e}}}}$ (см. ниже), но при наличии диффузионного потока, связанного с термодиффузией.
Распределение температуры в коре НЗ определяется уравнением теплопроводности, которое в стационарном случае имеет вид
Здесь $\hat {\kappa }$ – тензор теплопроводности, $f$ задает источники и стоки тепла. В данной работе мы ищем стационарное распределение температуры в коре НЗ и предполагаем отсутствие стоков и источников $f = 0$.В коре нейтронной звезды материя находится в особом состоянии кулоновского кристалла, в котором энергия электростатического взаимодействия между ионами существенно меньше энергии Ферми электронов. В таких условиях столкновения высокоэнергетических электронов с ионами приближенно можно рассматривать как столкновения со свободными частицами, т.е. как столкновения в газе. В пренебрежении во всех членах отношением масс электрона и иона ${{m}_{e}}{\text{/}}{{m}_{N}} \ll 1$ эти различия несущественны.
Тензор теплопроводности $\hat {\kappa }$ для сильно вырожденных электронов в магнитном поле получен в приближении Лоренца методом Чепмена-Энскога [18, 19]. Тензор учитывает потоки тепла вдоль и поперек магнитного поля, а также холловский поток тепла. Он записывается в декартовых координатах следующим образом [6]
(2)
$\left\{ \begin{gathered} {{\kappa }_{{ij}}} = \frac{{k_{B}^{2}T{{n}_{e}}}}{{m_{e}^{*}}}\tau \left( {{{\kappa }^{{(1)}}}{{\delta }_{{ij}}} + {{\kappa }^{{(2)}}}{{\varepsilon }_{{ijk}}}\frac{{{{B}_{k}}}}{B} + {{\kappa }^{{(3)}}}\frac{{{{B}_{i}}{{B}_{j}}}}{{{{B}^{2}}}}} \right), \hfill \\ {{\kappa }^{{(1)}}} = \frac{{5{{\pi }^{2}}}}{6}\left( {\frac{1}{{1 + {{{(\omega \tau )}}^{2}}}} - \frac{6}{5}\frac{{{{{(\omega \tau )}}^{2}}}}{{{{{(1 + {{{(\omega \tau )}}^{2}})}}^{2}}}}} \right), \hfill \\ {{\kappa }^{{(2)}}} = - \frac{{4{{\pi }^{2}}}}{3}\omega \tau \left( {\frac{1}{{1 + {{{(\omega \tau )}}^{2}}}} - \frac{3}{4}\frac{{{{{(\omega \tau )}}^{2}}}}{{{{{(1 + {{{(\omega \tau )}}^{2}})}}^{2}}}}} \right), \hfill \\ {{\kappa }^{{(3)}}} = \frac{{5{{\pi }^{2}}}}{6}{{(\omega \tau )}^{2}}\left( {\frac{1}{{1 + {{{(\omega \tau )}}^{2}}}} + \frac{6}{5}\frac{1}{{{{{(1 + {{{(\omega \tau )}}^{2}})}}^{2}}}}} \right), \hfill \\ \end{gathered} \right.$(3)
$\left\{ \begin{gathered} {{\kappa }_{{e \bot }}} = \frac{{k_{B}^{2}T{{n}_{e}}}}{{m_{e}^{*}}}\tau {{\kappa }^{{(1)}}}, \hfill \\ {{\kappa }_{{e\parallel }}} = \frac{{k_{B}^{2}T{{n}_{e}}}}{{m_{e}^{*}}}\tau ({{\kappa }^{{(1)}}} + {{\kappa }^{{(3)}}}). \hfill \\ \end{gathered} \right.$Отметим, что в лабораторной физике обычно используется другое определение коэффициента теплопроводности, когда зануляется не вектор диффузии ${{{\mathbf{d}}}_{{\mathbf{e}}}}$, а весь диффузионный поток электронов, связанный со скоростью диффузии $\left\langle {{{{\mathbf{v}}}_{{\mathbf{e}}}}} \right\rangle $. Как следует из решения уравнения Больцмана для нерелятивистского Лоренцевского электронного газа в отсутствие магнитного поля, в общем случае при наличии $\nabla T$ и ${{{\mathbf{d}}}_{{\mathbf{e}}}}$, выражения для теплового потока ${{{\mathbf{q}}}_{{\mathbf{e}}}}$ и диффузионной скорости электронов $\left\langle {{{{\mathbf{v}}}_{{\mathbf{e}}}}} \right\rangle $, определяюшей электрический ток, записываются в следующем виде [23]:
(4)
$\begin{gathered} {{{\mathbf{q}}}_{{\mathbf{e}}}} = - \frac{{640{{k}_{B}}}}{\Lambda }\frac{{{{m}_{e}}{{{({{k}_{B}}T)}}^{4}}}}{{{{n}_{N}}{{Z}^{2}}{{e}^{4}}{{h}^{3}}}}\left( {{{G}_{5}} - \frac{1}{2}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{G}_{4}}} \right) \cdot \nabla T - \\ \, - \frac{{128}}{\Lambda }\frac{{{{m}_{e}}{{{({{k}_{B}}T)}}^{5}}}}{{{{n}_{N}}{{Z}^{2}}{{e}^{4}}{{h}^{3}}}}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{G}_{4}} \cdot {{{\mathbf{d}}}_{{\mathbf{e}}}}, \\ \left\langle {{{{\mathbf{v}}}_{{\mathbf{e}}}}} \right\rangle = - \frac{{128{{k}_{B}}}}{\Lambda }\frac{{{{m}_{e}}{{{({{k}_{B}}T)}}^{3}}}}{{{{n}_{N}}{{n}_{e}}{{Z}^{2}}{{e}^{4}}{{h}^{3}}}}\left( {{{G}_{4}} - \frac{5}{8}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{G}_{3}}} \right) \cdot \nabla T - \\ \, - \frac{{32}}{\Lambda }\frac{{{{m}_{e}}{{{({{k}_{B}}T)}}^{4}}}}{{{{n}_{N}}{{n}_{e}}{{Z}^{2}}{{e}^{4}}{{h}^{3}}}}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{G}_{3}} \cdot {{{\mathbf{d}}}_{{\mathbf{e}}}}, \\ \end{gathered} $В лабораторных условиях считается равным нулю вектор $\left\langle {{{{\mathbf{v}}}_{{\mathbf{e}}}}} \right\rangle $, откуда находится связь ${{{\mathbf{d}}}_{{\mathbf{e}}}}$ и $\nabla T$. Подставляя эту связь в верхнюю строку (4), мы получаем другое выражение для потока тепла
(5)
${\mathbf{q}}_{{\mathbf{e}}}^{'} = - \frac{{128{{k}_{B}}}}{\Lambda }\frac{{{{m}_{e}}{{{({{k}_{B}}T)}}^{4}}}}{{{{n}_{N}}{{Z}^{2}}{{e}^{4}}{{h}^{3}}}}\left( {5{{G}_{5}} - 4\frac{{G_{4}^{2}}}{{{{G}_{3}}}}} \right) \cdot \nabla T.$Во внешних слоях нейтронных звезд текут электрические токи, возникает термоэлектрический эффект [24], поддерживающий магнитное поле в коре и оболочке, и средняя скорость электронов не равна нулю. Перенос тепла и электропроводность определяются уже не одним, а четырьмя процессами – теплопроводностью, диффузией, термодиффузией и диффузионным термоэффектом [25]. В данной работе мы пренебрегаем всеми процессами, кроме теплопроводности, полагая равной нулю не среднюю скорость электронов, а вектор диффузии. Отметим, что оба подхода являются приближенными, и мы оставляем полное согласованное рассмотрение всех четырех процессов для будущей работы.
2.2. Конфигурация магнитного поля в коре
Конфигурация магнитного поля задается постоянным магнитным диполем в центре звезды
(7)
${\mathbf{B}} = \frac{{{{B}_{{{\text{pd}}}}}R_{{{\text{NS}}}}^{3}}}{2}\frac{{3({\mathbf{d}} \cdot {\mathbf{r}}){\mathbf{r}} - {\mathbf{d}}{{r}^{2}}}}{{{{r}^{5}}}},$(8)
${\mathbf{B}} = {{B}_{{{\text{pq}}}}}R_{{{\text{NS}}}}^{4}\left( {\frac{{{{r}^{2}} - 5{{z}^{2}}}}{{2{{r}^{7}}}}{\mathbf{r}} - \frac{{{{{\mathbf{e}}}_{{\mathbf{z}}}}z}}{{{{r}^{5}}}}} \right),$2.3. Распределение плотности в коре НЗ
Плотность $\rho $ явным образом входит в тензор теплопроводности (2) и в эффективную массу электрона. Для получения профиля плотности в коре НЗ было решено уравнение Толмена-Оппенгеймера-Волкова для невращающихся НЗ при нулевой температуре:
(9)
$\left\{ \begin{gathered} \frac{{dP}}{{dr}} = \frac{{ - G\left( {\rho + \tfrac{P}{{{{c}^{2}}}}} \right)\left( {m + 4\pi {{r}^{3}}\tfrac{P}{{{{c}^{2}}}}} \right)}}{{r\left( {r - \tfrac{{2Gm}}{{{{c}^{2}}}}} \right)}}, \hfill \\ \frac{{dm}}{{dr}} = 4\pi {{r}^{2}}\rho , \hfill \\ P = P(\rho ). \hfill \\ \end{gathered} \right.$Рис. 1.
Зависимость плотности (слева) в НЗ и массы НЗ (справа) от расстояния до центра НЗ для центральной плотности ${{\rho }_{c}} = 1 \times {{10}^{{15}}}$ г/см3.

Уравнение состояния взято из работы [27], результаты которой базируются на работах [28, 29]. Уравнение состояния в [27] рассчитано одним и тем же методом для коры и ядра НЗ при помощи микроскопических расчетов теории ядерной материи при нулевой температуре. Ядро НЗ при таком уравнении состояния состоит из нейтронов, протонов, электронов и мюонов.
Как и в работе [12], уравнение теплопроводности решается нами не до внешней границы внутренней коры с $\rho = {{\rho }_{{{\text{drip}}}}} = 4 \times {{10}^{{11}}}$ г/см3, а до $\rho = {{\rho }_{{{\text{out}}}}} = {{10}^{{10}}}$ г/см3, чтобы как можно больше расширить область решения трехмерной задачи. Здесь ${{\rho }_{{{\text{drip}}}}}$ задает плотность, при которой начинается испарение нейтронов из перегруженных нейтронами ядер. Таким образом, радиус внутренней границы коры ${{R}_{{{\text{in}}}}} = 10.594$ км при $\rho = {{\rho }_{{{\text{in}}}}} = 2 \times {{10}^{{14}}}$ г/см3, а радиус внешней границы коры ${{R}_{{{\text{out}}}}} = 11.618$ км при $\rho = {{10}^{{10}}}$ г/см3; толщина такой коры составляет $1.024$ км. Для полученного численно распределения плотности в коре была получена аналитическая аппроксимация решения в виде:
(10)
$\begin{gathered} lg\rho = - 5.185{{(r - {{R}_{{{\text{in}}}}})}^{2}} + 1.06(r - {{R}_{{{\text{in}}}}}) + \\ \, + 14.22 + 0.13 + 0.45exp( - 10(r - {{R}_{{{\text{in}}}}})) - \\ \, - 0.35exp( - 3(r - {{R}_{{{\text{in}}}}} - 0.11)) - \\ \, - 0.27exp( - 10\left| {r - {{R}_{{{\text{in}}}}} - 0.79} \right|), \\ \end{gathered} $Отметим здесь также, что в данной работе во внешней оболочке (см. ниже) рассматривается полностью ионизированная плазма железа с $Z = 26$ и $A = 56$, а в коре учитывается нейтронизация вещества. Эффективные значения $Z$ и $A$ как функции плотности в коре НЗ взяты из работы [30] для $\rho < {{\rho }_{{{\text{drip}}}}}$, и из [31] для $\rho > {{\rho }_{{{\text{drip}}}}}$.
3. ОДНОМЕРНАЯ МОДЕЛЬ ВНЕШНЕЙ ЗАМАГНИЧЕННОЙ ОБОЛОЧКИ НЕЙТРОННОЙ ЗВЕЗДЫ
3.1. Уравнение тепловой структуры внешней оболочки
Внешние слои нейтронных звезд, при $\rho < $ < 1010 г/см3, имеют толщину $ \sim {\kern 1pt} 100$ метров, при этом в данной области происходят очень большие перепады плотности и температуры. С вычислительной точки зрения пространственно разрешить такую область на трехмерной сетке не удается. При параметрах внешней оболочки необходимо учитывать процессы радиационного переноса, поскольку в приповерхностной области они становятся доминирующими. Тепловая структура оболочки в данной работе исследуется в стационарном, локальном, плоско-параллельном приближении, для расчета связи локальной температуры поверхности ${{T}_{s}}$ с локальной температурой ${{T}_{b}}$ при $\rho = {{10}^{{10}}}$ г/см3 на дне оболочки. На всей площади поверхности принималось, что радиальный градиент температуры и тепловой поток поперек оболочки много больше, чем вдоль нее [10]. Ниже дан вывод уравнения, описывающего тепловую структуру оболочки, приведенный в работе [10]. В одномерном приближении уравнение теплопроводности имеет вид [23, 32]:
(11)
$F \equiv \sigma T_{s}^{4} = \kappa \frac{{dT}}{{dz}} = \frac{{16\sigma }}{3}\frac{{{{T}^{3}}dT}}{{d\tau }},\quad \kappa = \frac{{16\sigma {{T}^{3}}}}{{3K\rho }}.$Интегрирование уравнения (11) дает профиль температуры в оболочке $T \approx {{T}_{s}}{{\left( {\tfrac{3}{4}\tau + \tfrac{1}{2}} \right)}^{{1/4}}}$, где $\tau = \int_{ - \infty }^z \,K\rho dz$ – оптическая толщина оболочки. Постоянная интегрирования отвечает приближению Эддингтона [23, 32] ($\tau = \tfrac{2}{3}$ на излучающей поверхности).
При $z \ll {{R}_{{{\text{NS}}}}}$ релятивистское уравнение гидростатического равновесия (первое уравнение системы (9)) может быть приведено к Ньютоновской форме: $\tfrac{{dP}}{{dz}} = {{g}_{s}}\rho $, где $P$ – давление, ${{g}_{s}} = $ $ = G{{M}_{{{\text{NS}}}}}{\text{/}}(R_{{{\text{NS}}}}^{2}\sqrt {1 - {{r}_{g}}{\text{/}}{{R}_{{{\text{NS}}}}}} )$ ускорение свободного падения на поверхности НЗ. Из этого уравнения вместе с (11) можно получить уравнение тепловой структуры оболочки
Перенос тепла в оболочке определяется суммой двух процессов – лучистой и электронной теплопроводностью. Таким образом, эффективный коэффициент теплопроводности $\kappa = {{\kappa }_{r}} + {{\kappa }_{e}}$. Его можно выразить через коэффициенты теплопроводности вдоль (${{\kappa }_{\parallel }}$) и поперек (${{\kappa }_{ \bot }}$) силовых линий магнитного поля в виде [33](13)
$\kappa = {{\kappa }_{\parallel }}co{{s}^{2}}{{\theta }_{B}} + {{\kappa }_{ \bot }}si{{n}^{2}}{{\theta }_{B}},$(14)
$\begin{gathered} {{({{{\hat {\kappa }}}_{e}} \cdot \nabla T)}_{z}} = {{\kappa }_{{e \bot }}}\nabla T + ({{\kappa }_{{e\parallel }}} - {{\kappa }_{{e \bot }}})(\vec {B} \cdot \nabla T) \times \\ \times \;cos{{\theta }_{B}}{\text{/}}B. \\ \end{gathered} $(15)
${{\kappa }_{{e \bot }}} \cdot \nabla T + ({{\kappa }_{{e\parallel }}} - {{\kappa }_{{e \bot }}})\nabla Tco{{s}^{2}}{{\theta }_{B}},$Для коэффициентов лучистой теплопродности в работе [34] получены значения для случаев вдоль $({{\kappa }_{{r\parallel }}})$ и поперек $({{\kappa }_{{r \bot }}})$ магнитного поля при учете свободно-свободного поглощения и томсоновского рассеяния. Аналогичные рассуждения для тензора лучистой теплопроводности приводят к формуле (13). Непрозрачность в этом случае равна
Как было отмечено в [35], уравнение (12) может быть неприменимо в областях, где поле очень велико и близко к тангенциальному. В этом случае тепловой поток по нормали к поверхности может быть сильно подавлен и стать сравнимым с тепловым потоком вдоль оболочки, параллельно полю. В данной работе этот эффект не рассматривается.
Уравнение (12) решалось численно адаптивным методом Рунге–Кутта 4–5 порядка точности с переменным шагом расчетной сетки. В качестве граничного условия на поверхности излучающей оболочки принимается $T = {{T}_{s}}$, при этом давление на поверхности ${{P}_{s}}$ находится из условия Эддингтона ${{P}_{s}} \approx \tfrac{{2{{g}_{s}}}}{{3{{K}_{s}}}}$ [23]. При известной зависимости ${{K}_{s}}({{T}_{s}},{{\rho }_{s}})$ для непрозрачности, и ${{P}_{s}}({{T}_{s}},{{\rho }_{s}})$ для уравнения состояния, условие Эддингтона однозначно определяет поверхностные значения ${{P}_{s}}$ и ${{\rho }_{s}}$ при заданном ${{T}_{s}}$.
3.2. Уравнение состояния в оболочке
Во внешней оболочке в данной модели мы рассматриваем полностью ионизированную плазму железа с вырожденными электронами и невырожденными нерелятивистскими ядрами, при этом пренебрегается кулоновским взаимодействием между электронами и ионами, и не рассматриваются эффекты квантования уровней энергии электронов в магнитном поле (квантование Ландау). В таком приближении давление представлено суммой давлений идеальных газов электронов и ядер
где давление ядер $P_{{{\text{id}}}}^{{(N)}} = {{n}_{N}}{{k}_{B}}T$, а давление релятивистских электронов произвольной степени вырождения может быть записано c помощью интегралов Ферми–Дирака [36, 37]:(17)
$P_{{{\text{id}}}}^{{(e)}} = \frac{{{{{(2{{m}_{e}})}}^{{3/2}}}}}{{3{{\pi }^{2}}{{\hbar }^{3}}{{\beta }^{{5/2}}}}}({{I}_{{3/2}}}(\chi ,\tau ) + \frac{\tau }{2}{{I}_{{5/2}}}(\chi ,\tau )).$(18)
${{I}_{\nu }}(\chi ,\tau ) = \int\limits_0^\infty {\frac{{{{u}^{\nu }}\sqrt {1 + \tau u{\text{/}}2} }}{{exp(u - \chi ) + 1}}} \,du,$В пределе $\tau \to 0$ интегралы Ферми–Дирака превращаются в обычные нерелятивистские интегралы Ферми ${{I}_{\nu }}(\chi )$. Химический потенциал в таком случае может быть получен из соотношения
где $\theta = T{\text{/}}{{T}_{F}}$, ${{T}_{F}} = {{m}_{e}}{{c}^{2}}{\text{/}}{{k}_{B}}[\sqrt {1 + x_{r}^{2}} - 1]$ – температура Ферми, ${{x}_{r}} = {{p}_{{fe}}}{\text{/}}{{m}_{e}}c$, а ${{X}_{\nu }}$ – функция, обратная к интегралу Ферми, ее высокоточная аналитическая аппроксимация получена в работе [38]. Точность нерелятивистских формул быстро падает при $T > {{10}^{7}}$ К, поэтому к данной аппроксимации должна быть добавлена поправка, взятая из работы [37](20)
$\chi \, = \,{{\chi }^{{{\text{nonrel}}}}}\, - \,\frac{3}{2}log\left[ {1\, + \,\left( {\frac{\tau }{{1 + \tau {\text{/}}2\theta }}} \right)\frac{{1\, + \,{{q}_{1}}\sqrt \tau \, + \,{{q}_{2}}{{q}_{3}}\tau }}{{1\, + \,{{q}_{2}}\tau }}} \right],$3.3. Непрозрачности
Ввиду аддитивности коэффициента теплопроводности, полный коэффициент непрозрачности плазмы вдоль нормали к оболочке НЗ находится из коэффициентов фотонной и электронной непрозрачности следующим образом [23]:
где ${{K}_{e}}$ и ${{K}_{r}}$ – электронная и фотонная непрозрачности соответственно [23, 32]. Электронная непрозрачность может быть получена из аналогии с лучистой теплопроводностью: Здесь ${{\kappa }_{e}}$ является коэффициентом теплопроводности вдоль нормали к оболочке НЗ, (13) с учетом (3) для вырожденных электронов, однако во внешних слоях оболочки электроны могут быть невырождены, поэтому в невырожденной области необходимо использовать формулы для невырожденных электронов. Они также получены в работе [6] методом Чепмена-Энскога для двух- и трехполиномиального разложения решения уравнения Больцмана по полиномам Сонина–Лагерра. Для случая вдоль поля коэффициент теплопроводности невырожденных электронов запишется следующим образом:(23)
$\kappa _{{e\parallel }}^{{{\text{nd}}}} = \frac{5}{2}\frac{{k_{B}^{2}T{{n}_{e}}}}{{{{m}_{e}}}}{{\tau }_{{{\text{nd}}}}}\frac{{25}}{{4(1 + \sqrt 2 {\text{/}}Z)}},$Коэффициент теплопроводности для сильно вырожденной материи вдоль поля равен $\kappa _{\parallel }^{{{\text{sd}}}} = \tfrac{{5{{\pi }^{2}}}}{6}\tfrac{{{{k}^{2}}T{{n}_{e}}}}{{m_{e}^{*}}}\tau $. Поперек поля коэффициент подавляется на фактор $\left( {\tfrac{1}{{1 + {{{(\omega \tau )}}^{2}}}} - \tfrac{6}{5}\frac{{{{{(\omega \tau )}}^{2}}}}{{{{{(1 + {{{(\omega \tau )}}^{2}})}}^{2}}}}} \right)$ при $\omega \tau \ll 2\pi $, а при $\omega \tau > 1.5$ мы также переходим к приближенному соотношению $\tfrac{1}{{1 + {{{(\omega \tau )}}^{2}}}}$ также с учетом условия непрерывности ${{\kappa }_{ \bot }}$.
Для использования формул выше в расчетах необходимо сшить невырожденный и сильно вырожденный пределы, например, следующим образом:
Основной вклад в радиационную непрозрачность вносят свободно-свободное и связанно-свободное поглощение, а также томсоновское рассеяние на электронах. В отсутствие магнитного поля Томсоновская непрозрачность в нерелятивистском пределе записывается следующим образом [39]:
(24)
${{K}_{{Th}}} = \frac{{{{n}_{e}}{{\sigma }_{T}}}}{\rho } = \frac{{8\pi }}{3}{{\left( {\frac{{{{e}^{2}}}}{{{{m}_{e}}{{c}^{2}}}}} \right)}^{2}}\frac{{{{n}_{e}}}}{\rho },$Сечение свободно-свободного поглощения с учетом спонтанного и вынужденного излучения в условиях локального термодинамического равновесия в нерелятивистском случае дается следующей формулой [23]:
(25)
$\sigma _{{aff}}^{*} = \frac{{4\pi }}{{3\sqrt 3 }}\frac{{{{Z}^{2}}{{e}^{6}}}}{{m_{e}^{2}chv{{\nu }^{3}}}}{{g}_{{ff}}}(1 - {{e}^{{ - h\nu /{{k}_{B}}T}}}),$(26)
$\alpha _{{ff}}^{\nu } = \frac{{4\pi }}{{3\sqrt 3 }}\frac{{8\pi {{Z}^{2}}{{e}^{6}}}}{{A{{m}_{u}}c{{h}^{4}}{{\nu }^{3}}}}{{g}_{{ff}}}{{k}_{B}}Tlog\left( {\frac{{{{e}^{\chi }} + 1}}{{{{e}^{{\chi - h\nu /{{k}_{B}}T}}} + 1}}} \right).$(27)
$K_{{ff}}^{{{\text{nd}}}} = 4.34 \times {{10}^{{22}}}\frac{\rho }{{{{T}^{{7/2}}}}}\frac{{{{Z}^{2}}}}{A},$(28)
$K_{{ff}}^{{{\text{sd}}}} = 0.036\frac{{32{{\pi }^{2}}}}{{3\sqrt 3 }}\frac{{{{e}^{6}}{{g}_{{ff}}}}}{{{{m}_{u}}chk_{B}^{2}}}\frac{{{{Z}^{2}}}}{{A{{T}^{2}}}}.$Сечение связанно-свободного поглощения дается следующей формулой [23] в нерелятивистском пределе:
(29)
$\begin{gathered} \alpha _{{bf}}^{\nu } = \frac{4}{3}\sqrt {\frac{{2\pi }}{3}} \frac{{{{e}^{6}}{{h}^{2}}}}{{m_{e}^{{3/2}}c{{m}_{u}}{{{({{k}_{B}}T)}}^{{7/2}}}}}\frac{{{{Z}^{2}}}}{A}{{n}_{e}}{{g}_{{bf}}} \times \\ \, \times \left[ {\frac{1}{n}\frac{{{{E}_{b}}}}{{{{k}_{B}}T}}ex{{p}^{{{{E}_{b}}/{{k}_{B}}T}}}{{{\left( {\frac{{{{k}_{B}}T}}{{h\nu }}} \right)}}^{3}}{{q}_{{bf}}}} \right], \\ {{E}_{b}} = \frac{{2{{\pi }^{2}}{{m}_{e}}{{Z}^{2}}{{e}^{4}}}}{{{{h}^{2}}{{n}^{2}}}}, \\ {{q}_{{bf}}} = {{\left( {1 + exp\left( {\chi - \frac{{h\nu }}{{{{k}_{B}}T}} + \frac{{{{E}_{b}}}}{{{{k}_{B}}T}}} \right)} \right)}^{{ - 1}}}, \\ \end{gathered} $(30)
$K_{{bf}}^{{{\text{nd}}}} = 7.23 \times {{10}^{{24}}}\frac{\rho }{{{{T}^{{7/2}}}}}\frac{{{{Z}^{2}}}}{A}\frac{{{{g}_{{bf}}}}}{t},$(31)
$\alpha _{{bf}}^{\nu } = {{K}_{0}}\sum\limits_{n = 1}^\infty \,\frac{{{{E}_{b}}}}{{n{{k}_{B}}T}}\frac{{{{e}^{{ - \chi }}}}}{{{{x}^{3}}}}\frac{{{{e}^{x}} - 1}}{{{{e}^{{x - \tfrac{{{{E}_{b}}}}{{{{k}_{B}}T}} - \chi }}} + 1}},$Для использования формул (27), (28) для ff-переходов и (30), (32) для bf-переходов в расчетах, их необходимо непрерывно сшить, например, следующим образом:
(33)
${{K}_{{ff,bf}}} = K_{{ff,bf}}^{{{\text{nd}}}}\frac{1}{{1 + {{e}^{{m\chi }}}}} + K_{{ff,bf}}^{{{\text{sd}}}}\frac{{{{e}^{{m\chi }}}}}{{\varepsilon + {{e}^{{m\chi }}}}},$Мы учли влияние магнитного поля на непрозрачность таким же образом, как и в [10]. Авторы этой работы построили аналитическую аппроксимацию полученных численно свободно-свободных и томсоновских непрозрачностей в магнитном поле [34]. Росселандовы непрозрачности вдоль и поперек поля записываются следующим образом:
(34)
$\begin{gathered} \frac{{{{K}_{{r\parallel }}}(\rho ,T,B)}}{{{{K}_{r}}(\rho ,T,0)}} = \frac{{1 + {{A}_{1}}{{u}^{2}}}}{{1 + {{A}_{1}}{{u}^{2}} + {{A}_{2}}{{u}^{3}} + {{{({{A}_{3}}u)}}^{2}}{{u}^{2}}}}, \\ \frac{{{{K}_{{r \bot }}}(\rho ,T,B)}}{{{{K}_{r}}(\rho ,T,0)}} = \frac{{1 + {{A}_{4}}{{u}^{2}}}}{{1 + {{{({{A}_{5}}u)}}^{{3.5}}} + {{{({{A}_{6}}u)}}^{4}}}}, \\ {{A}_{n}} = {{a}_{n}} - {{b}_{n}}{{f}^{{{{c}_{n}}}}},\quad f = \frac{{{{K}_{{ff}}}}}{{{{K}_{{ff}}} + {{K}_{{Th}}}}}. \\ \end{gathered} $3.4. Аппроксимационные соотношения ${{T}_{s}}$–${{T}_{b}}$
В ходе расчетов были получены наборы распределений температуры в оболочке НЗ для разных значений ${{T}_{s}}$, $B$ и $\theta $, связывающие локальную температуру на поверхности НЗ ${{T}_{s}}$ с температурой, вдоль радиуса, на дне оболочки ${{T}_{b}}$, по заданному значению индукции магнитного поля $B$ и угла $\theta $ между направлением магнитной силовой линии и нормалью к поверхности НЗ, которые считаются постоянными во внешней оболочке. Обзор существующих к настоящему моменту ${{T}_{s}}{\kern 1pt} - {\kern 1pt} {{T}_{b}}$-соотношений может быть найден в [11].
Как было отмечено в [9], ${{T}_{s}}{\kern 1pt} - {\kern 1pt} {{T}_{b}}$-соотношение зависит от значения коэффициентов теплопроводности в “полосе чувствительности” (sensitivity strip) на плоскости $\rho {\kern 1pt} - {\kern 1pt} T$, находящейся около “точки поворота” (turning point), где ${{\kappa }_{e}} \sim {{\kappa }_{r}}$. Точка поворота в случае теплопереноса при наличии магнитного поля сдвигается в область более высоких плотностей с ростом поля. Вдоль магнитного поля этот эффект провоцируется уменьшением непрозрачности, а поперек поля – уменьшением непрозрачности и подавлением коэффициента электронной теплопроводности поперек полю.
На рис. 2 представлены графики распределения температуры в оболочке НЗ, для поверхностной температуры ${{T}_{s}} = {{10}^{6}}$ К. Нижние сплошные отвечают распределению температуры вдоль $({{\theta }_{B}} = 0)$, а верхние пунктирные – поперек $({{\theta }_{B}} = \pi {\text{/}}2)$ магнитному полю. На рис. 3 изображены графики распределения температуры в оболочке НЗ с фиксированной температурой на дне оболочки для звезды с дипольным магнитным полем при различных его значениях ${{B}_{p}}$ на магнитном полюсе. Отметим, что для диполя значение поля на экваторе ${{B}_{e}} = 0.5{{B}_{p}}$. В табл. 2 представлены температуры поверхности на магнитном полюсе и экваторе и их отношения для различных значений ${{B}_{p}}$, и ${{T}_{b}} = {{10}^{8}}$ К.
Рис. 2.
Распределение температуры как функции плотности в оболочке НЗ для ${{T}_{s}} = {{10}^{6}}$ К в однородном магнитном поле с $B = {{10}^{{11}}}$ Гс (слева) и $B = {{10}^{{13}}}$ Гс (справа). Сплошные кривые соответствуют магнитным полюсам, штриховые – экватору.

Рис. 3.
Распределение температуры как функции плотности в оболочке НЗ для ${{T}_{b}} = {{10}^{8}}$ К для звезды с дипольным магнитным полем, для различных его значений на полюсе, ${{B}_{p}} = {{10}^{{11}}}$ Гс (слева), ${{10}^{{12}}}$ Гс (центр) и ${{10}^{{13}}}$ Гс (справа). Сплошные кривые соответствуют магнитным полюсам, штриховые – экватору.

Таблица 2.
Температуры поверхности НЗ на полюсе $(\theta = 0)$ и экваторе $(\theta = \pi {\text{/}}2)$ и их отношения
| $lg{{B}_{p}}$ | 11 | 12 | 13 |
|---|---|---|---|
| ${{T}_{s}}(\theta = 0){\text{/}}{{10}^{6}}K$ | 1.02 | 1.03 | 1.16 |
| ${{T}_{s}}(\theta = \pi {\text{/}}2){\text{/}}{{10}^{6}}K$ | 0.71 | 0.35 | 0.18 |
| ${{T}_{{s\parallel }}}{\text{/}}{{T}_{{s \bot }}}$ | 1.43 | 2.94 | 6.44 |
Мы построили таблицы решений уравнения на тепловую структуру (12) для разных значений угла ${{\theta }_{B}}$, модуля индукции поля $B$ и температуры на дне оболочки ${{T}_{b}}$. Заметим, что в граничное условие уравнения (12) входит поверхностная температура ${{T}_{s}}$, поэтому для построения таблиц от ${{T}_{b}}$ необходимо решать уравнение на тепловую структуру, “подбирая” по ${{T}_{s}}$ необходимое значение ${{T}_{b}}$, в расчетах мы находили его с точностью 0.25%. В двумерных табл. 3 и 4 представлены решения уравнения [12] для некоторых ${{T}_{b}}$ и $B$ при ${{\theta }_{B}} = 0$ и ${{\theta }_{B}} = \pi {\text{/}}2$ соответственно.
Таблица 3.
Соотношение ${{T}_{s}} - {{T}_{b}}$ для ${{T}_{s}}$ в единицах ${{10}^{6}}K$ при ${{\theta }_{B}} = 0$ (${{T}_{b}}$ в единицах ${{10}^{9}}K$)
| ${{T}_{{b9}}}$ | $lg{{B}_{p}} = 11.7$ | 12 | 12,7 | 13 |
|---|---|---|---|---|
| 0.04 | 0.5721 | 0.5904 | 0.6672 | 0.6927 |
| 0.08 | 0.8930 | 0.9019 | 0.9931 | 1.0316 |
| 0.20 | 1.6021 | 1.6066 | 1.6723 | 1.7337 |
| 0.60 | 3.1664 | 3.1681 | 3.1818 | 3.2253 |
| 1.00 | 4.3058 | 4.3022 | 4.3057 | 4.3383 |
Таблица 4.
Соотношение ${{T}_{s}} - {{T}_{b}}$ для ${{T}_{s}}$ в единицах ${{10}^{6}}K$ при ${{\theta }_{B}} = \pi {\text{/}}2$ (${{T}_{b}}$ в единицах ${{10}^{9}}K$)
| ${{T}_{{b9}}}$ | $lg{{B}_{p}} = 11.7$ | 12 | 12.7 | 13 |
|---|---|---|---|---|
| 0.04 | 0.1636 | 0.1291 | 0.0894 | 0.0803 |
| 0.08 | 0.2917 | 0.2331 | 0.1495 | 0.1328 |
| 0.20 | 0.6502 | 0.5338 | 0.3417 | 0.2844 |
| 0.60 | 1.7487 | 1.4672 | 0.9712 | 0.8118 |
| 1.00 | 2.7193 | 2.2949 | 1.5321 | 1.2911 |
Мы сравнили полученное нами соотношение ${{T}_{s}} - {{T}_{b}}$ с аналогичным соотношением из работы [10]. Основные отличия между моделями тепловой структуры заключаются в том, что по сравнению с [10] мы использовали более простое уравнение состояния в оболочке, но учли связанно-свободное поглощение и эффекты электронного вырождения на радиационных непрозрачностях (32), (28), а также использовали отличные от [10] коэффициенты электронной теплопроводности (3). На рис. 4 представлено сравнение ${{T}_{s}}{\kern 1pt} - {\kern 1pt} {{T}_{b}}$ для двух значений дипольного магнитного поля, с $B = {{10}^{{12}}}$ Гс (слева) и ${{10}^{{12}}}$ Гс (справа) на полюсе. В обоих случаях разница температур поверхности ${{T}_{s}}$ не превышает 20% от [10]. Температура поверхности НЗ на магнитном полюсе (вдоль поля) получилась в наших расчетах немного выше, чем в [10] ввиду того, что используемый нами коэффициент электронной теплопроводности вдоль поля выше, чем в [7]. С ситуацией поперек поля все несколько сложнее: с ростом магнитного поля переход от лучистой к электронной теплопроводности (полоса чувствительности) происходит в существенно вырожденной области, в которой радиационная непрозрачность сильно подавляется ввиду вырождения. По этой причине градиент температуры в областях поперек поля ниже для сильного магнитного поля (см. нижнюю синюю кривую на правой панели рис. 4), чем в [10], хотя коэффициент электронной теплопроводности (3) сильнее подавлен поперек поля.
Рис. 4.
Сравнение соотношений ${{T}_{s}} - {{T}_{b}}$ из данной работы и [10] для магнитного экватора (красные линии) и полюса (синие линии) для дипольного магнитного поля. Штриховые линии соответствуют [10], сплошные линии – данной работе. Слева представлены результаты для ${{B}_{{{\text{pd}}}}} = {{10}^{{12}}}$ Гс, справа – для ${{B}_{{{\text{pd}}}}} = {{10}^{{13}}}$ Гс.

Для оценки поправок, связанных с влиянием эффектов общей теории относительности на конфигурацию дипольного магнитного поля в оболочке, рассмотренных в [10], следуя [41], была рассчитана модель оболочки НЗ при температуре поверхности коры ${{T}_{b}} = 1 \times {{10}^{8}}$ К. Распределение температуры в этом варианте дано на рис. 5 для этого и ньютоновского случаев. Для сравнения там же дано распределение температуры, построенное аналогичным образом в [10]. Из рисунка видно, что эффекты ОТО являются незначительными, и различия в температурах определяются другими физическими эффектами.
Рис. 5.
Сравнение поверхностных температур НЗ ${{T}_{s}}$ (в единицах ${{10}^{6}}$ К) для фиксированной температуры коры ${{T}_{b}} = 1 \times {{10}^{8}}$ К и индукцией дипольного магнитного поля ${{B}_{{{\text{pd}}}}} = {{10}^{{13}}}$ Гс на полюсе. Толстая штриховая и сплошная линии на левой панели отвечают полученному в данной работе распределению температуры с учетом и без учета эффектов общей теории относительности соответственно. Сплошная толстая линия – распределение температуры из работы [10] с учетом эффектов ОТО. На правой панели представлено увеличение левого рисунка в области магнитного экватора.

4. КРАЕВАЯ ЗАДАЧА ДЛЯ ТРЕХМЕРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
Предполагается, что поток тепла излучается с поверхности НЗ, а температура на внутреннем радиусе коры ${{T}_{{{\text{core}}}}}$ считается одинаковой по всему ядру, ввиду достаточно большой теплопроводности. Эта температура уменьшается со временем при остывании ядра НЗ достаточно медленно, после быстрого этапа с излучением нейтрино, так что эволюцию НЗ можно представить в виде последовательности остывающих моделей со стационарным распределением температуры по звезде.
Таким образом, значение поверхностной температуры ${{T}_{s}}$ определяется решением стационарной краевой задачи для уравнения теплопроводности в шаровом слое с заданной температурой ${{T}_{{{\text{core}}}}}$ на внутренней границе, и с условием излучения чернотельного спектра с поверхности на внешней границе, когда поток тепла определяется законом Стефана–Больцмана ${{F}_{s}} = \sigma T_{s}^{4}$. Во внешней оболочке, ввиду малости ее массы, поток тепла ${{F}_{s}}$ считается постоянным, поэтому на внешней границе коры, которая является также внутренней границей внешней оболочки, этот поток тепла равен радиальному потоку тепла из ядра при теплопроводности. Это задает граничные условия в виде
(35)
$T{{{\text{|}}}_{{{\text{in}}}}} = {{T}_{{{\text{core}}}}},\quad \kappa ({\mathbf{B}},\rho ,T){{\nabla }_{r}}T + {{F}_{s}}{{{\text{|}}}_{{{\text{out}}}}} = 0,$5. РЕЗУЛЬТАТЫ РАСЧЕТОВ
В результате расчетов по трехмерной программе были получены распределения температуры внутри коры, и по поверхности НЗ. На рис. 6 представлено распределение температуры в коре НЗ с плотностями $\rho = {{10}^{{10}}}{\kern 1pt} - {\kern 1pt} 2 \times {{10}^{{14}}}$ г/см3 с температурой ядра ${{T}_{{{\text{core}}}}} = 2 \times {{10}^{8}}$ К, для дипольного магнитного поля (7) с индукцией на полюсе ${{B}_{{{\text{pd}}}}} = {{10}^{{13}}}$ Гс.
Рис. 6.
Распределение температуры в коре НЗ для дипольного магнитного поля (7) с индукцией на полюсе ${{B}_{{{\text{pd}}}}} = $ = 1013 Гс, и ${{T}_{{{\text{core}}}}} = 2 \times {{10}^{8}}$ К (здесь и далее температура $T$ представлена в единицах ${{10}^{6}}K$) для плотностей $\rho = {{10}^{{10}}}{\kern 1pt} - {\kern 1pt} 2 \times {{10}^{{14}}}$ г/см$^{3}$. Слева – сечение в плоскости Y–Z, справа – трехмерная проекция поверхности коры НЗ при плотности ${{\rho }_{{{\text{out}}}}} = {{10}^{{10}}}$ г/см3.
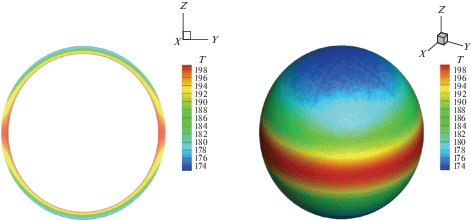
Распределение температуры в коре инвертировано по сравнению с поверхностным распределением температуры. Это объясняется тем, что сильнее всего коэффициент теплопроводности поперек поля подавляется во внешней оболочке, где $\omega \tau \gg 1$. Подавленный поток тепла на магнитном экваторе приводит к уменьшению градиента температуры в коре, поэтому на магнитном полюсе изменение температуры в коре выше, чем на экваторе.
На рис. 7 представлено найденное в расчетах распределение температуры по поверхности НЗ, соответствующее распределению из рис. 6, а также полуаналитическое распределение температуры из классической работы [33] с рассчитанными нами значениями температур на полюсе и экваторе НЗ:
(37)
${{T}_{s}}(B,\theta ) = {{[T_{s}^{4}(0)co{{s}^{2}}{{\theta }_{B}} + T_{s}^{4}(\pi {\text{/}}2)si{{n}^{2}}{{\theta }_{B}}]}^{{1/4}}}.$Рис. 7.
Распределение температуры на поверхности НЗ для дипольного магнитного поля с индукцией на полюсе ${{B}_{{{\text{pd}}}}} = {{10}^{{13}}}$ Гс, и ${{T}_{{{\text{core}}}}} = 2 \times {{10}^{8}}$ К как функции полярного угла $\theta $. Сплошная линия – полученная в расчетах зависимость, штриховая линия – зависимость, посчитанная по формуле (37).

Из рис. 7, 8 видно, что для чисто дипольных конфигураций магнитного поля угловая зависимость температуры хорошо описывается формулой Гринштейна и Хартке (37) из [33]. В наших расчетах получены следующие параметры. Для ${{T}_{{{\text{core}}}}} = 2 \times {{10}^{8}}$ К температура внешней границы коры на магнитном полюсе ${{T}_{{b\parallel }}} \approx 1.74 \times {{10}^{8}}$ K, на поверхности ${{T}_{{s\parallel }}} \approx 1.60 \times {{10}^{6}}$ K, а на экваторе ${{T}_{{b \bot }}} \approx 1.99 \times {{10}^{8}}$ K и ${{T}_{{s \bot }}} \approx 0.34 \times {{10}^{6}}$ K. Отношение температур ${{T}_{{s\parallel }}}{\text{/}}{{T}_{{s \bot }}}$ на поверхности равно $4.72$. Из рис. 7, 8 видно, что анизотропия в оболочке усиливается по мере охлаждения НЗ, так, при ${{T}_{{{\text{core}}}}} = {{10}^{9}}$ К отношение температур на полюсе и экваторе ${{T}_{{s\parallel }}}{\text{/}}{{T}_{{s \bot }}} = 2.55$, а при ${{T}_{{{\text{core}}}}} = 5 \times {{10}^{7}}$ К отношение ${{T}_{{s\parallel }}}{\text{/}}{{T}_{{s \bot }}} = 7.10$ В табл. 5 представлены полные светимости НЗ $L = 2\pi R_{{{\text{out}}}}^{2}\sigma \int_0^\pi \,{{T}^{4}}sin\theta d\theta $ и средние эффективные значения температуры. При этом для квадрупольных полей (${{B}_{{{\text{pq}}}}} = 1 \times {{10}^{{13}}}$) светимости НЗ меняются незначительно.
Рис. 8.
То же, что на рис. 7, для ${{T}_{{{\text{core}}}}} = 5 \times {{10}^{7}}$ К (слева) и ${{T}_{{{\text{core}}}}} = {{10}^{9}}$ К (справа).

Таблица 5.
Светимость и эффективная температура НЗ с дипольным магнитным полем
| ${{T}_{{{\text{core}}}}}$ | $5 \times {{10}^{7}}K$ | $2 \times {{10}^{8}}K$ | ${{10}^{9}}K$ |
|---|---|---|---|
| $L$, эрг/с | 1.6101e+32 | 3.6151e+33 | 1.3262e+35 |
| ${{T}_{{{\text{eff}}}}}$, K | 6.3966e+05 | 1.3924e+06 | 3.4268e+06 |
В качестве еще одного теста наши расчеты с дипольным полем правильнее всего сравнить с работами [12, 13] (случай т.н. “core-dipole configurations”), поскольку в них физическая постановка задачи близка к нашей (хотя в [13] рассмотрен случай сконденсировавшейся внешней оболочки). Наши результаты находятся в хорошем согласии с работой [12]. Так, для НЗ с температурой ядра ${{T}_{{{\text{core}}}}} = {{10}^{8}}$ К и индукцией дипольного поля на полюсах ${{B}_{{{\text{pd}}}}} = 1 \times {{10}^{{13}}}$ значения температур поверхности на магнитных полюсе и экваторе равны соответственно $1.09 \times {{10}^{6}}$ К и $0.18 \times {{10}^{6}}$ К, что визуально очень близко к аналогичным значениям в [12]. Угловая зависимость также воспроизводится с хорошей точностью. Расчеты с “core”-конфигурациями в [13] качественно близки к нашим, хотя в данной работе температура поверхности выше, чем у нас, при одних и тех же ${{T}_{{{\text{core}}}}}$.
На рис. 9, 10 представлено то же, что на рис. 6, 7, но для квадрупольного поля (8) с индукцией ${{B}_{{{\text{pq}}}}} = 1 \times {{10}^{{13}}}$ Гс на полюсе. При этом в распределении поверхностной температуры наблюдаются два “провала”. На рис. 10 представлено распределение температуры по поверхности НЗ, соответствующее распределению из рис. 9.
Рис. 9.
Распределение температуры в коре НЗ для квадрупольного поля (7) с индукцией на полюсе ${{B}_{{{\text{pq}}}}} = {{10}^{{13}}}$ Гс, и ${{T}_{{{\text{core}}}}} = 2 \times {{10}^{8}}$ К (здесь и далее в единицах ${{10}^{6}}$ К) для плотностей $\rho = {{10}^{{10}}} - 2 \times {{10}^{{14}}}$ г/см3. Слева – сечение в плоскости Y-Z, справа – трехмерная проекция поверхности коры НЗ при плотности ${{\rho }_{{{\text{out}}}}} = {{10}^{{10}}}$ г/см3.

Рис. 10.
Распределение температуры на поверхности НЗ для квадрупольного магнитного поля с индукцией ${{B}_{{{\text{pq}}}}} = 1 \times {{10}^{{13}}}$ Гс на полюсе для ${{T}_{{{\text{core}}}}} = 2 \times {{10}^{8}}$ К.

Далее мы рассмотрели соосные конфигурации дипольного и квадрупольного поля вместе. На рис. 11 дипольная составляющая магнитного поля осталась прежней для ${{T}_{{{\text{core}}}}} = 2 \times {{10}^{8}}$ К.
Рис. 11.
Распределение температуры на поверхности НЗ для суммы магнитных полей, слева – дипольно- (Bpq = 6 × × 1012 Гс), справа – квадрупольнодоминирующая (Bpq = 1.2 × 1013 Гс) конфигурация полей для ${{T}_{{{\text{core}}}}} = 2 \times {{10}^{8}}$ К.

При наличии слабого квадрупольного поля максимумы температуры сдвигаются в сторону от $\theta = \pi {\text{/}}2$ и становятся уже $2\pi $-периодичными по полярному углу, при этом если поле “в основном” дипольное, то имеется один “провал” температуры чуть выше магнитного экватора. В случае же, когда квадруполь доминирует, имеют место уже два смещенных “провала”.
В работе были проведены расчеты анизотропного распространения тепла во внешних слоях замагниченных НЗ для случаев, когда магнитное поле НЗ имеет осевую симметрию.
В дальнейшем мы планируем провести моделирование данной задачи в случае, когда в магнитном поле отсутствует осевая симметрия, а также рассмотреть наблюдательные проявления анизотропного распространения тепла.
Работа была выполнена при частичной поддержке грантов РФФИ 17-02-00760, 18-02-00619 и 18-29-21021, а также при частичной поддержке программы фундаментальных исследований РАН No.12 “Вопросы происхождения и эволюции Вселенной”.
Список литературы
J. A. Pons, F. M. Walter, J. M. Lattimer, et al., Astrophys. J. 564, 981 (2002).
D. L. Kaplan and M. H. van Kerkwijk, Astrophys. J. Lett. 628, L45 (2005).
D. L. Kaplan, S. R. Kulkarni, and M. H. van Kerkwijk, Astrophys. J. Lett. 588, L33 (2003).
F. Haberl, Mem. Soc. Astron. It. 75, 454 (2004).
Г. С. Бисноватый-Коган, Ю. Н. Куликов, В. М. Чечеткин, Астрон. журн. 53, 975 (1976).
G. S. Bisnovatyi-Kogan and M. V. Glushikhina, Plasma Physics Reports 44, 4, 355 (2018).
V. Urpin and D. G. Yakovlev, Sov. Astron. 24, 303 (1980).
E. Flowers and N. Itoh, Astrophys. J. 206, 218 (1986).
E. H. Gudmundsson, C. J. Pethick and R. I. Epstein, Astrophys. J. 272, 286 (1983).
A. Yu. Potekhin and D. G. Yakovlev, Astron. and Astrophys. 374, 213 (2001).
A. Yu. Potekhin, J. A. Pons, and D. Page, Space Science Rev. 191, 239 (2015).
U. Geppert, D. Kuker, and D. Page, Astron. and Astrophys. 426, 267 (2004).
J. F. Perez-Azorin, J. A. Miralles, and J. A. Pons, Astron. and Astrophys. 451, 1009 (2006).
U. Geppert, D. Kuker, and D. Page, Astron. and Astrophys. 457, 937 (2006).
D. N. Aguilera, J. A. Pons, and J. A. Miralles, Astron. and Astrophys. 486, 255 (2008).
J. A. Pons, J. A. Miralles, and U. Geppert, Astron. and Astrophys. 496, 207 (2009).
D. Vigano, N. Rea, J. A. Pons, D. N. Aguilera, and J. A. Miralles, Monthly Not. Roy. Astron. Soc. 434, 123 (2013).
С. И. Брагинский, Вопросы теории плазмы. Выпуск 1 (М.: ГосАтомИздат, 1963).
С. И. Брагинский, Журн. эксп. теор. физ. 6, 358 (1957).
Д. Г. Яковлев, В. А. Урпин, Астрон. журн. 57, 526 (1980).
С. Чепмен, Т. Каулинг, Математическая теория неоднородных газов (М.: Издательство иностранной литературы, 1960).
Дж. Займан, Электроны и фононы. Теория явлений переноса в твердых телах (М.: Издательство иностранной литературы, 1962).
Г. С. Бисноватый-Коган, Физические основы теории звездной эволюции (М.: Наука, 1989).
R. D. Blandford, J. H. Applegate, and L. Hernquist, Monthly Not. Roy. Astron. Soc. 204 1025 (1983).
G. S. Bisnovatyi-Kogan and M. V. Glushikhina, Plasma Physics Reports 44, 12, 1114 (2018).
Л. Д. Ландау, Е. М. Лифшиц Теоретическая физика. Теория поля (М.: Наука, 1988).
F. Douchin and P. Haensel, Astron. and Astrophys. 380, 151 (2001).
E. Chabanat, E. Bonche, E. Haensel, J. Meyer, and R. Schaeffer, Nucl. Phys. A 627, 710 (1997).
E. Chabanat, E. Bonche, E. Haensel, J. Meyer, and R. Schaeffer, Nucl. Phys. A 635, 231 (1998).
G. Baym, H. Bethe, and Ch. Pethick, Nucl. Phys. A 175, 255 (1971).
G. Baym, Ch. Pethick, and D. Sutherland, Astrophys. J. 170, 306 (1971).
G. B. Rybicki and A. P. Lightman, Radiative processes in astrophysics (WILEY-VCH, 2004).
G. Greenstein and G. J. Hartke, Astrophys. J. 271, 283 (1983).
N. A. Silant’ev and D. G. Yakovlev, Astrophys. Space Sci. 71, 45 (1980).
A. Y. Potekhin, G. Chabrier, and D. G. Yakovlev, Astrophys. Space Sci. 308, 353 (2007).
S. I. Blinnikov, N. V. Dunina-Barkovskaya, and D. K. Nadyozhin, Astrophys. J. Supp. Ser. 106, 171 (1996).
G. Chabrier and A. Yu. Potekhin, Phys. Rev. E 58, 4941 (1998).
H. M. Antia, Astrophys. J. Supp. Ser. 84, 101 (1993).
В. Б. Берестецкий, Е. М. Лифшиц, Л. П. Питаевский Квантовая электродинамика (М.: Наука, 1989).
М. Шварцшильд, Строение и эволюция звезд (М.: Эдиториал УРСС, 2004).
В. Л. Гинзбург, Л. М. Озерной, Журн. эксп. теор. физ. 47, 1030 (1964).
А. А. Самарский, Теория разностных схем (М.: Наука, 1989).
N. V. Ardeljan and K. V. Kosmachevskii, Comput. Math. Modelling 6, 209 (1995).
N. V. Ardelyan and I. S. Gush’in, Vestnik MSU 15, 3, 3 (1982).
Н. В. Арделян, К. В. Космачевский, С. В. Черниговский, Вопросы построения и исследования полностью консервативных разностных схем магнитной газодинамики (М.: МГУ, 1987).
N. V. Ardeljan, G. S. Bisnovatyi-Kogan, and S. G. Moiseenko, Astron. and Astrophys. 355, 1181 (2000).
N. V. Ardeljan, G. S. Bisnovatyi-Kogan, and S. G. Moiseenko, Monthly Not. Roy. Astron. Soc. 359, 333 (2005).
I. A. Kondratyev and S. G. Moiseenko, J. Phys. Conf. Ser. 1163, 012069 (2019).
А. А. Самарский, Ю. П. Попов, Разностные методы решения задач газовой динамики (М.: Наука, 1992).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


