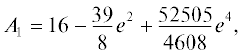Астрономический журнал, 2020, T. 97, № 4, стр. 348-352
Норма смещения положения небесного тела в одной задаче динамической астрономии
К. В. Холшевников 1, 2, *, Н. Батмунх 3, **, К. И. Оськина 1, ***, В. Б. Титов 1, ****
1 Санкт-Петербургский государственный университет
Санкт-Петербург, Россия
2 Институт прикладной астрономии РАН
Санкт-Петербург, Россия
3 Институт астрономии и геофизики Монгольской Академии наук
Улан-Батор, Монголия
* E-mail: kvk@astro.spbu.ru
** E-mail: monastro@yandex.ru
*** E-mail: zegzithsa@gmail.com
**** E-mail: tit@astro.spbu.ru
Поступила в редакцию 29.10.2019
После доработки 22.11.2019
Принята к публикации 22.11.2019
Аннотация
Широко применяющийся в небесной механике метод осреднения вводит среднюю орбиту, слабо отклоняющуюся от оскулирующей при условии малости возмущающих сил. Разность $\delta {\mathbf{r}}$ положений небесного тела на средней и оскулирующей орбите является квази-периодической функцией времени. Представляет интерес оценка нормы уклонения $\left\| {\delta {\mathbf{r}}} \right\|$. Ранее мы получили точное выражение среднеквадратической нормы для одной задачи небесной механики: точка нулевой массы движется под действием притяжения к центральному телу и малого возмущающего ускорения ${\mathbf{F}}$; вектор ${\mathbf{F}}$ постоянен в сопутствующей системе отсчета с осями, направленными по радиусу-вектору, трансверсали и вектору площадей. Здесь мы решили аналогичную задачу, предполагая вектор ${\mathbf{F}}$ постоянным в системе отсчета с осями, направленными по касательной, главной нормали и вектору площадей. Оказалось, что ${{\left\| {\delta {\mathbf{r}}} \right\|}^{2}}$ пропорциональна ${{a}^{6}}$, где $a$ – большая полуось. Величина ${{\left\| {\delta {\mathbf{r}}} \right\|}^{2}}{{a}^{{ - 6}}}$ является взвешенной суммой квадратов компонент ${\mathbf{F}}$. Коэффициенты квадратичной формы зависят лишь от эксцентриситета и представлены рядом Маклорена по четным степеням $e$, сходящимся, по крайней мере, при $e < 1$. Вычислены коэффициенты рядов до ${{e}^{4}}$ включительно, так что поправочные члены имеют порядок ${{e}^{6}}$.
1. ВВЕДЕНИЕ
В методе осреднения важную роль играет переход от оскулирующих элементов к средним [1–5]. Оценка норм их разностей обычно не представляет труда, но и не представляет сколько-нибудь значительного интереса. В самом деле, нас интересуют отклонения не элементов, а координат и/или скоростей. Формулы для нормы разностей координат, выраженных через разности элементов, приведены в [6]. Там же они применены к задаче о движении с возмущающим ускорением, постоянным в системе отсчета ${{\mathcal{O}}_{1}}$, связанной с радиусом-вектором.
Здесь мы выведем аналогичные формулы в задаче о движении с возмущающим ускорением ${\mathbf{F}}$, постоянным в системе отсчета ${{\mathcal{O}}_{2}}$, связанной с вектором скорости. В этой системе ось $x$ направлена по вектору скорости частицы, ось $y$ – по главной нормали к оскулирующей орбите, ось $z$ – по бинормали. Компоненты ${\mathbf{F}}$ обозначим через ${{\varkappa }^{2}}\mathfrak{T}$, ${{\varkappa }^{2}}\mathfrak{N}$, ${{\varkappa }^{2}}W$, где ${{\varkappa }^{2}}$ – гравитационный параметр. Постоянные $\mathfrak{T}$, $\mathfrak{N}$, $W$ имеют размерность длины в степени $ - 2$. Умноженные на ${{a}^{2}}$, они предполагаются малыми первого порядка. Величинами второго порядка малости мы пренебрегаем.
2. РАЗНОСТИ ОСКУЛИРУЮЩИХ И СРЕДНИХ ЭЛЕМЕНТОВ И КООРДИНАТ
Ограничиваясь первым порядком, заменим разности координат $\delta {\mathbf{r}}$ и элементов $\delta {{\epsilon }_{k}}$ дифференциалами. С такой точностью они приведены в [6]:
(1)
$\begin{gathered} {{(\delta {\mathbf{r}})}^{2}} = \delta {{r}^{2}} + {{r}^{2}}{{(\delta u + c\delta \Omega )}^{2}} + \\ + \;{{r}^{2}}\mathop {\left( {sinu\delta i - scosu\delta \Omega } \right)}\nolimits^2 . \\ \end{gathered} $Выразим первые два слагаемых справа в (1) через приращения независимых элементов [6]:
(2)
$\delta r = \frac{r}{a}\delta a + \frac{{{{a}^{2}}}}{r}(e - cosE)\delta e + \frac{{{{a}^{2}}esinE}}{r}\delta M,$(3)
$\begin{gathered} r(\delta u + c\delta \Omega ) = \frac{{{{a}^{2}}sinE}}{{r\eta }}(2 - {{e}^{2}} - ecosE)\delta e + \\ + \;r(\delta g + c\delta \Omega ) + \frac{{{{a}^{2}}\eta }}{r}\delta M. \\ \end{gathered} $Опираясь на структуру рядов для приращений элементов [7] и соотношения (2), (3), получим
(5)
$r(\delta u + c\delta \Omega ) = {{a}^{3}}[{{\Phi }_{5}}(e,E)\mathfrak{T} + {{\Phi }_{4}}(e,E)\mathfrak{N}],$(6)
$\begin{gathered} {{\Phi }_{n}}(e, - E) = {{( - 1)}^{{n - 1}}}{{\Phi }_{n}}(e,E), \\ {{\Phi }_{n}}( - e,E + \pi ) = {{\Phi }_{n}}(e,E). \\ \end{gathered} $Средствами компьютерной алгебры получим значения ${{a}_{{nk}}}$ с точностью до ${{e}^{5}}$:
Замечание 1. Коэффициенты ${{a}_{{1k}}}$ точны. Ряд для каждого из остальных выписанных ${{a}_{{nk}}}$ начинается с члена порядка ${{e}^{k}}$. Весьма вероятно, что это справедливо и в общем случае. Но доказать это нам пока не удалось.
Замечание 2. Функции ${{\Phi }_{n}}$ представлены рядами Фурье по эксцентрической аномалии, коэффициенты которых – ряды Маклорена по степеням эксцентриситета. Можно представить ${{\Phi }_{n}}$ рядами Маклорена по степеням $e$, коэффициенты которых – тригонометрические многочлены от $E$. Нетрудно перейти к тригонометрическим многочленам от средней аномалии. Но этого ни в коем случае делать не надо. Радиус сходимости рядов в первом случае равен единице, а во вто-ром – пределу Лапласа $0.662743$ [8, 9].
Замечание 3. К сожалению, в статье [7] допущена опечатка. В формулах (9) и (11) для ${{u}_{1}}$ и $\mathcal{I}{{u}_{1}}$ следует изменить знак. Опечатка повлекла ошибки в формуле (11) для ${v}$. Следует читать:
3. НОРМА СМЕЩЕНИЯ
Стандартной нормой для функций небесной механики служит среднеквадратичная норма по средней аномалии
(7)
${{\left\| f \right\|}^{2}} = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {{{f}^{2}}} dM = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {(1 - ecosE)} {{f}^{2}}dE.$Из соотношений (1), (4), (5) следует
(8)
$\begin{gathered} {{a}^{{ - 6}}}{{(\delta {\mathbf{r}})}^{2}} = (\Phi _{2}^{2} + \Phi _{5}^{2}){{\mathfrak{T}}^{2}} + (\Phi _{3}^{2} + \Phi _{4}^{2}){{\mathfrak{N}}^{2}} + \\ + \;\Phi _{1}^{2}{{W}^{2}} + 2({{\Phi }_{2}}{{\Phi }_{3}} + {{\Phi }_{4}}{{\Phi }_{5}})\mathfrak{T}\mathfrak{N}. \\ \end{gathered} $(9)
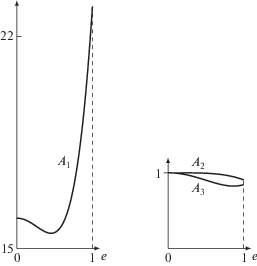
${{\varrho }^{2}}\;\mathop = \limits^{{\text{def}}} \;{{\left\| {\delta {\mathbf{r}}} \right\|}^{2}} = {{a}^{6}}({{A}_{1}}{{\mathfrak{T}}^{2}} + {{A}_{2}}{{\mathfrak{N}}^{2}} + {{A}_{3}}{{W}^{2}}).$(10)
$\begin{gathered} (1 - ecosE)\Phi _{n}^{2} = \\ = \;\frac{1}{2}\sum\limits_{k = 0}^\infty {\sum\limits_{m = 0}^\infty {{{a}_{{nk}}}} } {{a}_{{nm}}}[cos(k - m)E + cos(k + m)E] - \\ \end{gathered} $(11)
$\begin{gathered} \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {(1 - ecosE)} \Phi _{n}^{2}dE = \\ = \;a_{{n0}}^{2} - e{{a}_{{n0}}}{{a}_{{n1}}} + \frac{1}{2}\sum\limits_{k = 1}^\infty {(a_{{nk}}^{2} - e{{a}_{{nk}}}{{a}_{{n,k + 1}}})} . \\ \end{gathered} $(12)
$\frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {(1 - ecosE)} \Phi _{n}^{2}dE\frac{1}{2}\sum\limits_{k = 1}^\infty {(a_{{nk}}^{2} - e{{a}_{{nk}}}{{a}_{{n,k + 1}}})} .$С помощью средств компьютерной алгебры получим
Поправочные члены для ${{A}_{1}}$, ${{A}_{2}}$ имеют порядок ${{e}^{6}}$, а формула для ${{A}_{3}}$ точна.Установим некоторые свойства функций ${{A}_{n}}(e)$. Вычислим производные:
(15)
$\begin{gathered} min{{A}_{3}}(e) = {{A}_{3}}\left( {\sqrt {\frac{3}{4}} } \right) = \frac{{211}}{{256}} = 0.824219, \\ max{{A}_{1}}(e) = {{A}_{1}}(1) = 22\frac{{2393}}{{4608}} = 22.519314, \\ \end{gathered} $Отметим, что, как и в системе ${{\mathcal{O}}_{1}}$ [6], $\varrho $ зависит только от компонент вектора возмущающего ускорения, большой полуоси и эксцентриситета оскулирующего эллипса. От ориентации орбиты $\varrho $ не зависит. Сингулярности при $e = 0$ и $sini = 0$ отсутствуют.
Простая формула (9) позволяет легко найти наибольшее значение $\varrho $ для данной орбиты, если о возмущающем ускорении известно лишь, что вектор ${\mathbf{F}}$ находится внутри некоторого эллипсоида, ориентированного вдоль осей сопутствующей системы координат ${{\mathcal{O}}_{2}}$,
(17)
$\frac{{{{\mathfrak{T}}^{2}}}}{{b_{1}^{2}}} + \frac{{{{\mathfrak{N}}^{2}}}}{{b_{2}^{2}}} + \frac{{{{W}^{2}}}}{{b_{3}^{2}}} \leqslant 1,$(18)
$max{{\varrho }^{2}} = {{a}^{6}}\mathop {max}\limits_n {\text{\{ }}{{A}_{n}}b_{n}^{2}{\text{\} }}.$Пусть одна из величин ${{b}_{n}}$ равна нулю. Например, пусть ${{b}_{1}} = 0$. Это означает, что эллипсоид вырождается в эллипс, то есть $\mathfrak{T} = 0$. Формула (18) сохраняет силу, причем наибольшее значение ищется на множестве $n \in {\text{\{ }}2,3{\text{\} }}$.
Пусть две из величин ${{b}_{n}}$ равны нулю. Например, пусть ${{b}_{1}} = {{b}_{2}} = 0$. Это означает, что эллипсоид вырождается в отрезок, то есть $\mathfrak{T} = \mathfrak{N} = 0$. Формула (18) переходит в
Пусть ${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = b \ne 0$. Это равносильно фиксации модуля возмущающего ускорения $F = {{\varkappa }^{2}}b = {{\varkappa }^{2}}\sqrt {{{\mathfrak{T}}^{2}} + {{\mathfrak{N}}^{2}} + {{W}^{2}}} $. Формула (18) принимает вид
(19)
$max{{\varrho }^{2}} = {{a}^{6}}{{b}^{2}}max{\text{\{ }}{{A}_{1}},{{A}_{2}},{{A}_{3}}{\text{\} }}.$В заключение сравним полученные результаты с аналогичными для нормы смещения в задаче с возмущающим ускорением, постоянным в системе отсчета ${{\mathcal{O}}_{1}}$, связанной с радиусом-вектором [6]. Как уже отмечалось, формулы главного результата (9) идентичны с точностью до замены компонент возмущающего ускорения. Функции ${{A}_{n}}(e)$ в обоих случаях – ряды по четным степеням эксцентриситета. При $n = 3$ они совпадают, являясь многочленами четвертой степени. Так и должно быть, поскольку они отвечают одинаковой компоненте $W$ возмущающего ускорения. При $n = 1$ и $n = 2$ в системе ${{\mathcal{O}}_{1}}$ функции ${{A}_{n}}(e)$ являются многочленами шестой степени, тогда как в системе ${{\mathcal{O}}_{2}}$ – бесконечными рядами. Одинаковы лишь их свободные члены, как и должно быть, поскольку при нулевом эксцентриситете триедры систем ${{\mathcal{O}}_{1}}$ и ${{\mathcal{O}}_{2}}$ совпадают с точностью до направлений и нумерации.
Список литературы
Д. Брауер, Дж. Клеменс, Методы небесной механики (М.: Мир, 1964).
В. М. Волосов, Б. И. Моргунов, Методы осреднения в теории нелинейных колебательных систем (М.: Наука, 1971).
Е. А. Гребеников, Ю. А. Рябов, Новые качественные методы небесной механики (М.: Наука, 1971).
Г. Е. О. Джакалья, Методы теории возмущений для нелинейных систем (М.: Наука, 1979).
А. Морбиделли, Современная небесная механика (Москва, Ижевск: ИКИ, 2014).
Н. Батмунх, Т. Н. Санникова, К. В. Холшевников, В. Ш. Шайдулин, Астрон. журн. 93, 331 (2016).
Т. Н. Санникова, К. В. Холшевников, Астрон. журн. 91, 1060 (2014).
М. Ф. Субботин, Введение в теоретическую астрономию (М.: Наука, 1968).
А. Уинтнер, Аналитические основы небесной механики (М.: Наука, 1967).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал