1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 97, № 5, 2020

Астрономический журнал, 2020, T. 97, № 5, стр. 399-407

Орбитальный распад массивных рентгеновских двойных звезд

С. В. Чернов 1, *

1 Физический институт им. П.Н. Лебедева РАН, Астрокосмический центр
Москва, Россия

* E-mail: chernov@lpi.ru

Поступила в редакцию 28.06.2019
После доработки 20.12.2019
Принята к публикации 20.12.2019

Полный текст (PDF)

Аннотация

В работе рассматриваются две модели, способные объяснить изменение орбитального периода с течением времени у массивных рентгеновских двойных звезд. Первая модель объясняет орбитальный распад за счет действия динамических приливных сил, вторая модель – за счет изменения момента инерции массивной звезды вследствие эволюции самой звезды. Данные модели применяются к системам LMC X-4 и Cen X-3.

1. ВВЕДЕНИЕ

Рентгеновские двойные звезды были открыты спутником “Ухуру” в начале семидесятых годов прошлого века [1]. С тех пор эти системы постоянно исследуются. В частности, для некоторых систем удалось достаточно точно измерить изменение орбитального периода с течением времени [2]. Это может быть важно по следующим причинам. Если предположить, что причина орбитального распада связана с приливными взаимодействиями [3–5], то изучая орбитальный распад, можно понять природу диссипации приливного потока в звездах [6], т.к. именно диссипация приводит к орбитальному распаду. Тем самым можно непосредственно изучать физику эволюции звезд в двойной системе с учетом влияния звезд друг на друга [4].

В данной работе рассматриваются две массивные рентгеновские двойные системы, LMC X-4 и Cen X-3. Для них удалось измерить уменьшение орбитального периода с течением времени. Для системы LMC X-4 это уменьшение равно ${{\dot {P}}_{{{\text{orb}}}}}{\text{/}}{{P}_{{{\text{orb}}}}} = $ $ = \;( - 1.00 \pm 0.05) \times {{10}^{{ - 6}}}$ yr‒1 [2, 7], для системы Cen X-3 соответственно ${{\dot {P}}_{{{\text{orb}}}}}{\text{/}}{{P}_{{{\text{orb}}}}} = ( - 1.800 \pm 0.001) \times $ $ \times \;{{10}^{{ - 6}}}$ yr‒1 [2, 8].

В предыдущих работах было рассмотрено несколько моделей, способных объяснить орбитальный распад в массивных рентгеновских двойных системах. В работе [9] было рассмотрено быстрое изменение орбитального периода за счет приливных взаимодействий между нейтронной звездой и массивным компонентом в системе Cen X-3. В работе [10] рассмотрен орбитальный распад в системах LMC X-4 и Cen X-3 за счет переноса массы (ветра) от массивного компонента к нейтронной звезде и за счет приливной эволюции. В работе [7] обсужден орбитальный распад за счет изменения момента инерции звезды вследствие ее эволюции.

В данной работе рассмотрены две модели, способные объяснить изменение орбитального периода с течением времени. Первая модель объясняет орбитальный распад за счет действия динамических приливных сил в режиме умеренно большой диссипации [6]. В отличие от предыдущих работ [9, 10], мы учитываем динамические приливные взаимодействия, исходя из первых принципов [6], и используем более реалистичные модели звезд для расчетов приливных потоков. Вторая модель связана с изменением момента инерции звезды вследствие ее эволюции [9]. В процессе эволюции водородная оболочка массивной звезды может значительно увеличиваться, вследствие чего изменяется момент инерции звезды. Это приводит к изменению углового момента самой звезды, а т.к. суммарный угловой момент системы (орбитальный угловой момент плюс угловой момент звезды) сохраняется, то это приводит к изменению орбитального углового момента и, следовательно, к изменению орбитального периода двойной системы. В отличие от других работ [7], при моделировании звезд учитываются неустойчивости, которые приводят к дополнительному перемешиванию вещества внутри звезды и перераспределению углового момента в звездах, что также может внести свой вклад в процесс орбитального распада этих систем. Помимо этого, в данной работе учитывается модель звездного ветра от массивных звезд, которая также может уносить на бесконечность угловой момент тесной двойной системы, тем самым изменяя его.

Изменение орбитального периода за счет динамических приливов для других систем, таких как системы экзопланет, содержащие горячие Юпитеры, были рассмотрены в работе [11, 12].

2. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим две массивные рентгеновские двойные системы LMC X-4 и Cen X-3 [2], параметры которых представлены в табл. 1. Один компонент этих систем является нейтронной звездой с массой порядка полторы массы Солнца, а второй – массивной звездой с массой около 20 масс Солнца. Эти массивные звезды относятся к классу горячих OB звезд с эффективной температурой порядка 35 000 К. Орбита в таких системах практически круговая. Отношение угловой скорости вращения звезды к орбитальной угловой скорости порядка единицы, что говорит о том, что вращение массивного ОВ компонента практически синхронно с его орбитальным обращением. К синхронизации частот и циркуляризации орбиты приводят приливные взаимодействия [6]. Поэтому вначале рассмотрим орбитальный распад за счет действия динамических приливных сил.

Таблица 1.  

Параметры двойной системы [2]

Параметр LMC X4 Cen X-3
${{M}_{{ns}}},\;{{M}_{ \odot }}$ 1.57 ± 0.11 1.57 ± 0.16
${{P}_{s}}$, c 13.5 4.8
${{M}_{{{\text{opt}}}}},\;{{M}_{ \odot }}$ 18.3 ± 1 23.7 ± 1.4
${{R}_{{{\text{opt}}}}},\;{{R}_{ \odot }}$ 7.4 ± 0.4 11.4 ± 0.7
${{T}_{{{\text{eff}}}}} \times {{10}^{4}}$, K 3.5–3.6 3.3–3.7
${{P}_{{{\text{orb}}}}}$, d 1.4083790 2.08704106
e 0.006 ± 0.002 <0.0016
$\Omega {\text{/}}{{\Omega }_{{{\text{orb}}}}}$ 0.97 ± 0.13 0.75 ± 0.13
$\mathop {\dot {P}}\nolimits_{{\text{orb}}} {\text{/}}{{P}_{{{\text{orb}}}}}$, yr‒1 –1.00 × 10–6 –1.800 × 10–6

Примечание. ${{M}_{{ns}}}$ и ${{P}_{s}}$ – масса и период вращения нейтронной звезды, ${{M}_{{{\text{opt}}}}}$, ${{R}_{{{\text{opt}}}}}$ и ${{T}_{{{\text{eff}}}}}$ – масса, радиус и эффективная температура массивной звезды, ${{P}_{{{\text{orb}}}}}$ и $e$ – орбитальный период и эксцентриситет двойной системы, $\Omega {\text{/}}{{\Omega }_{{{\text{orb}}}}}$ – отношение скорости вращения массивной звезды к орбитальной скорости, ${{\dot {P}}_{{{\text{orb}}}}}{\text{/}}{{P}_{{{\text{orb}}}}}$ – изменение орбитального периода со временем.

2.1. Динамические приливы

Суть динамических приливов заключается в следующем. Нейтронная звезда, двигаясь по орбите, возбуждает в массивной звезде собственные колебания вблизи двойной резонансной частоты, диссипация которых приводит к обмену энергии и углового момента между орбитальным движением и массивной звездой и, следовательно, к орбитальному распаду. Последний проявляется в виде изменения орбитального периода с течением времени.

В работе [6] была выведена общая формула скорости диссипации энергии (и углового момента) за счет динамических приливов из первых принципов. Для вывода этой формулы рассматривалось уравнение Навье–Стокса. Были рассмотрены частные случаи: предел малых вязкостей и умеренно большие вязкости. (Понятие малой вязкости описано в [6], умеренно большие вязкости рассмотрены ниже). В звездах рассматривают радиационную и конвективную вязкость. Оказывается, что оба этих вида диссипации недостаточны, чтобы описать наблюдательные проявления. Этот вывод был получен в работе [11] для систем с экзопланетами. В рассмотренных двойных системах ситуация аналогичная. Поэтому стоит проблема понимания природы диссипации собственных мод. В нашей модели для описания наблюдательных проявлений был рассмотрен режим умеренно больших вязкостей. Удивительно, что в этом режиме коэффициент вязкости выпадает из окончательного ответа. Поэтому установить источник диссипации в этом режиме сложно. Режим умеренно больших вязкостей соответствует режиму, рассмотренному Заном в работе [13] (см. также [14]). С другой стороны, в этом режиме удается объяснить изменение орбитального периода для многих систем, не только рентгеновских массивных двойных звезд, рассмотренных в этой статье, но и в системах с экзопланетами, а также в системах “черная дыра + маломассивная звезда”.

Изменение орбитального периода с течением времени за счет динамических приливных взаимодействий задается формулой [6]

(1)
$\frac{{{{{\dot {P}}}_{{{\text{orb}}}}}}}{{{{P}_{{{\text{orb}}}}}}} = \frac{{3a{{{\dot {E}}}_{I}}}}{{G{{M}_{{ns}}}{{M}_{{{\text{opt}}}}}}},$
где $a$ – большая полуось орбиты, $G$ – гравитационная постоянная, ${{\dot {E}}_{I}}$ – скорость изменения энергии за счет вязких диссипаций. При выводе этой формулы предполагалось, что спектр возмущений достаточно плотный, то есть разность между соседними частотами много меньше самой частоты: $d\omega {\text{/}}dj \ll \omega $, где $j$ – номер собственной частоты. Мы будем считать, что диссипация в таких системах происходит в режиме умеренно большой диссипации [6]. Это означает, что характерный темп вязкой диссипации на резонансной частоте много больше, чем разница между резонансной частотой и соседней [6]. Это будет происходить в случае, когда характерное время распада моды либо из-за вязкости, либо из-за нелинейных эффектов много меньше времени распространения волнового пакета в лучистой области звезды с частотами порядка резонансной, которая, в свою очередь, имеет порядок обратного расстояния между собственными частотами нормальных мод [6]. В режиме умеренно большой вязкости скорость изменения энергии за счет вязких диссипаций определяется формулой с учетом вращения звезды [6],
(2)
${{\dot {E}}_{I}} = - \pi \sum\limits_{m,k} \,\left( {1 + \frac{{m\Omega }}{{{{\omega }_{{m,k}}}}}} \right)\frac{{A_{{mk}}^{2}Q_{j}^{2}}}{{\left| {\tfrac{{d\omega }}{{dj}}} \right|}},$
где ${{\omega }_{{mk}}} = k{{\Omega }_{{{\text{orb}}}}} - m\Omega $, ${{Q}_{j}}$ – интеграл перекрытия, который служит мерой эффективности возбуждения нормальных мод в звезде приливными силами [15], ${{A}_{{mk}}}$ – коэффициенты разложения эллиптической орбиты по малому эксцентриситету (значение этих коэффициентов приведены в [6, Приложение А]).

В формуле (2) наибольший вклад в сумму дают следующие пары чисел: для системы LMC X-4 ($m,k$) = (2,1) и (2,3), для системы Cen X-3 ($m,k$) = = (2,1), (2,2) и (2,3) [6]. Если просуммировать по этим парам, то в результате получаем

${{\dot {E}}_{I}} = - \pi \left( {1 + \frac{{2\Omega }}{{{{\Omega }_{{{\text{orb}}}}} - 2\Omega }}} \right)\mathop {\frac{{A_{{21}}^{2}Q_{j}^{2}}}{{\left| {\tfrac{{d\omega }}{{dj}}} \right|}}}\nolimits_{|21} - $
(3)
$ - \;\pi \left( {1 + \frac{{2\Omega }}{{2{{\Omega }_{{{\text{orb}}}}} - 2\Omega }}} \right)\mathop {\frac{{A_{{22}}^{2}Q_{j}^{2}}}{{\left| {\tfrac{{d\omega }}{{dj}}} \right|}}}\nolimits_{|22} - $
$ - \;\pi \left( {1 + \frac{{2\Omega }}{{3{{\Omega }_{{{\text{orb}}}}} - 2\Omega }}} \right)\mathop {\frac{{A_{{23}}^{2}Q_{j}^{2}}}{{\left| {\tfrac{{d\omega }}{{dj}}} \right|}}}\nolimits_{|23} .$
В приведенной выше формуле, при равенстве $\Omega = {{\Omega }_{{{\text{orb}}}}}$ (полная синхронизация) в знаменателе получается бесконечность, но частота возмущения в этом случае равна нулю, т.к. $\omega = {{\omega }_{{22}}} = $ $ = 2{{\Omega }_{{{\text{orb}}}}} - 2\Omega = 0$. Интеграл перекрытия при нулевой частоте возмущения тождественно равен нулю, $Q = 0$, следовательно, членом (2,2) можно пренебречь в случае полной синхронизации (см. [6]). Аналогичный вывод получаем при рассмотрении предельного случая, когда $\Omega \to {{\Omega }_{{{\text{orb}}}}}$. Для системы Cen X-3 частота вращения массивной звезды составляет 0.75 от орбитальной частоты, слагаемое (2,2) в этом случае будет давать сравнимый вклад с остальными членами. Для круговой орбиты в случае полной синхронизации скорость изменения орбитального периода равна нулю, т.к. во вращающейся системе отчета приливные силы работы не совершают. Для некруговой орбиты скорость изменения орбитального периода определяется эксцентриситетом системы.

Подставляя коэффициенты ${{A}_{{m,k}}}$ [6] в (3), получаем окончательный выражение для скорости изменения энергии

(4)
$\begin{gathered} {{{\dot {E}}}_{I}} = - \frac{{6{{\pi }^{2}}}}{5}\frac{{{{G}^{2}}M_{{ns}}^{2}}}{{{{a}^{6}}}}\left[ {\frac{{{{\Omega }_{{{\text{orb}}}}}}}{{{{\Omega }_{{{\text{orb}}}}} - 2\Omega }}\mathop {\frac{{{{e}^{2}}Q_{j}^{2}}}{{16\left| {\tfrac{{d\omega }}{{dj}}} \right|}}}\nolimits_{|21} } \right. + \\ + \;\frac{{{{\Omega }_{{{\text{orb}}}}}}}{{{{\Omega }_{{{\text{orb}}}}} - \Omega }}\mathop {\frac{{(1 - 5{{e}^{2}})Q_{j}^{2}}}{{4\left| {\tfrac{{d\omega }}{{dj}}} \right|}}}\nolimits_{|22} \left. { + \frac{{3{{\Omega }_{{{\text{orb}}}}}}}{{3{{\Omega }_{{{\text{orb}}}}} - 2\Omega }}\mathop {\frac{{49{{e}^{2}}Q_{j}^{2}}}{{16\left| {\tfrac{{d\omega }}{{dj}}} \right|}}}\nolimits_{|23} } \right]. \\ \end{gathered} $
Это общая формула для расчета скорости диссипации энергии за счет динамических приливных сил в режиме умеренно больших вязкостей с учетом вращения звезды для массивных рентгеновских двойных систем. Подставляя (4) в (1), получаем окончательную формулу для подсчета изменения орбитального периода за счет динамических приливов.

2.2. Изменение момента инерции массивной звезды

Следующей моделью, позволяющей объяснить изменение орбитального периода с течением времени для массивных рентгеновских двойных звезд, является модель, учитывающая изменение момента инерции массивной звезды, которое возникает из-за эволюционного расширения водородной оболочки звезды.

В работе [9] было показано, что в режиме слабого трения изменение орбитального периода за счет изменения момент инерции звезды выражается формулой

(5)
$\frac{{{{{\dot {P}}}_{{{\text{orb}}}}}}}{{{{P}_{{{\text{orb}}}}}}} \approx - \frac{{\Omega \tfrac{{dln(I)}}{{dt}}}}{{{{\Omega }_{{{\text{orb}}}}}(\mu {{a}^{2}}{\text{/}}3I - 1)}},$
где $\mu $ – приведенная масса, $I$ – момент инерции звезды. Знак изменения орбитального периода зависит от отношения момента инерции нейтронной звезды относительно центра масс системы к моменту инерции массивной звезды. Если момент инерции нейтронной звезды относительно центра масс больше момента инерции массивной звезды, то орбитальный период системы уменьшается, и система стремится к синхронизованному состоянию [9]. В противном случае период увеличивается, и такое условие может приводить к асинхронизации.

К изменению момента инерции звезды могут приводить дополнительные эффекты, связанные с перемешиванием вещества в звездах из-за конвекции и перераспределения углового момента за счет различных видов неустойчивости, связанных с дифференциальным вращением звезды. В данной работе при моделировании звезды учитывались следующие виды неустойчивостей [16, 17]: конвекция, полуконвекция, овершутинг, термохалинная циркуляция, динамическая сдвиговая неустойчивость, вековая сдвиговая неустойчивость, меридиональная циркуляция Эддингтона–Свита, неустойчивость Солберга–Хойланда и неустойчивость Голдрайха–Шуберта–Фрике. Эти неустойчивости рассматривались в диффузном приближении. Решаются два уравнения [17]: уравнение перемешивания вещества

(6)
$\frac{{\partial {{X}_{n}}}}{{\partial t}} = \frac{\partial }{{\partial M}}\left[ {{{{(4\pi {{r}^{2}}\rho )}}^{2}}D\frac{{\partial {{X}_{n}}}}{{\partial M}}} \right] + \mathop {\left( {\frac{{d{{X}_{n}}}}{{dt}}} \right)}\nolimits_{{\text{nuc}}} $
и уравнение переноса углового момента
(7)
$\frac{{\partial \omega }}{{\partial t}} = \frac{1}{i}\frac{\partial }{{\partial M}}\left[ {{{{(4\pi {{r}^{2}}\rho )}}^{2}}i\nu \frac{{\partial \omega }}{{\partial M}}} \right] - \frac{\omega }{r}\left( {\frac{{\partial r}}{{\partial t}}} \right)\frac{{dlni}}{{dlnr}},$
где ${{X}_{n}}$ – массовая доля каждого элемента в звезде, $\rho $ – плотность, $D$ – коэффициент диффузии, $i$ – удельный момент инерции, $\nu $ – коэффициент турбулентной вязкости, а слагаемое $\mathop {\left( {\tfrac{{d{{X}_{n}}}}{{dt}}} \right)}\nolimits_{{\text{nuc}}} $ связано с изменением массовой доли каждого элемента за счет ядерных реакций. Значения коэффициентов диффузии и турбулентной вязкости даны в работе [17].

Помимо эффектов перемешивания вещества и переноса углового момента, в работе исследован ветер массивной звезды. Ветер непосредственно уносит угловой момент от звезды, тем самым изменяя орбитальный угловой момент двойной системы [4]. Так как рассматриваемые звезды быстро вращаются и достаточно горячие, то при учете ветра использовался так называемый $\Omega \Gamma $ предел, т.е. использовалась формула с учетом вращения и излучения [18, 19]:

(8)
$\begin{gathered} \dot {M}(\Omega ) = \dot {M}(0)\mathop {\left( {\frac{1}{{1 - \Omega }}} \right)}\nolimits^{0.43} ,\quad \Omega = \frac{v}{{{{v}_{{{\text{crit}}}}}}}, \\ v_{{{\text{crit}}}}^{2} = \frac{{GM}}{R}\left( {1 - \frac{L}{{{{L}_{{{\text{Edd}}}}}}}} \right), \\ \end{gathered} $
где $\dot {M}(0)$ – скорость потери массы за счет ветра без учета вращения и излучения звезды, $v$ – скорость вращения на поверхности звезды, ${{L}_{{{\text{Edd}}}}}$ – эддингтоновская светимость, $M$ – масса звезды, $R$ – радиус звезды. Величина $\dot {M}(0)$ взята из работы [20], где была выведена специально для массивных горячих звезд OB класса. Эта формула имеет двухтемпературный режим и зависит от пяти параметров звезды: массы, светимости, эффективной температуры, скорости убегания частиц и металличности.

Звезда моделировалась с помощью пакета программ MESA версии 7385 [21–23]. В начальный момент времени параметры звезды выбирались таким образом, чтобы в некоторый момент времени, называемый возрастом звезды, наблюдаемые параметры звезды (см. табл. 1), такие как масса, радиус, эффективная температура, угловая скорость вращения, были в пределах ошибок близки к наблюдаемым величинам. В табл. 2 представлены параметры моделирования такой звезды, наилучшим образом согласующиеся с наблюдениями. Осцилляции звезды вычислялись с помощью пакета программ GYRE [24] с учетом вращения в традиционном приближении. Момент инерции звезды вычислялся по формуле

(9)
$I = \int\limits_0^r {{{r}^{2}}dM} .$
Таблица 2.  

Численные параметры модели

Параметр LMC X4 Cen X3
${{M}_{{{\text{opt}}}}},\;{{M}_{ \odot }}$ 18.3 23.7
${{R}_{{{\text{opt}}}}},\;{{R}_{ \odot }}$ 7.38 11.5
${{T}_{{{\text{eff}}}}} \times {{10}^{4}}$, K 3.08 3.14
$\Omega {\text{/}}{{\Omega }_{{{\text{orb}}}}}$ 0.94 0.71
${{t}_{{{\text{age}}}}} \times {{10}^{6}}$, yr 4.12 5.18

3. РЕЗУЛЬТАТЫ

В данной главе представлены результаты вычислений для каждой из представленных выше моделей.

3.1. Динамические приливы

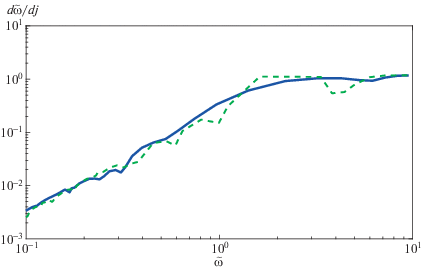
На рис. 1 показана зависимость безразмерного интеграла перекрытия от безразмерной собственной частоты. Интеграл перекрытия нормируется условием $Q = \tilde {Q}\sqrt M R$, а частоты – условием $\omega = \tilde {\omega }\sqrt {GM{\text{/}}{{R}^{3}}} $. Синяя сплошная кривая соответствует модели LMC X-4, а зеленая штриховая – модели Cen X-3. С уменьшением частоты происходит плавное уменьшение интеграла перекрытия. На рис. 2 показана зависимость разности между соседними частотами от собственной частоты. Синяя сплошная кривая соответствует модели LMC X-4, зеленая штриховая – модели Cen X-3. Для каждой модели звезд спектр оказался достаточно плотным в области двойной резонансной частоты, что подтверждает возможность использования формулы (1).

Рис. 1.

Зависимость модуля интеграла перекрытия от частоты для каждой модели.

Рис. 2.

Зависимость разности между соседними частотами от частоты для каждой модели.

На рис. 3 и рис. 4 показаны результаты изменения орбитального периода за счет действия динамических приливных сил для систем LMC X-4 и Cen X-3 соответственно. Рассмотрим каждый рисунок в отдельности.

Рис. 3.

Изменение орбитального периода в зависимости от орбитального периода для системы LMC X-4 за счет динамических приливов.

Рис. 4.

Изменение орбитального периода в зависимости от орбитального периода для системы Cen X-3 за счет динамических приливов.

На рис. 3 синяя сплошная кривая соответствует случаю, когда массивная звезда не вращается; черная пунктирная кривая соответствует случаю, когда угловая скорость вращения звезды составляет половину от орбитальной угловой скорости $\Omega = 0.5{{\Omega }_{{{\text{orb}}}}}$; красная штрих-пунктирная кривая соответствует случаю, когда угловая скорость вращения звезды составляет три четверти от орбитальной угловой скорости $\Omega = 0.75{{\Omega }_{{{\text{orb}}}}}$; зеленая штриховая кривая соответствует случаю полной синхронизации, когда угловая скорость вращения звезды равна орбитальной угловой скорости $\Omega = {{\Omega }_{{{\text{orb}}}}}$. Наблюдения (звездочка) показывают, что система LMC X-4 близка к полной синхронизации, $\Omega = (0.97 \pm 0.13){{\Omega }_{{{\text{orb}}}}}$ и, следовательно, зеленая штриховая кривая в пределах ошибок хорошо согласуется с наблюдениями.

На рис. 4 синяя сплошная кривая соответствует случаю, когда массивная звезда не вращается, красная штрих-пунктирная кривая соответствует случаю, когда угловая скорость вращения звезды составляет нижнюю допустимую границу ошибок от орбитальной угловой скорости $\Omega = 0.62{{\Omega }_{{{\text{orb}}}}}$, зеленая штриховая кривая соответствует наблюдаемой угловой скорости вращения звезды $\Omega = 0.75{{\Omega }_{{{\text{orb}}}}}$ и черная пунктирная кривая соответствует верхней ошибке угловой скорости вращения звезды $\Omega = 0.88{{\Omega }_{{{\text{orb}}}}}$. Из рис. 4 видно, что в пределах ошибок измерения угловой скорости вращения массивной звезды ($\Omega {\text{/}}{{\Omega }_{{{\text{orb}}}}} = 0.75 \pm 0.13$) динамические приливы хорошо согласуются с наблюдениями.

Расхождения теории с наблюдениями могут быть связаны с недостаточно точным определением параметров орбиты, особенно эксцентриситета, т.к. в режиме полной синхронизации приливный распад определяется эксцентриситетом системы [6].

3.2. Изменение момента инерции звезды

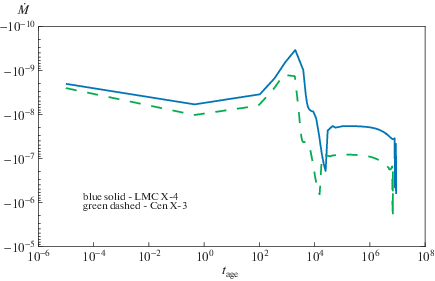
Сначала рассмотрим орбитальный распад за счет потери массы массивной звездой посредством звездного ветра. На рис. 5 показана зависимость скорости потери массы звезды в единицах массы Солнца за год от возраста звезды в годах. Сплошная синяя кривая соответствует звезде LMC X-4, а штриховая зеленая кривая – звезде Cen X-3. Для возраста звезды порядка ${{t}_{{{\text{age}}}}} \sim $ 106 лет скорость потери массы для обеих звезд $\dot {M} < {{10}^{{ - 7}}}{{M}_{ \odot }}$. В работе [25] приведен верхний предел на скорость потери массы для системы Cen X‑3, $\dot {M} \sim 3 \times {{10}^{{ - 6}}}{{M}_{ \odot }}$, что хорошо согласуется с численным моделированием. Следовательно, изменение орбитального периода со временем будет порядка ${{\dot {P}}_{{{\text{orb}}}}}{\text{/}}{{P}_{{{\text{orb}}}}} \sim \dot {M}{\text{/}}M < {{10}^{{ - 8}}}$, что на два порядка меньше, чем наблюдаемое значение. Стоит отметить, что та часть звездного ветра, которая аккрецирует на нейтронную звезду (большой телесный угол маломассивного компонента) не изменяет орбитальный угловой момент системы, а та часть звездного ветра, которая проходит сквозь ударную волну и уходит на бесконечность, приобретает существенную часть удельного орбитального момента маломассивного компонента (нейтронной звезды). К сожалению, численные расчеты с более точной оценкой приобретаемого веществом момента вращения в результате прохождения сквозь ударную волну пока отсутствуют. Конечно, особенно в системе Cen X-3, где оптический компонент практически заполняет свою полость Роша, есть потоки вещества, которые уходят на бесконечность через внешнюю точку Лагранжа ${{L}_{2}}$ и тоже уносят часть орбитального момента маломассивного компонента [26].

Рис. 5.

Зависимость скорости потерь массы звезды от возраста.

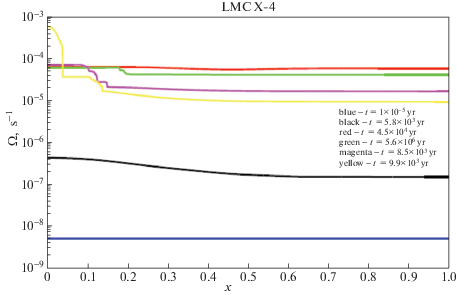
На рис. 6 показан график эволюции угловой скорости вращения звезды в ${{s}^{{ - 1}}}$ в зависимости от безразмерного радиуса для системы LMC X-4. Разным цветом показаны кривые для разных возрастов звезды. В начальный момент моделирования звезды $t = 0$ задавалось твердотельное вращение (синяя кривая) и по мере эволюции, вращение звезды частично становилось дифференциальным за счет рассмотренных в главе 2 неустойчивостей. Основные изменения происходят в ядре звезды, что и наблюдается на рис. 6. Оболочка звезды продолжает вращаться твердотельно во всем диапазоне эволюции звезды.

Рис. 6.

Зависимость угловой скорости вращения звезды от радиуса для системы LMC X-4.

На рис. 7 приведен график зависимости изменения орбитального периода в зависимости от возраста звезды за счет изменения момента инерции звезды для системы LMC X-4. Сплошная синяя кривая вычисляется по формуле (5), красная звездочка соответствует наблюдениям. Расхождение приблизительно составляет 2.5 раза.

Рис. 7.

Изменение орбитального периода в зависимости от орбитального периода для системы LMC X-4 за счет изменения момента инерции звезды.

На рис. 8 показан график зависимости изменения орбитального периода в зависимости от возраста звезды за счет изменения момента инерции звезды для системы Cen X-3. Сплошная синяя кривая вычисляется по формуле (5), красная звездочка соответствует наблюдениям. Расхождение приблизительно составляет 1.5 раза.

Рис. 8.

Изменение орбитального периода в зависимости от орбитального периода для системы Cen X-3 за счет изменения момента инерции звезды.

Таким образом, данная модель с расхождением приблизительно в два раза в состоянии объяснить наблюдательные проявления орбитального распада. Отличия могут быть связаны с необходимостью более точного моделирования и определения параметров звезды, с рассмотрением более общей модели трения (не только режим слабого трения).

4. ЗАКЛЮЧЕНИЕ

В работе рассмотрены две модели, которые способны (дополняя друг друга или по отдельности) объяснить изменения орбитального периода двойной системы с течением времени. Первая модель объясняет наблюдательные процессы за счет динамических приливов, вторая – за счет изменения момента инерции массивной звезды вследствие эволюции самой звезды. Звезды моделировались с учетом эффектов перемешивания вещества и перераспределения углового момента из-за неустойчивостей, связанных с конвекцией и с дифференциальным вращением звезды. В дополнение ко второй модели были учтены эффекты, связанные с потерей массы за счет звездного ветра массивной звезды. Так как звезда вращается, ветер также может уносить угловой момент массивной звезды и, следовательно, изменять орбитальный угловой момент.

Было показано, что в пределах наблюдательных ошибок можно подобрать параметры модели, которые с достаточно хорошей точностью способны объяснить изменение орбитального периода с течением времени.

Список литературы

  1. R. Giacconi, H. Gursky, E. Kellogg, E. Schreier, and H. Tananbaum, Astrphys. J. 167, L67 (1971).

  2. M. Falanga, E. Bozzo, A. Lutovinov, J. M. Bonnet-Bidaud, Y. Fetisova, and J. Puls, Astron. and Astrophys. 577, id. A130 (2015).

  3. С. В. Чернов, Письма в Астрон. журн. 43, 214 (2017).

  4. J. R. Hurley, C. A. Tout, and O. R. Pols, Monthly Not. Roy. Astron. Soc. 329, 897 (2002).

  5. S. V. Chernov, J. C. B. Papaloizou, and P. B. Ivanov, Monthly Not. Roy. Astron. Soc. 434, 1079 (2013).

  6. P. B. Ivanov, J. C. B. Papaloizou, and S. V. Chernov, Monthly Not. Roy. Astron. Soc. 432, 2339 (2013).

  7. A. M. Levine, S. A. Rappaport, and G. Zojcheski, Astrophys. J. 541, 194 (2000).

  8. R. L. Kelley, S. Rappaport, G. W. Clark, and L. D. Petro, Astrophys. J. 268, 790 (1983).

  9. A.M. Levine, S. Rappaport, J. E. Deeter, P. E. Boynton, and F. Nagase, Astrophys. J. 410, 328 (1993).

  10. S. Safi-Harb, H. Ogelmant, and K. Dennerl, Astrophys. J. 456, L37 (1996).

  11. S. V. Chernov, P. B. Ivanov, and J. C. B. Papaloizou, Monthly Not. Roy. Astron. Soc. 470, 2054 (2017).

  12. С. В. Чернов, ЖЭТФ 154(1), 85 (2018).

  13. J.-P. Zahn, Astron. and Astrophys. 57, 383 (1975).

  14. С. В. Чернов, Письма в Астрон. журн. 43(6), 474 (2017).

  15. W. H. Press and S. A. Teukolsky, Astrophys. J. 213, 183 (1977).

  16. A. S. Endal and S. Sofia, Astrphys. J. 220, 279 (1978).

  17. A. Heger, N. Langer, and S. E. Woosley, Astrophys. J. 528, 368 (2000).

  18. A. Maeder and G. Meynet, Astron. and Astrophys. 361, 159 (2000).

  19. D. B. Friend and D. C. Abbott, Astrophys. J. 311, 701 (1986).

  20. J. S. Vink, A. de Koter, and H. J. G. L. M. Lamers, Astron. and Astrophys. 369, 574 (2001).

  21. B. Paxton, L. Bildsten, A. Dotter, F. Herwig, P. Lesaffre, and F. Timmes, Astrophys. J. Suppl. 192, 3 (2011).

  22. B. Paxton, M. Cantiello, P. Arras, L. Bildsten, et al. A-strophys. J. Suppl. 208, 4 (2013).

  23. B. Paxton, P. Marchant, J. Schwab, E. B. Bauer, et al. Astrophys. J. Suppl. 220, 15 (2015).

  24. R. H. D. Townsend and S. A. Teitler, Monthly Not. Roy. Astron. Soc. 435, 3406 (2013).

  25. P. S. Wojdowski, D. A. Liedhal, and M. Sako, Astrophys. J. 547, 973, (2001).

  26. T. M. Tauris and E. P. J. van den Heuvel, arXiv:1401.0941 [astro-ph.SR] (2014).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал