Астрономический журнал, 2020, T. 97, № 5, стр. 408-420

1. ВВЕДЕНИЕ

В небесной механике для нахождения возмущений основным является метод Лагранжа, в котором используется разложение возмущающей функции по наклонам и эксцентриситетам орбит [1]. Однако подход Лагранжа при всей его несомненной ценности является весьма трудоемким, поэтому актуальными остаются поиски других способов решения задач о возмущениях в небесной механике. Новый шаг в решении проблемы в 1818 г. сделал Гаусс, который ввел представление о специальных кольцах. Гауссово кольцо получается при “размазывании” точечной массы $m$ по эллиптической орбите с одномерной плотностью вещества, обратной скорости движения спутника на данном участке траектории. Элемент массы кольца на угловом интервале $d{v}$ равен

Ньютоновский потенциал гауссова кольца выражается через полные эллиптические интегралы Лежандра и был найден в работе [2] (см. также книгу [3]). Отметим, что на практике указанный подход к нахождению возмущений может опираться на систему из нескольких колец Гаусса [4]. Подчеркнем, что в этом методе не рассматривается обратное влияние пробного тела на возмущающее кольцо. Условно назовем этот метод расчета возмущений прямым.

Однако в небесной механике часто встречаются и такие задачи, когда необходимо учитывать не только прямое влияние кольца на внешнее тело, но и обратное влияние возмущаемых тел на кольцо. Здесь основной интерес для нас представляет задача, в которой рассматривается взаимодействие между двумя (или несколькими) гравитирующими кольцами Гаусса. В таких задачах усреднение по быстрым переменным необходимо делать как для возмущающего, так и для возмущаемого тела. Условно назовем этот второй подход методом полного усреднения.

В указанных задачах для изучения эволюции взаимодействующих колец Гаусса необходимо знать взаимный гравитационный потенциал (или взаимную гравитационную энергию W_mut) этих колец. Эффективность метода, основанного на применении функции W_mut, была показана на примере исследования упрощенного варианта двупланетной задачи Солнце–Юпитер–Сатурн [5, 6]. В этих работах был найден взаимный потенциал двух однородных гравитирующих круглых колец, пересекающихся по диаметру под углом α друг к другу. С точностью до квадрата угла наклона α² включительно это выражение взаимной энергии колец равно

Здесь R₁ и R₂ – радиусы колец, а ${\rm K}\left( k \right)$ и $E\left( k \right)$ – полные эллиптические интегралы Лежандра первого и второго рода соответственно. Через W_mut легко найти момент сил M между кольцами

Момент сил между кольцами пропорционален углу $\alpha $ в первой степени, и этого достаточно при требуемой точности расчетов. Зная момент сил (4) и наделяя кольца соответствующим планетам угловым моментом, можно вычислить скорость прецессии узлов $\dot {\Omega }$ ≈ $25.6''$/год. Результат применения метода показал его адекватность (метод Лагранжа дает $\dot {\Omega }$ = $25.93''$/год [7]) и позволил дать простое и наглядное объяснение явлению вековой прецессии плоскостей орбит планет-гигантов.

Развивая данную тему, в работе [8] авторы отказались от упрощающего предположения о круговых кольцах. Предполагая кольца Гаусса компланарными слабо сжатыми эллипсами, выражение для взаимной гравитационной энергии было найдено в квадратичном по эксцентриситетам e₁ и e₂ приближении

Здесь $n = {{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}} \leqslant 1$ есть отношение больших полуосей колец, а β – угол между линиями их апсид. Заметим, что в (5) и (6) от угла $\beta $ зависит только коэффициент при смешанном члене W₁₂(n).

Предлагаемая работа продолжает указанную тематику: в ней задача о взаимной потенциальной энергии двух гауссовых колец решается в более общей постановке, когда оба кольца являются слабо эллиптическими и некомпланарными друг другу. Это позволяет применить новый метод для детального изучения вековой и долгопериодической эволюции орбит Юпитера и Сатурна в рамках двупланетной задачи. В разделе 2 дана постановка задачи. В разделе 3 получено выражение для взаимной энергии колец Гаусса, имеющих малые эксцентриситеты и небольшой наклон плоскостей друг к другу; результат представлен в виде ряда с точностью до членов четвертого порядка малости включительно. В разделе 4 выражение для взаимной энергии используется для вывода системы пяти дифференциальных уравнений, описывающих вековую эволюцию колец Гаусса. Получено решение этих уравнений эволюции. В разделе 5 разработанный математический аппарат применяется для более тщательного, чем ранее, исследования двупланетной задачи Солнце–Юпитер–Сатурн. В разделе 6 обсуждаются полученные результаты.

2. ПОСТАНОВКА ЗАДАЧИ

Даны два эллиптических кольца Гаусса с параметрами:

Здесь α_i, e_i – большая полуось и эксцентриситет i‑го кольца, ${{{v}}_{i}}$ – угол истинной аномалии на нем, (${{i}_{i}},{{\omega }_{i}},{{\Omega }_{i}}$) – углы наклона, аргументы перицентра и восходящего узла; ${{\mu }_{i}}\left( {{{{v}}_{i}}} \right)$ – распределение одномерной плотности вдоль кольца, m_i – масса кольца. Вклад во взаимную энергию колец от двух элементарных точечных масс $d{{m}_{1}}$ и $d{{m}_{2}}$ равен

Выражение для взаимной энергии двух эллиптических колец Гаусса можно получить теперь методом двукратного усреднения по средним движениям исходного выражения (8):

Введем декартову вспомогательную систему координат $O\xi \eta \zeta $, в которой ось $\eta $ направлена вдоль общей линии узлов колец Гаусса на восходящий узел, ось $\zeta $ – вдоль вектора углового момента 1-го кольца, а плоскость $O\xi \eta $ совпадает с плоскостью внешнего кольца под номером 1. В этой системе координат удобно находить взаимную энергию двух колец Гаусса, а также компоненты вектора ${\mathbf{M}}$ момента действующих сил. Радиус-вектор точки на k-ом кольце Гаусса (k = 1, 2) можно записать в виде ${{{\mathbf{r}}}_{k}}$ = ${{r}_{k}}\{ \cos {{u}_{k}}$, $\sin {{u}_{k}}\cos {{i}_{k}}$, $\sin {{u}_{k}}sin{{i}_{k}}\} $. Обозначим угол взаимного наклона плоскостей колец через $\Delta i = {{i}_{2}} - {{i}_{1}}$ (хотя в системе $O\xi \eta \zeta $ угол ${{i}_{1}} = 0$, но для симметрии в формулах мы его формально сохраним), тогда косинус угла между этими радиус-векторами будет равен $\cos \varphi $ = = $\cos {{u}_{1}}\cos {{u}_{2}}$ + $\sin {{u}_{1}}\sin {{u}_{2}}\cos \left( {\Delta i} \right)$, где ${{u}_{k}}$ = ${{{v}}_{k}} + {{\omega }_{k}}$, а ${{\omega }_{k}}$ – аргумент перицентра k-го кольца. С учетом закона распределения массы на каждом кольце (1), взаимную энергию (10) колец Гаусса можно представить двойным интегралом [5]

3. ВЗАИМНАЯ ЭНЕРГИЯ КОЛЕЦ. РАЗЛОЖЕНИЕ В РЯД

4. УРАВНЕНИЯ ЭВОЛЮЦИИ КОЛЕЦ ГАУССА

Под действием взаимных возмущений два гравитирующих кольца Гаусса не будут стационарными – они должны эволюционировать. Здесь нас интересует долгопериодическая и вековая эволюция эллиптических колец Гаусса (а значит, и соответствующих этим кольцам орбит).

4.5. Уравнения взаимной эволюции колец Гаусса в эклиптической системе отсчета

Теперь необходимо записать уравнения эволюции колец в основной, инерциальной системе отсчета. В качестве таковой естественно взять эклиптическую систему координат. Чтобы перейти в (40) от вспомогательной системы координат $O\xi \eta \zeta $ к эклиптической $O\xi {\text{'}}\eta {\text{'}}\zeta {\text{'}}$, необходимо выполнить преобразования, связанные с вращением первой системы отсчета вокруг оси $\zeta $ на угол $\Delta {{\bar {\omega }}_{2}}$, который может быть найден с помощью сферического треугольника, показанного на рис. 1 (соответствующие формулы см. в Приложении А).

Рис. 1.

Сферический треугольник в задаче о переходе к эклиптической системе координат. Здесь $\Delta i$ – угол между кольцами Гаусса; $\Delta \Omega {\text{'}}$ = $\Omega _{2}^{'}$ – $\Omega _{1}^{'}$ – разность долгот восходящих узлов колец Гаусса, отсчитываемая в некоторой плоскости (в нашем случае это плоскость эклиптики); $i_{1}^{'}$ и $i_{2}^{'}$ – наклонения, соответственно, первого и второго колец Гаусса к плоскости эклиптики; $\Delta {{\bar {\omega }}_{i}}$ – угол между линией узлов i-го кольца, лежащей в плоскости эклиптики, и общей линией узлов двух колец.

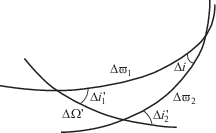
Итак, используя вспомогательные формулы (А2), уравнения эволюции (40) запишем в виде

$\frac{{d{{a}_{2}}}}{{dt}} = 0,$

$\frac{{d{{e}_{2}}}}{{dt}} = - \frac{{1 - e_{2}^{2}}}{{{{e}_{2}}}}\frac{{M_{\zeta }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}},$

(49)

$\frac{{di_{2}^{'}}}{{dt}} = \frac{{M_{\xi }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}\cos \left( {\Delta {{{\bar {\omega }}}_{2}}} \right) - \frac{{M_{\eta }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}\sin \left( {\Delta {{{\bar {\omega }}}_{2}}} \right),$

$\frac{{d\Omega _{2}^{'}}}{{dt}} = \frac{1}{{\sin i_{2}^{'}}}\left( {\frac{{M_{\xi }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}\sin \left( {\Delta {{{\bar {\omega }}}_{2}}} \right) + \frac{{M_{\eta }^{{\left( 2 \right)}}}}{{{{L}^{{\left( 2 \right)}}}}}\cos \left( {\Delta {{{\bar {\omega }}}_{2}}} \right)} \right),$

$\frac{{d\omega _{2}^{'}}}{{dt}} = - \left( {\frac{{d{{{v}}_{2}}}}{{dt}}} \right) - \cos i_{2}^{'}\frac{{d\Omega _{2}^{'}}}{{dt}}.$

Подставляя в уравнения (49) величины (42) и делая замены

(50)

$\begin{gathered} {{\omega }_{1}} = \omega _{2}^{'} - \Delta {{{\bar {\omega }}}_{1}},\quad {{\omega }_{2}} = \omega _{2}^{'} - \Delta {{{\bar {\omega }}}_{2}}, \\ \Delta i = \arccos (\cos i_{1}^{'}\cos i_{2}^{'} + \sin i_{1}^{'}\sin i_{2}^{'}\cos \Delta \Omega {\text{'}}) \equiv \\ \equiv \Delta i(i_{1}^{'},i_{2}^{'},\Delta \Omega {\text{'}}), \\ \end{gathered} $

получаем систему дифференциальных уравнений эволюции для оскулирующих элементов 2-го кольца под действием 1-го:

$\frac{{d{{a}_{2}}}}{{dt}} = 0,$

$\frac{{d{{e}_{2}}}}{{dt}} = - \frac{{G{{m}_{1}}}}{{16\pi a_{1}^{3}{{n}_{2}}{{n}^{3}}(1 + n){{{(1 - {{n}^{2}})}}^{2}}}} \times $

$ \times \;{{\left. {\sum\limits_{k + l + m = 1}^3 {e_{{klm}}^{{\left( 2 \right)}}} } \right|}_{\begin{subarray}{l} {{\omega }_{1}} = \omega _{1}^{'} - \Delta {{{\bar {\omega }}}_{1}} \\ {{\omega }_{2}} = \omega _{2}^{'} - \Delta {{{\bar {\omega }}}_{2}} \end{subarray} }}e_{1}^{k}e_{2}^{l}\Delta {{i}^{m}}(i_{1}^{'},i_{2}^{'},\Delta \Omega {\text{'}}),$

$\frac{{di_{2}^{'}}}{{dt}} = - \frac{{G{{m}_{1}}\Delta i(i_{1}^{'},i_{2}^{'},\Delta \Omega {\text{'}})}}{{8\pi a_{1}^{3}{{n}_{2}}{{n}^{3}}(1 + n){{{(1 - {{n}^{2}})}}^{2}}}} \times $

$ \times \;{{\left. {\sum\limits_{k + l = 2}^2 {i_{{kl}}^{{\left( 2 \right)}}} } \right|}_{\begin{subarray}{l} {{\omega }_{1}} = \omega _{1}^{'} - \Delta {{{\bar {\omega }}}_{1}} \\ {{\omega }_{2}} = \omega _{2}^{'} - \Delta {{{\bar {\omega }}}_{2}} \end{subarray} }}e_{1}^{k}e_{2}^{l}\cos \left( {\Delta {{{\bar {\omega }}}_{2}}} \right) + $

$ + \;\sin \left( {\Delta {{{\bar {\omega }}}_{2}}} \right)\frac{{G{{m}_{1}}}}{{8\pi a_{1}^{3}{{n}_{2}}{{n}^{3}}(1 + n){{{(1 - {{n}^{2}})}}^{2}}}} \times $

(51)

$ \times \;{{\left. {\sum\limits_{k + l + m = 0}^2 {\Omega _{{klm}}^{{\left( 2 \right)}}} } \right|}_{\begin{subarray}{l} {{\omega }_{1}} = \omega _{1}^{'} - \Delta {{{\bar {\omega }}}_{1}} \\ {{\omega }_{2}} = \omega _{2}^{'} - \Delta {{{\bar {\omega }}}_{2}} \end{subarray} }}e_{1}^{k}e_{2}^{l}\Delta {{i}^{{m + 1}}}(i_{1}^{'},i_{2}^{'},\Delta \Omega {\text{'}}),$

$\frac{{d\Omega _{2}^{'}}}{{dt}} = - \frac{{G{{m}_{1}}\Delta i(i_{1}^{'},i_{2}^{'},\Delta \Omega {\text{'}})}}{{8\pi a_{1}^{3}{{n}_{2}}{{n}^{3}}(1 + n){{{(1 - {{n}^{2}})}}^{2}}\sin i_{2}^{'}}} \times $

$ \times \;{{\left. {\sum\limits_{k + l = 2}^2 {i_{{kl}}^{{\left( 2 \right)}}} } \right|}_{\begin{subarray}{l} {{\omega }_{1}} = \omega _{1}^{'} - \Delta {{{\bar {\omega }}}_{1}} \\ {{\omega }_{2}} = \omega _{2}^{'} - \Delta {{{\bar {\omega }}}_{2}} \end{subarray} }}e_{1}^{k}e_{2}^{l}\sin \left( {\Delta {{{\bar {\omega }}}_{2}}} \right) - $

$ - \;\cos \left( {\Delta {{{\bar {\omega }}}_{2}}} \right)\frac{{G{{m}_{1}}}}{{8\pi a_{1}^{3}{{n}_{2}}{{n}^{3}}(1 + n){{{(1 - {{n}^{2}})}}^{2}}\sin i_{2}^{'}}}$

$ \times \;{{\left. {\sum\limits_{k + l + m = 0}^2 {\Omega _{{klm}}^{{\left( 2 \right)}}} } \right|}_{\begin{subarray}{l} {{\omega }_{1}} = \omega _{1}^{'} - \Delta {{{\bar {\omega }}}_{1}} \\ {{\omega }_{2}} = \omega _{2}^{'} - \Delta {{{\bar {\omega }}}_{2}} \end{subarray} }}e_{1}^{k}e_{2}^{l}\Delta {{i}^{{m + 1}}}(i_{1}^{'},i_{2}^{'},\Delta \Omega {\text{'}}),$

$\frac{{d\omega _{2}^{'}}}{{dt}} = - \cos i_{2}^{'}\frac{{d\Omega _{2}^{'}}}{{dt}} - \frac{{G{{m}_{1}}}}{{16\pi a_{1}^{3}{{n}_{2}}{{n}^{3}}(1 + n){{{(1 - {{n}^{2}})}}^{2}}}} \times $

$ \times \;{{\left. {\sum\limits_{k + l + m = 1}^3 {{\bar {v}}_{{klm}}^{{\left( 2 \right)}}} } \right|}_{\begin{subarray}{l} {{\omega }_{1}} = \omega _{1}^{'} - \Delta {{{\bar {\omega }}}_{1}} \\ {{\omega }_{2}} = \omega _{2}^{'} - \Delta {{{\bar {\omega }}}_{2}} \end{subarray} }}e_{1}^{k}e_{2}^{{l - 1}}\Delta {{i}^{m}}(i_{1}^{'},i_{2}^{'},\Delta \Omega {\text{'}}).$

Замечание 3. Уравнения (51) записаны в инерциальной (эклиптической) системе отсчета. Интересно, что в ней взаимный наклон колец $\Delta i{\text{'}} = i_{2}^{'} - i_{1}^{'}$, вообще говоря, уже не равен (см. вторую формулу в (50)) разности наклонов во вспомогательной системе отсчета, то есть $i_{2}^{'} - i_{1}^{'}$ ≠ ≠ ${{i}_{2}} - {{i}_{1}}$.

Замечание 4. Чтобы получить уравнения эволюции первого кольца под действием второго, нужно сделать перестановку индексов в уравнениях (51).

5. ПРИМЕНЕНИЕ МЕТОДА ВЗАИМНОЙ ЭНЕРГИИ К РЕШЕНИЮ ДВУПЛАНЕТНОЙ ЗАДАЧИ СОЛНЦЕ–ЮПИТЕР–САТУРН

Как известно, в небесной механике для изучения вековых и долгопериодических возмущений обычно применяется аналитический метод Лагранжа, основанный на разложении возмущающей функции в ряд по малым значениям эксцентриситетов и углов наклона орбит. Ранее этим методом Лаплас доказал замечательную теорему об устойчивости (в первом приближении) Солнечной системы. Численными расчетами было установлено, что в эволюции орбит планет и их спутников важную роль играют резонансы. Неожиданные эволюционные закономерности были открыты для орбит планет-гигантов. Оказалось, что на больших масштабах времени противоположные узлы орбит Юпитера и Сатурна на плоскости Лапласа совпадают и движутся вековым образом. Направление этого движения узлов попятное и скорость равна $\dot {\Omega }$ ≈ $25.93''$/год (Стокуэлл, в книге [7]). Характерным является синхронное движение узлов и периодические колебания в противофазе эксцентриситетов и наклонений орбит Юпитера и Сатурна. Согласно [13], период изменения взаимного наклона орбит равен T ≈ ≈ 51  000 лет, а эксцентриситетов T ≈ 70 000 лет.

В целом метод Лагранжа является весьма объемистым и трудоемким, о чем можно судить, например, по монографии ([13], раздел 7.3). Поэтому полученные ранее результаты по эволюции орбит Юпитера и Сатурна важно проверить другим методом, основанным на применении взаимной энергии колец Гаусса. Проблема сводится к изучению эволюции оскулирующих элементов колец под действием их взаимного гравитационного возмущения.

Расчеты по полученным выше формулам (51) дали следующие результаты (штрихи теперь опущены). На рис. 2 показана долгопериодическая зависимость от времени эксцентриситетов колец Юпитера и Сатурна.

Рис. 2.

Зависимость от времени эксцентриситета кольца Юпитера (сплошная линия) и Сатурна (штрихи), представляющие долгопериодическую эволюцию орбит планет под действием взаимного возмущения.

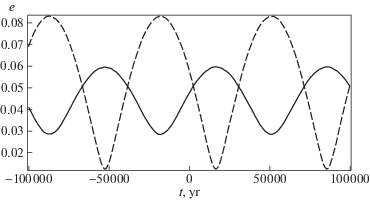
Мы нашли, что период и амплитуды этих долгопериодических колебаний эксцентриситетов имеют следующие значения:

Углы наклона колец к эклиптике также имеют долгопериодические колебания, см. рис. 3а. Период и амплитуды этих колебаний равны:

Рис. 3.

а). Зависимость от времени наклона (к эклиптике) кольца Юпитера (сплошная линия) и Сатурна (штрихи); б) биения угла наклона между кольцами Гаусса планет-гигантов.

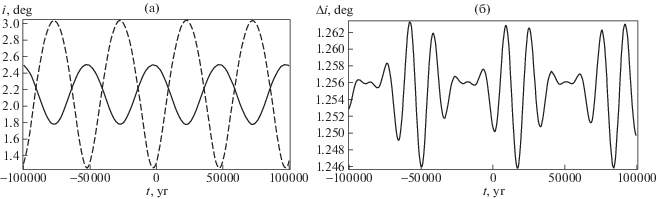
Интересно, что взаимный наклон колец в эклиптической системе отсчета имеет биения, которые показаны на рис. 3б. Период биений равен $T \approx 68.1 \times {{10}^{3}}$ лет.

Эволюция углов направления линий апсид у колец также имеет сложный характер (рис. 4a). Установлено, что эволюция перицентров характеризуется не только долгопериодическими колебаниями для долгот перицентров с периодом

Рис. 4.

а) зависимость долготы перицентра для орбиты Юпитера (сплошная линия) и Сатурна (штрихи); б) зависимость от времени угла $\Delta \varpi $ = ${{\varpi }_{2}} - {{\varpi }_{1}}$, в) зависимость от времени угла $\varpi $ (за вычетом векового компонента эволюции) для Юпитера (сплошная линия) и Сатурна (штрихи); г) зависимость $\Delta \varpi $ (также за вычетом векового компонента эволюции).

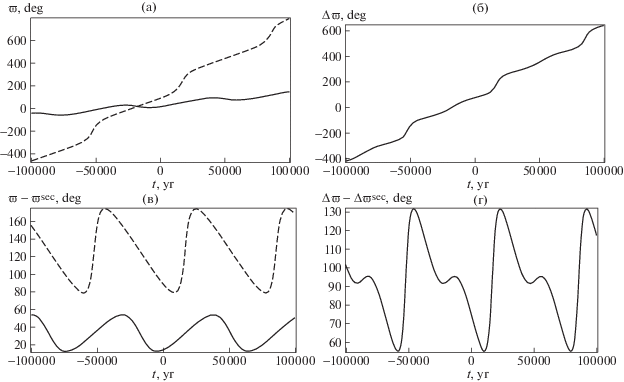
На рис. 4б показан график для разности углов $\Delta \varpi = {{\varpi }_{2}} - {{\varpi }_{1}}$. Период этого вращения равен ${{T}_{{\Delta \varpi }}} = 69.0 \times {{10}^{3}}$ лет.

Вычитая из $\varpi $ и $\Delta \varpi $ соответствующие вековые компоненты эволюции, вместо рис. 4а, б мы получим графики, показанные на рис. 4в, г. В сущности, график на рис. 4г представляет собой разность двух кривых, данных на рис. 4в.

В двупланетной задаче важно также найти прецессионное движение самих плоскостей двух колец. На рис. 5а, б это прецессионное движение колец представлено эволюцией долготы восходящего узла. Важно подчеркнуть, что указанная прецессия имеет не вековой характер, а описывается долгопериодическими поворотными колебаниями.

Рис. 5.

а) Зависимость изменения долготы восходящего узла для Юпитера (сплошная линия) и Сатурна (штрихи), представляющие вековую прецессию плоскостей орбит планет-гигантов под действием взаимного возмущения; б) разность долгот узлов орбиты Юпитера и Сатурна как функция времени.

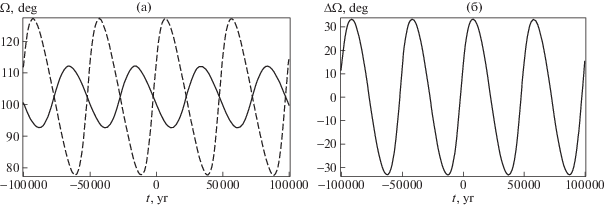
Особенно наглядно периодичность прецессионного движения орбит Юпитера и Сатурна показана на рис. 5б. Период и амплитуды колебаний долгот восходящих узлов и их разности соответственно равны:

Обратим внимание, что узлы в эклиптике у колец Юпитера и Сатурна не находятся строго в противофазе, как это имело бы место для узлов колец в плоскости Лапласа.

6. ОБСУЖДЕНИЕ И РЕЗУЛЬТАТЫ

В статье развит новый метод для изучения долгопериодических и вековых возмущений в динамической системе, которую можно моделировать двумя гравитирующими кольцами Гаусса. Установлено, что вместо усреднения полученного очень сложным образом выражения для возмущающей функции Лагранжа, проще и эффективнее сразу вычислить взаимную энергию двух колец Гаусса.

Основное внимание в работе уделяется задаче, где два кольца Гаусса имеют малые эксцентриситеты, небольшой угол взаимного наклона и произвольный угол между линиями апсид. При этих предположениях получено выражение для взаимной энергии колец W_вз в виде ряда с точностью до членов 4-го порядка малости включительно. Найдены и тщательно проверены все четырнадцать сложных коэффициентов, которые входят в выражение (14) для взаимной энергии двух колец Гаусса. Установлено, что выражение для взаимной энергии, записанное в виде ряда по степеням малых эксцентриситетов и малого взаимного наклона колец Гаусса, не содержит членов нечетных степеней по совокупности малых величин. Проверено, что член пятого порядка тождественно равен нулю, а шестого порядка не равен нулю, поэтому следующая поправка к выражению для взаимной энергии будет иметь сразу 6-й порядок малости.

Важным элементом в проведенных расчетах является учет того, что взаимная энергия инвариантна к преобразованиям переноса и повороту системы отсчета, поэтому можно выбрать систему отсчета для изучения вековых возмущений наиболее удобным образом. Именно так мы и поступили в разделе 2 с выбором вспомогательной системы координат $O\xi \eta \zeta $. В этой системе координат удобно находить взаимную энергию двух колец Гаусса, а значит, и вектор момента действующих сил. Но для практических приложений важным является переход к инерциальной системе координат $O\xi {\text{'}}\eta {\text{'}}\zeta {\text{'}}$, связанной с плоскостью эклиптики.

Выражение взаимной энергии ${{W}_{{{\text{mut}}}}}$ двух колец используется для вывода и решения системы пяти дифференциальных уравнений, описывающих их эволюцию. Решение уравнений эволюции также получено в виде степенных рядов.

Сравнение наших результатов с полученными традиционным методом разложения возмущающей функции Лагранжа на примере известной двупланетной задачи Солнце–Юпитер–Сатурн показало адекватность нового подхода. Более того, наши результаты в решении этой задачи дополняют и уточняют результаты других авторов. Дело в том, что, как уже говорилось, выражения для возмущающих функций получены у нас до членов 4-й степени малых величин, а в книге [13] только до членов 2-й степени малости. Кроме того, разработанный здесь принципиально новый метод получения возмущающей функции позволяет сразу изучать вековые и долгопериодические возмущения элементов орбит.

Новый метод позволил выявить неизвестные ранее особенности движений в двупланетной задаче. В частности, показано, что прецессионное движение плоскостей двух орбит описывается долгопериодическими поворотными колебаниями с периодом ${{T}_{\Omega }} = 49.9 \times {{10}^{3}}$ лет, причем амплитуды колебаний долгот восходящих узлов у обоих планет заметно различаются ${{A}_{{{{\Omega }_{1}}}}} = 19.5^\circ $, ${{A}_{{{{\Omega }_{2}}}}} = 49.5^\circ $. Отметим, что узлы в эклиптике у колец Юпитера и Сатурна не находятся строго в противофазе, как это имело бы место для узлов колец в плоскости Лапласа.

Отметим, наконец, что выражение возмущающей функции через взаимную гравитационную энергию может применяться не только к планетной задаче, где все наклонения должны быть малыми, но и к задаче с недавно обнаруженными у малых небесных тел кольцами уже не планетного типа [14–16].

ПРИЛОЖЕНИЕ А

Из сферического треугольника на рис. 1 получаем формулы

Тогда компоненты вектора момента сил (деленные на модуль углового момента 2-го кольца), действующего со стороны 1-го кольца на 2-е, преобразуются так

ПРИЛОЖЕНИЕ Б

КОЭФФИЦИЕНТЫ $i_{{kl}}^{{\left( 2 \right)}}$, ${\bar {v}}_{{klm}}^{{\left( 2 \right)}}$ $\Omega _{{klm}}^{{\left( 2 \right)}}$ В ПРАВЫХ ЧАСТЯХ УРАВНЕНИЙ (39)

Приводим точные выражения для оставшихся шестнадцати коэффициентов: