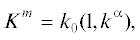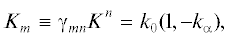Астрономический журнал, 2020, T. 97, № 5, стр. 421-431

Релятивистские редукции в высокоточных измерениях глобального гравитационного поля Земли с помощью мультипарной космической группировки

В. К. Милюков^1, *, И. Ю. Власов^1, **, М. В. Сажин^1, ***, О. С. Сажина^1, ****, В. Н. Семенцов^1, *****

¹ Московский государственный университет им. М.В. Ломоносова, Государственный астрономический институт им. П.К. Штернберга
Москва, Россия

^* E-mail: vmilyukov@yandex.ru
^** E-mail: i.vlasov78@mail.ru
^*** E-mail: sazhinm@gmail.com
^**** E-mail: cosmologia@yandex.ru
^***** E-mail: valera@sai.msu.ru

Поступила в редакцию 24.12.2019
После доработки 24.01.2020
Принята к публикации 24.01.2020

DOI: 10.31857/S0004629920060043

Полный текст (PDF)

Аннотация

В статье разработана теория релятивистских редукций для решения перспективных задач космической гравиметрии с целевой точностью до 1 пикометра.

1. ВВЕДЕНИЕ

Создание детальной модели гравитационного поля Земли с высокими пространственным и временным разрешениями, модели, которая может в будущем обеспечить в том числе навигацию по гравитационному полю, предполагает трехуровневую реализацию: глобальный, региональный и локальный уровни. Первый уровень картирования гравитационного поля Земли реализуется с помощью космических аппаратов (КА) на околоземной орбите.

Историю космической гравиметрии и градиентометрии следует начать уже со второго искусственного спутника Земли (ИСЗ), который был запущен в 1957 г. [1]. Высокоточные наблюдения его орбиты по регрессии долготы восходящего узла в течение трех месяцев позволили получить величину динамического сжатия Земли на порядок точнее, чем за 300 лет высокоточных триангуляционных наблюдений. В последние два десятка лет последовало бурное развитие методов космической гравиметрии и градиентометрии. Особенным успехом завершились космические миссии CHAMP [2], GRACE [3], GOCE [4], а также GRAIL [5]. В обзорных статьях эти космические миссии уже детально описаны (см., напр., [6]).

Современная космическая группировка спутников (далее просто космическая группировка), предназначенная для картирования глобального гравитационного поля Земли и создания моделей высокого разрешения, состоит из двух спутников-близнецов, которые расположены на геоцентрической круговой орбите с первоначальной высотой порядка 400–450 км. На более низких орбитах КА подвержены сильному тормозному воздействию атмосферы, на более высоких орбитах теряется чувствительность к амплитудам гармоник гравитационного поля Земли. Основная измеряемая величина в космической группировке – это межспутниковое расстояние. Необходимую точность его измерения обеспечивает лазерная система активного типа (ЛИС). Требуемая точность измерения межспутниковых расстояний на уровне 30 нм/Гц^1/2 приводит к требованию точности наведения порядка 1″–3″. Указанная величина точности соответствует уровню современных серийно выпускаемых звездных датчиков.

При движении КА на низких (400 км и ниже) геоцентрических орбитах необходимы компенсация негравитационных сил, действующих на КА, и контроль высоты. Автоматическая компенсация негравитационных ускорений (компенсация “сноса”) КА во время его движения по орбите приводит к значительным улучшениям траектории движения КА, приближая ее к так называемой “геодезической траектории”. В этой связи в будущих гравитационных миссиях система “компенсации сноса” будет обязательной частью состава служебных систем. В продолжение миссии GRACE 22 мая 2018 г. состоялся запуск двух спутников-близнецов GRACE Follow On (GRACE FO) [7]. Основная цель данной миссии – это обеспечение поступления данных для ежемесячных глобальных моделей гравитационного поля Земли высокого разрешения, начатых в миссии GRACE, т.е. мониторинг медленных временных вариаций гравитационного поля Земли. Два спутника GRACE FO находятся на той же орбите высотой 490 км (период обращения 90 мин) на расстоянии порядка 220 км друг от друга и используют ту же систему микроволновой связи $K$-диапазона, что и GRACE. Следовательно, ожидается тот же микронный уровень точности измерения межспутникового расстояния. Важно отметить принципиальный момент: спутники дополнительно оснащены лазерной интерферометрической системой, которая позволит поднять точность измерений на нанометровый уровень. Ожидаемая среднеквадратическая ошибка лазерных измерений 80 нм/Гц^1/2 в диапазоне частот 0.2–100 мГц.

Лазерная интерферометрическая система была создана коллаборацией двух организаций: JPL NASA (США) и Max Planck Institute for Gravitational Physics (Германия). Лазерная система была включена спустя три недели после запуска, и “первый свет” был получен практически с первой попытки. ЛИС приступила к выполнению научной фазы программы. Первые данные обработки лазерных измерений показали беспрецедентную точность: 100 пм/Гц^1/2 (пм – пикометр) на частоте порядка 1 мГц, а также хорошее согласие с данными основной измерительной системы микроволнового диапазона.

12 июня 2019 г. были опубликованы результаты анализа данных GRACE FO, так называемый продукт 2-го уровня. Этот первый выпуск продукта включает в себя девять ежемесячных моделей гравитационного поля Земли, построенных в трех центрах обработки данных (JPL, GFZ, CSR), а также соответствующие фоновые модели атмосферы и океана, охватывающие период с июня 2018 г. по апрель 2019 г. Последующие продукты 2-го уровня доступны на ежемесячной основе, начиная с июля 2019 г. В октябре 2019 г. состоялось рабочее совещание научных групп GRACE FO для обсуждения качества данных и результатов анализа.

В КНР в 2017 г. начала выполняться пятилетняя государственная программа “Precision gravity measurements”, в которой принимают участие ряд ведущих НИИ и ключевых университетов КНР. В рамках этой программы должна быть разработана миссия SAGM (Space Advanced Gravity Measurement), аналогичная GRACE: два космических аппарата на орбите вокруг Земли, оборудованные микроволновой системой измерения расстояния между спутниками. Запуск КА SAGM планируется на 2021–2022 гг.

В рамках проекта гравитационно-волнового детектора на околоземной орбите TianQin [8], который разрабатывается в КНР, предполагается в качестве второго этапа реализации проекта вывод на орбиту двух КА, связанных между собой оптической (лазерной) связью (космическая группировка типа GRACE FO). Предполагаемые параметры космической группировки следующие: высота полярной орбиты от 350 до 450 км, межспутниковое расстояние от 50 до 100 км. Точность измерения расстояния лазерной системой составит величину порядка 20 нм/Гц^1/2. Низкая орбита космической группировки предполагает использование системы компенсации инерциальных возмущений (технология “drag free”, т.е. “система, свободная от сноса”) на уровне порядка ${{10}^{{ - 12}}}$ м/с²/Гц^1/2. Ориентировочное время запуска: 2023–2024 гг.

Космические гравитационные группировки, состоящие из пары спутников, находящихся на одинаковых орбитах (GRACE, GRACE FO, GRAIL), имеют один существенный недостаток, связанный с ограничениями пространственно-временного разрешения моделей гравитационного поля Земли, которые создаются по данным гравитационной миссии.

Пространственное разрешение связано обратно пропорциональным отношением с временным разрешением. Чем лучше пространственное разрешение, тем хуже временное, и наоборот. Если мы имеем достаточное пространственное разрешение данных на временном интервале в один месяц (т.е. за месячный “период замыкания” орбит спутник покрывает треками поверхность Земли достаточно часто), то на более коротких интервалах (т.е. временное разрешение лучше) покрытие треками более редкое, т.е. угловое разрешение хуже.

Чтобы одновременно улучшить как угловое (пространственное), так и временное разрешение, необходимо рассматривать более сложные конфигурации спутников [9, 10]. Решением этой проблемы может быть мультипарная конфигурация, которая позволяет одновременно покрывать треками существенно разные участки поверхности Земли. Например, использование двух пар спутников, находящихся на разных орбитах, может существенно улучшить пространственное и временное разрешения. Основная задача таких конфигураций – обеспечить более равномерное покрытие на различных широтах и большую изотропность измерений, что в конечном итоге обеспечит более высокую точность гравитационных моделей Земли.

Для повышения точности пространственно-временного разрешения были предложены несколько типов расположения КА, основанных на конфигурации типа GRACE: все пары спутников, входящих в космическую группировку, имеют одинаковую орбитальную высоту и, следовательно, примерно одинаковые орбитальные периоды. Одна из таких конфигураций состоит из двух пар спутников типа GRACE, но имеет временной сдвиг относительно друг друга. Другими словами, две пары имеют одинаковое пространственное разрешение, но совершают движение по орбитам со сдвигом во времени, таким образом, проходя определенную широту в разные моменты времени. Максимальное расстояние между наземными треками в одни сутки составляет около 2600 км, что достигается для разности средних аномалий порядка $\pi $. Таким образом, космическая группировка состоит из двух пар спутников, каждая пара имеет одинаковые орбитальные элементы, но разные средние аномалии ($\Delta M = 180^\circ $).

Наиболее обсуждаемая конфигурация состоит из двух коллинеарных пар спутников, расположенных по типу GRACE: одна пара спутников находится на полярной орбите, а другая – на наклонной. Идея такой конфигурации впервые была предложена в работе [11] и получила название BENDER. Относительно наклонения второй орбиты имеются различные рекомендации, от величины порядка 63° до 75°. Обе пары спутников измеряют межспутниковые расстояния вдоль траектории полета (вдоль треков). Сочетание орбит с различным наклоном позволяет добиться более равномерного распределения плотности треков на различных широтах и большей изотропности измерений. Было выполнено численное моделирование гравитационного поля Земли для мультипарной конфигурации BENDER. Предполагалось, что спутники в конфигурации имеют на борту ЛИС и систему компенсации сноса. Результаты моделирования показали, что использование мультипарной конфигурации эффективно подавляет широтную зависимость ошибок моделей геофизических параметров Земли (ГПЗ) и приводит к однородному их распределению по поверхности Земли [12]. Мультипарные конфигурации позволяют повысить точность месячных моделей ГПЗ на два порядка по сравнению с GRACE, а также создавать модели ГПЗ на коротких временных интервалах с достаточным пространственным разрешением.

Точность измерения межспутникового расстояния в миссии GRACE FO приводит к необходимости учитывать релятивистские эффекты в наборах выходных данных ЛИС. Для релятивистской редукции данных наблюдений космических миссий типа GRACE FO был разработан аппарат, учитывающий влияние квадрупольного момента гравитационного поля Земли, влияние приливных сил планет Солнечной системы, а также влияние вращательных компонентов метрики на распространение света [13, 14]. В мультипарных группировках будущих гравитационных миссий, по данным которых будут строиться модели ГПЗ с существенно более высокой точностью, необходимо учитывать релятивистские эффекты следующего порядка малости.

Вариация межспутникового расстояния измеряется лучами света, при этом расстояние определяется как время света в пути между спутниками, деленное на скорость света. Время в пути отягощено задержками, связанными с релятивистскими эффектами. При распространении света в поле тяжести, время в пути зависит от величины этого поля. Для того, чтобы эффекты задержки не искажали измерения, необходимо учесть их влияние и провести редукцию измерений за этот эффект. Целью данной работы являются анализ гармоник гравитационного поля высокого порядка и их влияние на распространение лазерного луча между космическими аппаратами на околоземной орбите, а также вывод формул для редукции релятивистских эффектов.

2. МЕТРИЧЕСКИЙ ТЕНЗОР В ПРИБЛИЖЕНИИ СЛАБОГО ПОЛЯ

В статьях [13, 14] была построена теория релятивистских редукций для КА типа GRACE FO. Точность расчетов редукционных формул соответствовала точности измерений 1 нм. При этом было выяснено, что при редукциях необходимо принимать во внимание лишь несколько эффектов, связанных с гравитационным полем.

В космических миссиях следующего поколения точность измерений вырастет на несколько порядков и может достигнуть 1 пм. При повышении точности измерений на три порядка величины возникает много новых эффектов, которые необходимо принимать во внимание.

Оценим следующим образом точность, с которой необходимо проводить редукционные вычисления. Точность измерения межспутникового расстояния, деленная на расстояние между спутниками, есть хорошая оценка точности редукционных измерений. Для GRACE FO расстояния между спутниками составляет 270 км, точность измерений 1 нм; для спутников Луны GRAIL расстояние между КА 200 км, а точность измерения расстояния есть 1 мкм. Расстояние между КА NGSM будет порядка 100 км, а точность измерения расстояния будет 1 пм. Данные по разным космическим экспериментам приведены в табл. 1.

Таблица 1.

Оценка точности редукционных формул для различных космических миссий

Название КА	Расстояние между КА, км	Точность
GRACE-FO	270	$4 \times {{10}^{{ - 15}}}$
GRAIL	200	$5 \times {{10}^{{ - 12}}}$
NGSM	100	$1 \times {{10}^{{ - 17}}}$

Далее, в табл. 2 приведено несколько эффектов, которые надо принимать во внимание при построении редукционных формул. Так, если для GRAIL и GRACE FO нужно было принимать во внимание лишь монопольный и квадрупольный член гравитационного поля соответственно, то для космических миссий следующего поколения необходимо принимать во внимание несколько других эффектов, вполне возможно, включая квадратичные добавки по метрике.

Таблица 2.

Релятивистские поправки по порядку величины для околоземного пространства

Эффект	Порядок величины	Неопределенность
Гравитационный потенциал Земли (монопольная часть)	$\sim {\kern 1pt} 7 \times {{10}^{{ - 10}}}$	$ < {\kern 1pt} {{10}^{{ - 17}}}$
Центробежный потенциал ${{{v}}^{2}}{\text{/}}(2{{c}^{2}})$	$\sim {\kern 1pt} {{10}^{{ - 12}}}$	$ < {\kern 1pt} {{10}^{{ - 18}}}$
Гравитационный потенциал Земли (квадрупольная часть)	$\sim {\kern 1pt} 8 \times {{10}^{{ - 13}}}$	$ < {\kern 1pt} {{10}^{{ - 18}}}$
Гравитационный потенциал Земли (октупольная часть и выше)	$\sim {\kern 1pt} {{10}^{{ - 15}}}$	$ < {\kern 1pt} {{10}^{{ - 18}}}$
Вулканическая и сейсмическая активность	$\sim {\kern 1pt} {{10}^{{ - 16}}}$	?
Суммарное влияние внешних тел	$\sim {\kern 1pt} 2 \times {{10}^{{ - 17}}}$	$ < {\kern 1pt} {{10}^{{ - 18}}}$
Приливы коры Земли, океанские приливы	$\sim {\kern 1pt} {{10}^{{ - 18}}}$	$ < {\kern 1pt} {{10}^{{ - 18}}}$
Поправки порядка $O({{c}^{{ - 4}}})$	$\sim {\kern 1pt} {{10}^{{ - 18}}}$	$ < {\kern 1pt} {{10}^{{ - 18}}}$

В качестве ньютоновского потенциала гравитационного поля будем рассматривать разложение потенциала по сферическим функциям. Будут вычислены формулы для редукции только квадрупольной гармоники такого потенциала.

В этой статье используются обозначения, принятые в книге [15], а именно: буквы латинского алфавита $m$, $n,...$ ∈ $\{ 0,1,2,3\} $ обозначают индексы пространства-времени. Буквы греческого алфавита $\alpha $, $\beta ,...$ ∈ $\{ 1,2,3\} $ обозначают только пространственные индексы. Метрика ${{g}_{{mn}}}$ обозначает полный метрический тензор четырехмерного пространства-времени. Метрика ${{\gamma }_{{mn}}}$ принимается для обозначения пространства-времени Минковского:

${{\gamma }_{{mn}}} = {\text{diag}}( + 1, - 1, - 1, - 1).$

Будем разлагать метрику пространства-времени по степеням гравитационной постоянной $G$ и по обратным степеням скорости света $c$.

Приближенная метрика имеет вид суммы тензора Минковского и малых поправок:

${{g}_{{mn}}} = {{\gamma }_{{mn}}} + {{h}_{{mn}}}.$

Рассмотрим приближенный метод решения задачи о прохождении электромагнитной волны через медленно меняющееся гравитационное поле. Масштаб изменений этого поля значительно больше длины электромагнитной волны $\lambda $. При этом рассеяние назад или на большие углы пренебрежимо мало.

Флуктуации волнового поля определяются преимущественно теми неоднородностями гравитационного поля, которые лежат на пути волны, то есть в окрестности луча, который соединяет источник и наблюдателя. В указанном случае говорят о распространении волны в гравитационном поле с крупномасштабными неоднородностями. Существует несколько основных приближенных методов, используемых для решения таких задач. Рассмотрим только один из них: метод геометрической оптики.

Кратко напомним вывод уравнения геометрической оптики для простейшего случая монохроматической электромагнитной волны, которая распространяется в гравитационном поле с неподвижными или медленно движущимися неоднородностями.

Уравнения поля можно записать в виде

$A_{{m;n}}^{{;n}} + R_{m}^{n}{{A}_{n}} = 0.$

Здесь калибровка выбрана в виде

$A_{n}^{{;n}} = 0.$

В этих условиях можно полагать, что

$\lambda \;\triangledown \;h \ll 1.$

Кроме того, естественно предположить, что поле в каждой точке приближенно имеет структуру плоской волны

${{A}_{n}}({{x}^{a}}) = {{A}_{{n0}}}exp(iS({{x}^{a}})),$

где амплитуда ${{A}_{{n0}}}$ и эйконал $S({{x}^{a}})$ меняются медленно в масштабах длины волны $\lambda $. Воспользуемся малостью изменения амплитуды и эйконала. Тогда, следуя работам Дебая, нетрудно получить уравнение для $A$ и $S$. Разложим амплитуду в ряд по длине волны $\lambda $:

(1)

${{A}_{n}}({{x}^{a}}) = ({{A}_{{n0}}} - i\lambda {{A}_{{n1}}} - {{\lambda }^{2}}{{A}_{{n2}}} + ...).$

Коэффициент ${{A}_{{ni}}}$ в этом разложении в общем случае есть комплексное число. Вообще говоря, это число дает вклад в фазу результирующего электромагнитного поля. Подставив ряд (1) в уравнения поля и приравнивая члены при одинаковых степенях $\lambda $, получим систему уравнений для коэффициентов ${{A}_{{n0}}}$, ${{A}_{{n1}}}$, ${{A}_{{n2}}}$:

(2)

${{g}^{{mn}}}\frac{{\partial S}}{{\partial {{x}^{m}}}}\frac{{\partial S}}{{\partial {{x}^{n}}}} = 0,$

(3)

${{g}^{{mn}}}\frac{{\partial S}}{{\partial {{x}^{m}}}}\frac{{\partial {{A}_{{a0}}}}}{{\partial {{x}^{n}}}} + {{A}_{{a0}}}{{g}^{{mn}}}\left( {\frac{{{{\partial }^{2}}S}}{{\partial {{x}^{m}}\partial {{x}^{n}}}} - \Gamma _{{mn}}^{b}\frac{{\partial S}}{{\partial {{x}^{b}}}}} \right) = 0.$

Здесь (2) – уравнение эйконала, а (3) – уравнение переноса для амплитуд.

Будем анализировать только уравнение (2) для функции $S$. Оно определяет фазу электромагнитной волны и траекторию луча света. Уравнение (3) для амплитуды не представляет интереса, поскольку изменение амплитуды (или изменение потока света) представляет собой сумму постоянного члена (нулевого приближения) и переменного члена первого порядка по возмущениям метрики. Если возмущения фазы электромагнитной волны в гравитационном поле являются заметными величинами, которые легко измерить на современном технологическом уровне, то изменение амплитуды измерить практически невозможно.

Важно отметить, что приведенный метод является универсальным. Несмотря на то что он применяется для вычисления расстояния между спутниками, этот метод также приложим для вычисления расстояния между наземным телескопом и рефлектором на Луне, а также для вычисления расстояния между наземным телескопом и рефлектором на спутнике.

Конкретный вид метрического тензора, с которым нам предстоит работать ниже [13, 16], рассмотрим в рамках метрики слабого поля. Последняя представляется в виде стандартного постньютоновского разложения и реализует геоцентрическую систему координат (GCRF). Данная система координат не вращается и имеет начало отсчета в центре масс Земли. Соответствующая метрика в первом постньютоновском приближении имеет вид [13, 17–19]:

${{g}_{{00}}} = 1 - \frac{2}{{{{c}^{2}}}}{{w}_{{\text{E}}}} + \frac{2}{{{{c}^{4}}}}w_{{\text{E}}}^{2} + O({{c}^{{ - 6}}}),$

(4)

${{g}_{{0\alpha }}} = - {{\gamma }_{{\alpha \lambda }}}\frac{4}{{{{c}^{3}}}}w_{{\text{E}}}^{\lambda } + O({{c}^{{ - 5}}}),$

${{g}_{{\alpha \beta }}} = {{\gamma }_{{\alpha \beta }}} + {{\gamma }_{{\alpha \beta }}}\frac{2}{{{{c}^{2}}}}{{w}_{{\text{E}}}} + O({{c}^{{ - 4}}}).$

Здесь $w_{{\text{E}}}^{\lambda }$ – релятивистский векторный потенциал, отвечающий за вклад в гравитационное поле от вращения Земли (а также внешних по отношению к Земле тел, но в данном приближении вклад внешних тел крайне мал и им пренебрегаем).

Скалярный потенциал

${{w}_{{\text{E}}}} = U + u_{{\text{E}}}^{{{\text{tidal}}}} + O({{c}^{{ - 3}}})$

есть линейная суперпозиция гравитационного потенциала $U$ изолированной Земли и внешнего “приливного” потенциала $u_{{\text{E}}}^{{{\text{tidal}}}}$, создаваемого остальными телами Солнечной системы. Мультипольное разложение всех этих потенциалов будет приведено ниже при оценивании вклада соответствующих членов в фазу. Для решения уравнения эйконала необходимо знать компоненты $h_{1}^{{mn}}$, линейные по $G$ поправки к плоской метрике.

Из метрики (4) получаем

(5)

$\begin{gathered} h_{1}^{{00}} = \frac{2}{{{{c}^{2}}}}{{w}_{{\text{E}}}}, \\ h_{1}^{{0\alpha }} = \frac{4}{{{{c}^{3}}}}w_{{\text{E}}}^{\alpha }, \\ h_{1}^{{\alpha \beta }} = - \frac{2}{{{{c}^{2}}}}{{\gamma }^{{\alpha \beta }}}{{w}_{{\text{E}}}}. \\ \end{gathered} $

Решения уравнений для распространения луча в метрике (4) были получены в [13, 14]. В этих работах учитывались влияние квадрупольного момента гравитационного поля Земли, влияние приливных сил со стороны планет Солнечной системы, а также влияние вращательных компонентов метрики на распространение света. Для заданной точности измерения межспутниковых расстояний порядка 1 нм этого было достаточно.

Отметим, что важность релятивистских редукций была осознана уже в 1981 г. [20] при анализе каталогов гамма-источников. Сейчас редукционные формулы общей теории относительности являются необходимыми как в высокоточной навигации (см., напр., [21]), так и в высокоточных наблюдениях в астрометрии и астрофизике [22].

В будущих экспериментах точность измерений вырастет, и проведенного анализа уже будет недостаточно. В этой работе проведен анализ вклада членов гравитационного поля высоких порядков и их влияния на распространение света.

Следует отметить, что поправки $h_{2}^{{mn}}$ не могут быть получены из метрики (4), эта проблема будет решена в последующих работах.

3. ГРАВИТАЦИОННЫЙ ПОТЕНЦИАЛ ЗЕМЛИ

В связи с перспективой повышения точности в измерении расстояния между спутниками будущих миссий вплоть до ${{10}^{{ - 12}}}$ м возникает вопрос, какой порядок сферических гармоник следует учитывать в разложении гравитационного потенциала. Для решения этой проблемы будем работать с разложением земного потенциала по сферическим гармоникам в виде

(6)

$\begin{gathered} U = \frac{{GM}}{r}\sum\limits_{n = 0}^\infty \,\sum\limits_{m = 0}^n \,\mathop {\left( {\frac{{{{R}_{E}}}}{r}} \right)}\nolimits^n ({{C}_{{nm}}}cosm\varphi + \\ + \;{{S}_{{nm}}}sinm\varphi ){{{\bar {P}}}_{{nm}}}(cos\theta ), \\ \end{gathered} $

где $M$, ${{R}_{E}}$ – масса и радиус Земли соответственно, координаты точки даются стандартным набором сферических координат $(r,\theta ,\varphi )$, а ${{\bar {P}}_{{nm}}}$ обозначают нормализованные присоединенные полиномы Лежандра. Обычные присоединенные полиномы ${{P}_{{nm}}}$ определяются через производные от классических полиномов Лежандра ${{P}_{n}}$ как

${{P}_{{nm}}}(x) = {{(1 - {{x}^{2}})}^{{0.5m}}}\frac{{{{d}^{m}}}}{{d{{x}^{m}}}}{{P}_{n}}(x).$

Обращаем внимание на отсутствие в этом определении множителя ${{( - 1)}^{m}}$, называемого фазой Кондона-Шортли, что является обычной практикой в геодезии. Нормализованные присоединенные полиномы Лежандра ${{\bar {P}}_{{nm}}}$ вычисляются по правилу [23]

${{\bar {P}}_{{nm}}}(x) = \sqrt {{{K}_{m}}(2n + 1)\frac{{(n - m)!}}{{(n + m)!}}} {{P}_{{nm}}}(x)$

с множителем ${{K}_{m}} = 1$ при $m = 0$ и ${{K}_{m}} = 2$ при $m \ne 0$. Коэффициенты ${{C}_{{nm}}}$ и ${{S}_{{nm}}}$ в (6) носят название нормализованных гармоник; они вычислены и затабулированы для многочисленных моделей гравитационного поля Земли. Различия в численных значениях гармоник в современных моделях находятся за пределами точности рассматриваемой нами задачи, и для анализа поправки к фазе луча света выбрана модель GGM05C, содержащая гармоники по n = 360 и датированная 2015 годом [24]¹ ¹.

Поскольку в дальнейшем будем вычислять изменение фазы вдоль прямого пути, что проще делать в декартовых координатах, преобразуем нормализованные гармоники к виду однородных гармонических полиномов, которые являются функциями декартовых координат [25].

На первом этапе преобразований выразим нормированные функции в виде сферических гармоник согласно уравнениям:

$\begin{gathered} cosm\varphi {{{\bar {P}}}_{{nm}}}(cos\theta ) = \sqrt {{{K}_{m}}\pi } ({{Y}_{{nm}}}(\theta ,\varphi ) + Y_{{nm}}^{*}(\theta ,\varphi )), \\ sinm\varphi {{{\bar {P}}}_{{nm}}}(cos\theta ) = - i\sqrt {{{K}_{m}}\pi } ({{Y}_{{nm}}}(\theta ,\varphi ) - Y_{{nm}}^{*}(\theta ,\varphi )). \\ \end{gathered} $

Здесь ${{Y}_{{nm}}}(\theta ,\varphi )$ – обычные ортонормированные сферические функции, а индексы $n$, $m$ обозначают номер гармоники. Звездочка сверху функции означает комплексное сопряжение. Шаровые однородные сферические полиномы ${{u}_{{nm}}}\left( {x,y,z} \right)$ выражаются через сферические функции как

(7)

$\begin{gathered} {{u}_{{nm}}}(x,y,z) = {{r}^{n}}{{Y}_{{nm}}}(\theta ,\varphi ), \\ x = rsin\theta cos\varphi , \\ y = rsin\theta sin\varphi , \\ z = rcos\theta . \\ \end{gathered} $

Шаровые полиномы выражаются через декартовы координаты как

(8)

$\begin{gathered} {{u}_{{nm}}}(x,y,z) = \\ = {{B}_{{nm}}}\,\int\limits_0^{2\pi } exp( - im\xi )\mathop {\left( {z + ixsin\xi + iycos\xi } \right)}\nolimits^n d\xi , \\ {{B}_{{nm}}} = \frac{1}{{4\pi }}\frac{1}{{n!}}\sqrt {\frac{{2n + 1}}{\pi }(n - m)!(n + m)!} . \\ \end{gathered} $

Отметим, что размерность шаровых полиномов есть ${{u}_{{nm}}}(x,y,z)\sim {{r}^{n}}$. Будем использовать вид (8) для вычисления вариации эйконала или фазы.

Разложение гравитационного потенциала по рядам сферических функций заменим на разложение по ортогональным шаровым полиномам. Кроме того, для удобства вычислений введем новое обозначение ${{U}_{n}}$, которое имеет вид:

(9)

$\begin{gathered} {{U}_{n}} = \sum\limits_{m = 0}^n \,\left( {\frac{{R_{E}^{n}}}{{{{r}^{{2n + 1}}}}}} \right)\sqrt {{{K}_{m}}\pi } \text{[}({{C}_{{nm}}} - i{{S}_{{nm}}}){{u}_{{nm}}}(x,y,z) + \\ + \;({{C}_{{nm}}} + i{{S}_{{nm}}})u_{{nm}}^{*}(x,y,z)]. \\ \end{gathered} $

Тогда разложение гравитационного потенциала будет иметь вид:

(10)

$U = GM\,\sum\limits_{n = 0}^\infty \,{{U}_{n}}(x,y,z).$

При вычислении вариации эйконала будем работать с функциями ${{U}_{n}}$, а затем подставлять их в ряд (10) для вычисления вариации эйконала.

Сделаем еще одно упрощение для удобства дальнейшей работы с функциями ${{U}_{n}}$ и вычисления вариации оптического пути. Введем обозначения:

(11)

$\begin{gathered} {{Q}_{{nm}}} = {{B}_{{nm}}}\left( {{{C}_{{nm}}} - i{{S}_{{nm}}}} \right), \\ Q_{{nm}}^{*} = {{B}_{{nm}}}\left( {{{C}_{{nm}}} + i{{S}_{{nm}}}} \right). \\ \end{gathered} $

Теперь используем формулу (8) и получим выражение:

(12)

$\begin{gathered} {{U}_{n}} = \sum\limits_{m = 0}^n \,\left( {\frac{{R_{E}^{n}}}{{{{r}^{{2n + 1}}}}}} \right)\sqrt {{{K}_{m}}\pi } \times \\ \times \;\int\limits_0^{2\pi } \,d\xi [{{Q}_{{nm}}}exp( - im\xi ){{(z + ixsin\xi + iycos\xi )}^{n}} + \\ + \;Q_{{nm}}^{*}exp( + im\xi ){{(z - ixsin\xi - iycos\xi )}^{n}}]. \\ \end{gathered} $

Далее вычислим вариации оптического пути, используя (12) как основную формулу для описания зависимости гравитационного потенциала от координат.

4. ВЫЧИСЛЕНИЕ ОПТИЧЕСКОГО ПУТИ

Уравнения, которые описывают движение лучей света в слабом гравитационном поле, выводились неоднократно. В частности, для ситуации двух спутников на орбите эти уравнения подробно обсуждены в [13, 17, 19]. Обсудим эти уравнения лишь для того, чтобы в дальнейшем ссылаться на них.

Рассмотрим эйконал $S$ электромагнитной волны, который является скаляром и в приближении геометрической оптики удовлетворяет уравнению эйконала

${{g}^{{mn}}}{{S}_{{,m}}}{{S}_{{,n}}} = 0,$

здесь и далее индекс после запятой обозначает частную производную по соответствующей координате. В плоском пространстве волна распространяется прямолинейно, и эйконал линейно зависит от пространственных координат вдоль луча, оставаясь при этом фиксированным в любой движущейся вместе с волной точке волнового фронта. Введем постоянный вектор ${{K}^{m}}$, который направлен вдоль невозмущенной прямолинейной траектории луча и является нулевым, т.е. его компоненты удовлетворяют условию

${{\gamma }_{{mn}}}{{K}^{m}}{{K}^{n}} = 0.$

Удобно представить компоненты этого нулевого вектора как

(13)

(14)

где ${{k}_{0}} = \omega {\text{/}}c$, и $\omega $ есть постоянная угловая частота невозмущенной волны. Трехмерный единичный (относительно плоской метрики) вектор ${\mathbf{k}}$ имеет компоненты ${{k}^{\alpha }}$ и является касательным к пространственной проекции невозмущенной мировой линии сигнала. Для удобства обозначений не будем делать различий между верхним и нижним индексами компонентов этого вектора, т.е. по определению полагаем ${{k}^{\alpha }} = {{k}_{\alpha }}$, но в формулах будем помещать индексы в позициях, согласующихся со стандартным правилом суммирования Эйнштейна.

Вдоль мировой линии сигнала введем аффинный параметр $l$, что позволяет записать пространственную часть траектории в виде уравнения прямой линии с направляющим вектором ${\mathbf{k}}$.

$\{ {{x}^{m}}\} \equiv ({{x}^{0}} = l,{\mathbf{x}}(l) = {{{\mathbf{x}}}_{0}} + {\mathbf{k}}l + O({{G}^{2}})),$

при этом будем полагать, что в момент ${{t}_{0}}$ выхода луча от первого спутника, который находится в точке ${{{\mathbf{r}}}_{0}}$, значение аффинного параметра равно нулю.

Вернемся к рассмотрению эйконала или фазы. Так как сигнал распространяется в искривленном пространстве, то к нулевому невозмущенному приближению необходимо добавить возмущения. Поправку к фазе первого порядка по степени гравитационной постоянной $G$ обозначим как ${{\varphi }_{1}}$, решение для нее было исследовано в [13]. В нашей работе вычислим вариации фазы только от сферических гармоник ньютоновского потенциала. Таким образом, запишем разложение фазы вдоль луча в виде

$\begin{gathered} \varphi (t,{\mathbf{x}}) = {{\varphi }_{0}} + {{k}_{0}}(c(t - {{t}_{0}}) - {\mathbf{k}}({\mathbf{r}} - {{{\mathbf{r}}}_{0}})) + \\ + \;{{\varphi }_{1}}(t,{\mathbf{r}}) + \mathcal{O}({{G}^{2}}). \\ \end{gathered} $

Аналогично метрику представляем как сумму плоской метрики Минковского и возмущений первого порядка по $G$, соответственно $h_{1}^{{mn}}$ (их явный вид будет конкретизирован позже):

${{g}^{{mn}}} = {{\gamma }^{{mn}}} + h_{1}^{{mn}} + \mathcal{O}({{G}^{2}}).$

С учетом разложений метрики и фазы уравнение эйконала (4) дает уравнение для возмущений первого порядка в виде

$2{{K}^{m}}{{\varphi }_{{1,m}}} + {{K}_{m}}{{K}_{n}}h_{1}^{{mn}} = \mathcal{O}({{G}^{2}}).$

Так как нас интересует фаза на луче, то от частных производных удобно перейти к полным производным по времени; для возмущения фазы получаем

${{K}^{m}}{{\varphi }_{{1,m}}} = {{k}_{0}}\frac{{d{{\varphi }_{1}}}}{{dl}} + \mathcal{O}({{G}^{2}}),$

так что (15) переходит в

$2{{k}_{0}}\frac{{d{{\varphi }_{1}}}}{{dl}} + {{K}_{m}}{{K}_{n}}h_{1}^{{mn}} = \mathcal{O}({{G}^{2}}).$

Получаем вдоль невозмущенной прямолинейной траектории сигнала:

(15)

$\begin{gathered} {{\varphi }_{1}}(t,{\mathbf{r}}) = {{\varphi }_{1}}(t,{{{\mathbf{r}}}_{0}} + {\mathbf{k}}l) + \mathcal{O}({{G}^{2}}), \\ h_{1}^{{mn}}(t,{\mathbf{r}}) = h_{1}^{{mn}}(t,{{{\mathbf{r}}}_{0}} + {\mathbf{k}}l) + \mathcal{O}({{G}^{2}}). \\ \end{gathered} $

Далее под функциями $\varphi $ и ${{h}^{{mn}}}$ будем понимать функции в точках на невозмущенной траектории, как в правых частях (15), и для сокращения записи не будем указывать эту зависимость в уравнениях. Теперь получаем уравнения для линейной поправки к фазе:

(16)

$\frac{{d{{\varphi }_{1}}}}{{dl}} = - \frac{1}{{2{{k}_{0}}}}{{K}_{m}}{{K}_{n}}h_{1}^{{mn}}.$

В следующих разделах будут найдены решения этих уравнений и оценен их вклад в определение расстояния между спутниками: из (15) видно, что если значение поправки к фазе равно ${{\varphi }_{1}}$, то этому соответствует вклад в расстояние $\delta R = - {{\varphi }_{1}}{\text{/}}{{k}_{0}}$.

Далее везде будем вычислять вклад в расстояние между спутниками, называя этот вклад вариациями оптического пути.

Уравнение для изменения оптического пути вдоль траектории есть:

(17)

$\frac{{dR}}{{dl}} = \frac{1}{2}{{k}_{m}}{{k}_{n}}h_{1}^{{mn}}.$

5. РЕШЕНИЕ ДЛЯ ПОПРАВОК ПЕРВОГО ПОРЯДКА К ФАЗЕ

До сих пор наши рассуждения обладали некой общностью в том смысле, что оказывались применимы к физической ситуации достаточно слабого гравитационного поля, точнее, для случаев достаточно хорошей сходимости постминковского разложения полей на поправки с возрастающими степенями гравитационной постоянной $G$. Так как основной целью данной работы является описание ситуации околоземного гравитационного эксперимента, то можно конкретизировать вид метрического тензора; из всей совокупности членов, входящих в метрический тензор, оставим только гравитационный потенциал Земли в виде разложения по сферическим гармоникам.

Тогда вариации оптического пути из-за действия гравитационного поля есть:

(18)

$R = \frac{{{{r}_{g}}}}{2}\sum\limits_{n = 0}^\infty \,\int\limits_0^L \,{{U}_{n}}(l)dl,$

здесь ${{r}_{g}} = 2G{{M}_{E}}{\text{/}}{{c}^{2}}$, $L$ – расстояние между спутниками.

Введем обозначение:

${{R}_{n}} = \int\limits_0^L \,{{U}_{n}}(l)dl.$

Теперь выразим вариации оптического пути в виде ряда разложения по ортогональным шаровым полиномам, при этом поменяем порядок интегрирования по $\xi $ и $t$:

(19)

$\begin{gathered} {{R}_{n}} = \sum\limits_{m = 0}^n \,R_{E}^{n}\sqrt {{{K}_{m}}\pi } \int\limits_0^{2\pi } \,d\xi \left\{ {{{Q}_{{nm}}}exp( - im\xi )\;{{ \times }^{{^{{^{{^{{^{{}}}}}}}}}}}} \right. \\ \left. { \times \;\int\limits_0^L \,dl\frac{{{{{(z(l) + ix(l)sin\xi + iy(l)cos\xi )}}^{n}}}}{{{{r}^{{2n + 1}}}}} + H.C.} \right\}. \\ \end{gathered} $

Здесь обозначение $H.C.$ означает комплексное сопряжение.

Введем дополнительные обозначения:

$\begin{gathered} a = {{k}_{3}} + i{{k}_{1}}sin\xi + i{{k}_{2}}cos\xi , \\ \alpha = ({\mathbf{k}}{{{\mathbf{r}}}_{0}}), \\ \end{gathered} $

(20)

$\begin{gathered} b = {{z}_{0}} + i{{x}_{0}}sin\xi + i{{y}_{0}}cos\xi , \\ {{b}_{1}} = b - a\alpha , \\ \end{gathered} $

$\begin{gathered} {{l}_{1}} = l + \alpha , \\ f = \sqrt {r_{0}^{2} - {{\alpha }^{2}}} . \\ \end{gathered} $

Тогда

(21)

$\begin{gathered} z(l) + ix(l)sin\xi + iy(l)cos\xi = a{{l}_{1}} + b \\ r = \sqrt {l_{1}^{2} + {{f}^{2}}} . \\ \end{gathered} $

Кроме того, аффинный параметр теперь меняется в пределах ${{l}_{1}} \in \{ \alpha ,L + \alpha \} $. Теперь интеграл по аффинному параметру сводится к виду:

(22)

${{I}_{n}} = \int\limits_\alpha ^{L + \alpha } dl\frac{{{{{(al + b)}}^{n}}}}{{{{r}^{{2n + 1}}}}}.$

Это табличный интеграл, который берется аналитически. Общий вид выражается в виде гипергеометрической функции Аппеля ${{F}_{1}}(\alpha ;\beta ,\gamma ;\delta ;x,y)$ двух переменных x, y.

${{I}_{n}} = \frac{1}{{a(n + 1)}}\frac{{{{{(al + b)}}^{{n + 1}}}}}{{({{l}^{2}} + {{f}^{2}})(n + 1{\text{/}}2)}} \times $

(23)

$ \times \;\mathop {\left( {\frac{{iaf - l}}{{iaf + b}}} \right)}\nolimits^{n + 1/2} \mathop {\left( {\frac{{iaf - l}}{{iaf + b}}} \right)}\nolimits^{n + 1/2} \times $

$ \times \;{{F}_{1}}\left( {n + 1;n + 1{\text{/}}2,n + 1{\text{/}}2;n + 2;\frac{{al + b}}{{b - iaf}},\frac{{al + b}}{{b + iaf}}} \right).$

Однако можно получить более компактное выражение [26]. Будем пользоваться выражением, представленным в [26] для нескольких мультиполей низкого порядка.

5.1. Вклад квадрупольного компонента

Проведем расчет вклада в вариацию оптического пути от квадрупольного компонента гравитационного потенциала. Для этого нам надо вычислить интеграл вида:

(24)

$\begin{gathered} {{I}_{2}} = \int\limits_\alpha ^{L + \alpha } \,dl\tfrac{{{{{(al + {{b}_{1}})}}^{2}}}}{{{{{({{l}^{2}} + {{f}^{2}})}}^{{5/2}}}}} = \\ = \mathop {\left. {\tfrac{{{{a}^{2}}{{f}^{2}}{{l}^{3}} - 2a{{b}_{1}}{{f}^{4}} + b_{1}^{2}l(3{{f}^{2}} + 2{{l}^{2}})}}{{3{{f}^{4}}\mathop {({{l}^{2}} + {{f}^{2}})}\nolimits^{3/2} }}} \right|}\nolimits_\alpha ^{L + \alpha } . \\ \end{gathered} $

Величина a является безразмерной, величина b₁ имеет размерность длины. Для обратного преобразования к сферическим функциям уравняем размерность, умножив величину $a$ на ${{r}_{0}}$, и получим выражение вида:

(25)

${{I}_{2}} = {{(a{{r}_{0}})}^{2}}{{J}_{1}} - 2(a{{r}_{0}})b{{J}_{2}} + {{b}^{2}}{{J}_{3}}.$

где

${{J}_{1}} = \left. {\frac{{{{f}^{2}}{{l}^{3}} + 2\alpha {{f}^{4}} + {{\alpha }^{2}}l(3{{f}^{2}} + 2{{l}^{2}})}}{{3r_{0}^{2}{{f}^{4}}{{{({{l}^{2}} + {{f}^{2}})}}^{{3/2}}}}}} \right|_{\alpha }^{{L + \alpha }},$

(26)

${{J}_{2}} = \left. {\frac{{{{f}^{4}} + \alpha l(3{{f}^{2}} + 2{{l}^{2}})}}{{3{{r}_{0}}{{f}^{4}}{{{({{l}^{2}} + {{f}^{2}})}}^{{3/2}}}}}} \right|_{\alpha }^{{L + \alpha }},$

${{J}_{3}} = \left. {\frac{{l(3{{f}^{2}} + 2{{l}^{2}})}}{{3{{f}^{4}}{{{({{l}^{2}} + {{f}^{2}})}}^{{3/2}}}}}} \right|_{\alpha }^{{L + \alpha }}.$

Для того, чтобы вычислить вариации оптического пути, нам осталось вычислить интеграл по переменной $\xi $ и выразить полученную формулу в виде сферических функций.

(27)

$\begin{gathered} \int\limits_0^{2\pi } \,d\xi exp( - im\xi ){{I}_{2}}{{J}_{1}}\int\limits_0^{2\pi } \,d\xi exp( - im\xi ){{(a{{r}_{0}})}^{2}} + \\ + \;{{J}_{2}}\int\limits_0^{2\pi } \,d\xi exp( - im\xi )(a{{r}_{0}})b + {{J}_{3}}\int\limits_0^{2\pi } \,d\xi exp( - im\xi ){{b}^{2}}, \\ \end{gathered} $

причем

(28)

${{B}_{{2m}}}\int\limits_0^{2\pi } \,d\xi exp( - im\xi ){{(a{{r}_{0}})}^{2}} = {{u}_{{2m}}}({{X}_{0}},{{Y}_{0}},{{Z}_{0}}),$

где

(29)

$\begin{gathered} {{X}_{0}} = {{k}_{1}}{{r}_{0}}, \\ {{Y}_{0}} = {{k}_{2}}{{r}_{0}}, \\ {{Z}_{0}} = {{k}_{3}}{{r}_{0}}, \\ \end{gathered} $

а ${{u}_{{nm}}}({{X}_{0}},{{Y}_{0}},{{Z}_{0}})$ – однородный полином, который выражается через сферическую функцию как:

(30)

${{u}_{{2m}}}({{X}_{0}},{{Y}_{0}},{{Z}_{0}}) = r_{0}^{2}{{Y}_{{2m}}}\left( {\Theta ,\Phi } \right),$

(31)

$\begin{gathered} \Theta = arccos{{k}_{3}}, \\ \Phi = arctan\frac{{{{k}_{2}}}}{{{{k}_{1}}}}. \\ \end{gathered} $

Соответственно интеграл по переменной $\xi $ от третьего члена в интеграле ${{I}_{2}}$ есть:

(32)

$\begin{gathered} {{B}_{{2m}}}\int\limits_0^{2\pi } \,d\xi exp( - im\xi ){{b}^{2}} = \\ = {{u}_{{2m}}}({{x}_{0}},{{y}_{0}},{{z}_{0}}) = r_{0}^{2}{{Y}_{{2m}}}\left( {\theta ,\phi } \right). \\ \end{gathered} $

Интеграл от второго члена в ${{I}_{2}}$ не сводится к сферическим функциям, однако он имеет простой вид:

${{j}_{{2m}}} = \int\limits_0^{2\pi } \,d\xi exp( - im\xi )(a{{r}_{0}})b = {{k}_{3}}{{r}_{0}}{{z}_{0}}\int\limits_0^{2\pi } \,\xi exp( - im\xi ) + $

$ + \;i({{k}_{1}}{{r}_{0}}{{z}_{0}} + {{k}_{3}}{{r}_{0}}{{x}_{0}})\int\limits_0^{2\pi } \,d\xi exp( - im\xi )sin\xi + $

(33)

$\begin{gathered} + \;i({{k}_{2}}{{r}_{0}}{{z}_{0}} + {{k}_{3}}{{r}_{0}}{{y}_{0}})\int\limits_0^{2\pi } \,d\xi exp( - im\xi )cos\xi - \\ - \;({{k}_{1}}{{r}_{0}}{{x}_{0}})\int\limits_0^{2\pi } \,d\xi exp( - im\xi )si{{n}^{2}}\xi - \\ \end{gathered} $

$ - \;({{k}_{2}}{{r}_{0}}{{y}_{0}})\int\limits_0^{2\pi } \,d\xi exp( - im\xi )co{{s}^{2}}\xi - $

$ - \;({{k}_{2}}{{r}_{0}}{{x}_{0}} + {{k}_{1}}{{r}_{0}}{{y}_{0}})\int\limits_0^{2\pi } \,d\xi exp( - im\xi )sin\xi cos\xi .$

Теперь приведем значения величин ${{j}_{{2m}}}$.

(34)

$\begin{gathered} {{j}_{{20}}} = 2\pi {{k}_{3}}{{r}_{0}}{{z}_{0}} - \pi {{k}_{1}}{{r}_{0}}{{x}_{0}} - \pi {{k}_{2}}{{r}_{0}}{{y}_{0}}, \\ {{j}_{{21}}} = \frac{{i\pi }}{4}\left( {{{k}_{2}}{{r}_{0}}{{z}_{0}} + {{k}_{3}}{{r}_{0}}{{y}_{0}}} \right) + \frac{\pi }{4}\left( {{{k}_{1}}{{r}_{0}}{{z}_{0}} + {{k}_{3}}{{r}_{0}}{{x}_{0}}} \right), \\ {{j}_{{22}}} = \frac{\pi }{8}\left( {{{k}_{1}}{{r}_{0}}{{x}_{0}} - {{k}_{2}}{{r}_{0}}{{y}_{0}}} \right) + \frac{{i\pi }}{8}\left( {{{k}_{1}}{{r}_{0}}{{y}_{0}} + {{k}_{2}}{{r}_{0}}{{x}_{0}}} \right). \\ \end{gathered} $

Приведем значение ${{R}_{2}}$ – длины оптического пути с учетом воздействия квадрупольного компонента гравитационного поля.

(35)

$\begin{gathered} {{R}_{2}} = \sum\limits_{m = 0}^2 \,R_{E}^{2}\sqrt {{{K}_{m}}\pi } \{ ({{C}_{{2m}}} - i{{S}_{{2m}}})[{{J}_{1}}{{u}_{{2m}}}({{X}_{0}},{{Y}_{0}},{{Z}_{0}}) + \\ + \;{{J}_{2}}{{B}_{{2m}}}{{j}_{{2m}}} + {{J}_{3}}r_{0}^{2}{{Y}_{{2m}}}\left( {\theta ,\phi } \right)] + H.C.\} . \\ \end{gathered} $

Вариации оптического пути, вызванные квадрупольным компонентом гравитационного поля, теперь есть:

(36)

$R = \frac{1}{2}{{r}_{g}}{{R}_{2}}.$

Не приводя громоздкие вычисления, укажем лишь, что основные величины, которые определяют величину оптического пути, есть

$({\mathbf{k}}{{{\mathbf{r}}}_{0}}){\text{/|}}{{{\mathbf{r}}}_{0}}{\text{|}},\;L.$

Для произвольной орбиты эта формула имеет довольно сложный вид, ограничимся ее вычислением для круговой орбиты. Расстояние между КА на круговых орбитах определяется формулой:

$L = 2{{r}_{0}}sin\frac{\varphi }{2}.$

Здесь $a$ – большая полуось орбиты, $\varphi $ – угол между КА, наблюдаемые из центра Земли. Проекция единичного вектора, соединяющего КА, на вектор первого КА есть:

$({\mathbf{k}}{{{\mathbf{r}}}_{0}}) = - \frac{L}{2}.$

Приведем окончательный вид коэффициентов ${{J}_{1}}$, ${{J}_{2}}$, ${{J}_{3}}$:

${{J}_{1}} = \frac{{{{L}^{3}}}}{{6r_{0}^{5}}}\frac{{2r_{0}^{2} - \mathop {\left( {\frac{L}{2}} \right)}\nolimits^2 }}{{\left( {r_{0}^{2} - \mathop {\left( {\frac{L}{2}} \right)}\nolimits^2 } \right)}},$

(37)

${{J}_{2}} = \frac{{{{L}^{2}}}}{{6r_{0}^{4}}}\frac{{3r_{0}^{2} - \mathop {\left( {\frac{L}{2}} \right)}\nolimits^2 }}{{\left( {r_{0}^{2} - \mathop {\left( {\frac{L}{2}} \right)}\nolimits^2 } \right)}},$

${{J}_{3}} = \frac{L}{{3r_{0}^{3}}}\frac{{3r_{0}^{2} - \mathop {\left( {\frac{L}{2}} \right)}\nolimits^2 }}{{\left( {r_{0}^{2} - \mathop {\left( {\frac{L}{2}} \right)}\nolimits^2 } \right)}}.$

Теперь видно, что вариации оптического пути, созданные квадрупольным компонентом гравитационного поля Земли, выражаются в виде трех членов.

Первый член представляет собой однородный полином второй степени как функция компонентов единичного вектора, соединяющего два КА. Он пропорционален ${{L}^{3}}$. Поскольку расстояние между КА значительно меньше их расстояний до центра Земли, то и вклад первого члена в вариации оптического пути самый маленький.

Второй член представляет собой функцию от координат КА и от компонентов единичного вектора ${\mathbf{k}}$. Он пропорционален ${{L}^{2}}$.

Наконец, третий член является линейным по $L$ и зависит от квадрупольного компонента гравитационного поля Земли и от координат КА. Вклад этого члена в вариации оптического пути самый большой.

Величины ${{J}_{1}}$, ${{J}_{2}}$, ${{J}_{3}}$ могут быть аппроксимированы разложением в ряд по малому параметру $L{\text{/}}{{r}_{0}}$. Напишем разложение этих функций в ряд Тейлора по параметру $L$ вблизи точки $L = 0$, тогда коэффициенты ${{J}_{1}},\;{{J}_{2}},\;{{J}_{3}}$ есть:

(38)

$\begin{gathered} {{J}_{1}} = - \frac{{{{L}^{3}}}}{{3r_{0}^{7}}} - \frac{{{{L}^{5}}}}{{8r_{0}^{9}}} - \frac{{{{L}^{7}}}}{{24r_{0}^{{11}}}} + O({{L}^{8}}), \\ {{J}_{2}} = - \frac{{{{L}^{2}}}}{{2r_{0}^{6}}} - \frac{{5{{L}^{4}}}}{{24r_{0}^{8}}} - \frac{{7{{L}^{6}}}}{{96r_{0}^{{10}}}} + O({{L}^{7}}), \\ {{J}_{3}} = \frac{L}{{r_{0}^{5}}} + \frac{{5{{L}^{3}}}}{{12r_{0}^{7}}} + \frac{{7{{L}^{5}}}}{{48r_{0}^{9}}} + O({{L}^{6}}). \\ \end{gathered} $

Теперь видно, что линейный по $L$ член дает самый большой вклад в вариацию оптической длины.

У нас есть все формулы для окончательного вычисления вклада квадрупольного компонента и сравнения точной формулы (36) с формулами (31), (32) и (33) из статьи [13].

В работе [13] расстояние между космическими аппаратами $L$ обозначено как

${{d}_{{AB}}}{\text{/}}a.$

Расчет релятивистской редукции с точностью до нанометров содержит лишь линейные и квадратичные величины при разложении по малому параметру ${{d}_{{AB}}}{\text{/}}a$ [13]:

(39)

$\begin{gathered} {{R}_{2}} \approx 1.66 \times {{10}^{{ - 7}}}\;{\text{м}} \cdot \frac{L}{{270\;{\text{км}}}}({{\gamma }_{{\epsilon \lambda }}} + 3{{n}_{{A\epsilon }}}{{n}_{{A\lambda }}})j_{E}^{{\epsilon \lambda }} + \\ + \;9.85 \times {{10}^{{ - 9}}}{\text{м}} \cdot \mathop {\left( {\frac{L}{{270\;{\text{км}}}}} \right)}\nolimits^2 ({{n}_{{A\epsilon }}}{{k}_{\lambda }} + {{n}_{{A\lambda }}}{{k}_{\epsilon }})j_{E}^{{\epsilon \lambda }}. \\ \end{gathered} $

Будем считать, что расстояние между двумя спутниками есть $L \approx 100$ км, тогда вклад линейного члена по $L$ составляет

${{R}_{2}} \approx 6.14 \times {{10}^{{ - 8}}}\;{\text{м}},$

вклад квадратичного члена составляет

${{R}_{2}} \approx 9.01 \times {{10}^{{ - 10}}}\;{\text{м}},$

вклад третьей степени $\mathop {\left( {\frac{L}{{{{r}_{0}}}}} \right)}\nolimits^3 $ составляет

${{R}_{2}} \approx 1.32 \times {{10}^{{ - 11}}}\;{\text{м}},$

наконец, вклад четвертой степени $\mathop {\left( {\frac{L}{{{{r}_{0}}}}} \right)}\nolimits^4 $ составляет

${{R}_{2}} \approx 1.93 \times {{10}^{{ - 13}}}\;{\text{м}}.$

Для расчета с точностью до пикометров необходимо учитывать квадрат расстояния между КА, а также третью степень по величине $L$. Поэтому из коэффициента ${{J}_{3}}$ необходимо удерживать три члена, из коэффициента ${{J}_{2}}$ только два и из коэффициента ${{J}_{1}}$ только один член.

6. ЗАКЛЮЧЕНИЕ

В работе обсуждались эффекты общей теории относительности в постньютоновском приближении при распространении плоской электромагнитной волны в пространстве с гравитационным полем в окрестности протяженного тела. Произвольное по форме и распределению масс, а также вращению распределение материи представляется произвольным тензором энергии-импульса, который был положен в основу данного обсуждения. Была получена компактная замкнутая форма общерелятивистского решения, описывающая фазу плоской волны, учитывающая вклад гармоник гравитационного поля Земли высокого порядка. Результат вычислений представлен в форме вариации оптического пути между двумя космическими аппаратами.

Наша формулировка соответствует точностным требованиям космической миссии по измерению гармоник с большим мультипольным числом $l$ гравитационного поля Земли.

Поскольку рассматривались эффекты релятивизма, которые возникают на уровне точности измерений 1 пм, наш анализ релятивистских эффектов, представленных здесь, в основном, касался величин наибольших членов. В данной работе было получено точное решение для вклада квадрупольного момента гравитационного поля Земли в вариации оптического пути. Они зависят от координат КА и, следовательно, переменны во времени.

Наш анализ может быть использован для выбора орбиты кластера КА, включая члены, которые могут быть перенормированы в параметры орбиты. Более того, наши результаты могут быть легко расширены для анализа вкладов других мультипольных моментов гравитационного поля. Аналитическая модель, которую мы обсудили для измерения расстояния, является достаточно общей и может быть легко расширена на другие случаи.

Список литературы

С. Н. Яшкин, Геопрофи. Научно-технический журнал по геодезии, картографии и навигации № 4, 43 (2007).
Ch. Reigber, H. Luehr, P. Schwintzer, J. Adv. Space Res. 30, 129 (2002).
B. D. Tapley, S. Bettadpur, M. M. Watkins, and Ch. Reigber, Geophys. Res. Lett. 31(9), id. L09607 (2004).
A. Albertella, F. Migliaccio, and F. Sansó, Celestial Mechanics and Dynamical Astronomy 83(1), 1 (2002).
M. T. Zuber, D. E. Smith, M. M. Watkins, S. W. Asmar, et al., Science 339, 668 (2013).
В. К. Милюков, С.-Ц. Е, Астрон. журн. 95(12), 901 (2018).
M. Watkins, F. Flechtner, F. Webb, in GRACE Science Team Meeting Proceedings, held in Texas, Austin, September 21$ - $23, 2015.
Luo Jun, Chen Li-Sheng, Duan Hui-Zong, Gong Yun-Gui, et al., Classical and Quantum Gravity 33, id. 035010 (2016).
T. Reubelt, N. Sneeuw, and M. A. Sharifi, in Gravity, Geoid and Earth Observation: IAG Commission 2: Gravity Field, held in Chania, Crete, Greece, 23–27 June 2008 (2009).
T. van Dam, P. Visser, N. Sneeuw, M. Losch, et al., in The Earth System by Means of Satellites. Final Report. ESA Contract № 20403, November (2008).
P. L. Bender, D. Wiese, and R. S. Nerem, in Proc. Third Intern. Symp. “Formation Flying, Missions and Technologies, ESA/ESTEC”, held in Noordwijk, The Netherlands, April 23–25, 2008 (ESA SP-654, June 2008).
F. Flechtner, K-H. Neumayer, and Ch. Dahle, in GRACE Science Team Meeting Proceedings, held in Texas, Austin, September 21–23 (2015).
S. G. Turyshev, M. V. Sazhin, and V. T. Toth, Phys. Rev. D 89, id. 105029 (2014).
V. K. Milyukov, M. V. Sazhin, V. N. Sementsov, H.-Chi. Yeh, and C. Xue, Moscow University Phys. Bull. 74 (2), 197 (2019).
Л. Д. Ландау, Е. М. Лифшиц, Теория поля (М.: Наука, 1980).
M. Soffel, S. A. Klioner, G. Petit, P. Wolf, et al., Astron. J. 126(6), 2687, [astro-ph/0303376] (2003).
S. G. Turyshev, V. T. Toth, and M. V. Sazhin, Phys. Rev. D 87, id. 024020 (2013).
S. M. Kopeikin, M. Efroimsky, and G. Kaplan, Relativistic Celestial Mechanics of the Solar System (Wienheim, Germany: Wiley-VCH Verlag GmbH and Co. KGaA, 2011).
S. G. Turyshev and V. T. Toth, Intern. J. Modern Physics D 24(6), id. 1550039 (2015).
G. S. Bisnovaty-Kogan, I. V. Estulin, N. G. Haveson, V. G. Kurt, G. A. Mersov, and I. D. Novikov, Astrophys. Space Sci. 75, 219 (1981).
М. В. Сажин, И. Ю. Власов, О. С. Сажина, В. Г. Турышев. Астрон. журн. 87(11), 1043 (2010).
В. Е. Жаров, В. В. Орешко, В. А. Потапов, М. С. Пшир-ков, А. Е. Родин, М. В. Сажин, Астрон. журн. 96(2), 120 (2019).
W. Torge, Geodesy (Berlin, New York: Walter de Gruyter, 2001).
J. Ries, S. Bettadpur, R. Eanes, Z. Kang, et al., The Combined Gravity Model GGM05C (Potsdam: GFZ Data Services, 2016).
А. Ф. Никифоров, В. В. Уваров, Основы теории специальных функций (М.: Наука, 1974).
И. С. Градштейн, И. М. Рыжик, Таблицы интегралов, сумм, рядов и произведений (М.: ФизматГИЗ, 1963).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал