Астрономический журнал, 2020, T. 97, № 6, стр. 476-504
Принципы космической навигации по пульсарам
А. Е. Родин 1, *, В. В. Орешко 1, В. А. Потапов 1, М. С. Пширков 1, 2, М. В. Сажин 2
1 Физический институт им. П.Н. Лебедева РАН,
Пущинская радиоастрономическая обсерватория АКЦ ФИАН
Пущино, Россия
2 Московский государственный университет им. М. В. Ломоносова,
Государственный астрономический институт им. П. К. Штернберга
Москва, Россия
* E-mail: rodin@prao.ru
Поступила в редакцию 13.02.2020
После доработки 02.03.2020
Принята к публикации 02.03.2020
Аннотация
В работе рассмотрены принципы космической навигации по пульсарам, наблюдаемым в радиодиапазоне. Изложены требования к приемной аппаратуре, приведен список рекомендуемых пульсаров, изложен алгоритм определения местоположения космического аппарата в барицентрической системе координат и вычисления поправок к бортовой шкале времени.
1. ВВЕДЕНИЕ
Существует несколько определений понятия “космическая навигация”. Мы будем придерживаться определения, данного в учебниках по космической баллистике и космической навигации [1, 2]. Основной задачей навигации является определение координат и скоростей космических аппаратов по результатам измерений и обработки в определенной системе координат [3]. Способы решения этой задачи определяются в первую очередь системой координат, в которой она решается. На поверхности Земли для навигации еще совсем недавно использовались астрономические объекты, в настоящее время замену которым обеспечили глобальные навигационные спутниковые системы ГЛОНАСС, GPS, BeiDou, Galileo. Но даже при наличии современных технических средств ориентирование по звездам (астрономическим объектам) используют при морской навигации и ориентации космических аппаратов. Кроме этого, в основе глобальных навигационных систем лежит инерциальная система координат, определяемая радиоастрономическими методами по наблюдениям квазаров.
Для целей космической навигации в околоземном пространстве можно использовать существующие глобальные навигационные спутниковые системы. Они могут обеспечить полноценную навигацию космического аппарата (КА), требующую знания точного времени, положения, скорости. Однако эти спутниковые системы имеют ограниченные возможности определения местоположения КА относительно далеко от Земли или при потере связи из-за отказа или непредвиденных обстоятельств.
В пределах Солнечной системы способы навигации, используемые на Земле и околоземном пространстве, неприменимы или имеют ограниченные возможности. Сеть дальней космической связи (ДКС) помогает навигации КА далеко от Земли, определяя дальность и скорость ее изменения вдоль линии, соединяющей КА и наблюдателя. Точность определения этих величин снижается с увеличением дистанции от КА до земного наблюдателя из-за ослабления сигнала. Кроме того, свои ограничения накладывает нестабильность бортовых часов КА и погрешность определения их хода на длительных интервалах времени. Поэтому на больших расстояниях от Земли, по мере приближения к границе Солнечной системы, точность определения координат и вектора скорости КА существенно падает и несравнима с точностью навигации в околоземном пространстве.
Для дополнения существующих систем и разработки будущих навигационных систем необходимы альтернативные методы навигации в дальнем космосе. Одним из таких предлагаемых способов навигации является навигация с использованием в качестве опорных объектов нейтронных звезд – пульсаров. Обнаруженные более пятидесяти лет назад небесные объекты, пульсары обладают уникальным свойством – импульсным излучением с высокой стабильностью периода следования импульсов, поэтому они могут стать базисом для установления новой системы навигации по всей Солнечной системе и за ее пределами.
Концепция использования пульсаров в качестве навигационных средств основывается на измерении времен прихода импульсов и сравнении с прогнозируемым временем прибытия в данное место и в данную эпоху [4, 5]. Важными элементами в этих измерениях являются редукция наблюдаемого времени прибытия импульса пульсара в барицентр Солнечной системы и коррекция времени прибытия импульса. Параметрами этой коррекции являются эфемериды пульсара совместно с положением и скоростью наблюдателя относительно барицентра Солнечной системы.
Для целей космической навигации за рубежом активно рассматриваются рентгеновские пульсары. Значительную часть своей энергии эти пульсары излучают в рентгеновском диапазоне. Разработка прототипов таких систем идет в данное время в США и Европе [6–9]. В то же время нет принципиальных ограничений на использование радиоизлучения пульсаров. Теоретические алгоритмы навигации с использованием пульсаров едины для всех типов пульсаров, различия только в технической реализации аппаратуры регистрации момента прихода импульса. Далее мы рассмотрим предложения по созданию бортовых средств КА для наблюдений пульсаров в радиодиапазоне, сценария наблюдений и алгоритмов определения положения КА и поправок к бортовой шкале времени.
2. ТЕОРЕТИЧЕСКИЙ АЛГОРИТМ НАВИГАЦИИ КА ПО ПУЛЬСАРАМ
Навигационная система, основанная на пульсарах, должна включать в себя приемную антенну, многоканальный радиометр, часы на борту корабля, которые измеряют время прибытия импульсов пульсара, и базу данных известных моделей пульсаров. После идентификации пульсара и измерения времени прихода его импульсов эта информация может быть использована для определения или уточнения скорости, бортового времени и положения в пространстве. Методы определения этих величин описаны ниже.
Различные цели космической экспедиции могут требовать измерения скорости КА (включая направление, т.е. измерение всех трех компонентов вектора скорости). Скорость может быть измерена по эффекту Доплера. Поскольку пульсары излучают импульсные сигналы, которые носят периодический характер, то космический корабль, который движется относительно пульсара, будет воспринимать измеряемый период пульсара с поправкой на смещение Доплера. Измерение частоты прихода импульсов от пульсара и сравнение их с ожидаемой частотой пульсара позволяют измерить доплеровский сдвиг частоты. Этот сдвиг может быть преобразован в скорость вдоль луча зрения КА – пульсар. Совместные измерения доплеровского сдвига в периоде импульсов нескольких пульсаров (больше трех пульсаров, расположенных в разных направлениях от КА) позволят измерить трехмерную скорость КА таким же способом, как и определение положения.
Точные часы являются основополагающим компонентом системы навигации КА. Бортовые часы служат основой для процесса навигации и имеют решающее значение для бортовых систем связи. Атомные часы обеспечивают высокую стабильность обычно с точностью до 10–9–10–15 в течение дня. Для отслеживания движения источника радиосигналов с погрешностью в несколько десятых метра нужна точность хода часов около одной наносекунды. Для этого требуются часы, которые должны иметь стабильность порядка 10–13 в течение нескольких часов.
Возможно, наиболее значительным преимуществом пульсаров является возможность обеспечить измерение времени, сравнимое с точностью атомных часов, основываясь исключительно на небесных источниках. Приход импульсов пульсара на космический корабль с высокой периодичностью может быть использован для стабилизации бортовых часов с точностью, необходимой для работы систем связи. Время, полученное от пульсаров, не дает прямого измерения абсолютного времени; тем не менее, стабильный небесный источник импульсов может скорректировать вариации хода часов космического аппарата для поддержания точного времени.
Здесь может быть реализован способ коррекции времени с использованием фазовой автоподстройки частоты. В линию обратной связи может быть включена разность фаз между осциллятором локальных часов и опорного сигнала от пульсара, которая должна стремиться к нулю. Можно использовать итерации, чтобы разности фаз импульсов пульсара и часов на борту были сведены к нулю.
3. ИЗМЕРЕНИЕ ПОЛОЖЕНИЯ КА
По наблюдениям импульсов пульсара возможно определение положения космического аппарата. Координаты КА определяются относительно некоторой инерциальной системы. Основная инерциальная система, относительно которой можно осуществлять измерение положения КА, связана с барицентром Солнечной системы. Для некоторых задач космической навигации полезно также измерять положение корабля относительно барицентра (или геоцентра) Земли. Можно предложить несколько методов определения положения относительно Земли. Они похожи на методы космической навигации, основанные на оптических наблюдениях.
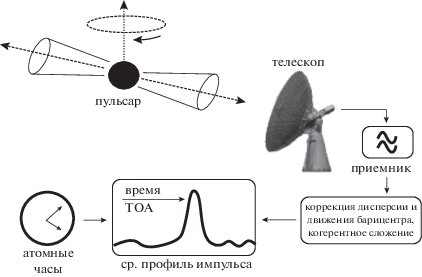
Основу концепции использования пульсаров в качестве навигационных средств составляют возможность измерения времен прихода импульсов и сравнение с прогнозируемым временем прибытия импульсов в данную эпоху и в данное место. Типичная итеративная процедура показана на рис. 1.
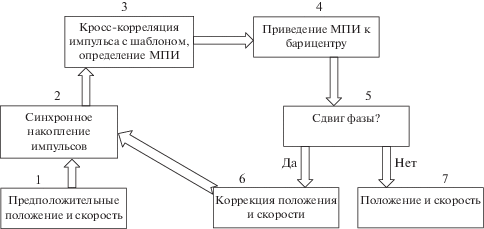
Важным этапом этих измерений является коррекция времени прихода наблюдаемого фотона относительно барицентра Солнечной системы. Параметрами этой процедуры являются эфемериды пульсара совместно с положением и скоростью наблюдателя. Положение КА немного отличается от предполагаемого, в результате измеренное положение импульса будет иметь фазовый сдвиг относительно пика предполагаемого импульса. Поэтому положение и скорость космического корабля можно включить в итерационный процесс для вычисления времени прихода импульса. Соответствующая итерационная цепочка показана на рис. 2.
Поясним итерационную цепочку более подробно. Первоначальный шаг заключается в том, что делается предположение о положении и скорости КА, которые берутся из запланированных параметров орбиты космического корабля (шаг 1). Итерационная цепочка начинается с наблюдения пульсара, в ходе которого регистрируются отдельные импульсы, которые накапливаются синхронно с видимым периодом пульсара, пока не будет достигнуто заданное отношение сигнал/шум (шаг 2). Полученный профиль импульса кросс-коррелируется с импульсом-шаблоном для определения момента прихода импульса (МПИ) (шаг 3).
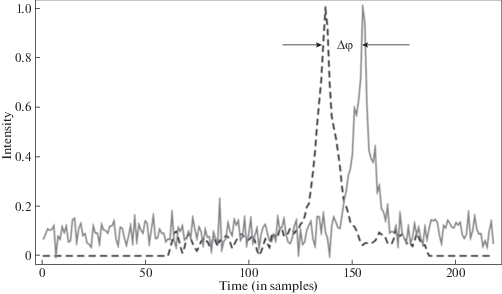
Измеренный МПИ относительно бортовой шкалы времени далее редуцируется путем преобразования к инерциальной системе (с учетом гравитационного поля в месте положения КА и его скорости), например, к барицентру Солнечной системы (шаг 4). Эта редукция, безусловно, требует сведений (предположенных или выведенных на предыдущем шаге) о положении космического аппарата и его скорости в качестве входных параметров. Из сравнения времени прихода наблюденного импульса и предсказания МПИ из вращательных эфемерид пульсара и первоначального положения и скорости КА можно измерить разность фаз (рис. 3).
В этой схеме фазовый сдвиг Δφ (шаг 5) по отношению к величине абсолютной фазы импульса соответствует разнице положения x = cP(Δφ + n). Здесь P – период пульсара, c – скорость света и n = 0, ±1, ±2, …– целое число, которое учитывает периодичность наблюдаемых импульсов. Если сдвиг фазы не равен нулю, то положение и скорость КА должны быть исправлены, соответственно необходима следующая итерация (шаг 6). Если сдвиг фазы равен нулю, или меньше определенного порога (погрешности измерения положения и скорости), то используемые в ходе итерации предыдущие значения положения и скорости были правильны (шаг 7) и соответствуют фактической орбите КА.
Здесь следует напомнить, что производится измерение положения и скорости КА вдоль линии “пульсар–КА”, другими словами, одномерное измерение.
Трехмерные величины положения и скорости могут быть получены из наблюдений, по крайней мере, трех различных пульсаров. Если также необходима калибровка бортовых часов, требуется наблюдение четвертого пульсара.
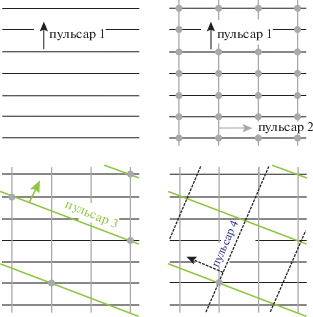
Поскольку положение КА выводится из значения фазы (или времени прихода импульса) периодического сигнала, то решение не единственно. Эта проблема снимается путем ограничения области возможных решений до конечного объема около первоначального предполагаемого значения, или путем наблюдения дополнительных пульсаров, как показано на рис. 4 [6].
При определении положения и скорости КА в пространстве возможны следующие подходы:
1) экстраполяция положения КА вперед на заданный интервал времени, исходя из знания положения и скорости аппарата в предыдущие моменты. При данном подходе траектория КА на ограниченном промежутке времени представляется полиномом невысокой степени, который с достаточной для данного промежутка точностью аппроксимирует орбиту. Таким образом, вычисление траектории КА сводится к вычислению набора коэффициентов полинома.
2) более общий подход, основанный на вычислении элементов мгновенной орбиты, на основе которых, в свою очередь, вычисляются текущее положение и скорость КА. Такой подход является более “компактным”, т.к. теоретически позволяет описать движение КА по всей орбите, если орбита является невозмущенной, что, однако, является нереализуемым на практике случаем.
3) способ без привлечения орбитальных элементов, когда орбита задается путем численного интегрирования с максимально возможной точностью. Далее измеренное положение сравнивается с предвычисленной орбитой.
Каждый из этих подходов имеет свои преимущества и недостатки. Так, первый подход является относительно менее затратным в смысле вычислительных ресурсов: метод вперед рассчитывает местоположение КА, исходя из предыдущей траектории и ограничений, накладываемых на величину скорости КА, его ускорения и т.д.
Второй подход, при котором определяется мгновенная орбита в виде набора кеплеровских элементов, позволяет легко обмениваться ими с потребителями, отслеживать их изменение во времени и таким образом изучать эволюцию орбиты. Так как реальная орбита из-за возмущений всегда изменяется во времени, то и в этом случае через определенные промежутки времени нужно будет заново вычислять орбитальные элементы, которые описывают фактическую орбиту, либо использовать производные элементов по времени.
Третий подход позволяет обойтись без промежуточных орбитальных элементов и связанных с этим дополнительных вычислений.
Также возможен еще один гипотетический случай, когда на борту КА произошел сбой, и часть времени КА летел по неизвестной траектории. Затем, когда функционирование КА восстановилось, требуется определить местоположение КА при полном отсутствии знаний о предыдущей орбите.
В дальнейших расчетах, говоря об орбитальных кеплеровских параметрах орбиты, будем использовать следующие обозначения: a – большая полуось орбиты, e – эксцентриситет орбиты, i – наклон орбиты к основной плоскости, Ω – долгота восходящего узла, ω – долгота перицентра, T – время пролета перицентра. Вначале рассмотрим принцип определения положения и приведем теоретические формулы для измерения положения.
3.1. Бортовой антенно-аппаратурный комплекс
Базовым элементом аппаратурного комплекса для наблюдений пульсаров на борту КА является приемная антенна. В основном именно технические возможности антенны определяют потенциальную чувствительность пульсарного комплекса. Определим основные положения, определяющие технические требования к бортовому антенно-аппаратурному комплексу КА для наблюдений пульсаров:
1. Антенно-аппаратурный комплекс должен обеспечить наблюдения реперных пульсаров с максимально возможным отношением сигнал/шум. Оптимальным диапазоном частот для наблюдений пульсаров на борту КА является диапазон 300–500 МГц как компромисс между падением потока на высоких частотах и влиянием межзвездной и межпланетной среды на низких частотах. Полоса рабочих частот антенны должна быть не менее 100 МГц.
2. Должна быть реализована высокая чувствительность системы: эффективная площадь антенны должна быть не менее 50 м2. Температура собственных шумов антенны должна быть минимально возможной, но не более 20 К.
3. Сектор сканирования луча антенны без смены ориентации КА должен быть максимально возможным, ±60° относительно оси антенны. Время перемещения луча не определено.
4. Масса и занимаемый объем антенны в сложенном состоянии должны быть минимальными.
5. Из-за высокой линейной поляризации излучения в импульсе необходимо принимать излучение в двух ортогональных линейных (либо круговых) поляризациях.
6. При наблюдении пульсаров необходимо использовать метод синхронного с периодом пульсара накопления сигнала или режим непрерывного накопления с последующим сложением с пробным периодом.
7. Приемно-регистрирующая система радиотелескопа должна обеспечивать компенсацию дисперсионного запаздывания импульса пульсара в рабочей полосе частот и регистрацию момента прихода импульса в бортовой шкале с погрешностью менее одной микросекунды.
Бортовая антенная система КА дециметрового диапазона радиоволн, в основном отвечающая необходимым техническим требованиям, может быть реализована тремя принципиально различающимися типами антенн.
3.2. ФАР с цифровым управлением
Практическая реализация перечисленных в предыдущих разделах технических требований к антенной системе и радиокомплексу КА может быть выполнена в виде фазированной антенной решетки с электронным управлением лучом антенны [10, 11]. По предварительным оценкам эффективность антенной системы на базе сканирующей ФАР может составить порядка 50–60 м2 в заданном частотном диапазоне 300–500 МГц. Тогда действительная физически создаваемая площадь антенны должна быть не менее 80–85 м2 с учетом коэффициента использования поверхности 0.6–0.65. При этом усиление антенны в заданном широкоугольном секторе сканирования для заданной эффективной площади антенны должно быть порядка 30–31.5 дБ с минимальными потерями в фидерном тракте и при условии использования малошумящих усилителей, размещаемых непосредственно вблизи антенных элементов ФАР.
3.3. Сферическая зеркальная антенна с цифровым управлением
Еще одним вариантом построения антенной системы является сферическая зеркальная антенна с эффективной площадью ~50–60 м2. Достоинством такой антенной системы является возможность обеспечить прием сигналов в широком угловом секторе обзора с ориентацией главного луча в заданных направлениях в пределах конического углового сектора с раствором порядка 100–120°.
В процессе разработки антенного устройства необходимо обеспечить ряд конструктивных особенностей, например, транспортировку космического аппарата в компактном транспортном положении на орбиту функционирования в космосе, развертывание панелей антенного устройства с гарантированной точностью и длительную работу в экстремальных условиях космического пространства.
3.4. Параболическая антенна с электромеханическим приводом
Наряду с ранее рассмотренными вариантами реализации антенных устройств с широкоугольным обзором и поиском излучающих радиоисточников в космическом пространстве с электронным управлением луча имеется возможность использования остронаправленных антенн зеркально-параболического типа с электромеханическим приводом. Антенны такого типа широко распространены, характеристики хорошо известны. Опыт реализации таких антенн, функционирующих в открытом космосе в течение более 30 лет, имеется в ОКБ МЭИ при эксплуатации известной системы “Целина”. Конструкторско-технологические трудности, связанные с работой вращающихся элементов привода в космосе, были решены путем использования специальных рениевых смазок и управляющих электромеханических устройств.
3.5. Приемно-усилительный тракт пульсарного комплекса
Основное назначение приемно-усилительного тракта пульсарного комплекса – усиление принимаемого сигнала до уровня достаточного для обработки и регистрации полезного сигнала, а также обеспечение максимально возможной чувствительности и помехоустойчивости приемно-регистрирующего комплекса. Схема построения и техническая реализация приемника в первую очередь зависят от рабочего диапазона частот, в нашем случае это диапазон 300–500 МГц. На этих частотах в настоящее время без больших технических сложностей реализуется прямая оцифровка сигнала с помощью АЦП с тактовой частотой 1000 МГц, доступных в достаточно широкой номенклатуре. Следовательно, для пульсарного приемника можно использовать схему приемника прямого усиления сигнала, без переноса спектра сигнала на промежуточные частоты, что существенно упрощает реализацию приемника и повышает надежность его работы.
Приемник пульсарного комплекса должен обеспечивать максимально возможную чувствительность пульсарного комплекса, из чего следует, что вклад собственных шумов приемника в системную температуру шума должен быть незначительным. Шумы системы приемно-регистрирующего комплекса включают в себя фоновое излучение Галактики на частоте 400 МГц Тф ≈ 20–100 К (в зависимости от направления), собственные шумы антенны Та ≈ 20 К и собственную температуру шума приемника Тпр. Принимая пороговое значение температуры шума системы Тсист = 100 К и среднее значение фоновой температуры Тф = 60 К, получаем, что температура шума приемника не должна превышать 20 К. Такое значение уровня шума для современных МШУ в этом диапазоне частот вполне достижимо и не требует охлаждения МШУ до криогенных температур.
Приемно-усилительный тракт должен обеспечивать усиление сигнала для устойчивой работы АЦП, исключающей влияние шумов квантования при аналого-цифровом преобразовании сигнала. Как правило, необходимый уровень сигнала на входе АЦП должен быть не менее 1–10 мВ. С учетом того, что на входе МШУ уровень сигнала, включая шумы системы, в полосе частот 100 МГц примерно равен 1–5 мкВ, приемный тракт должен обеспечить суммарное усиление примерно 80 дБ.
3.6. Приемно-регистрирующий комплекс КА для наблюдения пульсаров
Основными элементами комплекса являются:
• накопитель сигнала, обеспечивающий синхронное с наблюдаемым периодом интегрирование сигнала во времени;
• синтезатор периода пульсара, формирующий наблюдаемый период пульсара и обеспечивающий привязку момента начала регистрации к локальной шкале времени;
• компенсатор дисперсии, устраняющий дисперсионное запаздывание импульсов в широкой полосе частот;
• регистратор сигнала, обеспечивающий запись наблюдаемого сигнала на носитель информации для последующей обработки и анализа.
Технические требования к приемно-регистрирующему комплексу определяются диапазоном рабочих частот 350–450 (300–500) МГц, диапазоном наблюдаемых периодов пульсаров 0.0014–1 сек, необходимой точностью определения момента регистрации в бортовой шкале времени не хуже 0.1 мкс, максимальным временем накопления сигнала 104 с. Также принципиальное значение имеет выбор способа компенсации дисперсионного запаздывания сигнала. В работе [12] было показано, что для бортового пульсарного комплекса возможно использование только метода последетекторной компенсации дисперсии сигнала с использованием цифровой обработки сигналов на основе БПФ [13].
В ПРАО АКЦ ФИАН в последние годы был разработан цифровой приемно-регистрирующий комплекс для наблюдений пульсаров в дециметровом диапазоне радиоволн. Он предназначен для работы с трактом промежуточной частоты в полосе 100 МГц и, в основном, удовлетворяет вышеназванным техническим требованиям [14].
3.7. Принцип определения местоположения
Для определения положения КА необходимо предварительное знание его орбиты с точностью Pc/2, где P – период вращения пульсара, c – скорость света. Это позволяет избежать потери фазы (номера импульса) при определении положения КА. Большинство пульсаров имеют периоды от 8 с до 1.4 мс, что позволяет определять орбиту с различной степенью точности в зависимости от решаемой задачи.
Вначале рассмотрим приближенное уравнение
(1)
${{t}_{i}} - {{\tilde {t}}_{i}} = \frac{1}{c}({{\vec {n}}_{i}} \cdot \vec {r}),~\quad (i = 1,2,3,4),$Уравнение (1) есть система линейных уравнений относительно $\vec {r}$ – точного положения КА в Солнечной системе. Чтобы определять три координаты КА, необходимо наблюдать, по крайней мере, три пульсара. Еще один пульсар необходимо наблюдать для ведения времени. Таким образом, для точной навигации нужно вести мониторинг минимум четырех пульсаров.
Формула для определения радиус-вектора КА записывается в следующем виде [4, 15]:
(2)
$\vec {r} = \frac{{{{A}_{1}}{\kern 1pt} [{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}] + {{A}_{2}}{\kern 1pt} [{{{\vec {n}}}_{1}} \times {{{\vec {n}}}_{3}}] + {{A}_{3}}{\kern 1pt} [{{{\vec {n}}}_{1}} \times {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }}_{2}}]}}{{({{{\vec {n}}}_{1}} \cdot [{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}])}},$(3)
$c({{t}_{2}} - {{\tilde {t}}_{2}}) = ({{\vec {n}}_{2}} \cdot {\mathbf{\vec {r}}}) - \frac{1}{{2{{R}_{2}}}}{{[{{\vec {n}}_{2}} \times {\mathbf{\vec {r}}}]}^{2}} + {{\gamma }_{2}} + \frac{{D{{M}_{2}}}}{{{{f}^{2}}}},$(4)
${{A}_{2}} = ({{\vec {n}}_{2}} \cdot {\mathbf{\vec {r}}}) - \frac{1}{{2{{R}_{2}}}}{{[{{\vec {n}}_{2}} \times {\mathbf{\vec {r}}}]}^{2}},$Второй член правой части уравнений (4) имеет величину 1.2 мкс для КА на расстоянии r = 1 а.е. от барицентра и пульсара на расстоянии R = 1 кпк.
Навигацию по пульсарам целесообразно использовать в дальнем космосе, когда расстояние от барицентра может значительно превышать 10 а.е. В этом случае поправки за сферичность фронта волны от пульсара могут достигать 120 мкс или даже более. Такие поправки вполне сравнимы с задержкой Шапиро и должны учитываться при вычислении положения КА.
С точностью, достаточной для целей навигации, решение уравнений (4) можно записать как
(5)
$\vec {r} = \frac{{({{A}_{1}} + \delta {{A}_{1}})[{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}] + ({{A}_{2}} + \delta {{A}_{2}})[{{{\vec {n}}}_{1}} \times {{{\vec {n}}}_{3}}] + ({{A}_{3}} + \delta {{A}_{3}})[{{{\vec {n}}}_{1}} \times {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }}_{2}}]}}{{({{{\vec {n}}}_{1}} \cdot [{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}])}}.$Поскольку набор пульсаров для целей навигации будет определен заранее, то релятивистские поправки и поправки за межзвездную и межпланетную плазму можно вычислить заранее. Остаются только поправки за нестационарный солнечный ветер, которые требуют вычисления в текущее время.
Уравнения (2) и (5) позволяют вычислять положения КА по трем пульсарам, так что уравнения (3) являются определенными линейными уравнениями. В действительности для определения положения можно использовать не три, а значительно большее число пульсаров, скажем k. Тогда для определения трех координат возникает k уравнений. Система становится переопределенной, и в этом случае используется метод наименьших квадратов.
Вернемся к решению задачи навигации по трем пульсарам. Решение уравнения (2) зависит от знаменателя $({{\vec {n}}_{1}} \cdot [{{\vec {n}}_{2}} \times {{\vec {n}}_{3}}])$. Если эта величина мала, то решение становится плохо определенным. Это происходит в том случае, когда все три пульсара находятся близко друг к другу на небесной сфере. Величина $({{\vec {n}}_{1}} \cdot [{{\vec {n}}_{2}} \times {{\vec {n}}_{3}}])$ называется определителем Грама.
Отметим также, что скалярное произведение двух единичных векторов в направлении на пульсары равно косинусу угла между этими пульсарами. Единичный вектор в направлении на пульсар определяется через экваториальные координаты как $\vec {n} = \left( {cos\delta cos\alpha ,\,cos\delta sin\alpha ,\,sin\delta } \right)$, а через эклиптические как
Пользуясь этими определениями, можно вычислить определитель Грама и оценить качество выбранных пульсаров как навигационных реперов. Критерием плохой определенности системы является равенство определителя Грама ошибке определения времени прихода импульсов по отношению к периоду между импульсами. Качество пульсаров как навигационных реперов мы оценим ниже.
Для уменьшения количества итераций можно использовать пульсары с различными значениями периодов. В случае нулевой итерации можно использовать набор пульсаров с периодами примерно 1 сек. Тогда нулевое приближение положения КА достаточно знать с точностью до 150 000 км, что является достаточно простой задачей. В качестве второй итерации уже можно использовать набор миллисекундных пульсаров, которые позволяют определить положение КА с точностью лучше, чем 300 м.
3.8. Определение орбиты по положению и скорости
Для быстрого определения элементов орбиты КА могут использоваться одномоментные измерения его положения r0 и скорости v0 в момент времени t0. Будем придерживаться подхода, изложенного в книге [16]. Предполагаем, что векторы r0 и v0 не коллинеарны. Плоскость орбиты определяется с помощью единичного вектора нормали, вычисляемого из векторного произведения радиус-вектора и скорости
(6)
${{{\mathbf{c}}}^{0}} = \frac{{{{{\mathbf{r}}}_{0}} \times {{{\mathbf{v}}}_{0}}}}{{\left| {{{{\mathbf{r}}}_{0}} \times {{{\mathbf{v}}}_{0}}} \right|}}.$Составляющие вектора c0 обозначим через cx, cy, cz. Тогда наклонение орбиты и долготу восходящего узла можно вычислить из соотношений
по формуламИз модуля векторного произведения площадей $C = \left| {{{{\mathbf{r}}}_{0}} \times {{{\mathbf{v}}}_{0}}} \right|$ определяем параметр орбиты
а с помощью интеграла энергии $V_{0}^{2} - \frac{{2\mu }}{{{{r}_{0}}}} = h$ определяем эксцентриситет орбитыПо величине эксцентриситета однозначно определяется тип орбиты. При e < 1 орбита эллиптическая, при e > 1 – гиперболическая, в случае e = 1 – параболическая.
Истинная аномалия ${{\vartheta }_{0}}$ в момент времени t0 определяется из формул для радиальной и трансверсальной составляющей скорости КА
(9)
$\sin {{\vartheta }_{0}} = \frac{{{{V}_{{r0}}}}}{e}\sqrt {\frac{p}{\mu }} ,\quad \cos {{\vartheta }_{0}} = \frac{1}{e}\left( {{{V}_{{n0}}}\sqrt {\frac{p}{\mu }} - 1} \right),$Аргумент широты u0 определяется из следующих соотношений:
(10)
$\begin{gathered} \cos {{u}_{0}} = {\mathbf{r}}_{\Omega }^{0} \cdot \frac{{{{{\mathbf{r}}}_{0}}}}{{\left| {{{{\mathbf{r}}}_{0}}} \right|}}, \\ \sin {{u}_{0}} = \left| {{\mathbf{r}}_{\Omega }^{0} \times \frac{{{{{\mathbf{r}}}_{0}}}}{{\left| {{{{\mathbf{r}}}_{0}}} \right|}}} \right|\operatorname{sign} {{r}_{{0z}}}\quad (0 \leqslant {{u}_{0}} \leqslant 2\pi ), \\ \end{gathered} $Время пролета через перицентр T определяется исходя из знания типа орбиты – эллиптическая или гиперболическая. При эллиптической орбите предварительно вычисляется эксцентрическая аномалия по формуле
(12)
$\operatorname{tg} \frac{{{{E}_{0}}}}{2} = \sqrt {\frac{{1 - e}}{{1 + e}}} \operatorname{tg} \frac{{{{\vartheta }_{0}}}}{2},$(15)
$\operatorname{tg} \frac{{{{H}_{0}}}}{2} = \sqrt {\frac{{e - 1}}{{e + 1}}} \operatorname{tg} \frac{{{{\vartheta }_{0}}}}{2},$(16)
$T = {{t}_{0}} - \frac{{{{a}^{{3/2}}}}}{{\sqrt \mu }}(e\operatorname{sh} {{E}_{0}} - {{E}_{0}}),$В случае параболической орбиты время пролета перицентра вычисляется по формуле
3.9. Определение местоположения КА по орбитальным параметрам
Введем прямоугольную систему координат Oxyz. Начало системы координат в точке O выбирается в зависимости от решаемой задачи и определяется удобством последующих вычислений координат КА. Например, при определении местоположения КА в межпланетных перелетах центр координатной системы удобно выбрать совпадающим с барицентром Солнечной системы. При определении местоположения ИСЗ центр координат выбирается в центре масс Земли и т.д.
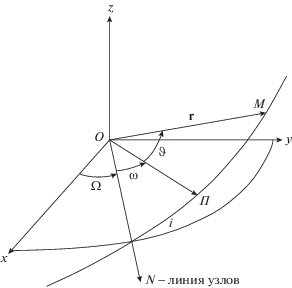
Пересчет полярных координат КА $(\vartheta ,{\mathbf{r}})$ из плоскости орбиты в прямоугольную систему координат Oxyz будем осуществлять с помощью последовательных поворотов на углы $\vartheta $, ω, i, Ω (рис. 5). Для этого введем матрицы поворота вокруг осей Ox, Oy, Oz:
(18)
${{{\mathbf{R}}}_{y}}(\varphi ) = \left( {\begin{array}{*{20}{c}} {\cos \varphi }&0&{ - \sin \varphi } \\ 0&1&0 \\ {\sin \varphi }&0&{\cos \varphi } \end{array}} \right),$(19)
$ = \left( {\begin{array}{*{20}{c}} {\cos \Omega }&{\sin \Omega }&0 \\ { - \sin \Omega }&{\cos \Omega }&0 \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos i}&{\sin i} \\ 0&{ - \sin i}&{\cos i} \end{array}} \right) \times $(20)
$\begin{gathered} x = r[\cos (\vartheta + \omega )\cos \Omega - \sin (\vartheta + \omega )\sin \Omega \cos i], \\ y = r[\cos (\vartheta + \omega )\sin \Omega - \sin (\vartheta + \omega )\cos \Omega \cos i], \\ z = r[\sin (\vartheta + \omega )\sin i]. \\ \end{gathered} $Рис. 5.
Положение орбиты в прямоугольной системе 0xyz и основные углы поворота для расчета прямоугольных координат КА.
Эти формулы пригодны для орбит всех типов – эллиптических, параболических, гиперболических, но в каждом случае нужно подставлять свои значения радиус-вектора r и истинной аномалии $\vartheta $ [17, 18].
3.10. Оценивание параметров траектории КА и их погрешности
Для оценки погрешности измерений в зависимости от статистики измерений рассмотрим траекторию КА на ограниченном интервале времени. Для ее описания будем использовать модель, представляющую собой детерминированную функцию ${\mathbf{r}}(\lambda ,t)$ неизвестных меняющихся неслучайных параметров $\lambda = {{({{\lambda }_{0}},{{\lambda }_{1}},...,{{\lambda }_{\kappa }})}^{T}}$ ((*)T – операция транспонирования) и времени t [19]. Функцию ${\mathbf{r}}(\lambda ,t)$ считаем дифференцируемой по всем параметрам λi (i = 1, 2, …, κ). Рассмотрим частный случай, когда траектория описывается полиномом κ-й степени:
(21)
${\mathbf{r}}({\mathbf{\lambda }},t) = {{\lambda }_{0}} + {{\lambda }_{1}}t + {{\lambda }_{2}}{{t}^{2}} + ... + {{\lambda }_{\kappa }}{{t}^{\kappa }}.$Коэффициенты λ0, λ1, λ2, … полинома имеют смысл координаты, скорости, ускорения и т.д. Степень полинома κ зависит от орбиты КА (околоземная, окололунная или межпланетная), промежутка времени, на который необходимо предвычислить положение КА, и заданной точности предсказания.
Вектор неизвестных параметров ${\mathbf{\lambda }} = ({{\lambda }_{0}},{{\lambda }_{1}},...,$ ${{\lambda }_{\kappa }}{{)}^{T}}$ траектории ${\mathbf{r}}({\mathbf{\lambda }},t)$ подлежит оцениванию по результатам наблюдения процесса $y(t) = {\mathbf{r}}({\mathbf{\lambda }},t) + \xi (t)$, где в качестве шума ξ(t) выступают аппаратурные погрешности измерений МПИ и фазовые вариации вращения пульсара.
Считаем, что число измерений n > κ. В этом случае нахождение вектора параметров $\lambda $ осуществляется методом наименьших квадратов. Введем векторы-столбцы размерности κ + 1 и n
(22)
${\mathbf{\lambda }} = \left( {\begin{array}{*{20}{c}} {{{\lambda }_{0}}} \\ {{{\lambda }_{1}}} \\ \vdots \\ {{{\lambda }_{\kappa }}} \end{array}} \right),\quad y = \left( {\begin{array}{*{20}{c}} {{{y}_{1}}} \\ {{{y}_{2}}} \\ \vdots \\ {{{y}_{n}}} \end{array}} \right),$(23)
${\mathbf{C}} = \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ \vdots \\ 1 \end{array}\;\begin{array}{*{20}{c}} {{{t}_{1}}} \\ {{{t}_{2}}} \\ \vdots \\ {{{t}_{n}}} \end{array}\;\begin{array}{*{20}{c}} {t_{1}^{2}} \\ {t_{2}^{2}} \\ \vdots \\ {t_{n}^{2}} \end{array}\;\begin{array}{*{20}{c}} {...} \\ {...} \\ \ddots \\ {...} \end{array}\;\begin{array}{*{20}{c}} {t_{1}^{\kappa }} \\ {t_{2}^{\kappa }} \\ \vdots \\ {t_{n}^{\kappa }} \end{array}} \right),\quad {\mathbf{H}} = \left( {\begin{array}{*{20}{c}} {1{\text{/}}\sigma _{1}^{2}}&0&{...}&0 \\ 0&{1{\text{/}}\sigma _{2}^{2}}&{...}&0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0&{...}&{1{\text{/}}\sigma _{n}^{2}} \end{array}} \right).$Тогда система нормальных уравнений для определения параметров траектории $\lambda $ запишется в виде
а решение в виде где ${\mathbf{\hat {\lambda }}} = {{({{\hat {\lambda }}_{0}},{{\hat {\lambda }}_{1}},...,{{\hat {\lambda }}_{\kappa }})}^{T}}$ – МНК-оценки коэффициентов полинома. Корреляционная матрица погрешностей оценок $\hat {\lambda }$ вычисляется с помощью формулы(26)
${{{\mathbf{K}}}_{{{\mathbf{\hat {\lambda }}}}}} = {{({{{\mathbf{C}}}^{T}}{\mathbf{HC}})}^{{ - 1}}}.$Рассмотрим конкретный практический случай, когда траектория описывается полиномом 2‑й степени, т.е. учитываются скорость и ускорение КА:
(27)
${\mathbf{r}}({\mathbf{\lambda }},t) = {{{\mathbf{r}}}_{n}} + {{{\mathbf{\dot {r}}}}_{n}}(t - {{t}_{n}}) + {{{\mathbf{\ddot {r}}}}_{n}}{{(t - {{t}_{n}})}^{2}},$(28)
${\mathbf{C}} = \left( {\begin{array}{*{20}{c}} 1&{{{t}_{1}} - {{t}_{n}}}&{{{{({{t}_{1}} - {{t}_{n}})}}^{2}}} \\ 1&{{{t}_{2}} - {{t}_{n}}}&{{{{({{t}_{2}} - {{t}_{n}})}}^{2}}} \\ \vdots & \vdots & \vdots \\ 1&{{{t}_{{n - 1}}} - {{t}_{n}}}&{{{{({{t}_{{n - 1}}} - {{t}_{n}})}}^{2}}} \\ 1&0&0 \end{array}} \right).$(29)
$ \times \;\left( {\begin{array}{*{20}{c}} 1&{{{t}_{1}} - {{t}_{n}}}&{{{{({{t}_{1}} - {{t}_{n}})}}^{2}}} \\ 1&{{{t}_{2}} - {{t}_{n}}}&{{{{({{t}_{2}} - {{t}_{n}})}}^{2}}} \\ \vdots & \vdots & \vdots \\ 1&{{{t}_{{n - 1}}} - {{t}_{n}}}&{{{{({{t}_{{n - 1}}} - {{t}_{n}})}}^{2}}} \\ 1&0&0 \end{array}} \right) = $Для упрощения дальнейших выкладок предположим, что измерения производятся через равные промежутки времени длиной T0. Такой случай можно заложить на этапе планирования миссии. Также этот вариант полезен для быстрых практических оценок точности получаемых параметров. Тогда
(30)
$\sum\limits_{i = 1}^n {{{{({{t}_{i}} - {{t}_{n}})}}^{3}}} = - T_{0}^{3}\sum\limits_{i = 1}^{n - 1} {{{i}^{3}}} = - T_{0}^{3}\frac{{{{{(n - 1)}}^{2}}{{n}^{2}}}}{4},$Подставляя эти выражения в матрицу CTHC и обращая ее, получим корреляционную матрицу ошибок
(31)
${{{\mathbf{K}}}_{{{\mathbf{\hat {\lambda }}}}}} = {{({{{\mathbf{C}}}^{T}}{\mathbf{HC}})}^{{ - 1}}} = {{\sigma }^{2}}\left( {\begin{array}{*{20}{c}} {\frac{{9n(n - 1) + 6}}{{n(n + 1)(n + 2)}}}&{\frac{{18(2n - 1)}}{{({{n}^{2}} + 3n + 2)n{{T}_{0}}}}}&{\frac{{30}}{{({{n}^{2}} + 3n + 2)nT_{0}^{2}}}} \\ {\frac{{18(2n - 1)}}{{({{n}^{2}} + 3n + 2)n{{T}_{0}}}}}&{\frac{{12(8n - 11)(2n - 1)}}{{({{n}^{5}} - 5{{n}^{3}} + 4n)T_{0}^{2}}}}&{\frac{{180}}{{({{n}^{3}} + {{n}^{2}} - 4n - 4)nT_{0}^{3}}}} \\ {\frac{{30}}{{({{n}^{2}} + 3n + 2)nT_{0}^{2}}}}&{\frac{{180}}{{({{n}^{3}} + {{n}^{2}} - 4n - 4)nT_{0}^{3}}}}&{\frac{{180}}{{({{n}^{5}} - 5{{n}^{3}} + 4n)T_{0}^{4}}}} \end{array}} \right).$Выражения для быстрой оценки СКО определяемых параметров получим, если примем еще одно упрощающее предположение: число измерений n должно быть относительно велико, скажем n ≥ 7–10. Тогда
(32)
$\left( {\begin{array}{*{20}{c}} {{{\sigma }_{r}}} \\ {{{\sigma }_{{\dot {r}}}}} \\ {{{\sigma }_{{\ddot {r}}}}} \end{array}} \right) \approx \sigma \left( {\begin{array}{*{20}{c}} {\frac{3}{{\sqrt n }}} \\ {\frac{{14}}{{\sqrt {{{n}^{3}}} {{T}_{0}}}}} \\ {\frac{{13}}{{\sqrt {{{n}^{5}}} T_{0}^{2}}}} \end{array}} \right).$Вектор оценок радиус-вектора, скорости и ускорения КА определяется следующим выражением
(33)
$\begin{gathered} {\mathbf{\hat {\lambda }}} = \left( {\begin{array}{*{20}{c}} {\frac{{9n(n - 1) + 6}}{{n(n + 1)(n + 2)}}}&{\frac{{18(2n - 1)}}{{({{n}^{2}} + 3n + 2)n{{T}_{0}}}}}&{\frac{{30}}{{({{n}^{2}} + 3n + 2)nT_{0}^{2}}}} \\ {\frac{{18(2n - 1)}}{{({{n}^{2}} + 3n + 2)n{{T}_{0}}}}}&{\frac{{12(8n - 11)(2n - 1)}}{{({{n}^{5}} - 5{{n}^{3}} + 4n)T_{0}^{2}}}}&{\frac{{180}}{{({{n}^{3}} + {{n}^{2}} - 4n - 4)nT_{0}^{3}}}} \\ {\frac{{30}}{{({{n}^{2}} + 3n + 2)nT_{0}^{2}}}}&{\frac{{180}}{{({{n}^{3}} + {{n}^{2}} - 4n - 4)nT_{0}^{3}}}}&{\frac{{180}}{{({{n}^{5}} - 5{{n}^{3}} + 4n)T_{0}^{4}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1&{...}&1&1 \\ {{{t}_{1}} - {{t}_{n}}}&{...}&{{{t}_{{n - 1}}} - {{t}_{n}}}&0 \\ {{{{({{t}_{1}} - {{t}_{n}})}}^{2}}}&{...}&{{{{({{t}_{{n - 1}}} - {{t}_{n}})}}^{2}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{y}_{1}}} \\ \vdots \\ {{{y}_{{n - 1}}}} \\ {{{y}_{n}}} \end{array}} \right) = \\ = \left( {\begin{array}{*{20}{l}} {\frac{3}{{n(n + 1)(n + 2)}}\sum\limits_{i = 1}^n {[2 + 2i(5i - 3) + 3n - 8ni + {{n}^{2}}]} {{y}_{i}}} \\ {\frac{6}{{n({{n}^{4}} - 5{{n}^{2}} + 4){{T}_{0}}}}\sum\limits_{i = 1}^n {[30{{i}^{2}}(n - 1) + (n + 2)(n + 1)(4n - 3) + i(22 - 28{{n}^{2}})]{{y}_{i}}} } \\ {\frac{{30}}{{n({{n}^{4}} - 5{{n}^{2}} + 4)T_{0}^{2}}}\sum\limits_{i = 1}^n {[6{{i}^{2}} - 6i(n + 1) + (n + 1)(n + 2)]{{y}_{i}}} } \end{array}} \right). \\ \end{gathered} $Таким образом, оценки радиус-вектора, скорости и ускорения в случае n равноотстоящих и равноточных измерений можно записать в общем виде
(34)
${{{\mathbf{\hat {r}}}}_{n}} = \sum\limits_{i = 1}^n {{{b}_{{ri}}}} {{y}_{i}},\quad {{{\mathbf{\hat {\dot {r}}}}}_{n}} = \sum\limits_{i = 1}^n {{{b}_{{\dot {r}i}}}} {{y}_{i}},\quad {{{\mathbf{\hat {\ddot {r}}}}}_{n}} = \sum\limits_{i = 1}^n {{{b}_{{\ddot {r}i}}}} {{y}_{i}},$Эти коэффициенты представляют импульсные характеристики дискретных фильтров, на выходе которых имеем оценки дальности, скорости и ускорения.
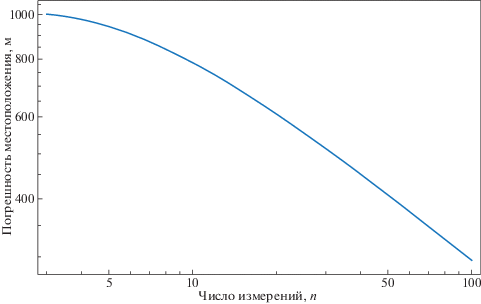
Графики уменьшения погрешности параметров траектории в зависимости от количества измерений n, проводимых через интервал времени T0, показаны на рис. 6–8.
Рис. 7.
Погрешность измерения скорости КА в зависимости от числа измерений n при разных интервалах измерений T0.
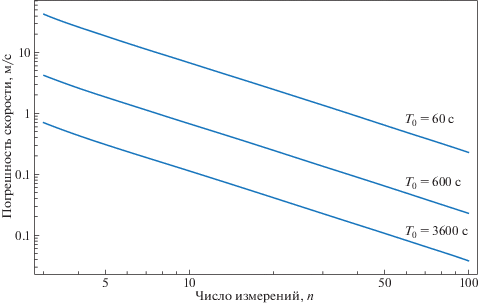
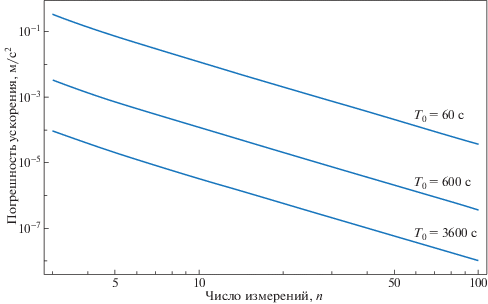
Рис. 8.
Погрешность измерения ускорения КА в зависимости от числа измерений n при разных интервалах измерений T0.
Отдельно стоит проанализировать график погрешности радиус-вектора. При увеличении числа измерений с трех до ста видно, что погрешность уменьшается с 1000 до 300 м – медленнее, чем в $\sqrt {100{\text{/}}3} \approx 6$ раз. Особенно явно этот эффект виден при небольшом числе измерений. Это связано со сложным поведением элемента корреляционной матрицы, ответственного за радиус-вектор. Таким образом, простое увеличение числа измерений во времени не приводит к ожидаемому улучшению точности радиус-вектора.
Альтернативным способом увеличить статистику измерений являются использование более четырех пульсаров и вычисление параметров траектории по всем их возможным комбинациям.
4. СПИСКИ РЕПЕРНЫХ ПУЛЬСАРОВ ДЛЯ НАВИГАЦИИ КА
Прямое определение положения КА методом, подобным методу решения задачи определения положения объекта по спутникам системы глобального позиционирования, когда положение объекта находится квазимгновенно при минимуме априорной информации о начальном положении и скорости объекта, для задачи навигации по пульсарам трудноразрешимо по следующим соображениям:
• Отсутствие “временных меток” (неразличимость импульсов), которые позволяли бы определять счетный номер импульса, что приводит, в общем случае, к неопределенности определения МПИ пульсара с точностью до периода. Теоретическая возможность использования пульсаров, генерирующих гигантские импульсы, которые имеют уникальную структуру и исключительную мощность, что в свою очередь позволяет регистрировать отдельный импульс даже с использованием антенны умеренной эффективной площади, на практике ограничивается следующими соображениями: (а) необходимостью знать временную привязку такого импульса, что требует обмена информации с наземным пунктом наблюдения пульсара, (б) малым числом пульсаров, регулярно генерирующих достаточно мощные гигантские импульсы
• Техническая сложность реализации одновременного наблюдения нескольких пульсаров (не менее 3 для решения задачи навигации и не менее 4 для решения задачи уточнения хода бортовых часов)
• Достаточно большое время накопления слабого сигнала радиопульсара в сравнении со временем изменения положения КА в пространстве (типичные времена накопления 1000 и более секунд при скорости КА в единицы километров в секунду)
С учетом вышеуказанного, реалистичным методом определения положения КА является уточнение расчетного положения КА относительно вычисленного по изначально заданному положению и скорости в заданной системе отсчета и/или уточнение параметров орбиты КА, который и будет рассматриваться далее в качестве базового.
Для выработки сценария наблюдений и выбора набора пульсаров, подходящего для его реализации, ограничим круг основных навигационных задач, которые могут быть решены методом хронометрирования пульсаров:
1. Грубое определение положения КА в пространстве с точностью до сотен километров. Данная задача возникает при навигации в дальнем космическом пространстве на перелетных орбитах к планетам Солнечной системы или при перелете к Луне, когда произошла потеря информации о положении КА, а восстановление ее радиометрическим методами невозможно. При этом исходное положение КА может быть известно (в направлении на реперный пульсар) с достаточно малой точностью – в общем случае не хуже сP/2. Данное требование связано с тем, что если ошибка в первоначальном определении положения КА (во временной мере) превосходит половину периода пульсара, то невозможно однозначно определить правильный счетный номер опорного импульса (происходит т.н. “потеря фазы”), который необходимо знать для определения поправки к положению КА. Например, при периоде собственного вращения пульсара ~1 с, неопределенность начального положения КА должна составлять около 150 тыс. км, что, очевидно, достигается при любых разумных начальных условиях. Для миллисекундного пульсара (с периодом от единиц до десятков миллисекунд) потеря фазы возможна при ошибке определения первоначального положения от ~200 (для одного из самых быстрых миллисекундных пульсаров B1937+21) до нескольких сотен километров.
2. Высокоточное определение положения и скорости и ускорения КА по наблюдениям пульсаров с точностью до десятков километров. Данная задача может возникнуть при дальних космических перелетах или перелетах к Луне.
3. Уточнение параметров орбит в дальних космических перелетах. Данная задача, очевидно, сводится к предыдущей.
4. Уточнение параметров орбит КА вокруг Земли, Луны и планет Солнечной системы. Данная задача сводится к многократным продолжительным наблюдениям группы реперных пульсаров с вычислением МПИ для каждого наблюдения и последующего решения систем уравнений относительно невязок орбитальных параметров КА с минимизацией СКО остаточных уклонений (ОУ – разницей между вычисленными и наблюденными МПИ пульсаров). Отметим, что это единственно возможный подход с учетом того факта, что периоды обращения КА вокруг тел Солнечной системы на низких орбитах соизмеримы со временем цикла наблюдения 3–4 реперных пульсаров, необходимым для вычисления положения КА.
Перечисленные задачи приводят к следующим требованиям к постановке наблюдений и выбору пульсаров:
• Решение первой и, в ограниченных пределах, третьей задачи обеспечивается наблюдениями группы мощных (секундных и миллисекундных) пульсаров с СКО ОУ МПИ порядка десятков и сотен микросекунд (рис. 9). Для надежного определения положения пульсаров в пространстве желательно обеспечить сохранение фазы пульсара между двумя наблюдениями (уход фазы за время между наблюдениями должен быть меньше 1/2 наблюдаемого периода пульсара). Ожидаемая точность привязки интегрального импульса в сеансе наблюдения – не хуже 1 мс, что обеспечивает определение положения КА в направлении на пульсар до 300 км.
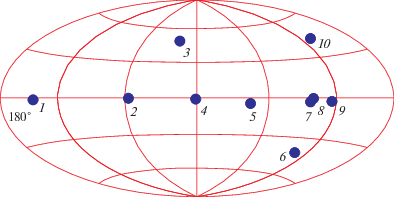
Рис. 9.
Опорные пульсары из табл. 2 (“сценарий грубого определения”). Карта в галактических координатах, долгота растет справа налево. Пульсары обозначены следующим образом: 1 – B0329+54, 2 – B1937+21, 3 – B1534+12, 4 – B1749-28, 5 – B1449-64, 6 – J0437-4715, 4 – B1449-64, 7 – B0833-45, 8 – B0835-41, 9 – B0740-28, 10 – B0950+08.
• Решение 2-й, 3-й и 4-й задачи обеспечивается наблюдениями групп менее мощных миллисекундных пульсаров (рис. 10). Точность привязки интегрального импульса в сеансе наблюдения в пределах нескольких десятков мкс, что обеспечивает точность определения положения КА в пределах от единиц до нескольких десятков км.
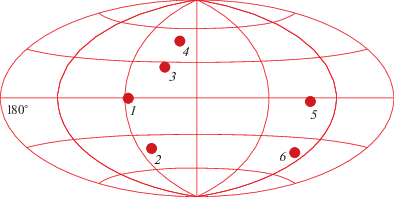
Рис. 10.
Опорные пульсары из табл. 3 и 4 (“сценарий точного определения”). Карта в галактических координатах, долгота растет справа налево. Пульсары обозначены следующим образом: 1 – B1937+21, 2 – J2145–0750, 3 – J1713+0747, 4 – B1534+12, 5 – B0833-45, 6 – J0437–4715.
Достижение сколько-нибудь приемлемого отношения сигнал/шум возможно только при использовании режима синхронного накопления (суммирования с наблюдаемым периодом) импульсов пульсара, который позволяет улучшать отношение сигнал/шум как N1/2, где N – количество просуммированных импульсов.
Оценим значение сигнал/шум для цифрового приемника в режиме многоканального приема излучения пульсара. Радиометрический выигрыш при таком режиме наблюдений обеспечивается тем, что общая полоса частот разбивается на несколько частотных каналов, в каждом из которых реализуется додетекторная компенсация дисперсии пульсара. Радиометрический выигрыш в этом случае равен корню квадратному из числа частотных каналов. В случае последетекторной компенсации дисперсии сигнал оцифровывается с интервалом выборки (определяемым теоремой Котельникова), производятся его Фурье-преобразование в энергетический частотный спектр и суммирование со сдвигом полученных частотных каналов на величину дисперсионной задержки импульса. В этом случае радиометрический выигрыш также равен корню квадратному из числа каналов частотного спектра. Таким образом, в случае использования цифровой обработки сигнала для приемно-регистрирующего комплекса, формула для вычисления отношения сигнал/шум имеет вид:
(35)
$S{\text{/}}N = \frac{{S{{A}_{{{\text{eff}}}}}{{{\left( {{{n}_{{{\text{pol}}}}}{{N}_{{{\text{ch}}}}}} \right)}}^{{1/2}}}}}{{2k{{T}_{{{\text{sys}}}}}}}{{\left( {\frac{T}{P}} \right)}^{{1/2}}}\frac{P}{W},$При разумных предположениях о форме импульса (квазигауссовый, одно- или двухкомпонентный симметричный сигнал с хорошо разделяемыми компонентами) величина погрешности определения одиночного МПИ при наивыгоднейшем с точки отношения сигнал/шум выборе постоянной времени детектора оценивается сверху как [20]
где W – ширина импульса, если постоянная времени детектора τ = W.В случае, когда регистрируется несколько точек на импульсе, формула для погрешности определения МПИ запишется как (данная оценка может считаться корректной при S/N > 5 для суммарного импульса [20]):
где W – длительность импульса пульсара; Δt – интервал между отсчетами на импульсе; S/N – отношение сигнал/шум.Подставляя (38) в (40), получим оценку точности определения МПИ δt:
где S0 – параметр, имеющий размерность спектральной плотности потока (Вт/м2/Гц или Ян), который зависит только от характеристик антенны и режима наблюдений:(39)
${{S}_{0}} = \frac{{0.6k{{T}_{{{\text{sys}}}}}}}{{{{A}_{{{\text{eff}}}}}\sqrt {{{n}_{{{\text{pol}}}}}T\Delta f} }}.$(40)
$\begin{gathered} {{S}_{0}} = 3.7\;{\text{мЯн}}\,\left( {\frac{{{{T}_{{{\text{sys}}}}}}}{{100\;{\text{K}}}}} \right){{\left( {\frac{{\Delta f}}{{100\;{\text{МГц}}}}} \right)}^{{ - 1/2}}} \times \\ \times \;{{\left( {\frac{T}{{1000\;{\text{с}}}}} \right)}^{{ - 1/2}}}{{\left( {\frac{{{{A}_{{{\text{eff}}}}}}}{{50\;{{{\text{м}}}^{2}}}}} \right)}^{{ - 1}}}. \\ \end{gathered} $Для обеспечения качественного определения МПИ необходимо, чтобы это изменение не превосходило относительную ширину импульса W/P (данный критерий также достаточно произволен и установлен феноменологически как обобщение опыта хронометрирования пульсаров). Из этого выводится выражение для максимально возможной продолжительности Tmax:
Этот предел не является фундаментальным, общее время накопления может быть и значительно большим при условии, что оно разбивается на отдельные сегменты малой продолжительности T < Tmax. Этот подход отработан при наземных наблюдениях миллисекундных пульсаров и может быть применен при определении положения во время движения по орбитам вокруг тел различных тел Солнечной системы, когда ускорения достигают больших значений.Характерные значения ускорения a и соответствующие максимальные времена когерентного накопления Tmax меняются в широких пределах: для перелетной траектории на расстоянии r от Солнца a мало:
Наблюдения пульсаров на низких частотах имеют свои достоинства, такие как значительно больший поток, и недостатки. Основным недостатком является более сильное воздействие межзвездной и межпланетной сред на распространение сигнала и в итоге на наблюдения. Прежде всего это воздействие будет заключаться в спорадическом возникновении межзвездных мерцаний, которые могут значительно увеличивать наблюдаемую ширину импульса, что в свою очередь будет снижать точность определения положения. Вторым важным эффектом является дисперсия сигнала, приводящая к тому, что сигнал на низких частотах запаздывает относительно сигнала на высоких. Дисперсионная задержка относительно свободного распространения (или, эквивалентно, распространения сигнала бесконечной частоты) на частоте f выражается следующей формулой:
(42)
$\Delta {{t}_{{{\text{disp}}}}} = 4.15\left( {\frac{1}{{{{f}^{2}}}}} \right){\text{DM}}\;{\text{мс}},$Таблица 1.
Вариации меры дисперсии и соответствующие ошибки определения МПИ для ярких миллисекундных пульсаров [21–23]
| PSR | σDM, 10–4 пк см–3 | δtDM, мкс |
|---|---|---|
| J0437-4715 | <1* | <2.6 |
| J1643-1224 | 3 | 8 |
| J1713+0747 | 2 | 5.2 |
| J1744-1134 | 4 | 10 |
| B1937+21 | <1** | <2.6 |
| J2145-0750 | 1.5 | 4 |
| * – верхняя оценка, ** – верхняя оценка на годовом интервале; поскольку пульсар обладает существенным вековым ходом меры дисперсии, для сохранения указанной точности желательна передача информации о текущем значении DM на борт КА с периодичностью 1 раз в год | ||
Кроме величины δt, связанной с конечным временем наблюдения, и δtDM, в полную ошибку определения положения δtполн вносит вклад еще член, описывающий собственный шум пульсара, который может характеризоваться, например, вариацией ОУ МПИ σTOA.
Для задачи определения положения КА были отобраны пульсары, которые позволяют достичь достаточно высокой точности за приемлемое время наблюдений. Для сценария грубого определения положения КА был выбран уровень точности δtполн ~ 1 мс, что соответствует точности определения положения 300 км, и время накопления менее 10 000 секунд. Кандидаты должны допускать надежное хронометрирование, т. е. при наблюдении должен достигаться уровень S/N > 10. Кандидаты, удовлетворяющие этим условиям и их свойства, приведены в табл. 2.
Таблица 2.
Свойства 10 пульсаров, которые позволяют достичь S/N > 10 за время наблюдения менее 10 000 с, но не обладают собственной стабильностью, достаточной для решения точной навигационной задачи. Данный набор пульсаров пригоден для решения грубой навигационной задачи (δt = 100–1000 мкс). Tsky взята из данных наблюдений на частоте 408 МГц [22] (см. рис. 9). Trec принимается равной 100 К
| PSR | Гал. широта, l,° | Гал. долгота, b,° | Tsky, K | S400, мЯн | P, мс |
|---|---|---|---|---|---|
| B0329+54 | 144.99 | –1.22 | 57 | 1500 | 710 |
| J0437-4715 | 253.39 | –41.96 | 18 | 550 | 5.7 |
| B0740-28 | 243.773 | –2.444 | 32 | 296 | 16 |
| B0833-45 | 263.552 | –2.787 | 214 | 5000 | 89 |
| B0835-41 | 260.904 | –0.336 | 51 | 197 | 751 |
| B0950+08 | 228.908 | 43.697 | 15 | 400 | 253 |
| B1449-64 | 315.733 | –4.427 | 75 | 230 | 179 |
| B1534+12 | 19.848 | 48.341 | 39 | 36 | 38 |
| B1749-28 | 1.540 | –0.961 | 419 | 1100 | 562 |
| B1937+21 | 57.51 | –0.29 | 97 | 240 | 1.6 |
Дальнейшее уточнение положения возможно лишь при наблюдении миллисекундных пульсаров, чаще всего обладающих более слабым потоком. В связи с этим порог обнаружения для них был понижен до S/N > 5. В табл. 3 и табл. 4 приведены эти пульсары и их свойства.
Таблица 3.
Свойства шести пульсаров, которые позволяют достичь полной точности определения МПИ менее 50 мкс за время наблюдения 10 000 сек и менее при достижении порогового отношения сигнал/шум S/N > 5 (“сценарий точного определения”). Tsky взята из данных наблюдений на частоте 408 МГц [22] (см. рис. 10). Trec принимается равной 100 К. Жирным шрифтом выделены пульсары, для которых отношение S/N превосходит 10 при продолжительности наблюдений в 10 000 с
| PSR | Гал. широта, l,° | Гал. долгота, b,° | Tsky, K | S, мЯн | P, мс |
|---|---|---|---|---|---|
| J0437-4715 | 253.39 | –41.96 | 18 | 550 | 5.7 |
| B0833-45 | 263.55 | –2.79 | 214 | 5000 | 89 |
| B1534+12 | 19.85 | 48.34 | 39 | 36 | 38 |
| J1713+0747 | 28.75 | 25.22 | 59 | 36 | 4.6 |
| B1937+21 | 57.51 | –0.29 | 97 | 240 | 1.6 |
| J2145-0750 | 47.78 | –42.08 | 26 | 100 | 16 |
Таблица 4.
Свойства шести пульсаров, которые позволяют достичь полной точности определения МПИ менее 50 мкс за время наблюдения 10 000 сек и менее при достижении порогового отношения сигнал/шум S/N > 5 (“сценарий точного определения”). Обозначения в таблице: S/N – отношение сигнал/шум при продолжительности сеанса наблюдений 10 000 сек, T(S/N = 5) – продолжительность наблюдений, необходимая для достижения отношения сигнал/шум S/N = 5, δt – ошибка определения МПИ при продолжительности сеанса наблюдений 10 000 с, δtDM – ошибка, вызванная случайными вариациями меры вращения DM, σTOA – среднеквадратичное отклонение рядов ОУ МПИ соответствующих пульсаров, δtполн – полная ошибка определения. Жирным шрифтом выделены пульсары, для которых отношение S/N превосходит 10 при продолжительности наблюдений в 10 000 с, * – верхний предел
| PSR | S/N | T(S/N = 5), 103 с | δt, мкс | σTOA, мкс | δtDM, мкс | δtполн, мкс |
|---|---|---|---|---|---|---|
| J0437-4715 | 47 | 0.11 | 0.5 | 0.3 | 2.6 | 2.7 |
| B0833-45 | 184 | 0.01 | 0.22 | 40 | 10* | 40 |
| B1534+12 | 13 | 1.5 | 3.3 | 40 | 10* | 40 |
| J1713+0747 | 5.4 | 8.6 | 0.75 | 0.4 | 5.2 | 5.3 |
| B1937+21 | 68 | 0.05 | 0.1 | 0.7 | 2.6 | 2.8 |
| J2145-0750 | 5.1 | 9.6 | 3.6 | 1.8 | 4.0 | 5.7 |
Для расчетов использовались следующие параметры приемной аппаратуры и антенны Aeff – эффективная площадь = 50 м2, число поляризаций npol = 2, ширина полосы приемника Δf = = 100 МГц, центральная частота наблюдений f = = 400 МГц, температура приемника Trec = 100 K.
5. АЛГОРИТМ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ КА И ПОПРАВОК К БОРТОВОЙ ШКАЛЕ
5.1. Редукция МПИ к барицентру Солнечной системы
Редукция МПИ в барицентр Солнечной системы сводится к вычислению разности МПИ $t - \tilde {t}{\text{\;}}$ в барицентр и точку наблюдения с радиус-вектором ${\mathbf{\vec {r}}}$. Формула редукции записывается в следующем виде [3, 24]:
(43)
$t - \tilde {t} = \frac{1}{c}{\mathbf{\vec {n}}} \cdot {\mathbf{\vec {r}}} - \frac{1}{{2cR}}{{[{\mathbf{\vec {n}}} \times {\mathbf{\vec {r}}}]}^{2}} + \gamma + \Delta {{t}_{{{\text{DM}}}}},$(44)
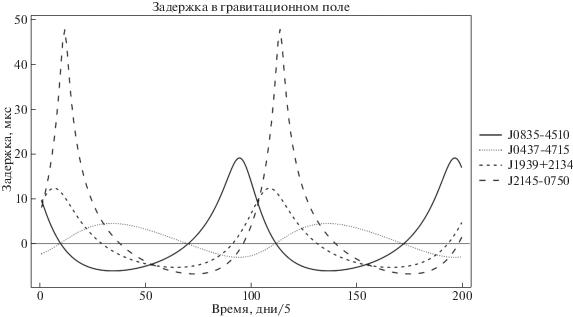
$\gamma = - \mathop \sum \limits_p \frac{{2G{{M}_{p}}}}{{{{c}^{3}}}}\ln [1 - {\mathbf{\vec {n}}} \cdot {{{\mathbf{\vec {n}}}}_{{rp}}}],$Далее в иллюстративных целях была взята перелетная орбита к Марсу со следующими параметрами: a = 1.19 а.е., e = 0.16, i = 1.7°, ω = 90°, Ω = = 76°, TП = 51 975. График задержки Шапиро показан на рис. 11.
Задержка сигнала в среде ΔtDM вычисляется по следующей формуле
(45)
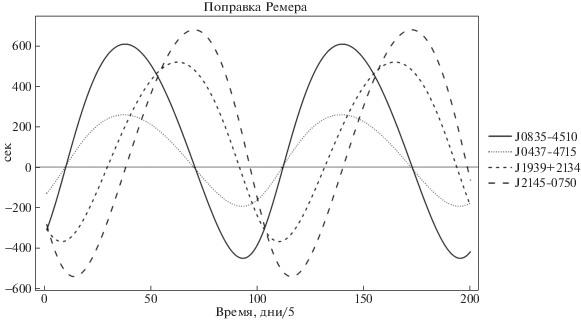
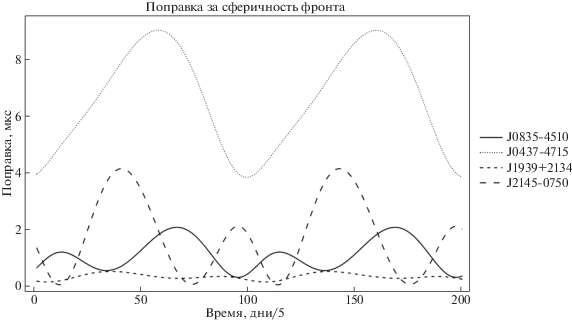
$\Delta {{t}_{{{\text{DM}}}}} = \frac{{{\text{DM}}}}{{2.410331 \times {{{10}}^{{ - 16}}}{{f}^{2}}}},$Первый член в правой части уравнения (43) называется поправкой Ремера. Она дает основной вклад в разность $t - \tilde {t}.$ Второй член справа в уравнении (43) вызван сферичностью фронта пульсарного сигнала. Рис. 12 показывает график задержки Ремера для четырех пульсаров, на рис. 13 показан график поведения задержки, вызванной сферичностью фронта сигнала.
Барицентрический момент времени t используется далее для вычисления вращательной фазы пульсара N по формуле
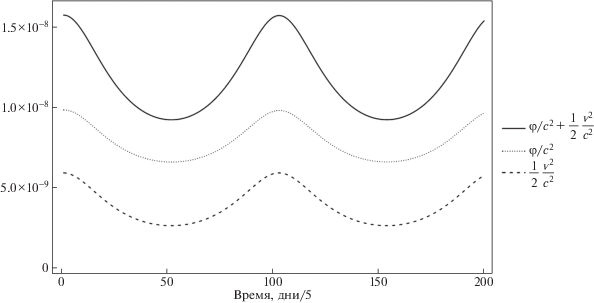
где $\nu ,\;\dot {\nu }$ – частота и производная частоты вращения пульсара на эпоху вращательных параметров t0, ε(t) – шумовая составляющая, которая включает собственные шумы вращения пульсара, неточность модели задержки, вклад бортовой шкалы. В идеальном случае при ε(t) = 0 идеальной модели и абсолютно точных вращательных параметрах N(t) должно быть большим целым числом, на практике же оно отличается от целого на величину ≪1. В единицах времени это отличие выражается следующим образом где R[*] – функция округления до ближайшего целого.Разность $t - \tilde {t}$ должна быть выражена в одной шкале времени, например TCB – шкале барицентрического координатного времени. Для этого необходимо МПИ, измеренные по бортовой шкале времени (по собственному времени КА), перевести в шкалу TCB. Запишем уравнение, связывающее собственное τ и координатное время t [3]:
(48)
$\frac{{d\tau }}{{dt}} = 1 - \frac{1}{{{{c}^{2}}}}\left( {\varphi + \frac{{{{{v}}^{2}}}}{2}} \right) + O\left( {\frac{{{{{v}}^{4}}}}{{{{c}^{4}}}}} \right).$(49)
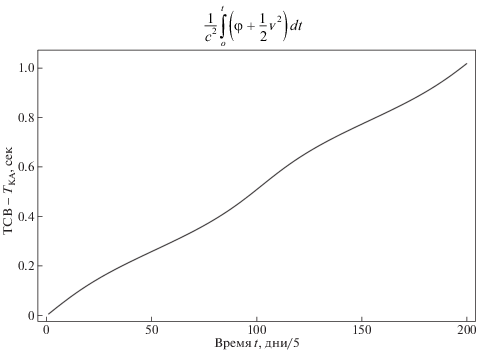
$\varphi = \mathop \sum \limits_p \frac{{G{{M}_{p}}}}{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{p}}} \right|}},$После интегрирования получим
(50)
$t = \tau + \mathop \smallint \limits_{{{t}_{0}}}^t \frac{1}{{{{c}^{2}}}}\left( {\varphi + \frac{{{{{v}}^{2}}}}{2}} \right)dt,$Анализ погрешностей всех малых поправок, входящих в модель (3.3), показывает, что они вычисляются с достаточным запасом точности, исходя из знания априорной орбиты, и укладываются в заданную точность определения орбиты КА.
5.2. Система уравнений для нахождения поправок к положению КА и бортовой шкале
Как уже было сказано ранее, формула для определения радиус-вектора КА записывается в следующем виде:
(51)
$\widehat {\vec {r}} = \frac{{{{A}_{1}}[{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}] + {{A}_{2}}[{{{\vec {n}}}_{1}} \times {{{\vec {n}}}_{3}}] + {{A}_{3}}[{{{\vec {n}}}_{1}} \times {{{\vec {n}}}_{2}}]}}{{({{{\vec {n}}}_{1}} \cdot [{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}])}},$(52)
$\begin{gathered} {{A}_{2}}\, = \,({{{\vec {n}}}_{2}} \cdot \vec {r})\, = \,c({{t}_{2}}\, - \,{{{\tilde {t}}}_{2}})\, + \,\frac{1}{{2{{R}_{2}}}}{{[{{{\vec {n}}}_{2}} \times \vec {r}]}^{2}}\, - \,{{\gamma }_{2}}\, - \,\frac{{{\text{D}}{{{\text{M}}}_{2}}}}{{{{f}^{2}}}}, \\ {{A}_{3}}\, = \,({{{\vec {n}}}_{3}} \cdot \vec {r})\, = \,c({{t}_{3}}\, - \,{{{\tilde {t}}}_{3}})\, + \,\frac{1}{{2{{R}_{3}}}}{{[{{{\vec {n}}}_{3}} \times \vec {r}]}^{2}}\, - \,{{\gamma }_{3}}\, - \,\frac{{{\text{D}}{{{\text{M}}}_{3}}}}{{{{f}^{2}}}}, \\ \end{gathered} $(53)
$\widehat {\vec {r}} = \vec {r} + \delta \vec {r} = \frac{{({{A}_{1}} + \delta A)[{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}] + ({{A}_{2}} + \delta A)[{{{\vec {n}}}_{1}} \times {{{\vec {n}}}_{3}}] + \left( {{{A}_{3}} + \delta A} \right)[{{{\vec {n}}}_{1}} \times {{n}_{2}}]}}{{({{{\vec {n}}}_{1}} \cdot [{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}])}},\quad \delta A = с\Delta \tau .$(54)
$\begin{gathered} \delta \vec {r} = \delta A\frac{{[{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}] + [{{{\vec {n}}}_{1}} \times {{{\vec {n}}}_{3}}] + [{{{\vec {n}}}_{1}} \times {{n}_{2}}]}}{{({{{\vec {n}}}_{1}} \cdot [{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}])}},~ \\ \delta A = с\Delta \tau . \\ \end{gathered} $(55)
$\vec {r} = \frac{{({{A}_{1}} - {{A}_{2}})[{{{\vec {k}}}_{2}} \times {{{\vec {k}}}_{3}}] + ({{A}_{2}} - {{A}_{3}})[{{{\vec {k}}}_{1}} \times {{{\vec {k}}}_{3}}] + ({{A}_{3}} - {{A}_{4}})[{{{\vec {k}}}_{1}} \times {{{\vec {k}}}_{2}}]}}{{({{{\vec {k}}}_{1}} \cdot [{{{\vec {k}}}_{2}} \times {{{\vec {k}}}_{3}}])}},$В уравнения (51), (53)–(55) в знаменатель входит псевдоскаляр – смешанное произведение векторов. Очевидно, что знаменатель должен как можно сильнее отличаться от нуля, иначе мы получим ухудшение точности вычисления координат КА. Это достигается таким выбором пульсаров, чтобы они по возможности были близки к ортогональной тройке векторов. Для используемых пульсаров величина $({{\vec {n}}_{1}} \cdot [{{\vec {n}}_{2}} \times {{\vec {n}}_{3}}]) = 0.284$ и $({{\vec {k}}_{1}} \cdot [{{\vec {k}}_{2}} \times {{\vec {k}}_{3}}]) = 0.316$. В ГНСС величина, обратная смешанному произведению, имеет сокращение DOP (Dilution of Precision, фактор снижения точности) и всегда приводится для используемой конфигурации спутников.
Векторное уравнение (54) представляет собой систему трех уравнений, записанных для каждой из координат. Поправка бортовой шкалы Δτ находится путем вычисления среднего из найденных трех значений.
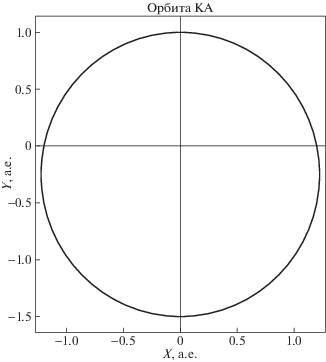
В качестве иллюстрации применения изложенного выше метода рассмотрим перелетную орбиту к Марсу. За основу возьмем гомановский эллипс (рис. 16) с уже приведенными ранее кеплеровскими параметрами:
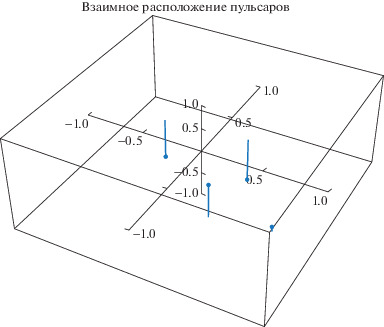
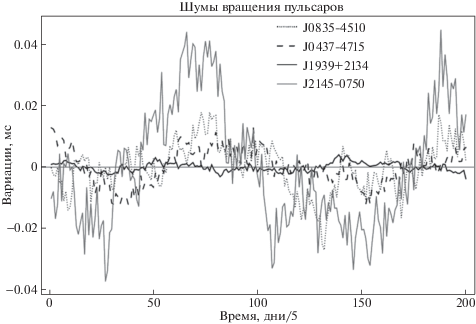
В качестве навигационных пульсаров возьмем следующие: J0835–4510, J0437–4715, J1939+2134, J2145–0750. Их взаимное расположение в эклиптической системе координат показано на рис. 17. Проекция на эклиптику показана тонкими линиями.Остаточные уклонения барицентрических МПИ показаны на рис. 18. Взяты модельные значения, которые представляют собой суперпозицию фазового шума случайных блужданий и белого шума. Ход бортовой шкалы был сгенерирован как шум случайных блужданий в частоте (рис. 19).
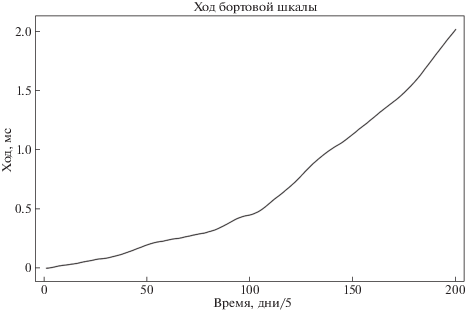
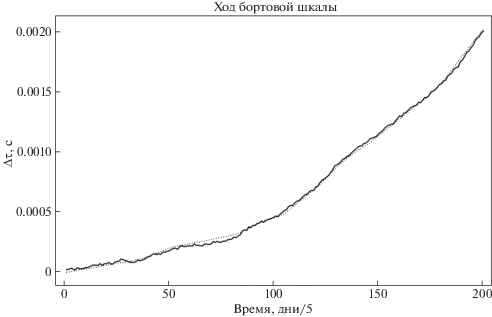
Вычисляя орбиту КА по уравнениям (51) и (53), получим вектор невязок по координатам x, y, z (рис. 20). На рис. 21 показан вектор $\delta \vec {r} = \widehat {\vec {r}} - \vec {r}$ в координатах (x, y)$.$ Из этого рисунка хорошо видно, что если не учитывать ход бортовой шкалы Δτ, то это приведет к смещению координат определяемой орбиты прямо пропорциональному величине Δτ$.$ На рис. 22 показан вычисленный по уравнению (52) ход бортовой шкалы (сплошная линия). Модельный ход шкалы показан пунктирной линией. Точность восстановления хода бортовой шкалы напрямую зависит от шумов вращения пульсаров.
Рис. 21.
Смещение орбиты в координатах (x, y), вызванное неучетом хода бортового стандарта. Отклонения от прямой линии вызваны влиянием собственных шумов пульсаров.
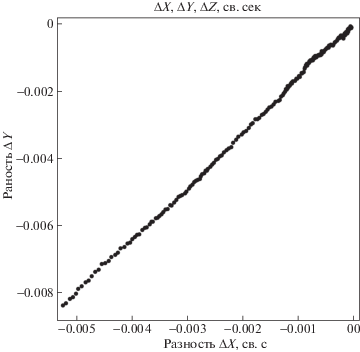
Рис. 22.
Ход бортовой шкалы времени КА, восстановленный по уравнению (52) (сплошная линия). Модельный ход шкалы показан пунктиром.
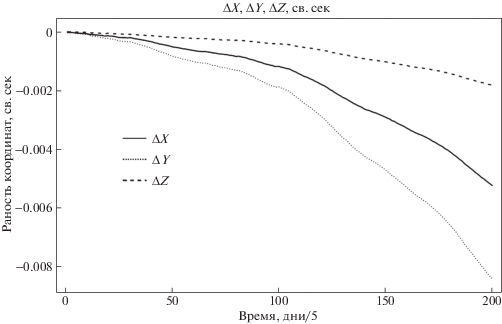
На рис. 23 приведены невязки (Δx, Δy) между радиус-вектором КА, вычисленным по формуле (53) с учетом поправок бортовой шкалы, и теоретическим радиус-вектором, заданным кеплеровскими элементами.
Рис. 23.
Невязки (∆x, ∆y) между радиус-вектором КА, вычисленным по формуле (53) с учетом хода бортовой шкалы, и теоретическим радиус-вектором КА, заданным кеплеровскими элементами.
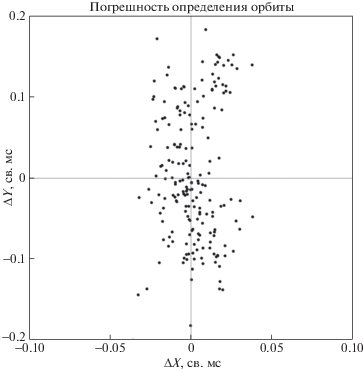
Среднеквадратичные отклонения σx, σy, σz невязок (Δx, Δy, Δz) зависят от ориентации пульсарных единичных векторов относительно координатных осей и знаменателя $({{\vec {n}}_{1}} \cdot [{{\vec {n}}_{2}} \times {{\vec {n}}_{3}}])$. Для их вычисления можно использовать следующее векторное уравнение:
(56)
$({{\sigma }_{x}}~{{\sigma }_{y}},~{{\sigma }_{z}}) = \frac{{\sqrt {\sigma _{1}^{2} + \sigma _{2}^{2}} ~[{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}] + \sqrt {\sigma _{2}^{2} + \sigma _{3}^{2}} ~[{{{\vec {n}}}_{1}} \times {{{\vec {n}}}_{3}}] + \sqrt {\sigma _{3}^{2} + \sigma _{4}^{2}} ~[{{{\vec {n}}}_{1}} \times {{{\vec {n}}}_{2}}]}}{{({{{\vec {n}}}_{1}} \cdot [{{{\vec {n}}}_{2}} \times {{{\vec {n}}}_{3}}])}}.$Улучшить точность измерений местоположения КА можно не только за счет увеличения количества измерений МПИ, но и за счет комбинирования разных четверок пульсаров. В самом деле, даже если использовать набор шести самых стабильных миллисекундных пульсаров из табл. 4, то количество комбинаций (и решений) определяется известной формулой ${{N}_{{{\text{комб}}}}} = \left( {\begin{array}{*{20}{c}} k \\ l \end{array}} \right) = \frac{{k{\kern 1pt} !}}{{l{\kern 1pt} !\left( {k - l} \right){\kern 1pt} !}}$ = = 15, что резко улучшает конечную точность определения координат КА. В качестве примера на рис. 24 приведен график хода бортовой шкалы времени, восстановленный по одному и пятнадцати измерениям.
Рис. 24.
Ход бортовой шкалы, восстановленный по одному измерению (серая линия) и 15 измерениям (синяя линия).

Использование в качестве весов для усредненного решения геометрического фактора ${{({{\vec {n}}_{1}} \cdot [{{\vec {n}}_{2}} \times {{\vec {n}}_{3}}])}^{2}}$ не приводит к улучшению точности определения местоположения и поправок шкалы КА.
6. ЗАКЛЮЧЕНИЕ
Развитие новых наблюдательных и космических технологий открывает новые перспективы в решении фундаментальных задач астрономии и исследования космического пространства. В настоящее время единственным средством для высокоточного измерения собственного времени и положения КА в глубоком космосе является использование уникальных возможностей, предоставляемых наблюдениями высокостабильных реперных пульсаров [25, 26].
В части разработки предложений по созданию бортовых средств для наблюдений пульсаров были проведены исследования по бортовой антенне КА и аппаратуре регистрации для наблюдений пульсаров.
Рассмотрены три возможных варианта бортовой антенны КА для наблюдений пульсаров: фазированная антенная решетка, сферическая зеркальная антенна и параболическая зеркальная антенна. Проанализированы различные типы излучателей для ФАР, проведены расчеты технических параметров рассматриваемых вариантов антенн. Считаем, что оптимальным вариантом бортовой антенны является параболическая зеркальная антенна, обеспечивающая рабочий диапазон частот 300–500 МГц, температуру шума антенны ≈20 К, эффективную площадь антенны ≈50–60 м2 при диаметре раскрыва 9–10 м. Предложено использовать для создания антенн трансформируемые ферменные конструкции, обеспечивающие высокий коэффициент трансформации из транспортного положения в рабочее.
Разработан вариант приемника с цифровой обработкой сигналов, обеспечивающего синхронное с периодом пульсара накопление сигнала и компенсацию дисперсионного запаздывания импульса в широкой полосе частот. Предложенный вариант приемника с полосой регистрируемых частот 105 МГц испытан на радиотелескопе БСА ФИАН. Система программно-фазового запуска регистрации и синтеза периода пульсара обеспечивает длительное накопление сигнала и определение момента регистрации с дискретностью ±10 нс в локальной шкале времени. Разработанные программно-математические методы для фазовых наблюдений пульсаров показали сохранение наблюдаемой фазы импульса пульсара на интервале в несколько суток в реальных наблюдениях пульсаров.
С учетом предложенных бортовых средств КА был уточнен список реперных пульсаров для навигации. Разработаны сценарии для наблюдений реперных пульсаров в различных условиях. Максимально достижимая точность определения координат и скорости КА обеспечивается пульсарами из табл. 4. Минимальная погрешность определения координат в этом случае равна 3.8 км.
Для практического применения разработан алгоритм определения положения КА и поправок к бортовой шкале времени. Приведена пошаговая последовательность действий для редукции МПИ к барицентру Солнечной системы и последующего определения координат КА и поправки к бортовой шкале времени. Для проверки разработанного алгоритма были проведены модельные расчеты для пульсаров из табл. 4 для определения поправок к бортовой шкале времени. Результаты моделирования показывают значения, близко совпадающие с теоретическими оценками предельных погрешностей определения координат КА.
Список литературы
Н. М. Иванова, Л. Н. Лысенко, Баллистика и навигация космических аппаратов (М.: Изд-во МГТУ им. Н.Э. Баумана, 2016).
D. Vallado, Fundamentals of Astrodynamics and Applications (Springer, 2007).
В. Е. Жаров, Сферическая астрономия (Фрязино, 2006).
A. E. Rodin, Y. P. Ilyasov, M. Sekido, and M. Imae, “Space navigation with pulsars”. Japan patent 3780345, 17 March 2006.
M. V. Sazhin, V. E. Zharov, V. K. Milyukov, M. S. Pshirkov, V. N. Sementsov, and O. S. Sazhina. “Space Navigation by X-Ray Pulsars”, Moscow University Physics Bulletin 73, 141 (2018).
S. I. Sheikh, D. J. Pines, P. S. Ray, K. S. Wood, M. N. Lovellette, and M. T. Wolff, J. Guidance, Control, and Dynamics 29, 49 (2006).
A. A. Emadzadeh and J. L. Speyer Navigation in Space by X-Ray Pulsars (Springer, 2011).
W. Becker, M.G. Bernhardt, and A. Jessner, Acta Futura 7, 11 (2013).
W. Becker, in Neutron Stars and Pulsars, Astrophysics and Space Science Library, ed. by W. Becker, 357, 91 (Springer, Berlin, Germany, 2009).
В. И. Гусевский, Зарубежная радиоэлектроника, Успехи современной радиоэлектроники 3, 50 (2001).
В. И. Гусевский, Э. А. Лидский, С. В. Рыжков, Изв. вузов, “Радиоэлектроника” 2, 37 (1991).
В. В. Орешко и др., “Разработка научно-методического обеспечения навигационного обеспечения космических миссий по пульсарам”, ПРАО АКЦ ФИАН, Пущино, (2017).
А. Б. Сергиенко Цифровая обработка сигналов (СПб: “Питер”, 2006).
С. В. Логвиненко, В. В. Орешко, Труды Всероссийской радиоастрономической конференции ВАК-2007, Казань, КГУ, 484 (2007).
А. Е. Родин, Труды ИПА РАН 27, 287 (2013).
Д. Е. Охоцимский, С. Ю. Сихарулидзе Основы механики космического полета (Москва: Наука, 1990).
Г. А. Гурзадян Теория межпланетных перелетов (Москва: Наука, 1992).
Г. Н. Дубошин Небесная механика. Основные задачи и методы (Москва: Наука, 1968).
Ю. Г. Сосулин Теоретические основы радиолокации и радионавигации (Москва: Радио и связь, 1992).
Ю. П. Илясов, А. Д. Кузьмин, Т. В. Шабанова, Ю. П. Шитов, Труды ФИАН 199, М.: ФИАН, 1989, с. 154.
X. P. You, G. Hobbs, W. A. Coles, et al., Monthly Not. Roy. Astron. Soc. 378, 493 (2007).
C. G. T. Haslam, C. J. Salter, H. Stoffel, and W. E. Wilson, Astron. and Astrophys. Supp. Ser. 47, 1 (1982).
J. Y. Donner, J. P. W. Verbiest, C. Tiburzi, et al., Astron. and Astrophys. 624, A22 (2019).
A. Murray Vectorial astrometry (Bristol: Hilger, 1983).
A. E. Rodin and V. A. Fedorova, Astronomy Reports 62, 378 (2018).
V. E. Zharov, V. V. Oreshko, V. A. Potapov, M. S. Pshirkov, A. E. Rodin, and M. V. Sazhin, Astronomy Reports 63, 112 (2019).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал