Астрономический журнал, 2021, T. 98, № 1, стр. 3-9
Сравнение пространственных свойств входов в черные дыры и кротовые норы
И. Д. Новиков 1, 2, 3, С. В. Репин 1, *
1 Физический институт им. П.Н. Лебедева РАН, Астрокосмический центр
Москва, Россия
2 The Niels Bohr International Academy, The Niels Bohr Institute
Copenhagen, Denmark
3 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: repinsv@lebedev.ru
Поступила в редакцию 30.06.2020
После доработки 30.08.2020
Принята к публикации 30.08.2020
Аннотация
Проведено сравнение пространственных свойств входов в сферически-симметричные черные дыры, кротовые норы с нулевой и положительной массами. Свойства изучались с точки зрения балка и браны. Найдены конкретные выражения для входов и показано, что в обоих представлениях пространственные воронки входов в кротовые норы наиболее крутые у Шварцшильдовских черных дыр, и наименее крутые у кротовых нор с нулевой массой.
1. ВВЕДЕНИЕ
Целью настоящей работы является выяснение отличий между геометрическими пространственными свойствами окрестности различных релятивистских объектов в рамках общей теории относительности (ОТО). Следует подчеркнуть, что эти отличия не ведут прямо к различию в видимости этих объектов внешним наблюдателем. Дело в том, что различие в видимости связано не только с различием пространственных свойств этих объектов, но, в еще большей степени, с различием в траекториях лучей света в различных гравитационных полях вокруг этих тел. Мы исследуем эти вопросы в наших других работах (см., напр., [1–4]). Они разбираются также в многочисленных работах других авторов (см., напр., [5–8]). Тем не менее отличия пространственных свойств важны по следующим причинам: 1) для анализа физических процессов вблизи входов; 2) в релятивистской теории так же, как в нерелятивистской теории, свойства процессов зависят от геометрических свойств отверстий, в которые происходит течение; 3) с точки зрения принципиальной возможности отличить эти объекты друг от друга чисто геометрическим путем, не привлекая для этого гравитацию, свет и другие процессы. Полученные отличия можно будет в будущем использовать как дополнительные критерии в наблюдательных проявлениях этих объектов.
Все расчеты в статье выполнены при $G = 1$, $c = 1$.
2. ОБЪЕКТЫ В ГИПЕРПРОСТРАНСТВЕ (БАЛКЕ)
В этом разделе мы рассмотрим релятивистские объекты в гиперпространстве.
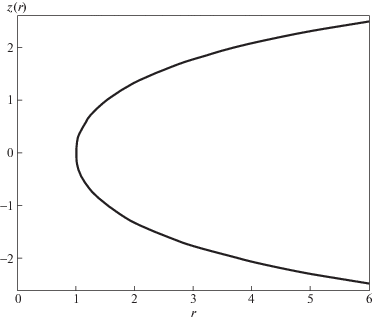
Рассмотрим сферически-симметричные черные дыры (ЧД). Определим форму поверхности вращения в трехмерном балке, внутренняя геометрия которой в бране (в нашей Вселенной) совпадает с двумерной геометрией экваториальной “плоскости” ЧД. Определение и описание терминов “балк” и “брана” даны работе [6]. Как показано в [9], эта поверхность вращения в цилиндрических координатах $(r,\varphi ,z)$ в балке есть
где ${{r}_{g}} = 2m$ – гравитационный радиус. Она соответствует двумерной метрике экваториального сечения ЧД. В полярных координатах в бране (в нашей Вселенной)(2)
$d{{l}^{2}} = {{\left( {1 - \frac{{{{r}_{g}}}}{r}} \right)}^{{ - 1}}}d{{r}^{2}} + {{r}^{2}}d{{\varphi }^{2}}.$(4)
$d{{l}^{2}} = \frac{{{{r}^{2}}}}{{{{r}^{2}} - {{q}^{2}}}}d{{r}^{2}} + {{r}^{2}}d{{\varphi }^{2}}.$(5)
$\begin{gathered} d{{l}^{2}} = d{{r}^{2}} + d{{z}^{2}} + {{r}^{2}}d{{\varphi }^{2}} = \\ \, = d{{r}^{2}}\left( {1 + \mathop {\left( {\frac{{dz}}{{dr}}} \right)}\nolimits^2 } \right) + {{r}^{2}}d{{\varphi }^{2}}. \\ \end{gathered} $(6)
$1 + \mathop {\left( {\frac{{dz}}{{dr}}} \right)}\nolimits^2 = \frac{{{{r}^{2}}}}{{{{r}^{2}} - {{q}^{2}}}}$(8)
${{z}_{{{\text{Th}}}}} = \pm qln\left( {r + \sqrt {{{r}^{2}} - {{q}^{2}}} } \right) + {{z}_{0}}.$Напомним, что в метрике КН$_{{{\text{Th}}}}$ нигде нет гравитационных ускорений, в том числе и вне выходов из КН$_{{{\text{Th}}}}$. Это означает, в частности, что эквивалентная масса каждого из входов равна нулю, $m = 0$.
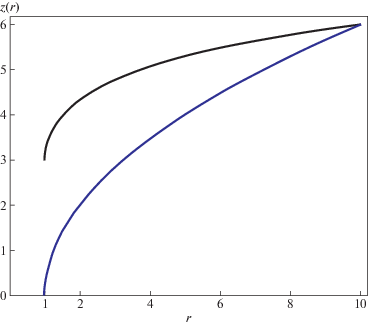
Сравним входы в ЧД и КН$_{{{\text{Th}}}}$. Они описываются поверхностями, получающимися при вращении вокруг $z = 0$ кривых ${{z}_{{\text{S}}}}$ (1) и ${{z}_{{{\text{Th}}}}}$ (8). Обе поверхности стремятся стать горизонтальными при $r \to \infty $. Однако при любом конечном $r$ они отличаются от плоскости, а геометрия на них – от эвклидовой. Степень отличия при данном $r$ может быть охарактеризована отличием разности $dl$ длин двух близких окружностей ${{r}_{1}} = {\text{const}}$ и ${{r}_{2}} = {\text{const}}$ от $2\pi dr$, где ${{r}_{2}} = {{r}_{1}} + dr$,
где ${{g}_{{11}}}$ – метрический коэффициент соответствующих метрик. Для нашего случая(10)
$\mathop {({{g}_{{11}}})}\nolimits_{\text{S}} = \mathop {\left( {1 - \frac{{{{r}_{g}}}}{r}} \right)}\nolimits^{ - 1} ,$(11)
$\mathop {({{g}_{{11}}})}\nolimits_{{\text{Th}}} = \frac{{{{r}^{2}}}}{{{{r}^{2}} - {{q}^{2}}}}.$Сравнение (10) и (11) при ${{r}_{g}} = q$ показывает, что искажение эвклидовости геометрии при продвижении от больших $r$ к входам происходит более плавно для КН, чем для ЧД, а рис. 2 показывает, что воронка ЧД является более “глубокой”, чем в случае КН.
Чтобы исключить недоразумения, напомним, что формально поверхность барна в случае ЧД обрывается при $r = {{r}_{g}}$, в то время как в случае КН после достижения $r = q$ поверхность продолжается к другому выходу из КН (см. рис. 1).
Обратимся теперь к случаю КН с массой $m \ne 0$. Такая модель была рассмотрена Эллисом [11] (см. также [14]). Пространственная метрика кротовой норы с массой $m{\kern 1pt} *$:
(16)
$\begin{gathered} d{{l}^{2}} = {{e}^{{E(\rho )}}}d{{\rho }^{2}} + \\ + \;{{e}^{{E(\rho )}}}({{\rho }^{2}} + {{n}^{2}} - {{m}^{2}})(d{{\vartheta }^{2}} + si{{n}^{2}}\vartheta d{{\varphi }^{2}}), \\ \end{gathered} $(17)
$E(\rho ) = \frac{{2m}}{{\sqrt {{{n}^{2}} - {{m}^{2}}} }}\left( {\frac{\pi }{2} - arctan\frac{\rho }{{\sqrt {{{n}^{2}} - {{m}^{2}}} }}} \right).$Та же метрика в экваториальной “плоскости” $\theta = \pi {\text{/}}2$:
(18)
$d{{l}^{2}} = {{e}^{{E(\rho )}}}d{{\rho }^{2}} + {{e}^{{E(\rho )}}}({{\rho }^{2}} + {{n}^{2}} - {{m}^{2}})d{{\varphi }^{2}}.$Метрику в экваториальной плоскости КН$_{{{\text{El}}}}$ можно записать в виде:
(20)
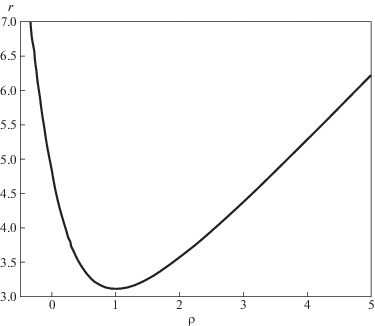
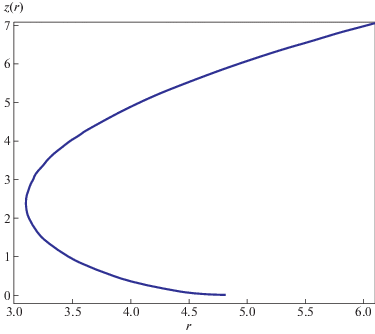
$d{{l}^{2}} = \frac{{{{\rho }^{2}} + {{n}^{2}} - {{m}^{2}}}}{{\mathop {\left( {\rho - m} \right)}\nolimits^2 }}d{{r}^{2}} + {{r}^{2}}d{{\varphi }^{2}}.$Представим теперь вид КН$_{{{\text{El}}}}$ в балке, как мы делали это выше для КН$_{{{\text{Th}}}}$. Поступая аналогично, получаем для ${{z}_{{{\text{El}}}}}(r)$ функцию, найденную численно при $m = 1$, $n = \sqrt 2 $ и представленную на рис. 4.
Форма качественно похожа на рис. 1, только горловина смещена вправо и вверх. На рис. 4 горловине соответствует точка поворота кривой. Ветвь, идущая вниз направо, уходит ко второму выходу. Попытки продолжить решение для ${{z}_{{{\text{El}}}}}(r)$ приводят к мнимым значениям для интеграла $z(\rho )$ для $\rho < 0$ и $z < 0$. Формально это означает невозможность поместить фигуру вращения в плоский трехмерный балк $(r,z,\varphi )$. Удивляться этому не приходится, ибо, как мы знаем, эта вторая ветвь ведет к выходу с отрицательной массой $m{\kern 1pt} * < 0$. Это означает, что вдали от выхода метрика должна соответствовать решению Шварцшильда с отрицательной массой. Но из формулы (1) видно, что для ${{z}_{{\text{S}}}}$ при ${{r}_{g}} < 0$ и $r > 0$ получаются мнимые значения, т.е. такая брана не может быть вложена в трехмерный плоский балк.
Возвращаясь к правому входу с $m{\kern 1pt} * > 0$, сравним его со входом в ЧД. Будем считать, что ${{r}_{g}}$ равно размеру горловины $r(m)$. Выше мы видели, что $r(m) > 2m{\kern 1pt} *$. Асимптотика отклонений от эвклидовой геометрии здесь определяется для обоих случаев КН$_{{{\text{El}}}}$ и ЧД величиной массы. Поэтому
Значит, в случае КН$_{{{\text{El}}}}$, как и в случае с КН$_{{{\text{Th}}}}$, при переходе от больших $r$ к входам искажение эвклидовости нарастает медленнее у КН$_{{{\text{El}}}}$, чем у ЧД.3. РЕЛЯТИВИСТСКИЕ ОБЪЕКТЫ В БРАНЕ
Обратимся теперь к свойствам пространства отверстий, оставаясь в трехмерной бране (в нашем случае в двумерном экваториальном сечении браны). Определим физическое радиальное расстояние от гравитационного радиуса ${{r}_{g}}$ до точки с координатой $r$ (в единицах ${{r}_{g}}$):
(22)
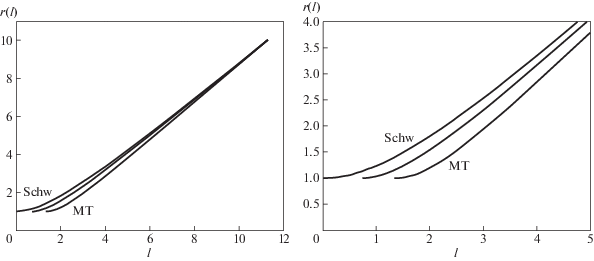
$\begin{gathered} {{l}_{{\text{S}}}} = \int\limits_1^r \,\sqrt {{{g}_{{{{{11}}_{{\text{S}}}}}}}} dr = \sqrt {r(r - 1)} + \\ + \;\frac{1}{2}ln(2r + 2\sqrt {r(r - 1)} - 1). \\ \end{gathered} $Рис. 5.
Зависимость $r(l)$ для метрики Шварцшильда. Расстояние $l$ отсчитывается от гравитационного радиуса.
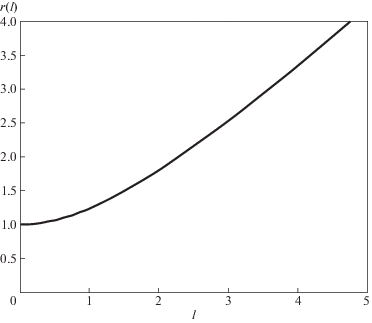
Аналогичное выражение для метрики Морриса–Торна для физического расстояния от горловины $r = q$ (в единицах $q$):
График обратной функции $r = r({{l}_{{{\text{Th}}}}}) = \sqrt {{{l}^{2}} + {{q}^{2}}} $ дан на рис. 6.Рис. 6.
Зависимость $r(l)$ для метрики Морриса–Торна. Расстояние $l$ отсчитывается от горловины, где $r = q$.
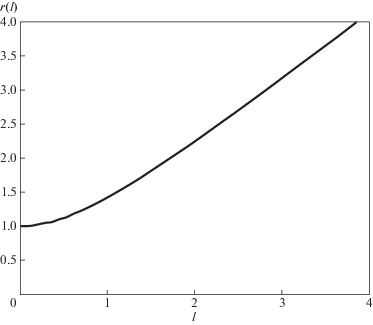
Наконец, обратимся к метрике Эллиса (16), (17). Для выхода из КН с $m > 0$ расстояние от горловины ${{r}_{{min}}}$ до точки с координатой $r$ записывается в виде:
(24)
${{l}_{{{\text{El}}}}} = \int\limits_{{{r}_{{min}}}}^r \,\sqrt {\frac{{{{\rho }^{2}} + {{n}^{2}} - {{m}^{2}}}}{{{{{(\rho - m)}}^{2}}}}} {\kern 1pt} dr.$Рис. 7.
Зависимость $r(l)$ для метрики Эллиса. Расстояние $l$ отсчитывается от горловины, где $r = {{r}_{{min}}}$.

На рис. 8 показаны $l(r)$ для всех трех случаев. При этом значения $r$ при $l = 10$ положены равными. Рисунок показывает, что при продвижении от $r = 10$ к входам искажение эвклидовости быстрее всего происходит для метрики Шварцшильда и медленнее всего для метрики Морриса–Торна.
4. ЗАКЛЮЧЕНИЕ
Отметим прежде всего, что обычный способ описывать и изображать входы в ЧД и КН как практически очень похожие не вполне корректен. Оба метода визуализации входов и в балке, и в бране показывают существенную разницу между метриками. Наиболее крупная воронка у метрики Шварцшильда. Указанную разницу следует учитывать при описании процессов у входов в ЧД и КН.
Список литературы
Я. Б. Зельдович, И. Д. Новиков, Релятивистская астрофизика (М.: Наука, 1967).
V. Frolov and I. Novikov, Black Hole Physics. Basic Concepts and New Developments (Kluwer Academic Publishers, 1998).
И. Д. Новиков, Н. С. Кардашев, А. А. Шацкий, Успехи физ. наук 177, 1017 (2007).
S. V. Repin, D. A. Kompaneets, I. D. Novikov, and V. A. Mityagina, arXiv:1802.04667 [gr-qc] (2018).
C. W. Misner, K. S. Thorne, and J. A. Wheeler, Gravitation (San Francisco: Freeman and Company, 1973).
K. Торн, Интерстеллар, наука за кадром (М.: ИД Манн, Иванов и Фербер, 2015).
R. Shaikh and S. Kar, Phys. Rev. D 96, id. 044037 (2017), arXiv:1705.11008 [gr-qc].
N. Tsukamoto, Phys. Rev. D 101, id. 104021 (2020), arXiv:2004.00822v2 [gr-qc].
Л. Д. Ландау, Е. М. Лифшиц, Теория поля (М.: Физматлит, 2012).
M. S. Morris and K. S. Thorne, American J. Physics 56, 395 (1988).
H. Ellis, J. Math. Phys. 14, 104 (1973).
K. A. Bronnikov, G. Clément, C. P. Constantinidis, and J. C. Fabris, Phys. Letters A 243 (3), 121 (1998).
K. A. Bronnikov, Acta Phys. Pol. 84, 251 (1973).
A. G. Doroshkevich, N. S. Kardashev, D. I. Novikov, and I. D. Novikov, Astron. Rep. 52, 616 (2008).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал