Астрономический журнал, 2021, T. 98, № 11, стр. 901-921
Автомодельное возмущение аккреционного диска вокруг сливающихся черных дыр
А. Г. Жилкин 1, *, Д. В. Бисикало 1
1 Институт астрономии Российской академии наук
Москва, Россия
* E-mail: zhilkin@inasan.ru
Поступила в редакцию 07.06.2021
После доработки 26.07.2021
Принята к публикации 27.07.2021
Аннотация
В работе исследуется возможность электромагнитного отклика от слияния двух черных дыр, окруженных общим аккреционным диском. При слиянии черных дыр масса конечного объекта уменьшается за счет излучения гравитационных волн и, как следствие, диск испытывает возмущения, проявляющиеся в том числе и в формировании ударных волн достаточно высокой интенсивности. На основе результатов численного моделирования мы выполнили анализ автомодельного решения, описывающего эволюцию возмущенного аккреционного диска с учетом эффекта вертикального расширения, приводящего к адиабатическому охлаждению вещества, нагретого ударными волнами. Разработанная методика позволяет корректно оценить нагрев вещества ударными волнами, и, соответственно, определить параметры возникающего электромагнитного излучения от диска, включая кривую блеска, спектр излучения, а также продолжительность вспышки.
1. ВВЕДЕНИЕ
С 2015 г., когда были экспериментально обнаружены гравитационные волны [1], начинается новая страница в астрономии. Возможность использовать “мультиканальный” (multi-messenger) подход позволяет достичь более глубокого понимания природы астрофизических объектов. Согласно теоретическим представлениям [2, 3], наибольшей интенсивностью гравитационно-волнового излучения обладают двойные черные дыры [4], а наибольшую вероятность обнаружения имеют двойные черные дыры звездных масс [5, 6]. И действительно, начиная с 2015 г. на детекторах LIGO и Virgo было обнаружено несколько гравитационно-волновых событий, сопровождающих слияние пар черных дыр [1, 7–11]. Возникает вопрос: а как нам добиться реализации “мультиканального” подхода для этих событий, или, другими словами, возникает ли электромагнитный отклик при слиянии черных дыр и можно ли его наблюдать?
В исследованиях черных дыр часто делается предположение о том, что эти объекты окружены аккреционными дисками. Сценарии формирования диска вокруг двойной сверхмассивной черной дыры, а также вокруг двойной черной дыры звездной массы указывались нами в работах [12, 13]. Рассмотрим задачу про возмущение аккреционного диска или оболочки вокруг сливающихся черных дыр. Согласно ОТО потеря энергии двойной черной дыры при излучении гравитационных волн приводит к формированию конечного объекта с массой на несколько процентов меньше исходной [3]. Кроме того, потеря импульса из-за отклонения от симметрии может привести к тому, что объект получает импульс отдачи (kick) [14] и в результате этого он приобретает скорость до 1000 км/с [15]. Вещество, окружающее сливающиеся черные дыры, испытывает возмущение [16], которое может привести к увеличению светимости и квазипериодическим вспышкам. Эффект отдачи черной дыры и последующее за этим гравитационное возмущение могут возбуждать в аккреционном диске ударные волны [17], а сами возмущения метрики вызывают в диске механические напряжения, которые могут диссипировать на вязкой шкале времени [18] или превращаться в ударные волны [19]. Нагрев вещества диска ударными волнами должен приводить к резкому увеличению яркости диска, что можно расценивать как электромагнитный отклик системы на эффект слияния двойной черной дыры.
Для случая слияния сверхмассивных черных дыр в ядрах галактик с полной массой ${{10}^{6}}\,{{M}_{ \odot }}$ потеря массы в 5% приводит к росту светимости аккреционного диска до ${{10}^{{43}}}$ эрг/с [20]. Эффект импульса отдачи может приводить к такому же росту светимости, однако его величина существенным образом зависит от плохо определенных параметров сливающейся двойной черной дыры [21, 22]. Отклик примерно такой же величины можно ожидать и для черных дыр звездных масс. В работе [23] было показано, что рост светимости аккреционного диска может достигать ${{10}^{{42}}}{\kern 1pt} - {\kern 1pt} {{10}^{{43}}}$ эрг/с, при этом максимум энергии излучения будет расположен в рентгеновской части спектра даже для случая волн плотности вместо ударных. В наших работах [12, 24] для моделей, параметры которых соответствовали событию GW170814 [10], были рассчитаны болометрические кривые блеска, спектры электромагнитного излучения и получены оценки длительности вспышки. Как оказалось, основная часть энергии электромагнитного излучения высвечивается в рентгеновском и гамма-диапазонах, и такого рода вспышки могут быть зарегистрированы инструментами, существующими в настоящее время.
Анализ результатов численных расчетов, проведенных в работах [12, 24], позволил заключить, что при определенном характере распределения плотности и температуры в исходном невозмущенном аккреционном диске режим распространения ударных волн в возмущенном диске с течением времени становится автомодельным. В частности, расстояние, пройденное фронтом ударной волны за время $t$, описывается степенным законом ${{t}^{{2/3}}}$, а ее скорость затухает со временем как ${{t}^{{ - 1/3}}}$. В работе [13] мы получили полное автомодельное решение этой задачи с использованием необходимой информации об ударных волнах, взятой из численных расчетов. Из автомодельного решения можно получить алгебраические интегралы углового момента и адиабатичности, а также найти асимптотические соотношения для автомодельных функций. Такая аналитическая модель на основе автомодельного решения позволяет приближенно оценивать величину электромагнитного отклика гравитационно-волнового события без проведения трудоемких численных расчетов. В данной работе мы уточнили разработанную ранее модель путем учета вертикального расширения диска, приводящие к адиабатическому охлаждению вещества за ударными волнами. Использованная методика позволяет приблизить модель к реальной физической картине и получить достоверные оценки электромагнитного отклика от сливающихся черных дыр звездных масс.
Статья организована следующим образом. В разделе 2 описаны постановка задачи и основные уравнения. В разделе 3 представлены автомодельные уравнения и проведен их анализ. В разделе 4 описаны результаты расчетов. В разделе 5 обсуждаются характеристики электромагнитного отклика. В разделе 6 содержатся основные выводы работы. В Приложении приведены некоторые детали численного метода и аналитического решения задачи.
2. ОСНОВНЫЕ УРАВНЕНИЯ
С помощью гравитационно-волновых детекторов LIGO и Virgo были проведены две завершенные серии наблюдений O1 (с 12 сентября 2015 г. по 19 января 2016 г.) и O2 (с 30 ноября 2016 г. по 26 августа 2017 г.). Третья серия наблюдений O3 началась 1 апреля 2019 г. и должна была завершиться 30 апреля 2020 г. Однако в конце марта 2020 г. наблюдения были прекращены из-за пандемии коронавируса. В завершенных сериях наблюдений O1 и O2 было обнаружено 10 событий слияния двойных черных дыр [11], из которых только 5 не имеют артефактов. Эти события представлены в табл. 1 вместе с оценками масс компонентов, доли теряемой массы и расстояния до соответствующего объекта. Как видно из таблицы, все эти объекты соответствуют черным дырам звездной массы. При этом доля теряемой массы при слиянии черных дыр составляет величину порядка 2–6%. В качестве исследуемого объекта в данной работе будем рассматривать событие GW170814, соответствующее слиянию двойной черной дыры с массами компонентов 30.5 и 25.3 ${{M}_{ \odot }}$. Для определенности будем считать, что потеря массы в этом событии составляла 5%.
Таблица 1.
Параметры сливающихся двойных черных дыр по данным гравитационно-волновых наблюдений
| Объект | ${{M}_{1}}{\text{/}}{{M}_{ \odot }}$ | ${{M}_{2}}{\text{/}}{{M}_{ \odot }}$ | $\Delta M{\text{/}}({{M}_{1}} + {{M}_{2}})$, % | $D$, Мпс | Ссылка |
|---|---|---|---|---|---|
| GW150914 | $36_{{ - 4}}^{{ + 5}}$ | $29_{{ - 4}}^{{ + 4}}$ | 3.3–5.2 | $410_{{ - 180}}^{{ + 160}}$ | [1] |
| GW151226 | $14.2_{{ - 3.7}}^{{ + 8.3}}$ | $7.5_{{ - 2.3}}^{{ + 2.3}}$ | 2.9–5.4 | $440_{{ - 190}}^{{ + 180}}$ | [7] |
| GW170104 | $31.2_{{ - 6.0}}^{{ + 8.4}}$ | $19.4_{{ - 5.9}}^{{ + 8.3}}$ | 2.3–5.7 | $880_{{ - 390}}^{{ + 450}}$ | [8] |
| GW170608 | $12_{{ - 2}}^{{ + 7}}$ | $7_{{ - 2}}^{{ + 2}}$ | 2.8–5.1 | $340_{{ - 140}}^{{ + 140}}$ | [9] |
| GW170814 | $30.5_{{ - 3.0}}^{{ + 5.7}}$ | $25.3_{{ - 4.2}}^{{ + 2.8}}$ | 4.0–5.8 | $540_{{ - 210}}^{{ + 130}}$ | [10] |
При исследовании черных дыр часто предполагается, что они окружены аккреционными дисками. Внутренний радиус аккреционного диска вокруг одиночной черной дыры равен $3{{R}_{{\text{g}}}}$, где ${{R}_{{\text{g}}}} = 2GM{\text{/}}{{c}^{2}}$ – гравитацонный радиус, $G$ – гравитационная постоянная, $c$ – скорость света. Внутри этой зоны устойчивых круговых орбит не существует [3]. Предположим, что двойная черная дыра также окружена общим аккреционным диском. Конечная стадия слияния черных дыр происходит очень быстро, за доли секунды. Процесс стремительного слияния черных дыр начинается, когда расстояние между ними составляет $A = 3{{R}_{{{\text{g}},1}}} + 3{{R}_{{{\text{g}},2}}} = 3{{R}_{{\text{g}}}}$, где ${{R}_{{{\text{g}},1}}}$ и ${{R}_{{{\text{g}},2}}}$ – гравитационные радиусы компонентов, ${{R}_{{\text{g}}}}$ – гравитационный радиус, вычисленный по их суммарной массе $M = {{M}_{1}} + {{M}_{2}}$ (гравитационный радиус аккретора) [25–28]. Внутренний радиус аккреционного диска вокруг двойной черной дыры примерно в два раза превышает расстояние между центрами черных дыр. Такой вывод следует из оценок устойчивости орбит относительно приливных сил [12, 13] и хорошо согласуется с результатами численного моделирования двойных систем с круговыми орбитами компонентов, отношение масс которых близко к единице [29–32].
До момента слияния сближение черных дыр происходит медленно и поэтому, благодаря действию вязких сил, аккреционный диск успевает подстроиться к изменяющемуся межкомпонентному расстоянию. Следовательно, можно считать, что непосредственно перед слиянием черных дыр внутренний радиус диска ${{r}_{{\text{d}}}}$ примерно в 6 раз превосходит гравитационный радиус аккретора ${{R}_{{\text{g}}}}$. Это позволяет при описании свойств такого аккреционного диска пренебрегать релятивистскими эффектами и использовать теорию Шакуры и Сюняева [33]. В этой модели скорость аккреции $\dot {M}$ определяется темпом диссипации углового момента, возникающего вследствие турбулентной вязкости. Интенсивность турбулентности описывается безразмерным параметром $\alpha $, значение которого не превышает единицы. Критический темп аккреции определяется величиной эддингтоновской светимости
(1)
${{\dot {M}}_{{{\text{cr}}}}} = 1.8 \times {{10}^{{ - 9}}}\frac{m}{\chi }\frac{{{{M}_{ \odot }}}}{{{\text{year}}}},$В модели [33] в аккреционном диске выделяются три характерные зоны (A, B и C), в которых распределение гидродинамических величин определяется относительным вкладом газового давления и давления излучения, а также механизмом непрозрачности. В зоне A преобладает давление излучения, а в зонах B и C им можно пренебречь по сравнению с газовым давлением. В зонах A и B непрозрачность определяется томсоновским рассеянием, а в зоне C непрозрачность обеспечивается свободно-свободными переходами. Вертикальная структура диска в этих зонах различается довольно сильно, но радиальные зависимости плотности и температуры оказываются близкими к степенным с почти одинаковыми показателями степени.
В данной работе мы будем рассматривать только зону B [13]. Поэтому для описания профилей плотности и температуры в невозмущенном аккреционном диске можно использовать следующие выражения:
(2)
$\rho = 7.03{{\alpha }^{{ - 7/10}}}{{m}^{{ - 7/10}}}{{\dot {m}}^{{2/5}}}{\kern 1pt} \mathop {\left( {\frac{{3{{R}_{{\text{g}}}}}}{r}} \right)}\nolimits^{33/20} \;{\text{г/с}}{{{\text{м}}}^{3}},$(3)
$T = 3.1 \times {{10}^{8}}{{\alpha }^{{ - 1/5}}}{{m}^{{ - 1/5}}}{{\dot {m}}^{{2/5}}}{\kern 1pt} \mathop {\left( {\frac{{3{{R}_{{\text{g}}}}}}{r}} \right)}\nolimits^{9/10} \;{\text{К}},$Поэтому в нашей модели для задания начальных условий мы используем следующие степенные распределения плотности и температуры в невозмущенном диске:
(4)
${{\rho }_{0}}(r) = {{\rho }_{*}}\mathop {\left( {\frac{r}{{{{r}_{*}}}}} \right)}\nolimits^{ - {{k}_{d}}} ,$(5)
${{T}_{0}}(r) = {{T}_{*}}\mathop {\left( {\frac{r}{{{{r}_{*}}}}} \right)}\nolimits^{ - {{k}_{t}}} ,$Уравнения гравитационной газовой динамики, описывающие эволюцию геометрически тонкого аккреционного диска после слияния черных дыр, в осесимметричном случае в цилиндрических координатах ($r$, $\varphi $, $z$) можно записать в следующем виде:
(6)
$\frac{{\partial \rho }}{{\partial t}} + {{{v}}_{r}}\frac{{\partial \rho }}{{\partial r}} + {{{v}}_{z}}\frac{{\partial \rho }}{{\partial z}} + \rho \left[ {\frac{1}{r}\frac{\partial }{{\partial r}}(r{{{v}}_{r}}) + \frac{{\partial {{{v}}_{z}}}}{{\partial z}}} \right] = 0,$(7)
$\begin{gathered} \frac{{\partial {{{v}}_{r}}}}{{\partial t}} + {{{v}}_{r}}\frac{{\partial {{{v}}_{r}}}}{{\partial r}} + {{{v}}_{z}}\frac{{\partial {{{v}}_{r}}}}{{\partial z}} - \frac{{{v}_{\varphi }^{2}}}{r} + \frac{1}{\rho }\frac{{\partial P}}{{\partial r}} + \\ \, + (1 - \xi )\frac{{GM}}{{{{r}^{2}}}} = 0, \\ \end{gathered} $(8)
$\frac{{\partial {{{v}}_{z}}}}{{\partial t}} + {{{v}}_{r}}\frac{{\partial {{{v}}_{z}}}}{{\partial r}} + {{{v}}_{z}}\frac{{\partial {{{v}}_{z}}}}{{\partial z}} + \frac{1}{\rho }\frac{{\partial P}}{{\partial z}} + (1 - \xi )\frac{{GM}}{{{{r}^{3}}}}z = 0,$(9)
$\frac{{\partial {{{v}}_{\varphi }}}}{{\partial t}} + {{{v}}_{r}}\frac{{\partial {{{v}}_{\varphi }}}}{{\partial r}} + {{{v}}_{z}}\frac{{\partial {{{v}}_{\varphi }}}}{{\partial z}} + \frac{{{{{v}}_{r}}{{{v}}_{\varphi }}}}{r} = 0,$(10)
$\frac{{\partial \varepsilon }}{{\partial t}} + {{{v}}_{r}}\frac{{\partial \varepsilon }}{{\partial r}} + {{{v}}_{z}}\frac{{\partial \varepsilon }}{{\partial z}} + \frac{P}{\rho }\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}(r{{{v}}_{r}}) + \frac{{\partial {{{v}}_{z}}}}{{\partial z}}} \right] = 0.$В случае геометрически тонких дисков мы можем пренебречь подробным описанием вертикальной структуры для исследования эффектов ударного нагрева и адиабатического расширения. Вместо этого можно использовать простое приближение, когда вертикальная скорость ${{{v}}_{z}}$ в любой момент времени остается пропорциональной высоте $z$ (аналог закона Хаббла в космологии):
В плоскости симметрии диска вертикальный компонент скорости ${{{v}}_{z}} = 0$. В нашей модели все уравнения (6)–(10) мы записываем для плоскости симметрии диска. В этом случае члены вида ${{{v}}_{z}}\partial {\text{/}}\partial z$ в конвективных производных исчезают во всех уравнениях. С учетом этого замечания и приближения (11) уравнения (6)–(10) (кроме уравнения (8)) примут вид:(12)
$\frac{{\partial \rho }}{{\partial t}} + {{{v}}_{r}}\frac{{\partial \rho }}{{\partial r}} + \rho \frac{1}{r}\frac{\partial }{{\partial r}}(r{{{v}}_{r}}) + \rho \psi = 0,$(13)
$\frac{{\partial {{{v}}_{r}}}}{{\partial t}} + {{{v}}_{r}}\frac{{\partial {{{v}}_{r}}}}{{\partial r}} - \frac{{{v}_{\varphi }^{2}}}{r} + \frac{1}{\rho }\frac{{\partial P}}{{\partial r}} + (1 - \xi )\frac{{GM}}{{{{r}^{2}}}} = 0,$(14)
$\frac{{\partial {{{v}}_{\varphi }}}}{{\partial t}} + {{{v}}_{r}}\frac{{\partial {{{v}}_{\varphi }}}}{{\partial r}} + \frac{{{{{v}}_{r}}{{{v}}_{\varphi }}}}{r} = 0,$(15)
$\frac{{\partial \varepsilon }}{{\partial t}} + {{{v}}_{r}}\frac{{\partial \varepsilon }}{{\partial r}} + \frac{P}{\rho }\frac{1}{r}\frac{\partial }{{\partial r}}(r{{{v}}_{r}}) + \frac{{P\psi }}{\rho } = 0.$Допустим, что давление в диске в произвольный момент времени определяется выражением
где $H$ – локальная полутолщина диска. Тогда из уравнения для вертикальной скорости (8) с помощью соотношения (11) можно получить уравнения для коэффициента $\psi $,(17)
$\frac{{\partial \psi }}{{\partial t}} + {{{v}}_{r}}\frac{{\partial \psi }}{{\partial r}} + {{\psi }^{2}} - \frac{{2P}}{{\rho {{H}^{2}}}} + (1 - \xi )\frac{{GM}}{{{{r}^{3}}}} = 0.$(19)
${{{v}}_{z}}(r,H(r,t),t) = \frac{{\partial H}}{{\partial t}} + {{{v}}_{r}}\frac{{\partial H}}{{\partial r}}.$(20)
$\frac{{\partial H}}{{\partial t}} + {{{v}}_{r}}\frac{{\partial H}}{{\partial r}} - \psi H = 0.$Для замыкания полученной системы уравнений (12)–(15), (17), (20) следует учесть уравнения состояния, определяющие зависимости давления $P$ и внутренней энергии $\varepsilon $ от плотности $\rho $ и температуры $T$. Поскольку в данной работе мы рассматриваем только зону B аккреционного диска, то давление излучения мы не учитываем. Однако следует отметить, что в сильно возмущенных областях этой зоны, где возникают ударные волны большой интенсивности, температура может возрастать настолько, что эффекты давления излучения могут играть существенную роль [12]. Уравнения состояния можно записать в виде:
где ${{A}_{{{\text{gas}}}}} = 2{{k}_{{\text{B}}}}{\text{/}}{{m}_{{\text{p}}}}$ – газовая постоянная, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, ${{m}_{{\text{p}}}}$ – масса протона, $\gamma $ – показатель адиабаты. Для полностью ионизованной водородной плазмы средний молекулярный вес следует принять равным $1{\text{/}}2$, а показатель адиабаты $\gamma = 5{\text{/}}3$.В качестве начальных условий для плотности и температуры используются выражения (4) и (5). Начальные распределения для давления и внутренней энергии можно получить из уравнений состояния (21) и (22),
(23)
${{P}_{0}}(r) = {{\rho }_{*}}c_{*}^{2}\mathop {\left( {\frac{r}{{{{r}_{*}}}}} \right)}\nolimits^{ - {{k}_{d}} - {{k}_{t}}} ,$(24)
${{\varepsilon }_{0}} = \frac{{c_{*}^{2}}}{{\gamma - 1}}\mathop {\left( {\frac{r}{{{{r}_{*}}}}} \right)}\nolimits^{ - {{k}_{t}}} ,$(25)
${{v}_{\varphi }}(r,0) = {{c}_{*}}\mathop {\left[ {{{\mu }^{2}} - ({{k}_{d}} + {{k}_{t}})\mathop {\left( {\frac{r}{{{{r}_{*}}}}} \right)}\nolimits^{1 - {{k}_{t}}} } \right]}\nolimits^{1/2} \mathop {\left( {\frac{r}{{{{r}_{*}}}}} \right)}\nolimits^{ - 1/2} ,$(26)
${{H}_{0}}(r) = {{r}_{*}}\frac{{\sqrt 2 }}{\mu }\mathop {\left( {\frac{r}{{{{r}_{*}}}}} \right)}\nolimits^{\tfrac{{3 - {{k}_{t}}}}{2}} .$Для численного решения описанных выше уравнений использовалась неявная полностью консервативная разностная схема Самарского–Попова [38], некоторые детали которой описаны в [39] (см. Приложение A). Следует подчеркнуть, что в этой схеме выполняются не только разностные аналоги законов сохранения массы, импульса и энергии, но и дополнительные соотношения, описывающие баланс по определенным видам энергии. Кроме того, в нашем случае в схеме выполняется разностный аналог закона сохранения удельного углового момента. Численная модель определяется следующими параметрами: показателями ${{k}_{d}}$ и ${{k}_{t}}$ начальных профилей плотности и температуры, долей теряемой массы $\xi $ и числом Маха $\mu $. Отметим, что в частном случае $\psi = 0$ эта численная модель переходит в более простую модель, рассмотренную нами в работе [24], в которой не учитываются эффекты, обусловленные адиабатическим расширением диска.
Будем считать, что безразмерная масса $m = 55$ соответствует гравитационно-волновому событию GW170814 (см. табл. 1). Выберем в качестве характерного радиуса ${{r}_{*}}$, который определяет пространственный масштаб исследуемой задачи, внутренний радиус невозмущенного диска, ${{r}_{{\text{d}}}} = 6{{R}_{{\text{g}}}}$. Тогда с учетом распределения температуры в невозмущенном диске (5) из (27) находим
Если зафиксировать здесь значение параметра $\dot {m}$, то в пределе при $\alpha \to 0$ мы можем получить сколь угодно малые значения параметра $\mu $. Наоборот, если мы зафиксируем значения параметра $\alpha $, то в пределе при $\dot {m} \to 0$ можно получить сколь угодно большие значения параметра $\mu $. Например, в случае $\alpha = 0.01$, $\dot {m} = 1$ получаем значение $\mu = 49.23$. В случае $\alpha = 0.01$, $\dot {m} = 0.01$ получаем значение $\mu = 123.65$. Отсюда видно, что возможные значения параметра $\mu $ лежат в довольно широких пределах.Поскольку мы рассматриваем только зону B аккреционного диска, то характерный радиус ${{r}_{*}}$ можно определить и как внутренний радиус этой зоны ${{r}_{{{\text{AB}}}}}$. Величину этого радиуса можно найти из условия равенства давления излучения и газового давления [33],
(29)
${{r}_{{{\text{AB}}}}} = 159.3{{\alpha }^{{2/21}}}{{m}^{{2/21}}}{{\dot {m}}^{{16/21}}}{{R}_{{\text{g}}}}.$Как показывают наши расчеты [12, 13, 24], степень возмущения аккреционного диска в результате слияния черных дыр и потери массы за счет излучения гравитационных волн определяется величиной параметра $\mu $. Электромагнитный отклик от гравитационно-волнового события оказывается тем выше, чем больше значение $\mu $. В связи с этим, следует заметить, что в случае сверхмассивных черных дыр значения параметра $\mu $ могут быть намного больше по сравнению с приведенными выше оценками для черных дыр звездной массы. В самом деле, выберем в качестве характерного радиуса ${{r}_{ * }}$ внутренний радиус невозмущенного диска. Тогда, задавая безразмерную массу, например, равной $m = {{10}^{8}}$, получаем
Отсюда в случае $\alpha = 0.01$, $\dot {m} = 1$ получаем значение $\mu = 208.05$, а в случае $\alpha = 0.01$, $\dot {m} = 0.01$ параметр $\mu = 522.59$. Для более массивных черных дыр можно получить еще большие значения параметра $\mu $.3. АВТОМОДЕЛЬНОЕ РЕШЕНИЕ
3.1. Автомодельные уравнения
Анализ численных решений, полученных нами в работе [24], позволил прийти к выводу о том, что возникающие в возмущенном диске ударные волны имеют автомодельный характер. В частности, расстояние, пройденное фронтом ударной волны за время $t$, описывается степенным законом ${{t}^{{2/3}}}$, а ее скорость затухает со временем как ${{t}^{{ - 1/3}}}$. В работе [12] мы исследовали возможность построения соответствующего автомодельного решения. Однако полностью получить его не удалось из-за трудностей, связанных с аналитическим определением положения ударных волн. Полное автомодельное решение было получено нами в работе [13] на основе сравнения автомодельного и численного решений.
Автомодельное решение описывает эволюцию возмущенного диска, когда ударные волны уходят достаточно далеко от его внутренней границы. Можно считать, что эта область соответствует зоне B аккреционного диска, причем давление излучения уже не оказывает существенного влияния на динамику вещества за фронтом ударных волн. В работе [13] при построении автомодельного решения эффекты, связанные с адиабатическим расширением диска, мы также не учитывали. Именно такая упрощенная численная модель рассматривалась нами в работе [24]. В данной работе мы рассматриваем автомодельное решение, учитывающее адиабатическое охлаждение диска.
Заметим, что в нашей модели начальные распределения всех величин за исключением азимутальной скорости ${{v}_{\varphi }}$ и, соответственно, углового момента $l = r{{v}_{\varphi }}$ описываются степенны́ми функциями радиуса $r$. Однако нетрудно видеть, что в случае ${{k}_{t}} = 1$ (что близко к $9{\text{/}}10$ в модели [33] для зоны B) это распределение также оказывается степенным,
(32)
${{l}_{0}}(r) = {{r}_{*}}{{c}_{*}}{{({{\mu }^{2}} - {{k}_{d}} - 1)}^{{1/2}}}\mathop {\left( {\frac{r}{{{{r}_{*}}}}} \right)}\nolimits^{1/2} .$Будем искать решение в следующем виде [40]:
где функции ${{\rho }_{0}}(r)$, ${{l}_{0}}(r)$, ${{\varepsilon }_{0}}(r)$ и ${{H}_{0}}(r)$ определяются (для случая ${{k}_{t}} = 1$) выражениями (4), (32), (24) и (26). Автомодельные функции $\sigma $, $u$, $\Lambda $, $w$, $\Psi $ и $h$ зависят от автомодельной переменной $\lambda $, которую выберем в виде(39)
$\lambda = \frac{r}{{{{r}_{*}}}}\mathop {\left( {\frac{{{{t}_{*}}}}{t}} \right)}\nolimits^\delta ,$В автомодельных переменных уравнения (12)–(15), (17) и (20) могут быть записаны в виде:
(40)
$(u - \delta )\frac{{dln\sigma }}{{dln\lambda }} + \frac{{du}}{{dln\lambda }} + (2 - {{k}_{d}})u + \Psi = 0,$(41)
$\begin{gathered} (u - \delta )\frac{{du}}{{dln\lambda }} + u(u - 1) + \\ + \;\frac{w}{{{{\lambda }^{3}}}}\left( {\frac{{dln\sigma }}{{dln\lambda }} + \frac{{dlnw}}{{dln\lambda }} - {{k}_{d}} - 1} \right) - \\ - \;({{\mu }^{2}} - {{k}_{d}} - 1)\frac{{{{\Lambda }^{2}}}}{{{{\lambda }^{3}}}} + (1 - \xi )\frac{{{{\mu }^{2}}}}{{{{\lambda }^{3}}}} = 0, \\ \end{gathered} $(43)
$\begin{gathered} (u - \delta )\frac{{dlnw}}{{dln\lambda }} + (\gamma - 1)\frac{{du}}{{dln\lambda }} + \\ \, + (2\gamma - 3)u + (\gamma - 1)\Psi = 0, \\ \end{gathered} $(44)
$(u - \delta )\frac{{d\Psi }}{{dln\lambda }} + \Psi (\Psi - 1) - \frac{w}{{{{h}^{2}}}}\frac{{{{\mu }^{2}}}}{{{{\lambda }^{3}}}} + (1 - \xi )\frac{{{{\mu }^{2}}}}{{{{\lambda }^{3}}}} = 0,$3.2. Автомодельные ударные волны
Фронту ударной волны в автомодельном решении соответствует постоянное значение автомодельной переменной ${{\lambda }_{s}} = {\text{const}}$. Отсюда следует, что положение ударной волны
(46)
${{r}_{s}} = {{\lambda }_{s}}{{r}_{*}}\mathop {\left( {\frac{t}{{{{t}_{*}}}}} \right)}\nolimits^\delta \propto {{t}^{\delta }},$На ударной волне должны выполняться условия Гюгонио, связывающие между собой величины перед разрывом (будем их помечать индексом 1) и после разрыва (будем их помечать индексом 2). Несложный анализ, проведенный нами в [13], приводит к следующим соотношениям для автомодельных функций:
(50)
${{V}_{2}} = \frac{{\gamma - 1}}{{\gamma + 1}}\frac{1}{{{{V}_{1}}}}\left( {V_{1}^{2} + \frac{2}{{\gamma - 1}}{{W}_{1}}} \right),$(51)
${{W}_{2}} = \mathop {\left( {\frac{{\gamma - 1}}{{\gamma + 1}}} \right)}\nolimits^2 \frac{1}{{V_{1}^{2}}}\left( {V_{1}^{2} + \frac{2}{{\gamma - 1}}{{W}_{1}}} \right)\left( {\frac{{2\gamma }}{{\gamma - 1}}V_{1}^{2} - {{W}_{1}}} \right),$Из условий Гюгонио, в частности, следует, что плотность потока массы $j = \sigma V$ и угловой момент $\Lambda $ остаются непрерывными при переходе через фронт ударной волны. Поскольку на ударных волнах $j \ne 0$, то $u$ не может равняться $\delta $ ни слева, ни справа от разрыва, $u \ne \delta $. Более того, все ударные волны в диске распространяются от центра к периферии. Следовательно, $j < 0$ и значит должно быть $u < \delta $.
3.3. Алгебраические интегралы
Из автомодельных уравнений (40)–(45) можно получить два алгебраических интеграла, выражающих законы сохранения углового момента и энтропии. Прежде всего из уравнений (40) и (45) находим
(54)
$(u - \delta )\left( {\frac{{dln\sigma }}{{dln\lambda }} + \frac{{dlnh}}{{dln\lambda }}} \right) + \frac{{du}}{{dln\lambda }} + (3 - {{k}_{d}})u = 0.$(55)
$\begin{gathered} (u - \delta )\left[ {\frac{{dln\sigma }}{{dln\lambda }} + \frac{{dlnh}}{{dln\lambda }} - 2(3 - {{k}_{d}})\frac{{dln\Lambda }}{{dln\lambda }}} \right] + \\ \, + \frac{{du}}{{dln\lambda }} = 0. \\ \end{gathered} $Для вывода второго алгебраического интеграла сначала из уравнений (43) и (45) находим
(58)
$\begin{gathered} (u - \delta )\left[ {\frac{{dlnw}}{{dln\lambda }} + (\gamma - 1)\frac{{dlnh}}{{dln\lambda }}} \right] + \\ \, + (\gamma - 1)\frac{{du}}{{dln\lambda }} + (3\gamma - 4)u = 0. \\ \end{gathered} $(59)
$\begin{gathered} (u - \delta )\left\{ {(3\gamma - 4)\frac{{dln\sigma }}{{dln\lambda }} + [{{k}_{d}}(\gamma - 1) - 1]\frac{{dlnh}}{{dln\lambda }} - } \right. \\ \, - \left. {(3 - {{k}_{d}})\frac{{dlnw}}{{dln\lambda }}} \right\} + [{{k}_{d}}(\gamma - 1) - 1]\frac{{du}}{{dln\lambda }} = 0. \\ \end{gathered} $(60)
$\frac{{{{\sigma }^{{3\gamma - 4}}}{{h}^{{{{k}_{d}}(\gamma - 1) - 1}}}}}{{{{w}^{{3 - {{k}_{d}}}}}}}{{\left| {u - \delta } \right|}^{{{{k}_{d}}(\gamma - 1) - 1}}} = {\text{const}}.$(61)
${{w}^{{3 - {{k}_{d}}}}}{{\delta }^{{{{k}_{d}}(\gamma - 1) - 1}}} = {{\sigma }^{{3\gamma - 4}}}\mathop {\left( {h\left| {u - \delta } \right|} \right)}\nolimits^{{{k}_{d}}(\gamma - 1) - 1} .$Аналитическая модель возмущения аккреционного диска в результате слияния двойной черной дыры, описанная в нашей недавней работе [13], не учитывала эффекты адиабатического нагрева-охлаждения, обусловленные вертикальными движениями. Данная модель этот эффект учитывает. Для перехода к более простой модели [13] следует положить $\Psi = 0$. В этом частном случае из уравнений (42) и (45) получаем соотношение $h = {{\Lambda }^{2}}$. Подставляя его в алгебраический интеграл углового момента (57), находим
Выражая отсюда ${{\Lambda }^{2}}$, можно написать С учетом этого соотношения из алгебраического интеграла адиабатичности (во внешней области возмущенного диска) получаем(64)
${{w}^{{2 - {{k}_{d}}}}}{{\delta }^{{{{k}_{d}}(\gamma - 1) - 1}}} = {{\sigma }^{{2\gamma - 3}}}{{\left| {u - \delta } \right|}^{{{{k}_{d}}(\gamma - 1) - 1}}}.$3.4. Асимптотики автомодельных функций
Исследуем асимптотику автомодельных функций в пределе при $\lambda \to \infty $. Эта асимптотика описывает рост возмущений в аккреционном диске на малых временах. С другой стороны, она соответствует состоянию диска в произвольный момент времени на больших расстояниях $r \gg {{r}_{*}}$ от центрального объекта. С учетом предельных при $\lambda \to \infty $ значений автомодельных функций $\sigma = 1$, $u = 0$, $\Lambda = 1$, $w = 1$, $\Psi = 0$, $h = 1$ искомое решение можно представить в виде: $u = {{u}_{1}}$, $\sigma = 1 + {{\sigma }_{1}}$, $\Lambda = 1 + {{\Lambda }_{1}}$, $w = 1 + {{w}_{1}}$, $\Psi = {{\Psi }_{1}}$, $h = 1 + {{h}_{1}}$, где ${{u}_{1}}$, ${{\sigma }_{1}}$, ${{\Lambda }_{1}}$, ${{w}_{1}}$, ${{\Psi }_{1}}$, ${{h}_{1}}$ – малые величины.
Заметим, что в уравнении движения (41) основным членом в пределе больших $\lambda $, который определяет нужную асимптотику, является последнее слагаемое в левой части. Отбрасывая в этом уравнении все малые по сравнению с ним величины, приходим к уравнению:
где штрихом обозначена производная по автомодельной переменной $\lambda $. Отсюда находим Аналогичным образом можно поступить с уравнением (44),(67)
$\delta \lambda \Psi _{1}^{'} + {{\Psi }_{1}} + \frac{{\xi {{\mu }^{2}}}}{{{{\lambda }^{3}}}} = 0.$(69)
$\delta \lambda \sigma _{1}^{'} - \lambda u_{1}^{'} - (2 - {{k}_{d}}){{u}_{1}} - {{\Psi }_{1}} = 0.$(73)
$\delta \lambda w_{1}^{'} - (\gamma - 1)\lambda u_{1}^{'} - (2\gamma - 3){{u}_{1}} - (\gamma - 1){{\Psi }_{1}} = 0.$(75)
${{h}_{1}} = \frac{1}{{24}}[2{{\mu }^{2}} - 5({{k}_{d}} + 1)]\frac{{\xi {{\mu }^{2}}}}{{{{\lambda }^{6}}}}.$(78)
$\frac{{\rho - {{\rho }_{0}}}}{{{{\rho }_{0}}}} = \frac{1}{2}{{k}_{d}}\xi GM\frac{{{{t}^{2}}}}{{{{r}^{3}}}},$(80)
$\frac{{\varepsilon - {{\varepsilon }_{0}}}}{{{{\varepsilon }_{0}}}} = \frac{1}{2}\xi GM\frac{{{{t}^{2}}}}{{{{r}^{3}}}},$(81)
$\frac{{H - {{H}_{0}}}}{{{{H}_{0}}}} = \frac{1}{{24}}[2{{\mu }^{2}} - 5({{k}_{d}} + 1)]\xi GM\frac{{{{t}^{4}}}}{{{{r}^{6}}}}.$Асимптотика автомодельных функций в противоположном пределе при $\lambda \to 0$ описывает переход возмущенного аккреционного диска к новому стационарному состоянию на больших временах $t \gg {{t}_{*}}$. В силу автомодельности задачи она также соответствует состоянию диска вблизи центрального объекта в произвольный момент времени. Предположим, что в пределе при $\lambda \to 0$ автомодельные функции $u \to 0$, $\sigma \to {{\sigma }_{0}}$, $w \to {{w}_{0}}$, $\Lambda \to {{\Lambda }_{0}}$, $\Psi \to 0$, $h \to {{h}_{0}}$. Тогда из уравнения (41) можно получить соотношение
(82)
$({{k}_{d}} + 1){{w}_{0}} + ({{\mu }^{2}} - {{k}_{d}} - 1)\Lambda _{0}^{2} = (1 - \xi ){{\mu }^{2}}.$4. РЕЗУЛЬТАТЫ РАСЧЕТОВ
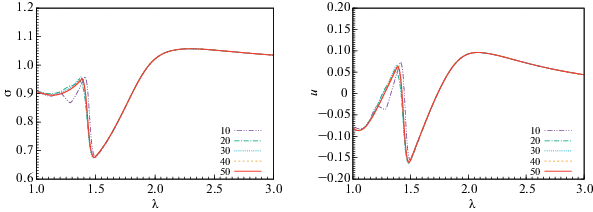
В предыдущем разделе 3 мы показали, что автомодельное решение исследуемой задачи существует. При этом мы подробно исследовали некоторые его свойства. Результаты численных расчетов полной задачи позволяют утверждать, то с течением времени решение действительно сходится к автомодельному. Сходимость численного решения уравнений (33)–(36) к автомодельному решению демонстрирует рис. 1. На рисунке показаны численные зависимости $\sigma (\lambda )$ (слева) и $u(\lambda )$ (справа) для различных моментов времени $t{\text{/}}{{t}_{*}}$. Решения соответствуют значению параметра $\mu = 5$. В результате слияния черных дыр и потери массы аккреционный диск возмущается и в нем формируется ударная волна слабой интенсивности, распространение которой происходит по автомодельному закону $\lambda = 1.428$ с показателем автомодельности $\delta = 2{\text{/}}3$. При этом в области перед ударной волной решение становится автомодельным практически сразу. Расчеты для больших значений $\mu $ показывают, что выход на автомодельный режим происходит гораздо быстрее. Таким образом, наряду с численным решением имеет смысл рассматривать и автомодельное решение.
Рис. 1.
Сходимость численного решения, описывающего возмущение аккреционного диска в результате слияния черных дыр и потери массы, к автомодельному решению для модели с параметром $\mu = 5$. Представлены численные зависимости $\sigma (\lambda )$ (слева) и $u(\lambda )$ (справа) для различных моментов времени $t/{{t}_{ * }}$.
Мы провели серию численных расчетов возмущения аккреционного диска, возникающего в результате слияния черных дыр и потери массы. С учетом оценок, приведенных в конце раздела 2, мы задавали значения параметра $\mu $ в диапазоне $50 \leqslant \mu \leqslant 200$ (см. табл. 2).
Таблица 2.
Характеристики автомодельных решений
| $\mu $ | ${{\lambda }_{1}}$ | ${{\lambda }_{2}}$ | ${{\lambda }_{3}}$ | ${{\sigma }_{0}}$ | ${{w}_{0}}$ | ${{I}_{\mu }}$ |
|---|---|---|---|---|---|---|
| 50 | 2.464 | 1.975 | 1.697 | 0.654 | 1.931 | 5.571 |
| 100 | 3.779 | 3.028 | 2.585 | 0.403 | 5.069 | 297.066 |
| 150 | 4.891 | 3.941 | 3.382 | 0.295 | 9.425 | 3741.66 |
| 200 | 5.897 | 4.765 | 4.075 | 0.233 | 15.15 | 25 304.2 |
Примечание. Приведены: $\mu $ – число Маха, ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, ${{\lambda }_{3}}$ (в порядке убывания) – автомодельные координаты ударных волн, ${{\sigma }_{0}}$ и ${{w}_{0}}$ – значения автомодельных функций $\sigma (\lambda )$ и $w(\lambda )$ в пределе при $\lambda \to 0$, ${{I}_{\mu }}$ – параметр, определяющий болометрическую светимость возмущенного диска согласно (89).
В работе [13] мы рассматривали чисто одномерную модель возмущенного аккреционного диска и строили автомодельное решение с помощью следующей методики. Сначала для достаточно большого значения автомодельной переменной $\lambda = {{\lambda }_{{max}}}$ вычислялись значения автомодельных функций по формулам, которые описывают асимптотику решения в пределе при $\lambda \to \infty $. Эти значения использовались в качестве начальных условий. Далее, задавая некоторый шаг автомодельной переменной $\Delta \lambda < 0$, с помощью численного метода находились значения величин для $\lambda < {{\lambda }_{{max}}}$. Количество ударных волн и положения их фронтов ${{\lambda }_{s}}$, где индекс $s$ определяет номер ударной волны, из самого автомодельного решения простым способом найти не удается. Эту необходимую информацию об ударных волнах мы брали из соответствующего численного решения. Как только в процессе численного интегрирования автомодельных уравнений автомодельная переменная $\lambda $ становилась равной ${{\lambda }_{1}}$, значение функций в точке $\lambda + \Delta \lambda $ вычислялись с помощью условий Гюгонио (48)–(53). После этого процедура интегрирования продолжалась дальше до следующей ударной волны.
В данной работе мы рассматриваем модель, соответствующую 1.5-мерному приближению, в котором учитываются вертикальные движения вещества в аккреционном диске. Это приводит к значительно более сложному характеру решения. В результате с помощью описанной выше методики получить полное автомодельное решение не удается. Проблема возникает вследствие того, что в данном случае использованная нами численная схема Рунге–Кутты 4-го порядка становится неустойчивой в окрестности особых точек (см. Приложение C), которые располагаются сразу за ударными волнами. Для корректного решения этой проблемы необходимо использовать какой-либо более специализированный численный метод. Поскольку у нас и так уже есть автомодельное решение, полученное с помощью численного моделирования полной задачи, то мы не стали этого делать. Автомодельное решение, полученное с помощью численного расчета полной задачи, с учетом найденных асимптотик, алгебраических интегралов углового момента и адиабатичности, а также информации об ударных волнах позволяет в полной мере оценивать величину и спектральные характеристики электромагнитного отклика от соответствующего гравитационно-волнового события.
Полученные решения для всех моделей представлены на рис. 2–7. Эти рисунки показывают, что во всех моделях в возмущенном аккреционном диске формируются три ударные волны, следующие друг за другом. Автомодельные координаты ${{\lambda }_{s}}$ этих ударных волн указаны в табл. 2. В модели с максимальным параметром $\mu = 200$ на самом деле формируется еще одна четвертая ударная волна, которой отвечает автомодельная координата ${{\lambda }_{s}} = 3.622$, но она имеет очень слабую интенсивность. Область сильного возмущения, где расположены ударные волны, сосредоточена в сравнительно узком интервале автомодельной переменной $2 < \lambda < 10$. С ростом значения параметра $\mu $ энергия возмущения перераспределяется между ударными волнами, которые осуществляют разгрузку этого возмущения. Угловой момент $\Lambda (\lambda )$ (см. рис. 4), а также автомодельные функции $\Psi (\lambda )$ (см. рис. 6) и $h(\lambda )$ (см. рис. 7) остаются непрерывными на ударных волнах, как и следует из полученных нами условий Гюгонио (49) и (53). Остальные автомодельные функции на ударных волнах испытывают скачки.
Рис. 2.
Автомодельная функция $\sigma (\lambda )$ для моделей с параметром $\mu $, равным 50, 100, 150 и 200.

Рис. 3.
Автомодельная функция $u(\lambda )$ для моделей с параметром $\mu $, равным 50, 100, 150 и 200.

Рис. 4.
Автомодельная функция $\Lambda (\lambda )$ для моделей с параметром $\mu $, равным 50, 100, 150 и 200.

Рис. 5.
Автомодельная функция $w(\lambda )$ для моделей с параметром $\mu $, равным 50, 100, 150 и 200.

Рис. 6.
Автомодельная функция $\Psi (\lambda )$ для моделей с параметром $\mu $, равным 50, 100, 150 и 200.
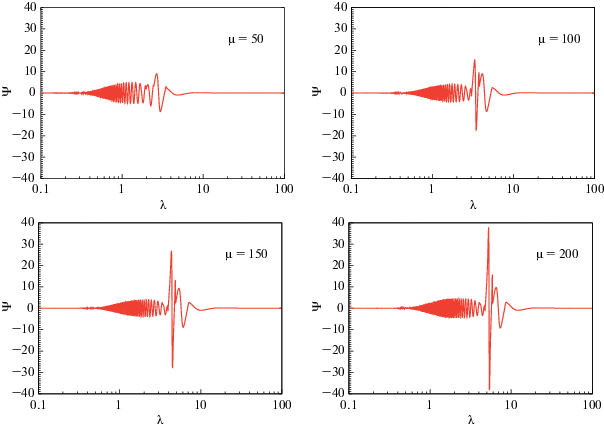
Рис. 7.
Автомодельная функция $h(\lambda )$ для моделей с параметром $\mu $, равным 50, 100, 150 и 200.
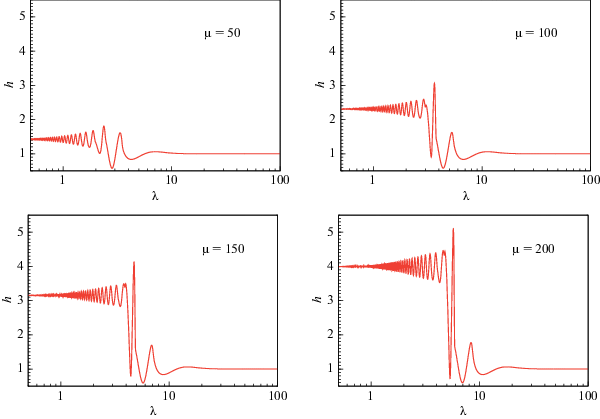
Анализ рисунков позволяет заключить, что интенсивность первой (самой внешней) ударной волны постепенно падает, в то время как интенсивности внутренних ударных волн постепенно нарастают. Особенно это касается второй (промежуточной) ударной волны. Так, в случае μ = 200 основная энергия возмущения сосредоточена во второй ударной волне. Интересно отметить, что перед каждой ударной волной располагаются нелинейные предвестники, распространяющиеся впереди них. Особенно их хорошо видно на распределении $w(\lambda )$ (см. рис. 5). При этом перед самой внешней ударной волной имеются сразу два таких предвестника, а предвестник перед самой внутренней ударной волной имеет слабую интенсивность.
Во внешней области перед ударными волнами автомодельное решение является гладким и при больших $\lambda $ описывается асимптотическими выражениями, полученными в разделе 3.4. Во внутренней области за ударными волнами при малых $\lambda $ автомодельное решение также переходит в соответствующую асимптотику при $\lambda \to 0$. По полученным результатам расчета непосредственной проверкой можно убедиться, что алгебраический интеграл углового момента (57) удовлетворяется во всей области изменения автомодельной переменной. В то же время алгебраический интеграл адиабатичности (61) строго совпадает с полученным решением только во внешней области до первой ударной волны.
В области за ударными волнами структура аккреционного диска становится существенно нестационарной. Распределение радиальной скорости $u(\lambda )$ имеет колебательный характер и она много раз меняет знак (см. рис. 3). Это означает, что одни части диска движутся наружу (${{v}_{r}} > 0$), а другие, наоборот, внутрь (${{v}_{r}} < 0$). Сильные вариации испытывает и вертикальная структура диска. Автомодельная функция $\Psi (\lambda )$, которая определяет вертикальную скорость (см. уравнения (11) и (37)), быстро изменяется во времени с явно выраженным колебательным характером (см. рис. 6). Это приводит к квазипериодическим изменениям полутолщины диска $h(\lambda )$ (см. рис. 7), амплитуда которых постепенно затухает.
После прохождения нелинейных и ударных волн в диске формируется новое стационарное состояние, в котором радиальная и вертикальная скорости равны нулю. Это новое состояние характеризуется более низкой плотностью, более высокой температурой и увеличенной толщиной диска. Анализ полученного решения (см. табл. 2) позволяет заключить, что в результате вертикального расширения диска плотность в плоскости симметрии во всех моделях (в модели с параметром $\mu = 50$ в $1.53$ раза) падает более, чем в 2 раза по сравнению с невозмущенным состоянием.
5. ЭЛЕКТРОМАГНИТНЫЙ ОТКЛИК
Прохождение ударных волн по диску приводит к нагреву вещества. Новое стационарное состояние диска, которое начинает формироваться в его внутренней части за ударными волнами, характеризуется более высокой температурой. В результате светимость аккреционного диска резко возрастает. Это явление можно расценивать как электромагнитный отклик объекта на эффект слияния черных дыр и потерю массы за счет излучения гравитационных волн.
Болометрическую светимость аккреционного диска (если смотреть на него с одной стороны) можно рассчитать с помощью выражения
(85)
$L(t) = 2{{\pi }^{2}}\int\limits_{{{r}_{{\text{d}}}}}^\infty \,drr{{\sigma }_{{{\text{SB}}}}}T_{{{\text{eff}}}}^{4}(r,t),$В геометрически тонком аккреционном диске для оценки эффективной температуры можно использовать простое приближение, в котором считается, что ${{T}_{{{\text{eff}}}}} = fT$, где коэффициент $f$ определяется конкретным процессом переноса тепловой энергии в вертикальном направлении [12, 24]. Если перенос тепловой энергии осуществляется путем лучистой теплопроводности, то можно принять, что коэффициент $f = 0.1$. Если же перенос энергии в вертикальном направлении определяется конвекцией, то перепад температуры можно оценить величиной $f = 0.5$.
Светимость возмущенного аккреционного диска можно оценить с помощью построенного автомодельного решения. Температура в плоскости симметрии диска в автомодельном решении определяется выражением
Следовательно, болометрическая светимость (85) может быть представлена в виде(87)
$L(t) = 2\pi {{\sigma }_{{{\text{SB}}}}}{{f}^{4}}T_{*}^{4}r_{*}^{2}\mathop {\left( {\frac{{{{t}_{*}}}}{t}} \right)}\nolimits^{4/3} \int\limits_{{{{({{t}_{ * }}/t)}}^{{2/3}}}}^\infty \,\frac{{{{w}^{4}}(\lambda )d\lambda }}{{{{\lambda }^{3}}}},$(88)
$\int\limits_{{{{({{t}_{ * }}/t)}}^{{2/3}}}}^1 \,\frac{{{{w}^{4}}(\lambda )d\lambda }}{{{{\lambda }^{3}}}} = \frac{{w_{0}^{4}}}{2}\left[ {\mathop {\left( {\frac{t}{{{{t}_{*}}}}} \right)}\nolimits^{4/3} - 1} \right].$(89)
${{I}_{\mu }} = \int\limits_1^\infty \,\frac{{{{w}^{4}}(\lambda )d\lambda }}{{{{\lambda }^{3}}}}$(90)
$L(t) = 2\pi {{\sigma }_{{{\text{SB}}}}}{{f}^{4}}T_{*}^{4}r_{*}^{2}\mathop {\left( {\frac{{{{t}_{*}}}}{t}} \right)}\nolimits^{4/3} \left\{ {\frac{{w_{0}^{4}}}{2}\left[ {\mathop {\left( {\frac{t}{{{{t}_{*}}}}} \right)}\nolimits^{4/3} - 1} \right] + {{I}_{\mu }}} \right\}.$Полученные зависимости $L(t)$, нормированные на предельное значение ${{L}_{{max}}}$, для моделей с различными параметрами $\mu $ показаны на рис. 8. Анализ этих кривых блеска позволяет заключить, что светимость возмущенного диска за время порядка нескольких характерных времен ${{t}_{ * }}$ (это составляет несколько секунд) достигает постоянного значения ${{L}_{{max}}}$. Рост светимости определяется фактором $w_{0}^{4}$, значения которого для различных моделей приведены в табл. 2. С увеличением параметра $\mu $ интенсивность электромагнитного отклика существенно возрастает. Если в модели светимость возрастает всего на порядок, то в модели $\mu = 200$ рост светимости составляет уже более 4 порядков величины.
Рис. 8.
Автомодельная зависимость болометрической светимости от времени $L(t)$ для моделей с параметрами $\mu $, равными 50, 100, 150 и 200.

В дальнейшем нагретое вещество будет постепенно остывать за счет радиативного охлаждения и светимость возмущенного диска будет медленно уменьшаться. В гидродинамической модели и в автомодельном решении этот эффект мы не учитывали. Однако характерное время охлаждения ${{t}_{{{\text{cool}}}}}$ нетрудно оценить [13]. Объемный коэффициент охлаждения в диффузионном приближении переноса излучения может быть записан в виде
(92)
${{\Lambda }_{{{\text{cool}}}}} = \frac{{4{{\sigma }_{{{\text{SB}}}}}{{T}^{4}}}}{{3\kappa \rho {{H}^{2}}}},$Спектральная плотность потока излучения с одной стороны диска в перпендикулярном направлении,
(94)
${{F}_{\nu }}(t) = 2{{\pi }^{2}}\int\limits_{{{r}_{{\text{d}}}}}^\infty \,drr{{B}_{\nu }}({{T}_{{{\text{eff}}}}}(r,t)),$(95)
${{B}_{\nu }}(T) = \frac{{2h{{\nu }^{3}}}}{{{{c}^{2}}}}\mathop {\left( {{{e}^{{\tfrac{{h\nu }}{{{{k}_{{\text{B}}}}T}}}}} - 1} \right)}\nolimits^{ - 1} ,$Полученные спектры электромагнитного излучения, соответствующие автомодельному решению, представлены на рис. 9. Спектры для радиативных дисков ($f = 0.1$) для различных моделей показаны на левой панели рис. 9, а для конвективных дисков ($f = 0.5$) на правой панели. При этом жирные линии описывают спектры возмущенных дисков, а тонкие линии соответствуют спектрам невозмущенных дисков. Значения потоков ${{F}_{\nu }}$ приведены в абсолютных величинах. Закрашенная вертикальная полоса указывает оптический диапазон спектра.
Рис. 9.
Спектры электромагнитного излучения ${{F}_{\nu }}$, полученные из автомодельного решения для радиативного (слева) и конвективного (справа) дисков. Жирные линии описывают спектры возмущенных дисков, а тонкие линии описывают соответствующие спектры невозмущенных дисков. Закрашенной полосой показан оптический диапазон спектра.

Как видно из рисунка, основная энергия излучения сосредоточена в диапазоне от 1 до 100 кэВ, что соответствует мягкому и жесткому рентгену. Кроме того, значительная доля энергии излучения приходит и в гамма-диапазоне ($ \geqslant {\kern 1pt} 100$ кэВ). В обоих случаях (радиативные и конвективные диски) максимальный поток излучения в процессе вспышки возрастает, как правило, на два порядка величины. При этом частота, на которой достигается максимум, смещается в область высоких частот. В случае конвективных дисков поток излучения на два порядка величины превышает поток от радиативных дисков. Кроме того, максимальное значение потока от конвективных дисков по сравнению с радиативными дисками смещено в область жесткого рентгеновского излучения. В видимой области спектра поток излучения возрастает примерно на порядок. При этом наибольший относительный эффект вспышки проявляется для наибольшего значения параметра $\mu = 200$. Поэтому следует ожидать, что в случае слияния сверхмассивных черных дыр поток излучения от возмущенного аккреционного диска должен возрастать в существенно большей степени, в том числе и в оптическом диапазоне спектра.
6. ЗАКЛЮЧЕНИЕ
Мы рассмотрели одну возможность электромагнитного отклика от слияния двух черных дыр. Сценарий основан на предположении, что двойная черная дыра окружена аккреционным диском. При слиянии черных дыр масса продукта уменьшается за счет излучения гравитационных волн. В результате аккреционный диск получает некоторую дополнительную энергию, достаточную, чтобы вывести его из равновесного состояния. Возмущение диска приводит к формированию в нем нелинейных и ударных волн высокой интенсивности, распространяющихся из центральной области на периферию. Ударные волны нагревают вещество, что приводит к резкому росту потока электромагнитного излучения от диска. В рамках такой модели оказывается возможным рассчитать кривую блеска, спектральную плотность потока излучения, а также оценить характерную продолжительность вспышки. Результаты расчетов показывают, что в случае объекта GW170814 всплеск светимости от аккреционного диска может оказаться вполне достаточным для регистрации этого отклика современными наблюдательными инструментами.
В работе исследовано автомодельное решение, описывающее эволюцию возмущенного аккреционного диска после слияния черных дыр и потери массы. При этом показатель автомодельности оказывается равным 2/3. Решение описывает структуру возмущенного диска в области (так называемая зона B), в которой доминирует газовое давление, а непрозрачность вещества определяется процессами томсоновского рассеяния электронов. В отличие от нашей предыдущей работы [13] в данной статье мы учли эффект, обусловленный адиабатическим охлаждением диска. Для построения автомодельного решения мы использовали результаты численного моделирования. Из автомодельных уравнений получены алгебраические интегралы углового момента и адиабатичности, выражающие соответствующие законы сохранения. Алгебраический интеграл углового момента удовлетворяется во всей области изменения автомодельной переменной. Алгебраический интеграл адиабатичности удовлетворяется только в областях гладкости решения, поскольку на ударных волнах энтропия испытывает скачок. Мы также нашли асимптотические соотношения для автомодельных функций, описывающие как развитие начального возмущения, так и переход диска к новому стационарному состоянию.
С помощью полученного автомодельного решения задачи можно приближенно оценивать величину электромагнитного отклика гравитационно-волнового события без проведения трудоемких численных расчетов. Анализ полученных автомодельных решений показывает, что для параметров, соответствующих событию GW170814, рост светимости диска может составить от одного до четырех порядков величины. В видимой области спектра поток излучения возрастает примерно на порядок. Этого может оказаться вполне достаточно для регистрации этого отклика современными наблюдательными инструментами.
Следует подчеркнуть, что интенсивность электромагнитного отклика существенно возрастает с увеличением числа Маха на внутренней границе диска. Мы рассматривали случай слияния черных дыр звездной массы, для которых характерное значение этого параметра составляет порядка сотни. Для сверхмассивных черных дыр этот параметр может быть существенно больше. Поэтому следует ожидать, что в случае слияния сверхмассивных черных дыр поток электромагнитного излучения от возмущенного аккреционного диска должен возрастать в существенно большей степени, в том числе и в оптическом диапазоне спектра.
Список литературы
B. P. Abbott, R. Abbott, T. D. Abbott, M. R. Abernathy, et al., Astrophys. J. Letters 818, id. L22 (2016).
Л. Д. Ландау, Е. М. Лифшиц, Теория поля (М.: Физматлит, 2012).
C. W. Misner, K. S. Thorne, and J. A. Wheeler, Gravitation (San Francisco: W. H. Freeman, 1973).
J. P. A. Clark and D. M. Eardley, Astrophys. J. 215, 311 (1977).
A. V. Tutukov and L. R. Yungelson, Monthly Not. Roy. Astron. Soc. 260, 675 (1993).
V. M. Lipunov, K. A. Postnov, and M. E. Prokhorov, Astron. Letters 23, 492 (1997).
B. P. Abbott, R. Abbott, T. D. Abbott, M. R. Abernathy, et al., Phys. Rev. Lett. 116, id. 241103 (2016).
B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, et al., Phys. Rev. Lett. 118, id. 221101 (2017).
B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, et al., Astrophys. J. Letters 851, id. L35 (2017).
B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, et al., Phys. Rev. Lett. 119, id. 141101 (2017).
B. P. Abbott, R. Abbott, T. D. Abbott, S. Abraham, et al., Phys. Rev. X 9, id. 031040 (2019).
Д. В. Бисикало, А. Г. Жилкин, Е. П. Курбатов, Успехи физ. наук 189, 1213 (2019).
D. V. Bisikalo and A. G. Zhilkin, Monthly Not. Roy. Astron. Soc. 494, 5520 (2020).
A. Peres, Phys. Rev. 128, 2471 (1962).
J. D. Bekenstein, Astrophys. J. 183 657 (1973).
N. Bode and S. Phinney, in American Physical Society, APS April Meeting, April 14–17, 2007, Abstracts (Washington, DC: American Physical Society, 2007), id. S1.010.
M. Megevand, M. Anderson, J. Frank, E. W. Hirsch-mann, L. Lehner, S. L. Liebling, P. M. Motl, and D. Neil-sen, Phys. Rev. D 80, id. 024012 (2009).
B. Kocsis and A. Loeb, Phys. Rev. Lett. 101, id. 041101 (2008).
А. М. Черепащук, Успехи физ. наук 186, 1001 (2016).
L. R. Corrales, Z. Haiman, and A. MacFadyen, Monthly Not. Roy. Astron. Soc. 404, 947 (2010).
M. J. Fitchett, Monthly Not. Roy. Astron. Soc. 203, 1049 (1983).
H. Pietilä, P. Heinamaki, S. Mikkola, and M. J. Valtonen, Celestial Mechanics and Dynamical Astronomy 62, 377 (1995).
S. E. de Mink and A. King, Astrophys. J. Letters 839, id. L7 (2017).
Д. В. Бисикало, А. Г. Жилкин, Е. П. Курбатов, Астрон. журн. 96, 3 (2019).
F. Pretorius, Phys. Rev. Lett. 95, id. 121101 (2005).
M. Campanelli, C. O. Lousto, P. Marronetti, and Y. Zlochower, Phys. Rev. Lett. 96, id. 111101 (2006).
J. G. Baker, J. Centrella, Dae-Il Choi, M. Koppitz, and J. van Meter, Phys. Rev. Lett. 96, id. 111102 (2006).
M. I. Cohen, J. D. Kaplan, and M. A. Scheel, Phys. Rev. D 85, id. 024031 (2012).
P. Artymowicz and S. H. Lubow, Astrophys. J. 421, 651 (1994).
D. B. Bowen, V. Mewes, S. C. Noble, M. Avara, M. Campanelli, and J. H. Krolik, Astrophys. J. 879, id. 76 (2019).
П. В. Кайгородов, Д. В. Бисикало, А. М. Фатеева, А. Ю. Сытов, Астрон. журн. 87(12), 1170 (2010).
А. Ю. Сытов, П. В. Кайгородов, А. М. Фатеева, Д. В. Бисикало, Астрон. журн. 88, 862 (2011).
N. I. Shakura and R. A. Sunyaev, Astron. and Astrophys. 24, 337 (1973).
V. M. Lipunov, G. Borner, and R. S. Wadhwa, Astrophysics of Neutron Stars (Springer, 1992).
J. M. Bardeen, Nature 226, 64 (1970).
K. S. Thorne, Astrophys. J. 191, 507 (1974).
L.-X. Li and B. Paczynski, Astrophys. J. Letters 534, L197 (2000).
A. A. Samarskii and I. P. Popov, Difference methods for solving problems of gas dynamics (2nd revised and enlarged edition) (Moscow: Nauka, 1980).
D. V. Bisikalo and A. G. Zhilkin, Ann. Brazilian Acad. Sci. 93 (Suppl. 1), e20200801 (2021).
L. I. Sedov, Similarity and dimensional methods in mechanics (Moscow: Mir Publ., 1982).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


