1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 98, № 2, 2021

Астрономический журнал, 2021, T. 98, № 2, стр. 132-148

Ограничения параметров черной дыры и плазмы в окрестности источника Стрелец A*

С. В. Чернов 1, *

1 Астрокосмический центр, Физический институт им. П.Н. Лебедева РАН
Москва, Россия

* E-mail: chernov@lpi.ru

Поступила в редакцию 27.04.2020
После доработки 27.09.2020
Принята к публикации 07.10.2020

Полный текст (PDF)

Аннотация

В работе получены оценки параметров аккреционных потоков плазмы и центральной черной дыры путем сравнения численных расчетов МГД моделей с наблюдениями для центра нашей Галактики Стрелец $A{\kern 1pt} *$ в радиодиапазоне. Аккреционный поток моделировался как распределение торообразной двухтемпературной электрон-протонной плазмы. Предполагается, что протоны нагреваются за счет эффектов вязкой диссипации, а электроны теряют энергию за счет синхротронного излучения. Считается, что кулоновские взаимодействия между протонами и электронами неэффективны. Из сравнения с наблюдениями спектральной плотности потока излучения и поляризации (линейной и круговой) для сверхмассивной черной дыры в источнике Стрелец $A{\kern 1pt} *$ были получены следующие ограничения: параметр вращения (спин) черной дыры равен $a \approx 0.6$, температура электронов составляет долю ${{T}_{p}}{\text{/}}3 < {{T}_{e}} < {{T}_{p}}$ от температуры протонов, наблюдатель расположен под углом $i \approx 50^\circ $ к оси вращения черной дыры, темп аккреции много меньше эддингтоновского предела $\dot {M} \sim {{10}^{{ - 8}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 10}}}{{\dot {M}}_{{{\text{Edd}}}}}$. Ограничения на магнитное поле получить не удалось из-за маленькой выборки по параметру плазмы $\beta = 2{{p}_{{gas}}}{\text{/}}{{p}_{{mag}}}$.

1. ВВЕДЕНИЕ

Стрелец $A{\kern 1pt} *$ (Sgr $A{\kern 1pt} *$) является компактным источником нетеплового радиоизлучения в центре нашей Галактики Млечный путь, внутри которого расположена сверхмассивная черная дыра [1]. Это радиоизлучение происходит из горячей, разреженной торообразной электрон-протонной плазмы, которая вращается вокруг черной дыры со скоростью около 100 км/с [2]. Размер центральной области – порядка одной астрономической единицы [3]. Считается, что масса черной дыры $M \approx 4 \times {{10}^{6}}\;{{M}_{ \odot }}$, а расстояние до нее $R \approx 8.2$ кпк [4–6]. Параметр вращения (спин) черной дыры определить достаточно сложно и надежные данные по измерению спина черной дыры отсутствуют. В работе [7] по сейсмологии аккреционного диска путем измерения квазипериодических осцилляций была получена оценка параметра вращения черной дыры, равная $a \approx 0.44$. В работе [8] автор получил оценку величины параметра вращения черной дыры, равной $a \approx 0.65$.

Считается, что торообразная плазма представляет из себя аккреционный диск, который вращается вокруг черной дыры [2]. Согласно современным представлениям, аккреционные диски можно разделить на два типа [9]. Первый тип – геометрически тонкие, оптически толстые диски, которые излучают чернотельное излучение [10]. Второй тип – геометрически толстые, но оптически тонкие диски, которые практически прозрачны к излучению [11]. Предполагается, что аккреционные диски содержат мелкомасштабное магнитное поле, которое генерируется и усиливается за счет магниторотационной неустойчивости. Светимость многих активных галактических ядер лежит в диапазоне ${{L}_{{{\text{Edd}}}}} > {{L}_{{bol}}} > 0.01{{L}_{{{\text{Edd}}}}}$ [12]. В отличие от большинства галактик в нашей Галактике дело обстоит совершенно противоположно. Максимум светимости приходится на субмиллиметровый диапазон. Предполагая, что болометрическая светимость по порядку величины соответствует светимости в субмиллиметровом диапазоне, получаем ${{L}_{{bol}}} \approx {{L}_{{submm}}} \sim {{10}^{{35}}}$ эрг/с [13, 14], что составляет малую долю эддингтоновского предела $({{10}^{{ - 8}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 9}}}){{L}_{{{\text{Edd}}}}}$ [13–15], где

(1)
${{L}_{{{\text{Edd}}}}} = \frac{{4\pi GM{{m}_{p}}c}}{{{{\sigma }_{T}}}} \approx {{10}^{{38}}}\frac{M}{{{{M}_{ \odot }}}}\;{\text{эрг/с}},$
а темп аккреции порядка $\dot {M} \sim {{10}^{{ - 7}}}{{\dot {M}}_{{{\text{Edd}}}}}$ и меньше [15], где
(2)
$\mathop {\dot {M}}\nolimits_{{\text{Edd}}} = \frac{{{{L}_{{{\text{Edd}}}}}}}{{\eta {{c}^{2}}}},$
и коэффициент $\eta $ здесь, и везде ниже, выбирается равным $\eta = 0.057$ [15], где $G$ – гравитационная постоянная, ${{m}_{p}}$ – масса протона, $c$ – скорость света, ${{\sigma }_{T}}$ – томсоновское сечение. Такая малая светимость центра нашей Галактики обусловлена малым темпом аккреции и низкой радиационной эффективностью аккрецирующего потока [1]. Такие диски являются геометрически толстыми и оптически тонкими [11, 15–17].

В данной работе нас будет интересовать сантиметровое, миллиметровое и субмиллиметровое радиоизлучение из центра нашей Галактики. Как было сказано выше, максимум светимости приходит на субмиллиметровую область спектра. В спокойном состоянии плотность потока в этой области спектра приблизительно равна 3 Ян [13]. Это излучение имеет как линейную, так и круговую поляризацию. Впервые линейная поляризация была измерена в работе [18], круговая поляризация в работе [19]. Считается, что источником линейной поляризации является синхротронное излучение. Круговая поляризация плохо изучена и составляет, как правило, доли процентов от интенсивности излучения. Считается, что круговая поляризация возникает из линейной поляризации (реполяризация) за счет фарадеевского преобразования. Она имеет постоянную отрицательную хиральность (handedness). Постоянное значение хиральности предполагает стабильную конфигурацию магнитного поля. Линейная поляризация отсутствует на сантиметровых длинах волн [19, 20] и достигает десяти процентов в миллиметровой и субмиллиметровой областях спектра [18, 21–23]. Предполагается, что линейная поляризация подвержена значительному фарадеевскому вращению, поэтому средняя мера вращения достаточно большая, $RM \approx - 5 \times {{10}^{5}}$ рад/м2 [14]. Считается, что линейная поляризация возникает в области $ \sim {\kern 1pt} 10{{R}_{g}}$ (${{R}_{g}} = 2GM{\text{/}}{{c}^{2}}$) от горизонта событий [24] и интерпретируется как внутренняя линейная поляризация.

Источник Sgr $A{\kern 1pt} *$ также проявляет вспышечную активность во всем наблюдаемом диапазоне длин волн от радио до гамма [25–29]. Продолжительность таких вспышек около часа [26, 27, 30, 31], что соответствует масштабам в несколько гравитационных радиусов, и считается, что эти области расположены во внутренних частях аккреционного диска, в ближайшей окрестности черной дыры [26, 32]. Если это так, то вспышечная активность даст важную информацию о механизмах излучения вблизи черной дыры [13]. Плотность потока излучения во время вспышки, в зависимости от диапазона, может меняться от нескольких процентов в радиодиапазоне до двух порядков в рентгеновском диапазоне. Также наблюдается корреляция между вспышками в различных диапазонах [13, 27]. Существуют много различных моделей, которые способны объяснить вспышечную активность: это модели аккреционных неустойчивостей, пересоединение магнитных силовых линий, расширяющие сгустки плазмы и другие модели [26, 27, 31], но на сегодняшний день единая самосогласованная модель отсутствует. По задержкам вспышек в разных диапазонах можно оценить параметры протон-электронной плазмы в непосредственной окрестности черной дыры. Предполагая электронейтральность плазмы и равнораспределение между энергией частиц и энергией магнитного поля, можно оценить следующие величины: плотность релятивистских электронов ${{n}_{e}} \approx 3.5 \times {{10}^{2}}$ см–3, температуру теплового газа $T \approx 5 \times {{10}^{9}}$ K и величину магнитного поля $B \approx 11$ Гс [33].

Для объяснения низкой светимости источника Sgr $A{\kern 1pt} *$ рассматриваются радиационно неэффективные модели аккреции плазмы на черную дыру [11]. В таком приближении излучением плазмы можно пренебречь, но само вещество нельзя рассматривать в одножидкостном приближении, так как температура электронов будет отлична от температуры протонов [1, 34]. Таким образом, задача сводится к отдельному вычислению аккреционного потока и соответствующих величин (магнитного поля, термодинамических величин, темпа аккреции), связанных с протонами, и затем к вычислению излучательной способности аккреционного диска за счет релятивистских электронов (синхротронных электронов). Главной проблемой данных моделей является неопределенность температуры электронов. В упрощенной постановке считается, что температура электронов связана с температурой протонов некоторой постоянной величиной ${{T}_{e}}{\text{/}}{{T}_{p}} = {\text{const}}$ [35]. В более сложных моделях рассматривают связь между температурами электронов и протонов отдельно в диске и в джете [36].

В данной работе строятся аналогичные МГД модели [35, 36], а затем для каждой модели отдельно вычисляются спектральная плотность потока излучения и поляризация (как линейная, так и круговая) и сравниваются с наблюдениями [37, 38]. Новизной данной работы является то, что плотность потока излучения сравнивается с наблюдениями не на одной частоте (230 ГГц), как в большинстве работ [39], а в некотором диапазоне частот (1–900 ГГц). Помимо этого, также сравниваются с наблюдениями линейная и круговая поляризация [37, 38] в диапазоне частот 80–400 и 2‒400 ГГц соответственно. Благодаря этому можно более строго определить ограничения на параметры плазмы из наблюдений.

В работе [39] рассматривалась численная осесимметричная магнитогидродинамическая модель эволюции торообразного распределения электрон-протонной плазмы вокруг черной дыры. При сравнении с наблюдениями были получены следующие значения параметров модели: параметр вращения черной дыры $a \approx 0.94$, отношение температуры протонов к температуре электронов ${{T}_{i}}{\text{/}}{{T}_{e}} \sim 3$ и наклонение $i \approx 85^\circ $. В работе [37] при сравнении численной модели с наблюдениями, как плотности потока, так и поляризации, были получены следующие оценки: параметр вращения черной дыры $a = 0.5$, наклонение $i = 75^\circ $, температура электронов ${{T}_{e}} = 3.1 \times $ × 1010 K, темп аккреционного потока $\dot {M} = 4.6 \times $ $ \times {{10}^{{ - 8}}}\,{{M}_{ \odot }}$/год.

Везде ниже время $t$ будет измеряться в компьютерных единицах. Для перевода в физические единицы $t$ необходимо умножить на фактор ${{t}_{g}} = GM{\text{/}}{{c}^{3}}$. Пространственные масштабы измеряются в единицах $GM{\text{/}}{{c}^{2}}$.

2. ЧИСЛЕННАЯ МОДЕЛЬ

В данном разделе рассматривается численная постановка задачи и ограничения, которые предполагаются в данной МГД модели. Будет рассмотрена модель излучения и представлены наблюдательные данные, которые использовались для сравнения с численной моделью.

2.1. Магнитогидродинамическая модель

Рассматривается радиационно неэффективный геометрически толстый, оптически тонкий идеальный аккреционный диск. При моделировании такие диски позволяют пренебречь излучением во всей области диска, что значительно облегчает решение численной задачи. Для моделирования идеальной замагниченной плазмы вокруг вращающейся черной дыры использовался двухмерный осесимметричный свободный код HARM2d [40, 41]. Рассматривалось осесимметричное распределение торообразной электрон-протонной плазмы. Предполагалось, что ось вращения черной дыры сонаправлена с осью вращения диска (обратный случай был рассмотрен в работе [42]), но наблюдатель смотрит на аккреционный диск под разными углами в диапазоне $cosi = (0;\;0.2;\;0.40;\;0.6428)$, где угол наклонения $i$ отсчитывается от оси вращения черной дыры. Для моделирования выбиралась торообразная проблема (TORUS–PROBLEM) с численным разрешением ${{N}_{r}} \times {{N}_{\theta }}$ = 250 × 250 точек. Начальное гидростатическое равновесие торообразной плазмы описано в работое [43] со следующими численными параметрами: внутренний радиус численной области ${{R}_{{in}}} = 0.9(1 + \sqrt {1 - {{a}^{2}}} )$, где $a$ – параметр вращения черной дыры, внешний радиус численной области ${{R}_{{out}}} = 50$, и с параметрами аккреционного диска: внутренний радиус диска ${{r}_{{in}}} = 6$, максимальное давление (плотность) задавалось в точке ${{r}_{{max}}} = 12$. Максимальный внешний радиус диска равен ${{r}_{{out}}} \approx 37$ гравитационных радиусов для $a = 0.95$, тем самым рассматривается распределение плазмы в ближайшей окрестности черной дыры.

В данной работе рассмотрены три значения параметра вращения черной дыры. Слабое вращение $a = 0.2$, умеренное вращение $a = 0.6$ и быстрое вращение $a = 0.95$. Начальное состояние плазмы описывалось гидродинамическими уравнениями с двумя значениями показателя адиабаты: $\Gamma = 4{\text{/}}3$ и 5/3, что соответствует релятивистскому и нерелятивистскому распределению температуры протонов соответственно. Считалось, что показатель адиабаты является постоянной величиной во всей области плазмы. В работе [44] рассмотрен случай, в котором показатель адиабаты $\Gamma $ зависел от температуры и было показано, что показатель адиабаты меняется от величины $\Gamma = 5{\text{/}}3$ в средней области диска до величины $\Gamma = 4{\text{/}}3$ в полярных областях. Полоидальное магнитное поле задавалось через векторный потенциал [40, 41]

(3)
${{A}_{\phi }} \sim max(\rho - 0.2;0),$
где $\rho $ – плотность плазмы. Амплитуда векторного потенциала нормируется параметром $\beta \, = \,2{{p}_{{gas}}}{\text{/}}{{p}_{{mag}}}$, которое определяется отношением газового давления к магнитному давлению. Этот параметр является ключевым в данной задаче. Такое распределение магнитного поля представляет из себя вложенные замкнутые петли в полоидальной плоскости. Рассматривались два значения параметра $\beta = 10$ и $\beta = 100$.

На рис. 1 показан пример начального (в момент $t = 0$) торообразного распределения плотности электрон-протонной плазмы для модели со следующими параметрами $\Gamma = 4{\text{/}}3$, $\beta = 100$, $a = 0.2$. Величина $\beta = 100$ приблизительно соответствует начальной величине магнитного поля $B \approx 0.03$ Гс.

Рис. 1.

Пример начального распределения плотности плазмы (показано цветом) вокруг черной дыры для модели с параметрами $\Gamma = 4{\text{/}}3$, $\beta = 100$ и $a = 0.2$. Черным полукругом изображена черная дыра.

Моделирование выполнялось до момента времени $t = 15\,000$, кроме моделей с параметрами $\Gamma = 5{\text{/}}3$, $\beta = 10$, для которых моделирование выполнялось до момента времени $t = 1800$. Орбитальный период в точке максимального давления приблизительно равен 264, что для момента времени $t = 15\,000$ приблизительно соответствует 57 орбитальным периодам. На рис. 2 показан пример зависимости темпа аккреции от времени для модели с параметрами $\Gamma = 4{\text{/}}3$ и $\beta = 100$. Темп аккреции определяется формулой [45]

(4)
$\dot {M} = \int\limits_0^\pi \,\int\limits_0^{2\pi } \,\sqrt { - g} \rho {{u}^{r}}d\phi d\theta ,$
где $g$ – определитель метрики Керра, ${{u}^{r}}$ –радиальная скорость. Синяя сплошная кривая показана для случая $a = 0.2$, зеленая штриховая – для случая $a = 0.6$, красная штрихпунктирная – для случая $a = 0.95$. Из рис. 2 видно, что при временах больше $t \approx 4000$ решение заведомо выходит на квазистационарное решение с медленно изменяющимся с течением времени потоком.

Рис. 2.

Пример зависимости темпа аккреции плазмы в компьютерных единицах с течением времени для модели с параметрами $\Gamma = 4{\text{/}}3$, $\beta = 100$ и трех значений $a$. Синяя сплошная кривая показана для случая $a = 0.2$, зеленая штриховая – для случая $a = 0.6$, красная штрихпунктирная – для случая $a = 0.95$.

Другим важным параметром в данных моделях является отношение магнитного потока к потоку частиц. Данный параметр определяется следующим образом [45]:

(5)
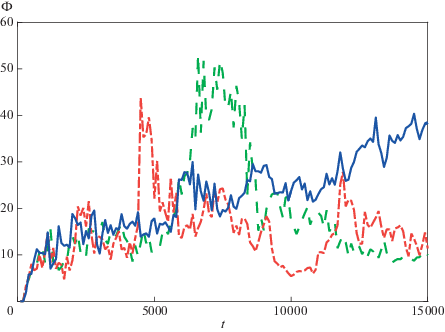
$\phi = \frac{1}{{\sqrt {\langle \dot {M}\rangle } }}\frac{{4\pi }}{2}\int\limits_0^\pi \,\int\limits_0^{2\pi } \,\sqrt { - g} {\text{|}}{{B}^{r}}{\text{|}}d\phi d\theta ,$
где ${{B}^{r}}$ – радиальное магнитное поле. Величина $\varphi $ вычисляется на гравитационном радиусе. Если величина этого параметра больше $ \sim {\kern 1pt} 50$ [45], то данная модель соответствует диску с захваченным магнитным полем (Magnetically Arrested Disks, MAD), в противном случае аккреционный диск является обычным диском со стандартной и нормальной эволюцией (Standard and Normal Evolution, SANE). В нашей работе все смоделированные аккреционные диски относятся к классу SANE. Считается, что именно такие диски описывают аккреционный поток в источнике Стрелец $A{\kern 1pt} *$.

На рис. 3 показан пример зависимости величины $\varphi $ от времени для модели с параметрами $\Gamma = 4{\text{/}}3$ и $\beta = 100$. Синяя сплошная кривая соответствует случаю $a = 0.2$, зеленая штриховая – случаю $a = 0.6$, и красная штрихпунктирная – случаю $a = 0.95$. Из рис. 3 видно, что кривые заведомо меньше критического значения $\phi \approx 50$ на всем рассмотренном промежутке времени. Синяя кривая стремится к величине $\phi \sim 50$, а красная кривая имеет среднее значение $\phi \approx 15$.

Рис. 3.

Зависимость параметра $\varphi $ от времени для моделей с параметрами $\Gamma = 4{\text{/}}3$, $\beta = 100$ и тремя значениями $a$. Синяя сплошная кривая соответствует случаю $a = 0.2$, зеленая штриховая – случай $a = 0.6$ и красная штрихпунктирная соответствует случаю $a = 0.95$.

Смоделированные МГД модели зависят от четырех физических параметров. Это масса черной дыры $M$, параметр вращения черной дыры $a$, показатель адиабаты $\Gamma $ и отношение газового давления к магнитному давлению $\beta $. Масса черной дыры фиксируется наблюдениями, поэтому остаются три свободных параметра, которые варьировались в диапазоне: $\Gamma = \left( {\tfrac{4}{3};\;\tfrac{5}{3}} \right)$, $a = (0.2;\;0.6;\;0.95)$, $\beta = (10;\;100)$. Для каждого набора параметров выбирались три различных промежутка времени $t = (5000;\;10\,000;\;15\,000)$, с которым затем вычислялись характеристики излучения (см. раздел 2.2). Для модели с параметрами Γ = 5/3 и β = 10 промежутки времени равны t = (600; 1200; 1800). Всего было рассмотрено 36 МГД моделей.

2.2. Модель излучения

Для вычисления свойств излучения плазмы каждой из 36 МГД моделей использовался свободный код grtrans [46]. Предполагалось, что свободные релятивистские электроны излучают синхротронное излучение в заданном распределении магнитного поля, которое определялось путем решения идеальных МГД уравнений (см. раздел 2.1). Функция распределения излучающих частиц, электронов задавалась в виде релятивистского распределения Максвелла, с некоторой температурой электронов ${{T}_{e}}$, которая определяется параметром $\mu $ (см. ниже). В случае, когда плотность аккрецирующей плазмы достаточно низкая, а это будет при темпе аккреции меньше, чем $\dot {M} < {{10}^{{ - 3}}}{{\dot {M}}_{{{\text{Edd}}}}}$, кулоновские столкновения между электронами и протонами будут достаточно редкими, следовательно, электроны и протоны будут иметь различную температуру [1]. Равновесная температура будет определяться балансом следующих процессов: турбулентный (вязкий) нагрев протонов, радиационное охлаждение электронов и передача энергии от протонов к электронам. При низких плотностях электрон-электронные столкновения редки и тепловое равновесие между электронами будет достигаться за более продолжительный промежуток времени. Даже если функция распределения электронов достаточно быстро термолизуется, в аккреционных дисках существуют процессы, такие как магнитное пересоединение, ударные волны, которые могут ускорить малую долю электронов до релятивистской нетепловой функции распределения. Эта функция распределения может существовать продолжительное время из-за редких столкновений между электронами [15].

Существует несколько подходов для того, чтобы выразить температуру электронов через температуру протонов. Отношение температур протонов и электронов можно фиксировать глобально [35, 47] или локально, в зависимости от рассматриваемой области (джет или диск) [36]. В данной работе фиксируем температуру электронов глобально в диске следующим соотношением:

(6)
$\mu = 1{\text{/}}(1 + {{T}_{p}}{\text{/}}{{T}_{e}}),$
где ${{T}_{p}}$ – температура протонов, ${{T}_{e}}$ – температура электронов [46].

Модель излучения зависит от трех свободных параметров. Это температура электронов ${{T}_{e}}$ (параметр $\mu $), темп аккреционного потока $\dot {M}$ и угол наклона наблюдателя $i$ к оси вращения черной дыры. Рассматривались три значения отношения температур: случай, когда температуры протонов и электронов равны ($\mu = 1{\text{/}}2$), случай, когда температура электронов составляет одну треть от температуры протонов ($\mu = 1{\text{/}}4$) и случай ($\mu = 1{\text{/}}8$), когда температура электронов много меньше температуры протонов (${{T}_{e}} = \tfrac{1}{7}{{T}_{p}} \ll {{T}_{p}}$). Более сложные зависимости с учетом истечения плазмы (джетов) были рассмотрены в работе [48]. Рассматривались четыре случая положения наблюдателя относительно оси вращения черной дыры. Три случая, когда наблюдатель расположен под углом к аккреционному диску ($cosi = 0.6428$, 0.4, 0.2), и один случай, когда наблюдатель расположен на краю диска ($cosi = 0$). Свободный параметр – темп аккреции $\dot {M}$ – выбирался в диапазоне $4 \times {{10}^{{14}}} < \dot {M} < 4 \times {{10}^{{20}}}$ гр/с таким образом, чтобы в пределах ошибки наилучшим образом удовлетворить наблюдениям в субмиллиметровой области спектра.

Для каждой из 36 МГД моделей вычислялись четыре параметра Стокса (спектральная плотность потока и поляризация) в зависимости от параметров излучения ($\mu $, $i$ и $\dot {M}$). Решалась полная система уравнений переноса с учетом релятивистских эффектов, поглощения и фарадеевских эффектов (преобразования и вращения) в метрике вращающейся черной дыры Керра [46]. Спектры вычислялись в диапазоне частот от $\nu = 3 \times {{10}^{9}}$ до $1 \times {{10}^{{13}}}$ Гц.

Приведенные выше модели были применены к источнику Стрелец $A{\kern 1pt} *$ с массой, равной $M = $ $ = 4 \times {{10}^{6}}\,{{M}_{ \odot }}$ и расстоянием до центра Галактики $D = 8.2$ кпк. Построены изображения в картинной плоскости, разрешение которых было выбрано равным $250 \times 250$ пикселей.

2.3. Наблюдательные данные

В данном разделе представлены наблюдательные данные по измерению спектральной плотности потока излучения и поляризации для источника Стрелец $A{\kern 1pt} *$, собранные из многочисленных статей (ссылки см. ниже).

Существует огромное количество литературы по наблюдению спектральной плотности потока излучения из объекта Стрелец $A{\kern 1pt} *$. Данные были взяты из работ [14, 18, 19, 21–23, 32, 33, 49–69]. Излучение наблюдается во всей области частот, от радио до гамма, с максимумом в области субмиллиметров. В данной работе будем рассматривать диапазон частот от $\nu \approx 3$ до $ \approx {\kern 1pt} {{10}^{3}}$ ГГц. Предполагается, что излучение генерируется за счет аккреции газа на черную дыру. Из-за маленького темпа аккреции (много меньше эддингтоновской предела) болометрическая светимость Sgr $A{\kern 1pt} *$ достаточно низкая. Считается, что источником субмиллиметрового излучения являются релятивистские электроны, которые излучают синхротронное излучение в неоднородном магнитном поле. Излучение является переменным с характерными временами от нескольких часов до месяцев.

Данные по линейной поляризации были взяты из работ [14, 21–23, 52, 57, 58, 70]. Линейная поляризация не наблюдается в сантиметровом диапазоне длин волн [20, 56], в то время как в миллиметровом и субмиллиметровом диапазонах длин волн наблюдается величина до $10\% $ [14]. Линейную поляризацию интерпретируют как внутреннюю линейную поляризацию, которая образуется за счет синхротронного излучения в ближайшей окрестности черной дыры внутри области порядка $10{{R}_{g}}$. Магнитное поле не является однородным на таких масштабах, а имеет более сложную структуру.

В табл. 1 представлены данные по линейной поляризации (параметры Стокса Q и U), которые использовались при сравнении с численными моделями. Из работы [21] были взяты только значения параметра Стокса U, так как ошибки измерения параметра Стокса Q сравнимы с наблюдательными данными. Данные из работы [52] для параметра Q, полученные 17.10.2002, и для параметра U, полученные 27.12.2003, не учитывались из-за больших ошибок наблюдений.

Таблица 1.  

Наблюдательные значения параметров Стокса Q и U линейной поляризации, которые использовались в работе при сравнении с численными моделями

$\nu $, Ггц Q, mJy U, mJy $\nu $, Ггц Q, mJy U, mJy
82.8 20 34 [22]   –78 –113 [52]
  31 9 [22]   –131 –104 [52]
  29 16 [22] 230.6 100 –176 [23]
  29 18 [22] 231.9 –244 –7 [23]
  55 21 [22]   –93 –196 [23]
86.3 –10 –11 [22]   15 –180 [23]
  7 –15 [22]   –91 –120 [23]
  30 –19 [22]   –223 26 [23]
215 –92 –136 [52] 239.96 88.882 106.037 [14]
  –86 –86 [52]   –132.402 –228.727 [14]
  –89 –111 [52]   126.549 –138.611 [14]
220.6 48 –153 [23] 241.96 81.717 107.850 [14]
221.9 –224 28 [23]   –129.888 –234.454 [14]
  –109 –157 [23]   131.360 –142.502 [14]
  –25 –165 [23] 331.7 104 –138 [57]
  –105 –110 [23]   41 –273 [57]
  –193 53 [23]   29 –164 [57]
223.96 140.533 79.584 [14]   31 –67 [57]
  –176.558 –190.601 [14]   29 –175 [57]
  82.909 –121.412 [14] 338.0 94 –214 [23]
225.96 132.145 84.040 [14]   29 –181 [23]
  –167.737 –191.118 [14]   109 –276 [23]
  85.942 –120.428 [14]   225 –203 [23]
226.9 77.6 –205.6 [58] 341.7 145 –97 [57]
  –214.7 –112.6 [58]   42 –267 [57]
  170.3 123.8 [58]   58 –169 [57]
230   –83 [21]   38 –35 [57]
    –241 [21]   37 –243 [57]
    –104 [21] 343 85.6 155.3 [58]
    –65 [21] 348 126 –177 [23]
  –69 –57 [52]   45 –166 [23]
  –91 –64 [52]   148 –228 [23]
  –80 –60 [52]   240 –220 [23]
  –180 –96 [52]      

Данные по круговой поляризации были взяты из работ [14, 19, 21, 49–52, 57, 58, 71]. Наблюдения были проведены на частотах $\nu = 1.4;\;4.8;\;8.4;\;15;$ $230;\;340$ ГГц. Круговая поляризация переменная и превышает абсолютную величину линейной поляризации при частотах выше 15 ГГц [49]. Во всех наблюдениях знак круговой поляризации (хиральность) отрицательный и абсолютная величина не превышает $ \leqslant {\kern 1pt} 1\% $ [14]. Происхождение круговой поляризации не до конца понято, и считается, что круговая поляризация образуется за счет фарадеевского преобразования линейной поляризации. Данные статьи [21] не использовались из-за большой ошибки наблюдений, в статье [51] был дан только верхний предел на величину круговой поляризации, данные из работ [52, 57] были взяты только те, ошибка которых меньше самих наблюдательных данных. В табл. 2 представлены данные по круговой поляризации (параметр Стокса V), которые использовались при сравнении с численными моделями. Наблюдается значительная переменность величины параметра Стокса V, что может быть связано как с источником поляризации, так и со средой.

Таблица 2.  

Наблюдательные значения параметра Стокса V круговой поляризации, которые использовались в работе при сравнении с численными моделями

$\nu $, Ггц V, mJy ${{m}_{c}}$, % $\nu $, Ггц V, mJy ${{m}_{c}}$, %
1.4 –0.995 –0.21 [50] 223.96 –50.173 –1.24 [14]
4.8 –1.8 –0.34 [19]   –30.207 –0.88 [14]
  –1.5 –0.30 [19]   –39.496 –1.49 [14]
  –2.6 –0.42 [19] 225.96 –49.793 –1.26 [14]
  –2.7 –0.42 [71]   –29.792 –0.89 [14]
  –2.6 –0.35 [71]   –36.879 –1.43 [14]
  –2.0 –0.34 [71] 226.9 –42.7 –1.1 [58]
  –2.7 –0.31 [50]   –42.2 –1.2 [58]
  –2.1 –0.37 [50]   –42.6 –1.1 [58]
  –2.4 –0.31 [50] 239.96 –54.265 –1.33 [14]
8.4 –1.9 –0.32 [19]   –34.542 –1.01 [14]
  –0.87 –0.16 [19]   –33.426 –1.22 [14]
  –2.1 –0.29 [19] 241.96 –55.053 –1.34 [14]
  –2.7 –0.34 [50]   –31.992 –0.93 [14]
  –2.6 –0.27 [50]   –30.809 –1.12 [14]
  –1.8 –0.36 [50] 331.7 –19 –0.61 [57]
15 –5.8 –0.62 [50] 341.7 –37 –1.14 [57]
215 –36 –5.22 [52] 343 –50.7 –1.6 [58]
  –82 –5.47 [52]      
217.8 –47 –6.62 [52]      
  –89 –5.82 [52]      

В работе [37] диапазон частот был разделен на группы, внутри которых наблюдательные данные усреднялись, и эти усреднения непосредственно сравнивались с численными решениями. В данной работе мы сравниваем наблюдательные данные, взятые непосредственно из табл. 1 и табл. 2, полученные на определенных частотах, с численными решениями.

3. РЕЗУЛЬТАТЫ

В предыдущем разделе были рассмотрены 36 МГД моделей распределения электрон-протонной плазмы в окрестности вращающейся черной дыры (см. раздел 2.1). Для каждой МГД модели вычислялась спектральная плотность потока и поляризация излучения в зависимости от параметров задачи (см. раздел 2.2). Среди всех рассмотренных МГД моделей с различными параметрами излучения лучше всех описывают наблюдательные данные две модели со следующими параметрами: первая модель – $\Gamma = 5{\text{/}}3$, $\beta = 10$, $a = 0.6$, $\mu = 1{\text{/}}4$, $cosi = 0.6428$, $t = 1200$, $\dot {M} = $ $ = (3{\kern 1pt} - {\kern 1pt} 3.5) \times {{10}^{{15}}}$ гр/с; вторая модель – $\Gamma = 4{\text{/}}3$, β = = 100, $a = 0.6$, $\mu = 1{\text{/}}2$, $cosi = 0.6428$, $t = 5000$, $\dot {M} = (4{\kern 1pt} - {\kern 1pt} 5) \times {{10}^{{17}}}$ гр/с. Остальные модели плохо согласуются с наблюдательными данными по одному или по всем параметрам Стокса.

Рассмотрим каждую модель в отдельности.

3.1. Первая модель

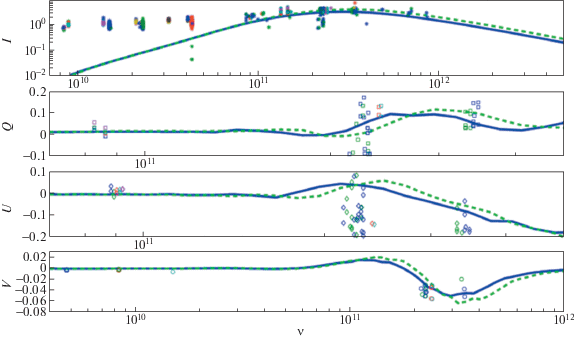
На рис. 4 приведено сравнение параметров Стокса I, Q, U, V наблюдательных данных, измеренных в янских, с данными, полученными численным моделированием, в зависимости от частоты (в Герцах). Сверху вниз звездочками, квадратами, ромбами и кругами показаны наблюдательные данные для параметров Стокса I, Q, U, V соответственно. Синяя сплошная линия соответствует потоку вещества, равному $\dot {M} = 3.85 \times {{10}^{{ - 10}}}{{\dot {M}}_{{{\text{Edd}}}}}$, зеленая штриховая линия – $\dot {M} = 4.49 \times {{10}^{{ - 10}}}{{\dot {M}}_{{{\text{Edd}}}}}$. Данные кривые хорошо описывают наблюдательные данные по спектральной плотности потока излучения в миллиметровой и в субмиллиметровой области спектра в диапазоне частот от $\nu \approx 4 \times {{10}^{{10}}}$ до $ \approx {\kern 1pt} {{10}^{{12}}}$ Гц, но при меньших частотах наклон численных кривых становится круче наклона наблюдательных данных. То же относится и к круговой поляризации. Кроме того, круговая поляризация Стрелец $A{\kern 1pt} *$ в диапазоне частот от $\nu \approx 4 \times {{10}^{9}}$ до $ \approx {\kern 1pt} 4 \times {{10}^{{11}}}$ Гц имеет отрицательные значения. Численные кривые в диапазоне частот от $\nu \approx 4 \times {{10}^{{10}}}$ до $ \approx {\kern 1pt} {{10}^{{12}}}$ Гц достаточно хорошо воспроизводят эти значения, но при меньших частотах наблюдаются расхождения с наблюдениями. С линейной поляризацией дело обстоит гораздо проще в связи с тем, что на низких частотах ($\nu \approx 5 \times {{10}^{{10}}}$ Гц) линейная поляризация не наблюдается. В миллиметровой и в субмиллиметровой области спектра данные численной модели достаточно хорошо описывают наблюдательные данные параметра Q и хуже параметра U линейной поляризации.

Рис. 4.

Графики сравнения численных вычислений параметров Стокса (в янских) с наблюдательными данными в зависимости от частоты (в герцах) для модели с параметрами $\Gamma = 5{\text{/}}3$, $\beta = 10$, $a = 0.6$, $\mu = 1{\text{/}}4$, $cosi = 0.6428$, $t = 1200$, $\dot {M} = (3{\kern 1pt} - {\kern 1pt} 3.5) \times {{10}^{{15}}}$ г/с. Наблюдательные данные для параметров Стокса I, Q, U, V показаны (сверху вниз) звездочками, квадратами, ромбами и кругами соответственно. Синяя сплошная линия соответствует потоку вещества, равному $\dot {M} = 3.85 \times {{10}^{{ - 10}}}{{\dot {M}}_{{{\text{Edd}}}}}$, зеленая штриховая линия – $\dot {M} = 4.49 \times {{10}^{{ - 10}}}{{\dot {M}}_{{{\text{Edd}}}}}$.

На рис. 5 показана зависимость величины темпа аккреции $\dot {M}$ на черную дыру от времени для данной модели. При временах порядка $t \approx 150$ темп аккреции выходит на квазистационарное решение. Таким образом, первая модель заведомо находится в квазистационарном состоянии. Эволюция замагниченной торообразной плазмы определяется магниторотационной неустойчивостью, которая, в свою очередь, развивает турбулентность. В результате чего происходит аккреция плазмы на черную дыру [36].

Рис. 5.

Зависимость темпа аккреции в компьютерных единицах от времени для модели с параметрами $\Gamma = 5{\text{/}}3$, $\beta = 10$, $a = 0.6$, $\mu = 1{\text{/}}4$, $cosi = 0.6428$, $t = 1200$, $\dot {M} = (3{\kern 1pt} - {\kern 1pt} 3.5) \times {{10}^{{15}}}$ г/с, которая наилучшим образом соответствует наблюдательным данным.

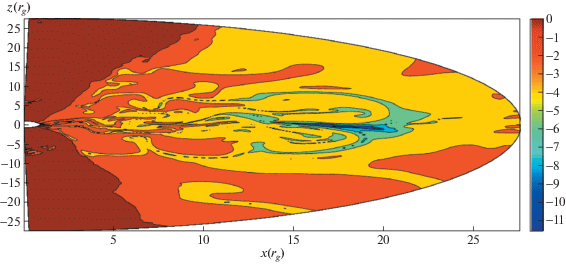
На рис. 6 цветом показано логарифмическое распределение отношения плотности энергии магнитного поля к плотности энергии плазмы ${{B}^{2}}{\text{/}}\rho $, где ${{B}^{2}}$ – квадрат магнитного поля. Белый кружок в начале координат изображает черную дыру. Этот рисунок качественно показывает границу Пойтинга доминирующего истечения (джета), ветра (короны) и радиационно неэффективного аккреционного диска [72]. Граница истечения и ветра приближенно определяется равенством магнитной энергии и энергии плазмы. В данном случае это происходит, когда ${{B}^{2}}{\text{/}}\rho \approx 0.5$. Граница ветра и аккреционного диска приближенно определяется равенством нулю интеграла Бернулли, когда $Be \approx 0$. Если интеграл Бернулли больше нуля, $Be > 0$, то плазма перестает быть гравитационно связанной и может уходить на бесконечность. Из рис. 6 видно, что в аккреционном диске развивается магниторотационная неустойчивость, в результате чего происходит медленная квазистационарная аккреция замагниченной плазмы (с полоидальным магнитным полем) на черную дыру. При прохождении эргосферы магнитное поле изгибается вдоль азимутального направления, образуя истечение плазмы (джета) из черной дыры, которое распространяется вдоль оси $z$, образуя коническую форму. Стоит заметить, что величина ${{B}^{2}}{\text{/}}\rho $ внутри истечения слабо зависит как от радиуса $r$, так и от угла $\theta $, но плотность плазмы сильно зависит от радиуса $r$. Это приводит к тому, что не наблюдается накапливания магнитного поля вдоль оси $z$ [72] и оно становится однородным во всей области истечения.

Рис. 6.

Логарифмическое распределение отношения плотности энергии магнитного поля к плотности энергии плазмы вокруг черной дыры для модели с параметрами $\Gamma = 5{\text{/}}3$, $\beta = 10$, $a = 0.6$, $\mu = 1{\text{/}}4$, $cosi = 0.6428$, $t = 1200$, $\dot {M} = (3{\kern 1pt} - {\kern 1pt} 3.5) \times {{10}^{{15}}}$ г/с.

Крупномасштабное полоидальное магнитное поле существует только в области истечения плазмы, когда ${{B}^{2}}{\text{/}}\rho > 0.5$. Поток Пойтинга непосредственно истекает из черной дыры, что свидетельствует о том, что процесс истечения происходит за счет процесса Блендфорда–Знаека [34]. Вычисление параметра $\phi $ показало, что эта модель относится к классу аккреционных дисков со стандартной и нормальной эволюцией (класс SANE), т.к. параметр $\phi \approx 28$ приблизительно в два раза меньше предельного значения $\phi \approx 50$.

На рис. 7 изображены образы черной дыры на частоте 375 ГГц (субмиллиметровая область с длиной волны $\lambda = 0.8$ мм) для данной численной модели. На такой частоте явно наблюдются фотонное кольцо и диск вблизи черной дыры [16]. Небольшое увеличение яркости связано с проявлением фотонных орбит и линзирования, которое непосредственно зависит от параметра вращения черной дыры.

Рис. 7.

Карты параметров Стокса – плотность потока и поляризация излучения (в янских) со стороной от –13 М до 13 М на частоте 375 ГГц ($\lambda = 0.8$ мм). Показаны параметры Стокса I, Q (верхняя панель) и U, V (нижняя панель) соответственно.

Численное моделирование линейной поляризации показало, что она имеет пятнистую структуру, в каждой области которой имеется своя поляризация с определенным знаком. Просуммировав по всей области карты, можно получить результирующую линейную поляризацию, которая непосредственно наблюдается. Суммарное значения параметра Стокса Q линейной поляризации имеет положительный знак, а параметра Стокса U – отрицательный знак. Знак круговой поляризации, как видно из рис. 7, как положительный, так и отрицательный, но суммарное значение имеет отрицательную хиральность и составляет величину порядка одного процента (см. табл. 2), что приближенно и наблюдается (см. рис. 4).

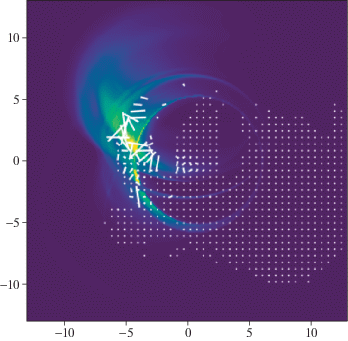
На рис. 8 показан образ спектральной плотности потока излучения, на который наложена линейная поляризация, изображенная штрихами. Длина штриха соответствует величине линейной поляризации. Наибольшее значение линейной поляризации наблюдается в области уярчения за счет линзирования и имеет хаотическое направление, что означает присутствие нерегулярного магнитного поля.

Рис. 8.

Плотность потока излучения в янских (параметр Стокса I, см. рис. 7), штрихами показана линейная поляризация.

3.2. Вторая модель

Результаты для второй модели схожи с результатами первой модели, но есть и отличия. На рис. 9 приведено сравнение наблюдательных данных параметров Стокса I, Q, U, V (в янских) с данными, полученными численным моделированием, в зависимости от частоты (в герцах). Сверху вниз звездочками, квадратами, ромбами и кругами показаны наблюдательные данные для параметров Стокса I, Q, U, V соответственно. Синяя сплошная линия соответствует потоку вещества, равному $\dot {M} = 5.13 \times {{10}^{{ - 8}}}{{\dot {M}}_{{{\text{Edd}}}}}$, зеленая штриховая линия – $\dot {M} = 6.41 \times {{10}^{{ - 8}}}{{\dot {M}}_{{{\text{Edd}}}}}$. Данные кривые так же хорошо описывают наблюдательные данные, что и первая модель, в том же диапазоне для всех четырех параметров Стокса. Отличие заключается в том, что кривые, которые описывают параметр Стокса Q, более гладкие и плавно изменяются во всем диапазоне частот от $8 \times {{10}^{{10}}}$ до $4 \times {{10}^{{11}}}$ Гц. Во всем этом диапазоне кривые положительны. То же относится и к параметру Стокса U. Кривые более гладкие и везде отрицательные в том же частотном диапазоне.

Рис. 9.

Графики сравнения численных вычислений параметров Стокса (в янских) с наблюдательными данными в зависимости от частоты (в герцах) для модели с параметрами $\Gamma = 4{\text{/}}3$, $\beta = 100$, $a = 0.6$, $\mu = 1{\text{/}}2$, $cosi = 0.6428$, $t = 5000$, $\dot {M} = (4{\kern 1pt} - {\kern 1pt} 5) \times {{10}^{{17}}}$ г/с. Сверху вниз звездочками, квадратами, ромбами и кругами показаны наблюдательные данные для параметров Стокса I, Q, U, V соответственно. Синяя сплошная линия соответствует потоку вещества, равному $\dot {M} = 5.13 \times {{10}^{{ - 8}}}{{\dot {M}}_{{{\text{Edd}}}}}$, зеленая штриховая линия – $\dot {M} = 6.41 \times {{10}^{{ - 8}}}{{\dot {M}}_{{{\text{Edd}}}}}$.

На рис. 10 показана зависимость величины темпа аккреции $\dot {M}$ на черную дыру от времени. В данном случае при временах порядка $t \approx 2500$ темп аккреции выходит на квазистационарное решение, что означает, что данная модель заведомо находится в квазистационарном состоянии.

Рис. 10.

Зависимость плотности потока плазмы в компьютерных единицах от времени для модели с параметрами $\Gamma = 4{\text{/}}3$, $\beta = 100$, $a = 0.6$, $\mu = 1{\text{/}}2$, $cosi = 0.6428$, $t = 5000$, $\dot {M} = (4{\kern 1pt} - {\kern 1pt} 5) \times {{10}^{{17}}}$ гр/с, которая наилучшим образом соответствует наблюдательным данным.

На рис. 11 цветом показано логарифмическое распределение отношения плотности энергии магнитного поля к плотности энергии плазмы ${{B}^{2}}{\text{/}}\rho $. Белый кружок в начале координат изображает черную дыру. Отличие данной модели от первой заключается в следующем. Граница Пойтинга доминирующего истечения определяется соотношением ${{B}^{2}}{\text{/}}\rho \approx 1$. Это отношение ${{B}^{2}}{\text{/}}\rho $ внутри истечения плазмы зависит от радиуса $r$, но не от угла $\theta $. Плотность плазмы также зависит только от радиуса $r$, как и в первой модели. Из рис. 11 видно, что в аккреционном диске плазма не успела перемешаться, наблюдается плавная аккреция, но в то же время развивается магниторотационная неустойчивость, что в конечном счете приведет к перемешиванию плазмы. Крупномасштабное полоидальное магнитное поле также наблюдается только в истекающей плазме. Процесс истечения происходит за счет процесса Блендфорда–Знаека [34]. Вычисление параметра $\varphi $ показало, что эта модель относится к классу аккреционных дисков со стандартной и нормальной эволюцией (класс SANE), т.к. параметр $\phi \approx 16$ приблизительно в три раза меньше предельного значения $\phi \approx 50$.

Рис. 11.

Логарифмическое распределение отношения плотности энергии магнитного поля к плотности энергии плазмы вокруг черной дыры для модели с параметрами $\Gamma = 4{\text{/}}3$, $\beta = 100$, $a = 0.6$, $\mu = 1{\text{/}}2$, $cosi = 0.6428$, $t = 5000$, $\dot {M}(4{\kern 1pt} - {\kern 1pt} 5) \times {{10}^{{17}}}$ гр/с.

На рис. 12 изображены образы черной дыры на частоте 375 ГГц ($\lambda = 0.8$ мм) для второй численной модели. Здесь более резко наблюдаются фотонное кольцо и образ аккреционного диска над фотонным кольцом. Это связано с тем, что магнитное поле вблизи черной дыры более сильное по величине, чем в первой модели.

Рис. 12.

Образы параметров Стокса – плотность потока и поляризация излучения (в янских) со стороной от –13 М до 13 М на частоте 375 ГГц ($\lambda = 0.8$ мм). Показаны параметры Стокса I, Q (верхняя панель) и U, V (нижняя панель) соответственно.

Численное моделирование линейной поляризации показало, что она имеет более крупную пятнистую структуру. Это связано с тем, что магнитное поле вблизи черной дыры имеет более регулярную структуру. То же самое наблюдается и в образе круговой поляризации.

На рис. 13 показан образ спектральной плотности потока излучения, на который наложена линейная поляризация, изображенная штрихами. Здесь также максимум линейной поляризации имеет хаотическое направление, что характеризуется нерегулярной структурой магнитного поля.

Рис. 13.

Плотность потока излучения в янских (параметр Стокса I), на которую штрихами наложена линейная поляризация.

3.3. Выводы

Общие выводы заключаются в следующем. Наблюдательные данные лучше всего описываются моделью с умеренным вращением черной дыры, когда спин порядка $a \approx 0.6$, что согласуется с наблюдениями по квазипериодическим осцилляциям [7, 8]. Наблюдатель расположен под углом к оси вращения черной дыры, равным $i \approx 50^\circ $. Менее точно можно объяснить наблюдательные данные и при углах наклонения в диапазоне $50^\circ < i < 70^\circ $, но при углах наклонения в диапазоне $i \approx 70^\circ {\kern 1pt} - {\kern 1pt} 90^\circ $ наблюдательные данные не воспроизводятся полностью. Температура электронов равна или чуть меньше температуры протонов ${{T}_{p}}{\text{/}}3 < {{T}_{e}} < {{T}_{p}}$. Случай, когда температура электронов много меньше температуры протонов, ${{T}_{e}} \ll {{T}_{p}}$, исключается полностью. Величину магнитного поля ограничить не удалось. Это связано с маленькой выборкой величины параметра $\beta $, рассмотренной в данной работе. Поток вещества на черную дыру достаточно мал и составляет малую долю от эддингтоновского предела. Для первой модели $\dot {M} \approx 4 \times {{10}^{{ - 10}}}{{\dot {M}}_{{{\text{Edd}}}}}$, для второй модели $\dot {M} \approx 6 \times {{10}^{{ - 8}}}{{\dot {M}}_{{{\text{Edd}}}}}$, что значительно меньше потока вещества на радиусе Бонди, а это в свою очередь означает существование крупномасштабного истечения (ветра).

Если мы хотим сравнить численное моделирование только со спектральной плотностью потока излучения без поляризации, то это можно сделать с хорошей точностью и для других моделей с другими параметрами, например, для $a = 0.2$, $a = 0.95$ и $\mu = 1{\text{/}}8$. Таким образом, ограничить параметры плазмы и параметр вращения черной дыры только по наблюдениям спектральной плотности потока излучения в данных моделях затруднительно. Для всех рассмотренных моделей наблюдения описываются значительно лучше для наблюдателя, расположенного под углом $50^\circ < i < 70^\circ $, чем под углом $i \approx 70^\circ {\kern 1pt} - {\kern 1pt} 90^\circ $. Это означает, что наблюдатель смотрит на черную дыру в центре нашей Галактики не строго в плоскости вращения черной дыры, а находится над ней.

Полученные образы на рис. 7 и 12 должны непосредственно наблюдаться в будущих наблюдениях проекта Телескоп горизонта событий и Миллиметрон при наблюдениях Стрелец $A{\kern 1pt} *$ на частоте 375 ГГц.

4. ЗАКЛЮЧЕНИЕ

Были рассмотрены простейшие МГД модели торообразной электрон-протонной плазмы в ближайшей окрестности черной дыры, которые относятся к радиационно неэффективным типам аккреционных дисков, т.е. к дискам, в которых пренебрегают радиационными эффектами. В зависимости от параметра $\phi $ такие диски относятся к классу либо аккреционных дисков с нормальной и стандартной эволюцией (SANE), либо к аккреционным дискам с захваченным магнитным полем (MAD). Оба этих класса характеризуются темпом аккреции, значительно меньшим эддингтоновского предела. В работе рассматривались аккреционные диски, принадлежащие классу SANE. Для каждой модели такого диска вычислялись спектральные параметры синхротронного излучения (параметры Стокса) и сравнивались с наблюдениями.

Для сравнения с наблюдениями был выбран источник, расположенный в центре нашей галактики Млечный Путь. Это достаточно массивная черная дыра, которая излучает в миллиметровом и в субмиллиметровом диапазонах спектра. Сопоставляя результаты численных расчетов с наблюдениями, удалось оценить параметры плазмы и параметр вращения черной дыры. Оказалось, что наилучшее соответствие между численными моделями и наблюдательными данными достигается для умеренного вращения черной дыры $a \approx 0.6$, когда наблюдатель расположен под углом $i \approx 50^\circ $, а температура излучающих электронов порядка или чуть меньше температуры протонов. Были построены карты спектральной плотности потока излучения и поляризации для численных моделей, которые наилучшим образом согласуются с наблюдательными данными.

Помимо этого, данные модели имеют ряд недостатков [34], связанных с неучетом многих явлений, таких как нагрев электронов за счет пересоединения магнитных силовых линий, постоянного отношения температуры электронов к температуре протонов как в диске, так и в джете, и с проблемами устойчивости относительно тепловых возмущений.

Список литературы

  1. F. K. Baganoff, Y. Maeda, M. Morris, M. W. Bautz, et al., Astrophys. J. 591, 891 (2003).

  2. F. Yusef-Zadeh, H. Bushouse, M. Wardle, C. Heinke, et al., Astrophys. J. 706, 348 (2009).

  3. Z.-Q. Shen, K. Y. Lo, M.-C. Liang, P. T. P. Ho, and J.‑H. Zhao, Nature 438, 62 (2005).

  4. S. Gillessen, F. Eisenhauer, S. Trippe, T. Alexander, R. Genzel, F. Martins, and T. Ott, Astrophys. J. 692, 1075 (2009).

  5. A. Boehle, A. M. Ghez, R. Schodel, L. Meyer, et al., A-strophys. J. 830, id. 17 (2016).

  6. S. S. Doeleman, J. Weintroub, A. E. E. Rogers, R. Plambeck, et al., Nature 455, 78 (2008).

  7. Y. Kato, M. Miyoshi, R. Takahashi, H. Negoro, and R. Matsumoto, Monthly Not. Roy. Astron. Soc. 403, L74 (2010).

  8. V. I. Dokuchaev, General Relativ. and Gravit. 46, 1832 (2014).

  9. F. Yuan and R. Narayan, Ann. Rev. Astron. Astrophys. 52, 529 (2014).

  10. N. I. Shakura and R. A. Sunyaev, Astron. and Astrophys. 24, 337 (1973).

  11. R. Narayan and I. Yi, Astrophys. J. Letters 428, L13 (1994).

  12. Г. А. Хорунжев, С. Ю. Сазонов, Р. А. Буренин, А. Ю. Тка-ченко, ПАЖ 38(8), 539 (2012).

  13. M. Subroweit, M. Garcia-Marin, A. Eckart, A. Borkar, M. Valencia-S., G. Witzel, B. Shahzamanian, and C. Straubmeier, Astron. and Astrophys. 601, id. A80 (2017).

  14. G. C. Bower, A. Broderick, J. Dexter, S. Doeleman, et al., Astrophys. J. 868, id. 101 (2018).

  15. A. A. Chael, R. Narayan, and A. Sadowski, Monthly Not. Roy. Astron. Soc. 470, 2367 (2017).

  16. S. M. Ressler, A. Tchekhovskoy, E. Quataert, and C. F. Gammie, Monthly Not. Roy. Astron. Soc. 467, 3604 (2017).

  17. П. Б. Иванов, Е. В. Михеева, В. Н. Лукаш, А. М. Малиновский, С. В. Чернов, А. С. Андрианов, В. И. Костенко, С. Ф. Лихачев, Успехи физ. наук 189, 449 (2019).

  18. D. K. Aitken, J. Greaves, A. Chrysostomou, T. Jenness, W. Holland, J. H. Hough, D. Pierce-Price, and J. Richer, Astrophys. J. 534, L173 (2000).

  19. G. C. Bower, H. Falcke, and D. C. Backer, Astrophys. J. 523, L29 (1999).

  20. G. C. Bower, D. C. Backer, J.-H. Zhao, M. Goss, and H. Falcke, Astrophys. J. 521, 582 (1999).

  21. G. C. Bower, M. C. H. Wright, H. Falcke, and D. C. Backer, Astrophys. J. 588, 331 (2003).

  22. J.-P. Macquart, G. C. Bower, M. C. H. Wright, D. C. Backer, and H. Falcke, Astrophys. J. 646, L111 (2006).

  23. D. P. Marrone, J. M. Moran, J.-H. Zhao, and R. Rao, Astrophys. J. 654, L57 (2007).

  24. M. D. Johnson, V. L. Fish, S. S. Doeleman, D. P. Marrone, et al., Science 350, 1242 (2015).

  25. M. Garcia-Marin, A. Eckart, A. Weiss, G. Witzel, et al., Astrophys. J. 738, 158 (2011).

  26. G. Trap, A. Goldwurm, K. Dodds-Eden, A. Weiss, et al., Astron. ans Astrophys. 528, id. A140 (2011).

  27. D. P. Marrone, F. K. Baganoff, M. R. Morris, J. M. Moran, et al., Astrophys. J. 682, 373 (2008).

  28. V. L. Fish, S. S. Doeleman, C. Beaudoin, R. Blundell, et al., Astrophys. J. Letters 727, L36 (2011).

  29. A. M. Ghez, S. A. Wright, K. Matthews, D. Thompson, et al., Astrophys. J. 601, L159 (2004).

  30. J. C. Mauerhan, M. Morris, F. Walter, and F. K. Baganoff, Astrophys. J. 623, 25 (2005).

  31. F. Yusef-Zadeh, M. Wardle, C. Heinke, C. D. Dowell, D. Roberts, F. K. Baganoff, and W. Cotton, Astrophys. J. 682, 361 (2008).

  32. A. Borkar, A. Eckart, C. Straubmeier, D. Kunneriath, et al., Monthly Not. Roy. Astron. Soc. 458, 2336 (2016).

  33. F. Yusef-Zadeh, H. Bushouse, C. D. Dowell, M. Wardle, et al., Astrophys. J. 644, 198 (2006).

  34. В. С. Бескин, Осесимметричные стационарные течения в астрофизике (M.: Физматлит, 2005).

  35. M. Moscibrodzka, C. F. Gammie, J. C. Dolence, H. Shiokawa, and P. K. Leung, Astrophys. J. 706, 497 (2009).

  36. M. Moscibrodzka, H. Falcke, H. Shiokawa, and C. F. Gammie, Astron. and Astrophys. 570, id. A7 (2014).

  37. R. V. Shcherbakov, R. F. Penna, and J. C. McKinney, As-trophys. J. 755, id. 133 (2012).

  38. J. Dexter, A. Jimenez-Rosales, S. M. Ressler, A. Tchekhovskoy, et al., Monthly Not. Roy. Astron. Soc. 494, 4168(2020).

  39. M. Moscibrodzka, C. F. Gammie, J. Dolence, H. Shiokawa, and P. K. Leung, arXiv:1002.1261 [astro-ph.HE] (2010).

  40. C. F. Gammie, J. C. McKinney, and G. Toth, Astrophys. J. 589, 444 (2003).

  41. S. C. Noble, C. F. Gammie, J. C. McKinney, and L. D. Zan-na, Astrophys. J. 641, 626 (2006).

  42. C. J. White, J. Dexter, O. Blaes, and E. Quataert, a-rXiv:2001.02361 [astro-ph.HE] (2020).

  43. L. G. Fishbone and V. Moncrief, Astrophys. J. 207, 962 (1976).

  44. A. Sadowski, M. Wielgus, R. Narayan, D. Abarca, J. C. McKinney, and A. Chael, Monthly Not. Roy. Astron. Soc. 466, 705 (2017).

  45. A. Sadowski, R. Narayan, J. C. McKinney, and A. Tche-khovskoy, Monthly Not. Roy. Astron. Soc. 439, 503 (2014).

  46. J. Dexter, Monthly Not. Roy. Astron. Soc. 462, 115 (2016).

  47. J. Dexter, E. Agol, P. C. Fragile, and J. C. McKinney, A-strophys. J. 717, 1092 (2010).

  48. M. Moscibrodzka, H. Falcke, and H. Shiokawa, A-stron. and Astrophys. 586, id. A38 (2016).

  49. G. C. Bower, M. C. H. Wright, H. Falcke, and D. C. Ba-cker, Astrophys. J. 555, L103 (2001).

  50. G. C. Bower, H. Falcke, R. J. Sault, and D. C. Backer, Astrophys. J. 571, 843 (2002).

  51. M. Tsuboi, H. Miyahara, R. Nomura, T. Kasuga, and A. Miyazaki, Astron. Nachricht. 324, 431 (2003).

  52. G. C. Bower, H. Falcke, M. C. Wright, and D. C. Backer, Astrophys. J. 618, L29 (2005).

  53. T. An, W. M. Goss, J.-H. Zhao, X. Y. Hong, S. Roy, A. P. Rao, and Z.-Q. Shen, Astrophys. J. 634, L49 (2005).

  54. S. Roy and A. P. Rao, Monthly Not. Roy. Astron. Soc. 349, L25 (2004).

  55. M. E. Nord, T. Lazio, W. Joseph, N. E. Kassim, W. M. Goss, and N. Duric, Astrophys. J. 601, L51 (2004).

  56. G. C. Bower, M. C. H. Wright, D. C. Backer, and H. Falcke, Astrophys. J. 527, 851 (1999).

  57. D. P. Marrone, J. M. Moran, J.-H. Zhao, and R. Rao, Astrophys. J. 640, 308 (2006).

  58. D. J. Muñoz, D. P. Marrone, J. M. Moran, and R. Rao, Astrophys. J. 745, id. 115 (2012).

  59. G. C. Bower, S. Markoff, J. Dexter, M. A. Gurwell, et al., Astrophys. J. 802, id. 69 (2015).

  60. G. C. Bower, J. Dexter, K. Asada, C. D. Brinkerink, et al., Astrophys. J. Letters 881, id. L2 (2019).

  61. H. B. Liu, M. C. H. Wright, J.-H. Zhao, E. A. C. Mills, et al., Astron. and Astrophys. 593, id. A44 (2016).

  62. H. B. Liu, M. C. H. Wright, J.-H. Zhao, C. D. Brinkerink, et al., Astron. and Astrophys. 593, id. A107 (2016).

  63. H. Falcke, W. M. Goss, H. Matsuo, P. Teuben, J.‑H. Zhao, and R. Zylka, Astrophys. J. 499, 731 (1998).

  64. R. M. Herrnstein, J.-H. Zhao, G. C. Bower, and W. M. Goss, Astron. J. 127, 3399 (2004).

  65. K. Y. Lo, Z.-Q. Shen, J.-H. Zhao, and P. T. P. Ho, Astrophys. J. 508, L61 (1998).

  66. A. Miyazaki, T. Tsutsumi, and M. Tsuboi, Astrophys. J. 611, 97 (2004).

  67. J.-H. Zhao, K. H. Young, R. M. Herrnstein, P. T. P. Ho, T. Tsutsumi, K. Y. Lo, W. M. Goss, and G. C. Bower, Astrophys. J. 586, 29 (2003).

  68. J. Dexter, B. Kelly, G. C. Bower, D. P. Marrone, J. Stone, and R. Plambeck, Monthly Not. Roy. Astron. Soc. 442, 2797 (2014).

  69. T. P. Krichbaum, D. A. Graham, M. Bremer, W. Alef, A. Witzel, J. A. Zensus, and A. Eckart, J. Physics: Conference Series 54, 328 (2006).

  70. F. Yusef-Zadeh, M. Wardle, W. D. Cotton, C. O. Heinke, and D. A. Roberts, Astrophys. J. 668, L47 (2007).

  71. R. J. Sault and J.-P. Macquart, Astrophys. J. 526, L85 (1999).

  72. M. Nakamura, K. Asada, K. Hada, H.-Y. Pu, et al., Astrophys. J. 868, id. 146 (2018).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал