Астрономический журнал, 2021, T. 98, № 2, стр. 149-159
Изменения орбитальных периодов затменно-двойных систем RY Aqr, AK Vir и AX Vul
1 Московский государственный университет им. М.В. Ломоносова,
Государственный астрономический институт им. П.К. Штернберга
Москва, Россия
* E-mail: hfh@sai.msu.ru
Поступила в редакцию 28.04.2020
После доработки 30.08.2020
Принята к публикации 30.08.2020
Аннотация
В затменно-двойных системах RY Aqr, AK Vir и AX Vul изучены изменения орбитального периода. Показано, что изменения периодов этих систем можно представить с одинаковой точностью двумя способами: либо в виде суперпозиции векового уменьшения и циклических изменений, либо только в виде циклических колебаний. Циклические изменения периодов AK Vir и AX Vul вполне можно объяснить световым уравнением вследствие присутствия третьего тела в системе. Циклические изменения периода RY Aqr можно объяснить как световым уравнением, так и магнитными циклами. Вековое уменьшение периодов может быть вызвано магнитным торможением.
1. ВВЕДЕНИЕ
Наблюдательными проявлениями процессов, происходящих в тесных двойных системах (ТДС), являются изменения орбитальных параметров, в частности, периода. Наиболее удобным инструментом для изучения периодов ТДС служат затменно-двойные звезды. Изменения орбитального периода делятся на вековые (монотонные) и циклические. Вековые изменения периода связывают с процессами обмена веществом между компонентами и потерей вещества системой в целом. В зависимости от физических процессов, происходящих в двойной системе, период может увеличиваться или уменьшаться [1–3]. Количественные оценки скорости уменьшения (или увеличения) периода помогут сделать выбор среди имеющихся теоретических моделей. Поэтому важно быть уверенным, что в системе действительно происходит вековое изменение периода. Например, при больших периодах движения в долгопериодической орбите и при недостаточно продолжительных рядах наблюдений моментов минимумов можно ошибочно интерпретировать части долгопериодических синусоидальных изменений периода как параболы [4–7]. В других случаях допустима двоякая интерпретация изменений орбитального периода: их можно представить либо суперпозицией монотонного изменения периода и циклических изменений, либо только циклическими изменениями (см., например, [7]). Ясность в вопрос о характере изменения периода в таких системах могут внести дальнейшие наблюдения моментов минимумов. До выяснения этого вопроса эти системы лучше не использовать в работах, посвященных сравнению наблюдений с теоретическими моделями.
В представленной работе рассматриваются как раз такие затменно-двойные системы, изменения орбитальных периодов которых допускают двоякую интерпретацию. При этом точность представления практически одинакова для обоих случаев. Для исследования изменений периода каждой из затменно-двойных систем были использованы моменты минимумов из базы данных B. R. N. O. [8]. Начальные значения параметров световых уравнений определялись методом перебора в области их возможных значений. Затем они уточнялись методом дифференциальных поправок [9] совместно с линейными или квадратичными элементами. Одновременно вычислялись ошибки определения параметров.
2. ИЗМЕНЕНИЯ СО ВРЕМЕНЕМ ОРБИТАЛЬНОГО ПЕРИОДА RY AQR
Переменность звезды RY Aqr (HD 203069, BD –11 5574, V = 8.82m, P = 1.9666d) открыла Г.С. Ливит [10]. Эфемериды и основные характеристики кривой блеска были получены в работе [11]. Первый подробный фотометрический анализ опубликовал Дуган [12]. Поппер [13] построил кривые лучевых скоростей для обоих компонентов и определил массы компонентов и их спектральные классы. Кривые блеска были решены в работах [14] и [15]. В работе [14] были также изучены изменения периода RY Aqr, но имевшиеся к тому времени данные не позволяли сделать определенные выводы об их природе, было лишь сделано предположение, что они могут быть следствием светового уравнения с периодом ∼70 лет. Сойдуган [16] интерпретировал изменения периода RY Aqr как световое уравнение с периодом 89.7 года. Он нашел функцию масс тройной системы f(m) = 0.178 ${{М}_{ \odot }}$ и минимальную массу третьего тела 1.06 ${{М}_{ \odot }}$. В работе [15] изменения периода RY Aqr были представлены в виде суперпозиции векового уменьшения периода со скоростью 8.6 × 10–7 сут/год и его циклических изменений с периодом 72.69 года. Масса третьего тела получилась довольно большой (1.59 ${{М}_{ \odot }}$), а вклад третьего тела в светимость системы довольно маленьким (6.5% в фильтре V). При этом из-за слишком большого модулирующего периода авторы отвергли идею, что циклические изменения орбитального периода могут быть вызваны магнитными колебаниями, и предположили, что третье тело – белый карлик. Однако масса белого карлика не может быть больше 1.4 ${{М}_{ \odot }}$. К сожалению, графики, приведенные в работе [15], не дают представления о том, насколько хорошо данная интерпретация удовлетворяет наблюдениям. В работе [17] изменения периода RY Aqr также представлены в виде суперпозиции векового уменьшения периода и его циклических изменений с периодом 55 лет за счет третьего тела массой 1.11 ${{М}_{ \odot }}$. Приведенная в этой работе теоретическая кривая плохо представляет наблюдения.
Для RY Aqr имеется 165 моментов главного минимума: 115 визуальных, 1 фотографический и 49 минимумов из фотоэлектрических и ПЗС-наблюдений. Для вторичного минимума имеется 10 моментов. Поскольку вторичный минимум очень мелкий, его моменты определяются с намного меньшей точностью, чем моменты главного минимума, и они не использовались в анализе. На рис. 1 приведены отклонения (O – C)1 наблюдаемых (О) моментов минимумов RY Aqr от вычисленных (C) с линейными элементами:
(1)
$\begin{gathered} C \equiv {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2452499.955 + \\ + \;{{1.9665889}^{{\text{d}}}} \times Т, \\ \end{gathered} $Рис. 1.
Отклонения (O – C)1 наблюдаемых (О) моментов минимумов RY Aqr от вычисленных (C) с линейными элементами (1). Сплошная линия – теоретическая кривая для светового уравнения с параметрами из табл. 1. В нижней части рисунка приведена зависимость от времени значений (O – C)2, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом светового уравнения. Фотографический момент минимума обозначен треугольником, визуальные наблюдения – маленькими точками, фотоэлектрические и ПЗС – большими точками.

Изменения периода RY Aqr можно представить непосредственно световым уравнением, тогда теоретические моменты минимумов вычисляются по формуле:
(2)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2452499.955(5) + \\ + \;1.9665889{{(5)}^{{\text{d}}}} \times T + LTE, \\ \end{gathered} $Таблица 1.
Параметры гипотетической долгопериодической орбиты RY Aqr
| Параметр | Только 3-е тело | Парабола + 3-е тело |
|---|---|---|
| P3 | (47 800 ± 300) сут = (130.9 ± 0.8) лет | (31 600 ± 300) сут = (86.5 ± 0.8) лет |
| A3 | (0.120 ± 0.003) сут | (0.059 ± 0.004) сут |
| e3 | 0.28 ± 0.03 | 0.30 ± 0.07 |
| ω3 | 2° ± 1° | 330° ± 3° |
| JD3 | 2 434 900 ± 260 | 2 433 580 ± 240 |
| ${{a}_{3}}\sin {{i}_{3}}$ | (3.11 ± 0.08) × 109 км = (20.8 ± 0.5) а.е. | (1.53 ± 0.10) × 109 км = (10.2 ± 0.7) а.е. |
Изменения периода RY Aqr можно также представить суперпозицией параболы и светового уравнения:
(3)
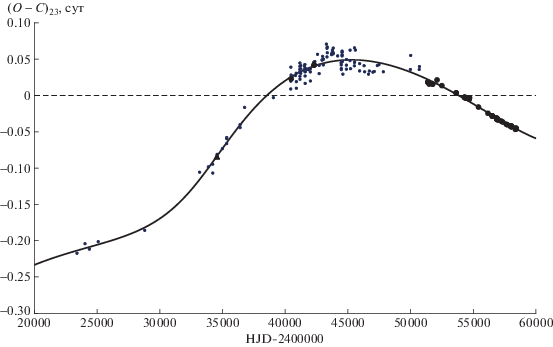
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2452500.009(5) + \\ + \;1.9665862{{(13)}^{d}}T--{{(9.3 \pm 1.1)}^{{\text{d}}}} \times \\ \times \;{{10}^{{--10}}}{{T}^{2}} + LTE. \\ \end{gathered} $Параметры светового уравнения для этого случая также приведены в табл. 1. Зависимость от времени остатков (O – C)21, полученных вычитанием из наблюдаемых моментов минимумов теоретической параболы с параметрами из представления (3), приведена на рис. 2. Сплошная линия на этом рисунке – теоретическая кривая для светового уравнения с параметрами из второго столбца табл. 1. В нижней части рис. 2 приведена зависимость от времени значений (O – C)22, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом квадратичных элементов (3) и светового уравнения. На рис. 3 приведены изменения со временем отклонений (О – С)23 наблюдаемых моментов минимумов RY Aqr от вычисленных с линейными элементами (3). Сплошная линия на этом рисунке – сумма теоретических кривых для параболы (3) и светового уравнения с параметрами из второго столбца табл. 1. Из рисунка видно, что эта кривая неплохо описывает изменения орбитального периода RY Aqr. Обратная парабола означает, что происходит вековое уменьшение периода. Его скорость вычисляется по формуле: dP/dt = 2Q/P, где Q – коэффициент при квадратичном члене в представлении моментов минимумов [1]. Используя величины из представления (3), получаем dP/dt = –3.4 × 10–7 сут/год. Вековое уменьшение периода может быть вызвано потерей углового момента системы вследствие магнитного торможения [19–21].
Рис. 2.
Зависимость от времени остатков (O – C)21, полученных вычитанием из наблюдаемых моментов минимумов RY Aqr теоретической параболы с параметрами из представления (3). Сплошная линия – теоретическая кривая для светового уравнения с параметрами из второго столбца табл. 1. Внизу приведена зависимость от времени значений (O – C)22, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом квадратичных элементов (3) и светового уравнения. Обозначения как на рис. 1.

Интерпретируя циклические изменения периода как движение в долгопериодической орбите с параметрами, приведенными в табл. 1, можно оценить массу третьего тела, вычислив функцию масс:
(4)
$f({{M}_{3}}) = \frac{{4{{\pi }^{2}}}}{G}\frac{{a_{3}^{3}{{{\sin }}^{3}}{{i}_{3}}}}{{P_{3}^{2}}} = \frac{{M_{3}^{3}{{{\sin }}^{3}}{{i}_{3}}}}{{{{{({{M}_{1}} + {{M}_{2}} + {{M}_{3}})}}^{2}}}}.$Из рис. 1–2 видно, что оба представления, и с линейными элементами, и с квадратичными, хорошо удовлетворяют наблюдениям. Рассмотрим возможную природу третьего тела в каждом случае.
1) Линейные элементы + световое уравнение. В этом случае для третьего тела получается масса М3 > 1.81 ${{М}_{ \odot }}$. Звезда главной последовательности такой массы имела бы светимость больше светимости всей затменно-двойной системы. Однако величина третьего света, найденная в работе [15], составляет 6.5%. Третий компонент может быть нейтронной звездой, тем более что в системе обнаружено рентгеновское излучение [22].
2) Квадратичные элементы + световое уравнение. Для этого случая масса третьего компонента М3 > 0.969 ${{М}_{ \odot }}$. Это может быть как нейтронная звезда, так и белый карлик.
3) В обоих случаях третье тело может быть, в свою очередь, тесной двойной системой.
Альтернативная причина циклических изменений периода – проявление магнитной активности звезды позднего спектрального класса, имеющей конвективную оболочку. Вторичный компонент RY Aqr имеет спектральный класс ∼ K и попадает в число звезд, имеющих конвективную оболочку. В модели Эппелгейта [23] амплитуда модуляций орбитального периода ΔP и амплитуда осцилляций Δ(О – С) на диаграмме О – С связаны соотношением: ΔP/P0 = 2πΔ(О – С)/Pmod. Период циклических изменений орбитального периода RY Aqr при линейных элементах, пожалуй, слишком велик, чтобы отнести его на счет магнитных колебаний. Однако период циклических изменений при квадратичных элементах вполне можно отнести на счет таких колебаний. Например, в работе [23] в качестве примера рассматривается SV Cam, у которой период циклических колебаний ∼80 лет. Принимая для радиуса и светимости вторичного компонента значения согласно [15] и используя приближенные соотношения из работы [23], находим оценки величины переносимого (от ядра звезды к ее оболочке и обратно) углового момента ΔJ, количества энергии, необходимого для переноса углового момента во внешнюю часть звезды, ΔE, напряженности магнитного поля B активного компонента и изменений его светимости ΔL. Эти величины приведены в табл. 2. Полученные оценки магнитных и энергетических величин вполне укладываются в допустимые рамки. Возможные колебания светимости вторичного компонента невелики. Следовательно, магнитные колебания могут быть причиной циклических изменений орбитального периода RY Aqr.
3. ИЗМЕНЕНИЯ СО ВРЕМЕНЕМ ОРБИТАЛЬНОГО ПЕРИОДА AK VIR
Переменность звезды AK Vir (BD –17 3997, V = = 10.0m, P = 1.1936d) открыл Хоффмайстер [24] и определил, что это затменно-переменная типа Алголя. Соловьев [25] построил кривую блеска из визуальных наблюдений. Фотометрические наблюдения AK Vir
в системе UBV были проведены в работах [26, 27]. Последнее определение эфемерид сделано в работе [28]. Для этой системы нет ни решения кривой блеска, ни спектроскопических наблюдений.
Проблемы с получением кривой блеска AK Vir связаны, по-видимому, с присутствием звезды
BD –17 3996 на расстоянии 44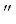 от нее [29]. В работе [30] определены приближенные характеристики компонентов. Исследование изменений периода
не проводилось.
от нее [29]. В работе [30] определены приближенные характеристики компонентов. Исследование изменений периода
не проводилось.
Для затменно-двойной системы AK Vir имеется 74 момента главного минимума: 56 визуальных и 18 из фотоэлектрических и ПЗС-наблюдений. Наблюдений моментов вторичного минимума нет. На рис. 4 приведены отклонения (O – C)1 наблюдаемых (О) моментов минимумов AK Vir от вычисленных (C) с линейными элементами:
Рис. 4.
Отклонения (O – C)1 наблюдаемых (О) моментов минимумов AK Vir от вычисленных (C) с линейными элементами (5). Сплошная линия – теоретическая кривая для светового уравнения с параметрами из табл. 3. В нижней части рисунка приведена зависимость от времени значений (O – C)2, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом светового уравнения. Визуальные наблюдения обозначены маленькими точками, фотоэлектрические и ПЗС– большими точками.

На этом рисунке визуальные наблюдения обозначены маленькими точками, фотоэлектрические и ПЗС-наблюдения – большими точками. Эти изменения периода можно представить непосредственно световым уравнением:
(6)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2442576.381(5) + \\ + \;1.1935960{{(1)}^{{\text{d}}}} \times T + LTE. \\ \end{gathered} $Таблица 3.
Параметры гипотетической долгопериодической орбиты AK Vir
| Параметр | Только 3-е тело | Парабола + 3-е тело |
|---|---|---|
| P3 | (22 600 ± 250) сут = (61.9 ± 0.7) лет | (22 000 ± 300) сут = (60.2 ± 0.8) лет |
| A3 | (0.0188 ± 0.0016) сут | (0.021 ± 0.003) сут |
| e3 | 0.57 ± 0.14 | 0.69 ± 0.10 |
| ω3 | 285° ± 7° | 338° ± 8° |
| JD3 | 2 430 200 ± 300 | 2 432 500 ± 300 |
| ${{a}_{3}}\sin {{i}_{3}}$ | (4.9 ± 0.4) × 108 км = (3.3 ± 0.3) а.е. | (5.4 ± 0.8) × 108 км = (3.6 ± 0.5) а.е. |
Изменения периода AK Vir можно также представить суперпозицией параболы и светового уравнения:
(7)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2442576.393(4) + \\ + \;1.19359576{{(14)}^{{\text{d}}}} \times T--{{(6.7 \pm 2.8)}^{{\text{d}}}} \times \\ \times \;{{10}^{{--11}}} \times {{T}^{2}} + LTE. \\ \end{gathered} $Параметры светового уравнения для этого случая также приведены в табл. 3. Зависимость от времени остатков (O – C)21, полученных вычитанием из наблюдаемых моментов минимумов теоретической параболы с параметрами из представления (7), приведена на рис. 5. Сплошная линия на этом рисунке – теоретическая кривая для светового уравнения с параметрами из второго столбца табл. 3. В нижней части рис. 5 приведена зависимость от времени значений (O – C)22, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом квадратичных элементов (7) и светового уравнения.
Рис. 5.
Зависимость от времени остатков (O – C)21, полученных вычитанием из наблюдаемых моментов минимумов AK Vir теоретической параболы с параметрами из представления (7). Сплошная линия – теоретическая кривая для светового уравнения с параметрами из второго столбца табл. 3. Внизу приведена зависимость от времени значений (O – C)22, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом квадратичных элементов (7) и светового уравнения. Обозначения как на рис. 4.
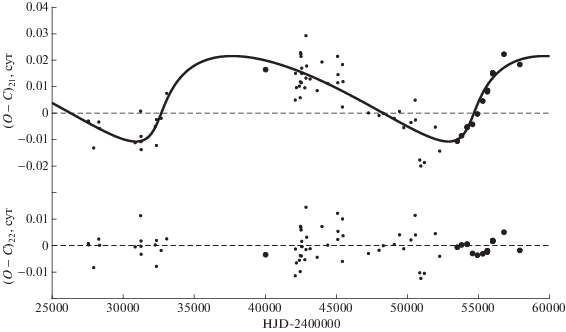
Световые уравнения в затменно-двойной системе AK Vir, полученные для линейных и квадратичных элементов, имеют близкие периоды и амплитуды и различаются в основном формой кривой. Коэффициент при квадратичном члене довольно мал, поэтому график для суммы параболы и светового уравнения почти не отличается от рис. 5. Скорость уменьшения периода, соответствующая квадратичным элементам (7), dP/dt = = ‒4.1 × 10–8 сут/год. Для уточнения характера изменения периода AK Vir нужны новые наблюдения.
Используя найденные нами параметры долгопериодической орбиты, приведенные в табл. 3, можно оценить массу третьего тела в AK Vir, вычислив функцию масс. В случае непосредственного представления диаграммы О – С световым уравнением f(M3) = 0.00902 ${{М}_{ \odot }}$, в случае суперпозиции параболы и светового уравнения f(M3) = = 0.0133 ${{М}_{ \odot }}$. Для масс компонентов затменно-двойной системы имеются лишь оценки, полученные в работе [30]: М1 = 2.05 ${{М}_{ \odot }}$, М2 = 0.43 ${{М}_{ \odot }}$. Считая i3 = 90°, находим нижнюю границу для массы третьего тела: М3 > 0.42 ${{М}_{ \odot }}$ для первого случая и М3 > 0.49 ${{М}_{ \odot }}$ для второго. То есть значения массы третьего компонента для обоих случаев примерно одинаковы, и это приближенные оценки, так как для компонентов затменно-двойной системы нет надежных определений масс. Для этой системы нет решения кривой блеска, так что вопрос о третьем свете остается открытым. Однако можно предполагать, что третье тело является звездой главной последовательности.
4. ИЗМЕНЕНИЯ СО ВРЕМЕНЕМ ОРБИТАЛЬНОГО ПЕРИОДА AX VUL
Переменность звезды AX Vul (HD 340621, V = = 11.0m, P = 2.0248d) открыл Хоффмайстер [31] и определил, что это затменно-переменная типа Алголя. Спектральный класс системы был определен в работе [32]: A1V. В течение долгого времени для этой системы публиковались только моменты минимумов и эфемериды. Диаграмма О – С, приведенная в атласе [33], показывает, что орбитальный период системы меняется. В работе [34] изменения орбитального периода затменно-двойной системы AX Vul были представлены в виде суперпозиции векового уменьшения периода (dP/dt ≈ –1.17 × 10–7 сут/год) и светового уравнения с периодом 43 года. В той же работе из решения кривых блеска в фильтре V были получены фотометрические элементы орбиты. Вследствие накопления точных фотоэлектрических определений моментов минимумов AX Vul следует пересмотреть изменения ее периода.
Для затменно-двойной системы AX Vul имеется 143 момента главного минимума: 111 визуальных, 14 фотографических и 18 минимумов из фотоэлектрических и ПЗС-наблюдений. Для вторичного минимума имеется всего 4 момента минимума. На рис. 6 приведены отклонения (O – C) наблюдаемых (О) моментов минимумов AX Vul от вычисленных (C) с линейными элементами, полученными методом наименьших квадратов с использованием всех имеющихся моментов главного минимума:
(8)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2444853.3804(9) + \\ + \;2.0248365{{(2)}^{{\text{d}}}} \times Т. \\ \end{gathered} $Рис. 6.
Отклонения (O – C) наблюдаемых (О) моментов минимумов AX Vul от вычисленных (C) с линейными элементами (8). Фотографические наблюдения обозначены треугольниками, визуальные – маленькими точками, фотоэлектрические и ПЗС – большими точками.
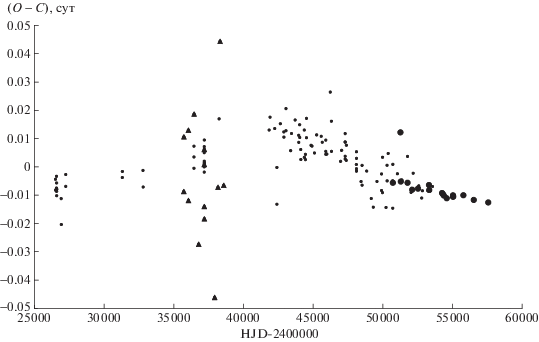
На этом рисунке фотографические наблюдения обозначены треугольниками, визуальные – маленькими точками, фотоэлектрические и ПЗС – большими точками. В дальнейшем анализе не использовались фотографические точки, а также две сильно отскакивающие точки: визуальная JD = 2442403.315 и фотоэлектрическая JD = = 2451276.174. Остальные моменты главного минимума AX Vul были представлены выражением:
(9)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2444853.3844(11) + \\ + \;2.0248363{{(1)}^{{\text{d}}}} \times T + LTE. \\ \end{gathered} $При вычислениях фотоэлектрические и ПЗС точки брались с весом 5, визуальные – с весом 1. Значения параметров светового уравнения в AX Vul приведены в табл. 4. На рис. 7 приведены отклонения (O – C)1 наблюдаемых моментов минимумов AX Vul от вычисленных с линейными элементами из представления (9). Сплошная линия на этом рисунке – теоретическая кривая для светового уравнения с параметрами из табл. 4. В нижней части рис. 7 приведена зависимость от времени значений (O – C)2, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом светового уравнения.
Таблица 4.
Параметры гипотетической долгопериодической орбиты AX Vul
| Параметр | Только 3-е тело | Парабола + 3-е тело |
|---|---|---|
| P3 | (33 300 ± 200) сут = (91.2 ± 0.5) лет | (17 000 ± 200) сут = (46.5 ± 0.5) лет |
| A3 | (0.0110 ± 0.0005) сут | (0.0046 ± 0.0005) сут |
| e3 | 0.38 ± 0.08 | 0 |
| ω3 | 120° ± 4° | 0 |
| JD3 | 2 444 700 ± 120 | 2 455 400 ± 100 |
| ${{a}_{3}}\sin {{i}_{3}}$ | (2.85 ± 0.13) × 108 км = (1.90 ± 0.09) а.е. | (1.19 ± 0.13) × 108 км = (0.80 ± 0.09) а.е. |
Рис. 7.
Отклонения (O – C)1 наблюдаемых моментов минимумов AX Vul от вычисленных с линейными элементами из представления (9). Сплошная линия – теоретическая кривая для светового уравнения с параметрами из табл. 4. Внизу приведена зависимость от времени значений (O – C)2, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом светового уравнения. Обозначения как на рис. 4.

Изменения периода AX Vul можно также представить суперпозицией параболы и светового уравнения:
(10)
$\begin{gathered} {\text{HJD}}({\text{Min}}\;{\text{I}}) = 2444853.3869(6) + \\ + \;2.02483523{{(11)}^{{\text{d}}}} \times T--{{(3.8 \pm 0.2)}^{{\text{d}}}} \times \\ \times \;{{10}^{{--10}}} \times {{T}^{2}} + LTE. \\ \end{gathered} $Вычисления проводились с теми же весами, что и в предыдущем случае. Параметры светового уравнения для этого случая также приведены в табл. 4. Зависимость от времени остатков (O – C)21, полученных вычитанием из наблюдаемых моментов минимумов теоретической параболы с параметрами из представления (10), приведена на рис. 8. Сплошная линия на этом рисунке – теоретическая кривая для светового уравнения с параметрами из второго столбца табл. 4. В нижней части рис. 8 приведена зависимость от времени значений (O – C)22, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом квадратичных элементов (10) и светового уравнения. На рис. 9 приведены изменения со временем отклонений (О – С)23 наблюдаемых моментов минимумов AX Vul от вычисленных с линейными элементами (10). Сплошная линия на этом рисунке – сумма теоретических кривых для параболы (10) и светового уравнения с параметрами из табл. 4. Из рисунка видно, что эта кривая неплохо описывает изменения орбитального периода AX Vul. Используя значение величин из представления (10), получим для скорости уменьшения периода dP/dt = –1.4 × 10–7 сут/год. Характеристики изменения орбитального периода AX Vul в этом случае близки к полученным в работе [34].
Рис. 8.
Зависимость от времени остатков (O – C)21, полученных вычитанием из наблюдаемых моментов минимумов AX Vul теоретической параболы с параметрами из представления (10). Сплошная линия – теоретическая кривая для светового уравнения с параметрами из второго столбца табл. 4. Внизу приведена зависимость от времени значений (O – C)22, полученных вычитанием из наблюдаемых моментов минимумов теоретических, вычисленных с учетом квадратичных элементов (10) и светового уравнения. Обозначения как на рис. 4.

Рис. 9.
Изменения со временем отклонений (О – С)23 наблюдаемых моментов минимумов AX Vul от вычисленных с линейными элементами (10). Сплошная линия на этом рисунке – сумма теоретических кривых для параболы (10) и светового уравнения с параметрами из второго столбца табл. 4. Обозначения как на рис. 4.

Используя найденные нами параметры долгопериодической орбиты, приведенные в табл. 4, можно оценить массу третьего тела, вычислив функцию масс. В случае непосредственного представления диаграммы О – С световым уравнением f(M3) = 0.000833 ${{М}_{ \odot }}$, в случае суперпозиции параболы и светового уравнения f(M3) = = 0.000234 ${{М}_{ \odot }}$. Для масс компонентов затменно-двойной системы имеются лишь оценки, полученные в работе [30]: М1 = 2.25 ${{М}_{ \odot }}$, М2 = 0.54 ${{М}_{ \odot }}$. Считая i3 = 90°, находим нижнюю границу для массы третьего тела: М3 > 0.20 ${{М}_{ \odot }}$ для первого случая и М3 > 0.13 ${{М}_{ \odot }}$ для второго. То есть в обоих случаях для массы третьего компонента получается небольшое значение, это может быть звезда главной последовательности. Оценок вклада третьего света в светимость этой системы не делалось.
5. ЗАКЛЮЧЕНИЕ
Изменения орбитальных периодов затменно-двойных систем RY Aqr, AK Vir и AX Vul хорошо представляются как суперпозицией обратной параболы и светового уравнения, так и одним только световым уравнением.
Для RY Aqr в обоих случаях масса третьего тела получается очень большой при небольшом третьем свете. Приходится предположить, что третий компонент либо нейтронная звезда (в случае линейных эфемерид), либо белый карлик (в случае квадратичных эфемерид). Третье тело может быть также тесной двойной системой. В случае квадратичных эфемерид причиной циклических изменений орбитального периода RY Aqr могут быть также магнитные колебания.
Для AK Vir в обоих случаях получается небольшое значение для массы третьего тела. При этом коэффициент при квадратичном члене определяется с очень большой ошибкой. Изменения орбитального периода AK Vir вполне можно объяснить только световым уравнением.
Для AX Vul в обоих случаях для массы третьего компонента получается приемлемое значение, а коэффициент при квадратичном члене определяется с хорошей точностью. Для окончательного решения вопроса о характере изменения орбитального периода AX Vul требуются дальнейшие наблюдения.
Список литературы
Х. Ф. Халиуллин, Астрон. журн. 51, 395 (1974).
N. Nanouris, A. Kalimeris, E. Antonopolou, and H. Rjvithis-Livaniou, Astron. and Astrophys. 535, 126 (2011).
N. Nanouris, A. Kalimeris, E. Antonopolou, and H. Rjvithis-Livaniou, Astron. and Astrophys. 575, 64 (2015).
А. И. Халиуллина, Астрон. журн. 92, 587 (2015).
А. И. Халиуллина, Астрон. журн. 93, 795 (2016).
А. И. Халиуллина, Астрон. журн. 94, 619 (2017).
А. И. Халиуллина, Астрон. журн. 94, 849 (2017).
B. R. N. O. Project Eclipsing Binaries database, http://var2.astro.cz/EN/brno/index.php.
А. И. Халиуллина и Х. Ф. Халиуллин, Астрон. журн. 61, 393 (1984).
E. C. Pickering, Harvard College Obs. Circ. № 142 (1908).
E. Zinner, Astron. Nachr. 195, 453 (1913).
R. S. Dugan, Contr. from the Princeton Univer. Obs. № 6, 1 (1924).
D. M. Popper, Astrophys. J. Supp. 71, 595 (1989).
B. E. Helt, Astron. and Astrophys. 172, 155 (1987).
D. Manzoori and A. Salar, Astron. J. 152, 26 (2016).
F. Soydugan, Astron. Nachr. 329, 587 (2008).
D. E. Tvardovskyi, Annales Astronomiae Novae 1, 231 (2020).
Д. Я. Мартынов, в кн.: М. С. Зверев, Б. В. Кукаркин, Д. Я. Мартынов, П. П. Паренаго, Н. Ф. Флоря и В. П. Цесевич, Переменные звезды, т. 3, Гостехиздат (1947), стр. 464–490.
S. Rappaport, F. Verbunt, and P. C. Joss, Astrophys. J. 275, 713 (1983).
N. Ivanova and R. E. Taam, Astrophys. J. 599, 516 (2003).
C. Knigge, I. Baraffe, and J. Patterson, Astrophys. J. Supp. 194, 28 (2011).
N. E. White and F. E. Marshall, Astrophys. J. Lett. 268, L117 (1983).
J. H. Applegate, Astrophys. J. 385, 621 (1992).
C. Hoffmeister, Astron. Nachr. 236, 233 (1929).
А. В. Соловьев, Переменные звезды 12, 262 (1958).
D. S. Hall, Inform. Bull. Var. Stars, № 344, 1 (1969).
D. S. Hall, and S. L. Weedman, Publ. Astron. Soc. Pacif. 83, 69 (1971).
J. M. Kreiner, Acta Astron. 54, 207 (2004).
N. N. Samus, E. V. Kazarovets, O. V. Durlevich, N. N. Ki-reeva, and E. N. Pastukhova, Astronomy Reports 61, 80 (2017).
М. А. Свечников и Э. Ф. Кузнецова, Каталог приближенных фотометрических и абсолютных элементов затменных переменных звезд (Свердловск, Изд-во Урал. ун-та, 1990).
C. Hoffmeister, Astron. Nachr. 240, 195 (1930).
E. M. Halbedel, Inform. Bull. Var. Stars № 2549 (1984).
J. M. Kreiner, C.-H. Kim, and I.-S. Nha, An Atlas of O–C Diagrams of Eclipsing Binary Stars, Parts 1–6. Pedagogical University Press, Cracow (2001), http://www.as.up.krakow.pl/o-c/.
F. Soydugan, A. Erdem, S. S. Doğru, F. Aliçavuş, E. Soydugan, C. Çiçek, and O. Demircan, New Astron. 16, 253 (2011).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал