Астрономический журнал, 2021, T. 98, № 2, стр. 160-176

1. ВВЕДЕНИЕ

За последние десятилетия были проведены несколько космических экспериментов по измерению гравитационного поля Земли с низкоорбитальных космических аппаратов (КА). Особенно успешным был эксперимент с двумя КА GRACE. В течение его работы с 2002 по 2017 г. КА провели беспрецедентно точные измерения гравитационного поля Земли, открывая тем самым новую эру для изучения временных вариаций гравитационного поля Земли из космоса. По наблюдениям GRACE месячная модель гравитационного поля Земли рассчитывается с точностью лучше, чем 0.1 мгал и с пространственным разрешением примерно 400 км [1–4]. Эти модели теперь успешно применяются во многих областях геофизики, в том числе в изучении колебаний уровня моря, потери массы полярного ледяного покрова, масс пресной воды, колебаний грунтовых вод и т.д. Сейчас на орбите вокруг Земли работают два новых КА, GRACE Follow on (GRACE-FO), которые продолжают изучение гравитационного поля Земли с более высокой точностью. Готовятся новые экспедиции для изучения гравитационного поля Земли с еще большей точностью. Кроме того, готовятся космические эксперименты с кластером спутников на высоких орбитах вокруг Земли для детектирования гравитационных волн [5]. Основной принцип измерения гравитационного поля посредством пары спутников – измерение изменений расстояния между ними. Если для экспедиций типа GRACE точность измерения между КА составляла порядка 1 мкм, то в случае космических детекторов гравитационных волн точность измерения должна быть уже на шесть порядков выше и составлять примерно 1 пикометр (пм).

Релятивистские редукции в космических экспериментах на низких орбитах неоднократно рассматривались для различных конфигураций и характеристик кластеров КА [6]. В связи с постепенным улучшением точности измерений необходимо обновить и формулы редукции для них. В нашу задачу входит написать формулы для редукции измерений расстояния между двумя КА с учетом вторых поправок по гравитационному полю Земли, что уже необходимо для измерений указанной выше точности. Для этого мы будем работать с фазой сигнала, которым обмениваются спутники, и в данной статье получим выражение для фазы, в котором учтены все гравитационные поправки, достаточные для редукции измерений расстояния между спутниками с точностью в 1 пм. Используемый нами метод был развит в работах [7, 8], где планка желаемой точности была установлена на уровне 1 нанометра в расстоянии между спутниками; полученные там результаты были приняты как часть модели реального анализа результатов миссии GRACE-FO. Рассматриваемый нами фазовый подход может быть применен для анализа измерений в околоземном эксперименте с парой спутников, обменивающихся сигналами, по запаздыванию которых делается вывод о расстоянии между спутниками и скорости его изменения. В качестве конкретного примера такого эксперимента мы будем работать с конфигурацией миссии GRACE-FO.

Здесь следует упомянуть, что помимо релятивистских эффектов оптический путь лучей света искажают также ионосфера и атмосфера. Эффект искажения оптического пути, вносимый ионосферой, зависит от частоты обратно пропорционально квадрату частоты. Поэтому, если на стандартных частотах K (27 ГГц) и Ka (32 ГГц) вариации оптического пути составляют примерно 1 см, то для лазерного излучения (282 ТГц) соответствующие вариации есть примерно 100 пм. Эту вариацию можно редуцировать при наблюдении на двух частотах. Для верхней атмосферы ситуация сложнее. Несмотря на значительные высоты (400–500 км) существует остаточная нейтральная атмосфера, которая также искажает оптический путь. Причем искажение пути не зависит от частоты излучения.

Существуют несколько моделей атмосферы на высотах превышающих 100 км. Они строились на основе наблюдений за полетами спутников и ракет, а также на основе наблюдений радарного эха. Плотность газов на таких высотах определяется годом, днем года, всемирным временем, высотой, геодезической широтой и долготой, местным солнечным временем, потоком солнечного излучения (для предыдущего дня и среднего трехмесячного значения) и магнитным индексом. Можно провести оценки вариации оптического пути. На высоте 400 км они составляют от 78 до 216 пм, а на высоте 500 км они составляют от 12 до 47 пм. Более подробные вычисления этих эффектов и возможности их редукции являются предметом отдельного исследования.

Обрисуем в общих чертах геометрию миссии GRACE-FO [8] (см. рис. 1).

Спутник GRACE-FO-A движется по траектории с координатами ${{\vec {x}}_{{\text{A}}}}(t)$ и в геоцентрический момент времени ${{t}_{1}}$ испускает сигнал ко второму спутнику GRACE-FO-B, который движется по траектории ${{\vec {x}}_{{\text{B}}}}(t)$ и принимает сигнал в момент ${{t}_{2}}$ (эту часть мы будем называть сигналом “туда”, после чего второй спутник мгновенно ретранслирует сигнал обратно к первому (сигнал “обратно”), и момент регистрации обратного сигнала первым спутником будем обозначать как ${{t}_{3}}$. Геоцентрическими координатами события испускания сигнала “туда” являются $(c{{t}_{1}},{{\vec {x}}_{{\text{A}}}}({{t}_{1}}))$, событие приема этого сигнала имеет координаты $(c{{t}_{2}},{{\vec {x}}_{{\text{B}}}}({{t}_{2}}))$, и координаты приема обратного сигнала есть $(c{{t}_{3}},{{\vec {x}}_{{\text{A}}}}({{t}_{3}}))$. Таким образом, для описания фазы при распространении сигнала “туда” мы полагаем ${{\vec {x}}_{0}} = {{\vec {x}}_{{\text{A}}}}({{t}_{1}})$ и $\vec {x} = {{\vec {x}}_{{\text{B}}}}({{t}_{2}})$. Обратный сигнал в данной работе мы не рассматриваем, откладывая это для следующей статьи, в которой будет рассмотрено конструирование наблюдаемых величин. Поэтому для краткости мы не будем указывать в формулах зависимость от конкретных моментов времени; как общее правило, все величины с индексом A берутся в момент ${{t}_{1}}$, а с индексом B – в момент ${{t}_{2}}$. В связи с этим удобно ввести ряд обозначений, упрощающих описание геометрии задачи: единичные вектора координат спутников ${{\vec {n}}_{{\text{A}}}} = {{\vec {x}}_{{\text{A}}}}{\text{/}}{{r}_{{\text{A}}}}$, ${{\vec {n}}_{{\text{B}}}} = {{\vec {x}}_{{\text{B}}}}{\text{/}}{{r}_{{\text{B}}}}$, где ${{r}_{{\text{A}}}} = {\text{|}}{{\vec {x}}_{{\text{A}}}}{\text{|}}$ и ${{r}_{{\text{B}}}} = {\text{|}}{{\vec {x}}_{{\text{B}}}}{\text{|}}$; вектор, соединяющий точки испускания и приема ${{\vec {R}}_{{{\text{AB}}}}} = {{\vec {x}}_{{\text{B}}}} - {{\vec {x}}_{{\text{A}}}}$, его длина ${{R}_{{{\text{AB}}}}} = {\text{|}}{{\vec {R}}_{{{\text{AB}}}}}{\text{|}}$ и единичный вектор ${{\vec {N}}_{{{\text{AB}}}}} = {{\vec {R}}_{{{\text{AB}}}}}{\text{/}}{{R}_{{{\text{A}}B}}}$. Отсюда следует, что единичный вектор $\vec {k}$ вдоль невозмущенной траектории сигнала представим в виде $\vec {k} = {{\vec {N}}_{{{\text{AB}}}}} + \mathcal{O}(G)$. Отметим, что так как оба спутника движутся по почти идентичным и почти круговым орбитам (на высоте $h \simeq 450$ км над поверхностью Земли), то расстояние ${{d}_{{{\text{AB}}}}}(t)$ между ними для многих оценок можно считать постоянным, так что ${{R}_{{{\text{AB}}}}} = {{d}_{{{\text{AB}}}}}({{t}_{1}}) + \mathcal{O}({{c}^{{ - 1}}}) \simeq {{d}_{{{\text{AB}}}}} = 270$ км там, где не требуется учет эксцентриситета. Расстояние между спутниками ${{d}_{{{\text{AB}}}}} = 270$ км было использовано для оценок в [8], и в нашей работе мы будем полагать его таким же.

Наши обозначения во многом совпадают с использованными в классической работе [9]. Латинские буквы $m,\;n,\;...$ обозначают пространственно-временные индексы и имеют значения от 0 до 3, а греческие буквы $\alpha ,\;\beta ,\;...$ соответствуют пространственным индексам и имеют значения от 1 до 3. Метрика Минковского обозначается как ${{\eta }_{{mn}}} = {\text{diag}}( + 1, - 1, - 1, - 1)$. Для пространственно-временных индексов мы используем стандартное правило суммирования Эйнштейна, при этом манипулирование индексами производится посредством полной метрики ${{g}_{{mn}}}$ (или, с соответствующим комментарием, с помощью плоской метрики ${{\eta }_{{mn}}}$). Для чисто пространственных величин мы не делаем различия между верхними и нижними индексами (во избежание путаницы со знаками). Например, для компонентов трехмерного вектора $\vec {k}$ мы полагаем ${{k}^{\alpha }} \equiv {{k}_{\alpha }}$, т.е. в трехмерных объектах индексы меняют уровень посредством свертки с трехмерным символом Кронекера (единичной матрицей) ${{\delta }_{{\alpha \beta }}} = {\text{diag}}(1,\;1,\;1)$. Прочие обозначения поясняются по мере появления в тексте.

2. УРАВНЕНИЕ ДЛЯ ФАЗЫ СИГНАЛА ВО ВТОРОМ ПРИБЛИЖЕНИИ

Рассмотрим фазу $\varphi $ электромагнитной волны, которая является скаляром и в приближении геометрической оптики удовлетворяет уравнению эйконала

здесь и далее индекс после запятой обозначает частную производную по соответствующей координате. В плоском пространстве волна распространяется прямолинейно, и фаза линейно зависит от пространственных координат вдоль луча, оставаясь при этом фиксированной в любой движущейся вместе с волной точке волнового фронта. Для описания такого приближения введем постоянный (по отношению к метрике Минковского) вектор ${{K}^{m}}$, который направлен вдоль невозмущенной прямолинейной траектории луча и является нулевым, т.е. его компоненты удовлетворяют условию Так как в дальнейшем естественным образом происходит расщепление четырехмерных величин на пространственную и временную часть, то будет удобным представить компоненты этого нулевого вектора как где ${{k}_{0}} = \omega {\text{/}}c$, $\omega $ есть постоянная угловая частота невозмущенной волны. Трехмерный единичный (относительно плоской метрики) вектор $\vec {k}$ имеет компоненты ${{k}^{\alpha }}$ и является касательным к пространственной проекции невозмущенной мировой линии сигнала. Для удобства обозначений мы не будем делать различий между верхним и нижним индексами компонентов этого вектора, т.е. по определению полагаем ${{k}^{\alpha }} = {{k}_{\alpha }}$, но в формулах будем помещать индексы в позициях, согласующихся со стандартным правилом суммирования Эйнштейна.

Параметризация мировой линии сигнала координатным временем $t$ позволяет записать пространственную часть траектории в виде уравнения прямой линии с направляющим вектором $\vec {k}$, с добавлением поправки $\mathop {\vec {\xi }}\nolimits_1 (t)$ (первого порядка по $G$), описывающей искривление реальной траектории. Точный вид этой поправки в рассматриваемой задаче оказывается несущественным, так что в общем виде координаты вдоль луча представимы как

Вернемся к рассмотрению фазы. Так как сигнал распространяется в искривленном пространстве, то к нулевому невозмущенному приближению необходимо добавить возмущения. Поправку к фазе первого порядка по степени гравитационной постоянной $G$ обозначим как ${{\varphi }_{1}}$, решение для нее было детально исследовано в работе [8]; в нашей работе мы доведем соответствующую ей точность в определении расстояния между спутниками до одного пикометра, а также получим решение для нелинейной части возмущения ${{\varphi }_{2}}$, квадратичной по $G$. Таким образом, запишем разложение фазы вдоль луча в виде Здесь и далее точка между векторами обозначает трехмерное декартово скалярное произведение. Аналогично, метрику представляем как сумму плоской метрики Минковского и возмущений первого и второго порядка по $G$, соответственно $h_{1}^{{mn}}$ и $h_{2}^{{mn}}$ (их явный вид будет конкретизирован позже): С учетом разложений метрики и фазы уравнение эйконала (1) дает уравнение для возмущений первого и второго порядка в виде Так как нас интересует фаза на луче, то от частных производных удобно перейти к полным производным по времени; для произвольной функции $f(t,\vec {x})$, при зависимости координат траектории от времени в виде (5), справедливо соотношение Из этого, беря в качестве функции $f$ возмущения фазы, получаем так что (8) переходит в Последний член в левой части этого уравнения можно удалить, выполнив разложение в ряд Тэйлора около невозмущенной прямолинейной траектории сигнала: Далее под функциями $\varphi $ и ${{h}^{{mn}}}$ будем понимать функции в точках на невозмущенной траектории, как в правых частях (12), и для сокращения записи не будем указывать эту зависимость в уравнениях. Теперь, собирая отдельно члены первого и второго порядка по $G$, получаем уравнения для линейной и квадратичной поправок к фазе: В следующих разделах будут найдены решения этих уравнений и оценен их вклад в определение расстояния между спутниками. Переход от фазы к расстояниям можно проделать следующим образом: перепишем уравнение (6) в виде так что функция $\mathcal{R}({{\vec {x}}_{{\text{0}}}},\vec {x})$ представляет собой полное расстояние, пройденное сигналом с момента излучения ${{t}_{0}}$ по момент приема $t$; в соответствии с (6), она зависит от поправок к фазе как Из этого видно, что линейная и квадратичная поправки к фазе вносят коррекции в расстояние соответственно как $\Delta {{r}_{1}} = - {{\varphi }_{1}}{\text{/}}{{k}_{0}}$ и $\Delta {{r}_{2}} = - {{\varphi }_{2}}{\text{/}}{{k}_{0}}$. Из уравнений (16), (13) и (14) можно заключить, что $\Delta r \simeq h{{d}_{{{\text{AB}}}}}$, так что члены $h$ величиной около 3.7 × 10^–18 в метрическом тензоре приводят к поправкам в районе 1 пм в измерении расстояния между спутниками (для конфигурации G-RACE‑FO с ${{d}_{{{\text{AB}}}}} = 270$ км).

3. РЕШЕНИЕ ДЛЯ ПОПРАВОК ПЕРВОГО ПОРЯДКА К ФАЗЕ

В этом разделе будет получено решение для ${{\varphi }_{1}}$ – поправки первого порядка по гравитационной постоянной, и оценен вклад в измеренное расстояние от различных ее составляющих. До сих пор наши рассуждения обладали некой общностью в том смысле, что применимы к физической ситуации достаточно слабого гравитационного поля, точнее, для случаев достаточно хорошей сходимости постминковского разложения полей на поправки с возрастающими степенями гравитационной постоянной $G$. Так как основной целью данной работы является описание ситуации околоземного гравитационного эксперимента, то следует конкретизировать вид метрического тензора; мы будем работать в рамках метрики слабого поля, представленной в виде стандартного разложения и реализующей так называемую геоцентрическую систему координат (GCRF). Данная система координат является кинематически невращающейся и имеет начало отсчета в центре масс Земли, и контравариантные компоненты соответствующей ей метрики имеют вид

где $W$ и ${{W}^{\alpha }}$ обозначают соответственно релятивистский скалярный и векторный потенциал. Поправки второго порядка $h_{2}^{{nm}}$ здесь оставлены в общем виде, и речь о них пойдет в разделе о решении для возмущения фазы второго порядка. Отброшенные в (17) члены имеют порядок ${{c}^{{ - 5}}}$ по скорости света, и их величины оценены в районе орбиты околоземного спутника (на высоте 500 км от поверхности Земли). Как было сказано выше, члены порядка $4 \times {{10}^{{ - 18}}}$ в метрике приводят к поправкам в расстоянии на уровне 1 пм, поэтому влиянием отброшенных в (17) членов можно пренебречь при нашей точности. Далее рассмотрим, что конкретно имеется в виду под метрическими потенциалами $W$ и ${{W}^{\alpha }}$.

Основная, линейная по $G$ часть метрики (17), соответствует рекомендованному МАС [10, 11] представлению метрического тензора в геоцентрической системе координат и описывается посредством двух релятивистских потенциалов $W$ и ${{W}^{\alpha }}$, каждый из которых состоит из трех частей различной природы. Скалярный потенциал описывает влияние массы тел и записывается как

т.е. является линейной суперпозицией релятивистского скалярного гравитационного потенциала ${{U}_{{\text{E}}}}$ изолированной Земли (он отличается от классического ньютоновского потенциала релятивистскими поправками), внешнего “приливного” потенциала ${{U}_{{{\text{tidal}}}}}$, создаваемого остальными телами Солнечной системы (его главная часть квадратична по расстоянию от начала координат и тоже близка к классическому приливному потенциалу), и поправки ${{U}_{{{\text{iner}}}}}$, возникающей из-за отклонения движения начала координат (центра масс Земли) от геодезической. Такое отклонение возникает в основном из-за отличия формы Земли от сферической, что приводит к взаимодействию квадрупольного момента Земли с внешним гравитационным полем (в первую очередь с полем Луны). Величина ${{U}_{{{\text{iner}}}}}$ линейна по расстоянию от начала координат и пропорциональна негеодезическому ускорению Земли. В работе [12] такое ускорение оценено как $4 \times {{10}^{{ - 11}}}$ м/с², что соответствует членам порядка $6 \times {{10}^{{ - 21}}}$ в метрике для околоземного пространства. Таким образом, величиной ${{U}_{{{\text{iner}}}}}$ в нашей точности можно пренебречь. Внешний потенциал дает поправки к метрике около ${{10}^{{ - 16}}}$ и соответствующие члены должны быть учтены в пикометровой модели. Наконец, главный вклад происходит от скалярного потенциала Земли, члены с ним в метрике имеют величину $1.3 \times {{10}^{{ - 9}}}$.

Векторный потенциал описывает влияние вращения массивных тел и дается похожим разложением

т.е. разделяется на аналогичные по смыслу части: он является линейной суперпозицией релятивистского векторного гравитационного потенциала $U_{{\text{E}}}^{\alpha }$ изолированной Земли, внешнего “приливного” потенциала $U_{{{\text{tidal}}}}^{\alpha }$, создаваемого остальными телами Солнечной системы, и поправки $U_{{{\text{iner}}}}^{\alpha }$, отвечающей релятивистской прецессии, которая возникает из-за наличия вращения геоцентрической системы координат относительно динамически невращающейся системы. За подробностями, касающимися этой поправки, отсылаем читателя к работе [10]. Отметим, что соответствующие ей члены в метрике имеют величину около $7 \times {{10}^{{ - 17}}}$ и должны быть оставлены в модели. Приливный вклад от вращения внешних тел, собранный в $U_{{{\text{tidal}}}}^{\alpha }$, дает в метрике члены не более $3 \times {{10}^{{ - 20}}}$, и поэтому далее учитываться не будет. За подробностями, касающимися его структуры, отсылаем читателя к работам [13, 14]. Вращательный потенциал Земли $U_{{\text{E}}}^{\alpha }$ приводит к поправкам в метрике на уровне $8 \times {{10}^{{ - 16}}}$ и должен учитываться в нашей модели. По причине малости вращательных эффектов поправка второго порядка $h_{2}^{{0\alpha }}$ в пикометровой модели не требуется и была отнесена к отброшенным членам в разложении компонентов метрики ${{g}^{{0\alpha }}}$ в (17).

С учетом этих оценок линейные по $G$ поправки $h_{1}^{{mn}}$ к плоской метрике достаточно полагать равными

Следует отметить, что поправки второго порядка $h_{2}^{{mn}}$ лежат за пределами точности разложения метрики в первом постньютоновском приближении. Соответствующая им квадратичная по $G$ поправка к фазе будет найдена и оценена в разделе 4. Уравнение (13) для линейной поправки к фазе выражается с учетом (20) через потенциалы как Здесь члены расположены в порядке убывания значимости. Для удобства разобьем поправку ${{\varphi }_{1}}$ на четыре составляющие, соответствующие по порядку членам с разными потенциалами в (21): и далее получим решения и оценки для каждой из этих поправок по отдельности.

Последний член в (21) описывает поправку к фазе за счет вращательных инерциальных эффектов:

“Инерциальный” векторный потенциал $U_{{{\text{iner}}}}^{\alpha }$ по своей смысловой нагрузке является потенциалом для релятивистской силы Кориолиса, возникающей из-за вращения геоцентрической системы координат относительно инерциальной системы [10]. Обозначая угловую скорость этого вращения как ${{\vec {\Omega }}_{{{\text{iner}}}}}$, данный потенциал записывается в виде векторного произведения Угловая скорость такого вращения разделяется на сумму трех так называемых релятивистских прецессий: геодезическую (составляет около /столетие), Лензе–Тирринга (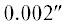/столетие) и Томаса (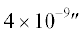/столетие). Для пикометровой точности достаточен учет только первого из этих типов прецессии. Геодезическая прецессия возникает как следствие вращения системы координат, связанной с Землей, вокруг центра масс Солнечной системы, и с достаточной точностью полная угловая скорость представима в виде где ${{\vec {v}}_{{\text{E}}}}$ и ${{\vec {a}}_{{\text{E}}}}$ обозначают соответственно барицентрическую скорость и ускорение центра масс Земли, и по величине оценивается как ${{\Omega }_{{{\text{iner}}}}} \simeq 3 \times $ $ \times {{10}^{{ - 15}}}$ рад/с. Вклад от данного эффекта в измеренное расстояние между спутниками GRACE-FO может достигать 18 пм, так что он должен учитываться в нашей модели. Решение уравнений (23)–(25) может быть найдено точно (считая скорость и ускорение Земли неизменными на малом промежутке времени полета сигнала, составляющем менее 1 мс), и отождествляя начальное событие с положением спутника A в момент испускания сигнала, а конечное событие – с положением спутника B в момент приема сигнала, получаем для сигнала от A к B “прецессионную” поправку к фазе здесь погрешность оценена по отброшенным в (25) членам.

Предпоследний член в уравнении (21) соответствует вкладу внешнего потенциала в поправку к фазе; обозначив эту поправку как $\varphi _{1}^{{{\text{tidal}}}}$, имеем для нее уравнение

Внешний “приливный” потенциал ${{U}_{{{\text{tidal}}}}}$ с достаточной точностью определен как часть суммарного ньютоновского потенциала внешних тел, которая является квадратичной (и выше) по расстоянию от начала координат, плюс релятивистские поправки, имеющие порядок малости $\mathcal{O}({{c}^{{ - 2}}}):$Здесь суммирование ведется по всем телам $b$ Солнечной системы, исключая Землю, ${{U}_{b}}(\vec {x})$ и ${{U}_{b}}(\vec {0})$ обозначают соответственно значения потенциала тела $b$ в текущей точке $\vec {x}$ и в начале координат $\vec {0}$; градиент потенциала тела $b$ в начале координат обозначен как $\vec {\nabla }{{U}_{b}}(\vec {0})$. Наконец, ${{\vec {r}}_{b}}$ есть геоцентрический радиус-вектор центра масс тела $b$, ${{r}_{b}}$ – его модуль, и ${{\vec {n}}_{b}} \equiv {{\vec {r}}_{b}}{\text{/}}{{r}_{b}}$. Во втором равенстве в первой сумме собраны вторые производные внешнего потенциала, т.е. эта сумма является квадрупольной частью внешнего потенциала. Во второй сумме собраны третьи производные, что дает октупольную часть внешнего потенциала. В данном выражении пренебрегается постньютоновскими поправками к потенциалу и более высокими, чем третья, производными в разложении в ряд Тэйлора в окрестности начала координат. Это оправдано тем, что вклад внешнего потенциала в определение расстояния, как будет показано ниже, достаточно мал и находится на уровне нескольких десятков пикометров.

Оценим, какую поправку в расстояние между спутниками дают гравитационные потенциалы внешних тел. Для этого достаточно считать правую часть дифференциального уравнения (27) постоянной на времени полета сигнала. Это является хорошим приближением, так как расстояние между спутниками ${{d}_{{{\text{AB}}}}} = 270$ км сигнал проходит всего за 0.9 мс. Тогда приливная поправка к фазе оценивается как $\varphi _{1}^{{{\text{tidal}}}} \simeq - \frac{{{{d}_{{{\text{AB}}}}}}}{c}\frac{{2{{k}_{0}}}}{c}{{U}_{{{\text{tidal}}}}}$, и по (16) поправка к расстоянию составляет $\Delta {{r}_{{{\text{tidal}}}}} \simeq \frac{{2{{d}_{{{\text{A}}B}}}}}{{{{c}^{2}}}}{{U}_{{{\text{tidal}}}}}$. Для указанных ранее параметров орбиты спутников в миссии GRACE-FO максимальный вклад квадрупольной части приливного поля Солнца и Луны в нахождение расстояния между спутниками оценивается по этой формуле как 11 и 30 пм соответственно. Следующий ближайший по малости квадрупольный вклад оказывается от потенциала Венеры и составляет порядка 0.0013 пм. Наибольший эффект от октупольных членов в разложении (28) происходит от поля Луны и составляет не более 0.58 пм, следующий по малости вклад равен $5 \times {{10}^{{ - 4}}}$ пм (от поля Солнца). Таким образом, для точности в 1 пм можно пренебречь всей второй суммой в (28), а в первой сумме сохранить только члены для Луны и Солнца. При этих условиях уравнение (27) может быть решено точно. Отождествляя начальное событие с положением спутника A в момент испускания сигнала, а конечное событие – с положением спутника B в момент приема сигнала, получаем для сигнала от A к B приливную поправку к фазе

в которой содержится только сумма вкладов от квадрупольных приливных потенциалов Луны (M) и Солнца (S). Оценка точности здесь дана по отброшенным членам с октупольным приливным потенциалом Луны.

Перейдем к рассмотрению влияния на фазу векторного гравитационного потенциала; такую поправку обозначим через $\varphi _{1}^{{{\text{spin}}}}$, и соответствующий ей второй член в (21) приводит к дифференциальному уравнению

С достаточной точностью векторный потенциал определен как где ${{\sigma }^{\alpha }}(t,\vec {x}{\kern 1pt} ')$ обозначает релятивистскую плотность импульса материи вращающейся Земли, и интегрирование ведется по объему Земли. Во второй части уравнения выполнено мультипольное разложение и сохранен только ведущий спиновый момент (плотность момента импульса) ${{\vec {S}}_{{\text{E}}}}$, который имеет стандартное определение в виде интеграла по объему Земли, Отметим известный факт, что для однородного шара с радиусом $R$ и массой $M$, вращающегося твердотельно с угловой скоростью $\Omega $, такое определение спина дает значение $S = \tfrac{2}{5}\Omega M{{R}^{2}}$. Остальные члены мультипольного разложения и постньютоновские поправки к потенциалу пренебрежимо малы: согласно оценкам в работе [10], отброшенные в (31) члены имеют величину примерно в ${{10}^{4}}$ раз меньшую, чем главный дипольный спиновый член. При таком выражении для векторного потенциала может быть найдено точное решение уравнения (30): для прохождения сигнала от A к B, что соответствует поправке порядка 200 пм при измерении расстояния между спутниками (величина отброшенного члена дана по приведенной выше оценке отброшенных спиновых мультиполей). Таким образом, поправка (33) должна быть учтена в окончательной формулировке выражения для фазы. Отметим, что альтернативная форма записи решения (33) была получена в [8], где сначала проводилось интегрирование по времени, а затем разложение по мультиполям.

Наиболее сложной является ситуация с вкладом $\varphi _{1}^{{\text{E}}}$ от скалярного потенциала Земли. В уравнении (21) ему отвечает первое слагаемое, так что эта поправка подчиняется уравнению

В работе [8], посвященной созданию модели, обеспечивающей нанометровую точность в измерении расстояния, было получено точное решение уравнения (34), имеющее вид Здесь интегрирование производится по объему Земли, и ${{\sigma }_{{\text{E}}}}(t,\vec {x}{\kern 1pt} ')$ обозначает релятивистскую массовую плотность материи. Отброшенные члены соответствуют ряду постньютоновских поправок к определению скалярного потенциала Земли и по величине составляют порядка ${{10}^{{ - 9}}}$ от величины основного интеграла, представленного здесь.

Далее, раскладывая в ряд логарифм под знаком интеграла, в [8] были получены монопольная и квадрупольная поправки к фазе; для определения массы Земл ${{M}_{{\text{E}}}}$ и ее квадрупольного момента $J_{{\text{E}}}^{{\alpha \beta }}$ в (35) было проделано мультипольное разложение

и выполняя мультипольное разложение в (35), получаем поправку к фазе в форме Первый (логарифмический) член представляет собой классический эффект Шапиро от точечной массы ${{M}_{E}}$, он является доминирующим по величине среди всех поправок к фазе и приводит для сигнала от A к B в миссии GRACE-FO к поправке в расстоянии порядка 350 мкм. Для круговых орбит этот вклад постоянен во времени; при наличии небольшого эксцентриситета $e \sim 0.001$ появляется дополнительная поправка порядка 0.35 мкм с периодом, равным периоду обращения спутников. Группа членов с $J_{{\text{E}}}^{{\alpha \beta }}$ представляет собой квадрупольный вклад в фазу и приводит к поправке (периодической) в несколько десятых микрометра. Следующие члены мультипольного разложения (октупольный и прочие) здесь отброшены; они были оценены в [8] как дающие поправку в расстояние менее 1 нм.

В связи с перспективами повышения точности в измерении расстояния между спутниками миссии GRACE-FO до ${{10}^{{ - 12}}}$ м возникает вопрос, до каких порядков следует продолжить мультипольное разложение (38) и имеет ли вообще смысл в задаче с повышенной точностью оперировать такого рода разложением, так как уже квадрупольная поправка выглядит не слишком компактно, а следующие члены разложения усложняются еще больше [15]. Для решения этой проблемы мы обратимся к более удобному для практики, чем мультипольное, разложению потенциала по сферическим гармоникам. Для релятивистского скалярного потенциала такое разложение имеет вид [10]:

где ${{R}_{{\text{E}}}}$ обозначает радиус Земли, ${{P}_{{lm}}}$ – присоединенные полиномы Лежандра. Коэффициенты ${{C}_{{lm}}}(t,r)$ и ${{S}_{{lm}}}(t,r)$ являются функциями времени и геоцентрического расстояния, а именно Коэффициенты ${{C}_{{lm}}}(t)$ и ${{S}_{{lm}}}(t)$ описывают разложение релятивистского геопотенциала в геоцентрической системе координат; они соотносятся (путем релятивистского преобразования между вращающимися и невращающимися координатами) с приблизительно постоянными коэффициентами ${{C}_{{lm}}}$ и ${{S}_{{lm}}}$ в моделях геопотенциала во вращающихся вместе с Землей координатах. Наборы $\{ C(t),S(t)\} $ и $\{ C,S\} $ отличаются на множитель порядка $1 + O({{(r{{\Omega }_{{\text{E}}}}{\text{/}}c)}^{2}})$ из-за преобразования между системами координат; для орбит с высотой 500 км над поверхностью это составляет около $1 + O(3 \times {{10}^{{ - 12}}})$, что приводит к поправкам в измерение расстояния между спутниками GRACE-FO порядка ${{10}^{{ - 3}}}$ пм. Релятивистские поправки в (40) имеют тот же порядок малости. Наконец, характерные времена изменения гармоник ${{C}_{{lm}}}$ и ${{S}_{{lm}}}$ много больше динамической шкалы в нашей задаче, описываемой миллисекундными интервалами в обмене сигналами между спутниками, так что на протяжении распространения сигналов можно пренебречь временной зависимостью гармоник. Все это позволяет нам представить релятивистский геопотенциал в районе орбит спутников в виде стандартного разложения с так называемыми нормализованными (постоянными) гармониками ${{C}_{{lm}}}$ и ${{S}_{{lm}}}$, которые вычислены и затабулированы для многочисленных моделей гравитационного поля Земли. Различия в численных значениях гармоник в разных современных моделях находятся за пределами точности рассматриваемой нами задачи, и для анализа поправки к фазе $\varphi _{1}^{{\text{E}}}$ мы выбрали модель GGM05C, содержащую гармоники по $l = 360$ и датированную 2015 годом [16]. Таблицы с численными значениями гармоник этой модели, как и множества других, можно найти в открытом доступе на сайте icgem.gfz-potsdam.de.

В разложении (41) координаты точки $\vec {x}$ даются стандартным набором сферических (геоцентрических невращающихся) координат $(r,\theta ,\phi )$. Необходимо отметить, что азимутальная координата $\phi $ для фиксированной точки должна пониматься как линейная функция времени вида $\phi = {{\phi }_{0}} - {{\Omega }_{{\text{E}}}}t$ по причине того, что гармоники ${{C}_{{lm}}}$ и ${{S}_{{lm}}}$ относятся к вращающейся вместе с Землей системе координат; в результате этого в фиксированной в геоцентрической системе координат точке $\vec {x}$ значение потенциала ${{U}_{{\text{E}}}}(t,\vec {x})$ является переменным во времени. Другой важный момент, на котором здесь следует заострить внимание, это использование в разложении (41) так называемых нормализованных присоединенных полиномов Лежандра ${{\bar {P}}_{{lm}}}$. Обычные присоединенные полиномы ${{P}_{{lm}}}$ определяются через производные от классических полиномов Лежандра ${{P}_{l}}$ как

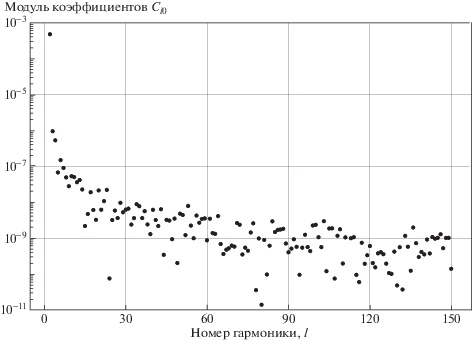
(обращаем внимание на отсутствие в этом определении множителя ${{( - 1)}^{m}}$, называемого фазой Кондона–Шортли, что является обычной практикой в геодезии). Нормализованные присоединенные полиномы Лежандра $\mathop {\bar {P}}\nolimits_{lm} $ вычисляются по правилу [17] с множителем $K = 1$ при $m = 0$ и $K = 2$ при $m \ne 0$. В разложениях с большими порядками гармоник использование нормализованных полиномов вместо обычных объясняется вычислительной необходимостью, так как максимальные значения обычных полиномов слишком быстро растут с увеличением порядка, что делает их неудобными при численных вычислениях.

Для иллюстрации темпа сходимости ряда (41) на рис. 2 представлена зависимость модуля коэффициентов ${{C}_{{l0}}}$ от номера гармоники $l$, начиная с квадрупольного члена $l = 2$ и далее по $l = 150$. Коэффициенты убывают очень медленно, и сходимость разложения (41), помимо знакопеременности, обусловлена убыванием фактора расстояния ${{({{R}_{{\text{E}}}}{\text{/}}r)}^{l}}$. Однако спутники GRACE-FO находятся на низкой орбите с высотой $h \simeq 450$ км, так что для них ${{R}_{{\text{E}}}}{\text{/}}r \simeq 0.934$, и для сотой гармоники фактор расстояния составляет всего около ${{10}^{{ - 3}}}$. Октупольный момент дает вклад в расстояние между спутниками порядка 1 нм, так что приходится говорить о нескольких десятках гармоник, дающих вклад не менее 1 пм. Более того, возможен накопительный эффект – отброшенные за малостью высокие гармоники в сумме могут давать достаточно большую поправку.

Все это приводит к необходимости детального анализа влияния различных гармоник. Обозначим $\Delta {{d}_{l}}$ вклад от гармоник $l$ (просуммированный по $m$) в вычисление расстояния между спутниками. Из (16), (34) и разложения (41) следует, что для произвольного момента испускания сигнала $t$ эти величины могут быть вычислены как

где сферические координаты $(r{\kern 1pt} ',\theta {\kern 1pt} ',\phi {\kern 1pt} ')$ вычисляются для точек на прямолинейном отрезке траектории сигнала от A к B по стандартным формулам сферической тригонометрии (заметим, что геоцентрическая долго-та   ϕ' должна быть дополнительно сдвинута на $ - {{\Omega }_{{\text{E}}}}(t + t{\kern 1pt} ')$ для перехода к вращающейся вместе с Землей системе координат, в которой заданы гармоники $C$ и $S$).

Численный анализ вклада каждой гармоники проведем следующим образом. Будем считать, что спутник А шлет сигнал к спутнику В один раз в секунду, и для каждого такого события вычислим поправки в измеряемое при этом расстояние, разделяя по отдельности вклады от каждой гармоники, так что для каждой гармоники можно будет рассмотреть динамику во времени. Для орбиты пары спутников сделаем упрощающее предположение, что они движутся синхронно на фиксированном расстоянии ${{d}_{{{\text{AB}}}}} = 270$ км друг от друга по круговой околополярной орбите с геоцентрическим радиусом $r = {{R}_{{\text{E}}}} + 450$ км и наклоном $89^\circ $ к экватору (параметры орбиты близки к реальным для GRACE-FO). Для такой орбиты вычисляем координаты спутников ${{\vec {x}}_{{\text{A}}}}(t)$ и ${{\vec {x}}_{{\text{B}}}}(t)$ с шагом в одну секунду на протяжении 15 их оборотов, что составляет около одних земных суток. Для каждого такого секундного шага, соответствующего моменту $t$, вычисляем величины $\Delta {{d}_{l}}(t)$ по определению (44) для всех номеров гармоник l. Для этого интервал интегрирования ${{d}_{{{\text{AB}}}}}{\text{/}}c \simeq $ $ \simeq 9 \times {{10}^{{ - 4}}}$ секунды делится на 64 равных отрезка и интегрирование выполняется численно по методу Ромберга. При таком методе интегрирования численные ошибки лежат далеко за пределами желаемой нами точности вычислений, и на полученные результаты будем далее в тексте ссылаться как на точные.

В результате описанных действий мы для каждой гармоники проследили зависимость поправок к расстоянию между спутниками от времени на протяжении 15 оборотов спутников (примерно 1 сут). Этого вполне достаточно для оценки максимального вклада различных гармоник. В качестве иллюстрации полученных результатов на рис. 3 приведен ряд графиков зависимости от времени для поправок к расстоянию от некоторых гармоник. В верхнем ряду слева показано, как зависит от времени самый крупный (после монопольного) вклад от квадрупольных $(l = 2)$ гармоник земного потенциала. Видно, что максимальный по модулю вклад в измеренное расстояние между спутниками (для GRACE-FO) составляет немного более 300 нм. Справа в верхнем ряду приведена зависимость суммарного вклада от всех гармоник, больших квадрупольной, т.е. для всех порядков с $l \geqslant 3$. Видно, что максимальное значение составляет около трех нанометров. Это следует понимать так, что ошибка при учете только монопольной и квадрупольной составляющей потенциала Земли достигала бы 3 нм. В верхнем ряду масштабы осей $y$ взяты разными из-за отличия значений эффектов примерно на два порядка. В каждом следующем ряду на рис. 3 масштабы осей сделаны одинаковыми для лучшей визуализации при сравнении вкладов индивидуальных гармоник (левый столбец) с $l = 3,\;4,\;58,\;70$ с суммарными вкладами всех последующих гармоник (соответственно с $l \geqslant 4,\;5,\;59,\;71,$ правый столбец).

По графикам во втором ряду видно, что октупольные гармоники приводят к максимальным поправкам около двух нанометров, в то время как все остальные гармоники с $l \geqslant 4$ суммарно могут давать те же два нанометра. Похожая ситуация наблюдается и в третьем ряду, где максимальный эффект около 1 нм дают как гармоники с $l = 4$, так и суммарно с $l \geqslant 5$. В четвертом ряду слева представлен график для первой по порядку гармоники, вклад которой оказывается менее одного пикометра (гармоника с $l = 58$). Однако по соответствующему правому графику видно, что все последующие гармоники суммарно могут давать эффект в три раза больший. Наконец, в нижнем ряду справа показан суммарный вклад всех гармоник с порядками $l \geqslant 71$, который оказывается ниже желаемой планки в 1 пм. При этом гармоники с $l = 70$ приводят к поправкам не более 0.2 пм (график в нижнем ряду слева). Для двух последних рядов в графиках справа хорошо заметны резкие пики, в которых вклады высоких гармоник усиливают друг друга; все это позволяет говорить о значительном накопительном эффекте, имеющем здесь место. Формальное отбрасывание всех гармоник с индивидуальными вкладами, меньшими одного пикометра, приводит к ошибкам при измерении расстояния не в 1 пм, а в 3 пм, как видно из второго снизу ряда на рис. 3. Точность в 1 пм для конфигурации GRACE-FO обеспечивается учетом всех гармоник потенциала вплоть по $l = 70$.

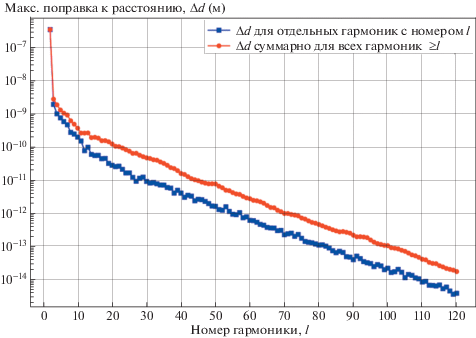
На рис. 4 проиллюстрирована важность накопительного эффекта в целом. Из набора полученных данных о временнóй зависимости поправок от каждой гармоники, пять примеров которых были представлены на рис. 3, можно вычислить максимальные вклады в измерение расстояния для каждой гармоники, которые наблюдаются на интервале в 15 оборотов спутников. Модуль таких максимальных вкладов в зависимости от номера гармоники $l$ представлен нижней линией на рис. 4. Верхняя линия изображает аналогичный максимальный вклад от суммы всех гармоник с номерами $ \geqslant \,{\kern 1pt} l$. Вертикальное расстояние между линиями показывает величину накопленного эффекта от всех гармоник, больших данной. Значительное расхождение линий хорошо демонстрирует существенное влияние такого накопительного эффекта: видно, что для всех гармоник выше примерно двадцатой, величина суммарного эффекта от гармоник $ \geqslant \,{\kern 1pt} l$ в 3–5 раз превосходит величину эффекта от гармоники номер $l$. Мы можем заключить, что каждая гармоника, начиная с $l = 58$, дает максимальную поправку менее 1 пм, однако для обеспечения точности в 1 пм при анализе фазовой информации необходимо учитывать все гармоники земного потенциала вплоть по номер $l = 70$. Так как при построении модели распространения фазы имеются ошибки из других источников, повысим здесь планку точности в 10 раз и потребуем, чтобы отброшенные гармоники земного потенциала приводили к ошибке в   измерении расстояния между спутниками GRACE-FO не более, чем в 0.1 пм. Из рис. 4 видно, что для этого нужно полностью учитывать первые 100 гармоник. Отметим, что есть вероятность того, что на бóльших временах мониторинга спутников, чем те 15 оборотов, которые рассматривали мы, будут появляться более высокие пики от сумм высоких гармоник, так что наша оценка необходимого числа гармоник может быть занижена на несколько единиц.

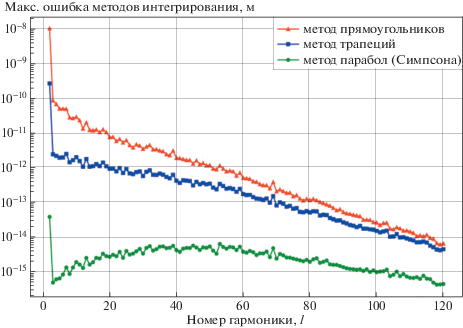
Возникает вопрос, каким образом можно адекватно включить в процедуру анализа фазы такое большое число гармоник земного потенциала. В работе [8] представлен механизм аналитического вычисления поправок к фазе для произвольной гармоники и выведены формулы для монопольного и квадрупольного вкладов, но не был найден общий вид формул для других гармоник, так как в этом не было необходимости в связи с ограничением планируемой точности эксперимента в 1 нм. Даже если такие формулы получить, то выражения для вклада каждой следующей гармоники будут содержать в несколько раз больше членов, чем для предыдущей, поэтому общий вид такого разложения скорее представляет только теоретический, а не практический интерес. При реальной обработке эксперимента приходится прибегнуть к той или иной форме численного интегрирования, по типу использованного нами при вычислении поправок (44). Не вдаваясь в детали реализации конкретных методов обработки наблюдений, мы изучили вопрос, какой из численных методов взятия интегралов (44) достаточен по точности для пикометровой модели. Мы исследовали, помимо метода Ромберга, еще 3 более быстрых метода интегрирования и сравнили получившиеся результаты с “точными” (полученными методом Ромберга и описанными выше). На рис. 5 для каждой гармоники приведены абсолютные значения максимальных расхождений между упрощенными методами интегрирования и методом Ромберга в вычислении расстояния между спутниками. Верхняя кривая соответствует ошибкам при интегрировании методом прямоугольников (по одной точке, функция считается постоянной на интервале интегрирования и равной своему значению, например, на левой границе). Можем заключить, что точность этого метода не является удовлетворительной. Средняя кривая показывает ошибки при интегрировании методом трапеций (по двум точкам, функция аппроксимируется отрезком прямой, соединяющей значения на концах интервала интегрирования). Видно небольшое увеличение точности, но его все равно недостаточно для пикометровой точности. Наконец, нижняя кривая соответствует ошибкам при интегрировании методом Симпсона (по трем точкам, функция аппроксимируется параболой). Этот метод оказывается вполне пригодным, и даже для квадрупольных гармоник дает наибольшее расхождение около 0.04 пм.

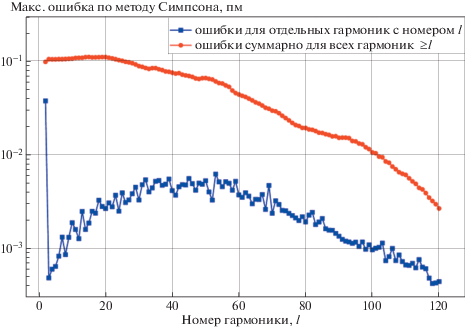
Выясним, какова точность интегрирования методом Симпсона суммарного эффекта от всех гармоник земного потенциала. Это следует проанализировать, так как возможна ситуация, когда ошибки интегрирования накапливаются при сложении большого количества членов. Действительно, на рис. 6 нижняя линия является копией нижней линии с рис. 5 и представляет собой ошибки для индивидуальных гармоник $l$ в методе Симпсона. Верхняя линия показывает максимальные ошибки при интегрировании совокупности гармоник со всеми номерами $ \geqslant {\kern 1pt} l$. Видно, что метод парабол гарантирует точность численного интегрирования в 0.1 пм для полного разложения потенциала по гармоникам. Окончательно мы приходим к выводу, что учет 100 первых гармоник земного потенциала и численное интегрирование в (44) по методу Симпсона приводят к ошибкам в вычислении расстояния между спутниками GRACE-FO не более 0.2 пм.

Таким образом, для вычисления поправки к фазе $\varphi _{1}^{{\text{E}}}$ от скалярного потенциала Земли представим потенциал ${{U}_{{\text{E}}}}$ в виде разложения, содержащего 100 первых гармоник ${{U}_{l}}$:

где гармоники ${{U}_{l}}$ определены через коэффициенты ${{C}_{{lm}}}$ и ${{S}_{{lm}}}$ из модели потенциала Земли как Решение уравнения (34) для ньютоновской поправки к фазе будем записывать в виде суммы логарифмического члена Шапиро, описывающей влияние монопольной части потенциала, и формулы Симпсона (из численного интегрирования методом парабол) для гармоник с $l = 2$ по 100: Данная формула является основным результатом исследования влияния скалярного потенциала Земли на фазу сигнала.

Напомним, что полная поправка первого порядка к фазе была разбита в (22) на 4 части, и в заключение этого раздела соберем вместе полученные результаты.

Скалярный потенциал Земли приводит к фазовой поправке в виде (48), с вкладом в расстояние от монопольной части на уровне 350 мкм, от квадрупольной – до 320 нм, и суммарно от гармоник с номерами от 3 по 100 – до 3 нм.

Релятивистская поправка, связанная с вращением Земли (гравимагнитный эффект) дается выражением (33) и приводит к поправкам в расстояние до 200 пм.

Влияние внешних по отношению к Земле тел (достаточно принимать во внимание только Луну и Солнце) может достигать 40 пм и дается формулой (29).

Наконец, вращение Земли вокруг Солнца приводит к геодезической прецессии, что оказывает влияние на фазу сигнала (26) на уровне 18 пм. Приведем единое выражение для поправки к фазе первого порядка:

Напоминаем, что все координаты ${{\vec {x}}_{{\text{A}}}}$ вычисляются в момент испускания сигнала ${{t}_{1}}$, а координаты ${{\vec {x}}_{{\text{B}}}}$ – в момент приема ${{t}_{2}}$. То же относится и к прочим выводимым из них величинам. Оценка погрешности в (49) получена как сумма погрешностей четырех рассмотренных частей фазы.

4. РЕШЕНИЕ ДЛЯ ПОПРАВОК ВТОРОГО ПОРЯДКА К ФАЗЕ

Уравнение (14), которому подчиняется поправка второго порядка по $G$, запишем в более развернутом виде, разделяя компоненты ${{K}_{m}}$ на временную и пространственные в соответствии с (4), а также учитывая отсутствие явной зависимости от времени у поправок первого порядка ${{\varphi }_{1}}$, что видно из итогового результата (49) предыдущего раздела. Получаем

Как было получено в предыдущей главе, доминирующим членом в ${{\varphi }_{1}}$ является поправка от монопольного эффекта Шапиро, которая дает вклад в измерение расстояния примерно $3.5 \times {{10}^{{ - 4}}}$ м, а все остальные поправки как минимум на 3 порядка меньше. По грубой оценке, поправки второго порядка получают дополнительный множитель порядка ${{U}_{{\text{E}}}}{\text{/}}{{c}^{2}} \sim 6.5 \times {{10}^{{ - 10}}}$, поэтому ожидаемая величина поправок в расстоянии за счет ${{\varphi }_{2}}$ должна находиться в районе $2 \times {{10}^{{ - 13}}}$ м. Это ниже принятой нами планки в 1 пм, однако находится недалеко от нее, поэтому желательна более аккуратная оценка. В силу малости рассматриваемой поправки второго порядка, в функции ${{\varphi }_{1}}$ в (50) достаточно сохранить только эффект Шапиро (логарифмический член в (49)), а остальными поправками пренебречь; тогда необходимые здесь производные от фазы по пространственным координатам вычисляются как Добавление сюда производных от более высоких гармоник земного потенциала излишне, так как максимальное значение производной от вклада гармоники с номером $n$ растет примерно пропорционально $n$, и этого недостаточно, чтобы соответствующие члены попали в диапазон значений выше 1 пм.

Покажем, что третий и четвертый члены в (50) можно сразу исключить из рассмотрения. Они связаны с влиянием гравимагнитной составляющей гравитационного поля Земли, и поэтому вклад от них достаточно мал. В предыдущем разделе показано, что поправка в расстоянии от линейного возмущения метрики $h_{1}^{{0\alpha }}$ находится на уровне $2 \times {{10}^{{ - 10}}}$ м; во втором приближении аналогичный по своей природе третий член в (50), пропорциональный $h_{2}^{{0\alpha }}$, имеет следующий порядок малости, т.е. его вклад подавлен примерно в ${{10}^{{10}}}$ раз. Очевидно, такой поправкой к фазе мы пренебрегаем. Для четвертого члена в (50) приведем более точную оценку. Оставляя в мультипольном разложении векторного гравитационного потенциала Земли только главный спиновый член (31), получаем

Для твердотельного однородного шара с радиусом ${{R}_{{\text{E}}}}$, вращающегося с угловой скоростью ${{\Omega }_{{\text{E}}}}$, спиновый момент ${\text{|}}{{\vec {S}}_{{\text{E}}}}{\text{|}} = \tfrac{2}{5}{{M}_{{\text{E}}}}{{\Omega }_{{\text{E}}}}R_{{\text{E}}}^{2}$, поэтому вклад члена (52) в измерение расстояния между спутниками оценивается как где, как обычно, мы полагаем время распространения сигнала от спутника A к B $\Delta t \simeq 9 \times {{10}^{{ - 4}}}$ с. Соответственно, этой поправкой тоже можно пренебречь.

Для вычисления квадратичных по $G$ поправок $h_{2}^{{00}}$ и $h_{2}^{{\alpha \beta }}$, входящих в (50), поступим следующим образом. Мы показали, что во втором приближении вклад гравимагнитного поля Земли пренебрежимо мал. Также мал вклад от несферичности Земли и от гравитационного поля внешних тел (такие поправки к расстоянию оцениваются как поправки первого порядка, умноженные на релятивистский фактор ${{U}_{{\text{E}}}}{\text{/}}{{c}^{2}} \sim 6.5 \times {{10}^{{ - 10}}}$, т.е. составляют менее ${{10}^{{ - 16}}}$ м). Это говорит о том, что для описания гравитационного поля во втором приближении достаточно считать Землю изолированным сферически симметричным телом. В то время как поправка первого порядка к фазе была нами получена в полной модели с учетом несферичности и вращения Земли, для второго порядка будем представлять поле Земли в качестве метрики Шварцшильда, записанной в подходящих координатах. Координатами, в которых метрика Шварцшильда при разложении по малому параметру дает монопольное приближение нашей метрики (17), являются изотропные координаты; интервал в них имеет вид [18]

Такая метрика является диагональной, и несложно вычислить квадратичные поправки в обратной метрике при разложении по степеням $G$: В таком виде подставим эти поправки в первые два слагаемые уравнения (50), а производные (51) – в последние два слагаемых, и в результате получим достаточно компактное уравнение для поправки второго порядка к фазе: Точки с координатами $\vec {x}$, как и ранее, берутся на прямолинейной невозмущенной траектории сигнала, так что координаты точек зависят от времени как $\vec {x}(t) = {{\vec {x}}_{0}} + \vec {k}c(t - {{t}_{0}})$. С учетом этого данное уравнение оказывается возможным проинтегрировать точно, и нами было найдено его решение в следующем виде: Для сигнала от спутника A к B в качестве начальной и конечной точек выступают ${{\vec {x}}_{0}} = {{\vec {x}}_{{\text{A}}}}$ и $\vec {x} = {{\vec {x}}_{{\text{B}}}}$. Сделаем некоторые упрощения для оценки вклада от (57) в расстояние между спутниками. Во всех знаменателях, а так же под корнем в числителе внутри арктангенса, считаем $\vec {k} \cdot \vec {x}$ и $\vec {k} \cdot {{\vec {x}}_{0}} \ll {{r}_{0}}$, так как вектор $\vec {k}$ вдоль луча близок к перпендикуляру к радиусу-вектору спутника. Расстояние между спутниками ${\text{|}}\vec {x} - {{\vec {x}}_{0}}{\kern 1pt} {\text{|}}$ мало по сравнению с радиусом орбиты ${{r}_{0}}$, так что для малого $\alpha $ используем приближение $arctan\alpha \simeq \alpha $. Орбиты спутников считаем круговыми, так что ${{r}_{0}} = r$. Наконец, для разности координат спутников имеем точное равенство $\vec {x} - {{\vec {x}}_{0}} = c\vec {k}\Delta t$. В таком случае для (57) справедлива оценка При $\Delta t = 9 \times {{10}^{{ - 4}}}$ с значение этой поправки составляет $3 \times {{10}^{{ - 14}}}$ м. Таким образом, можно констатировать, что квадратичные поправки к фазе оказываются за пределами точности измерения расстояния в 1 пм.

5. ЗАКЛЮЧЕНИЕ

В качестве главного итога данной работы нами получено аналитическое выражение для фазы сигнала, которым обмениваются спутники в эксперименте типа GRACE-FO. Фаза была проанализирована методом возмущений, и для возмущений первого порядка по гравитационной постоянной найдены все поправки, достаточные для обработки измерения расстояния с точностью в 1 пм. Затем было показано, что возмущения второго порядка приводят к поправкам в расстоянии между спутниками GRACE-FO на уровне 0.03 пм и тем самым могут не учитываться в пикометровой модели. Итоговое выражение для фазы сигнала, испущенного спутником А в геоцентрический момент времени ${{t}_{1}}$, и принимаемого на спутнике В в момент ${{t}_{2}}$, получается комбинированием формулы разложения фазы на возмущения (6) и решением (49) для возмущения фазы первого порядка:

Здесь логарифмический член (монопольный эффект Шапиро) записан в более удобном виде с использованием соотношения [7]: Уравнение (59) связывает начальную и конечную фазу точки волнового фронта сигнала; так как фаза точки не изменяется $(\varphi ({{t}_{1}},{{\vec {x}}_{{\text{A}}}}) = \varphi ({{t}_{2}},{{\vec {x}}_{{\text{B}}}}))$, то (59) в сущности задает связь между временем движения сигнала ${{t}_{2}} - {{t}_{1}}$ и расстоянием между спутниками. В следующей публикации будет рассмотрен вопрос об использовании результата (59) для формулировки наблюдаемых величин в эксперименте типа GRACE-FO.

Авторы признательны профессору В.Г. Турышеву за многочисленные комментарии и помощь в структурировании материала.