Астрономический журнал, 2021, T. 98, № 4, стр. 281-304

Популяционный синтез экзопланет с учетом изменения орбит за счет звездной эволюции

А. С. Андрюшин^1, *, С. Б. Попов^1, 2, **

¹ Московский государственный университет им. М.В. Ломоносова, Физический факультет
Москва, Россия

² Московский государственный университет им. М.В. Ломоносова, Государственный астрономический институт им. П.К. Штернберга
Москва, Россия

^* E-mail: andriushin.as14@physics.msu.ru
^** E-mail: sergepolar@gmail.com

Поступила в редакцию 16.10.2020
После доработки 26.11.2020
Принята к публикации 16.12.2020

DOI: 10.31857/S0004629921040010

Полный текст (PDF)

Аннотация

В работе методом популяционного синтеза исследована эволюция орбит экзопланет на поздних стадиях звездной эволюции. Эволюция звезд прослежена, начиная со стадии Главной последовательности до стадии белого карлика. Для расчета эволюционных треков использован пакет MESA. Проведен расчет статистики поглощенных, выброшенных из системы и выживших планет к моменту превращения родительских звезд в белые карлики с учетом изменения темпа звездообразования в Галактике за все время ее существования. Рассмотрены планеты у звезд в интервале начальных масс (1–8) ${{M}_{ \odot }}$, поскольку менее массивные звезды не успевают уйти с Главной последовательности за время жизни Галактики, а более массивные не приводят к образованию белых карликов. Установлено, что для принятых в работе начальных распределений планет на плоскости “a – M_pl” большинство (около 60%) планет, родившихся у звезд в исследуемом диапазоне масс, поглощается родительскими звездами на стадии гиганта. Небольшая доля планет (менее процента) оказывается выброшена из своих систем из-за воздействия улетающего от звезды потока вещества. Оцененное число “убежавших” планет с массами в интервале от 0.04 массы Земли до 13 масс Юпитера в Галактике приближенно равно 300 млн.

1. ВВЕДЕНИЕ

С момента открытия первых экзопланет прошло около трех десятилетий [1, 2]. За это время число подтвержденных внесолнечных планет, открытых с помощью таких инструментов как Kepler, HARPS, HIRES, TESS и др., превысило 4300¹ ¹. Из них более ста – планеты вокруг проэволюционировавших звезд: красных гигантов и субгигантов. Статистика обнаружения планет вокруг белых карликов более скромная: среди немногочисленных примеров – планета у звезды WD 0806–661 [3], недавно открытый кандидат у WD 1856+534 [4], а также объекты в двойных системах “белый карлик + звезда Главной последовательности (ГП)” (NN Ser, Gliese 86).

Однако существует гораздо большее число примеров – порядка 1000 – обнаружения вокруг белых карликов и в их атмосферах “планетных останков” – продуктов разрушения планет и (или) астероидов. Такие выводы позволяют сделать анализ наблюдаемого химического состава атмосфер карликов и обнаружения вокруг них околозвездных дисков из пыли и обломков пород [5, 6]. Таким образом, можно считать установленным фактом, что объекты планетных масс могут не только остаться в системе после сброса звездой оболочки на поздних стадиях эволюции, но и перейти на низкие орбиты вокруг компактного объекта. Это делает актуальным анализ свойств планет на поздних стадиях эволюции и их предшествующей истории.

Чтобы адекватно трактовать растущий объем данных по экзопланетам у проэволюционировавших звезд и иметь возможность судить по этим данным о том, какую эволюцию претерпела наблюдаемая планетная система, необходимо теоретическое осмысление процессов, обусловливающих эволюцию планетных систем, в частности, на тех этапах жизни данных систем, когда их родительская звезда уходит с ГП. Модель эволюции планетных систем под влиянием эволюции их родительских звезд позволила бы в отношении открываемых и наблюдаемых планет у проэволюционировавших звезд делать предположения о прошлом данных систем. Кроме того, желательно, чтобы модель также обладала и предсказательным потенциалом для планетных систем у звезд ГП.

Моделированию эволюции планетных систем звезд после стадии ГП за последние 10 лет было посвящено много работ. Ключевые результаты и нерешенные вопросы обсуждаются, например, в обзоре [7]. Эволюция планетных систем на поздних стадиях жизни звезды происходит под воздействием разных факторов и на разных уровнях в зависимости от того, какими являются значение большой полуоси орбиты и масса субзвездного объекта (например, планеты или астероида) в период жизни звезды на ГП, от того как на этот объект в дальнейшем (после ухода звезды с ГП) могут влиять такие факторы, как потеря массы родительской звездой, приливные эффекты в системе “звезда + планета”, излучение (эффект Ярковского, YORP-эффект), магнитные поля. Воздействие указанных факторов может проявляться как в изменении орбиты субзвездного объекта, так и в изменении его физических параметров (массы и размера, температуры, состава поверхности и атмосферы и др.). Оно может оказаться настолько сильным, что объект окажется выброшенным из системы, а, может, случится так, что на стадии гиганта родительская звезда поглотит его и он перестанет существовать. И в этой связи стоит добавить, что помимо упомянутых уже примеров планет у белых карликов и звезд-гигантов есть и известные примеры свободных планет: WISE J085510.83–071442.5 [8], SDSS J1110+0116 [9], PSO J318.5–22 [10] и др. Отдельно стоит выделить обнаружение свободной планеты земной массы [11]. Число обнаруженных свободных планет растет, и среди них могут оказаться и такие, которые стали свободными после того, как были выброшены из своих родительских планетных систем в результате потери звездой массы за счет сильного звездного ветра.

Финальная судьба планетных систем определяется не только звездной эволюцией, но и начальными параметрами планет. Есть большое количество современных работ, которые посвящены теории формирования планет и моделированию планетных систем (см. обзор в [12]). Наряду с детальным изучением отдельных систем (например, Солнечной) или разработкой деталей различных стадий процесса образования планет и эволюции их орбит важное место занимает построение популяционных моделей, которые на более грубом уровне включают в себя процессы формирования и эволюции объектов в широком диапазоне начальных параметров. Популяционному синтезу экзопланет посвящены, например, работы Кристофа Мордасини, Яна Алиберта и др. [13–16]. В нашей статье мы активно используем результаты этих исследований.

Целью данной работы является моделирование планетных орбит с учетом эволюции звезды после стадии ГП, а также расчет статистики поглощенных, выброшенных из системы и выживших планет к моменту превращения их родительской звезды в белый карлик с учетом истории звездообразования в Галактике.

В разделе 2 представлена модель, которая лежит в основе нашего популяционного синтеза, описаны осуществляемые в нашем моделировании начальные распределения планет по массам и орбитам, а также используемые в работе эволюционные модели звезд. В разделе 3 кратко описан программный код для популяционного синтеза, написанный в пакете MatLab. Раздел 4 посвящен результатам работы, а раздел 5 – их обсуждению. В заключительном разделе кратко суммированы основные результаты данной работы.

2. МОДЕЛЬ

Осуществляемые в работе популяционный синтез и моделирование эволюции экзопланетных систем основаны на современных представлениях о формировании планетных систем и звездной эволюции, а также на простой модели, связывающей эволюцию звезды и изменение орбиты планет. В рамках данной простой модели не ведется учет возможных изменений орбиты в результате межпланетных гравитационных взаимодействий. Что касается двойных и кратных звездных систем, то модель пригодна только для той их части, где расстояние между родительской звездой и планетой значительно превышает расстояние до второй звезды в системе (для двойных, где планета обращается на большом расстоянии от пары близких друг к другу звезд, модель не работает, так как при этом эволюционные треки звезд из-за взаимного влияния во многих случаях будут отличны от используемых в данной работе).

2.1. Модель эволюции орбиты

Задача об эволюции орбиты за счет изотропной потери массы центральным более массивным телом хорошо известна. Изменение большой полуоси орбиты, эксцентриситета и истинной аномалии со временем в общем случае при этом описывается следующими дифференциальными уравнениями (см. [17, 18]):

(1)

$\frac{{da}}{{dt}} = a\frac{{1 + {{e}^{2}} + 2ecos(f)}}{{1 - {{e}^{2}}}}\frac{{{{{\dot {M}}}_{{{\text{tot}}}}}}}{{{{M}_{{{\text{tot}}}}}}},$

(2)

$\frac{{de}}{{dt}} = (e + cos(f))\frac{{{{{\dot {M}}}_{{{\text{tot}}}}}}}{{{{M}_{{{\text{tot}}}}}}},$

(3)

$\frac{{df}}{{dt}} = - \frac{{sin(f)}}{e}\frac{{{{{\dot {M}}}_{{{\text{tot}}}}}}}{{{{M}_{{{\text{tot}}}}}}} + \frac{{n{{{(1 + ecos(f))}}^{2}}}}{{{{{(1 - {{e}^{2}})}}^{{3/2}}}}},$

где $f$ – истинная аномалия, $a$ – большая полуось орбиты, $e$ – эксцентриситет орбиты, ${{\dot {M}}_{{{\text{tot}}}}}$ – темп потери массы системой, который в нашем случае связан лишь со звездой (${{\dot {M}}_{{{\text{tot}}}}} \equiv {{\dot {M}}_{ \star }}$), ${{M}_{{{\text{tot}}}}}$ – суммарная масса системы “звезда + планета” (для наших систем ${{M}_{{{\text{tot}}}}} \approx {{M}_{ \star }}$, где ${{M}_{ \star }}$ – масса звезды), $n$ – среднее движение ($n = 2\pi \sqrt {{{M}_{{{\text{tot}}}}}{\text{/}}{{a}^{3}}} $). Дополняют систему уравнения для наклонения орбиты $i$, долготы восходящего узла $\Omega $, долготы перицентра $\varpi $ и аргумента перицентра $\omega $ [17]:

$\left\{ \begin{gathered} \frac{{di}}{{dt}} = \frac{{d\Omega }}{{dt}} = 0, \hfill \\ \frac{{d\varpi }}{{dt}} = \frac{{d\omega }}{{dt}} = \frac{{sin(f)}}{e}\frac{{{{{\dot {M}}}_{{{\text{tot}}}}}}}{{{{M}_{{{\text{tot}}}}}}}. \hfill \\ \end{gathered} \right.$

Система этих уравнений не имеет полного аналитического решения, однако есть режимы потери массы, при которых аналитическое решение имеет место. Нас интересует один из этих режимов, для определения которого вводится безразмерный параметр потери массы $\psi $, определяемый следующим образом:

(4)

$\psi = \frac{1}{{2\pi }}\mathop {\left( {\frac{a}{{1\;{\text{а}}.{\text{е}}.}}} \right)}\nolimits^{3/2} \mathop {\left( {\frac{{{{M}_{ \star }}}}{{{{M}_{ \odot }}}}} \right)}\nolimits^{ - 3/2} \frac{{{{{\dot {M}}}_{ \star }}}}{{{{M}_{ \odot }}\;{\text{го}}{{{\text{д}}}^{{ - 1}}}}}.$

В случаях, когда $\psi \ll 1$ имеет место режим, который именуют адиабатическим и при котором эволюция орбиты медленная и описывается простой аналитической формулой:

(5)

$a(\Delta t) = {{a}_{{in}}}\mathop {\left( {1 - \frac{{\Delta t{{{\dot {M}}}_{ \star }}}}{{{{M}_{{{\text{tot}}}}}}}} \right)}\nolimits^{ - 1} .$

Здесь $\Delta t$ – длительность эволюционной стадии, $a(\Delta t)$ – значение большой полуоси орбиты в конце эволюционной стадии, ${{a}_{{{\text{in}}}}}$ – значение большой полуоси орбиты в начале эволюционной стадии, ${{M}_{{{\text{tot}}}}}$ – текущая суммарная масса звезды и планеты (масса планет считается постоянной). Изменение массы звезды при этом описывается следующей формулой:

(6)

${{M}_{ \star }}(\Delta t) = {{M}_{{{\text{in}}}}} - \Delta t{{\dot {M}}_{ \star }},$

где ${{M}_{ \star }}(\Delta t)$ – масса звезды в конце эволюционной стадии, ${{M}_{{{\text{in}}}}}$ – масса звезды в начале эволюционной стадии.

Для случаев, когда $\psi $ приближается к единице, точнее $\psi > 0.1$, мы решаем численно систему из четырех дифференциальных уравнений, три из которых приведены выше, а четвертое описывает эволюцию темпа потери массы (см. раздел 3).

2.2. Начальные распределения планет

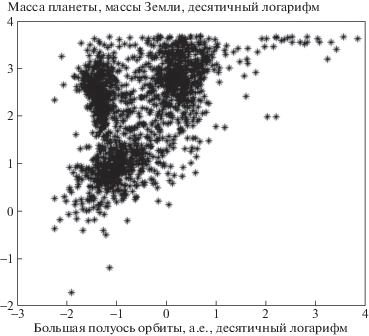
Ключевым моментом в нашем моделировании является выбор начальных распределений параметров планет. В настоящий момент они известны недостаточно хорошо, поэтому можно использовать различные подходы для их задания. Например, в качестве распределения экзопланет по массам и большим полуосям орбит можно было бы взять за основу данные одного из каталогов подтвержденных экзопланет (см. рис. 1). Однако современные наблюдательные данные отягощены различными эффектами селекции. Поэтому мы приняли решение воспользоваться результатами теоретического моделирования планетных систем.

Рис. 1.

Распределение подтвержденных экзопланет на плоскости “большая полуось орбиты планеты – масса планеты” по данным сайта exoplanet.eu. На рисунке приведены данные примерно по 1700 планетам, включая те, у которых в качестве массы известен только нижний предел $Msin(i)$. Не включены планеты у пульсаров и белых карликов.

За последние годы популяционные модели формирования планетных систем получили значительное развитие. В нашем моделировании при создании начального распределения планет на плоскости “большая полуось орбиты планеты–масса планеты” (“a–M_pl”) мы ориентировались на статью Алиберта и др. [15], представляющую результаты моделирования формирования планетных систем из протопланетных дисков. В этой работе авторами рассчитаны распределения по массам и большим полуосям на момент окончания бурной начальной динамической эволюции планетной системы. Акцент делается на том, что расчеты проводились с учетом взаимодействий между планетными эмбрионами и планетами. Начальные орбиты эмбрионов имели значение в интервале от 0.1 до 20 а.е., начальные массы – 0.01 массы Земли, масса центральной звезды принималась равной одной массе Солнца, металличность звезды выбиралась случайным образом из металличностей звезд списка объектов CORALIE. Внутренний радиус диска считался равным 0.05 а.е., масса дисков имела значения в диапазоне от 0.01 до 0.03 ${{M}_{ \odot }}$, поверхностная плотность на расстоянии 5.2 а.е. – от 0 до 10 г/см² с длинным “хвостом” распределения вплоть до 50 г/см².

Аналогично подходу, использованному в работе Попкова и Попова [19], посвященной частоте слияний экзопланет со звездами в результате приливной эволюции и ухода с ГП, мы аппроксимируем представленную в работе [15] диаграмму “a–M_pl” несколькими группами распределений (см. рис. 2).

Рис. 2.

Начальное распределение планет по массам и большим полуосям орбиты (показана популяция из 15 000 планет).

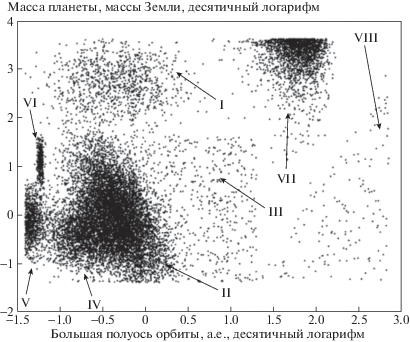
Каждая из групп I, IV–VI аппроксимируется двумерным логнормальным распределением, которое состоит из двух одномерных:

(7)

$p(x) = \frac{1}{{x\sqrt {2\pi {{\sigma }^{2}}} }}exp\left( { - \frac{{{{{(ln(x) - \zeta )}}^{2}}}}{{2{{\sigma }^{2}}}}} \right),$

где $\sigma $ и $\zeta $ – параметры распределения (см. табл. 1).

Таблица 1.

Группы начальных распределений планет на плоскости “a–M_pl” и их параметры

Группа	Распределение	Параметры	Доля планет
I	Двумерное логнормальное	${{\zeta }_{a}} = ln(0.5)$ ${{\zeta }_{M}} = ln(500)$ ${{\sigma }_{a}} = 0.9$ ${{\sigma }_{M}} = 1$	6.72%
II	Двумерное нормальное в логарифме	${{\zeta }_{a}} = lg(0.5)$ ${{\zeta }_{M}} = 0$ ${{\sigma }_{a}} = 0.25$ ${{\sigma }_{M}} = 0.45$ $\rho = - 0.8$	46.78%
III	Равномерное в логарифме	$lg({{a}_{{min}}}) = - 0.7$ $lg({{M}_{{min}}}) = - 1.39$ $lg({{a}_{{max}}}) = 1.3$ $lg({{M}_{{max}}}) = 1.6$	5.19%
IV	Двумерное логнормальное	${{\zeta }_{a}} = ln(0.2)$ ${{\zeta }_{M}} = ln(0.4)$ ${{\sigma }_{a}} = 0.5$ ${{\sigma }_{M}} = 0.8$	17.61%
V	Двумерное логнормальное	${{\zeta }_{a}} = ln(0.045)$ ${{\zeta }_{M}} = ln(0.7)$ ${{\sigma }_{a}} = 0.2$ ${{\sigma }_{M}} = 0.8$	6.04%
VI	Двумерное логнормальное	${{\zeta }_{a}} = ln(0.06)$ ${{\zeta }_{M}} = ln(12)$ ${{\sigma }_{a}} = 0.05$ ${{\sigma }_{M}} = 0.5$	2.72%
VII	Нормальное в логарифме (для масс)	${{\zeta }_{M}}$ = 23 ${{m}_{{Jup}}}$ ${{\sigma }_{M}}$ = 20 ${{m}_{{Jup}}}$	13.95%
	“Максвелловское” (для орбит)	$a$ = 40
VIII	“Треугольное” равномерное в логарифме	$lg({{a}_{{min}}}) = lg(20)$ $lg({{M}_{{min}}}) = lg(0.04)$ $lg({{M}_{{max}}}) = lg(1200)$ $lg({{a}_{{max}}}) = lg(700)$	1%

Примечание. Единицы измерения – а.е. и массы Земли, если не указано другое.

Группа II аппроксимируется двумерным нормальным в логарифме распределением (bivariate Gauss distribution) следующего вида:

(8)

$\begin{gathered} p(x,y) = \frac{1}{{2\pi xy{{\sigma }_{x}}{{\sigma }_{y}}\sqrt {1 - {{\rho }^{2}}} }} \times \\ \times \;exp\left( { - \frac{{{{\phi }^{2}}{\text{/}}\sigma _{x}^{2} + {{\psi }^{2}}{\text{/}}\sigma _{y}^{2} - 2\rho \psi \phi {\text{/}}{{\sigma }_{x}}{{\sigma }_{y}}}}{{2(1 - {{\rho }^{2}})}}} \right), \\ \end{gathered} $

где $\phi = lg(x) - {{\zeta }_{x}}$, $\psi = lg(y) - {{\zeta }_{y}}$, а ${{\sigma }_{x}}$, ${{\sigma }_{y}}$, ${{\zeta }_{x}}$, ${{\zeta }_{y}}$, $\rho $ – параметры распределения (табл. 1). Группа III аппроксимируется двумерным равномерным в логарифмическом масштабе распределением.

Поскольку в статье [19] внимание было сосредоточено на тех планетах, которые могут слиться со своими звездами, т.е. на относительно близких к своим звездам, постольку в указанной работе авторы ограничиваются в своем моделировании перечисленными шестью группами планет, которые описывают большую часть полученного Алибертом и др. распределения на плоскости “a‒M_pl”. Анализ рис. 5 в [15] позволяет утверждать, что на нем есть еще одна немногочисленная группа планет (на нашем рис. 2 это груп-па VIII) – объектов, которые оказались на больших орбитах в результате гравитационного взаимодействия с другими телами в многопланетных системах на ранних стадиях их жизни. Согласно [15] доля таких планет в рассмотренной нами популяции составляет немногим менее 1%.

Данная группа описывается двумерным равномерным в логарифмическом масштабе “треугольным” распределением, в котором “гипотенуза” задана прямой, соединяющей на плоскости “a–M_pl” точки с координатами ($lg(20)$, $lg(0.1)$) и ($lg(700)$, $lg(1200)$), а “катеты” определены в табл. 1.

Также мы добавили группу, которой нет в работе [15]. Это планеты, образовавшиеся в результате фрагментации самогравитирующего протопланетного диска. В описании данной группы мы следовали работе Форгана и др. [20]. Аппроксимируя нормальным распределением в логарифмической шкале распределение масс околозвездных дисков, как это сделано в статье Мордасини [16, рис. 4, табл. 2] (см. также рис. 3), и полагая, что такое распределение характерно для всего диапазона масс звезд в нашей работе, мы посчитали долю планетных систем, в которых будут присутствовать планеты, образовавшиеся в результате самогравитации фрагментов диска. Необходимо отметить, что в этих подсчетах сделано несколько предположений на основе результатов [20]. Следуя этой работе, во-первых, такие планеты могут образовываться лишь в дисках с массами в интервале от 0.125 до 0.4 массы звезды (более легкие диски вряд ли будут самогравитирующими, а более тяжелые очень быстро аккрецируют на звезду). Во-вторых, принималось, что среднее число фрагментов диска, которые могут стать планетами в данной системе, равно четырем. Наконец, в-третьих, в среднем выживает около 40% из этих фрагментов. С учетом написанного доля $\delta $ планет данной группы в популяции была вычислена по следующей формуле:

(9)

$\begin{gathered} \delta = 0.4 \times 4 \times \\ \times \;\frac{{\int\limits_{lg(0.125)}^{lg(0.4)} {exp\left( { - \tfrac{{{{{(x + 1.66)}}^{2}}}}{{2 \times {{{0.6}}^{2}}}}} \right){\text{/}}\sqrt {2\pi \times {{{0.6}}^{2}}} dx} }}{{\int\limits_{lg(0.001)}^{lg(1)} {exp\left( { - \tfrac{{{{{(x + 1.66)}}^{2}}}}{{2 \times {{{0.6}}^{2}}}}} \right){\text{/}}\sqrt {2\pi \times {{{0.6}}^{2}}} dx} }} \approx \\ \approx 0.1395. \\ \end{gathered} $

Рис. 3.

Распределение по массам околозвездных дисков по данным из работы [16]. Параметры распределения: $\sigma = 0.6$, $\mu = - 1.66$. Отмечен интервал масс, в котором в самогравитирующем диске могут образовываться планеты.

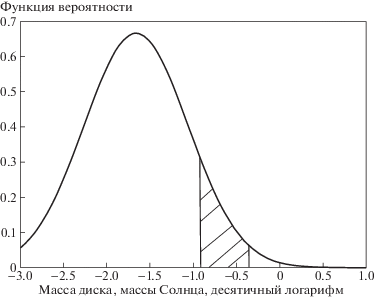
При выборе функций для задания распределений данной группы планет в качестве ориентира служили распределения, приведенные в работе [20, рис. 3, рис. 7]. Распределение больших полуосей орбиты приближено функцией, схожей с распределением Максвелла: $f(x) = \sqrt {\tfrac{2}{\pi }} \tfrac{{{{x}^{2}}}}{{{{\kappa }^{3}}}}exp\left( { - \tfrac{{{{x}^{2}}}}{{2{{\kappa }^{2}}}}} \right)$, где $\kappa $ – параметр распределения, а распределение по массам нормальное в логарифме (см. табл. 1).

Доля каждой из первых шести групп планет в популяции определена по данным работы [19] и скорректирована путем пропорционального вычитания из каждой планет седьмой и восьмой групп. Процентное соотношение разных групп приведено в четвертом столбце табл. 1.

Независимо от того, к какой группе принадлежат планеты, для всей популяции в нашей работе определены нижний и верхний пределы по массе. Наименее массивные планеты – не легче 0.04 массы Земли, наиболее массивные – не массивнее 13 масс Юпитера (около 4120 масс Земли). Нижняя граница выбрана, таким образом, с ориентиром на массу наименее массивной планеты Солнечной системы, а также с учетом того, что на сегодняшний момент достоверно известно всего три экзопланеты с массами меньше этого предела² ². Верхняя же граница связана с нижним пределом на массу бурых карликов.

Для численного расчета орбит планет при больших значениях параметра $\psi $ необходимы значения эксцентриситета и истинной аномалии. Для всей популяции мы принимали начальное значение истинной аномалии $f = 0$, а распределение начального эксцентриситета задавалось равномерным в диапазоне $0.01 < e < 0.1$. На наш взгляд, данные наблюдений и/или моделирования не позволяют с достаточной точностью задать распределение этого параметра. Фиксирование начального эксцентриситета на значениях 0.1 и 0.01 приводили к следующему изменению ключевых результатов: число поглощенных планет менялось на уровне 1%, число выброшенных планет – на уровне $0.04\% $.

2.3. Эволюционные треки

Для построения эволюционных треков был использован пакет библиотек MESA (Modules for Experiments in Stellar Astrophysics, Release 10398) [21]. Были построены эволюционные треки звезд с металличностью $Z = 0.02$ для следующих начальных масс: от 1 до 2.6 ${{M}_{ \odot }}$ с шагом 0.1 ${{M}_{ \odot }}$, затем – для масс 2.8, 3.0 и 3.25 ${{M}_{ \odot }}$, наконец далее с шагом 0.25 ${{M}_{ \odot }}$ до 8 ${{M}_{ \odot }}$ включительно. Также были построены треки для менее массивных звезд, но в итоге они не использовались в моделировании, так как стадия красного гиганта у маломассивных звезд достигается за время, превышающее возраст Галактики (см. подраздел 5.1). При создании каждого из треков в файле входных настроек (inlist-файл) до начала расчета трека указывались начальная масса звезды, ее металличность, библиотеки, определяющие непрозрачность, используемое при расчетах уравнение состояния, темпы ядерных реакций в звезде, а также множество других параметров, которые можно сделать отличными от их значений, прописанных в настройках по умолчанию. В частности, при построении всех треков в файле входных настроек для расчета темпов потери массы на стадии красного гиганта (Red Giant Branch – RGB) мы указывали формулу Реймерса [22]:

(10)

$\frac{{{{{\dot {M}}}_{ \star }}}}{{{{M}_{ \odot }}\;{\text{го}}{{{\text{д}}}^{{ - 1}}}}} = 4 \times {{10}^{{ - 13}}}{{\eta }_{R}}\left( {\frac{L}{{{{L}_{ \odot }}}}} \right)\left( {\frac{R}{{{{R}_{ \odot }}}}} \right)\mathop {\left( {\frac{{{{M}_{ \star }}}}{{{{M}_{ \odot }}}}} \right)}\nolimits^{ - 1} .$

Здесь $L$ – текущая светимость звезды, $R$ – текущий радиус звезды, $M$ – ее текущая масса (все три величины – в солнечных единицах), ${{\eta }_{R}}$ – свободный параметр, значения которого для звезд с начальной массой до 3 ${{M}_{ \odot }}$ задавались в интервале 0.1–0.7 и на RGB, и на AGB, а для более массивных звезд – в том же интервале на RGB и от 0.5 до 7 на AGB (см. подраздел 5.2). Для расчета темпов потери вещества на стадии асимптотической ветви гигантов (Asymptotic Giant Branch – AGB) использовалась формула Блёкера [22]:

(11)

$\begin{gathered} \frac{{{{{\dot {M}}}_{ \star }}}}{{{{M}_{ \odot }}\;{\text{го}}{{{\text{д}}}^{{ - 1}}}}} = 4 \times {{10}^{{ - 13}}}{{\eta }_{R}}\left( {\frac{L}{{{{L}_{ \odot }}}}} \right)\left( {\frac{R}{{{{R}_{ \odot }}}}} \right)\mathop {\left( {\frac{{{{M}_{ \star }}}}{{{{M}_{ \odot }}}}} \right)}\nolimits^{ - 1} \times \\ \, \times 4.83 \times {{10}^{{ - 9}}}\mathop {\left( {\frac{L}{{{{L}_{ \odot }}}}} \right)}\nolimits^{2.7} \mathop {\left( {\frac{{{{M}_{ \star }}}}{{{{M}_{ \odot }}}}} \right)}\nolimits^{ - 2.1} . \\ \end{gathered} $

Все построенные треки, подготовленные для моделирования, доведены до стадии белого карлика. В качестве критерия наступления данной стадии служило падение светимости (за счет остывания) ниже критического значения (см. рис. 4) после окончания потери массы. Модели звезд с начальной массой больше 3 ${{M}_{ \odot }}$ также удалось довести до стадии белого карлика. При этом асимптотическая ветвь гигантов заканчивается в используемых в работе моделях массивных звезд стадией тепловых вспышек (Thermal Pulse Asymptotic Giant Branch – TPAGB), ограничивающейся одним или двумя кратковременными повышениями светимости (и темпа потери массы). В ходе них теряется большая часть гелиево-водородной оболочки звезды (см. рисунки в Приложении), после чего трек “поворачивает” в сторону увеличения эффективной температуры, и звезда переходит на стадию планетарной туманности, на которой тоже происходит потеря массы (несколько десятых ${{M}_{ \odot }}$).

Рис. 4.

Диаграмма Герцшпрунга–Рассела от стадии ГП до стадии белых карликов для некоторых треков, использованных в моделировании. Указаны начальные массы.

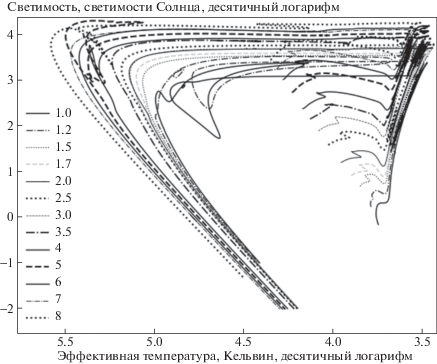
Рис. 5.

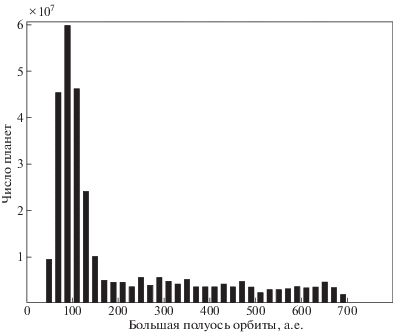
История звездообразования в Галактике, использованная в моделировании. Ширина бина составляет 50 млн. лет. Число звезд в выборке – 500 000. Нормировка произведена таким образом, что масса всех сформировавшихся звезд Галактики в диапазоне от 1 до 8 масс Солнца равна $19.55 \times {{10}^{9}}\;{{M}_{ \odot }}$.

Началом эволюционного трека для звезд с начальной массой менее 3 ${{M}_{ \odot }}$ была стадия до ГП, в более массивных – начало ГП. Результатом расчета звездного эволюционного трека для каждой из указанных выше начальных масс является группа profile-файлов, каждый из которых описывает структуру звезды на соответствующей стадии ее эволюции, и history-файл, содержащий информацию об изменении основных параметров звезды от одной стадии к другой. В число параметров, изменение которых фиксируется в history, входят текущий возраст звезды, ее эффективная температура, ее светимость, масса, радиус, темп потери массы, содержание водорода, гелия в центре звезды и многие другие. History-файлы рассчитанных нами в MESA треков содержат информацию об изменении основных параметров звезды на протяжении от примерно 1200 (для некоторых моделей массивных звезд) до 30 000 эволюционных стадий, большинство из которых соответствует эволюции звезды после ГП, в том числе асимптотической ветви и ветви красных гигантов.

Из параметров, содержащихся в history-файлах, непосредственно для популяционного синтеза нам нужны темп потери массы, радиус звезды и соответствующий возраст звезды, либо длительность текущей стадии эволюции. Основной процедурой популяционного синтеза был расчет орбиты планеты на каждой эволюционной стадии родительской звезды. В этой связи одной из задач было не перегрузить программный код слишком большим объемом вычислений из-за большого числа эволюционных стадий. Другая задача состояла в том, чтобы при исключении “лишних” эволюционных стадий отслеживать, что оставшиеся стадии и соответствующие им темпы потери массы дают такую же (в пределах погрешности) конечную массу звезды, т.е. белого карлика, которая получалась в расчете MESA. Третья задача – не исключить в качестве “лишней” стадию, на которой радиус звезды достигает текущего максимума (поскольку увеличивающаяся в размерах звезда может поглотить близкую планету).

Решая эти задачи и работая с полученными по данным history-файлов зависимостями темпа потери массы от времени и радиуса звезды от времени (в том числе в их графическом представлении), мы сделали усеченные версии треков, содержащие, в зависимости от массы звезды, от 30 до 170 эволюционных стадий. Самыми длинными получились те, где происходит наибольшее количество тепловых вспышек на стадии TPAGB (пример фрагмента такого трека приведен в Приложении). Массы белых карликов, получаемые по усеченным трекам, систематически больше масс по данным исходных треков в пределах 1%. Первая стадия в каждом из треков оказывалась самой длительной. Это стадия ГП. Темп потери массы на ГП рассчитывался как среднее значение от темпа потери в начале и в конце стадии ГП. Началом ГП мы считали этап, когда центральное содержание водорода уменьшилось на одну сотую по сравнению с его начальным содержанием, а окончанием ГП – момент, когда центральное содержание водорода стало меньше одной сотой от начального. Во всех усеченных треках для каждой из стадий прописывались ее длительность, средний темп потери массы на данной стадии и радиус звезды в конце стадии. В некоторых треках массивных звезд сохранены отдельные “стадии”, длительность которых не превышает нескольких лет. Это сделано в тех случаях, когда темп потери массы очень высок (выше, чем ${{10}^{{ - 4}}}\;{{M}_{ \odot }}$/год, см. Приложение).

3. ПОПУЛЯЦИОННЫЙ СИНТЕЗ. ПРОГРАММНЫЙ КОД

Первым шагом в программном коде, написанном в пакете MatLab, в качестве одной из констант назначается общее число пар “звезда + планета”. Это число определяет количество повторений в цикле описанных ниже процедур, а также число планет каждой из групп распределений в плоскости “a–M_pl”. Каждой паре “звезда + планета” в программном коде случайным образом (с использованием встроенного в MatLab генератора псевдослучайных чисел), в соответствии с описанными начальными распределениями, приписывались значения большой полуоси орбиты планеты, массы планеты и массы звезды (начальное распределение звезд по массам задано функцией Солпитера $dN{\text{/}}dM \sim {{M}^{{ - 2.3}}}$ [23, 24]). Генерируемые массы звезд лежат в интервале от 1 до 8 ${{M}_{ \odot }}$.

Также задаются начальное значение эксцентриситета и истинная аномалия орбиты планеты, которая выбирается одинаковой для всех систем. На первом шаге определяется бин в истории звездообразования (“возрастная группа”) для звезды и соответствующий данной группе максимально возможный возраст звезды. Для этого вся история звездообразования в Галактике делится на несколько этапов (см. рис. 5) с разными темпами звездообразования, следуя аппроксимации в работе [25, рис. 1]. При этом предполагается, что на протяжении всей истории звездообразования начальное распределение звезд по массам задается функцией Солпитера. Для каждого этапа рассчитывается отношение суммарной массы сформировавшихся за это время звезд к общей массе звезд Галактики в интервале от 1 до 8 ${{M}_{ \odot }}$, которая равна $19.55 \times {{10}^{9}}\;{{M}_{ \odot }}$, поскольку суммарную начальную массу всех звезд Галактики, сформировавшихся за время ее жизни, считаем равной $50 \times {{10}^{9}}\;{{M}_{ \odot }}$ [25]. Данное отношение определяет диапазон величин случайных чисел, соответствующих звездам, сформировавшимся на данном этапе истории звездообразования. Далее, используя генератор псевдослучайных чисел, мы получаем величину, определяющую “возрастную группу” звезды. Затем, повторно прибегая к генератору псевдослучайных чисел, а также к условным операторам, разыгрываем максимально возможный возраст звезды.

Затем рассчитывается коэффициент ${{N}_{{{\text{planets}}}}}$, определяющий число планет у звезды. Формула для расчета данного коэффициента взята из работы [19]:

(12)

$\begin{gathered} {{N}_{{{\text{planets}}}}} = \\ = \;\left\{ \begin{gathered} {{({{M}_{ \star }}{\text{/}}{{M}_{ \odot }})}^{{1.2}}}{{N}_{{{\text{planet,sun}}}}}, \hfill \\ {\text{если}}\quad {{M}_{ \star }} < 1.5\;{{M}_{ \odot }}; \hfill \\ 10,\quad {\text{если}}\quad {{M}_{ \star }} > 1.5\;{{M}_{ \odot }}. \hfill \\ \end{gathered} \right. \\ \end{gathered} $

Здесь ${{N}_{{{\text{planet,sun}}}}} = 8$ – число планет в Солнечной системе. Данный коэффициент позволяет рассчитать среднее число планет у звезды, которое используется как дополнительный множитель при получении конечных распределений планет (см. ниже ф-лу (13)).

На следующем шаге значение массы звезды в текущей паре сравнивается с теми массами звезд, для которых построены эволюционные треки, и для дальнейшей работы осуществляется выбор наиболее близкой по массе модели и считывается соответствующий файл усеченного трека. То есть, распределение по массам бинировано в соответствии с выбранными значениями начальным масс треков, рассчитанных в MESA. Значение большой полуоси орбиты и значение массы звезды на первой эволюционной стадии трека назначаются равными начальным значениям орбиты и массы звезды.

Далее рассчитывается параметр $\psi $. Если его величина менее 0.1, то значения большой полуоси орбиты и массы звезды на момент окончания данной эволюционной стадии определяются по формулам (5) и (6) соответственно, эксцентриситет и истинная аномалия не меняются. Если $\psi \geqslant 0.1$, то с использованием классического метода Рунге–Кутты четвертого порядка численно решается система из уравнений (1)–(3) и условия ${{\dot {M}}_{ \star }} = {\text{const}}$, где константа определяется считываемым из файла значением темпа потери массы на данной стадии. Шаг сетки выбирается с ориентацией на длительность эволюционной стадии: минимальный шаг (0.1 год) выбирается для очень коротких стадий и для стадий, когда $\psi > 3$. Для стадий длительностью более 100 лет применяется шаг, равный 5 годам, при длительности стадии более 1000 лет – 50 годам, для всех остальных – 1 год.

После решения указанной системы уравнений для следующей эволюционной стадии помимо новых значений массы звезды и большой полуоси орбиты планеты имеются новые значения эксцентриситета и истинной аномалии. Перед переходом к следующей эволюционной стадии текущее значение орбиты сравнивается с текущим радиусом звезды, а текущий возраст, рассчитываемый как сумма всех прошедших эволюционных стадий, с максимально возможным возрастом.

Если значение перицентрического расстояния планеты и текущее значение радиуса звезды становятся равны или радиус оказывается больше орбиты планеты, то индекс поглощенных планет увеличивается на единицу.

Число эволюционных стадий в треке (равное числу строк в файле усеченного трека) определяет число повторений расчета значения текущей массы звезды. Оно также определяет число повторений расчета значения большой полуоси орбиты планеты, если величина $\psi $ не превышает 0.1.

Вычисления останавливаются, если текущий возраст звезды на какой-то стадии достигает или превышает изначально определенный для нее конечный возраст.

Если эксцентриситет на каком-то этапе достигает величины $e \geqslant 0.998$ (в том числе, в середине эволюционной стадии), то индекс “убежавших” из системы планет увеличивается на единицу, изменение элементов орбиты прекращается (до конца эволюции на всех следующих стадиях сохраняются их значения, фиксированные в момент, когда эксцентриситет стал больше 0.998), масса звезды продолжает рассчитываться в соответствии с темпами потери как на текущей, так и на каждой следующей эволюционной стадии по формуле (6). Мы варьировали критическое значение эксцентриситета в диапазоне от 0.99 до 0.999, что не приводило к существенному изменению числа “убежавших” (и поглощенных) планет. При критическом значении $e > 0.999$ мы сталкиваемся с неустойчивостью в работе кода.

Значения элементов орбиты, а также значения массы и радиуса звезды в конце каждой эволюционной стадии фиксируются (т.е. их значения доступны в том числе после окончания выполнения всей программы).

Код предусматривает также откат назад по времени, уменьшение шага до 0.01 года и численное решение системы из уравнений (1)–(3) и уравнения ${{\dot {M}}_{ \star }} = {\text{const}}$ с уменьшенным шагом по времени в случае, если при текущей сетке значение эксцентриситета оказалось меньше нуля.

Для окончательной оценки числа “убежавших” и поглощенных планет и получения конечных распределений выживших планет по орбитам и эксцентриситету в Галактике (для заявленного выше диапазона начальных масс звезд) используется коэффициент ${{N}_{{{\text{planets}}}}}$ из формулы 12 и множитель $k$ (см. ниже ф-лу (14)). Так что искомое число $N$ соответствующих тем или иным характеристикам планет (например, убежавших или поглощенных и т.д.) в Галактике определяется следующим выражением:

(13)

$N = k\frac{{{{N}_{{{\text{calc}}}}}\sum\limits_{n = 1}^{{{N}_{{{\text{tot}}}}}} \,{{N}_{{{\text{planets}},n}}}}}{{{{N}_{{{\text{tot}}}}}}},$

где ${{N}_{{{\text{calc}}}}}$ – число планет с соответствующими характеристиками, получившееся в моделировании, ${{N}_{{{\text{tot}}}}}$ – общее число пар “звезда + планета” в моделировании, равное 500 000, коэффициент $k$:

(14)

$\begin{gathered} k = \frac{{\int\limits_1^8 \,{{M}^{{ - 2.3}}}dM}}{{{{N}_{{{\text{tot}}}}}}} \times \\ \times \;\frac{{{{M}_{{{\text{Gal}}}}}}}{{\int\limits_{0.1}^{0.5} \,{{M}^{{ - 0.3}}}dM + \int\limits_{0.5}^{150} \,{{M}^{{ - 1.3}}}dM}}, \\ \end{gathered} $

где ${{M}_{{{\text{Gal}}}}}$ – масса всех звезд Галактики ($50 \times {{10}^{9}}\;{{M}_{ \odot }}$, см. [25]), ${{N}_{{{\text{tot}}}}} = 500\,000$, как и в формуле (13). Для этих параметров получаем $k \approx 17{\kern 1pt} {\kern 1pt} 851$.

4. РЕЗУЛЬТАТЫ

4.1. Распределение по орбитам. “Убежавшие” планеты

В результате эксперимента из популяции в 500 000 планет около 60.2% оказываются поглощены родительскими звездами на стадии красного гиганта (RGB и AGB), порядка 0.3% покинули свои планетные системы и превратились в “убежавшие”, пополнив популяцию планет, для которых в английском языке используется термин “free-floating planets”. Используя формулы (13) и (14), мы на основе полученной статистики “убежавших” планет оценили их число в Галактике и получили значения в диапазоне около 278–297 млн.

При этом в тех диапазонах масс звезд, которые не охвачены в коде, по нашему предположению звезды практически не производят “убежавшие” планеты либо из-за недостаточной потери массы и звездного ветра в случае малых масс звезд, либо из-за короткого времени жизни околозвездного диска, затрудняющего формирование планет, в случае массивных звезд с мощным потоком излучения [26]. Разумеется, какое-то количество планет может покидать свои системы из-за динамического взаимодействия с другими объектами, но такой канал не рассматривается в данной работе.

Из выживших планет у звезд, прошедших все эволюционные стадии (т.е. ставших белыми карликами), минимальные значения большой полуоси орбиты наблюдаются у планет из I–IV групп распределения “a–M_pl” (наименьшее значение около 1.036 а.е. у планеты из группы II с начальным значением орбиты около 0.538 а.е. и начальным эксцентриситетом $e \approx 0.01$, мало изменившимся за время жизни звезды). Максимальные орбиты – у планет VII и VIII групп, “убежавшие” планеты тоже принадлежали только VII и VIII группам. Большинство убежавших планет имели начальные орбиты, близкие к 100 а.е. (см. рис. 6).

Рис. 6.

Распределение начальных орбит “убежавших” планет. Бин – 20 а.е. Число объектов нормировано на параметры Галактики.

Как видно на рис. 7, из V и VI групп (см. также рис. 2) ни одной планеты у звезд, которые успели доэволюционировать до стадии белого карлика, не выжило: они оказались поглощены расширившимися оболочками родительских звезд на стадии гиганта. Это связано с тем, что звезды к моменту превращения в красный гигант успевают сбросить такую долю массы, что орбиты планет увеличиваются мало и близкие к звезде планеты указанных групп оказываются поглощенными; наименее массивные звезды сбрасывают на RGB большую долю своей массы, чем на AGB, но и радиус их растет значительнее на этой стадии. Стоит отметить также, что из звезд популяции, не успевших проэволюцировать до стадии белого карлика, тоже есть такие, которые поглотили свои планеты.

Рис. 7

Распределение планет по массам и большим полуосям орбиты в конечной стадии эволюции, полученное в моделировании. Вверху – для звезд популяции, проэволюционировавших до стадии белого карлика (БК), внизу – для всех звезд. Знаком “+” обозначены планеты у звезд, не дошедших до стадии БК. Чтобы не загромождать рисунок, показано 100 000 точек, т.е. 20% от рассмотренной в моделировании популяции.

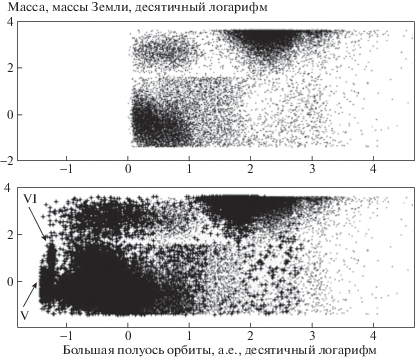
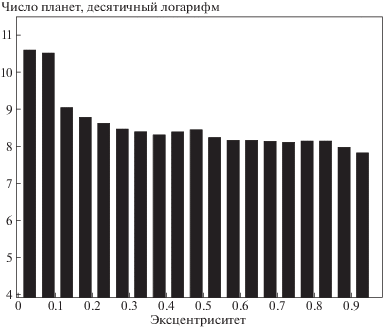
Значительная группа планет перешла на высокоэксцентричные орбиты (рис. 8). Поскольку формальным критерием покидания планетой своей родительской системы считалось достижения значения эксцентриситета $e = 0.998$, то среди выживших планет есть несколько примеров с эксцентриситетом $e > 0.99$ и орбитой более, чем ${{10}^{5}}$ а.е., а у пары планет даже более парсека. Понятно, что такие планеты можно считать связанными лишь по указанному выше формальному признаку, принимая же во внимание, например, галактические приливы, их стоит относить к числу “убежавших”. Тем не менее в приводимой здесь статистике они не включены в число “убежавших”. Это объясняется тем, что количество планет с орбитами более ${{10}^{4}}$ а.е., но формально не покинувших свои родительские системы, получилось относительно небольшим – около $0.03 \pm 0.003\% $ от рассмотренной популяции, а в пересчете на Галактику – около 30 млн. планет.

Рис. 8.

Распределение выживших планет по эксцентриситету орбиты для звезд, проэволюционировавших до стадии белого карлика. Бин – 0.05. Число объектов нормировано на параметры Галактики.

Распределение остальных выживших планет по орбитам у белых карликов представлено на рис. 9. В частности, на нем видно наличие локального максимума в распределении числа планет в районе 100–200 а.е. Данный максимум связан с наличием достаточно многочисленной группы планет, имеющих большие начальные значения большой полуоси орбиты (см. также рис. 2, 7 и табл. 1).

Рис. 9.

Конечное распределение планет по большим полуосям орбиты у звезд, проэволюционировавших до стадии белого карлика. Слева – бин по 20 а.е., справа – по 200 а.е. Число объектов нормировано на параметры Галактики.

4.2. Будущее Земли

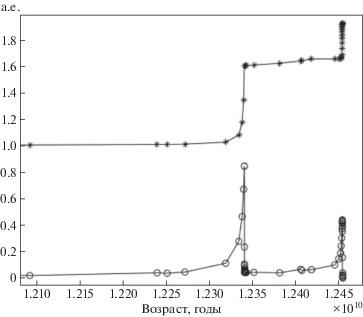
С тем же программным кодом, который описан в работе, проведен эксперимент для пары “Земля + Солнце” (текущий возраст Солнца принят равным 4.58 млрд. лет).

В нашей модели Земля к моменту превращения Солнца в белый карлик массой около 0.52 ${{M}_{ \odot }}$ не будет поглощена звездой на стадии красного гиганта и будет иметь большую полуось орбиты около 1.922 а.е. (рис. 10). Однако существуют исследования, которые показывают, что Земля будет поглощена Солнцем, когда последнее будет находиться на стадии красного гиганта. Так, по расчетам, представленным в работе Шрёдера и Смита [27], Земля будет поглощена из-за действия приливных эффектов, которые не учитываются в нашей работе. Однако даже учет приливов, судя по максимальной величине радиуса Солнца в нашей модели, не привел бы к поглощению Земли. Полученное нами по трекам MESA максимальное значение радиуса звезды с начальной массой в 1 ${{M}_{ \odot }}$ уступает значениям, которые приведены в работе [27]: 185 ${{R}_{ \odot }}$, или 0.844 а.е., против порядка 255 ${{R}_{ \odot }}$, или около 1.188 а.е. в нашей модели. Надо, однако, отметить, что эволюционная модель для Солнца в указанной работе получена для металличности $Z = 0.0188$, более близкой к реальной солнечной металличности, чем значение $Z = 0.02$, использованное во всех треках в нашем моделировании. Также отметим, что помимо радиусов отличается и время, которое проживает Солнце до достижения им пика стадии гиганта (в моделях Шрёдера это происходит примерно на 20 млн. лет раньше, ср. рис. 10 в нашей работе и рисунок из работы [27, рис. 1]).

Рис. 10.

Результат расчета эволюции орбиты Земли (звездочки, верхняя кривая) и эволюция радиуса Солнца (кружки, нижняя кривая) с использованием трека MESA для звезды с начальной массой 1 ${{M}_{ \odot }}$.

4.3. “Убежавшие” планеты и планеты у массивных звезд и звезд-гигантов

В базах данных по экзопланетам на данный момент очень мало наблюдательных примеров планет у звезд массой 3 и более масс Солнца. Среди подтвержденных примеров: o UMa b, Hip 79098 (AB) b, HD 17092 b, HD 13189 b, HD 119445, $\nu $ Oph b и с, BD+20 2457 b и c³ ³^{, 4}⁴. Причем четыре последние скорее представляют собой бурые карлики, чем планеты. Есть исследования и наблюдательные программы, посвященные поиску планет у звезд-гигантов, в ходе которых у более чем ста звезд массивнее 2.7 ${{M}_{ \odot }}$ не обнаружено ни одной планеты [28]. Обсуждая эти результаты, авторы [28] отстаивают позицию, согласно которой условия в протопланетных дисках звезд с начальными массами выше 2.5–3 ${{M}_{ \odot }}$ таковы, что там в принципе не могут сформироваться планеты-гиганты. Вместе с тем есть и другие исследования, посвященные планетам у звезд с массами в интервале от 6 до 8 ${{M}_{ \odot }}$ [26] и показывающие теоретическую возможность выживания планет у таких звезд.

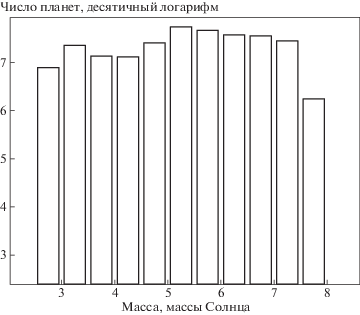
Массивные звезды интересуют нас потому, что именно они теряют в ходе своей эволюции до стадии белого карлика достаточное количество массы и достигают на соответствующих стадиях своей эволюции таких темпов потери массы, которые могут приводить в потере планет (см. рис. 11). В нашем моделировании наименее массивная звезда, планета при которой оказалась “убежавшей” в конце эволюции, имеет начальную массу 2.6 ${{M}_{ \odot }}$ (начальная орбита данной планеты, принадлежащей к VIII группе распределения “a–M_pl”, составляет ${{a}_{{{\text{in}}}}} \approx 663$ а.е.). Для “убежавших” планет из VII группы распределения “a–M_pl” наименее массивными звездами были звезды с массой начиная от 3.5 ${{M}_{ \odot }}$.

Рис. 11.

Распределение начальных масс звезд, планеты которых оказались выброшены из родительских планетных систем. Бин – 0.5 ${{M}_{ \odot }}$. Число объектов нормировано на параметры Галактики.

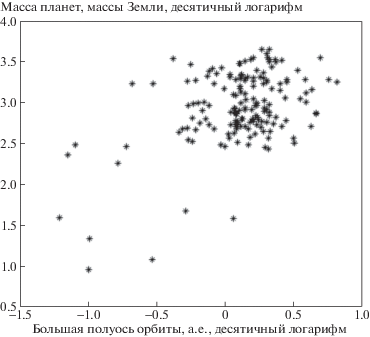
Поскольку звезда теряет массу, то интересны могут быть наблюдательные примеры не только звезд массивнее 3 ${{M}_{ \odot }}$, но и планет у несколько менее массивных звезд, находящихся на эволюционной стадии гигантов и уже потерявших некоторую долю своей массы. Примеров планет у гигантов значительно больше, чем у звезд, массивнее 3 ${{M}_{ \odot }}$, около 150 объектов⁵ ⁵, открытых в большинстве случаев по вариации лучевой скорости. Большинство этих планет обращаются на орбитах с большой полуосью менее 5 а.е. (рис. 12). Примеров планет с большой полусью более 10 а.е. у звезд-гигантов пока нет совсем (правда, есть несколько примеров у субгигантов: TYC 8998–760–1 b⁶ ⁶, $\kappa $ And b⁷ ⁷, 51 Eri b⁸ ⁸).

Рис. 12.

Распределение экзопланет на плоскости “a–M_pl” у звезд-гигантов и субгигантов по данным каталога exoplanet.eu.

Наше моделирование показывает, что в среднем для “убежавших” планет с меньшими начальными орбитами суммарная сброшенная звездой масса должна быть, очевидно, больше, чем для изначально удаленных от своих звезд планет. Самая близкая из “убежавших” планет в моделировании имеет начальную орбиту ${{a}_{{{\text{in}}}}} \approx 52$ а.е. и эксцентриситет, близкий к $e = 0.1$, она была выброшена звездой с начальной массой 7.5 ${{M}_{ \odot }}$. В этом свете можно было бы сделать вывод, что по наблюдательным данным из каталогов экзопланет среди уже открытых планет кандидата в будущие “убежавшие” планеты не найти. Однако среди подтвержденных планет у звезд-гигантов есть несколько примеров с большим значением эксцентриситета: у планеты HD 76920 b значение эксцентриситета составляет $e = 0.856$, а большая полуось орбиты равна $a = 1.15$ а.е., у HD 75458 b $e = 0.713$ при орбите $a = 1.275$ а.е., у HD 238914 b – $e = 0.56$, $a = 5.7$ а.е., у HD 102272 c – $e = 0.68$, $a = 1.57$ а.е., у HD 14067 b – $e = 0.533$, $a = 3.4$ а.е., у Hip 97233 b – $e = 0.61$, $a = 2.55$ а.е., у HD 1690 b – $e = 0.64$, $a = 1.3$ а.е., у Kepler–432 c – $e = 0.64$, $a = 1.188$ а.е., у BD+48 740 b – $e = 0.76$, $a = 1.7$ а.е.⁹ ⁹ Среди указанных систем есть такие, где звезда имеет массу около 1.5 и даже $ \sim {\kern 1pt} 2$ ${{M}_{ \odot }}$ и в зависимости от темпов, с которыми она большую часть этой массы потеряет, эксцентриситет орбиты планеты теоретически в будущем может оказаться больше единицы, т.е. планета окажется более не связанной со своей звездой. Если рассмотреть не только планеты у проэволюционировавших звезд, но также и у звезд ГП, то там также можно найти кандидатов в будущие “убежавшие” планеты.

5. ОБСУЖДЕНИЕ

5.1. Массы белых карликов

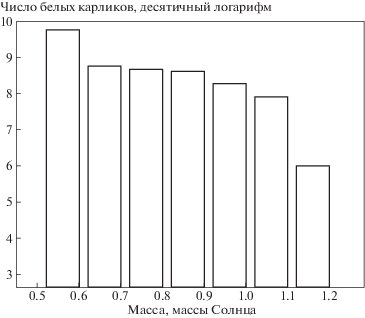
В моделировании 82–83% звезд рассмотренной популяции успевают проэволюционировать и превратиться в белые карлики. Результирующее распределение белых карликов по массе изображено на рис. 13. Самый массивный белый карлик, получившийся в наших расчетах, имеет массу около 1.16 ${{M}_{ \odot }}$, самый легкий – 0.519 ${{M}_{ \odot }}$. Сравнение c современными теоретическими и наблюдательными данными по белым карликам показывает относительно неплохую корреляцию наших результатов с этими данными с учетом того, что наше моделирование не включает эволюцию маломассивных звезд малой металличности (ср. рис. 13 с данными работ [29–31]).

Рис. 13.

Распределение белых карликов по массам для звезд с начальными массами в интервале (1–8) ${{M}_{ \odot }}$ согласно результатам нашего моделирования. Бин равен 0.1 ${{M}_{ \odot }}$. Число объектов нормировано на параметры Галактики.

Как было упомянуто в подразделе 2.3, время жизни звезд с массой менее 1 ${{M}_{ \odot }}$ и металличностью $Z = 0.02$ до превращения их в белый карлик, согласно расчетам в MESA, превышает время жизни Галактики. Так, для звезды с начальной массой 0.9 ${{M}_{ \odot }}$ время жизни на ГП составляет около 13.3 млрд. лет, а чтобы звезда достигла пика ветви гигантов, нужно еще примерно 4.5 млрд. лет. Звезда с массой 0.95 ${{M}_{ \odot }}$ живет на ГП приблизительно 10.6 млрд. лет, и, прежде чем она достигнет после этого своего максимального радиуса на ветви гигантов, проходит еще более 4 млрд. лет.

Мы провели сравнение этих результатов, полученных в MESA, с результатами расчетов эволюционных треков, проведенных разными научными группами. В частности, в статье [32], представляющей эволюционные модели маломассивных звезд, приведены следующие времена жизни на ГП для звезд с металличностью $Z = 0.02$ и начальной массой 0.8 и 0.9 ${{M}_{ \odot }}$: 22.7 и 14 млрд. лет соответственно. Для звезды начальной массой 0.95 ${{M}_{ \odot }}$ проведено сравнение с треками PARSEC падуанской группы [33]: за 13.7–13.8 млрд. лет центральное содержание водорода звезды указанной начальной массы успевает упасть больше, чем в сто раз (т.е. можно говорить об окончании стадии ГП), но звезда еще далека даже до того, чтобы достичь стадии гиганта, не говоря уже о белом карлике. Таким образом, сравнение с современными передовыми расчетами звездной эволюции позволяет считать наш выбор интервала масс звезд-прародителей белых карликов уместным, поскольку в моделировании нас интересовало положение дел, которое может иметь место в современной нам Галактике.

5.2. Эволюционные треки

Поскольку полученные с помощью пакета MESA значения радиусов звезд и их темпов потери массы на разных стадиях эволюции играют в нашем моделировании определяющую роль в итоговой статистике планет, то они заслуживают обсуждения и сравнения их с известными расчетами. Выше мы уже обсуждали различия для звезд с массой 1 ${{M}_{ \odot }}$. Для более массивных звезд сравнение наших результатов с другими усложняется наличием стадии TPAGB, когда радиус за $n$-е количество пульсаций звезды то увеличивается, то возрастает, и далеко не все треки рассчитаны до конца TPAGB. В табл. 2 приведены сравнения для некоторых начальных масс.

Таблица 2.

Сравнение максимальных радиусов звезд по данным разных треков

Начальная масса, ${{M}_{ \odot }}$	PARSEC	SSE	MESA
2	1.147	1.869	1.536
5	2.16	4.98	1.899
6*	3.034	5.97	2.252

Примечание. Радиусы звезд для разных треков приведены в единицах а.е.

* К моменту начала стадии TPAGB у звезды с массой $6\;{{M}_{ \odot }}$ радиус составляет 2.95 а.е.

Среди использованных в моделировании треков, построенных в MESA, максимальный радиус достигается у звезды начальной массы 6 ${{M}_{ \odot }}$. Он составляет $ \approx $2.3 а.е. Судя по проведенному нами сравнению, максимальные радиусы полученных в MESA моделей меньше, чем в моделях SSE, а многие из доступных треков PARSEC не доведены до конца стадии TPAGB.

Что касается темпов потери массы, то в MESA для треков наиболее массивных звезд (от 3.5 ${{M}_{ \odot }}$) мы получили на отдельных очень кратковременных стадиях эволюции очень большие значения, которые не соответствуют существующим наблюдениям. Самое большое значение (${{10}^{{ - 2.2}}}\,{{M}_{ \odot }}$/год) получено для моделей с начальными массами в 6.0 и $7.5\;{{M}_{ \odot }}$, в которых звезда теряет массу с такой интенсивностью в течение примерно пятидесяти лет. Интересно, что при неизменных прочих настройках в inlist-файле трека использование меньших значений параметра ${{\eta }_{R}}$ в формуле (11) давало на коротком эволюционном отрезке наибольшие по модулю значения темпов потери массы. Большие же значения данного параметра давали в свою очередь меньший абсолютный максимум значений темпов потери, но зато на более длительном отрезке времени.

Расчеты звездной эволюции с темпами потери массы, близкими к полученным нами ((4–7) × $ \times \;{{10}^{{ - 4}}}\,{{M}_{ \odot }}$/год), в конце стадии AGB и при сбросе планетарной туманности можно найти в работах [34, 35]. До $ \sim {\kern 1pt} {{10}^{{ - 3}}}{\kern 1pt} {{M}_{ \odot }}$ в год доходят оценки звездного “суперветра” для некоторых из наблюдаемых OH/IR звезд [36–39] и др. Именно в контексте обсуждения больших темпов потери массы в звездах типа Миры Кита и звездах OH/IR в работе Блёкера была предложена приведенная выше формула (11), используемая в MESA. Реальные темпы потери в случае ряда используемых в работе моделей на коротких временны́х отрезках могут быть значительно (на два порядка) меньше. Вместе с тем звезды соответствующих начальных масс, достигая стадии белого карлика, теряют ту же долю массы, что и при больших темпах потери. В случае массивных звезд важным для судьбы обращающихся вокруг них планет является то, что эти звезды теряют за время эволюции после начала ГП много больше половины своей массы. Благодаря этому и становится возможным то, что планеты оказываются более не связанными с родительской звездой.

5.3. Развитие модели

На пути к усовершенствованию модели можно учесть неоднородность химического состава звезд популяции. Как уже было указано, все эволюционные треки звезд в MESA были рассчитаны для начальной металличности $Z = 0.02$. Ориентируясь же на современные модели химической эволюции Млечного пути, следует отразить неоднородность металличности звездного населения тонкого и толстого диска и, возможно, балджа Галактики [41, 40 ]. Для этого необходимо дополнить сетку треков, рассчитав эволюцию звезд с металличностью $Z \approx 0.005$, соответствующей пику распределения для звезд толстого диска (см. [40, рис. 3]) и, возможно, металличностью $Z \approx 0.04$ для звезд балджа (см. [41, рис. 5]).

Важным фактором, определяющим полученную в работе статистику по планетам, являются принимаемые предположения об их начальном распределении на плоскости “a–M_pl”. Данное распределение может сильно отличаться от используемого здесь. Также важно, что для разных масс звезд используется одно и то же распределение. Это является существенным упрощением, которое делается из-за отсутствия данных популяционных расчетов, для разных масс звезд. По всей видимости, соответствующие данные появятся в ближайшие 1–2 года (об этом говорят первые работы большого цикла, которые начала публиковать бернская группа [42–44].

Также очень существенным параметром для полученной в работе статистики является используемый темп потери массы звездой. Необходимо отметить, что решающим фактором, который побудил нас работать с данной сеткой рассчитанных в MESA треков, был удачный расчет эволюции звезд вплоть до стадии белого карлика, в результате чего финальные массы звездных остатков были получены непосредственно. Таким образом, нам не пришлось прибегать к сторонним источникам или к аппроксимационным формулам, связывающим начальную и конечную массы звезд, чтобы для каждого трека определить массу звезды в конце эволюции. Если удастся получить эволюционные треки, доведенные до стадии белого карлика, с более убедительной эволюцией темпов потери массы, радиуса звезды и других физических характеристик звезд, чем в MESA, то они будут привлечены для совершенствования модели.

В текущем программном коде мы не учитывали влияния приливов между родительской звездой и планетой на тесных орбитах. Можно попытаться оценить, как изменится финальная статистика поглощенных и выживших планет, основываясь на полученных нами распределениях и на данных о приливном поглощении планет звездами-гигантами. Однако пока расчеты приливного взаимодействия все еще имеют ряд неопределенностей.

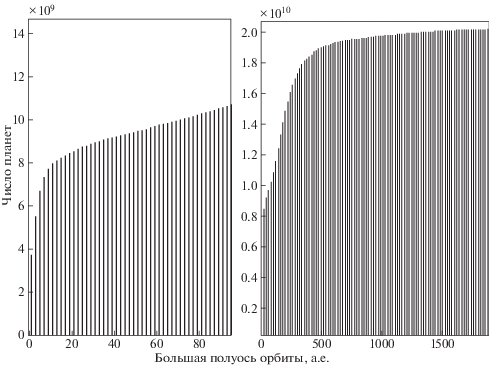
Приливные эффекты могут повлиять на результаты расчетов для планет, близких к белым карликам. В нашем моделировании получилось, что в конце эволюции (на стадии белого карлика) на близких к своим звездам орбитах находится достаточно большое число выживших планет (рис. 14): в пределах 2 а.е. – около 3.7 млрд., что составляет менее одной пятой всех выживших планет (около 18%), а в пределах 4 а.е. – около 30%. Однако если посмотреть, каково распределение по массам этих планет, то видно, что из выживших близких к своим звездам планет лишь небольшая доля (планеты из группы I) имеют юпитерианские массы, среди других же близких к родительским звездам выживших планет средние массы в группе III составляют около 1–5 масс Земли (массивнее 0.15 массы Юпитера не встречается), в группе II – менее одной массы Земли (самые массивные также около 0.15 массы Юпитера). Такие результаты дают основание полагать, что учет приливных эффектов увеличит долю поглощенных планет не более чем на несколько процентов по сравнению с полученными нами результатами, поскольку роль приливов важнее для массивных планет.

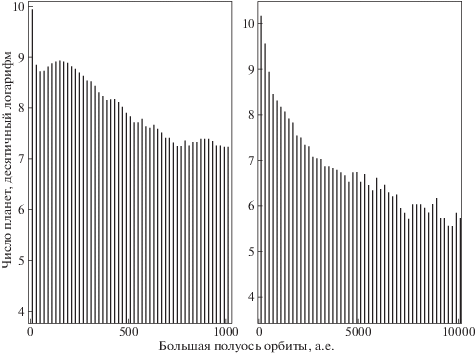
Рис. 14.

Интегральное распределение выживших планет по орбитам у белых карликов. Слева: бин – 2 а.е., справа: бин – 20 а.е. Число объектов нормировано на параметры Галактики.

Наконец, есть ряд плохо известных параметров, связанных с общей нормировкой числа планет. Например, мы использовали конкретный вид зависимостей, представленных в уравнении (12). Вероятнее всего в будущем, например, после увеличения статистики числа известных планет по данным спутников Gaia и PLATO, можно будет с большей точностью задать количество планет в разных типах систем. Пока же мы использовали упрощенную форму зависимости числа планет от массы, что приводит к некоторой систематической неопределенности в полном числе поглощенных, выживших и выброшенных планет.

6. ЗАКЛЮЧЕНИЕ

В работе методом популяционного синтеза проведено изучение свойств планет на поздних стадиях эволюции звезд. С помощью пакета M-ESA эволюция звезд прослежена от стадии Главной Последовательности до формирования белого карлика. Проведен расчет статистики поглощенных, выброшенных из системы и выживших планет к моменту превращения их родительских звезд в белый карлик. Установлено, что при принимаемых в работе начальных распределениях планет на плоскости “a–M_pl” большинство ($ \sim {\kern 1pt} 60\% $) планет, родившихся у звезд в интервале масс от 1 до 8 ${{M}_{ \odot }}$, поглощается их родительскими звездами на стадии гиганта. Небольшая доля планет ($ \sim {\kern 1pt} 0.3\% $) оказывается выброшена из своих систем из-за воздействия улетающего от звезды потока вещества. Оценено число “убежавших” планет с массами в интервале от 0.04 массы Земли до 13 масс Юпитера в Галактике. Оно составило около 300 млн. объектов.

Список литературы

A. Wolszczan and D. A. Frail, Nature 355, 145 (1992).
M. Mayor and D. Queloz, Nature 378, 355 (1995).
K. L. Luhman, A. J. Burgasser, and J. J. Bochanski, A-strophys. J. Letters 730, id. L9 (2011).
A. Vanderburg, S. A. Rappaport, S. Xu, I. Crossfield, et al., Nature 585, 363 (2020).
D. Koester, B. T. Gänsicke, and J. Farihi, Astron. and Astrophys. 566, id. A34 (2014).
C. J. Manser, B. T. Gänsicke, N. P. Gentile Fusillo, R. Ashley, E. Breedt, M. Hollands, P. Izquierdo, and I. Pelisoli, Monthly Not. Roy. Astron. Soc. 439, 2127 (2020).
D. Veras, Royal Society Open Science 3, id. 150571 (2016).
M. R. Zapatero Osorio, N. Lodieu, V. J. S. Béjar, E. L. Mar-tin, et al., Astron. and Astrophys. 592, id. A80 (2016).
J. Gagné, A. J. Burgasser, J. K. Faherty, D. Lafreniere, R. Christine P., Astrophys. J. Letters 808, id. L20 (2015).
M. C. Liu, E. A. Magnier, N. R. Deacon, K. N. Allers, et al., Astrophys. J. Letters 777, id. L20 (2013).
P. Mroz, R. Poleski, A. Gould, A. Udalski, et al., Astrophys. J. Letters 903, id. L11 (2020).
S. N. Raymond and A. Morbidelli, arXiv:2002.05756 [astro-ph.EP] (2020).
C. Mordasini, Planetary population synthesis. Handbook of exoplanets, edited by H. J. Deeg, and J. A. Belmonte (Springer International Publishing AG, 2018), p. 143.
M. Schlecker, C. Mordasini, A. Emsenhuber, H. Klahr, T. Henning, R. Burn, Y. Alibert, and W. Benz, arXiv:2007.05563 [astro-ph.EP] (2020).
Y. Alibert, F. Carron, A. Fortier, S. Pfyffer, W. Benz, C. Mordasini, and D. Swoboda, Astron. and Astrophys. 558, id. A109 (2013).
C. Mordasini, Y. Alibert, and W. Benz, Astron. and Astrophys. 501, 1139 (2009).
D. Veras, M. C. Wyatt, A. J. Mustill, A. Bonsor, and J. J. Eldridge, Monthly Not. Roy. Astron. Soc. 417, 2104 (2011).
J. D. Hadjidemetriou, Icarus 2, 440 (1963).
A. V. Popkov and S. B. Popov, Monthly Not. Roy. Astron. Soc. 490, 2390 (2019).
D. H. Forgan, C. Hall, F. Meru, and W. K. M. Rice, Monthly Not. Roy. Astron. Soc. 474, 5036 (2018).
B. Paxton, L. Bildsten, A. Dotter, F. Herwig, P. Lesaffre, and F. Timmes, Astron. and Astrophys. Suppl. Ser. 192, id. 3 (2011).
T. Blocker, Astron. and Astrophys. 297, 727 (1995).
E. E. Salpeter, Astrophys. J. 121, 161 (1955).
P. Kroupa and T. Jerabkova, Nature Astron. 3, 482 (2019).
M. Haywood, M. D. Lehnert, P. Di Matteo, O. Snaith, M. Schultheis, D. Katz, and A. Gomez, Astron. and Astrophys. 589, id. A66 (2016).
D. Veras, P.-E. Tremblay, J. J. Hermes, C. H. McDonald, G. M. Kennedy, F. Meru, and B. T. Gänsicke, Monthly Not. Roy. Astron. Soc. 493, 765 (2020).
K.-P. Schröder and R. Connon Smith, Monthly Not. Roy. Astron. Soc. 386, 155 (2008).
S. Reffert, C. Bergmann, A. Quirrenbach, T. Trifonov, and A. Künstler, Monthly Not. Roy. Astron. Soc. 574, id. A116 (2015).
S. J. Kleinman, S. O. Kepler, D. Koester, I. Pelisoli, et al., Astrophys. J. Suppl. 204, id. 5 (2013).
S. O. Kepler, D. Koester, A. D. Romero, G. Ourique, and I. Pelisoli, in: 20th European White Dwarf Workshop, Proc. of a Conference held at University of Warwick, Coventry, West Midlands, United Kingdom, 25–29 July 2016, edited by P.-E. Tremblay, B. Gänsicke, and T. Marsh (San Francisco: Astronomical Society of the Pacific, 2017), ASP Conf. Ser. 509, p. 421.
P. -E. Tremblay, J. Cummings, J. S. Kalirai, B. T. Gänsicke, N. Gentile-Fusillo, and R. Raddi, Monthly Not. Roy. Astron. Soc. 461, 2100 (2016).
C. Charbonnel, W. Dáppen, D. Schaerer, P. A. Bernasconi, A. Maeder, G. Meynet, and N. Mowlavi, Astron. and Astrophys. Suppl. Ser. 135, 405 (1999).
A. Bressan, P. Marigo, L. Girardi, B. Salasnich, C. Dal Cero, S. Rubele, and A. Nanni, Monthly Not. Roy. Astron. Soc. 427, 127 (2012).
D. Schönberner, Astrophys. J. 272, 708 (1983).
R. Härm and M. Schwarzschild, Astrophys. J. 200, 324 (1975).
K. Justtanont, D. Teyssier, M. J. Barlow, M. Matsuura, B. Swinyard, L. B. F. M. Waters, and J. Yates, Astron. and Astrophys. 556, id. A101 (2013).
T. De Jong, Astrophys. J. 274, 252 (1983).
P. Goldreich and N. Scoville, Astrophys. J. 205, 144 (1976).
S. Höfner and H. Olofsson, Astron. and Astrophys. Rev. 26, id. 1 (2018).
A. Micali, F. Matteucci, and D. Romano, Monthly Not. Roy. Astron. Soc. 43, 1648 (2013).
F. Matteucci, E. Spitoni, D. Romano, and A. Rojas Arriagada, in Frontier Research in Astrophysics II, held 23–28 May 2016 in Mondello (Palermo), Italy (-FRAPWS2016). Online at https://pos.sissa.it/cgi-bin/reader/conf.cgi?confid 9, id. 27 (2016).
A. Emsenhuber, C. Mordasini, R. Burn, Y. Alibert, W. Benz, and E. Asphaug, arXiv:2007.05561 [astro-ph.EP] (2020).
M. Schlecker, C. Mordasini, A. Emsenhuber, H. Klahr, Th. Henning, R. Burn, Y. Alibert, and W. Benz, arXiv:2007.05563 [astro-ph.EP] (2020).
A. Emsenhuber, C. Mordasini, R. Burn, Y. Alibert, W. Benz, and E. Asphaug, arXiv:2007.05562 [astro-ph.EP] (2020).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал