Астрономический журнал, 2021, T. 98, № 7, стр. 571-580

Исследование вековой эволюции циркумбинарных систем на моделях R-тороида и колец Гаусса

Б. П. Кондратьев^{1, 2, 3, *}, В. С. Корноухов^1, 2

¹ Московский государственный университет им. М.В. Ломоносова, Физический факультет
Mосква, Россия

² Московский государственный университет им. М.В. Ломоносова, Государственный астрономический институт им. П.К. Штернберга
Москва, Россия

³ Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия

^* E-mail: work@boris-kondratyev.ru

Поступила в редакцию 20.02.2021
После доработки 12.03.2021
Принята к публикации 31.03.2021

DOI: 10.31857/S0004629921080077

Полный текст (PDF)

Аннотация

Разработаны два метода изучения вековой (апсидальной и нодальной) прецессии орбит в циркумбинарных системах, состоящих из двойной звезды и экзопланеты. Первый метод основан на модели из трех R-тороидов и предназначен для исследования прецессии пробных орбит. Для экзосистем Kepler-413 и Kepler-453 найдены взаимная ориентация угловых моментов звездной пары ${{L}_{{12}}}$ и планеты ${{L}_{p}}$ относительно плоскости Лапласа, вычислены отношение $\gamma = \frac{{{{L}_{{12}}}}}{{{{L}_{p}}}}$ и зональные гармоники потенциала R-тороидов. Получены и решены уравнения для частот обоих типов прецессии, установлено доминирующее влияние тороидов звездной пары. Второй метод опирается на модель взаимодействующих колец Гаусса и предназначен для исследования вековой эволюции орбит звезд и планеты самой циркумбинарной системы. Такой подход позволил точно рассчитать периоды нодальной прецессии для звезд и планеты; например, в системе Kepler-413 эти периоды равны, соответственно, $T_{1}^{0} = 11.63 \pm 0.28$ лет, $T_{2}^{0} = 11.39 \pm 0.28$ лет, $\;T_{p}^{0} = 11.49 \pm 0.28$ лет. Выявлен тонкий эффект влияния планеты на нарушение резонанса 1:1 для периодов нодальной прецессии звезд.

Ключевые слова: циркумбинарные системы, вековые возмущения, эллиптические кольца Гаусса, R‑тороид, прецессия и эволюция оскулирующих орбит (для английской версии circumbinary systems, secular perturbations, elliptical Gauss rings, R-toroid, precession and evolution of osculating orbits)

1. ВВЕДЕНИЕ

В работе [1] была разработана модель R-тороида, предназначенная для исследования долгопериодических и вековых возмущений в небесной механике. Эта модель представляет 3D обобщение прецессирующего кольца Гаусса, и метод ее построения сводится к цепочке преобразований: 1D кольцо Гаусса – 2D R-кольцо – 3D R-тороид. В [1] были изучены форма, структура и гравитационный потенциал R-тороида, найдена взаимная энергия ${{W}_{{{\text{mut}}}}}$ R-тороида и внешнего кольца Гаусса; с помощью ${{W}_{{{\text{mut}}}}}$ получена система из шести дифференциальных уравнений, описывающих вековую эволюцию оскулирующих орбит в гравитационном поле R-тороида.

Было установлено, что в Солнечной системе модель R-тороида можно применять для оценки гравитационного влияния планет-гигантов на вековую эволюцию тел в рассеянном диске и в облаке Оорта. Перспективным является применение новой модели для изучения динамики экзопланет, о которых к настоящему времени накопилась огромная наблюдательная информация. В частности, с помощью модели R-тороида в [1] рассчитан профиль частот прецессии пробной орбиты в поле прецессирующей центральной звезды и планеты PTFO 8-8695b (об этой системе см. [2, 3]).

В обширной экзопланетной тематике наиболее актуальным является применение модели R-тороида к изучению эволюции орбит горячих юпитеров с коротким временем нодальной прецессии и циркумбинарных систем. Циркумбинарные системы состоят из тесной пары звезд и двигающейся вокруг них экзопланеты. Изучению движения таких тройных систем (планет с кратными орбитами) посвящено немало работ, см., например, [4–6]. Их важно изучать потому, что встречающиеся здесь орбитальные конфигурации и трехчастичные гравитационные взаимодействия позволяют проводить прямые и точные измерения масс и радиусов тел.

Данная работа посвящена решению двух задач. В первой исследуется апсидальная и нодальная прецессия пробных орбит в гравитационном поле трех R-тороидов. Во второй задаче методом взаимодействующих колец Гаусса изучается вековая эволюция орбит тел (двух звезд и экзопланеты) самой циркумбинарной системы. Здесь выявлен тонкий эффект нарушения синхронности в вековом движении центральной пары звезд под влиянием планеты.

План статьи следующий. В разделах 2, 3 дана постановка задачи, вводится плоскость Лапласа и находятся углы ориентации и угловые моменты в циркумбинарных системах Kepler-413 и Kepler-453. В подразделах 4.1–4.3 изучается прецессия пробных орбит в суммарном гравитационном поле трех R-тороидов. Применение метода к системе Kepler-413 излагается в подразделе 4.4, а в 4.5 дана сводка результатов для двух систем экзопланет. В разделе 5 через взаимную энергию колец Гаусса изучается эволюция орбит тел самой циркумбинарной системы. Получены уравнения для частоты прецессии линии узлов кольца Гаусса и изучается влияние планеты на нарушение резонанса в вековом движении узлов звездных орбит. Результаты работы обсуждаются в разделе 6.

2. ПОСТАНОВКА ЗАДАЧИ. ПЛОСКОСТЬ ЛАПЛАСА И УГЛЫ ОРИЕНТАЦИИ

Рассмотрим циркумбинарную систему, в которой одна экзопланета движется по внешней (отдаленной) орбите вокруг тесной пары звезд. Для описания движения тел в такой системе следует знать массы и орбитальные параметры двух звезд $({{M}_{1}},{{M}_{2}},{{a}_{1}},{{a}_{2}},{{e}_{{12}}},{{i}_{{12}}})$ и планеты $(m,{{a}_{p}},{{e}_{p}},{{i}_{p}})$. Здесь углы наклонов орбит звезд ${{i}_{{12}}}$ и планеты ${{i}_{p}}$ будем отсчитывать от общей для системы плоскости Лапласа (рис. 1).

Рис. 1.

Схема векторов угловых орбитальных моментов в циркумбинарной системе. Штрихами показана плоскость Лапласа.

Угловой момент орбитального эллиптического движения тела (на единицу массы) в заданной тройной системе запишем в виде

(1)

$L = \sqrt {\mu a(1 - {{e}^{2}})} ,$

где a и e – большая полуось и эксцентриситет орбиты, $\mu = G\bar {M}$ – аналог гравитационного параметра тела. Если начало координат находится в центре масс двойной звезды (принимается условие $m \ll {{M}_{1}} + {{M}_{2}}$), то отмеченные верхней чертой величины $\bar {M}$равны:

(2)

$\begin{gathered} {{{\bar {M}}}_{1}} = \frac{{M_{2}^{3}}}{{{{{({{M}_{1}} + {{M}_{2}})}}^{2}}}}; \\ {{{\bar {M}}}_{2}} = \frac{{M_{1}^{3}}}{{{{{({{M}_{1}} + {{M}_{2}})}}^{2}}}}. \\ \end{gathered} $

Через величины $\bar {M}$из (2) орбитальный угловой момент звездной пары равен

(3)

${{L}_{{12}}} = {{M}_{1}}\sqrt {G{{{\bar {M}}}_{1}}{{a}_{1}}(1 - e_{{12}}^{2})} + {{M}_{2}}\sqrt {G{{{\bar {M}}}_{2}}{{a}_{2}}(1 - e_{{12}}^{2})} ,$

где полуоси орбит каждой звезды (с фокусом в общем центре масс) связаны очевидными соотношениями

(4)

$\begin{gathered} {{a}_{1}} + {{a}_{2}} = {{a}_{{12}}}, \\ {{a}_{1}}{{M}_{1}} = {{a}_{2}}{{M}_{2}}. \\ \end{gathered} $

Тогда угловой орбитальный момент планеты массой $m$ будет равен

(5)

${{L}_{p}} = m\sqrt {G({{M}_{1}} + {{M}_{2}}){{a}_{p}}(1 - e_{p}^{2})} .$

Рассмотрим в данной системе плоскость Лапласа. По определению, эта плоскость должна быть нормальна вектору полного орбитального углового момента системы ${{{\mathbf{L}}}_{{{\text{Total}}}}} = {{{\mathbf{L}}}_{{12}}} + {{{\mathbf{L}}}_{p}}$. В заданных декартовых координатах (рис. 1) проекции векторов угловых моментов на оси $Oxy$ будут равны (см. также [7]):

(6)

$\begin{gathered} L_{{12}}^{{(x)}} = {{L}_{{12}}}\cos \left( {\frac{\pi }{2} - {{i}_{{12}}}} \right) = {{L}_{{12}}}\sin {{i}_{{12}}}, \\ L_{{12}}^{{(y)}} = {{L}_{{12}}}\sin \left( {\frac{\pi }{2} - {{i}_{{12}}}} \right) = {{L}_{{12}}}\cos {{i}_{{12}}}; \\ \end{gathered} $

(7)

$\begin{gathered} L_{p}^{{(x)}} = {{L}_{p}}\cos \left( {\frac{\pi }{2} + {{i}_{p}}} \right) = - {{L}_{p}}\sin {{i}_{p}}, \\ L_{p}^{{(y)}} = {{L}_{p}}\sin \left( {\frac{\pi }{2} + {{i}_{p}}} \right) = {{L}_{p}}\cos {{i}_{p}}, \\ \end{gathered} $

где ${{i}_{p}}$ и ${{i}_{{12}}}$ – вспомогательные углы наклона плоскостей орбит планеты и звезд к плоскости Лапласа. Указанное выше условие перпендикулярности плоскости Лапласа вектору ${{L}_{{{\text{Total}}}}}$ выполняется, если

(8)

${{L}_{p}}\sin {{i}_{p}} = {{L}_{{12}}}\sin {{i}_{{12}}}.$

Таким образом, для вспомогательных углов ${{i}_{p}}$ и ${{i}_{{12}}}$ получим систему двух уравнений

(9)

$\begin{gathered} \frac{{\sin {{i}_{p}}}}{{\sin {{i}_{{12}}}}} = \frac{{{{L}_{{12}}}}}{{{{L}_{p}}}} = \gamma , \\ {{i}_{p}} + {{i}_{{12}}} = \Delta i. \\ \end{gathered} $

Две формулы (9) можно объединить в одну и выразить наклон плоскости орбит двойной звезды ${{i}_{{12}}}$ к плоскости Лапласа через $\Delta i$

(10)

${{i}_{{12}}} = \arctan \frac{{\sin \Delta i}}{{\gamma + \cos \Delta i}}.$

В итоге, согласно формулам (3) и (5), отношение угловых орбитальных моментов двойной звезды и планеты в циркумбинарной системе будет равно

(11)

$\gamma = \frac{{{{L}_{{12}}}}}{{{{L}_{p}}}} = \sqrt {\frac{{1 - e_{{12}}^{2}}}{{1 - e_{p}^{2}}}} \left[ {\frac{{{{M}_{1}}\sqrt {{{{\bar {M}}}_{1}}{{a}_{1}}} + {{M}_{2}}\sqrt {{{{\bar {M}}}_{2}}{{a}_{2}}} }}{{m\sqrt {({{M}_{1}} + {{M}_{2}}){{a}_{p}}} }}} \right].$

3. ПРИМЕРЫ: СИСТЕМЫ KEPLER-413 И KEPLER-453

Согласно [8], для системы Kepler-413 известно следующее: массы двух звезд и планеты равны ${{M}_{1}}\, = \,0.820 \pm 0.015\,{{M}_{ \odot }}$, ${{M}_{2}} = 0.542 \pm 0.008\,{{M}_{ \odot }}$, m = $ = (67 \pm 21){{M}_{{{\text{Earth}}}}}$ (как видим, масса планеты известна весьма приближенно); полуоси орбит ${{a}_{{12}}} = 0.10148 \pm 0.00057.$ а.е., ${{a}_{p}} = 0.355 \pm 0.002$ а.е.; эксцентриситеты ${{e}_{{12}}} = 0.0365 \pm 0.0023$ (орбиты звезд почти круговые), ${{e}_{p}} = 0.1181 \pm 0.0018$; угол между плоскостью орбиты планеты и плоскостью орбит звезд $\Delta i = 4_{.}^{{^{ \circ }}}073 \pm 0_{.}^{{^{ \circ }}}113$.

По формуле (11), с учетом данных наблюдений для Kepler-413 находим отношение суммарного орбитального углового момента пары звезд к орбитальному угловому моменту планеты

(12)

$\gamma = \frac{{{{L}_{{12}}}}}{{{{L}_{p}}}} \approx 873.$

Поэтому для Kepler-413 по формуле (10) находим показанные на рис. 1 углы наклонов

(13)

$\begin{gathered} {{i}_{{12}}} = 0_{.}^{{^{ \circ }}}0047 \pm 0.0015, \\ {{i}_{p}} = 4_{.}^{{^{ \circ }}}07 \pm 0.11. \\ \end{gathered} $

Довольно большое значение $\gamma = {{{{L}_{{12}}}} \mathord{\left/ {\vphantom {{{{L}_{{12}}}} {{{L}_{p}}}}} \right. \kern-0em} {{{L}_{p}}}}$ из (12) объясняется тем, что в числителе стоит величина орбитального (а не спинового) углового момента звезд. Доминирующий характер углового момента звездной пары в системе Kepler-413 виден и в малом значении угла ${{i}_{{12}}} \approx 0_{.}^{{^{ \circ }}}005$ из (13).

Данные о второй циркумбинарной системе Kepler-453 были взяты из работы Welsh et al. [9] и приводятся в табл. 1. Здесь мы сталкиваемся с одной особенностью: массы звезд известны с хорошей точностью ${{M}_{1}} = 0.944 \pm 0.010\,{{M}_{ \odot }}$, ${{M}_{2}} = 0.1951 \pm $ $ \pm \;0.0020\,{{M}_{ \odot }}$, однако масса планеты Kepler-453b известна очень плохо. Полуоси орбит звезд и планеты равны ${{a}_{{12}}} = 0.18539 \pm 0.00066$ а.е., ${{a}_{p}} = 0.7903 \pm $ $ \pm \;0.0028$ а.е., причем эти орбиты почти круговые ${{e}_{{12}}} = 0.0524 \pm 0.00{\text{37,}}$ ${{e}_{p}} = 0.0359 \pm 0.0088.$ Угол взаимного наклона плоскости орбиты планеты и орбит звезд составляет $\Delta i = 2_{.}^{{^{ \circ }}}258 \pm 0_{.}^{{^{ \circ }}}039$. Минимальное значение полуоси круговой орбиты в Kepler-453 ${{a}_{{{\text{cr}}}}} \approx 24$ а.е.

Таблица 1.

Параметры для циркумбинарных систем Kepler-413 из [8] и Kepler-453 из [9]

Система	Kepler-413	Kepler-453
${{M}_{1}}$ [${{M}_{ \odot }}$]	$0.820 \pm 0.015$	$0.944 \pm 0.010$
${{M}_{2}}$ [${{M}_{ \odot }}$]	$0.542 \pm 0.008$	$0.1951 \pm 0.0020$
${{a}_{{12}}}$ [а.е.]	$0.10148 \pm 0.00057$	$0.18539 \pm 0.00066$
${{e}_{{12}}}$	$0.0365 \pm 0.0023$	$0.0524 \pm 0.0037$
$i_{{12}}^{'}$ [°]	$87.332 \pm 0.050$	$90.266 \pm 0.052$
${{\omega }_{{12}}}$ [°]	$279.74 \pm 0.62$	$263.05 \pm 0.48$
${{M}_{p}}\;\left[ {{{M}_{{{\text{Earth}}}}}} \right]$	$67 \pm 21$	$0.2 \pm 16.0$
${{a}_{p}}$ [а.е.]	$0.355 \pm 0.002$	$0.7903 \pm 0.0028$
${{e}_{p}}$	$0.1181 \pm 0.0018$	$0.0359 \pm 0.0088$
$i_{p}^{'}$ [°]	$89.929 \pm 0.024$	$89.4429 \pm 0.0091$
${{\omega }_{p}}$ [°]	$94.6 \pm 2.2$	$185.1 \pm 3.7$
$\Delta {{\Omega }_{p}}$ [°]	$3.139 \pm 0.080$	$2.103 \pm 0.055$
$\Delta i$ [°]	$4.073 \pm 0.113$	$2.258 \pm 0.039$

По формулам (10) и (11) для системы Kepler-453 находим

(14)

$\begin{gathered} \gamma \approx {\text{1628}}{\text{.9;}} \\ {{i}_{{12}}} = 0_{.}^{{^{ \circ }}}00002 \pm 0.00139, \\ {{i}_{p}} = 2_{.}^{{^{ \circ }}}26 \pm 0.04. \\ \end{gathered} $

Заметим, что в силу указанной выше некомпланарности орбит звезд и планеты относительно плоскости Лапласа, орбиты всех трех тел будут взаимно прецессировать. Эту прецессию мы рассматриваем в разделе 4. Появляющийся при этом тонкий эффект нарушения резонанса в периодах прецессии звезд обсуждается в разделах 5 и 6.

4. УРАВНЕНИЯ ВЕКОВОЙ ПРЕЦЕССИИ ПРОБНОЙ ОРБИТЫ

4.1. Зональные гармоники потенциала

Как показано в [1], зональные гармоники внешнего потенциала R-тороида равны

(15)

$\begin{gathered} C_{{20}}^{R} = - \frac{1}{2}\left( {1 + \frac{3}{2}e_{R}^{2}} \right)\frac{{3{{{\cos }}^{2}}{{i}_{R}} - 1}}{2}; \\ C_{{40}}^{R} = \frac{3}{8}\left( {1 + 5e_{R}^{2} + \frac{{15}}{8}e_{R}^{4}} \right)\frac{{35{{{\cos }}^{4}}{{i}_{R}} - 30{{{\cos }}^{2}}{{i}_{R}} + 3}}{8}. \\ \end{gathered} $

Здесь ${{e}_{R}},\;{{i}_{R}}$, соответственно, – эксцентриситет и наклон орбиты к плоскости Лапласа того тела, для которого создается модель R-тороида.

Для Kepler-413 расчет по формулам (15) с учетом найденных углов (13) и известных эксцентриситетов орбит дает следующие значения коэффициентов зональных гармоник потенциала

$C_{{20}}^{{(1)}} = C_{{20}}^{{(2)}} = - 0.5010 \pm 0.0001;$

(16)

$\begin{gathered} C_{{40}}^{{(1)}} = C_{{40}}^{{(2)}} = 0.3775 \pm 0.0003; \\ C_{{20}}^{p} = - 0.5066 \pm 0.0003; \\ \end{gathered} $

$C_{{40}}^{p} = 0.3912 \pm 0.0010.$

Для другой циркумбинарной системы Kepler-453, коэффициенты потенциалы были также рассчитаны и приводятся в табл. 2.

Таблица 2.

Рассчитанные по формулам (10), (11) и (15) коэффициенты 2-й и 4-й зональных гармоник R-тороидов звезд $C_{{20}}^{1}$, $C_{{20}}^{2}$, $C_{{40}}^{1}$, $C_{{40}}^{2}$ и планеты $C_{{20}}^{p}$, $C_{{40}}^{p}$. Далее представлены величины $\dot {\Omega }_{R}^{0}$ пробной планеты от отдельного тороида, где индекс $R = \left\{ {1,2,p} \right\}$; скорости прецессии линии узлов и линии апсид пробной планеты от всех тороидов $\dot {\Omega }_{{12p}}^{0}$, $\dot {\omega }_{{12p}}^{0}$; соответствующие периоды прецессии ${{(T_{\Omega }^{{12p}})}_{0}}$ и ${{(T_{\omega }^{{12p}})}_{0}}$. Все расчеты сделаны для вырожденного случая нулевых эксцентриситетов и наклона орбиты. Даны также наклоны орбитальных моментов звездной пары и планеты к суммарному угловому моменту ${{i}_{{12}}}$ и ${{i}_{p}}$

Система	Kepler-413	Kepler-453
$C_{{20}}^{1},\;C_{{20}}^{2}$	$ - 0.5010 \pm 0.0001$	$ - 0.5021 \pm 0.0003$
$C_{{40}}^{1},\;C_{{40}}^{2}$	$0.3775 \pm 0.0003$	$0.3802 \pm 0.0007$
$C_{{20}}^{p}$	$ - 0.5066 \pm 0.0003$	$ - 0.4998 \pm 0.0005$
$C_{{40}}^{p}$	$0.3912 \pm 0.0010$	$0.3745 \pm 0.0012$
$\dot {\Omega }_{1}^{0}$ [${{10}^{{ - 10}}}$ с^–1]	$ - 6.83 \pm 0.09$	$ - 18.86 \pm 0.15$
$\dot {\Omega }_{2}^{0}$ [${{10}^{{ - 10}}}$ с^–1]	$ - 5.55 \pm 0.08$	$ - 8.58 \pm 0.10$
$\dot {\Omega }_{p}^{0}$ [${{10}^{{ - 10}}}$ с^–1]	$ - 0.03 \pm 0.01$	$ - 0.0005 \pm 0.0420$
$\dot {\Omega }_{{12p}}^{0}$ [${{10}^{{ - 9}}}$ с^–1]	$ - 1.24 \pm 0.02$	$ - 2.74 \pm 0.02$
$\dot {\omega }_{{12p}}^{0}$ [${{10}^{{ - 9}}}$ с^–1]	$2.48 \pm 0.03$	$5.49 \pm 0.05$
${{(T_{\Omega }^{{12p}})}_{0}}$ [лет]	$160 \pm 2$	$72.6 \pm 0.6$
${{(T_{\omega }^{{12p}})}_{0}}$ [лет]	$80 \pm 1$	$36.3 \pm 0.3$
${{i}_{{12}}}$ [°]	$0.0047 \pm 0.0015$	$0.00002 \pm 0.00139$
${{i}_{p}}$ [°]	$4.07 \pm 0.11$	$2.26 \pm 0.04$

4.2. Прецессия пробных орбит в гравитационном поле R-тороида

Согласно [1], скорость прецессии линии узлов и линии апсид пробной орбиты под влиянием R‑тороида описывается дифференциальными уравнениями

(17)

${{\left( {\frac{{d\Omega }}{{dt}}} \right)}_{R}} = \dot {\Omega }_{R}^{0}{{\left( {\frac{{{{a}_{R}}}}{a}} \right)}^{{7/2}}}\frac{{\cos i}}{{{{{(1 - {{e}^{2}})}}^{2}}}};$

(18)

${{\left( {\frac{{d\omega }}{{dt}}} \right)}_{R}} = \dot {\omega }_{R}^{0}{{\left( {\frac{{{{a}_{R}}}}{a}} \right)}^{{7/2}}}\frac{{5{{{\cos }}^{2}}i - 1}}{{4{{{(1 - {{e}^{2}})}}^{2}}}},$

где используются коэффициенты

(19)

$\dot {\Omega }_{R}^{0} = \frac{3}{2}C_{{20}}^{R}\frac{{{{m}_{R}}}}{{{{{\bar {M}}}_{R}}}}\sqrt {\frac{{G{{{\bar {M}}}_{R}}}}{{a_{R}^{3}}}} ,\quad \dot {\omega }_{R}^{0} = - 2\dot {\Omega }_{R}^{0},$

равные частотам прецессии линии узлов и линии апсид пробной планеты под влиянием каждого из трех тороидов в вырожденном случае $(a = 1\;{\text{а}}.{\text{е}}.,\;e = 0,\;i = 0^\circ )$.

4.3. Прецессия пробных орбит в гравитационном поле трех R-тороидов

Напомним, что в данной работе для циркумбинарной системы рассматривается совокупность трех моделей R-тороида (для двух звезд и для планеты). Рассмотрим суммарное влияние силовых полей этих трех тороидов на прецессию пробных орбит. Прежде всего, для введенных выше коэффициентов можно написать уравнения

(20)

$\dot {\Omega }_{{12p}}^{0} = \dot {\Omega }_{1}^{0} + \dot {\Omega }_{2}^{0} + \dot {\Omega }_{p}^{0};\quad \dot {\omega }_{{12p}}^{0} = - 2\dot {\Omega }_{{12p}}^{0};$

(21)

${{(T_{\Omega }^{{12p}})}_{0}} = \frac{{2\pi }}{{\left| {\left( {\frac{{d\Omega }}{{dt}}} \right)_{{12p}}^{0}} \right|}};\quad {{(T_{\omega }^{{12p}})}_{0}} = \frac{1}{2}T_{\Omega }^{{12p}}.$

Следовательно, периоды узловой и апсидальной прецессии пробной планеты под влиянием трех тороидов будут равны

(22)

$T_{\Omega }^{{12p}} = {{(T_{\Omega }^{{12p}})}_{0}}{{\left( {\frac{a}{{{\text{1}}\;{\text{а}}{\text{.е}}{\text{.}}}}} \right)}^{{7/2}}}\frac{{{{{(1 - {{e}^{2}})}}^{2}}}}{{\cos i}};$

(23)

$T_{\omega }^{{12p}} = {{(T_{\omega }^{{12p}})}_{0}}{{\left( {\frac{a}{{{\text{1}}\;{\text{а}}{\text{.е}}{\text{.}}}}} \right)}^{{7/2}}}\frac{{4{{{(1 - {{e}^{2}})}}^{2}}}}{{5{{{\cos }}^{2}}i - 1}}.$

Из формул (22) и (23) находим отношение периодов нодальной и апсидальной прецессии для пробной орбиты (или же представляющего ее оскулирующего кольца Гаусса)

(24)

$\frac{{T_{\Omega }^{{12p}}}}{{T_{\omega }^{{12p}}}} = - \frac{{5{{{\cos }}^{2}}i - 1}}{{2\cos i}} \approx - 2\left( {1 - \frac{3}{4}{{i}^{2}} + O({{i}^{6}})} \right).$

Из (24) следует, что модуль отношения периодов нодальной и апсидальной прецессии для внешнего кольца Гаусса, имеющего малый наклон i и находящегося в гравитационном поле R-тороида, оказывается чуть меньше 2:

(25)

$\left| {\frac{{T_{\Omega }^{'}}}{{T_{\omega }^{'}}}} \right| \leqslant 2.$

Результат (25) подтвержден при моделировании экзопланеты KOI 120.01 [10].

Прецессия при больших углах наклона пробных орбит здесь не рассматривается.

4.4. Расчет прецессии орбиты пробной планеты в системе Kepler-413

В системе Kepler-413 значения больших полуосей пробных орбит в поле R-тороидов двойной звезды ограничены снизу $a > {{a}_{{{\text{cr}}}}} \approx 5.48$ а.е., а на таких расстояниях вкладом 4-й зональной гармоники из (16) можно пренебречь. Учитывая это, вклады в прецессию линии узлов пробной орбиты от обеих звезд и планеты Kepler-413b с учетом погрешностей входных величин представим уравнениями:

$\begin{gathered} {{\left( {\frac{{d\Omega }}{{dt}}} \right)}_{1}} = - \left[ {(6.83 \pm 0.09) \times {{{10}}^{{ - 10}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right] \times \\ \, \times {{\left( {\frac{{1\;{\text{а}}{\text{.е}}{\text{.}}}}{a}} \right)}^{{7/2}}}\frac{{\cos i}}{{{{{(1 - {{e}^{2}})}}^{2}}}}; \\ \end{gathered} $

(26)

$\begin{gathered} {{\left( {\frac{{d\Omega }}{{dt}}} \right)}_{2}} = - \left[ {(5.55 \pm 0.08) \times {{{10}}^{{ - 10}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right] \times \\ \, \times {{\left( {\frac{{1\;{\text{а}}{\text{.е}}{\text{.}}}}{a}} \right)}^{{7/2}}}\frac{{\cos i}}{{{{{(1 - {{e}^{2}})}}^{2}}}}; \\ \end{gathered} $

$\begin{gathered} {{\left( {\frac{{d\Omega }}{{dt}}} \right)}_{p}} = - \left[ {(0.03 \pm 0.01) \times {{{10}}^{{ - 10}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right] \times \\ \, \times {{\left( {\frac{{1\;{\text{а}}{\text{.е}}{\text{.}}}}{a}} \right)}^{{7/2}}}\frac{{\cos i}}{{{{{(1 - {{e}^{2}})}}^{2}}}}. \\ \end{gathered} $

Из (26) видно, что вклад в прецессию узла от R‑тороида планеты Kepler-413b составляет только $ \approx 0.3\% $ от вклада тороидов звездной пары. Фактически, вклад планеты теряется на уровне погрешности вкладов от тороидов звезд.

Складывая первое и второе выражения в (26), находим суммарное влияние R-тороидов звездной пары на прецессии линии узлов и линии апсид пробной орбиты:

${{\left( {\frac{{d\Omega }}{{dt}}} \right)}_{{12p}}} = - \left[ {(1.242 \pm 0.016) \times {{{10}}^{{ - 9}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right] \times $

(27)

$\begin{gathered} \, \times {{\left( {\frac{{1\;{\text{а}}{\text{.е}}{\text{.}}}}{a}} \right)}^{{7/2}}}\frac{{\cos i}}{{{{{(1 - {{e}^{2}})}}^{2}}}}; \\ {{\left( {\frac{{d\omega }}{{dt}}} \right)}_{{12p}}} = \left[ {(2.484 \pm 0.032) \times {{{10}}^{{ - 9}}}\;\frac{{{\text{рад}}}}{{\text{с}}}} \right] \times \\ \end{gathered} $

$\, \times {{\left( {\frac{{1\;{\text{а}}{\text{.е}}{\text{.}}}}{a}} \right)}^{{7/2}}}\frac{{5{{{\cos }}^{2}}i - 1}}{{4{{{(1 - {{e}^{2}})}}^{2}}}}.$

Соответственно, периоды нодальной и апсидальной прецессии для пробной орбиты в системе Kepler-413 будут равны

(28)

$\begin{gathered} T_{\Omega }^{{12p}} = \left[ {(160 \pm 2)\;{\text{лет}}} \right]{{\left( {\frac{a}{{1\;{\text{а}}{\text{.е}}{\text{.}}}}} \right)}^{{7/2}}}\frac{{{{{(1 - {{e}^{2}})}}^{2}}}}{{\cos i}}; \\ T_{\omega }^{{12p}} = \left[ {(80 \pm 1)\;{\text{лет}}} \right]{{\left( {\frac{a}{{1\;{\text{а}}{\text{.е}}{\text{.}}}}} \right)}^{{7/2}}}\frac{{4{{{(1 - {{e}^{2}})}}^{2}}}}{{5{{{\cos }}^{2}}i - 1}}. \\ \end{gathered} $

На рис. 2 (левая панель) показан график зависимости периода прецессии аргумента перицентра пробной орбиты от значения полуоси этой орбиты для системы Kepler-413. Минимальное значение большой полуоси пробной планеты (при котором модель R-тороида еще применима) находится по формуле

(29)

${{a}_{{cr}}} = {{\left( {\frac{\mu }{{4{{\pi }^{2}}}}} \right)}^{{1/3}}}{{T}_{\Omega }}^{{2/3}}.$

В частности, для данной в [8] величины ${{T}_{\Omega }} = $ = 11 лет нижнее значение полуоси круговой орбиты равно ${{a}_{{{\text{cr}}}}} = 5.48$ а.е., причем период прецессии аргумента перицентра будет равен ${{\left. {{{T}_{\omega }}} \right|}_{{\begin{array}{*{20}{c}} {e = 0} \\ {i = 0} \end{array}}}} = (30.8 \pm $ $ \pm \;0.4) \times {{10}^{3}}$ лет. Для системы Kepler-413 на рис. 3 (левая панель) построен график для периода нодальной прецессии от полуоси орбиты пробной планеты. При ${{a}_{{cr}}} = 5.48$ а.е. период прецессии восходящего узла равен ${{\left. {{{T}_{\Omega }}} \right|}_{{\begin{array}{*{20}{c}} {e = 0} \\ {i = 0} \end{array}}}} = (61.6 \pm 0.8) \times {{10}^{3}}$ лет, т.е. в два раза больше, как и должно быть (см. равенство (21)), чем ${{\left. {{{T}_{\omega }}} \right|}_{\begin{subarray}{l} e = 0 \\ i = 0 \end{subarray} }}$.

Рис. 2.

Графики зависимости периода прецессии аргумента перицентра орбиты пробной планеты ${{\left. {T_{\omega }^{{12p}}\left( a \right)} \right|}_{\begin{subarray}{l} e = 0 \\ i = 0 \end{subarray} }}$, измеряемого в годах, от ее полуоси в астрономических единицах, в вырожденном случае $e = 0$ и $i = 0$. График слева – для системы Kepler-413, справа – для системы Kepler-453. Для наглядности графики представлены в логарифмической шкале по обеим осям. В системе Kepler-413 для крайнего значения полуоси круговой орбиты ${{a}_{{{\text{cr}}}}} = 5.48$ а.е. период апсидальной прецессии равен ${{\left. {{{T}_{\omega }}} \right|}_{{\begin{array}{*{20}{c}} {e = 0} \\ {i = 0} \end{array}}}} = (30.8 \pm 0.4) \times {{10}^{3}}$ лет.

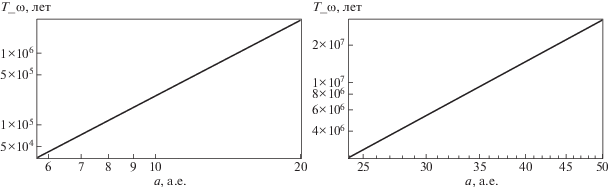
Рис. 3.

Графики зависимости периода прецессии долготы восходящего узла орбиты пробной планеты ${{\left. {T_{\Omega }^{{12p}}(a)} \right|}_{\begin{subarray}{l} e = 0 \\ i = 0 \end{subarray} }}$, измеряемого в годах, от ее полуоси, измеряемой в астрономических единицах, в вырожденном случае $e = 0$ и $i = 0$. График (в логарифмической шкале по обеим осям) слева – для системы Kepler-413, справа – для системы Kepler-453.

4.5. Сводка результатов для двух экзосиcтем

Все необходимые данные для циркумбинарных систем Kepler-413 из [8] и Kepler-453 (Welsh et al. 2015) из [9] представлены в табл. 1. Все необходимые величины, рассчитанные указанным выше методом по формулам (10), (11), (15) и (20‒23), даны в табл. 2.

Рассчитаем теперь по формулам (27) и (28) периоды прецессии пробной планеты в зависимости от большой полуоси орбиты в случае нулевых эксцентриситета и наклона орбиты к главной плоскости ($a = {{a}_{{cr}}}$, $e = 0$, $i = 0^\circ $).

Графики на рис. 2 и 3 построены от критического (наименьшего возможного в модели) значения полуоси пробной планеты ${{a}_{{cr}}}.$ Для системы Kepler-413 имеем оценку периода апсидальной прецессии $T_{\omega }^{{12p}} = (35.4 \pm 0.4) \times {{10}^{3}}$ лет, а для периода прецессии долготы восходящего узла $T_{\Omega }^{{12p}} = (70.7 \pm 0.8) \times {{10}^{3}}$ лет. Для системы Kepler-453, соответственно, находим $T_{\omega }^{{12p}} = (2.2 \pm 0.2) \times $ $ \times \;{{10}^{6}}$ лет и $T_{\Omega }^{{12p}} = (4.4 \pm 0.4) \times {{10}^{6}}$ лет.

5. ВЫЧИСЛЕНИЕ ПЕРИОДОВ ВЕКОВОЙ ПРЕЦЕССИИ ОРБИТ ТРЕХ ТЕЛ В ЦИРКУМБИНАРНОЙ СИСТЕМЕ МЕТОДОМ КОЛЕЦ ГАУССА

Выше рассматривалась вековая эволюция пробных орбит, теперь рассмотрим эволюцию орбит звезд центральной пары и экзопланеты самой циркумбинарной системы. Для этого циркумбинарную систему представим совокупностью трех взаимодействующих колец Гаусса.

5.1. Уравнения для частот прецессии колец Гаусса

Метод взаимодействующих колец Гаусса был разработан в статье [11]. Здесь мы используем формулы этого метода и ограничимся точностью до квадратов малых наклонов и эксцентриситетов. Вначале запишем уравнение для частоты прецессии линии узлов второго кольца Гаусса в системе координат, где главной плоскостью является плоскость первого кольца (индекс 1 относится к орбите звезды, а индекс 2 – к орбите планеты):

(30)

$\begin{gathered} \frac{{d{{\Omega }_{2}}}}{{dt}} = - \frac{{G{{m}_{1}}}}{{8\pi a_{1}^{3}{{n}_{2}}{{n}^{3}}(1 + n){{{(1 - {{n}^{2}})}}^{2}}}} \times \\ \times \;[\Omega _{{000}}^{{\left( 2 \right)}} + \Omega _{{002}}^{{\left( 2 \right)}}\Delta {{i}^{2}} + \Omega _{{200}}^{{\left( 2 \right)}}e_{1}^{2} + \Omega _{{020}}^{{\left( 2 \right)}}e_{2}^{2} + \Omega _{{110}}^{{\left( 2 \right)}}{{e}_{1}}{{e}_{2}}], \\ \end{gathered} $

где коэффициенты

(30.1)

$\begin{gathered} \Omega _{{002}}^{{\left( 2 \right)}} = \left( {\frac{{(1 + {{n}^{2}})(1 - 4n + {{n}^{2}})(1 + 4n + {{n}^{2}})}}{{{{{(1 - n)}}^{2}}}}} \right. \times \\ \, \times \left. {\mathop {E(k) - (1 - 5{{n}^{2}} + {{n}^{4}})K(k)}\limits_{_{{_{{}}}}} } \right)n; \\ \end{gathered} $

$\Omega _{{200}}^{{\left( 2 \right)}} = \left( {\frac{{1 + 21{{n}^{2}} + 47{{n}^{4}} + 3{{n}^{6}}}}{{{{{(1 - n)}}^{2}}}}E(k)} \right. - $

(30.2)

$\begin{gathered} \, - \left. {\mathop {(1 + 5{{n}^{2}} + 3{{n}^{4}})K(k)}\limits_{_{{_{{}}}}} } \right)n - \\ - \;\left( {\frac{{1 - 3{{n}^{2}} + 23{{n}^{4}} + 3{{n}^{6}}}}{{{{{(1 - n)}}^{2}}}}E(k) - } \right. \\ \end{gathered} $

$ - \;\left. {\mathop {(1 - {{n}^{2}} + 3{{n}^{4}})K(k)}\limits_{_{{_{{}}}}} } \right)2n{{\cos }^{2}}{{\omega }_{1}};$

$\Omega _{{110}}^{{\left( 2 \right)}} = \left( {\frac{{4 - 15{{n}^{2}} - 26{{n}^{4}} - 15{{n}^{6}} + 4{{n}^{8}}}}{{{{{(1 - n)}}^{2}}}}E(k) - } \right.$

(30.3)

$\begin{gathered} - \;\left. {\mathop {(4 - 11{{n}^{2}} + 4{{n}^{4}})(1 + {{n}^{2}})K(k)}\limits_{_{{_{{}}}}} } \right)\cos {{\omega }_{1}}\cos {{\omega }_{2}} + \\ + \;\left( {\frac{{4 - 21{{n}^{2}} - 110{{n}^{4}} - 21{{n}^{6}} + 4{{n}^{8}}}}{{{{{(1 - n)}}^{2}}}}E(k) - } \right. \\ \end{gathered} $

$\left. { - \;\mathop {(4 - {{n}^{2}})(1 - 4{{n}^{2}})(1 + {{n}^{2}})K(k)}\limits_{_{{_{{}}}}} } \right)\sin {{\omega }_{1}}\sin {{\omega }_{2}};$

$\Omega _{{020}}^{{\left( 2 \right)}} = \left( {\frac{{5 + 45{{n}^{2}} + 19{{n}^{4}} + 3{{n}^{6}}}}{{{{{(1 - n)}}^{2}}}}E(k) - } \right.$

(30.4)

$\begin{gathered} - \;\left. {\mathop {(5 + {{n}^{2}} + 3{{n}^{4}})K(k)}\limits_{_{{_{{}}}}} } \right)n - \\ - \;\left( {\frac{{3 + 23{{n}^{2}} - 3{{n}^{4}} + {{n}^{6}}}}{{{{{(1 - n)}}^{2}}}}E(k) - } \right. \\ \end{gathered} $

$ - \;\left. {\mathop {(3 - {{n}^{2}} + {{n}^{4}})K(k)}\limits_{_{{_{{}}}}} } \right)2n{{\cos }^{2}}{{\omega }_{2}};$

(30.5)

$\Omega _{{000}}^{{\left( 2 \right)}} = \left( {\frac{{1 + {{n}^{2}}}}{{{{{(1 - n)}}^{2}}}}E(k) - K(k)} \right)4n{{(1 - {{n}^{2}})}^{2}}.$

Здесь: ${{m}_{1}}$ – масса, ${{a}_{1}}$ – большая полуось, ${{e}_{1}}$ – эксцентриситет, ${{\omega }_{1}}$ – аргумент перицентра первого (возмущающего) кольца Гаусса; индекс 2 относится ко второму кольцу Гаусса со средним движением ${{n}_{2}}$; $\Delta i$ – угол взаимного наклона колец Гаусса; $K(k)$ и $E(k)$ – полные эллиптические интегралы Лежандра первого и второго рода; кроме того,

(30.6)

$k = \frac{{2\sqrt {{{a}_{1}}{{a}_{2}}} }}{{{{a}_{1}} + {{a}_{2}}}} = \frac{{2\sqrt n }}{{1 + n}} \leqslant 1,\quad n = \frac{{{{a}_{2}}}}{{{{a}_{1}}}}.$

На втором этапе следует учесть поправки к аргументам перицентров при переходе от картинной плоскости к плоскости первого кольца. Тогда из сферического треугольника $ABC,$ показанного на рис. 4, находим требуемые величины $\Delta {{\bar {\omega }}_{{12}}}$ и $\Delta {{\bar {\omega }}_{p}}$:

(31.1)

$\begin{gathered} \sin (\Delta {{{\bar {\omega }}}_{{12}}}) = \frac{{\sin i_{p}^{'}\sin (\Delta {{\Omega }_{p}})}}{{\sin (\Delta i)}}; \\ \cos (\Delta {{{\bar {\omega }}}_{{12}}}) = \\ = \frac{{ - \sin i_{{12}}^{'}\cos i_{p}^{'} + \cos i_{{12}}^{'}\sin i_{p}^{'}\cos (\Delta {{\Omega }_{p}})}}{{\sin (\Delta i)}}; \\ \end{gathered} $

(31.2)

$\begin{gathered} \sin (\Delta {{{\bar {\omega }}}_{p}}) = \frac{{\sin i_{{12}}^{'}\sin (\Delta {{\Omega }_{p}})}}{{\sin (\Delta i)}}; \\ \cos (\Delta {{{\bar {\omega }}}_{p}})\, = \,\frac{{\sin i_{p}^{'}\cos i_{{12}}^{'} - \cos i_{p}^{'}\sin i_{{12}}^{'}\cos (\Delta {{\Omega }_{p}})}}{{\sin (\Delta i)}}. \\ \end{gathered} $

Рис. 4.

Сферический треугольник при переходе от системы координат, связанных с картинной плоскостью $AB.$ Здесь $\Delta i$ – угол между плоскостью колец Гаусса звездной пары $AC$и плоскостью кольца планеты $BC$; $\Delta {{\Omega }_{p}}$ – разность долгот восходящих узлов колец Гаусса в картинной плоскости; $i_{{12}}^{'}$ и $i_{p}^{'}$ – наклонения, соответственно, звездного и планетного колец Гаусса к картинной плоскости; $\Delta {{\bar {\omega }}_{{12}}}\,(\Delta {{\bar {\omega }}_{p}})$ – угол между линией узлов звездного (планетного) кольца в картинной плоскости и общей линией узлов двух колец. Плоскость Лапласа проходит через точку $C.$

Наконец, на третьем этапе преобразований мы пренебрегаем малым влиянием планеты и переходим к плоскости Лапласа звездных колец Гаусса. Из геометрических соображений ясно, что плоскость Лапласа двух колец Гаусса проходит через их общую линию узлов (на рис. 4 плоскость Лапласа проходит через точку C). Для упрощения очень сложных расчетов в выбранной модели за начальный момент времени берется тот, с которого начинает действовать возмущение от планеты. Другими словами, до этого начального момента орбиты звезд мы считаем лежащими в одной плоскости (на рис. 4 эта плоскость проходит через дугу AC), не прецессирующими и с одинаковыми периодами движения звезд по ним.

Скорость узловой прецессии второго кольца (отметим ее верхним индексом L) относительно неподвижной плоскости Лапласа будет выражаться через прежнюю $\frac{{d{{\Omega }_{2}}}}{{dt}}$ формулой (30) (см. [10])

(32)

$\frac{{d\Omega _{2}^{L}}}{{dt}} = \frac{{\sin \Delta i}}{{\sin i_{2}^{L}}}\frac{{d{{\Omega }_{2}}}}{{dt}}.$

Учитывая, что в системах Kepler-413 и Kepler-453 орбиты звезд полагаются лежащими в одной плоскости, уравнение (32) для орбиты планеты и двух звезд на начальный момент времени можно представить в виде (индекс L можно опустить)

(33)

$\begin{gathered} {{\left( {\frac{{d{{\Omega }_{p}}}}{{dt}}} \right)}_{0}} = \frac{{\sin \Delta i}}{{\sin {{i}_{p}}}} \times \\ \times \;\left( {\frac{{d{{\Omega }_{2}}}}{{dt}}\left( \begin{gathered} {{a}_{1}} = {{a}_{1}},{{e}_{1}} = {{e}_{{12}}},{{\omega }_{1}} = {{\omega }_{{12}}} - \Delta {{{\bar {\omega }}}_{{12}}}, \hfill \\ {{a}_{2}} = {{a}_{p}},{{e}_{2}} = {{e}_{p}},{{\omega }_{2}} = {{\omega }_{p}} - \Delta {{{\bar {\omega }}}_{p}} \hfill \\ \end{gathered} \right) + } \right. \\ + \;\left. {\frac{{d{{\Omega }_{2}}}}{{dt}}\left( \begin{gathered} {{a}_{1}} = {{a}_{2}},{{e}_{1}} = {{e}_{{12}}},{{\omega }_{1}} = {{\omega }_{{12}}} - \Delta {{{\bar {\omega }}}_{{12}}} - \pi , \hfill \\ {{a}_{2}} = {{a}_{p}},{{e}_{2}} = {{e}_{p}},{{\omega }_{2}} = {{\omega }_{p}} - \Delta {{{\bar {\omega }}}_{p}} \hfill \\ \end{gathered} \right)} \right); \\ \end{gathered} $

(34)

$\begin{gathered} {{\left( {\frac{{d{{\Omega }_{1}}}}{{dt}}} \right)}_{0}} = \frac{{\sin \Delta i}}{{\sin {{i}_{{12}}}}} \times \\ \times \;\frac{{d{{\Omega }_{2}}}}{{dt}}\left( \begin{gathered} {{a}_{1}} = {{a}_{p}},{{e}_{1}} = {{e}_{p}},{{\omega }_{1}} = {{\omega }_{p}} - \Delta {{{\bar {\omega }}}_{p}}, \hfill \\ {{a}_{2}} = {{a}_{1}},{{e}_{2}} = {{e}_{{12}}},{{\omega }_{2}} = {{\omega }_{{12}}} - \Delta {{{\bar {\omega }}}_{{12}}} \hfill \\ \end{gathered} \right); \\ \end{gathered} $

(35)

$\begin{gathered} {{\left( {\frac{{d{{\Omega }_{2}}}}{{dt}}} \right)}_{0}} = \frac{{\sin \Delta i}}{{\sin {{i}_{{12}}}}} \times \\ \times \;\frac{{d{{\Omega }_{2}}}}{{dt}}\left( \begin{gathered} {{a}_{1}} = {{a}_{p}},{{e}_{1}} = {{e}_{p}},{{\omega }_{1}} = {{\omega }_{p}} - \Delta {{{\bar {\omega }}}_{p}}, \hfill \\ {{a}_{2}} = {{a}_{2}},{{e}_{2}} = {{e}_{{12}}},{{\omega }_{2}} = {{\omega }_{{12}}} - \Delta {{{\bar {\omega }}}_{{12}}} - \pi \hfill \\ \end{gathered} \right), \\ \end{gathered} $

где учтено, что аргументы перицентров отсчитываются от общей линии узлов для орбит звезд, а не от линий узлов, расположенных в картинной плоскости, с помощью формул (31.1), (31.2), а также учтено, что аргументы перицентров орбит звезд отстоят друг от друга на $\pi $ радиан.

Подчеркнем, что формулы (33)–(35) выражают принятые выше условия: на кольцо Гаусса внешней планеты действует гравитация обоих звездных колец Гаусса, а на кольцо Гаусса каждой из звезд возмущающее влияние оказывает только кольцо планеты. Другими словами, в данном подходе кольца Гаусса каждой звезды не оказывают возмущающего влияния друг на друга, так как в данной задаче трех тел орбиты звезд на начальный момент времени представлены орбитами синхронной пары, а такие орбиты (кольца) не должны возмущать друг друга.

5.2. Периоды прецессии орбит звезд и планеты в циркумбинарной системе. Эффект малого отклонения от резонанса

Прежде всего периоды нодальной прецессии колец Гаусса циркумбинарной системы в начальный момент времени, соответственно, равны

(36)

$T_{p}^{0}\, = \,\frac{{2\pi }}{{\left| {{{{\left( {\frac{{d{{\Omega }_{p}}}}{{dt}}} \right)}}_{0}}} \right|}};\quad T_{1}^{0}\, = \,\frac{{2\pi }}{{\left| {{{{\left( {\frac{{d{{\Omega }_{1}}}}{{dt}}} \right)}}_{0}}} \right|}};\quad T_{2}^{0}\, = \,\frac{{2\pi }}{{\left| {{{{\left( {\frac{{d{{\Omega }_{2}}}}{{dt}}} \right)}}_{0}}} \right|}}.$

Минимальное значение большой полуоси планеты (при котором модель R-тороида еще применима) находится по формуле (29) при подстановке уточненных значений $T_{1}^{0}$ и $T_{2}^{0}.$

Рассчитаем теперь начальные периоды прецессии линий узлов орбит двух звезд и планеты, а также минимальные значения больших полуосей орбиты пробной планеты по формуле (36) и по уточненной формуле (30) (табл. 3.)

Таблица 3.

Оценки начальных периодов прецессии линий узлов орбит звезд и планеты в плоскости Лапласа, отношений этих периодов и минимальной большой полуоси для орбиты пробной планеты

Система	Kepler-413	Kepler-453
$T_{p}^{0}$ [лет]	$11.49 \pm 0.28\;(11.47 \pm 0.28)$	$105 \pm 2\;(106 \pm 2)$
$T_{1}^{0}$ [лет]	$11.63 \pm 0.28\;(11.76 \pm 0.28)$	$112 \pm 2\;(112 \pm 2)$
$T_{2}^{0}$ [лет]	$11.39 \pm 0.28\;(11.28 \pm 0.28)$	$104 \pm 2\;(104 \pm 2)$
$T_{p}^{0}{\text{/}}T_{1}^{0}$	$0.988 \pm 0.001\;(0.975 \pm 0.001)$	$0.942 \pm 0.002\;(0.945 \pm 0.001)$
$T_{p}^{0}{\text{/}}T_{2}^{0}$	$1.008 \pm 0.001\;(1.017 \pm 0.001)$	$1.0120 \pm 0.0002\;(1.0114 \pm 0.0001)$
$T_{1}^{0}{\text{/}}T_{2}^{0}$	$1.021 \pm 0.002\;(1.043 \pm 0.002)$	$1.074 \pm 0.001\;(1.070 \pm 0.001)$
${{a}_{{{\text{cr}}}}}$ [а.е.]	$5.7$	$24$
В круглых скобках указан вариант оценок, соответствующий преобразованию ${{\omega }_{{12}}} \to {{\omega }_{{12}}} - \pi $.

Подставляя в формулы (36) известные нам значения величин, получим периоды нодальной прецессии для планет в системах Kepler-413 и Kepler-453, а также отношения этих периодов, см. табл. 3. Обратим внимание на то, что для обеих экзосистем выполняются строгие неравенства

(37)

$T_{1}^{0} > T_{p}^{0} > T_{2}^{0}.$

Для пояснения неравенств (37) заметим следующее. Если при построении плоскости Лапласа пренебречь малым влиянием кольца Гаусса от планеты, то вместо (37) выполнялись бы строгие равенства $T_{1}^{0} = T_{2}^{0} = 0$ (прецессии узлов вообще бы не было). Действительно, без влияния планеты орбиты звезд всегда лежали бы строго в одной плоскости, а движение по этим орбитам происходило бы синхронно с резонансом $1:1$. Но под влиянием в начальный момент времени притяжения планеты центр масс звездной пары и направления двух линий апсид немного сместятся относительно прежних положений; при этом орбиты звезд станут некомпланарными и появится вековая прецессия узлов этих орбит с периодами, немного различающимися между собой. Очевидно, что смещенный (относительно барицентра системы трех тел) центр масс пары звезд будет двигаться синхронно в противофазе с планетой. И хотя отклонения орбит звезд от их синхронных аналогов малы (что видно из табл. 3 по пересекающимся областям оценок начальных периодов уже в пределах $1\sigma $), эффект квазисинхронности орбит звезд все же проявляет себя и отражен в непересекающихся оценках (даже в пределах $3\sigma $) отношений периодов в табл. 2.

Таким образом, для возмущенных орбит звезд появятся вековые движения узлов, причем периоды движения не будут одинаковыми (синхронными). Но одновременно вековую прецессию узла получит и орбита самой планеты, причем направления движения узлов у звезд и планеты будут совпадать.

Чтобы разобраться в том, почему период прецессии узла планеты $T_{p}^{0}$ находится в середине неравенств (37), введем понятие среднего кольца Гаусса, которое составляется для колец звездной пары в синхронной конфигурации (напомним: речь идет о модели, в которой возмущаемые планетой орбиты звезд рассматриваются на начальный момент времени в состоянии синхронного орбитального движения). Тогда появившуюся из‑за возмущений прецессию плоскости орбиты планеты можно представить как следствие взаимодействия кольца Гаусса планеты с указанным средним кольцом Гаусса, созданного двумя кольцами звезд в синхронной конфигурации. Взаимодействие кольца планеты со средним кольцом Гаусса звезд и приводит к тому, что период прецессии узла орбиты планеты $T_{p}^{0}$ будет больше наименьшего $T_{2}^{0}$, и меньше наибольшего $T_{1}^{0}$ периодов прецессии колец звезд, как это имеет место в неравенствах (37).

6. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В первой части этой работы изучается прецессия пробных орбит в циркумбинарных системах, состоящих из двойной звезды и внешней экзопланеты. Следует подчеркнуть актуальность задач по исследованию пробных орбит в экзосистемах. Действительно, на современном этапе уверенных прямых наблюдений планетных систем у других звезд пока нет, и в этой ситуации исследование пробных орбит помогает лучше понять динамику экзосистем. О важности такой постановки задачи говорит и статья [6], где исследовалась устойчивость пробных орбит спутников экзопланет в циркумбинарных системах (причем сами спутники пока не обнаружены).

Для изучения прецессии пробных орбит был разработан новый метод, опирающийся на модель из трех R-тороидов. Этот метод применяется к экзосистемам Kepler-413 и Kepler-453. Для них была найдена ориентация угловых моментов звездной пары ${{L}_{{12}}}$ и экзопланеты ${{L}_{p}}$ относительно плоскости Лапласа, вычислены отношение ${{\gamma = {{L}_{{12}}}} \mathord{\left/ {\vphantom {{\gamma = {{L}_{{12}}}} {{{L}_{p}}}}} \right. \kern-0em} {{{L}_{p}}}}$ и зональные гармоники внешних гравитационных потенциала трех R-тороидов. Используя найденное в [1] выражение взаимной энергии тороида и кольца Гаусса, мы вывели уравнения для частот апсидальной и нодальной прецессии пробных орбит. Анализ решений этих уравнений показал, что в рассматриваемых системах основной вклад в прецессию орбит вносят R‑тороиды звездной пары.

Во второй части работы изучается эволюция орбит звезд и планеты самой циркумбинарной системы. Для решения этой задачи применяется разработанный в [11] метод взаимодействующих колец Гаусса. Важное значение здесь имеет вывод формулы для взаимной энергии колец в системе координат, где главной является плоскость Лапласа. С помощью взаимной энергии колец было получено уравнение для частоты прецессии линии узлов каждого кольца Гаусса. Решение этого уравнения позволило получить новую информацию об экзосистемах. Например, для системы Kepler-413 мы не только уточнили данный в [8] период нодальной прецессии орбиты планеты ${{T}_{p}} = $ 11 лет (у нас $T_{p}^{0} = 11.49 \pm 0.28$ лет), но и нашли неизвестные ранее периоды нодальной прецессии орбит центральной пары звезд $T_{1}^{0} = $ 11.63 ± ± 0.28 лет, $T_{2}^{0} = 11.39 \pm 0.28$ лет. Для экзосистемы Kepler-453 впервые были найдены все три периода прецессии узла: $T_{1}^{0} = 112 \pm 2~$ $(112 \pm 2)$ лет, $T_{2}^{0}\, = \,104 \pm 2~$ $(104 \pm 2)$ лет, $T_{p}^{0} = 105 \pm 2~$ $(106 \pm 2)$ лет.

В данной работе мы обратили внимание на тонкий эффект влияния планеты на нарушение резонанса $1:1$ периодов нодальной прецессии у пары звезд. Если при построении плоскости Лапласа пренебречь малым влиянием кольца Гаусса планеты, то вместо (37) выполнялись бы строгие равенства $T_{1}^{0} = T_{2}^{0} = 0$ и прецессия узлов отсутствовала. Это и понятно: без возмущений от планеты обе орбиты звезд лежали бы строго в одной плоскости, и движение по ним происходило синхронно с резонансом $1:1$. Но с учетом гравитационного влияния циркумбинарной планеты картина изменится: центр масс пары звезд немного сместится относительно барицентра системы трех тел и будет двигаться синхронно в противофазе с планетой. При этом появятся малые поправки к элементам невозмущенных орбит звезд, причем эти элементы будут зависеть от времени. Одновременно вековую прецессию узла получит и орбита самой планеты, причем направления движения узлов у звезд и планеты будут совпадать.

Для прояснения ситуации с влиянием планеты на движение звезд полезно ввести понятие среднего кольца Гаусса для звездной пары; это среднее кольцо создается из пары звездных колец Гаусса в синхронной конфигурации и позволяет выявить тонкий эффект влияния планеты на нарушение резонанса $1:1$ в периодах нодальной прецессии звезд. Таким образом, прецессию плоскости орбиты планеты можно рассматривать как результат взаимодействия кольца Гаусса этой планеты с указанным средним кольцом для пары звезд. Именно взаимодействие кольца планеты со средним кольцом Гаусса звезд позволяет объяснить неравенства (37).

Список литературы

Б. П. Кондратьев, В. С. Корноухов, Астрон. журн. 98, 434 (2021).
St. Raetz, T. O. B. Schmidt, S. Czesla, T. Klocová, et al., Monthly Not. Roy. Astron. Soc. 460, 2834 (2016).
J. W. Barnes, J. C. van Eyken, B. K. Jackson, D. R. Ciardi, J. J. Fortney, Astrophys. J. 774, id. 53 (2013).
Ch. Chen, A. Franchini, S. H. Lubow, R. G. Martin, Monthly Not. Roy. Astron. Soc. 490, 5634 (2019).
B. C. Bromley, S. J. Kenyon, Astron. J. 161, id. 25 (2021).
A. S. Hamers, M. X. Cai, J. Roa, N. Leigh, Monthly Not. Roy. Astron. Soc. 480, 3800 (2018).
B. P. Kondratyev, Solar System Research 46, 352 (2012).
V. B. Kostov, P. R. McCullough, J. A. Carter, M. Deleuil, et al., Astrophys. J. 784, 14 (2014).
Y. Judkovsky, A. Ofir, O. Aharonson, Astron. J. 160, id. 195 (2020).
W. F. Welsh, J. A. Orosz, D. R. Short, W. D. Cochran, et al., Astrophys. J. 809, id. 26 (2015).
Б. П. Кондратьев, В. С. Корноухов, Астрон. журн. 97, 408 (2020).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал