Астрономический журнал, 2021, T. 98, № 8, стр. 643-662

Асинхронные звезды в тесных двойных системах

С. В. Чернов^1, *

¹ Физический институт им. П.Н. Лебедева РАН, Астрокосмический центр
Москва, Россия

Поступила в редакцию 05.02.2021
После доработки 30.04.2021
Принята к публикации 30.04.2021

DOI: 10.31857/S0004629921090024

Аннотация

Спутник “Kepler” пронаблюдал более восьмисот тесных двойных систем [1], для которых удалось измерить не только орбитальные периоды, но и скорости вращения звезд. Оказалось, что многие звезды в тесных двойных системах не синхронизованы, т.е. период вращения звезды не точно равен орбитальному периоду. В работе рассмотрены две модели, способные объяснить асинхронность звезд либо за счет дифференциального вращения звезды, либо за счет ненулевого эксцентриситета двойной системы. Проведено численное моделирование эволюции звезды в двойной системы с учетом обратного влияния компаньона на звезду в зависимости от орбитальных параметров и показано, что тесная двойная система может находиться не только в синхронизованном, но также в несинхронизованном состоянии за время жизни звезды на главной последовательности. Данная модель применена к системе KIC 8736245.

Ключевые слова: тесные двойные системы, приливные взаимодействия, асинхронные звезды, эволюция звезд

1. ВВЕДЕНИЕ

Половина из всех наблюдаемых звезд находятся в двойных (кратных) системах. Причем многие двойные системы достаточно тесные, с орбитальным периодом меньше десяти дней, ${{P}_{{{\text{orb}}}}} \leqslant 10$. Эволюция звезд в двойных системах значительно отличается от эволюции одиночных звезд. Например, в тесных двойных системах значительную роль играют приливные силы [2, 3], которые приводят двойную систему в состояние равновесия с круговой орбитой, к выравниванию орбитальной плоскости с плоскостью, перпендикулярной вращению звезды, и в состояние синхронизации, когда орбитальный период становится равным периоду вращения звезды [4].

Благодаря миссии “Kepler” удалось пронаблюдать достаточно много тесных двойных систем и измерить не только орбитальный период, но и собственную скорость вращения звезд (период вращения) [1]. Оказалось, что многие тесные двойные системы не синхронизованы, а находятся либо в субсинхронизованном ${{P}_{{{\text{orb}}}}}{\text{/}}{{P}_{{{\text{rot}}}}} < 1$, либо в сверхсинхронизованном ${{P}_{{{\text{orb}}}}}{\text{/}}{{P}_{{{\text{rot}}}}} > 1$ состоянии [1].

В работе рассмотрены две модели, которые могут объяснить асинхронное состояние тесных двойных систем. Первая модель объясняет асинхронное состояние за счет дифференциального вращения звезды. При определении скорости вращения звезды измеряют скорость вращения на ее поверхности. Но звезды вращаются дифференциально. Следовательно, орбитальная скорость (или орбитальный период) за счет приливных взаимодействий должна быть равна не поверхностной скорости вращения звезды (периоду вращения звезды на ее поверхности), а некоторой “равновесной” скорости вращения, которая может и не совпадать со скоростью вращения звезды на ее поверхности.

Вторая модель объясняет асинхронное состояние за счет ненулевого эксцентриситета орбиты. Если орбита двойной системы эллиптическая, то система будет стремиться не к синхронизации, а к псевдосинхронизации [5]. Другими словами, скорость вращения звезды будет стремиться к орбитальной скорости компаньона в периастре. Это связано с тем, что приливные силы сильно зависят от расстояния между двумя небесными телами [6], и наибольший эффект возникает при минимальном сближении, т.е. в периастре.

Эти модели применены к тесной двойной системе KIC 8736245, в которой одна звезда находится в субсинхронизованном состоянии, а другая в сверхсинхронизованном [7].

В работе [8] представлены данные по вращению 950 звезд в системах экзопланет. Было показано, что для экзопланет с радиусом больше шести радиусов Земли, ${{R}_{p}} > 6{{R}_{ \oplus }}$, период вращения звезды ${{P}_{{{\text{rot}}}}}$ приблизительно равен орбитальному периоду ${{P}_{{{\text{orb}}}}}$ (т.е. система находится либо в синхронном, либо в асинхронном состоянии) в диапазоне $1 < {{P}_{{{\text{orb}}}}} < 10$ дней.

В работе [9] были определены периоды вращения звезд для восьми двойных систем. Оказалось, что для четырех систем, у которых орбитальный период меньше 10 дней, период вращения звезды синхронизован с орбитальным периодом. Все эти системы имеют нулевой эксцентриситет. Остальные четыре системы имеют эксцентриситет в диапазоне $0.22 < e < 0.47$ и отношение периода вращения к орбитальному периоду, $0.05 < {{P}_{{{\text{rot}}}}}{\text{/}}{{P}_{{{\text{orb}}}}} < 0.35$, соответствуют асинхронному вращению. Такие системы могут быть объяснены режимом псевдосинхронизации.

2. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим тесную двойную систему, состоящую из двух компонентов. Первый компонент является звездой с массой в одну массу Солнца, отметим его индексом 1. Второй компонент (компаньон) является точечным источником, масса которого варьировалась, пометим его индексом 2. Оба компонента движутся по эллиптической орбите вокруг общего центра масс. При моделировании эволюции звезды учитывалось влияние второго компонента на эволюцию первого, которое, помимо гравитационного взаимодействия, включает в себя следующие эффекты: потеря массы звездного компонента за счет ветра, аккреция доли массы ветра на компаньон, перетекание вещества, заполняющего полость Роша, влияния приливных взаимодействий на звезду, спин-орбитальное взаимодействие, магнитное торможение, гравитационное излучение.

Моделирование осуществлялось с помощью свободного кода MESA версии 11701 [10–12]. Код MESA был создан для решения уравнений эволюции звезды в одномерном приближении с учетом многочисленных эффектов, которые не учитываются при трехмерном моделировании. Также код MESA содержит пакет binary, который позволяет моделировать эволюцию звезды в тесных двойных системах с учетом влияния компаньона на эволюцию звезды. Кратко опишем вышесказанные эффекты и параметры моделирования.

2.1. Основные формулы и определения

Орбитальный угловой момент двойной системы определяется выражением

(1)

${{J}_{{{\text{orb}}}}} = {{M}_{1}}{{M}_{2}}\sqrt {\frac{{Ga(1 - {{e}^{2}})}}{{{{M}_{1}} + {{M}_{2}}}}} ,$

где ${{M}_{1}}$, ${{M}_{2}}$ – массы первого и второго компонентов соответственно, $G$ – гравитационная постоянная, $e$ – эксцентриситет, $a$ – большая полуось. Эволюция двойной системы определяется изменением параметров орбиты с течением времени. Производная по времени от выражения (1) дает [13]

(2)

$\frac{{\dot {a}}}{a} = 2\frac{{{{{\dot {J}}}_{{{\text{orb}}}}}}}{{{{J}_{{{\text{orb}}}}}}} - 2\frac{{{{{\dot {M}}}_{1}}}}{{{{M}_{1}}}} - 2\frac{{{{{\dot {M}}}_{2}}}}{{{{M}_{2}}}} + \frac{{{{{\dot {M}}}_{1}} + {{{\dot {M}}}_{2}}}}{{{{M}_{1}} + {{M}_{2}}}} + 2\frac{{e\dot {e}}}{{1 - {{e}^{2}}}}.$

Из формулы (2) видно, что изменение большой полуоси происходит либо за счет изменения орбитального углового момента, либо за счет изменения эксцентриситета системы, либо за счет изменения массы звезд.

Изменение массы $\dot {M}$ звезд может происходить за счет трех эффектов: потери массы за счет звездного ветра ${{\dot {M}}_{{{\text{wind}}}}}$, перетекание массы за счет заполнения полости Роша через точку Лагранжа ${{\dot {M}}_{{{\text{rlof}}}}}$ и за счет доли аккреции звездного ветра на компаньон. Cуммарную потерю массы первого компонента можно записать в виде [13]

(3)

${{\dot {M}}_{1}} = {{\dot {M}}_{{{\text{wind}},1}}} + {{\dot {M}}_{{{\text{rlof}}}}} - {{\varepsilon }_{{{\text{wind}},2}}}{{\dot {M}}_{{{\text{wind}},2}}},$

а второго компонента – в виде

(4)

${{\dot {M}}_{2}} = {{\dot {M}}_{{{\text{wind}},2}}} - {{\varepsilon }_{{{\text{rlof}}}}}{{\dot {M}}_{{{\text{rlof}}}}} - {{\varepsilon }_{{{\text{wind}},1}}}{{\dot {M}}_{{{\text{wind}},1}}},$

где ${{\varepsilon }_{{{\text{wind}}}}}$ – доля потери массы, которая аккрецирует на звезду за счет звездного ветра компаньона, ${{\varepsilon }_{{{\text{rlof}}}}}$ – доля потери массы, которая аккрецирует на компаньон за счет заполнения полости Роша. Суммарное количество массы, которое потеряет двойная системы при своей эволюции, определяется суммой потерь масс каждого компонента [13]

(5)

$\begin{gathered} {{{\dot {M}}}_{\infty }} = (1 - {{\varepsilon }_{{{\text{rlof}}}}}){{{\dot {M}}}_{{{\text{rlof}}}}} + (1 - {{\varepsilon }_{{{\text{wind}},1}}}){{{\dot {M}}}_{{{\text{wind}},1}}} + \\ \, + (1 - {{\varepsilon }_{{{\text{wind}},2}}}){{{\dot {M}}}_{{{\text{wind}},2}}}. \\ \end{gathered} $

Орбитальный угловой момент может изменяться за счет потери массы звезды (звездный ветер) ${{\dot {J}}_{{{\text{wind}}}}}$, либо за счет заполнения полости Роша и перетекания вещества на компаньон ${{\dot {J}}_{{{\text{rlof}}}}}$, либо за счет взаимодействия с окружающем диском ${{\dot {J}}_{{{\text{disk}}}}}$. Помимо этого будут учтены эффекты, связанные с гравитационным излучением ${{\dot {J}}_{{{\text{gr}}}}}$, магнитным торможением ${{\dot {J}}_{{{\text{mb}}}}}$ и спин-орбитальным взаимодействием ${{\dot {J}}_{{{\text{ls}}}}}$. Общая формула изменения орбитального углового момента имеет вид [12]

(6)

${{\dot {J}}_{{{\text{orb}}}}} = {{\dot {J}}_{{{\text{rlof}}}}} + {{\dot {J}}_{{{\text{wind}}}}} + {{\dot {J}}_{{{\text{disk}}}}} + {{\dot {J}}_{{{\text{gr}}}}} + {{\dot {J}}_{{{\text{mb}}}}} + {{\dot {J}}_{{{\text{ls}}}}}.$

Эволюция эксцентриситета определяется приливным взаимодействием двух звезд ${{\dot {e}}_{{{\text{tides}}}}}$, взаимодействием между двойной системой и диском ${{\dot {e}}_{{{\text{disk}}}}}$, а также за счет фазовой зависимости звездного ветра или перетекания массы за счет заполнения полости Роша ${{\dot {e}}_{{{\text{ml}}}}}$ (см. ниже) [13]. Общая формула изменение эксцентриситета запишется в виде

(7)

$\dot {e} = {{\dot {e}}_{{{\text{tides}}}}} + {{\dot {e}}_{{{\text{ml}}}}} + {{\dot {e}}_{{{\text{disk}}}}}.$

Рассмотрим каждый процесс в отдельности.

2.1.1. Перетекание вещества за счет заполнения полости Роша. Звезда в процессе своей эволюции может заполнять полость Роша. Это приводит к возможному перетеканию массы с одного компонента на другую. Радиус полости Роша определяется формулой Эгглтона [14]. Для первого компонента формула Эгглтона имеет вид

(8)

${{R}_{L}} = \frac{{1 - {{e}^{2}}}}{{1 + ecos\theta }}\frac{{0.49{{q}^{{2/3}}}a}}{{0.6{{q}^{{2/3}}} + ln(1 + {{q}^{{1/3}}})}},$

где $\theta $ – истинная аномалия, а $q = \tfrac{{{{M}_{1}}}}{{{{M}_{2}}}}$ – отношение масс звезд. Радиус полости Роша для второго компонента определяется заменой масс в отношении ${{q}_{2}} = \tfrac{{{{M}_{2}}}}{{{{M}_{1}}}}$. Темп обмена массы задавался по формуле Риттера, [15, 12 ]

(9)

${{\dot {M}}_{{{\text{rlof}}}}} = - {{\dot {M}}_{0}}exp\left( {\gamma ({{q}_{2}})\frac{{{{R}_{1}} - {{R}_{{L,1}}}}}{{{{H}_{{P,1}}}}}} \right),$

где ${{H}_{P}} = - dr{\text{/}}dlnP$ – масштаб неоднородности давления. Темп потери массы ${{\dot {M}}_{0}}$ определяется по формуле

(10)

${{\dot {M}}_{0}} = \frac{{2\pi }}{{\sqrt e }}{{F}_{1}}({{q}_{2}})\frac{{R_{{L1}}^{3}}}{{G{{M}_{1}}}}\mathop {\left( {\frac{{{{k}_{{\text{B}}}}{{T}_{{{\text{eff}}}}}}}{{{{m}_{p}}{{\mu }_{{{\text{ph}}}}}}}} \right)}\nolimits^{3/2} {{\rho }_{{{\text{ph}}}}},$

где $e \approx 2.72$ – основание натурального логарифма, ${{m}_{p}}$ – масса протона, ${{T}_{{{\text{eff}}}}}$ – эффективная температура донора, ${{k}_{{\text{B}}}}$ – постоянная Стефана–Больцмана, ${{\mu }_{{{\text{ph}}}}}$ и ${{\rho }_{{{\text{ph}}}}}$ – средний молекулярный вес и плотность в фотосфере. Функции ${{F}_{1}}({{q}_{2}})$ и $\gamma ({{q}_{2}})$ зависят только от отношения масс и определены в работе [15].

Для учета изменения углового момента использовалась $\alpha \beta \gamma \delta $ – модель [16]. В этой модели эффективность аккреции задается с помощью параметра ${{\varepsilon }_{{{\text{rlof}}}}}$, который определяется соотношением

(11)

${{\varepsilon }_{{{\text{rlof}}}}} = 1 - \alpha - \beta - \delta ,$

где $\alpha $, $\beta $, $\delta $ – доля массы, которая теряется в окрестности донора, аккретора и за счет тороидального диска, его радиус определяется соотношением ${{R}_{{{\text{toroid}}}}} = {{\gamma }^{2}}a$, где $\gamma $ – параметр задачи. В этой модели изменение углового момента задается формулой [16]

(12)

${{\dot {J}}_{{{\text{rlof}}}}} = \frac{{\alpha + \beta {{q}^{2}} + \delta \gamma {{{(1 + q)}}^{2}}}}{{1 + q}}\frac{{{{{\dot {M}}}_{{{\text{rlof}}}}}}}{{{{M}_{2}}}}{{J}_{{{\text{orb}}}}}.$

В данной работе коэффициенты $\alpha ,\;\beta ,\;\gamma ,\;\delta $ приняты равными $\alpha = 0.2$, $\beta = 0.3$, $\gamma = 0.4$ и $\delta = 0.1$.

2.1.2. Звездный ветер. Для учета потерь массы звездного компонента за счет ветра используется формула Реймерса [17]

(13)

${{\dot {M}}_{{{\text{wind}}}}} = - 4 \times {{10}^{{13}}}\eta \frac{{LR}}{M}\;{{M}_{ \odot }}{\text{/yr}}$

с коэффициентом $\eta = 0.5$. Фактор Тоута–Эгглто-на [18], который усиливает ветер за счет приливного влияния и магнитной активности, не учитывался. На скорость потерь звездного ветра влияют вращение и излучение, поэтому использовался так называемый $\Omega \Gamma $ предел, который учитывает поправки за счет вращения $\Omega $ и излучения $L$ звезды [11, 19, 20],

(14)

$\dot {M}(\Omega ) = \dot {M}(0)\mathop {\left( {\frac{1}{{1 - \Omega {\text{/}}{{\Omega }_{{{\text{crit}}}}}}}} \right)}\nolimits^\xi ,$

где $\Omega _{{{\text{crit}}}}^{2} = \left( {1 - \tfrac{L}{{{{L}_{{{\text{crit}}}}}}}} \right)\tfrac{{GM}}{{{{R}^{3}}}}$ – критическая угловая скорость на поверхности звезды, ${{L}_{{{\text{crit}}}}} = 4\pi cGM{\text{/}}k$ – эддингтоновская светимость, $k$ – непрозрачность, $\dot {M}(0)$ – скорость потерь массы без учета вращения и излучения. В данной работе величина $\xi $ выбирается равной $\xi = 0.43$ [21].

Предполагая, что ветер сферически симметричен, получаем потери углового момента за счет ветра [13],

(15)

${{\dot {J}}_{{{\text{wind}},1,2}}} = {{\dot {M}}_{{{\text{wind}},1,2}}}\mathop {\left( {\frac{{{{M}_{{2,1}}}}}{{{{M}_{1}} + {{M}_{2}}}}a} \right)}\nolimits^2 \frac{{2\pi }}{{{{P}_{{{\text{orb}}}}}}}\sqrt {1 - {{e}^{2}}} .$

Суммарное изменение углового момента двойной системы за счет ветра определяется соотношением ${{\dot {J}}_{{{\text{wind}}}}} = {{\dot {J}}_{{{\text{wind}},1}}} + {{\dot {J}}_{{{\text{wind}},2}}}$.

2.1.3. Аккреция звездного ветра. Часть звездного ветра звезды может аккрецировать на компаньон. Считая аккрецию сферически симметричной, средний темп аккреции на компаньон оценивается по формуле Бонди-Хойла [22],

(16)

${{\dot {M}}_{2}} = - \frac{1}{{\sqrt {1 - {{e}^{2}}} }}\mathop {\left( {\frac{{GM}}{{v_{w}^{2}}}} \right)}\nolimits^2 \frac{{{{\alpha }_{{{\text{BH}}}}}}}{{2{{a}^{2}}}}\frac{1}{{{{{(1 + {{v}^{2}})}}^{{3/2}}}}}{{\dot {M}}_{1}},$

где ${{v}^{2}} = \tfrac{{v_{{{\text{orb}}}}^{2}}}{{v_{w}^{2}}}$, а ${{v}_{w}}$ – скорость ветра. Скорость ветра оценивалась как $v_{w}^{2} \approx 2\beta \tfrac{{GM}}{R}$ с коэффициентом $\beta = \tfrac{1}{8}$. В данной работе коэффициент ${{\alpha }_{{{\text{BH}}}}}$ задавался равным ${{\alpha }_{{{\text{BH}}}}} = 3{\text{/}}2$ в соответствии с работой [23].

2.1.4. Изменение эксцентриситета за счет потери массы. Потеря массы за счет звездного ветра или за счет перетекания массы через заполнение полости Роша могже быть не постоянна в течение полного орбитального периода. Это может приводить к изменению эксцентриситета двойной системы [24]. Если двойная система теряет массу на бесконечности ${{\dot {M}}_{\infty }}(\theta )$, то изменение эксцентриситета определяется соотношением [13, 24]

(17)

${{\dot {e}}_{{{\text{loss}}}}} = \frac{{{\text{|}}{{{\dot {M}}}_{\infty }}(\theta ){\kern 1pt} {\text{|}}}}{{{{M}_{1}} + {{M}_{2}}}}(e + cos\theta ),$

где $\theta $ – истинная аномалия. Если потеря массы двойной системы на бесконечности постоянна во времени, то это не приводит к изменению эксцентриситета. Но если потеря массы $\dot {M}$ в периастре больше, чем в апоастре, то это приведет к увеличению эксцентриситета.

Часть звездного ветра звезды может аккрецировать на компаньон. Это будет приводить к изменению эксцентриситета. Формула изменения эксцентриситета за счет аккреции звездного ветра имеет вид [13]

(18)

${{\dot {e}}_{{{\text{acc}}}}} = 2\left| {{{{\dot {M}}}_{{{\text{acc}}}}}(\theta )} \right|\left( {\frac{1}{{{{M}_{1}}}} - \frac{1}{{{{M}_{2}}}}} \right)(e + cos\theta ).$

Суммарное изменение эксцентриситета определяется формулой

(19)

${{\dot {e}}_{{{\text{ml}}}}} = \int {\left( {{{{\dot {e}}}_{{{\text{loss}}}}}(\theta ) + {{{\dot {e}}}_{{{\text{acc}}}}}(\theta )} \right)d\theta } .$

2.1.5. Учет приливных сил. Приливные силы могут приводить к таким эффектам, как синхронизация частот и циркуляризация орбиты. Темп приливных взаимодействий определяется диссипацией приливного потока в звездах. Для учета приливных взаимодействий использовался формализм Хата [5] и Зана [25]. Рассматриваются два случая в зависимости от структуры звезды. В первом случае диссипация происходит в конвективной оболочке, во втором – в радиационной оболочке. Для описания эволюции орбитальных параметров используется формализм Хата [5], который в режиме слабого трения описывается формулами

(20)

$\begin{gathered} \dot {e} = - 27\left( {\frac{k}{T}} \right)\frac{{eq(1 + q)}}{{{{{(1 - {{e}^{2}})}}^{{13/2}}}}}\mathop {\left( {\frac{R}{a}} \right)}\nolimits^8 \times \\ \times \;\left( {{{f}_{3}}({{e}^{2}}) - \frac{{11}}{{18}}{{{(1 - {{e}^{2}})}}^{{3/2}}}{{f}_{4}}({{e}^{2}})\frac{\Omega }{\omega }} \right), \\ \end{gathered} $

(21)

$\begin{gathered} \dot {\Omega } = 3\left( {\frac{k}{T}} \right)\frac{{{{q}^{2}}}}{{{{r}_{g}}}}\mathop {\left( {\frac{R}{a}} \right)}\nolimits^6 \frac{\omega }{{{{{(1 - {{e}^{2}})}}^{6}}}} \times \\ \times \;\left( {{{f}_{2}}({{e}^{2}}) - {{{(1 - {{e}^{2}})}}^{{3/2}}}{{f}_{5}}({{e}^{2}})\frac{\Omega }{\omega }} \right), \\ \end{gathered} $

где ${{f}_{2}}$, ${{f}_{3}}$, ${{f}_{4}}$, ${{f}_{5}}$ – степенные функции эксцентриситета [5], $r_{g}^{2} = I{\text{/}}M{{R}^{2}}$, $I$ – момент инерции, ${{\omega }^{2}} = G({{M}_{1}} + {{M}_{2}}){\text{/}}{{a}^{3}}$, $k{\text{/}}T$ – диссипационный член, который определен ниже.

В случае, когда оболочка конвективная, отношение $\tfrac{k}{T}$ задается соотношением [26]

(22)

$\mathop {\left( {\frac{k}{T}} \right)}\nolimits_{{\text{conv}}} = \frac{2}{{21}}\frac{{{{f}_{{{\text{conv}}}}}}}{{{{\tau }_{{{\text{conv}}}}}}}\frac{{{{M}_{{{\text{env}}}}}}}{M}\;\mathop {{\text{yr}}}\nolimits^{ - 1} ,$

где ${{\tau }_{{{\text{conv}}}}}$ – характерное время оборота конвективной ячейки, определяется следующим соотношением

(23)

${{\tau }_{{{\text{conv}}}}} = 0.4311\,\mathop {\left( {\frac{{{{M}_{{{\text{env}}}}}{{R}_{{{\text{env}}}}}(R - {{R}_{{{\text{env}}}}}{\text{/}}2)}}{{3L}}} \right)}\nolimits^{1/3} ,$

где ${{M}_{{{\text{env}}}}}$, ${{R}_{{{\text{env}}}}}$ – масса и радиус оболочки. Если время оборота конвективной ячейки ${{\tau }_{{{\text{conv}}}}}$ больше орбитального периода, то диссипация будет подавлена на фактор $2{{\tau }_{{{\text{conv}}}}}{\text{/}}{{P}_{{{\text{orb}}}}}$ [27, 28]. Это определяется фактором ${{f}_{{{\text{conv}}}}}$, равным

(24)

${{f}_{{{\text{conv}}}}} = {\text{min}}\left[ {1,\mathop {\left( {\frac{{{{P}_{{{\text{orb}}}}}}}{{2{{\tau }_{{{\text{conv}}}}}}}} \right)}\nolimits^2 } \right].$

В случае, когда оболочка радиационная, то отношение $\tfrac{k}{T}$ задается по формуле Зана [25, 29]

(25)

$\mathop {\left( {\frac{k}{T}} \right)}\nolimits_{{\text{rad}}} = 1.9782 \times {{10}^{4}}\frac{{M{{R}^{2}}}}{{{{a}^{5}}}}{{(1 + q)}^{{5/6}}}{{E}_{2}}\;\mathop {{\text{yr}}}\nolimits^{ - 1} ,$

где численный фактор ${{E}_{2}}$ фитировался формулой

(26)

${{E}_{2}} = 1.592 \times {{10}^{{ - 9}}}{{M}^{{2.84}}}.$

Приведенные выше формулы качественно согласуются с наблюдениями, хотя и имеют серьезные недостатки [30].

2.1.6. Магнитное торможение. Звезды, подобные Солнцу, обладают конвективной оболочкой, в которой генерируется магнитное поле. Это магнитное поле может вносить существенный вклад в замедление вращения звезды из-за замагниченного ветра [31]. Следовательно, двойная система будет также изменять орбитальный угловой момент [22]. Раппапорт и др. [32] вывели формулу потерь углового момента звездой за счет магнитного торможения, которая имеет вид [22, 12 ]

(27)

$\begin{gathered} {{{\dot {J}}}_{{{\text{mb}}}}} = - 6.82 \times {{10}^{{34}}}\left( {\frac{{{{M}_{1}}}}{{{{M}_{ \odot }}}}} \right)\mathop {\left( {\frac{{{{R}_{1}}}}{{{{R}_{ \odot }}}}} \right)}\nolimits^{{{\gamma }_{m}}} \times \\ \, \times \mathop {\left( {\frac{{1d}}{{{{P}_{{{\text{orb}}}}}}}} \right)}\nolimits^3 \;[{\text{дин}}\;{\text{см}}]. \\ \end{gathered} $

Это выражение зависит от коэффициента ${{\gamma }_{m}}$, который выбирался равным ${{\gamma }_{m}} = 3$.

2.1.7. Спин-орбитальное взаимодействие. Как приливное взаимодействие, так и перетекание массы и звездный ветер могут сильно изменить угловой момент звезды. Поэтому необходимо учесть спин-орбитальное взаимодействие, которое будет изменять орбитальный угловой момент двойной системы. Учет этого эффекта основан на законе сохранения полного углового момента [12]. Изменение углового момента орбитального движения есть изменение вращательного углового момента звезды с учетом потерь массы за счет звездного ветра и перетекания вещества. Общее выражение имеет вид [12]

(28)

${{\dot {J}}_{{{\text{ls}}}}} = - \frac{1}{{\delta t}}\left( {\delta {{S}_{1}} - {{S}_{{1,{\text{lost}}}}}\frac{{{{{\dot {M}}}_{{{\text{wind}},1}}}}}{{{{{\dot {M}}}_{1}}}} + \delta {{S}_{2}} - {{S}_{{2,{\text{lost}}}}}} \right).$

2.1.8. Гравитационное излучение. Для общности был также включен эффект гравитационного излучения двух массивных тел. Гравитационное излучение эффективно для катаклизмических переменных с орбитальным периодом менее 3 ч. Знаменитый пульсар Халса-Тейлора имеет орбитальный период 7.75 ч. Изменение орбитального углового момента и эксцентриситета за счет гравитационного излучения определяется формулами [22]

(29)

${{\dot {J}}_{{{\text{gr}}}}} = - \frac{{32{{G}^{{7/2}}}}}{{5{{c}^{5}}}}\frac{{M_{1}^{2}M_{2}^{2}\sqrt {{{M}_{1}} + {{M}_{2}}} }}{{{{a}^{{7/2}}}}}\frac{{1 + \tfrac{7}{8}{{e}^{2}}}}{{{{{(1 - {{e}^{2}})}}^{2}}}},$

(30)

$\frac{{{{{\dot {e}}}_{{{\text{gr}}}}}}}{e} = - \frac{{304{{G}^{3}}}}{{15{{c}^{5}}}}\frac{{{{M}_{1}}{{M}_{2}}({{M}_{1}} + {{M}_{2}})}}{{{{a}^{4}}}}\frac{{1 + \tfrac{{121}}{{304}}{{e}^{2}}}}{{{{{(1 - {{e}^{2}})}}^{{5/2}}}}}.$

2.1.9. Другие эффекты. Другие эффекты, такие как слияние звездных компонентов, столкновения и эффект общей оболочки, не учитывались в данной работе.

2.2. Конвекция

В данном и в следующем разделах будут рассмотрены близкие процессы – конвекция и дифференциальное вращение. Эти процессы будут рассмотрены в диффузном приближении, с некоторым коэффициентом диффузии $D$ для каждого процесса. Предполагается, что суммарный коэффициент диффузии является суммой коэффициентов диффузии каждого процесса с некоторым весом ${{f}_{c}}$,

(31)

$\begin{gathered} D = {{D}_{{{\text{conv}}}}} + {{D}_{{{\text{sc}}}}} + {{D}_{{{\text{ov}}}}} + \\ \, + {{f}_{c}}({{D}_{{{\text{DSI}}}}} + {{D}_{{{\text{SHI}}}}} + {{D}_{{{\text{SSI}}}}} + {{D}_{{{\text{ES}}}}} + {{D}_{{{\text{GSF}}}}}). \\ \end{gathered} $

Весовой фактор ${{f}_{c}}$ определяет уменьшение коэффициентов диффузии за счет вращения для неустойчивостей, связанных с дифференциальным вращением, и принимает значения в диапазоне $0 \leqslant {{f}_{c}} \leqslant 1$.

Для дифференциального вращения необходимо будет знать коэффициент турбулентной вязкости, который отвечает за перераспределение углового момента в звездах. В данной работе коэффициент турбулентной вязкости приравнивается коэффициенту диффузии перераспределения вещества, но с одинаковым весом, равным единице [33],

(32)

$\begin{gathered} \nu = {{D}_{{{\text{conv}}}}} + {{D}_{{{\text{sc}}}}} + {{D}_{{{\text{ov}}}}} + \\ + \;{{D}_{{{\text{DSI}}}}} + {{D}_{{{\text{SHI}}}}} + {{D}_{{{\text{SSI}}}}} + {{D}_{{{\text{ES}}}}} + {{D}_{{{\text{GSF}}}}}, \\ \end{gathered} $

где ${{D}_{{{\text{conv}}}}}$ – коэффициент диффузии и турбулентной вязкости для процессов конвекции, ${{D}_{{{\text{sc}}}}}$ – полуконвекции, ${{D}_{{{\text{ov}}}}}$ – овершутинга, ${{D}_{{{\text{DSI}}}}}$ – динамической сдвиговой неустойчивости, ${{D}_{{{\text{SHI}}}}}$ – неустойчивости Солберга–Хойланда, ${{D}_{{{\text{SSI}}}}}$ – вековой сдвиговой неустойчивости, ${{D}_{{{\text{ES}}}}}$ – меридиональной циркуляции, ${{D}_{{{\text{GSF}}}}}$ – неустойчивости Голдрайха–Шуберта–Фрике. В данной работе фактор веса ${{f}_{c}}$ выбирается равным ${{f}_{c}} = 1{\text{/}}30$, как следует из теоретических соображений работы [34].

2.2.1. Конвекция. Звезда может находиться в гидродинамическом равновесии, но не находиться в тепловом равновесии одновременно. Это приводит к развитию конвекции. Конвекция будет происходить, если температурный градиент меньше адиабатического градиента [33],

(33)

${{\nabla }_{{{\text{ad}}}}} - \nabla \leqslant 0,$

где

(34)

${{\nabla }_{{{\text{ad}}}}} = \mathop {\left( {\frac{{\partial lnT}}{{\partial lnP}}} \right)}\nolimits_{{\text{ad}}} ,\quad \nabla = \left( {\frac{{\partial lnT}}{{\partial lnP}}} \right)$

– адиабатический и температурный градиенты соответственно. Этот критерий называется критерием Шварцшильда. Критерий Шварцшильда (33) не является верным по многим причинам. В частности, градиент молекулярного веса может препятствовать возникновению конвекции. Поэтому обобщенный критерий отсутствия конвекции имеет вид

(35)

${{\nabla }_{{{\text{ad}}}}} - \nabla + \frac{\phi }{\delta }{{\nabla }_{\mu }} \geqslant 0,$

где

$\begin{gathered} {{\nabla }_{\mu }} = \frac{{\partial ln\mu }}{{\partial lnP}},\quad \delta = - {{\left. {\frac{{\partial ln\rho }}{{\partial lnT}}} \right|}_{{\mu ,P}}}, \\ \phi = - {{\left. {\frac{{\partial ln\rho }}{{\partial ln\mu }}} \right|}_{{T,P}}}. \\ \end{gathered} $

Этот критерий называется критерием возникновения конвекции Леду. В данной работе для описания конвекции рассматривается критерий Леду (35) и применяется теория путей перемешивания, которая описывает конвекцию как диффузный процесс с коэффициентом диффузии, равным

(36)

${{D}_{{{\text{conv}}}}} = {{D}_{{{\text{mlt}}}}} = \frac{1}{3}{{\alpha }_{{{\text{mlt}}}}}{{H}_{p}}{{v}_{{{\text{conv}}}}},$

здесь ${{H}_{p}}$ – масштаб неоднородности давления, ${{v}_{{{\text{conv}}}}}$ – скорость конвективной ячейки. Численный параметр ${{\alpha }_{{{\text{mlt}}}}}$ в работе выбирался равным ${{\alpha }_{{{\text{mlt}}}}} = 1.8$.

Конвекция в звездах – достаточно быстрый процесс, в результате которого происходит выглаживание неоднородностей в конвективной области.

2.2.2. Полуконвекция. Полуконвекция происходит в случае, когда температурный градиент стабилизирует условие возникновения конвекции путем больших градиентов молекулярного веса. Граница области возникновения полуконвекции определяется соотношением

(37)

$\frac{\phi }{\delta }{{\nabla }_{\mu }} \geqslant \nabla - {{\nabla }_{{{\text{ad}}}}} \geqslant 0.$

Полуконвекция является вековой неустойчивостью в том смысле, что она происходит на тепловых временны́х масштабах. Коэффициент диффузии определяется выражением [11, 35]:

(38)

${{D}_{{{\text{sc}}}}} = {{\alpha }_{{{\text{sc}}}}}\left( {\frac{K}{{6{{c}_{p}}\rho }}} \right)\frac{{\nabla - {{\nabla }_{{{\text{ad}}}}}}}{{{{\nabla }_{{{\text{ad}}}}} - \nabla + \tfrac{\phi }{\delta }{{\nabla }_{\mu }}}},$

где ${{c}_{p}}$ – удельная теплоемкость при постоянном давлении, $K = \tfrac{{4ac{{T}^{3}}}}{{3k\rho }}$, $a$ – постоянная Стефана-Больцмана. Коэффициент ${{\alpha }_{{{\text{sc}}}}}$ в данной работе выбран равным ${{\alpha }_{{{\text{sc}}}}} = 0.01$.

2.2.3. Овершутинг. Овершутинг определяется вне Шварцшильдовской границы конвективной области, которая определена условием (33). На этой границе сила плавучести и, следовательно, ускорение конвективной ячейки, равна нулю. Но скорость конвективной ячейки не обязательно равна нулю на этой границе. Это приводит к тому, что конвективная ячейка продолжает движение вне конвективной области, определенной критерием Шварцшильда, но с замедлением. Такой процесс называется овершутинг. В данной работе овершутинг рассматривается через экспоненциальное затухание с коэффициентом диффузии, равным [11]

(39)

${{D}_{{{\text{ov}}}}} = {{D}_{{{\text{conv}}}}}exp\left( { - \frac{{2\Delta r}}{{{{f}_{{{\text{ov}}}}}{{H}_{p}}}}} \right),$

где $\Delta r$ – расстояние от начала границы конвективной области, ${{f}_{{{\text{ov}}}}}$ – безразмерный параметр, который определяет размер области овершутига. В данной работе этот параметр выбирался равным ${{f}_{{{\text{ov}}}}} = 0.004$.

2.3. Дифференциальное вращение

В данном разделе рассматриваются неустойчивости, которые приводят к перемешиванию вещества и перераспределению углового момента за счет дифференциального вращения звезды. Эти неустойчивости можно разделить на две группы в зависимости от характерных времен, на которых они действуют [36]. Это динамические и вековые неустойчивости. Первые действуют на характерных временах свободного падения ${{\tau }_{{{\text{dyn}}}}} = \sqrt {{{R}^{3}}{\text{/}}GM} $, а вторые на временах Кельвина–Гемгольца ${{\tau }_{{HK}}} = G{{M}^{2}}{\text{/}}LR$, где $L$ – светимость звезды [37]. Динамическое время на много порядков меньше, чем любые другие характерные времена эволюции звезды. На динамических временах перемешивание вещества и перераспределение углового момента происходит достаточно быстро (мгновенно). Например, для Солнца характерные времена равны ${{\tau }_{{{\text{dyn}}}}} \approx 1500$ c, ${{\tau }_{{HK}}} \approx {{10}^{{15}}}$ c.

Дифференциальное вращение звезд возникает либо за счет неустойчивости, либо за счет взаимодействия турбулентной конвекции с вращением [38]. В данной работе рассматривается пять видов неустойчивостей: динамическая сдвиговая неустойчивость, меридиональная циркуляция (циркуляция Эддингтона–Свита), вековая сдвиговая неустойчивость, неустойчивость Солберга–Хойланда, неустойчивость Голдрайха–Шуберта–Фрике. Данные виды неустойчивостей рассматриваются в диффузном приближении, с некоторыми коэффициентами диффузии и весовым эффективным фактором. Дифференциальное вращение переносит угловой момент и перераспределяет вещество внутри звезды [38]. Поэтому рассматриваются два уравнения [33, 36]. Уравнение перемешивания вещества,

(40)

$\frac{{\partial {{X}_{n}}}}{{\partial t}} = \frac{\partial }{{\partial M}}\left[ {{{{(4\pi {{r}^{2}}\rho )}}^{2}}D\frac{{\partial {{X}_{n}}}}{{\partial M}}} \right] + \mathop {\left( {\frac{{d{{X}_{n}}}}{{dt}}} \right)}\nolimits_{{\text{nuc}}} ,$

и уравнение переноса углового момента,

(41)

$\frac{{\partial \Omega }}{{\partial t}} = \frac{1}{i}\frac{\partial }{{\partial M}}\left[ {{{{(4\pi {{r}^{2}}\rho )}}^{2}}i\nu \frac{{\partial \Omega }}{{\partial M}}} \right] - \frac{\Omega }{r}\left( {\frac{{\partial r}}{{\partial t}}} \right)\frac{{dlni}}{{dlnr}},$

где $D$ – суммарный коэффициент диффузии каждого процесса, ${{X}_{n}}$ – массовая доля каждого элемента вида $n$, $i$ – удельный момент инерции звезды.

Вкратце рассмотрим каждую неустойчивость отдельно.

2.3.1. Динамическая сдвиговая неустойчивость. Динамическая сдвиговая неустойчивость возникает, когда энергия сдвигового потока становится сравнима с работой, совершаемой силами плавучести по адиабатическому переносу элемента массы в гравитационном поле [33]. Стабилизирующим фактором сдвигового потока является градиент плотности. Вдоль поверхности постоянной плотности любое дифференциальное вращение неустойчиво [36]. Условие устойчивости определяется числом Ричардсона $Ri$, которое при дифференциальном рассмотрении определяется как отношение силы плавучести к квадрату разности скоростей [33, 36, 39],

(42)

$Ri = \frac{{{{N}^{2}}}}{{\mathop {\left( {\tfrac{{d\Omega }}{{dlnr}}} \right)}\nolimits^2 }} > R{{i}_{{{\text{crit}}}}} \approx \frac{1}{4},$

где $N$ – частота Брунта-Вайсала. Коэффициент диффузии определяется характерным пространственным масштабом области неустойчивости ${{d}_{{{\text{inst}}}}}$, масштабом неоднородности давления ${{H}_{p}}$ и локальным динамическим временем ${{\tau }_{{{\text{dyn}}}}}$ [33]:

(43)

${{D}_{{{\text{DSI}}}}} = {{\left[ {{\text{min}}\{ {{d}_{{{\text{inst}}}}},{{H}_{p}}\} \left( {1 - {\text{max}}{\kern 1pt} \left\{ {\frac{{Ri}}{{R{{i}_{{{\text{crit}}}}}}},0} \right\}} \right)} \right]}^{2}}{\kern 1pt} {\text{/}}{{\tau }_{{{\text{dyn}}}}}.$

Считается, что неустойчивость достаточно слабая при малых отклонениях числа Ричардсона от критического значения $R{{i}_{{{\text{crit}}}}} \approx \tfrac{1}{4}$, поэтому был добавлен квадратичный фактор в соотношение (43).

2.3.2. Неустойчивость Солберга–Хойланда. Неустойчивость Солберга–Хойланда возникает в случае, когда направление суммарной силы, действующей на массовый элемент, будет иметь то же направление, что и смещение этого элемента [33]. Условие устойчивости против осесимметричных адиабатических возмущений можно разделить на два условия. Первое условие устойчивости на экваторе в вертикальном направлении определяется критерием вида [33]

(44)

${{R}_{{{\text{SH}}}}} = {{N}^{2}} + \frac{1}{{{{r}^{3}}}}\frac{d}{{dr}}{{({{r}^{2}}\Omega )}^{2}} \geqslant 0.$

Если удельный угловой момент $j \sim {{r}^{2}}\Omega $ не зависит от радиуса, то данный критерий сводится к критерию Леду возникновения конвекции. Если среда устойчива по отношению к конвекции, то данный критерий сводится к критерию устойчивости Рэлея вращающейся жидкости. Второе условие сводится к условию устойчивости дифференциального вращения вдоль поверхности постоянной энтропии и требует, чтобы на такой поверхности выполнялось условие $\partial j{\text{/}}\partial z \leqslant 0$ [39].

Коэффициент диффузии определяется аналогично динамической сдвиговой неустойчивости: характерным пространственным масштабом области неустойчивости ${{d}_{{{\text{inst}}}}}$, масштабом неоднородности давления ${{H}_{p}}$ и локальным динамическим временем ${{\tau }_{{{\text{dyn}}}}}$:

(45)

${{D}_{{{\text{SHI}}}}} = {{\left[ {{\text{min}}\{ {{d}_{{{\text{inst}}}}},{{H}_{p}}\} \left( {\frac{{r{{R}_{{{\text{SH}}}}}}}{g}} \right)} \right]}^{2}}{\text{/}}{{\tau }_{{{\text{dyn}}}}}.$

2.3.3. Вековая сдвиговая неустойчивость. Вековая сдвиговая неустойчивость аналогична динамической сдвиговой неустойчивости, только стабилизация происходит не за счет градиента плотности, а за счет градиента температур. Поэтому этот процесс происходит на масштабах времени Кельвина–Гемгольца ${{\tau }_{{HK}}}$, когда характерное время тепловой диффузии много меньше характерного времени диффузии углового момента. Это означает, что в среде обмен тепла происходит быстрее перераспределения углового момента. Условие в звезде определяется числом Прандтля, которое является отношением кинематической вязкости к коэффициенту температуропроводности ${\text{Pr}} = \tfrac{\nu }{\chi }$. Для звезд, как правило, $\Pr \ll 1$. В работе [36] было показано, что вековая сдвиговая неустойчивость определяется двумя условиями:

(46)

$R{{i}_{{s,1}}} = \frac{{PrR{{e}_{c}}}}{8}\frac{{\rho \delta }}{P}({{\nabla }_{{{\text{ad}}}}} - \nabla )\mathop {\left( {g\frac{{dlnr}}{{d\Omega }}} \right)}\nolimits^2 > R{{i}_{{{\text{crit}}}}},$

(47)

$R{{i}_{{s,2}}} = \frac{{\rho \phi {{\nabla }_{\mu }}}}{P}\mathop {\left( {g\frac{{dlnr}}{{d\Omega }}} \right)}\nolimits^2 > R{{i}_{{{\text{crit}}}}},$

где ${\text{R}}{{{\text{e}}}_{c}}$ – критическое число Рейнольдса. Второе условие связано с тем, что $\mu $-градиент (градиент среднего молекулярного веса) может стабилизировать вековую сдвиговую неустойчивость. Крупномасштабная скорость определяется как скорость турбулентного элемента и оценивается величиной [36]

(48)

${{v}_{{{\text{SSI}}}}} = \sqrt {\frac{\nu }{{{{{\operatorname{Re} }}_{c}}}}\frac{{d\Omega }}{{dlnr}}} $

и ограничивается скоростью звука [33].

Коэффициент диффузии определяется крупномасштабной скоростью турбулентного элемента ${{v}_{{{\text{SSI}}}}}$, масштабом неоднородности крупномасштабной скорости ${{H}_{{{v},ssi}}} = {\text{|}}dr{\text{/}}dln{{v}_{{{\text{SSI}}}}}{\kern 1pt} {\text{|}}$ и масштабом неоднородности давления ${{H}_{p}}$

(49)

$\begin{gathered} {{D}_{{{\text{SSI}}}}} = {\text{min}}\{ {{{v}}_{{{\text{SSI}}}}},{{c}_{s}}\} min\{ {{H}_{{{v},{\text{SSI}}}}},{{H}_{p}}\} \times \\ \, \times \mathop {\left( {1 - \frac{{max\{ R{{i}_{{s,1}}},R{{i}_{{s,2}}}\} }}{{{{R}_{{i,c}}}}}} \right)}\nolimits^2 . \\ \end{gathered} $

2.3.4. Меридиональная циркуляция. Вращающаяся звезда может не находиться одновременно в гидродинамическом и тепловом равновесии. Это связано с тем, что поверхности постоянной температуры и постоянного давления могут не совпадать [33]. Это приводит к развитию крупномасштабного меридионального течения. Скорость меридионального течения была оценена в работе [40]

(50)

$\begin{gathered} {{{v}}_{e}} = \frac{{{{\nabla }_{{{\text{ad}}}}}}}{{\delta ({{\nabla }_{{{\text{ad}}}}} - \nabla )}} \times \\ \, \times \frac{{{{\Omega }^{2}}{{r}^{3}}L}}{{{{G}^{2}}{{M}^{2}}}}\left[ {\frac{{2({{\varepsilon }_{n}} + {{\varepsilon }_{\nu }}){{r}^{2}}}}{L} - \frac{{2{{r}^{2}}}}{M} - \frac{3}{{4\pi \rho r}}} \right]. \\ \end{gathered} $

В работе [40] Киппенхан не учел влияние $\mu $-градиента, который может стабилизировать меридиональную циркуляцию. Эта стабилизирующая меридиональная скорость оценивается как [33]

(51)

${{v}_{\mu }} = \frac{{{{H}_{p}}}}{{{{\tau }_{{HK}}}}}\frac{{\phi {{\nabla }_{\mu }}}}{{\delta (\nabla - {{\nabla }_{{{\text{ad}}}}})}}.$

Тогда скорость меридионального течения определяется формулой ${{{v}}_{{{\text{ES}}}}} = {\text{max}}\{ {\text{|}}{{{v}}_{e}}{\kern 1pt} {\text{|}}\; - \;{\text{|}}{{{v}}_{\mu }}{\kern 1pt} {\text{|}},0\} $. Коэффициент диффузии определяется скоростью крупномасштабного течения ${{{v}}_{{{\text{ES}}}}}$, масштабом неоднородности скорости ${{H}_{{{v},{\text{ES}}}}} = {\text{|}}dr{\text{/}}dln{{{v}}_{{{\text{ES}}}}}{\kern 1pt} {\text{|}}$ и пространственным масштабом неустойчивости ${{d}_{{{\text{inst}}}}}$:

(52)

${{D}_{{{\text{ES}}}}} = {\text{min}}\{ {{d}_{{{\text{inst}}}}},{{H}_{{{v},{\text{ES}}}}}\} {{{v}}_{{{\text{ES}}}}}.$

2.3.5. Неустойчивость Голдрайха–Шуберта–Фрике. Неустойчивость Голдрайха–Шуберта–Фрике против осесимметричных возмущений исследовалась в работах [41, 42]. Они показали, что в невязкой среде, для которой $\Pr \ll 1$, неустойчивость возникает при условиях [33]

(53)

$\frac{{\partial j}}{{\partial r}} \geqslant 0,\quad \frac{{\partial \Omega }}{{\partial z}} = 0.$

Первое условие аналогично условию неустойчивости Солберга–Хойланда, но стабилизация происходит за счет градиента температуры. Второе условие означает бессдвиговое течение в вертикальной плоскости. Нарушение этого условия приводит к возбуждению меридионального течения [33]. Скорость крупномасштабного течения можно оценить по формуле [36]

(54)

${{v}_{g}} = \frac{{2{{H}_{T}}}}{{{{H}_{j}}}}\frac{{dln\Omega }}{{dlnr}}{{v}_{e}},$

где ${{H}_{T}} = - dr{\text{/}}dlnT$, ${{H}_{j}} = - dr{\text{/}}dlnj$ – масштабы неоднородности температуры и удельного углового момента соответственно. Принимая во внимание стабилизирующий эффект за счет $\mu $-градиента, результирующая скорость крупномасштабного течения оценивается как ${{v}_{{{\text{GSF}}}}} = {\text{max}}\{ {\text{|}}{{{v}}_{g}}{\kern 1pt} {\text{|}}\; - \;{\text{|}}{{{v}}_{\mu }}{\kern 1pt} {\text{|}}\} $. Коэффициент диффузии определяется скоростью крупномасштабного течения ${{{v}}_{{{\text{GSF}}}}}$, масштабом неоднородности скорости ${{H}_{{c,{\text{GSF}}}}} = {\text{|}}dr{\text{/}}dln{{{v}}_{{{\text{GSF}}}}}{\kern 1pt} {\text{|}}$ и масштабом неустойчивости ${{d}_{{{\text{inst}}}}}$ [33]:

(55)

${{D}_{{{\text{GSF}}}}} = min{\text{\{ }}{{d}_{{{\text{inst}}}}},{{H}_{{c,{\text{GSF}}}}}{\text{\} }}{{{v}}_{{{\text{GSF}}}}}.$

При малых градиентах угловой скорости циркуляция Эддингтона–Свита преобладает над неустойчивостью Голдрайха–Шуберта–Фрике. С увеличением градиента угловой скорости неустойчивость Голдрайха–Шуберта–Фрике начинает преобладать над циркуляцией Эддингтона–Свита.

2.4. Параметры моделирования

В работе проведено численное моделирование эволюции звезды в двойной системе в зависимости от начальных орбитальных параметров (орбитальный период, эксцентриситет, масса компаньона). В начальный момент времени $t = $ 10⁵ лет масса звезды задавалась равной одной массе Солнца ${{M}_{1}} = {{M}_{ \odot }}$ для всех параметров моделирования с металличностью $z$ равной $z = 0.02$. Масса компаньона варьировалась в диапазоне ${{M}_{2}} = [0.01;\;0.1;\;1;\;10]\,{{M}_{ \odot }}$. Нижний предел этого диапазона приблизительно соответствует десяти массам Юпитера [43], а верхний предел – массивным звездам [44]. Начальный эксцентри-ситет двойной системы выбирался равным $e = [0;\;0.2;\;0.4;\;0.6;\;0.8]$, а начальный орбитальный период задавался равным ${{P}_{{{\text{orb}}}}} = [5;\;7.5;\;10]$ дней. Всего было промоделировано 60 моделей эволюции звезд с различными начальными орбитальными параметрами. Моделирование проводилось с момента времени $t = $ 10⁵ лет либо до момента времени, когда орбитальный период становился приблизительно равным ${{P}_{{{\text{orb}}}}} \approx 0.6$ дней, либо до момента времени $t = $ 10¹⁰ лет, что приблизительно составляет время жизни звезды на главной последовательности для массы звезды, равной одной массе Солнца. В начальный момент моделирования $t = $ 10⁵ лет задавалось твердотельное вращение основной звезды с линейной скоростью на поверхности звезды, равной ${{v}_{{{\text{sur}}}}} = 2$ км/с для всех моделей. Это соответствует начальному периоду вращения поверхности основной звезды, равной ${{P}_{{{\text{rot}}}}} \approx 22$ дня. Например, период вращения поверхности Солнца на экваторе приблизительно равен ${{P}_{{{\text{rot}}}}} \approx 25$ дней. В начальный момент времени для всех моделей двойная система находилась в субсинхронизованном состоянии, так как ${{P}_{{{\text{orb}}}}}{\text{/}}{{P}_{{{\text{rot}}}}} < 1$.

3. РЕЗУЛЬТАТЫ

В данной главе представлены результаты эволюции параметров орбиты (эксцентриситета, орбитального периода и отношения периода вращения звезды к орбитальному периоду) тесной двойной системы в зависимости от возраста звезды.

3.1. Изменение эксцентриситета

Во всех моделях изменение эксцентриситета происходит за счет приливных взаимодействий. Только незначительное влияние на увеличение эксцентриситета вносит эффекты потери массы и аккреции (2.1.4) для следующих моделей с параметрами: ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, ${{P}_{{{\text{orb}}}}} = 5$ дней, $e = 0.6$; ${{M}_{2}}\, = \,0.01\;{{M}_{ \odot }}$, ${{P}_{{{\text{orb}}}}} = 5$ дней, $e = 0.8$; ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, ${{P}_{{{\text{orb}}}}} = 7.5$ дней, $e = 0.8$; ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, ${{P}_{{{\text{orb}}}}} = $ = 10 дней, $e = 0.8$ и ${{M}_{2}} = 0.1\;{{M}_{ \odot }}$, ${{P}_{{{\text{orb}}}}} = 5$ дней, $e = 0.8$. Увеличение эксцентриситета происходит в конце численного счета, когда орбитальный период становится близким к величине ${{P}_{{{\text{orb}}}}} \approx $ ≈ 0.6 дней. Для модели с параметрами ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, ${{P}_{{{\text{orb}}}}} = 5$ дней, $e = 0.8$ характерные времена изменения эксцентриситета за счет накачки в 5 раз больше, чем за счет приливных взаимодействий при возрасте основной звезды ${{t}_{{{\text{age}}}}} \approx 2.9 \times {{10}^{8}}$ лет. Это означает, что эксцентриситет двойной системы будет не уменьшаться за счет приливных сил, а увеличиваться за счет накачки эксцентриситета.

Изменение эксцентриситета двойной системы с течением времени (в годах) показано на рис. 1–4 для конфигураций орбит с начальным эксцентриситетом $e = 0.2$, 0.4, 0.6 и 0.8 соответственно. Разные цвета кривых означают следующее: синий цвет – начальный орбитальный период равен ${{P}_{{{\text{orb}}}}} = 5$ дней, зеленый – ${{P}_{{{\text{orb}}}}} = 7.5$ дней, красный – ${{P}_{{{\text{orb}}}}} = 10$ дней. Разный стиль кривых означает следующее: сплошная кривая соответствует массе компаньона ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, штрихпунктирная кривая – $0.1\;{{M}_{ \odot }}$, штриховая кривая – $1\,{{M}_{ \odot }}$ и пунктирная кривая – $10\;{{M}_{ \odot }}$.

Рис. 1.

Изменение эксцентриситета тесной двойной системы в зависимости от возраста основной звезды (в годах). Начальный эксцентриситет равен $e = 0.2$ для начальных орбитальных периодов ${{P}_{{{\text{orb}}}}} = 5$ дней (синий цвет), 7.5 дней (зеленый) и 10 дней (красный). Массы второго компаньона равны ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$ (показана сплошной кривой), $0.1\,{{M}_{ \odot }}$ (штрихпунктирные кривые), $1\,{{M}_{ \odot }}$ (штриховые кривые) и $10{{M}_{ \odot }}$ (пунктирные кривые).

Рис. 2.

То же, что на рис. 1, для $e = 0.4$.

Рис. 3.

То же, что на рис. 1, для $e = 0.6$.

Рис. 4.

То же, что на рис. 1, для $e = 0.8$.

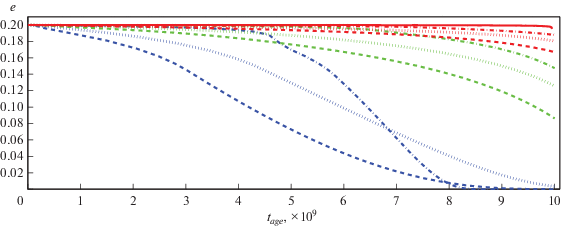
Приливные взаимодействия приводят к циркуляризации орбиты, что сводится к уменьшению эксцентриситета двойной системы (20). Поэтому эксцентриситет двойной системы будет стремиться к нулю с течением времени. Эффективность приливного потока зависит от отношения масс звезд, начального орбитального периода и эксцентриситета нелинейным образом (20). Из рис. 1–4 непосредственно видно, что чем меньше начальный орбитальный период, тем более быстро уменьшается эксцентриситет двойной системы (на рис. 1–4 синяя кривая быстрее достигает нулевого эксцентриситета, чем зеленая и красная, а зеленая кривая быстрее красной одного и того же стиля). Кривые разных начальных орбитальных периодов для заданной массы компаньона выходят из одной точки, но никогда не пересекаются. Зависимость от отношения масс звезд не такая очевидная. Это связано с тем, что в зависимости от массы компаньона изменяется также орбитальный период двойной системы, что, следовательно, приводит к изменению эксцентриситета (на рис. 1–4 это отображается в виде изломов). Это, в свою очередь, приведет к тому, что для более массивного компаньона эксцентриситет будет изменяться медленнее, чем для менее массивного за время жизни звезды на главной последовательности. На графиках это проявляется тем, что кривые одного цвета, но разного стиля – могут пересекаться.

Вывод заключается в следующем: изменение эксцентриситета происходит за счет приливных сил. Накачка эксцентриситета за счет потери массы и аккреции может происходить для маломассивного компаньона с коротким орбитальным периодом и с большим эксцентриситетом, но существенной роли на эволюцию орбиты это не сказывает.

3.2. Изменение орбитального углового момента

Для маломассивного компаньона с массами ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$ и $0.1\;{{M}_{ \odot }}$ основной вклад в изменение орбитального углового момента $\mathop {\dot {J}}\nolimits_{{\text{orb}}} $ вносит магнитное торможение (2.1.6) в течение всей эволюции звезды на главной последовательности. Звездный ветер (2.1.2) дает сравнимый вклад только для короткопериодической и сильно вытянутой орбиты с периодом, равным ${{P}_{{{\text{orb}}}}} = 5$ дней и эксцентриситетом $e = 0.6$ и 0.8.

Для моделей с массами компаньона ${{M}_{2}} = 1\;{{M}_{ \odot }}$ и $10\;{{M}_{ \odot }}$ все три эффекта – магнитное торможение (2.1.6), спин-орбитальное взаимодействие (2.1.7) и звездный ветер (2.1.2) – дают сравнимые вклады. В зависимости от параметров задачи и возраста основной звезды один из эффектов может преобладать над другими.

Вывод заключается в следующем: три эффекта (магнитное торможение, звездный ветер и спин-орбитальное взаимодействие) играют существенную роль. В зависимости от начальных параметров орбиты и времен эволюции преобладает один эффект над другим или все три эффекта дают значительный вклад в изменение орбитального углового момента.

3.3. Изменение орбитального периода

Изменение орбитального периода двойной системы вычисляется по формуле (2). В зависимости от параметров задачи, то или иное слагаемое вносит существенный вклад. В большинстве случаев основной вклад дает изменение орбитального углового момента (3.2). Изменение массы звезд (2.1.2) дает значительный вклад при массе компаньона равным ${{M}_{2}} = 1\;{{M}_{ \odot }}$ и $10\;{{M}_{ \odot }}$. Для высокоэллиптической орбиты с эксцентриситетами $e = 0.6$ и 0.8 существенный вклад также дает изменение эксцентриситета двойной системы (2.1.4).

На рис. 5, 6 и 7 показано изменение орбитального периода в днях с течением времени (в годах) для начального орбитального периода ${{P}_{{{\text{orb}}}}} = $ $ = [5;7.5;10]$ дней соответственно. Обозначения следующие: сплошная кривая соответствует массе компаньона ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, штрихпунктирная кривая – $0.1\;{{M}_{ \odot }}$, штриховая – $1\;{{M}_{ \odot }}$ и пунктирная – $10\;{{M}_{ \odot }}$. Цвет кривой соответствует эксцентриситету: $e = 0$ (черный), 0.2 (голубой), 0.4 (зеленый), 0.6 (красный) и 0.8 (фиолетовый).

Рис. 5.

Зависимость орбитального периода двойной системы (в днях) от возраста основной звезды (в годах). Начальный орбитальный период равен ${{P}_{{{\text{orb}}}}} = 5$ дней. Приведены кривые для начального эксцентриситета $e = 0$ (черный цвет), 0.2 (голубой), 0.4 (зеленый), 0.6 (красный), 0.8 (фиолетовый). Массы второго компаньона равны ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$ (сплошные кривые), $0.1\;{{M}_{ \odot }}$ (штрихпунктирные кривые), $1\;{{M}_{ \odot }}$ (штриховые кривые) и $10\;{{M}_{ \odot }}$ (пунктирные кривые).

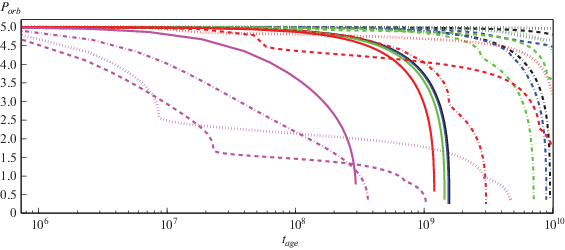
Рис. 6.

То же, что на рис. 5, для начального орбитального периода ${{P}_{{{\text{orb}}}}} = 7.5$ дней.

Рис. 7.

То же, что на рис. 5, для начального орбитального периода ${{P}_{{{\text{orb}}}}} = 10$ дней.

Для всех случаев, рассмотренных в работе, орбитальный период уменьшается с течением времени. Наибольший эффект достигается при большом эксцентриситете, $e = 0.8$, за счет быстрого изменения самого эксцентриситета. Дальше прослеживается зависимость: чем больше масса и меньше эксцентриситет, тем слабее изменяется орбитальный период. Для круговой орбиты $e = 0$ и массивного компаньона ${{M}_{2}} = 10\;{{M}_{ \odot }}$ орбитальный период двойной системы приблизительно остается постоянным в течение эволюции звезды на главной последовательности.

Выводы заключаются в следующем: изменение орбитального периода главным образом обусловлено изменением орбитального углового момента. Изменение эксцентриситета и массы звезд вносит существенный вклад только для некоторых орбитальных параметров. Изменение орбитального периода в тесных двойных системах можно непосредственно наблюдать и сравнивать с теоретическими предсказаниями [28, 43, 44].

3.4. Отношение периодов вращения основной звезды к орбитальному периоду

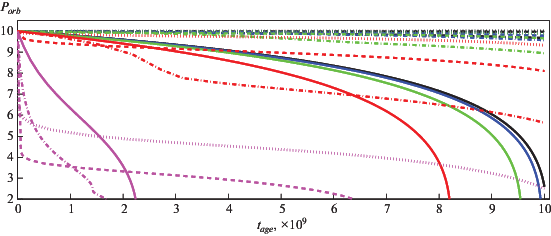
На рис. 8, 9 и 10 показаны графики зависимости отношения периода вращения звезды к орбитальному периоду с течением времени (в годах) для разных начальных значений орбитальных периодов ${{P}_{{{\text{orb}}}}} = 5$, 7.5 и 10 дней соответственно. Сплошными кривыми изображены случаи, когда масса компаньона равна ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, штрих-пунктирными – $0.1\;{{M}_{ \odot }}$, штриховыми – $1\;{{M}_{ \odot }}$ и пунктирными – $10\;{{M}_{ \odot }}$. Цвет кривой указывает на значение эксцентриситета: $e = 0$ (черный), 0.2 (синий), 0.4 (зеленый), 0.6 (красный) и 0.8 (фиолетовый).

Рис. 8.

Зависимость отношения периода вращения основной звезды к орбитальному периоду от времени (в годах) для начального орбитального периода двойной системы ${{P}_{{{\text{orb}}}}} = 5$ дней и для начальных эксцентриситетов $e = 0$ (черный цвет), 0.2 (синий), 0.4 (зеленый), 0.6 (красный) и 0.8 (фиолетовый). Массы второго компаньона равны ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$ (сплошные кривые), $0.1\;{{M}_{ \odot }}$ (штрих-пунктирные кривые), $1\;{{M}_{ \odot }}$ (штриховые кривые) и $10\;{{M}_{ \odot }}$ (пунктирные кривые).

Рис. 9.

То же, что на рис. 8, для начального орбитального периода двойной системы ${{P}_{{{\text{orb}}}}} = 7.5$ дней.

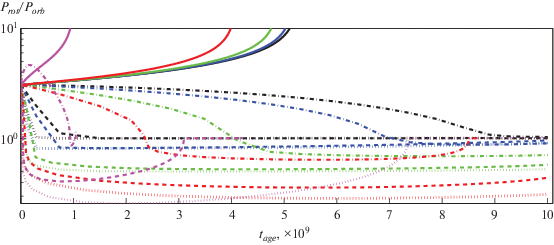
Рис. 10.

То же, что на рис. 8, для начального орбитального периода двойной системы ${{P}_{{{\text{orb}}}}} = 10$ дней.

Из рис. 8–10 видно, что все сплошные кривые, которые соответствуют массе компаньона ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, не стремятся к синхронизованному состоянию ни при каком эксцентриситете. Это связано с тем, что при малой массе компаньона приливные взаимодействия будут значительно слабее других эффектов. Рост величины ${{P}_{{{\text{rot}}}}}{\text{/}}{{P}_{{{\text{orb}}}}}$ происходит за счет быстрого уменьшения орбитального периода (см. рис. 5–7 ). С увеличением массы компаньона до ${{M}_{2}} = 0.1\;{{M}_{ \odot }}$ (штрих-пунктирные кривые) приливные взаимодействия начинают преобладать над другими эффектами. Для малых величин эксцентриситета $e = [0;\;0.2;\;0.4;\;0.6]$, двойная система стремится к синхронизованному состоянию, но в зависимости от начального орбитального периода (а следовательно, и от силы приливных взаимодействий) за время жизни основной звезды на главной последовательности двойная система либо синхронизуется, либо будет находиться в асинхронном состоянии. Для начального орбитального периода ${{P}_{{{\text{orb}}}}} = 5$ дней, синхронизация наступает за время жизни основной звезды на главной последовательности (черная, синяя и зеленая штрихпунктирные кривые на рис. 8). Для начального орбитального периода ${{P}_{{{\text{orb}}}}} = 7.5$ и 10 дней, синхронизация либо наступает, либо нет в зависимости от эксцентриситета. За время жизни основной звезды на главной последовательности здесь наблюдается асинхронное состояние (как сверхсинхронизованное, так и субсинхронизованное). Для эксцентриситета $e = 0.8$ ситуация более сложная. Отношение вращательного периода к орбитальному сначала увеличивается, потом уменьшается, а потом снова увеличивается. Это связано с тем, что при большом эксцентриситете приливные взаимодействия более эффективны в периастре, следовательно, преобладание различных эффектов может чередоваться в зависимости от орбитального периода, а следовательно, и с течением времени.

Для массы компаньона ${{M}_{2}} = 1\;{{M}_{ \odot }}$ (штриховые кривые) ситуация различается в зависимости от начального орбитального периода. При начальном орбитальном периоде, равном ${{P}_{{{\text{orb}}}}} = 5$ дней, вне зависимости от начального эксцентриситета, двойная система достигает синхронизованного состояния за время жизни основной звезды на главной последовательности. Для начальных орбитальных периодов ${{P}_{{{\text{orb}}}}} = 7.5$ и 10 дней наблюдаются либо синхронизация, либо асинхронное состояние (сверхсинхронизация). Синхронизация наблюдается для круговых (с малым эксцентриситетом) орбит. Для эксцентричных орбит имеет место асинхронное состояние, причем только сверхсинхронизация. Она наблюдается на продолжительном периоде жизни звезды на главной последовательности.

Для массы компаньона, равной ${{M}_{2}} = 1\;{{M}_{ \odot }}$ (пунктирные кривые) в зависимости от эксцентриситета и начального орбитального периода, двойная система будет стремиться либо к синхронизованному, либо к сверхсинхронизованному состоянию для любого эксцентриситета. Причем звезда может находиться в сверхсинхронизованном состоянии в течение всей жизни звезды на главной последовательности (синие, зеленые и красные пунктирные кривые на рис. 9 и 10 ).

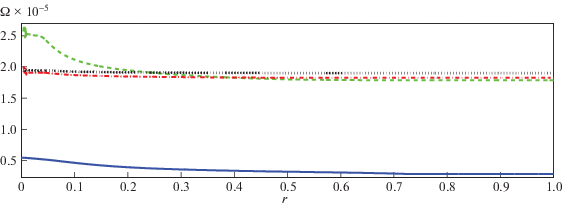
Выводы заключаются в следующем: для компаньона с массой больше одной массы Cолнца, ${{M}_{2}} \geqslant 1\;{{M}_{ \odot }}$, звезда находится либо в синхронизованном состоянии, либо в сверхсинхронизованном на главной последовательности. Для массы компаньона ${{M}_{2}} = 0.1\;{{M}_{ \odot }}$ звезда может находиться в любом состоянии в зависимости от эксцентриситета и начального орбитального периода. Для массы компаньона ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$ звезда не стремится к синхронизованному состоянию. Асинхронное состояние объясняется псевдосинхронизацией для орбит с ненулевым эксцентриситетом. Для орбит с нулевым эксцентриситетом асинхронное состояние объясняется диффиренциальным вращением. На рис. 11 показан пример зависимости угловой скорости вращения звезды (в единицах c^–1) от безразмерного радиуса звезды (синяя кривая) для модели с параметрами ${{M}_{2}} = 10\;{{M}_{ \odot }}$, ${{P}_{{{\text{orb}}}}} = 5$ дней, $e = 0$ и возрастом звезды $t = {{10}^{{10}}}$ лет. Горизонтальной зеленой штрих-пунктирной прямой показана орбитальная скорость двойной системы ${{\Omega }_{{{\text{orb}}}}} = 2\pi {\text{/}}{{P}_{{{\text{orb}}}}}$. Из рис. 11 видно, что равновесие достигается, когда орбитальная угловая скорость ${{\Omega }_{{{\text{orb}}}}}$ равна некоторой равновесной угловой скорости вращения звезды, которая, в свою очередь, не равна скорости вращения на поверхности звезды.

Рис. 11.

Зависимость скорости вращения звезды (в единицах ${{c}^{{ - 1}}}$) от безразмерного радиуса для модели с параметрами ${{M}_{2}} = 10\;{{M}_{ \odot }}$, ${{P}_{{{\text{orb}}}}} = 5$ дней, $e = 0$ и ${{t}_{{{\text{age}}}}} = {{10}^{{10}}}$ лет. Зеленой штрихпунктирной линией показана орбитальная скорость двойной системы ${{\Omega }_{{{\text{orb}}}}} = 2\pi {\text{/}}{{P}_{{{\text{orb}}}}}$.

Рассмотрим влияние компаньона на эволюцию угловой скорости дифференциального вращения основной звезды в зависимости от параметров орбиты (эксцентриситет, масса компаньона, начального орбитального периода). На рис. 12 показан пример эволюции угловой скорости вращения звезды (в единицах ${{c}^{{ - 1}}}$) в зависимости от безразмерного радиуса для модели с начальными параметрами: масса компаньона ${{M}_{2}} = 1\;{{M}_{ \odot }}$, начальный орбитальный период ${{P}_{{{\text{orb}}}}} = 7.5$ дней и эксцентриситет $e = 0.4$. Эта модель соответствует штриховой зеленой кривой на рис. 2, 6 и 9 .

Рис. 12.

Пример зависимости угловой скорости (в единицах ${{c}^{{ - 1}}}$) основной звезды от безразмерного радиуса $r$ для разных моментов времени.

Черная сплошная кривая соответствует начальному времени моделирования звезды $t = $ 10⁵ лет (начальное твердотельное вращение), синяя штрихпунктирная – $t = 5.8 \times {{10}^{8}}$ лет, зеленая штриховая – $t = 7.7 \times {{10}^{9}}$ лет, а красная пунктирная – $t = {{10}^{{10}}}$ лет. За время эволюции звезды из-за развития неустойчивостей ядро звезды начинает вращаться дифференциально, конвективная оболочка продолжает вращаться твердотельно. За счет приливных сил двойная система стремится к псевдосинхронизации. На поздних стадиях эволюции звезды ($t = {{10}^{{10}}}$ лет) это состояние соответствует периоду вращения на поверхности звезды ${{P}_{{{\text{rot}}}}} \approx 4$ дня. Орбитальный период равен ${{P}_{{{\text{orb}}}}} \approx 7$ дней, что соответствует угловой орбитальной скорости ${{\Omega }_{{{\text{orb}}}}} \approx {{10}^{{ - 5}}}$ с^–1. Отношение вращательного периода поверхности звезды к орбитальному равно ${{P}_{{{\text{rot}}}}}{\text{/}}{{P}_{{{\text{orb}}}}} \approx 0.57$. Угловая скорость вращения звезды меняется немонотонно. Сначала происходит рост угловой скорости вращения до некоторого максимального значения, а затем уменьшается. Звезда переходит в устойчивое псевдосинхронизованное состояние.

На рис. 13 показана зависимость угловой скорости вращения звезды (в единицах c^–1) от безразмерного радиуса для разных эксцентриситетов на поздних стадиях эволюции звезды ($t = {{10}^{{10}}}$ лет) для модели с начальным орбитальным периодом ${{P}_{{{\text{orb}}}}} = 7.5$ дней и массой компаньона ${{M}_{2}} = 1\;{{M}_{ \odot }}$.

Рис. 13.

Зависимость угловой скорости (в единицах ${{c}^{{ - 1}}}$) основной звезды от безразмерного радиуса $r$ при разных эксцентриситетах орбиты для момента времени $t = {{10}^{{10}}}$ лет.

Черная кривая соответствует эксцентриситету, равному $e = 0$, синяя – $e = 0.2$, зеленая – $e = 0.4$, красная – $e = 0.6$ и фиолетовая – $e = 0.8$. Из рис. 13 следует, что чем больше эксцентриситет двойной системы, тем больше угловая скорость вращения звезды.

На рис. 14 и 15 показана зависимость угловой скорости вращения основной звезды (в единицах c^–1) от безразмерного радиуса для разных масс компаньона в модели с начальным орбитальным периодом ${{P}_{{{\text{orb}}}}} = 7.5$ дней и начальными эксцентриситетами $e = 0$ и 0.4 соответственно.

Рис. 14.

Зависимость угловой скорости (в единицах ${{c}^{{ - 1}}}$) основной звезды от безразмерного радиуса $r$ для разных масс компаньона в момент времени $t = {{10}^{{10}}}$ лет для эксцентриситета $e = 0$.

Рис. 15.

То же, что на рис. 14, для эксцентриситета $e = 0.4$.

Синяя сплошная кривая соответствует массе компаньона ${{M}_{2}} = 0.01\;{{M}_{ \odot }}$, красная штрихпунктирная – $0.1\;{{M}_{ \odot }}$, зеленая штриховая – $1\;{{M}_{ \odot }}$ и черная пунктирная – $10\;{{M}_{ \odot }}$. Влияние приливных сил для маломассивного компаньона ${{M}_{2}} = 0.01$ (синяя сплошная кривая) достаточно слабое, поэтому влияние на эволюцию угловой скорости звезды тоже слабое. Для более массивного компаньона наблюдается более сложная зависимость и от массы, и от эксцентриситета.

4. ДВОЙНАЯ СИСТЕМА KIC 8736245

Приведенный выше формализм был применен к моделированию двойной системы KIC 8736245. Эта тесная двойная система состоит из двух поздних карликов типа K и M с орбитальным периодом ${{P}_{{{\text{orb}}}}} = 5.07$ дней. Орбита данной системы круговая с эксцентриситетом $e = 0$. Возраст звезд оценивается как ${{t}_{{{\text{age}}}}} \sim 7{\kern 1pt} - {\kern 1pt} 9$ млрд. лет. В табл. 1 представлены физические параметры звезд-компонентов. В работе [7] была определена скорость вращения каждой звезды. Оказалась, что одна звезда сверхсинхронизована ${{P}_{{{\text{orb}}}}}{\text{/}}{{P}_{{\operatorname{rot} 1}}} = 1.02$, а другая субсинхронизована ${{P}_{{{\text{orb}}}}}{\text{/}}{{P}_{{\operatorname{rot} 2}}} = 0.86$.

Таблица 1.

Физические параметры звезд в двойной системе KIC 8736245 [7]

Параметры	Звезды
Параметры	1	2
$M$, ${{M}_{ \odot }}$	0.987	0.782
$R$, ${{R}_{ \odot }}$	1.311	0.804
${{T}_{{{\text{eff}}}}}$, K	5811	5050
${{P}_{{{\text{rot}}}}}$, дни	4.98	5.87
${{P}_{{{\text{orb}}}}}{\text{/}}{{P}_{{{\text{rot}}}}}$	1.02	0.86
${{P}_{{{\text{rot}}}}}{\text{/}}{{P}_{{{\text{orb}}}}}$	0.98	1.16
[m/H]	–0.31	–0.31

Было проведено моделирование обеих звезд в двойной системе с учетом влияния каждой звезды друг на друга. Звезды моделировались в начальный период времени ${{t}_{i}} = $ 10⁵ лет до момента времени ${{t}_{f}} = 9 \times $ 10⁹ лет. Начальные параметры моделирования подгонялись таким образом, чтобы удовлетворить наблюдательным данным наилучшим образом в пределах ошибок при возрасте звезды ${{t}_{{{\text{age}}}}} \approx 8 \times $ 10⁹ лет. Оказалось, что наилучшим образом удовлетворяют этим требованиям звезды со следующими начальными характеристиками: первая звезда с массой ${{M}_{1}} = 0.99\;{{M}_{ \odot }}$ вращается достаточно быстро с поверхностной скоростью ${{v}_{1}} = 50$ км/c, вторая звезда с массой ${{M}_{2}} = 0.7825\;{{M}_{ \odot }}$ вращается достаточно медленно с поверхностной скоростью ${{v}_{2}} = 1{\text{/}}3$ км/c. Начальный орбитальный период двойной системы равен ${{P}_{{{\text{orb}}}}} = 5.08$ дней. Предполагается, что диссипация приливного потока происходит в конвективных оболочках звезд и, при равенстве времени оборота конвективной ячейки и орбитального периода, использовался квадратичный фактор подавления [27]. Характерные времена синхронизации для обоих звезд были увеличены в 10 раз.

Моделирование показало, что при возрасте ${{t}_{{{\text{age}}}}} = 8.18 \times {{10}^{{10}}}$ лет параметры звезд и орбиты наилучшим образом описывают наблюдательные данные. Первая звезда находится в сверхсинхронизованном состоянии с отношением периодов ${{P}_{{\operatorname{rot} 1}}}{\text{/}}{{P}_{{{\text{orb}}}}} = 0.99$, вторая звезда – в субсинхронизованном состоянии с отношением периодов ${{P}_{{\operatorname{rot} 2}}}{\text{/}}{{P}_{{{\text{orb}}}}} = 1.15$. Сверхсинхронизованное состояние первой звезды поддерживается за счет дифференциального вращения. Орбитальная скорость вращения равна некоторой равновесной скорости вращения звезды, расположенной между минимальной и максимальной скоростью вращения (аналогично рис. 11). Первая звезда, хоть и находится в сверхсинхронизованном состоянии, но она также стремится к субсинхронизованному состоянию и при возрасте ${{t}_{{{\text{age}}}}} = 9 \times $ 10⁹ лет, для обеих звезд выполняется неравенство ${{P}_{{{\text{orb}}}}}{\text{/}}{{P}_{{\operatorname{rot} 1,2}}} < 1$. Вторая звезда за время жизни на главной последовательности все время находится в субсинхронизованном состоянии и при временах ${{t}_{{{\text{age}}}}} = 9 \times $ × 10⁹ достигает равновесного состояния, когда субсинхронизация поддерживается дифференциальным вращением.

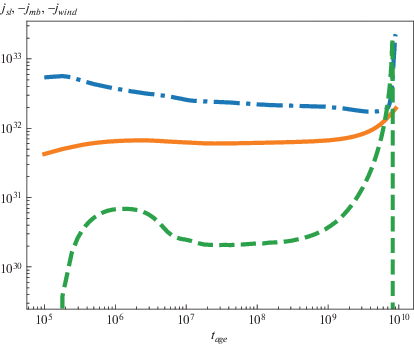
На рис. 16 показана зависимость изменения орбитального углового момента за счет магнитного торможения (${{\dot {J}}_{{{\text{mb}}}}} < 0$, штрихпунктирная кривая), спин-орбитального взаимодействия (${{\dot {J}}_{{{\text{sl}}}}} > 0$, штриховая кривая) и ветра (${{\dot {J}}_{{{\text{wind}}}}} < 0$, сплошная кривая). Спин-орбитальное взаимодействие увеличивает орбитальный угловой момент за счет быстровращающейся звезды. Магнитное торможение и ветер уменьшают орбитальный угловой момент.

Рис. 16.

Зависимость изменения орбитального углового момента от возраста звезды (в годах) за счет магнитного торможения (штрихпунктирная кривая), спин-орбитального взаимодействия (штриховая кривая) и ветра (сплошная кривая).

На рис. 17 показана зависимость орбитального периода двойной системы от времени. В изменение орбитального периода основной вклад вносят два эффекта: магнитное торможение и спин-орбитальное взаимодействие. Прогиб на графике означает, что спин-орбитальное взаимодействие преобладает над магнитным торможением и двойная система получает угловой момент из быстровращающейся первой звезды, тем самым увеличивая орбитальный период.

Рис. 17.

Зависимость орбитального периода (в днях) от возраста звезды (в годах).

На рис. 18 показано отношение вращательного периода к орбитальному в зависимости от возраста двойной системы. Синяя штрих-пунктирная кривая относится к первой звезде, сплошная красно-коричневая – ко второй звезде. Обе звезды стремятся к равновесному субсинхронизованному состоянию, причем первая звезда в процессе эволюции проходит через сверхсинхронизованное состояние. Субсинхронизованное состояние поддерживается за счет дифференциального вращения звезд.

Рис. 18.

Зависимость отношения вращательного периода к орбитальному от возраста звезды (в годах).

5. ЗАКЛЮЧЕНИЕ

В работе рассмотрена эволюция звезды в тесной двойной системе с учетом обратного влияния компаньона на звезду. Важную роль в такой системе играют приливные взаимодействия. Они приводят систему в состояние синхронизации, когда орбитальный период становится равным периоду вращения звезды. Наблюдения показывают, что не все звезды в тесных двойных системах находятся в состоянии синхронизации. Многие системы асинхронны. В работе исследованы две модели, которые объясняют асинхронное состояние за счет дифференциального вращения звезды и псевдосинхронизации эллиптической орбиты. Было показано, что тесная двойная система может достаточно продолжительно находиться в асинхронном состоянии за время жизни звезды на главной последовательности.

Измеряя более точно отношение вращательного периода к орбитальному, можно строить модели и изучать дифференциальное вращение звезды.

Список литературы

J. C. Lurie, K. Vyhmeister, S. L. Hawley, J. Adilia, et al., Astron. and Astrophys. 154, id. 250 (2017).
P. B. Ivanov, J. C. B. Papaloizou, and S. V. Chernov, Monthly Not. Roy. Astron. Soc. 432, 2339 (2013).
S. V. Chernov, J. C. B. Papaloizou, ande P. B. Ivanov, Monthly Not. Roy. Astron. Soc. 434, 1079 (2013).
P. Hut, Astron. and Astrophys. 92, 167 (1980).
P. Hut, Astron. and Astrophys. 99, 126 (1981).
С. В. Чернов, Письма в Астрон. журн. 43, 214 (2017).
T. Fetherolf, W. F. Welsh, J. A. Orosz, G. Windmiller, S. N. Quinn, D. R. Short, S. R. Kane, and R. A. Wade, Astron. J. 158, id. 198 (2019).
L. M. Walkowicz and G. S. Basri, Monthly Not. Roy. Astron. Soc. 436, 1883 (2013).
E. Marilli, A. Frasca, E. Covino, J. M. Alcala, et al., A-stron. and Astrophys. 463, 1081 (2007).
B. Paxton, L. Bildsten, A. Dotter, F. Herwig, P. Lesaffre, and F. Timmes, Astrophys. J. Suppl. 192, 3 (2011).
B. Paxton, L. Bildsten, A. Dotter, F. Herwig, P. Lesaffre, and F. Timmes, Astrophys. J. Suppl. 208, 4 (2013).
B. Paxton, P. Marchant, J. Schwab, E. B. Bauer, et al., Astrophys. J. Suppl. 220, 15 (2015).
J. Vos, R. H. Østensen, P. Marchant, and H. Van Winckel, Astron. and Astrophys. 579, id. A49 (2015).
P. P. Eggleton, Astrophys. J. 268, 368 (1983).
H. Ritter, Astron. and Astrophys. 202, 93 (1988).
T. M. Tauris and E. P. J. van den Heuvel, in Compact stellar X-ray sources, edited by W. Lewin and M. van der Klis, Cambridge Astrophysics Series, No. 39 (Cambridge, UK: Cambridge University Press, 2006), p. 623.
D. Reimers, Mem. Soc. Roy. Sciences Liege 8, 369 (1975).
C. A. Tout and P. P. Eggleton, Monthly Not. Roy. Astron. Soc. 231, 823 (1988).
D. B. Friend and D. C. Abbott, Astrophys. J. 311, 701 (1986).
A. Maeder and G. Meynet, Astron. and Astrophys. 361, 159 (2000).
N. Langer, Astron. and Astrophys. 329, 551 (1998).
J. R. Hurley, C. A. Tout, and O. R. Pols, Monthly Not. Roy. Astron. Soc. 329, 897 (2002).
H. M. J. Boffin and A. Jorissen, Astron. and Astrophys. 205, 155 (1988).
N. Soker, Astron. and Astrophys. 357, 557 (2000).
J.-P. Zahn, Astron. and Astrophys. 41, 329 (1975).
F. A. Rasio, C. A. Tout, S. H. Lubow, and M. Livio, Astrophys. J. 470, 1187 (1996).
P. Goldreich and P. D. Nicholson, Icarus 30, 301 (1977).
С. В. Чернов, ЖЭТФ 154, 85 (2018).
J.-P. Zahn, Astron. and Astrophys. 57, 383 (1977).
С. В. Чернов, Письма в Астрон. журн. 43, 474 (2017).
M. Goupil, K. Belkacem, C. Neiner, F. Lignieres, and J. Green (eds.), Studying stellar rotation and convection (Berlin, Heidelberg: Springer, 2013).
S. Rappaport, F. Verbunt, and P. Joss, Astrophys. J. 275, 713 (1983).
A. Heger, N. Langer, and S. E. Woosley, Astrophys. J. 528, 368 (2000).
B. Chaboyer and J.-P. Zahn, Astron. and Astrophys. 253, 173 (1992).
N. Langer, K. J. Fricke, and D. Sugimoto, Astron. and Astrophys. 126, 207 (1983).
A. S. Endal and S. Sofia, Astrophys. J. 220, 279 (1978).
A. S. Endal and S. Sofia, Astrophys. J. 232, 531 (1979).
Л. Л. Кичатинов, Успехи физ. наук 175, 475 (2005).
J.-L. Tassoul, Stellar rotation (Cambridge: Cambridge University Press, 2000).
R. Kippenhahn, IAU Symp 66, 20 (1974).
P. Goldreich and G. Schubert, Astrophys. J. 150, 571 (1967).
K. Fricke, Zeitschrift für Astrophysik 68, 317 (1968).
S. V. Chernov, J. C. B. Papaloizou, and P. B. Ivanov, Monthly Not. Roy. Astron. Soc. 470, 2054 (2017).
С. В. Чернов, Астрон. журн. 97(5), 399 (2020).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал