1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 98, № 8, 2021

Астрономический журнал, 2021, T. 98, № 8, стр. 663-680

МГД модель взаимодействия коронального выброса массы с горячим юпитером HD 209458b

А. Г. Жилкин 1, *, Д. В. Бисикало 1, Е. А. Колымагина 1

1 Институт астрономии РАН
Москва, Россия

* E-mail: zhilkin@inasan.ru

Поступила в редакцию 25.03.2021
После доработки 21.04.2021
Принята к публикации 30.04.2021

Полный текст (PDF)

Аннотация

Большинство горячих юпитеров обладают протяженными газовыми оболочками, выходящими за пределы их полостей Роша. Типичная оболочка гравитационно слабо связана с планетой и, следовательно, ее структура и свойства сильно подвержены влиянию возмущений звездного ветра, например, корональных выбросов массы. Ранее мы провели газодинамическое моделирование взаимодействия узконаправленного коронального выброса массы (КВМ) с оболочкой горячего юпитера HD 209458b. В этой работе исследуется влияние магнитного поля планеты и звездного ветра на структуру и динамику оболочки HD 209458b, подверженной воздействию такого же КВМ. Для этого разработана МГД модель взаимодействия КВМ с оболочкой. Предполагалось, что поле планеты имеет общепринятое значение и соответствует 1/10 магнитного момента Юпитера. Поле звезды предполагалось слабым (10–3 Гс), что обеспечивает сверх-альфвеновский режим обтекания планеты звездным ветром. Сравнение результатов МГД моделирования с газодинамическими расчетами показывает, что для использованных нами значений величины поля планеты и звезды влияние магнитного поля на оболочку не является определяющим и качественная картина течения не меняется. В то же время учет магнитных полей приводит к изменению количественных характеристик оболочки и темпа потери массы, что может иметь значение при определении эволюционного статуса экзопланеты.

Ключевые слова: численное моделирование, магнитная гидродинамика (МГД), горячие юпитеры, корональные выбросы массы (КВМ)

1. ВВЕДЕНИЕ

При наблюдении транзита части горячих юпитеров наблюдается сильное поглощение в некоторых спектральных линиях. Например, для типичного горячего юпитера HD 209458b [1] падение яркости родительской звезды в линии Ly-$\alpha $ может достигать $15\% $, что соответствует радиусу окружающего планету водородного облака в $4.3{{R}_{J}}$ [2], где ${{R}_{J}}$ – радиус Юпитера. Это значение превышает радиус соответствующей полости Роша $3.6{{R}_{J}}$. Следовательно, часть атмосферы выходит за область гравитационного влияния планеты и может быть потеряна под действием звездного ветра [3, 4]. Согласно полученным оценкам [5], потери массы для HD 209458b в результате испарения атмосферы составляют $(8{\kern 1pt} - {\kern 1pt} 40) \times {{10}^{{10}}}$ г/см.

Флуктуации звездного ветра могут вызывать существенные изменения структуры протяженной газовой оболочки горячих юпитеров. В результате такого воздействия темп потери массы может сильно варьироваться. К значительным возмущениям ветра, в частности, приводят гигантские выбросы вещества из короны звезды – корональные выбросы массы (КВМ). В работах [6, 7] была сделана оценка темпа потери массы экзопланетой HD 209458b при прохождении через широкий КВМ, т.е. в случае, когда планета не выходит за его границы. Было показано, что при параметрах КВМ, близких к солнечным, потерю массы за один выброс можно оценить значением ${{10}^{{15}}}$ г. Подобный КВМ приводил к срыву оболочки, выходящей за пределы полости Роша. Похожая ситуация наблюдалась и при касательном взаимодействии с выбросом, например, в случае узких КВМ [8]. В этом случае основная потеря массы происходила за счет взаимодействия с волной разрежения, следующей сразу за выбросом, и составила величину порядка $4 \times {{10}^{{15}}}$ г.

Указанные работы были выполнены на основе моделирования, не учитывающего ни магнитное поле планеты, ни магнитное поле звездного ветра. Однако, по всей видимости, включение в модель магнитного поля может оказать достаточно ощутимое влияние на эволюцию планеты и на темп потери массы, в частности. В работе [9] для горячего юпитера WASP 12b было отмечено заметное ослабление темпа потери массы по сравнению с чисто газодинамическим случаем даже при задании относительно слабого магнитного поля планеты (на уровне $0.1\,{{\mu }_{J}}$, где ${{\mu }_{J}} = 1.53 \times {{10}^{{30}}}$ Гс см3 – магнитный момент Юпитера [10]).

В работе [11] показано, что магнитное поле звездного ветра также является важным фактором, который необходимо учитывать. Это обусловлено тем, что большинство горячих юпитеров находятся в суб-альфвеновской зоне звездного ветра, где магнитное давление превышает динамическое давление. При этом с учетом орбитального движения планеты скорость обтекания оказывается близкой к альфвеновской скорости. В результате может реализоваться как сверх-альфвеновский [12], так и суб-альфвеновский [13] режимы обтекания. Отметим, что в случае суб-альфвеновского режима обтекания планеты звездным ветром головная ударная волна в структуре магнитосферы будет отсутствовать. При прохождении КВМ вблизи горячего юпитера возмущаются все параметры звездного ветра (в том числе и магнитное поле). Поэтому этот процесс может приводить к переключению между суб-альфвеновским и сверх-альфвеновским режимами обтекания. При этом должна существенным образом изменяться вся структура магнитосферы. В частности, может происходить как исчезновение, так и появление головной ударной волны вокруг горячего юпитера и его протяженной оболочки [14].

Целью настоящей работы является исследование вопроса о взаимодействии узких КВМ, проходящих касательно к планете, с характерными структурами оболочки горячего юпитера, имеющими место при невозмущенном звездном ветре. Предполагается, что обтекание планеты звездным ветром происходит в сверх-альфвеновском режиме. Проводится сравнение магнитогидродинамической и чисто газодинамической моделей. Статья организована следующим образом: в разделе 2 представлено описание физической модели задачи, структуры КВМ, а также математическая модель; в разделе 3 представлены результаты расчетов структуры протяженной оболочки HD 209458b с учетом магнитного поля системы, проведено сравнение с чисто газодинамическим случаем и вычислена потеря массы планеты для двух модельных КВМ; основные выводы работы кратко просуммированы в разделе 4.

2. ОПИСАНИЕ МОДЕЛИ

2.1. Основные уравнения

В работе исследуется двойная система, состоящая из горячего юпитера HD 209458b и его родительской звезды. Вследствие малости эксцентриситета орбиты планеты ($e = 0.082$) ее движение считается строго круговым. Сравнительно малая масса вещества протяженной оболочки горячего юпитера позволяет пренебречь его гравитационным влиянием. Это означает, что при переходе в неинерциальную систему отсчета, вращающуюся вместе с двойной системой, можно использовать приближение Роша.

Структуру течения в окрестности горячего юпитера можно описывать с помощью системы уравнений одножидкостной магнитной гидродинамики. При этом удобно явным образом выделять фоновое магнитное поле [9, 11, 15, 16], когда полное магнитное поле ${\mathbf{B}}$ представляется в виде суперпозиции фонового магнитного поля ${\mathbf{H}}$ и магнитного поля ${\mathbf{b}}$, индуцированного токами в самой плазме, ${\mathbf{B}} = {\mathbf{H}} + {\mathbf{b}}$. В нашей постановке задачи фоновое поле создается источниками, распределенными внутри звезды (или, точнее говоря, внутри короны), а также в недрах планеты. Поэтому в расчетной области эти источники отсутствуют и, следовательно, фоновое поле должно удовлетворять условию потенциальности, $\nabla \times {\mathbf{H}} = 0$. Это позволяет его частично исключить из уравнений магнитной гидродинамики [17, 18]. Кроме того, в нашей модели предполагается, что фоновое магнитное поле является стационарным, $\partial {\mathbf{H}}{\text{/}}\partial t = 0$.

С учетом вышеуказанных обстоятельств уравнения магнитной гидродинамики могут быть записаны в виде

(1)
$\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {\mathbf{v}}) = 0,$
(2)
$\begin{gathered} \frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}} \cdot \nabla ){\mathbf{v}} = - \frac{{\nabla P}}{\rho } - \frac{{{\mathbf{b}} \times \nabla \times {\mathbf{b}}}}{{4\pi \rho }} - \\ - \;\frac{{{\mathbf{H}} \times \nabla \times {\mathbf{b}}}}{{4\pi \rho }} + {\mathbf{f}}, \\ \end{gathered} $
(3)
$\frac{{\partial {\mathbf{b}}}}{{\partial t}} = \nabla \times ({\mathbf{v}} \times {\mathbf{b}} + {\mathbf{v}} \times {\mathbf{H}}),$
(4)
$\frac{{\partial \varepsilon }}{{\partial t}} + ({\mathbf{v}} \cdot \nabla )\varepsilon + \frac{P}{\rho }\nabla \cdot {\mathbf{v}} = 0.$
Здесь $\rho $ – плотность, ${\mathbf{v}}$ – скорость, $P$ – давление, $\varepsilon $ – удельная внутренняя энергия, ${\mathbf{f}}$ – внешняя сила, рассчитанная на единицу массы. Для замыкания этой системы уравнений используется уравнение состояния идеального газа
(5)
$P = (\gamma - 1)\rho \varepsilon ,$
где $\gamma = 5{\text{/}}3$ – показатель адиабаты. Неадиабатические процессы радиационного охлаждения газа в настоящей модели не учитываются. Из рассмотрения исключаются все процессы, связанные с переносом излучения, в том числе ускорение ветра электромагнитным излучением звезды вследствие радиационного давления. Это предположение является оправданным, так как протяженные оболочки горячих юпитеров почти полностью ионизованы вследствие их близости к родительской звезде [19]. Эффектами магнитной вязкости мы также пренебрегаем, поскольку процесс воздействия КВМ происходит на достаточно коротких промежутках времени.

В неинерциальной системе отсчета, вращающейся вместе с двойной системой с угловой скоростью Ω, положения центров звезды и планеты не изменяются. При этом удельная внешняя сила определяется выражением

(6)
${\mathbf{f}} = - \nabla \Phi - 2(\Omega \times {\mathbf{v}}).$
Здесь первое слагаемое в правой части описывает силу, обусловленную градиентом потенциала Роша
(7)
$\Phi = - \frac{{G{{M}_{{\text{s}}}}}}{{{\text{|}}{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{s}}}}{\kern 1pt} {\text{|}}}} - \frac{{G{{M}_{{\text{p}}}}}}{{{\text{|}}{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{p}}}}{\kern 1pt} {\text{|}}}} - \frac{1}{2}\mathop {\left[ {\Omega \times ({\mathbf{r}} - {{{\mathbf{r}}}_{{\text{c}}}})} \right]}\nolimits^2 ,$
где $G$ – гравитационная постоянная, ${{M}_{{\text{s}}}}$ – масса звезды, ${{M}_{{\text{p}}}}$ – масса планеты, ${{{\mathbf{r}}}_{{\text{s}}}}$ – радиус-вектор центра звезды, ${{{\mathbf{r}}}_{{\text{p}}}}$ – радиус-вектор центра планеты, ${{{\mathbf{r}}}_{{\text{c}}}}$ – радиус-вектор центра масс системы. Второе слагаемое в правой части (6) описывает силу Кориолиса.

Фоновое магнитное поле задавалось в виде

(8)
${\mathbf{H}} = {{{\mathbf{H}}}_{{\text{p}}}} + {{{\mathbf{H}}}_{{\text{s}}}}.$
Здесь первое слагаемое описывает собственное магнитное поле планеты, которое предполагалось чисто дипольным,
(9)
${{{\mathbf{H}}}_{{\text{p}}}} = \frac{\mu }{{{\text{|}}{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{p}}}}{\kern 1pt} {{{\text{|}}}^{3}}}}\left[ {3({\mathbf{d}} \cdot {{{\mathbf{n}}}_{{\text{p}}}}){{{\mathbf{n}}}_{{\text{p}}}} - {\mathbf{d}}} \right],$
где $\mu $ – магнитный момент, ${{{\mathbf{n}}}_{{\text{p}}}} = ({\mathbf{r}} - {{{\mathbf{r}}}_{{\text{p}}}}){\text{/|}}{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{p}}}}{\kern 1pt} {\text{|}}$, ${\mathbf{d}}$ – единичный вектор, направленный вдоль магнитной оси, вектор магнитного момента $\mu = \mu {\text{d}}$. Второе слагаемое в правой части (8) описывает радиальное магнитное поле звездного ветра, которое можно определить из уравнения Максвелла $\nabla \cdot {\mathbf{B}} = 0$. С учетом предполагаемой сферической симметрии звездного ветра получаем (см. раз-дел 2.2)
(10)
${{{\mathbf{H}}}_{{\text{s}}}} = \frac{{{{B}_{{\text{s}}}}R_{{\text{s}}}^{2}}}{{{\text{|}}{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{s}}}}{\kern 1pt} {{{\text{|}}}^{2}}}}{{{\mathbf{n}}}_{{\text{s}}}},$
где ${{R}_{{\text{s}}}}$ – радиус звезды, ${{B}_{{\text{s}}}}$ – среднее магнитное поле на поверхности звезды, а единичный вектор ${{{\mathbf{n}}}_{{\text{s}}}} = ({\mathbf{r}} - {{{\mathbf{r}}}_{{\text{s}}}}){\text{/|}}{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{s}}}}{\kern 1pt} {\text{|}}$. Непосредственной проверкой нетрудно убедиться, что такое фоновое магнитное поле, действительно, удовлетворяет условию потенциальности $\nabla \times {\mathbf{H}} = 0$. Собственное магнитное поле родительской звезды не учитывалось, поскольку в нашей модели считается, что орбита планеты располагается внутри гелиосферной области, где межпланетное магнитное поле определяется звездным ветром.

2.2. Звездный ветер

Для описания структуры звездного ветра в окрестности горячего юпитера мы используем модель, подробно описанную в нашей недавней работе [13] (см. также монографию [20]). Она опирается на хорошо изученные свойства солнечного ветра. Модель ветра является осесимметричной и не учитывает возможную секторную структуру магнитного поля ветра, а также наличие в нем гелиосферного токового слоя [21]. В рамках этой модели можно рассчитать структуру магнитного поля. Вследствие вращения звезды магнитные силовые линии постепенно закручиваются в виде спирали и поэтому на больших расстояниях магнитное поле ветра может быть с хорошей точностью описано с помощью простой модели Паркера [22]. Однако на близких расстояниях от звезды характер решения оказывается более сложным из-за наличия альфвеновской, а также быстрой и медленной магнитозвуковых особых точек [23] (см. также монографию [24]).

Для описания структуры ветра будем использовать инерциальную систему отсчета в сферических координатах ($r$, $\theta $, $\varphi $), центр которой совпадает с центром звезды. Поскольку нас интересует структура течения вблизи плоскости орбиты горячего юпитера, зависимость параметров ветра от угла $\theta $ можно не учитывать. В результате все величины оказываются зависящими только от радиальной координаты $r$. Из уравнений магнитной гидродинамики, описывающих стационарную структуру ветра, можно получить следующие выражения [13]:

(11)
$4\pi {{r}^{2}}\rho {{v}_{r}} = \dot {M},$
(12)
${{B}_{r}} = {{B}_{{\text{s}}}}\mathop {\left( {\frac{{{{R}_{{\text{s}}}}}}{r}} \right)}\nolimits^2 ,$
(13)
$\frac{{v_{r}^{2}}}{2} + \frac{{v_{\varphi }^{2}}}{2} + \frac{{c_{s}^{2}}}{{\kappa - 1}} - \frac{{G{{M}_{{\text{s}}}}}}{r} - \frac{{B_{\varphi }^{2}}}{{4\pi \rho }} - \frac{{{{B}_{r}}{{B}_{\varphi }}{{v}_{\varphi }}}}{{4\pi \rho {{v}_{r}}}} = Q.$
Величина $\dot {M}$ описывает темп уменьшения массы звезды за счет звездного ветра, а константа $Q$ определяет плотность потока энергии в звездном ветре, который равен $\dot {M}Q$. Плотность $\rho $, давление $P$ и температура $T$ ветра удовлетворяют уравнению состояния для идеального политропного газа,
(14)
$P = K{{\rho }^{\kappa }} = \frac{{2{{k}_{{\text{B}}}}}}{{{{m}_{{\text{p}}}}}}\rho T,$
где $K$ – константа, $\kappa $ – показатель политропы, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, ${{m}_{{\text{p}}}}$ – масса протона. Средний молекулярный вес вещества ветра считается равным $1{\text{/}}2$, что соответствует полностью ионизованной водородной плазме, состоящей только из электронов и протонов. Квадрат скорости звука определяется выражением

(15)
$c_{s}^{2} = \frac{{\kappa P}}{\rho }.$

Решение для азимутальных компонент скорости и магнитного поля можно записать в виде

(16)
${{v}_{\varphi }} = {{\Omega }_{{\text{s}}}}r\frac{{1 - {{\lambda }^{2}}r_{A}^{2}{\text{/}}{{r}^{2}}}}{{1 - {{\lambda }^{2}}}},$
(17)
${{B}_{\varphi }} = \frac{{{{B}_{r}}}}{{{{v}_{r}}}}{{\Omega }_{{\text{s}}}}r{{\lambda }^{2}}\frac{{1 - r_{A}^{2}{\text{/}}{{r}^{2}}}}{{1 - {{\lambda }^{2}}}}.$
Здесь ${{\Omega }_{{\text{s}}}}$ – угловая скорость собственного вращения звезды, а через $\lambda $ обозначено альфвеновское число Маха для радиальных компонент скорости и магнитного поля,
(18)
$\lambda = \frac{{\sqrt {4\pi \rho } {{v}_{r}}}}{{{{B}_{r}}}}.$
В альфвеновской точке $r = {{r}_{A}}$ значение параметра $\lambda $ оказывается равным 1. В суб-альфвеновской области $r < {{r}_{A}}$ скорость ветра оказывается меньше альфвеновской скорости. В сверх-альфвеновской области $r > {{r}_{A}}$, наоборот, скорость ветра превосходит альфвеновскую скорость. Выписанные соотношения позволяют алгебраическим образом получить распределения всех магнитогидродинамических величин, описывающих структуру ветра. При этом для выделения однозначного решения необходимо использовать условия непрерывности в трех особых точках ${{r}_{S}}$, ${{r}_{A}}$ и ${{r}_{F}}$, в которых радиальная скорость ветра оказывается равной медленной магнитозвуковой, альфвеновской и быстрой магнитозвуковой скоростям соответственно.

В качестве параметров модели задавались значения плотности ${{n}_{0}} = 1400$ см–3 и температуры ${{T}_{0}} = 7.3 \times {{10}^{5}}$ К на расстоянии ${{r}_{0}} = 10\;{{R}_{ \odot }}$ от звезды [25]. Свободным параметром модели ветра является величина среднего магнитного поля на поверхности звезды ${{B}_{{\text{s}}}}$. Получающиеся соответствующие распределения использовались в нашей численной модели для описания магнитогидродинамической структуры звездного ветра в окрестности горячего юпитера. В частности, радиальная скорость ветра на орбите планеты оказывалась равной порядка 130 км/с.

2.3. Модель КВМ

Возмущение звездного ветра во время прохождения в окрестности планеты КВМ в нашей модели основано на результатах измерений параметров солнечного ветра на орбите Земли, полученных с помощью космических аппаратов ACE, WIND и SOHO в мае 1998 г. во время соответствующего события [26]. Согласно этим данным, процесс прохождения КВМ можно разделить на три отдельные фазы. Первая фаза начинается с прохождения фронта МГД ударной волны. За ударной волной следует оболочка (sheath) нагребенного вещества. Вторая фаза (ранний КВМ) начинается с прохождения тангенциального МГД разрыва, который распространяется вслед за ударной волной. Наконец, третья фаза (поздний КВМ) отличается резким увеличением плотности по отношению к невозмущенному ветру. По завершению этой фазы параметры ветра возвращаются к исходным значениям.

Для описания процесса прохождения КВМ в окрестности горячего юпитера введем временные профили ${{f}_{q}}(t)$, которые определяют возмущения исходных параметров звездного ветра в точке наблюдения. Это означает, что значение некоторой величины $q$ (плотность, скорость и т.п.) в точке ${\mathbf{r}}$ в произвольный момент времени $t$ определяется следующим выражением:

(19)
$q({\mathbf{r}},t) = {{f}_{q}}(t){{q}_{{\text{w}}}}({\mathbf{r}}),$
где ${{q}_{{\text{w}}}}({\mathbf{r}})$ описывает невозмущенное стационарное состояние ветра. В простейшем случае можно использовать кусочно-постоянные функции ${{f}_{q}}(t)$, когда на каждой отдельной фазе КВМ возмущенные параметры ветра не зависят от времени. Однако эти временные профили ${{f}_{q}}(t)$ могут иметь и более общий вид [7]. Например, вместо кусочно-постоянных функций можно использовать кусочно-линейные функции. Этот подход позволяет описать КВМ различных типов, соответствующих наблюдаемым в солнечным ветре медленным, средним [27] и быстрым [28] КВМ.

Для описания узконаправленного КВМ будем считать, что он движется от звезды внутри некоторого конуса [8], вершина которого совпадает с центром звезды. Конфигурация такого выброса схематически представлена на рис. 1. Пространственная ориентация оси конуса в сферической системе координат определяется углами $\theta $ и $\varphi $. Угол при вершине конуса обозначим через $\alpha $. Эти три угла являются параметрами модели. Для описания процесса взаимодействия КВМ с протяженной оболочкой горячего юпитера на основе соотношения (19) необходимо в каждый момент времени определять участки границы расчетной области, пересекающиеся с конусом выброса. Тогда на этих участках соотношения (19) можно использовать для задания нестационарных граничных условий.

Рис. 1.

Модель узконаправленного коронального выброса массы. Цифрами обозначены: 1 – звезда, 2 – планета, 3 – газовая оболочка планеты, 4 – расчетная область, 5 – конус выброса (ось конуса показана пунктирной линией), 6 – область пространственной локализации выброса. Конфигурация выброса показана для двух моментов времени ${{t}_{1}}$ и ${{t}_{2}}$. В течение этого интервала времени $\Delta t = {{t}_{2}} - {{t}_{1}}$ вследствие орбитального движения планеты ориентация конуса выброса поворачивается на угол $\Delta \varphi = \Omega \Delta t$.

Обозначим через ${\mathbf{a}}$ единичный вектор вдоль оси конуса, а через ${\mathbf{n}} = {\mathbf{r}}{\text{/}}r$ единичный вектор, направленный из вершины конуса в точку наблюдения ${\mathbf{r}}$. Скалярное произведение ${\mathbf{a}} \cdot {\mathbf{n}}$ определяет косинус угла между осью конуса и направлением в точку наблюдения. Поэтому точка наблюдения оказывается внутри конуса выброса, если выполняется условие

(20)
$cos(\alpha {\text{/}}2) < {\mathbf{a}} \cdot {\mathbf{n}}.$
Кроме этого в неинерциальной системе отсчета, связанной орбитальным вращением с угловой скоростью $\Omega $, необходимо учесть, что азимутальный угол $\varphi $ ориентации выброса ${\mathbf{a}}$ изменяется со временем по закону
(21)
$\varphi = {{\varphi }_{0}} - \Omega (t - {{t}_{0}}),$
где ${{t}_{0}}$ – некоторый начальный момент времени, а ${{\varphi }_{0}}$ – соответствующая начальная азимутальная фаза. В качестве ${{t}_{0}}$ выбирается момент входа выброса в расчетную область. Эта ситуация показана на рис. 1 в виде конфигураций для двух последовательных моментов времени ${{t}_{1}}$ и ${{t}_{2}}$. В течение интервала времени ${{t}_{1}} \leqslant t \leqslant {{t}_{2}}$ из-за орбитального движения ориентация конуса выброса поворачивается в обратном направлении относительно планеты на угол $\Delta \varphi = \Omega ({{t}_{2}} - {{t}_{1}})$. Вещество выброса при этом успевает смещаться на некоторое расстояние в радиальном направлении от звезды.

Чтобы описанная модель была полной, необходимо задать скорости распространения границ, разделяющих фазы КВМ. Это позволяет однозначным образом определить фазу выброса в данной точке пространства в произвольный момент времени. Однако такая информация в экспериментальных данных отсутствует. Поэтому в нашей модели эти скорости задаются равными скоростям газа в данной фазе КВМ.

Следует заметить, что выброс будет иметь форму прямого конуса только в инерциальной системе отсчета. В неинерциальной системе отсчета, связанной с вращающейся двойной системой, форма конуса будет изогнутой в виде спирали. Этот эффект в нашей текущей модели КВМ не учитывается, но мы собираемся его учесть в последующих работах. Нетрудно оценить, что на масштабе $\Delta r$ использованной нами расчетной области ось конуса повернется на угол $\Delta \varphi = - \Omega \Delta r{\text{/}}{{v}_{{{\text{cme}}}}}$, где ${{v}_{{{\text{cme}}}}}$ – характерная скорость выброса. Для параметров наших расчетов угол поворота оси конуса $\Delta \varphi $ не превосходит 10°. При этом угол, под которым из центра звезды видна вся расчетная область, составляет 46°. Иными словами, неучет этого эффекта в наших расчетах вносит погрешность не более 20%.

2.4. Параметры модели и численный метод

В качестве объекта исследования мы используем типичный горячий юпитер HD 209458b, который имеет массу ${{M}_{{\text{p}}}} = 0.71{{M}_{{\text{J}}}}$ и фотометрический радиус ${{R}_{{\text{p}}}} = 1.38{{R}_{{\text{J}}}}$, где ${{M}_{{\text{J}}}}$ и ${{R}_{{\text{J}}}}$ – масса и радиус Юпитера. Родительская звезда характеризуется следующими параметрами: спектральный класс G0, масса ${{M}_{{\text{s}}}} = 1.1\;{{M}_{ \odot }}$, радиус ${{R}_{{\text{s}}}} = 1.2\;{{R}_{ \odot }}$. Период собственного вращения звезды ${{P}_{{{\text{rot}}}}} = 14.4$ сут, что соответствует угловой скорости ${{\Omega }_{{\text{s}}}} = 5.5 \times $ $ \times \;{{10}^{{ - 6}}}$ с–1 или линейной скорости на экваторе ${{v}_{{{\text{rot}}}}} = 4.2$ км/с. Большая полуось орбиты планеты $A = 10.2\;{{R}_{ \odot }}$, что соответствует периоду обращения вокруг звезды ${{P}_{{{\text{orb}}}}} = 84.6$ ч.

В начальный момент времени задавалась сферически-симметричная изотермическая атмосфера планеты, распределение плотности в которой определялось из условия гидростатического равновесия:

(22)
$\rho = {{\rho }_{{{\text{atm}}}}}exp\left[ { - \frac{{G{{M}_{{\text{p}}}}}}{{{{R}_{{{\text{gas}}}}}{{T}_{{{\text{atm}}}}}}}\left( {\frac{1}{{{{R}_{{\text{p}}}}}} - \frac{1}{{{\text{|}}{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{p}}}}{\kern 1pt} {\text{|}}}}} \right)} \right],$
где ${{\rho }_{{{\text{atm}}}}}$ – плотность на фотометрическом радиусе, ${{T}_{{{\text{atm}}}}}$ – температура атмосферы, ${{R}_{{{\text{gas}}}}}$ – газовая постоянная. Начальная толщина атмосферы определялась из условия равновесия по давлению с веществом звездного ветра. В расчетах температура атмосферы задавалась равной ${{T}_{{{\text{atm}}}}} = 7500$ К, а концентрация частиц на фотометрическом радиусе ${{n}_{{{\text{atm}}}}} = {{10}^{{11}}}$ см–3. Эти значения температуры и плотности соответствуют формированию квазизамкнутой оболочки для немагнитного случая. Предполагалось, что величина магнитного момента планеты составляет 0.1 от магнитного момента Юпитера, а ось магнитного диполя была наклонена на угол 30° по отношению к оси вращения планеты в противоположную от звезды сторону. При этом мы считали, что собственное вращение планеты является синхронизованным с орбитальным вращением, а ось собственного вращения коллинеарна оси орбитального вращения.

Параметры звездного ветра определялись на основе модели, описанной в разделе 2.2. Среднее магнитное поле на поверхности родительской звезды задавалось равным ${{B}_{{\text{s}}}} = {{10}^{{ - 3}}}$ Гс, что соответствует относительно слабому полю. Решение уравнений, описывающих структуру ветра, показывает, что при таком значении поля альфвеновская точка ${{r}_{A}}$ формально располагается внутри звезды. Быстрой магнитозвуковой точке соответствует радиус ${{r}_{F}} = 8.197\;{{R}_{ \odot }}$. Показатель политропы оказывается равным $\kappa = 1.112$. На орбите планеты, расположенной на расстоянии $10.2\;{{R}_{ \odot }}$ от центра звезды, параметры ветра оказываются следующими: температура ${{T}_{{\text{w}}}} = 7.3 \times {{10}^{5}}$ К, скорость ${{v}_{{\text{w}}}} = 130$ км/с, концентрация протонов ${{n}_{{\text{w}}}}$  = = 1400 см–3. Отсюда следует, что планета расположена в сверх-альфвеновской зоне ветра, поскольку на орбите планеты скорость ветра ${{v}_{{\text{w}}}}$ превышает альфвеновскую скорость ${{u}_{A}}$. При этом альфвеновское число Маха на орбите планеты оказывается равным $\lambda = 154.86$. С учетом орбитальной скорости планеты $143$ км/с находим, что отношение скорости обтекания планеты звездным ветром к альфвеновской скорости составляет значение 230.22. Таким образом, при используемых нами параметрах модели обтекание планеты звездным ветром происходит в существенно сверх-альфвеновском режиме.

Моделирование проводилось в декартовой системе координат, начало которой располагалось в центре горячего юпитера. Ось $x$ проходила через центры звезды и планеты и при этом была направлена от звезды к планете. Ось $y$ была направлена вдоль орбитального вращения планеты, а ось $z$ – вдоль ее оси собственного вращения. Использовалась расчетная область $ - 30 \leqslant x{\text{/}}{{R}_{{\text{p}}}} \leqslant 30$, $ - 30 \leqslant y{\text{/}}{{R}_{{\text{p}}}} \leqslant 30$, $ - 15 \leqslant z{\text{/}}{{R}_{{\text{p}}}} \leqslant 15$ с числом ячеек $N = 480 \times 480 \times 240$. Для повышения точности расчета сетка сгущалась к центру планеты.

Граничные условия задавались следующим образом. Внутри планеты на расстоянии $0.56{{R}_{{\text{p}}}}$ от центра устанавливалась твердая граница, на которой были заданы постоянные граничные условия, определяемые соотношением (22). Магнитное поле ${\mathbf{b}}$ при этом задавалось равным нулю. На высотах от $0.56{{R}_{{\text{p}}}}$ до $1.0{{R}_{{\text{p}}}}$ для гашения ударных волн в атмосфере планеты вводилась искусственная вязкость, аналогично работам [3, 4]. На участках внешних границ, через которые звездный ветер втекал в счетную область, граничные условия задавались из описанной выше модели звездного ветра. На участках, через которые вещество покидало счетную область, поддерживались условия свободного вытекания. На участках внешних границ, которые в данный момент времени попадали в конус выброса, использовались нестационарные граничные условия, определяемые из модели КВМ.

Для численного решения уравнений магнитной гидродинамики (1)–(4) мы используем комбинацию разностных схем Роу и Лакса-Фридрихса. Алгоритм решения состоит из нескольких последовательных этапов, возникающих в результате применения метода расщепления полной системы уравнений на отдельные подсистемы по физическим процессам. Первая подсистема соответствует идеальной магнитной гидродинамике с собственным магнитным полем плазмы ${\mathbf{b}}$ без учета фонового магнитного поля ${\mathbf{H}}$. В нашей численной модели для решения этой подсистемы использовалась схема Роу [29] (см. также монографию [15]) для уравнений магнитной гидродинамики с повышающей поправкой Ошера [30]. МГД вариант схемы Роу был представлен в численном коде таким образом, чтобы в отсутствие магнитного поля (${\mathbf{b}} = 0$) эта схема в точности переходила в схему Роу–Эйнфельдта–Ошера, использовавшуюся нами ранее в чисто газодинамических расчетах [3]. Более подробно использованная разностная схема описана в работе [31]. Вторая (альфвеновская) подсистема соответствует учету влияния фонового поля. Для численного решения второй подсистемы использовалась схема Лакса–Фридрихса с повышающими TVD (total variation diminishing) поправками [15]. Для очистки дивергенции магнитного поля ${\mathbf{b}}$ мы применяли метод обобщенного множителя Лагранжа [32]. При использовании этого метода к вышеописанным двум подсистемам добавляется еще одна подсистема, отвечающая за очистку дивергенции магнитного поля.

Моделирование осуществлялось посредством непрерывного расчета от начального состояния. Но его можно условно разбить на два отдельных этапа. На первом этапе моделирование проводилось до достижения квазистационарного решения, когда основные параметры течения переставали существенно изменяться со временем. Это соответствует формированию квази-замкнутой оболочки горячего юпитера. На втором этапе моделировалось взаимодействие сформировавшейся оболочки с КВМ. Как уже было описано выше, в данной работе используется упрощенная модель КВМ, состоящая из трех фаз: ударной волны, раннего КВМ и позднего КВМ. До входа в расчетную область КВМ распространяется внутри некоторого телесного угла, ось которого вращается по отношению к движущейся по орбите планете, а вершина совпадает с центром родительской звезды. Параметры звездного ветра, в том числе возмущенного, задаются с помощью изменяющихся во времени условий (19). Для проведения расчетов были выбраны модельные КВМ из работы [8], условно названные “долгий” и “короткий” КВМ, параметры которых указаны в табл. 1. В этой модели временные профили ${{f}_{q}}(t)$, которые определяют возмущения исходных параметров звездного ветра в точке наблюдения, для каждой величины $q$ описываются с помощью кусочно-постоянных функций.

Таблица 1.  

Параметры звездного ветра во время прохождения КВМ. Плотность $n$, скорость $v$, температура $T$ и магнитное поле $B$ нормированы на соответствующие параметры ${{n}_{{\text{w}}}}$, ${{v}_{{\text{w}}}}$, ${{T}_{{\text{w}}}}$ и ${{B}_{{\text{w}}}}$ невозмущенного звездного ветра

Тип КВМ долгий короткий
Фаза 1 2 3 1 2 3
Длительность, ч 1 1 1 0.17 0.17 0.17
$n{\text{/}}{{n}_{{\text{w}}}}$ 10 1 5 10 1 5
$T{\text{/}}{{T}_{{\text{w}}}}$ 5.07 0.79 0.3 5.07 0.79 0.3
${v}{\text{/}}{{{v}}_{{\text{w}}}}$ 13 13 13 6 6 6
$B{\text{/}}{{B}_{{\text{w}}}}$ 2.25 1.75 1.13 2.25 1.75 1.13

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

На рис. 2 представлено распределение десятичного логарифма плотности вещества в экваториальной плоскости расчетной области. На верхней панели показаны результаты вычислений для МГД случая, а на нижней панели – для чисто газодинамического случая. Число в правом верхнем углу указывает значение физического времени в орбитальных периодах ${{P}_{{{\text{orb}}}}}$ вращения планеты, прошедшее от начала расчета.

Рис. 2.

Распределение десятичного логарифма плотности (цвет) вещества в окрестности горячего юпитера HD 209458b для МГД случая (сверху) и чисто газодинамического случая (снизу) перед началом взаимодействия с выбросом. На графиках показана экваториальная плоскость счетной области. Число в правом верхнем углу соответствует физическому времени в орбитальных периодах, прошедшему с момента начала расчетов. Размеры счетной области нормированы на радиус планеты.

На момент времени $0.34{{P}_{{{\text{orb}}}}}$ в обоих случаях формируются квазистационарные течения с темпом потери массы $1.03 \times {{10}^{{10}}}$ г/с и $1.32 \times {{10}^{{10}}}$ г/с для МГД и чисто газодинамической моделей соответственно. Величина темпа потери массы ${{\dot {M}}_{{\text{p}}}}$ вычисляется на основе расчета потока массы через сферу радиусом $5{{R}_{{\text{p}}}}$, центр которой совпадает с центром горячего юпитера.

В обоих случаях наблюдается квази-замкнутая протяженная газовая (плазменная) оболочка с потоками вещества из точек Лагранжа ${{L}_{1}}$ и ${{L}_{2}}$. Поток из точки ${{L}_{1}}$ останавливается динамическим давлением звездного ветра. Однако в случае МГД модели остановка потока происходит на более близких к планете расстояниях [9].

3.1. Долгий КВМ

В модели долгого КВМ все три фазы прохождения выброса в окрестности планеты четко различимы (см. рис. 3–6). Хорошо заметны области нагребенного вещества в начале первой и третьей фаз. К моменту времени $0.378{{P}_{{{\text{orb}}}}}$ передний край КВМ достигает диска планеты, что приводит к дестабилизации потока через внутреннюю точку Лагранжа ${{L}_{1}}$ (рис. 3). К конце третьей фазы прохождения выброса поток вещества через точку ${{L}_{1}}$ полностью разрушается возмущенным ветром. При этом часть этого потока падает обратно на планету, а остаток выносится за пределы расчетной области (рис. 4). Приходящая после ударной волны область разрежения влечет за собой расширение оболочки горячего юпитера вплоть до 5–6 ${{R}_{{\text{p}}}}$ (против $2{{R}_{{\text{p}}}}$ при стационарном ветре) (рис. 5). Помимо этого в газодинамическом случае становится заметной фрагментация потока через точку ${{L}_{2}}$. По мере восстановления плотности звездного ветра расширение прекращается, а течения в оболочке стремятся восстановить первоначальную конфигурацию (рис. 6).

Рис. 3.

То же, что и на рис. 2. Взаимодействие протяженной оболочки горячего юпитера с долгим КВМ. Первая фаза КВМ достигла планеты, третья фаза вошла в расчетную область.

Рис. 4.

То же, что и на рис. 2. Взаимодействие протяженной оболочки горячего юпитера с долгим КВМ. Третья фаза КВМ достигла планеты.

Рис. 5.

То же, что и на рис. 2. Взаимодействие протяженной оболочки горячего юпитера с долгим КВМ. Планета находится в индуцированной прохождением КВМ области разрежения звездного ветра.

Рис. 6.

То же, что и на рис. 2. Взаимодействие протяженной оболочки горячего юпитера с долгим КВМ. Плотность звездного ветра восстанавливается.

Зависимость величины темпа потери массы ${{\dot {M}}_{{\text{p}}}}$ от времени для случая долгого КВМ для обеих моделей (рис. 7) имеет два пика, ассоциированных с взаимодействием планетарной оболочки с первой и третьей фазами прохождения выброса, отличающимися повышенной плотностью. При учете магнитного поля высота этих пиков достигает больших значений, чем в чисто газодинамическом случае. Примечательно, что третья фаза, менее плотная, чем первая, ответственна за снос большей массы вещества. Мы объясняем этот эффект тем, что первая фаза первично дестабилизирует оболочку планеты, тогда как третья фаза выносит вещество за пределы ограничивающей сферы, для которой проводился расчет величины темпа потери массы. Сразу после прохождения КВМ через область, занимаемую планетой, темп потери массы на некоторое время становится отрицательным, поскольку масса, сосредоточенная вблизи планеты, увеличивается. По-видимому, такой эффект связан с упомянутым выше падением вещества из разрушенного потока через внутреннюю точку Лагранжа ${{L}_{1}}$ обратно на горячий юпитер.

Рис. 7.

Зависимость темпа потери массы горячего юпитера (г/с) от физического времени с начала расчета (${{P}_{{{\text{orb}}}}}$) для МГД (слева) и чисто газодинамического (справа) вариантов моделирования для случая долгого КВМ.

Интегрирование темпа потери массы ${{\dot {M}}_{{\text{p}}}}$ на промежутке времени от $0.35{{P}_{{{\text{orb}}}}}$ до $0.598{{P}_{{{\text{orb}}}}}$ дает следующие значения для полной потери массы $\Delta {{M}_{{\text{p}}}}$ горячим юпитером, вызванной прохождением одного КВМ: $2.26 \times {{10}^{{14}}}$ г для МГД модели и $4.75 \times {{10}^{{14}}}$ г для чисто газодинамической модели.

3.2. Короткий КВМ

Короткий КВМ в нашей модели отличается от долгого, помимо длительности, скоростью и углом вхождения в расчетную область. Сам выброс при этом не оказывает такого же существенного воздействия на структуру течений вблизи планеты, однако он по-прежнему приводит к сильной дестабилизации оболочки. Уже на незначительном расстоянии от края расчетной области, параметры КВМ сглаживаются (рис. 8). Поэтому можно говорить о цельном КВМ без привязки к отдельной фазе. После прохождения выброса (рис. 9) наступает этап взаимодействия с областью разрежения, которая длится меньше по сравнению со случаем долгого КВМ (рис. 10).

Рис. 8.

То же, что и на рис. 2. Взаимодействие протяженной оболочки горячего юпитера с коротким КВМ. Передний край КВМ достиг планеты.

Рис. 9.

То же, что и на рис. 2. Взаимодействие протяженной оболочки горячего юпитера с коротким КВМ. Планета находится в индуцированной прохождением КВМ области разрежения звездного ветра.

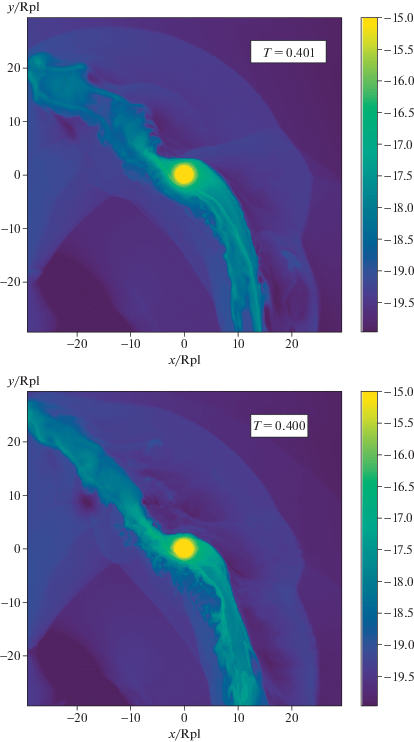
Рис. 10.

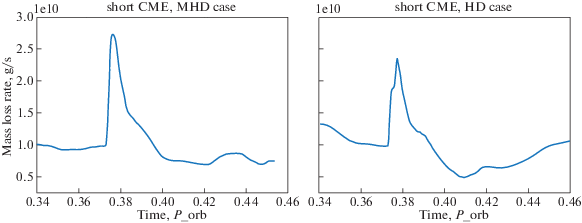
То же, что и на рис. 2. Взаимодействие протяженной оболочки горячего юпитера с коротким КВМ. Плотность звездного ветра восстанавливается.

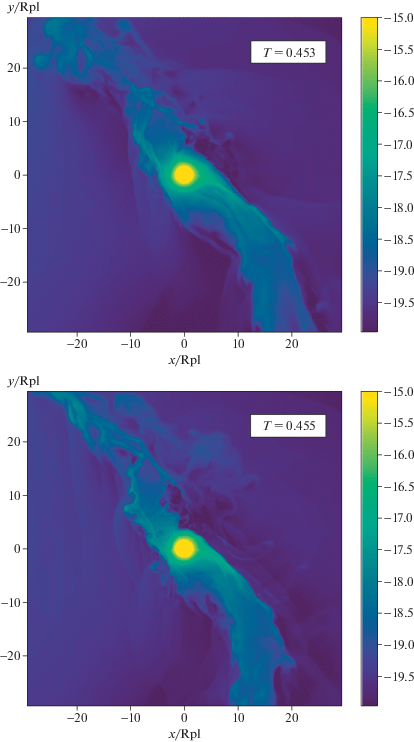
Аналогично случаю долгого КВМ максимальное значение темпа потери массы ${{\dot {M}}_{{\text{p}}}}$ оказывается больше в МГД случае (рис. 11). На графиках наблюдается провал, когда темп потери массы резко уменьшается. Однако значения темпа потери массы при этом не уходят в область отрицательных значений, что можно связать с коротким временем действия области разрежения. Общая потеря массы $\Delta {{M}_{{\text{p}}}}$ за один выброс составила $3.45 \times {{10}^{{14}}}$ г/с и $3.26 \times {{10}^{{14}}}$ г/с для МГД и газодинамической моделей соответственно. Близость полученных интегралов может быть связана, во-первых, с меньшим по времени влиянием короткого КВМ на область вблизи горячего юпитера, во-вторых, с тем, что короткий модельный выброс проходит по касательной к диску планеты.

Рис. 11.

То же, что и на рис. 7, но для случая короткого КВМ.

4. ЗАКЛЮЧЕНИЕ

Морфология течений в окрестности горячего юпитера определяется, по большей части, балансом динамического давления ветра и давления оболочки планеты. Таким образом, возмущения в звездном ветре, даже самые незначительные, способны влиять на структуру течений в окрестности атмосфер экзопланет, особенно если речь идет о частях оболочки, выходящих за полость Роша и демонстрирующих слабую гравитационную связь с планетой. Поэтому корональные выбросы массы важно рассматривать как одно из распространенных явлений в астрофизике, непосредственно влияющее на параметры звездного ветра и, как следствие, на эволюцию атмосфер экзопланет.

Качественный анализ структур, проведенный в настоящей работе, показал, что динамика основных течений вблизи горячего юпитера с одинаковой точностью описывается как МГД, так и чисто газодинамической моделями, с той разницей, что магнитное поле приводит к большей стабилизации некоторых потоков. Как для долгого, так и для короткого КВМ включение в рассмотрение, пусть и слабого, магнитного поля позволило избежать незначительной фрагментации истечения из точки Лагранжа ${{L}_{2}}$. Вполне возможно, что для упрощения расчетов при грубом определении основных закономерностей динамики вещества, можно пользоваться менее громоздкой газодинамической моделью. Однако следует отметить, что для систем с более сильным магнитным полем, чем в рассмотренной, именно МГД модель может помочь выявить существенно более тонкие эффекты.

Отдельно необходимо подчеркнуть влияние области разрежения, следующей сразу за КВМ и вносящей весомый вклад в дестабилизацию оболочки горячего юпитера. Падение давления звездного ветра приводит к увеличению области расширения оболочки и отдалению точки лобового столкновения непосредственно от поверхности планеты в 2–3 раза. Не так давно удалось пронаблюдать корональный выброс массы у другой звезды [33], поэтому в перспективе при достаточном количестве наблюдательных данных такой эффект можно наблюдать при интерпретации более раннего начала транзита у известных горячих юпитеров.

По результатам проведенных МГД и газодинамического моделирований можно сделать вывод, что включение в рассмотрение магнитного поля так же, как и в случае стационарного ветра [9], приводит к уменьшению потери массы в случае значительных возмущений параметров ветра. Примечателен тот факт, что хоть и разница в значениях интегральной потери массы планетой соответствует данному выводу, пики темпа потери массы выше именно в МГД случае. Не до конца изучен также вопрос влияния положения КВМ по отношению к горячему юпитеру. Показано, что геометрия выброса играет существенную роль в степени дестабилизации оболочки планеты за пределами полости Роша, однако точные закономерности найдены не были. Эти результаты открыты для дальнейших обсуждений.

По итогам работы общая потеря массы $\Delta {{M}_{{\text{p}}}}$ за выброс составила для МГД и газодинамической моделей соответственно $2.26 \times {{10}^{{14}}}$ г, $4.75 \times {{10}^{{14}}}$ г для долгого КВМ и $4.27 \times {{10}^{{14}}}$ г, $5.27 \times {{10}^{{14}}}$ г для короткого КВМ. Сравнение этих результатов с чисто газодинамическими расчетами [7] для широкого КВМ, когда планета на протяжении всего моделирования лежит внутри выброса ($\Delta {{M}_{{\text{p}}}} \approx {{10}^{{15}}}$ г), показало уменьшение общей потери массы, ассоциированной с КВМ. Однако разница составляет меньше порядка, что позволяет сделать вывод, что учет даже слабых узких КВМ, взаимодействующих с планетой лишь по касательной, необходим для исследования эволюции горячих юпитеров. Во-первых, стоит принять во внимание, что планеты, находящиеся столь близко к родительской звезде, способны подвергаться влиянию КВМ довольно часто. Во-вторых, частота КВМ зависит от возраста звезды, поэтому более молодые, чем Солнце, звезды будут в сумме оказывать более разрушительное влияние на оболочки таких планет.

Список литературы

  1. D. Charbonneau, T. M. Brown, D. W. Latham, and M. Mayor, Astrophys. J. 529, L45 (2000).

  2. A. Vidal-Madjar, A. Lecavelier des Etangs, J.-M. Desert, G. E. Ballester, et al., Nature 422, 143 (2003).

  3. Д. В. Бисикало, П. В. Кайгородов, Д. Э. Ионов, В. И. Шематович, Астрон. журн. 90, 779 (2013).

  4. D. Bisikalo, P. Kaygorodov, D. Ionov, V. Shematovich, et al., Astrophys. J. 764, 19 (2013).

  5. J. L. Linsky, H. Yang, K. France, C. S. Froning, et al., Astrophys. J. 717, 1291 (2010).

  6. Д. В. Бисикало, А. А. Черенков, Астрон. журн. 93, 139 (2016).

  7. A. Cherenkov, D. Bisikalo, L. Fossati, and C. Möstl, A-strophys. J. 846, 31, (2017).

  8. П. В. Кайгородов, Е. А. Ильина, Д. В. Бисикало, Астрон. журн. 96, 367 (2019).

  9. А. С. Аракчеев, А. Г. Жилкин, П. В. Кайгородов, Д. В. Бисикало, А. Г. Косовичев, Астрон. журн. 94, 927 (2017).

  10. K. G. Kislyakova, M. Holmström, H. Lammer, et al., Science 346, 981 (2014).

  11. А. Г. Жилкин, Д. В. Бисикало, Астрон. журн. 96, 547 (2019).

  12. А. Г. Жилкин, Д. В. Бисикало, П. В. Кайгородов, А-строн. журн. 97, 242 (2020).

  13. А. Г. Жилкин, Д. В. Бисикало, Астрон. журн. 97, 538 (2020).

  14. А. Г. Жилкин, Д. В. Бисикало, П. В. Кайгородов, А-строн. журн. 97, 145 (2020).

  15. Д. В. Бисикало, А. Г. Жилкин, А. А. Боярчук, Газодинамика тесных двойных звезд (М.: Физматлит, 2013).

  16. А. Г. Жилкин, Д. В. Бисикало, А. А. Боярчук, Усп. физ. наук 182, 121 (2012).

  17. T. Tanaka, J. Comp. Phys. 111, 381 (1994).

  18. K. G. Powell, P. L. Roe, T. J. Linde, T. I. Gombosi, and D. L. de Zeeuw, J. Comp. Phys. 154, 284 (1999).

  19. A. A. Cherenkov, D. V. Bisikalo, and A. G. Kosovichev, Monthly Not. Roy. Astron. Soc. 475, 605 (2018).

  20. Д. В. Бисикало, В. И. Шематович, П. В. Кайгородов, А. Г. Жилкин, Газовые оболочки экзопланет – горячих юпитеров (М.: Наука, 2020).

  21. M. J. Owens and R. J. Forsyth, Living Rev. Solar Phys. 10, 5 (2013).

  22. E. N. Parker, Astrophys. J. 128, 664 (1958).

  23. E. J. Weber and L. Davis Jr., Astrophys. J. 148, 217 (1967).

  24. В. Б. Баранов, К. В. Краснобаев, Гидродинамическая теория космической плазмы (М.: Наука, 1977).

  25. G. L. Withbroe, Astrophys. J. 325, 442 (1988).

  26. W. M. Farrell, J. S. Halekas, R. M. Killen, G. T. Delory, et al., J. Geophys. Res. Planets 117, id. E00K04 (2012).

  27. C. Möstl, K. Amla, J. R. Hall, P. C. Liewer, et al., Astrophys. J. 787, 119, (2014).

  28. Y. D. Liu, J. D. Richardson, C. Wang, and J. G. Luhmann, Astrophys. J. 788, L28, (2014).

  29. P. Cargo and G. Gallice, J. Comp. Phys. 136, 446 (1997).

  30. S. R. Chakravarthy and S. Osher, AIAA Papers N 85-0363 (1985).

  31. А. Г. Жилкин, А. В. Соболев, Д. В. Бисикало, М. М. Габ-деев, Астрон. журн. 96, 748 (2019).

  32. A. Dedner, F. Kemm, D. Kroner, C.-D. Munz, T. Schni-tzer, and M. Wesenberg, J. Comp. Phys. 175, 645 (2002).

  33. C. Argiroffi, F. Reale, et al., Nature Astronomy 3, 742 (2019).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал