1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 99, № 10, 2022

Астрономический журнал, 2022, T. 99, № 10, стр. 832-846

Динамика замагниченных аккреционных дисков молодых звезд

С. А. Хайбрахманов 1, 2, *, А. Е. Дудоров 2, 1

1 Уральский федеральный университет
Екатеринбург, Россия

2 Челябинский государственный университет
Челябинск, Россия

* E-mail: khaibrakhmanov@csu.ru

Поступила в редакцию 23.05.2022
После доработки 06.07.2022
Принята к публикации 18.07.2022

Полный текст (PDF)

Аннотация

В работе исследуется динамика аккреционных дисков молодых звезд с остаточным крупномасштабным магнитным полем. Авторская магнитогазодинамическая (МГД) модель аккреционных дисков обобщается для учета динамического влияния магнитного поля на скорость вращения газа и вертикальную структуру диска. С помощью развиваемой динамической МГД-модели рассчитывается структура аккреционного диска звезды типа Т Тельца солнечной массы для различных значений темпа аккреции $\dot {M}$ и размеров пылинок ${{a}_{d}}$. Расчеты радиальной структуры диска показывают, что при типичных значениях $\dot {M} = {{10}^{{ - 8}}}$ ${\kern 1pt} {{M}_{ \odot }}$/год и ${{a}_{d}} = 0.1$ мкм магнитное поле в диске является кинематическим, и электромагнитная сила не влияет на скорость вращения газа. В случае крупных пылинок, ${{a}_{d}} \geqslant 1$ мм, магнитное поле вморожено в газ и на радиальных расстояниях от звезды $r \gtrsim 30$ а.е. генерируется динамически сильное магнитное поле, натяжения которого замедляют скорость вращения на величину $ \lesssim {\kern 1pt} 1.5$% от кеплеровской скорости. Это эффект сравним с вкладом радиального градиента газового давления и может приводить к увеличению скорости радиального дрейфа пылинок в диске. В случае высокого темпа аккреции, $\dot {M} \geqslant {{10}^{{ - 7}}}$ ${{M}_{ \odot }}$/год, магнитное поле является динамически сильным и во внутренней области диска, $r < 0.2$ а.е. Расчеты вертикальной структуры показывают, что, в зависимости от условий на поверхности диска, вертикальный градиент магнитного давления может приводить как к уменьшению, так и увеличению характерной толщины диска по сравнению с гидростатической на 5–20%. Изменение толщины диска происходит вне области низкой степени ионизации и эффективной диффузии магнитного поля (“мертвой” зоны), которая при типичных параметрах простирается от $r = 0.3$ до 20 а.е.

Ключевые слова: аккреция, аккреционные диски, магнитные поля, магнитная газодинамика (МГД)

1. ВВЕДЕНИЕ

Аккреционные диски молодых звезд (АД МЗ) представляют собой геометрически тонкие вращающиеся газопылевые диски размерами $ \sim {\kern 1pt} 100{\kern 1pt} - {\kern 1pt} 1000$ а.е. и массами $ \sim {\kern 1pt} 0.001{\kern 1pt} - {\kern 1pt} 0.1\;{{M}_{ \odot }}$ (см. [1]). В процессе эволюции АД темп аккреции вещества на МЗ уменьшается от ${{10}^{{ - 6}}}$ до ${{10}^{{ - 9}}}$ ${{M}_{ \odot }}$/год. АД МЗ могут эволюционировать в протопланетные диски (ППД) – аналоги протосолнечной туманности, в которых условия благоприятны для образования планет. В последние годы это предположение получает прямые наблюдательные подтверждения [2, 3]. Процессы, связанные с формированием и динамикой протопланет также проявляются как кольца, спирали, вихри и другие субструктуры на картах излучения АД и ППД в инфракрасном и (суб)миллиметровом диапазонах спектра [4, 5]. Развитие техник проведения и анализа наблюдений позволяет исследовать структуру АД и ППД, в частности восстанавливать двумерные распределения температуры и определять компоненты скорости в дисках (см., напр., [6, 7]). Для интерпретации имеющихся и будущих наблюдений АД и ППД, а также объяснения происхождения и свойств внесолнечных планетных систем интерес представляет разработка теоретических моделей АД и ППД.

Современные наблюдательные данные позволяют утверждать, что АД и ППД МЗ имеют крупномасштабное магнитное поле. Первые указания на это были получены из поляриметрических исследований излучения окрестностей звезд типа Т Тельца [8]. Поляризационное картирование аккреционных дисков звезд типа Т Тельца и Ае/Ве звезд Хербига с пространственным разрешением порядка 50 а.е. показало, что крупномасштабное магнитное поле в дисках может иметь сложную геометрию [9]. Наличие магнитного поля косвенно подтверждается обнаружением истечений и джетов из молодых звездных объектов (см. обзор Франка и др. [10]). Надежные измерения интенсивности магнитного поля АД и ППД МЗ до сих пор затруднительны из-за ограничений на чувствительность и пространственное разрешение инструментов. Донати и др. [11] заявили о регистрации зеемановского уширения линий в диске звезды FU Ori и отметили, что в диске может присутствовать магнитное поле интенсивностью $B \sim 1$ кГс. Перспективным инструментом является измерение зеемановского расщепления молекулярных линий CN в субмиллиметровом диапазоне [12], с помощью которого пока удается получить лишь верхние оценки на интенсивность магнитного поля в поверхностных слоях дисков [13, 14]. Наконец, измерения остаточной намагниченности метеоритов дают косвенные оценки интенсивности магнитного поля протосолнечной туманности $ \sim {\kern 1pt} 0.1{\kern 1pt} - {\kern 1pt} 1$ Гс на расстоянии $1{\kern 1pt} - {\kern 1pt} 3$ а.е. от звезды [15, 16].

Наличие крупномасштабного магнитного поля в АД и ППД естественным образом объясняется в рамках теории остаточного магнитного поля, основанной на анализе наблюдательных данных и численных расчетах процесса образования звезд в результате гравитационного коллапса магнитных вращающихся протозвездных облаках (ПЗО). Согласно этой теории, магнитный поток ПЗО частично сохраняется в процессе коллапса ПЗО, и звезды с аккреционными дисками рождаются с остаточным крупномасштабным магнитным полем [17, 18]. При условии развитой циклонической конвекции в дифференциально вращающемся диске возможна также генерация магнитного поля за счет динамомеханизма [19, 20].

В первых работах по моделированию эволюции аккреционных дисков с крупномасштабным магнитным полем рассматривался вопрос об эффективности адвекции полоидального магнитного поля в турбулентных дисках [21, 22]. Рейес-Руиз и Степински [23] указали на то, что во вращающихся дисках происходит также генерация тороидального магнитного поля. Шу и др. [24] получили аналитическое решение для распределения полоидального магнитного поля в диске для предписанных коэффициента диффузии и степени отклонения скорости вращения газа от кеплеровской. В работе Лавлэйса и др. [25] рассчитана вертикальная структура стационарных аккреционных дисков в предположении, что поверхностные слои аккреционного диска являются нетурбулентными. В указанных статьях величина коэффициента диффузии предписывалась с помощью безразмерного магнитного числа Прандтля. Подход Лубова и др. [22] был развит в работе Гуилет и Огильви [26], в которых было постулировано и исследовано влияние турбулентной диффузии на эволюцию крупномасштабного полоидального магнитного поля. Авторы сделали аккуратное усреднение коэффициентов переноса по высоте диска и учли самосогласованное влияние магнитного поля на эти коэффициенты, что позволило описать более эффективное усиление магнитного поля в дисках. Окудзуми и Такеучи [27] получили стационарное распределение вертикального магнитного поля в диске с учетом только омической диффузии. Лицано и др. [28] рассчитали вертикальную структуру АД МЗ с предписанным вмороженным полоидальным магнитным полем. Они рассмотрели влияние вязкого и омического нагрева, а также нагрева излучением звезды на температуру диска.

Большинство численных магнитогазодинамических (МГД) расчетов эволюции АД с учетом омической диффузии и магнитной амбиполярной диффузии [29], а также с учетом эффекта Холла [30] проводились только в локальном приближении с использованием предписанной интенсивности и/или геометрии магнитного поля. Грессел и др. [31] выполнили первые глобальные расчеты с учетом магнитной амбиполярной диффузии и ионизации только рентгеновскими лучами и ультрафиолетовым излучением звезды. В расчетах исследовалась динамика диска в небольшой области от 1 до 5 а.е. от звезды. В ряде недавних работ проведены масштабные МГД-расчеты эволюции АД и ППД с целью исследования переноса углового момента посредством дискового ветра и попыток объяснения образования кольцевых структур в газе за счет МГД-процессов [32–35]. Недостатками указанных работ являются априорное задание коэффициентов диффузии магнитного поля и/или интенсивности магнитного поля в предположении о постоянстве плазменного параметра $\beta $ во всем диске.

В рамках теории остаточного магнитного поля Дудоров и Хайбрахманов разработали кинематическую МГД-модель АД МЗ [36–39]. Модель основана на приближениях базовой модели Шакуры и Сюняева [40, 41]. В дополнении к уравнениям базовой модели решается уравнение индукции с учетом омической и магнитной амбиполярной диффузий, магнитной плавучести и эффекта Холла, а также уравнения тепловой и ударной ионизации с учетом основных ионизационных и рекомбинационных эффектов. Расчеты с помощью модели в частности показали, что магнитное поле может быть динамически сильным в некоторых областях диска, $\beta \lesssim 1$, где $\beta $ – плазменный параметр (отношение газового давления к магнитному). В связи с этим необходима разработка динамической модели АД, в которой бы учитывалось влияние магнитного поля на структуру и эволюцию диска. Ранее модель Дудорова и Хайбрахманова была расширена для учета влияния диссипативных МГД-эффектов на тепловую структуру диска [42], а также градиента магнитного давления на вертикальную структуру диска [43]. В настоящей работе выполняется дальнейшее развитие модели. Впервые самосогласованно рассматривается влияние натяжений крупномасштабного магнитного поля на центробежное равновесие диска и определяется степень отклонения от кеплеровского вращения.

Статья организована следующим образом. В разделе 2 описывается постановка задачи. Уравнения модели, описывающие радиальную структуру диска, записываются в разделе 3.1, уравнения вертикальной структуры – в разделе 3.2. В разделе 4.1 приводятся основные параметры модели и методы решения уравнений. Результаты расчетов радиальной структуры диска с помощью развиваемой модели и влияние магнитного поля на скорость вращения вещества в диске приводятся и обсуждаются в разделе 4.2. Результаты расчетов вертикальной структуры диска и влияние магнитного поля на толщину диска описываются в разделе 4.3. В разделе 5 обсуждаются результаты работы и делаются выводы.

2. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим стационарный геометрически тонкий и оптически толстый аккреционный диск, масса которого мала по сравнению с массой звезды. Используем цилиндрические координаты $(r,\varphi ,z)$. Будем считать, что угловой момент переносится в радиальном направлении $r$ посредством турбулентности. Диск находится в центробежном равновесии по $r$ и магнитостатическом равновесии в вертикальном направлении $z$. Энергия, выделяемая в диске за счет турбулентного трения, уносится излучением в вертикальном направлении.

Вещество в аккреционных дисках молодых звезд представляет собой слабоионизованную газопылевую плазму. Для исследования динамики аккреционного диска с крупномасштабным магнитным полем используем систему уравнений диссипативной магнитной газодинамики,

(1)
$\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho v} \right) = 0,$
(2)
$\begin{gathered} \rho \left[ {\frac{{\partial {\mathbf{v}}}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{v}}} \right] = - \nabla \left( {p + \frac{{{{B}^{2}}}}{{8\pi }}} \right) + \\ \, + \rho {\mathbf{g}} + \frac{1}{{4\pi }}\left( {{\mathbf{B}} \cdot \nabla } \right){\mathbf{B}} + \operatorname{div} \hat {\sigma }{\kern 1pt} ', \\ \end{gathered} $
(3)
$\rho T\left[ {\frac{{\partial s}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right)s} \right] = \sigma _{{ik}}^{'}\frac{{\partial {{v}_{i}}}}{{\partial {{x}_{k}}}} + \nabla \cdot {\mathbf{F}},$
(4)
$\frac{{\partial {\mathbf{B}}}}{{\partial t}} = \nabla \times \left( {v \times {\mathbf{B}}} \right) + \eta {{\nabla }^{2}}{\mathbf{B}},$
где ${\mathbf{g}}$ – гравитационное ускорение, $s$ – энтропия на единицу объема, $\hat {\sigma }{\kern 1pt} '$ – тензор вязких напряжений ($\sigma _{{ik}}^{'}$ в индексных обозначениях, индексы $i$ и $k$ нумеруют пространственные координаты), ${\mathbf{F}}$ – плотность потока лучистой энергии, $\eta $ – коэффициент диффузии магнитного поля, включающий омическую и магнитную амбиполярную диффузию. Для остальных величин используются стандартные физические обозначения. Для замыкания системы уравнений (1)–(4) используем уравнение состояния идеального газа со средним молекулярным весом $\mu = 2.3$.

3. УРАВНЕНИЯ МГД-МОДЕЛИ АККРЕЦИОННЫХ ДИСКОВ

В приближении геометрически тонкого диска в исходных уравнениях можно пренебречь радиальными градиентами по сравнению с вертикальным, а последние заменить на конечные разности. В рассматриваемом случае маломассивного диска гравитационное ускорение определяется притяжением звезды,

(5)
${\mathbf{g}} = - \frac{{GM}}{{{{R}^{3}}}}{\mathbf{R}},$
где ${\mathbf{R}} = (r,{\kern 1pt} 0,{\kern 1pt} z)$ – радиус-вектор. В геометрически тонком диске $r$-компонента гравитационной силы доминирует, так что выполняются следующие соотношения для компонент вектора скорости газа: ${\text{|}}{{v}_{z}}{\kern 1pt} {\text{|}} \ll {\text{|}}{{v}_{r}}{\kern 1pt} {\text{|}} \ll {\text{|}}{{v}_{\varphi }}{\kern 1pt} {\text{|}}$. Эти приближения позволяют разделить переменные в уравнениях МГД и решать уравнения радиальной структуры (уравнения аккреции) и уравнения вертикальной структуры (уравнение магнитостатического равновесия) отдельно, полагая, что диск находится в центробежном равновесии.

Применимость стационарного приближения обусловлена тем, что основной динамический масштаб времени в рассматриваемом случае – кеплеровский период обращения, ${{t}_{{\text{k}}}}\, = \,1\;{\text{год}}\,{{(r{\text{/}}{\kern 1pt} 1\;{\text{а}}{\text{.е}}.{\kern 1pt} )}^{{3/2}}}$, – мал по сравнению со временем жизни диска ${{t}_{{{\text{disk}}}}} \sim 1{\kern 1pt} - {\kern 1pt} 10$ млн. лет.

3.1. Уравнения радиальной структуры

Система уравнений, описывающих радиальную структуру диска в кинематическом приближении, была получена Дудоровым и Хайбрахмановым [36–38]. Рассмотрим, как изменятся уравнения системы, если учесть динамические слагаемые, в частности, влияние магнитных натяжений на центробежное равновесие и диссипативных МГД-эффектов на тепловой баланс в диске.

Влияние магнитного поля на скорость вращения вещества в диске описывается радиальной компонентой уравнения движения (2),

(6)
$\begin{gathered} \rho {{\Omega }^{2}}r - \rho \frac{{GM}}{{{{r}^{2}}}}{{\left( {1 + \frac{{{{z}^{2}}}}{{{{r}^{2}}}}} \right)}^{{ - 3/2}}} + \frac{{\partial p}}{{\partial r}} + \\ + \;{\kern 1pt} \frac{{{{B}_{z}}}}{{4\pi }}\frac{{\partial {{B}_{r}}}}{{\partial z}} - \frac{\partial }{{\partial r}}\left( {\frac{{B_{z}^{2} + B_{\varphi }^{2}}}{{8\pi }}} \right) - \frac{{B_{\varphi }^{2}}}{{4\pi r}} = 0, \\ \end{gathered} $
где $\Omega = {{v}_{\varphi }}{\text{/}}r$ – угловая скорость газа. Градиентом газового давления, $\partial p{\text{/}}\partial r$, в геометрически тонком диске тоже можно пренебречь. Отметим, что в задачах о взаимодействии газа и пылинок в диске это слагаемое играет важную роль, т.к. вызываемое им небольшое отклонение от центробежного баланса обусловливает дрейф пылинок относительно газа [44]. Четвертое слагаемое в уравнении (6) описывает магнитные натяжения, а последние два – градиент магнитного давления. В геометрически тонком диске можно пренебречь последними двумя слагаемыми, поэтому
(7)
${{v}_{\varphi }} = \sqrt {\frac{{GM}}{r}{{{\left( {1 + \frac{{{{z}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{ - 3/2}}} - \frac{{r{{B}_{z}}}}{{4\pi \rho }}\frac{{\partial {{B}_{r}}}}{{\partial z}}} .$
Таким образом, основной вклад электромагнитной силы в центробежный баланс определяется $rz$-компонентой тензора напряжений Максвелла. В приближениях модели это слагаемое можно оценить как $(r{{B}_{z}}{\text{/}}4\pi \rho )({{B}_{r}}{\text{/}}H)$.

Влияние диссипативных МГД-эффектов – омической и магнитной амбиполярной диффузии – на тепловую структуру диска было включено в модель и исследовано в работе [42].

Итоговая система уравнений модели радиальной структуры диска с учетом рассмотренных динамических эффектов выглядит следующим образом:

(8)
$\dot {M} = - 2\pi r{{v}_{r}}\Sigma ,$
(9)
$\dot {M}{{\Omega }_{{\text{k}}}}f = 2\pi \alpha c_{{\text{T}}}^{2}\Sigma ,$
(10)
${{v}_{\varphi }} = \sqrt {\frac{{GM}}{r}{{{\left( {1 + \frac{{{{z}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{ - 3/2}}} - \frac{{r{{B}_{r}}{{B}_{z}}}}{{4\pi \Sigma }}} ,$
(11)
$H = \frac{{{{c}_{{\text{T}}}}}}{{{{\Omega }_{{\text{k}}}}}},$
(12)
${{\sigma }_{{{\text{sb}}}}}T_{{{\text{eff}}}}^{4} = \frac{3}{{8\pi }}\dot {M}\Omega _{{\text{k}}}^{2}f + {{\Gamma }_{{{\text{MGD}}}}},$
(13)
${{T}^{4}} = \frac{3}{8}{{\kappa }_{{\text{R}}}}\Sigma T_{{{\text{eff}}}}^{4},$
(14)
${{B}_{r}} = - \frac{{{{v}_{r}}H}}{\eta }{{B}_{z}},$
(15)
${{B}_{\varphi }} = - \frac{3}{2}{{\left( {\frac{H}{r}} \right)}^{2}}\frac{{{{v}_{\varphi }}H}}{\eta }{{B}_{z}} - \frac{1}{2}\left( {\frac{H}{r}} \right)\frac{{{{v}_{\varphi }}H}}{\eta }{{B}_{r}},$
(16)
${{B}_{z}} = \left\{ \begin{gathered} {{B}_{{z0}}}\frac{\Sigma }{{{{\Sigma }_{0}}}},\quad {{R}_{{\text{m}}}} \gg 1, \hfill \\ \sqrt {4\pi x{{\rho }^{2}}r{\text{|}}{{v}_{r}}{\kern 1pt} {\text{|}}} ,\quad {{R}_{{\text{m}}}} < 1, \hfill \\ \end{gathered} \right.$
где $\dot {M}$ – темп аккреции, $\Sigma = 2\langle \rho \rangle H$ – поверхностная плотность газа в диске, $\langle \rho \rangle $ – средняя по $z$ плотность газа, $H$ – шкала высоты диска, ${{\Omega }_{{\text{k}}}} = \sqrt {GM{\text{/}}{{r}^{3}}} $ – кеплеровская угловая скорость, $f = 1 - {{\left( {{{r}_{0}}{\text{/}}r} \right)}^{{1/2}}}$, ${{r}_{0}}$ – радиальная координата внутренней границы диска, ${{c}_{{\text{T}}}} = \sqrt {{{R}_{{\text{g}}}}T{\text{/}}\mu } $ – изотермическая скорость звука, $T$ – температура в экваториальной плоскости диска, ${{\sigma }_{{{\text{sb}}}}}$ – постоянная Стефана$ - $Больцмана, ${{T}_{{{\text{eff}}}}}$ – эффективная температура диска, ${{\Gamma }_{{{\text{MGD}}}}}$ – скорость нагрева за счет диссипативных МГД-эффектов на единицу площади диска, ${{\kappa }_{{\text{R}}}}$ – Росселандов средний коэффициент поглощения, ${{B}_{{z0}}} = {{B}_{z}}({{r}_{{{\text{out}}}}})$, ${{\Sigma }_{0}} = \Sigma ({{r}_{{{\text{out}}}}})$, ${{r}_{{{\text{out}}}}}$ – внешний радиус диска, ${{R}_{{\text{m}}}}$ – магнитное число Рейнольдса, $x$ – степень ионизации.

Обсудим кратко физический смысл уравнений модели. Уравнение (8) следует из уравнения непрерывности. Уравнение (9) представляет собой уравнение переноса углового момента. Уравнение (12) отражает баланс между поверхностными скоростями нагрева за счет турбулентного трения (первое слагаемое справа) и за счет диссипативных МГД-эффектов (второе слагаемое) и потоком излучения. Поверхностная скорость нагрева за счет омической и магнитно амбиполярной диффузий определяется как (см. [42]):

(17)
$\begin{gathered} {{\Gamma }_{{{\text{MGD}}}}} = \frac{{{{\nu }_{{\text{m}}}}}}{{4\pi }}{\kern 1pt} \frac{{B_{r}^{2} + B_{\varphi }^{2}}}{H} + \\ + \;\frac{{{{{\left( {{{B}_{r}}{{B}_{z}}} \right)}}^{2}} + {{{\left( {{{B}_{\varphi }}{{B}_{z}}} \right)}}^{2}} + {{{\left( {B_{r}^{2} + B_{\varphi }^{2}} \right)}}^{2}}}}{{32{{\pi }^{2}}{{R}_{{{\text{in}}}}}H}}, \\ \end{gathered} $
где ${{\nu }_{{\text{m}}}}$ – магнитная вязкость (коэффициент омической диффузии), ${{R}_{{{\text{in}}}}}$ – коэффициент трения между ионной и нейтральной компонентами плазмы.

Связь (13) между температурой в экваториальной плоскости диска и эффективной температурой получена из решения уравнения переноса излучения в диффузионном приближении. Решения (14), (15) уравнения индукции для компонент магнитного поля ${{B}_{r}}$ и ${{B}_{\varphi }}$ отражают баланс между адвекцией магнитного поля в соответствующих направлениях и диффузией в $z$-направлении. Вклад эффекта Холла в уравнение индукции был рассмотрен в [39], в настоящей работе он для ясности не учитывается. Решения (16) для вертикальной компоненты магнитного поля ${{B}_{z}}$ получены для случаев вмороженного магнитного поля (${{R}_{{\text{m}}}} \gg 1$) и эффективной магнитной амбиполярной диффузии (${{R}_{{\text{m}}}} < 1$).

Коэффициенты омической и амбиполярной диффузии магнитного поля зависят от степени ионизации вещества и рассчитываются в соответствии с работой [38]. Степень ионизации рассчитывается следуя Дудорову и Сазонову [45]. Рассматривается тепловая ионизация металлов и водорода, ударная ионизация космическими лучами, рентгеновским излучением и радиоактивными элементами. Учитываются лучистые рекомбинации и рекомбинации на пылевых гранулах.

3.2. Уравнения вертикальной структуры

Уравнения вертикальной структуры аккреционного диска с крупномасштабным магнитным полем выведены Дудоровым и Хайбрахмановым [43]. Полагается, что диск находится в магнитостатическом равновесии и основной вклад электромагнитной силы в баланс сил в $z$-направлении определяется градиентом тороиадального магнитного поля. Магнитостатическое равновесие устанавливается за время распространения МГД‑волн в $z$-направлении,

(18)
${{t}_{{\text{A}}}} \approx \frac{H}{{\sqrt {c_{{\text{T}}}^{2} + v_{{\text{A}}}^{2}} }} \sim \Omega _{{\text{k}}}^{{ - 1}}{{\left( {1 + \frac{2}{\beta }} \right)}^{{ - 1/2}}},$
где ${{v}_{{\text{A}}}}$ – альвеновская скорость. Оценка (18) показывает, что ${{t}_{{\text{A}}}} \sim {{t}_{{\text{k}}}} \ll {{t}_{{{\text{disk}}}}}$ при $\beta \sim 1$.

В модели полагается, что тепло, выделяющееся в результате турбулентного трения соседних слоев газа, уносится излучением в вертикальном направлении. Для оптически толстого диска поток излучения записывается в диффузионном приближении. В выбранных приближениях уравнения магнитостатического равновесия имеют вид:

(19)
$\frac{{dp}}{{dz}} = - \rho \frac{{GM}}{{{{r}^{3}}}}z - \frac{d}{{dz}}\left( {\frac{{B_{\varphi }^{2}}}{{8\pi }}} \right),$
(20)
$ - \frac{{16\sigma {{T}^{3}}}}{{3{{\kappa }_{{\text{R}}}}\rho }}\frac{{dT}}{{dz}} = {{\mathcal{F}}_{z}},$
(21)
$\frac{{d{{\mathcal{F}}_{z}}}}{{dz}} = \frac{3}{2}{\kern 1pt} \alpha {\kern 1pt} p{\kern 1pt} {{\Omega }_{{\text{k}}}},$
(22)
$\frac{{{{d}^{2}}{{B}_{\varphi }}}}{{d{{z}^{2}}}} = - \frac{3}{2}{\kern 1pt} \frac{{{{v}_{{\text{k}}}}{{B}_{z}}}}{\eta }\frac{z}{{{{r}^{2}}}},$
где ${{\mathcal{F}}_{z}}$ – $z$-компонента вектора плотности потока излучения ${\mathbf{F}}$, ${{v}_{{\text{k}}}} = {{\Omega }_{{\text{k}}}}r$ – кеплеровская скорость.

Обыкновенные дифференциальные уравнения первого порядка (19), (20) и (21) и уравнение второго порядка (22) образуют замкнутую систему уравнений относительно неизвестных $p$, $T$, ${{\mathcal{F}}_{z}}$ и ${{B}_{\varphi }}$ при заданных коэффициентах ${{\kappa }_{{\text{R}}}}(\rho ,{\kern 1pt} T)$, ${{v}_{{\text{k}}}}(r)$, $\eta (r)$ и ${{B}_{z}}(r)$ на некотором радиусе $r$. Будем решать уравнения в области $z \in [0,{\kern 1pt} {{z}_{{\text{s}}}}]$, где ${{z}_{{\text{s}}}}$ – координата фотосферы диска, которая характеризуется оптической толщиной $\tau = \int_{{{z}_{{\text{s}}}}}^\infty {{{\kappa }_{{\text{R}}}}\rho dz} = 2{\text{/}}3$. Граничные условия для давления, температуры и плотности потока излучения:

(23)
$p({{z}_{{\text{s}}}}) = {{p}_{{\text{s}}}},$
(24)
$T({{z}_{{\text{s}}}}) = {{T}_{{{\text{eff}}}}},$
(25)
${{\mathcal{F}}_{z}}(0) = 0,$
(26)
${{\mathcal{F}}_{z}}({{z}_{{\text{s}}}}) = \sigma T_{{{\text{eff}}}}^{4}.$
Давление на границе фотосферы ${{p}_{{\text{s}}}}$ можно оценить из приближенного решения уравнения гидростатического равновесия вблизи фотосферы (см. [46]):
(27)
${{p}_{{\text{s}}}} = \frac{2}{3}{\kern 1pt} \frac{{{{\Omega }_{{\text{k}}}}}}{{{{\kappa }_{{\text{R}}}}({{\rho }_{{\text{s}}}},{\kern 1pt} {{T}_{{{\text{eff}}}}})}}{\kern 1pt} {{z}_{{\text{s}}}}.$
При получении этой оценки принято, что $p(\tau = 0) \ll {{p}_{{\text{s}}}}$.

В силу экваториальной симметрии остаточного крупномасштабного магнитного поля ${{B}_{\varphi }}(z = 0) = 0$.

На поверхности диска для $\varphi $-компоненты магнитного поля можно рассмотреть как граничные условия типа Дирихле (I), так и Неймана (II).

В случае граничных условий типа I на поверхности диска интенсивность магнитного поля фиксируется:

(28)
${{B}_{\varphi }}({{z}_{{\text{s}}}}) = {{B}_{{{\text{ext}}}}},$
где величина ${{B}_{{{\text{ext}}}}}$ определяется моделью среды над диском. Например, в случае, если над диском формируется истечение, вызванное действием градиента тороидального магнитного поля [47], то ${{B}_{{{\text{ext}}}}} \sim {{B}_{z}}$ и плазменный параметр $\beta \sim 1$. В случае магнито-центробежного истечения Блэндфорда и Пэйна [48] на поверхности диска магнитное поле является квазирадиальным и ${{B}_{\varphi }} < {{B}_{r}} \sim {{B}_{z}}$.

В случае граничных условий типа II полагается, что среда над диском является вакуумом,

(29)
$\partial {{B}_{\varphi }}{\text{/}}\partial z({{z}_{{\text{s}}}}) = 0.$

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

4.1. Параметры и методы решения уравнений модели

Системы уравнений (8)–(16), (19–(22) совместно с уравнениями для расчета степени ионизации образуют замкнутую систему уравнений, описывающую радиальную и вертикальную структуру диска. Эти уравнения решаются в следующей последовательности.

На первом этапе система нелинейных алгебраических уравнений (8)–(16), описывающая радиальную структуру диска, решается методом простых итераций совместно с методом бисекции. В качестве начального приближения выбирается решение соответствующих уравнений в кинематическом приближении [38]. Полагается, что интенсивность магнитного поля ограничена максимальным значением, соответствующим равнораспределению магнитной энергии и тепловой энергии газа, ${{B}_{{{\text{eq}}}}} = \sqrt {8\pi p} $. Уравнения решаются в области от внутренней границы диска, ${{r}_{{{\text{in}}}}}$, до внешней границы, ${{r}_{{{\text{out}}}}}$, на логарифмической сетке, содержащей 200 узлов. Внутренняя граница диска определяется радиусом магнитосферы звезды, внешняя граница – как контактный разрыв с межзвездной средой. Индукция магнитного поля на внешней границе, ${{B}_{{z0}}}$, “сшивается” с индукцией магнитного поля межзвездной среды (см. [38]). Основными параметрами для уравнений радиальной структуры являются темп аккреции и параметр турбулентности, а также характеристики звезды. В качестве стандартных в данной работе выбраны параметры звезды типа Т Тельца солнечной массы: $\alpha = 0.01$, $\dot {M} = {{10}^{{ - 8}}}$ ${{M}_{ \odot }}$/год, радиус звезды ${{R}_{*}} = 2{\kern 1pt} \;{{R}_{ \odot }}$, светимость звезды ${{L}_{*}} = 1{\kern 1pt} \;{{L}_{ \odot }}$, индукция магнитного поля на поверхности звезды ${{B}_{*}} = 2$ кГс. Степень ионизации и коэффициенты диффузии магнитного поля рассчитываются для следующих стандартных параметров: радиус пылевой гранулы ${{a}_{d}} = 0.1$ мкм, скорость ионизации неэкранированными космическими лучами ${{\xi }_{0}} = 3 \times {{10}^{{ - 17}}}{\kern 1pt} $ с–1, пробег космических лучей ${{\Sigma }_{{{\text{CR}}}}} = 100$ г/см2, скорость ионизации за счет распада радиоактивных элементов ${{\xi }_{{{\text{RE}}}}} = 7.6 \times {{10}^{{ - 19}}}$ с–1, рентгеновская светимость звезды ${{L}_{{{\text{XR}}}}} = {{10}^{{30}}}$ эрг/с, энергия рентгеновских фотонов $k{{T}_{{{\text{XR}}}}} = 0.5$ кэВ. Коэффициент поглощения ${{\kappa }_{{\text{R}}}}$ рассчитывается с помощью интерполяции таблиц Семенова и др. [49] и OPAL [50].

На втором этапе обыкновенные дифференциальные уравнения (19)–(22), описывающие вертикальную структуру диска, решаются на каждом заданном $r$ методом Рунге–Кутты 4-го порядка точности с автоматическим выбором шага. Коэффициенты уравнений задаются из решения уравнений радиальной структуры. Координата фотосферы находится методом стрельбы. В случае, когда для магнитного поля на поверхности диска рассматриваются граничные условия первого рода, принято, что ${{B}_{{{\text{ext}}}}} = - 0.1{\kern 1pt} {{B}_{z}}$.

Итерационные процедуры на каждом этапе вычислений осуществляются для требуемой относительной точности ${{10}^{{ - 4}}}$.

Алгоритм решения уравнений модели реализован в программном комплексе “Belmondo” на языке программирования C++.

4.2. Радиальная структура диска

В данном разделе приводятся результаты расчетов радиальной структуры диска при различных параметрах и анализируется влияние магнитного поля на отклонение от кеплеровского вращения.

4.2.1. Кинематика. Для начала рассмотрим случай, соответствующий звезде типа Т Тельца солнечной массы при стандартных параметрах.

Обсудим кратко структуру диска в этом случае (детальный анализ см. в [38, 39]). На рис. 1 показаны радиальные профили поверхностной плотности, температуры, степени ионизации и компонент вектора магнитной индукции, а также профиль плазменного параметра $\beta $.

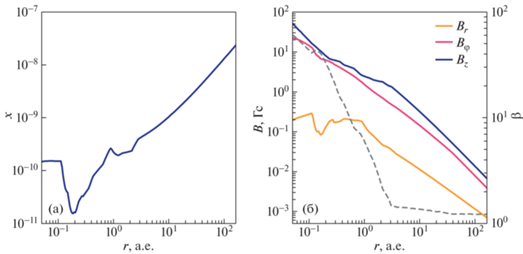
Рис. 1.

Радиальная структура диска при стандартных параметрах, приведены профили поверхностной плотности (а); эффективной температуры ${{T}_{{{\text{eff}}}}}$ и температуры в экваториальной плоскости (б); степени ионизации (в); и компонент вектора магнитной индукции (левая ось ординат, сплошные линии) и плазменного параметра (правая ось ординат, штриховая линия)(г). Кружочки на линиях отмечают точки, для которых было выполнено моделирование вертикальной структуры (см. далее рис. 4 и 5). Отрезки с числами указывают характерные наклоны профилей из аналитического решения уравнений модели [38].

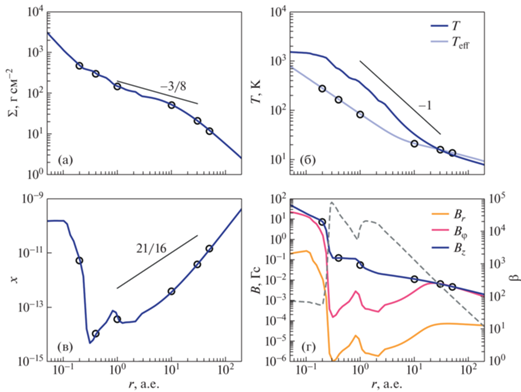
Рис. 1(а) и (б) показывают, что плотность и температура уменьшаются с расстоянием в диске. В области $1 < r < 30$ а.е. характерные наклоны профилей $\Sigma (r)$ и $T(r)$ составляют $ - 3{\text{/}}8$ и $ - 1$ соответственно, что согласуется с типичными наблюдательными значениями (см., напр., [1]). В области $r \lesssim 50$ а.е. диск области является оптически толстым по отношению к собственному излучению и $T > {{T}_{{{\text{eff}}}}}$.

Согласно рис. 1(в), профиль степени ионизации является немонотонным и имеет минимум ${{x}_{{{\text{min}}}}} \approx 5 \times {{10}^{{ - 15}}}$ вблизи ${{r}_{{{\text{min}}}}} \approx 0.3$ а.е. В области $r < {{r}_{{{\text{min}}}}}$ степень ионизации резко растет при приближении к звезде из-за тепловой ионизации металлов. В области $r > {{r}_{{{\text{min}}}}}$ степень ионизации возрастает при удалении от звезды из-за уменьшения плотности и более эффективной ионизации космическими лучами и рентгеновским излучением звезды.

Рис. 1(г) показывает, что в диске можно выделить три области с различной геометрией магнитного поля. В области $r < {{r}_{{{\text{min}}}}}$ магнитное поле является квазиазимутальным, ${{B}_{r}} < {{B}_{\varphi }} \sim {{B}_{z}}$. В этой области высокой степени ионизации магнитное поле вморожено в газ, поэтому происходит интенсивная генерация тороидального магнитного поля. В области ${{r}_{{{\text{min}}}}} < r \lesssim 20$ а.е. магнитное поле является квазиоднородным, ${{B}_{z}} \gg ({{B}_{r}},{\kern 1pt} {{B}_{\varphi }})$. Данная область является “мертвой” зоной, в которой степень ионизации мала, $x \lesssim {{10}^{{ - 12}}}$, и омическая диффузия препятствует усилению магнитного поля по сравнению с начальным значением. Во внешней по отношению к “мертвой” зоне части диска, $r > 20$ а.е., магнитное поле является квазиазимутальным. Эффективная магнитная амбиполярная диффузия подавляет усиление радиальной компоненты магнитного поля в этой области. Магнитное поле может быть квазирадиальным, ${{B}_{r}} \sim {{B}_{z}}$, в этой области при условии повышенных скоростей ионизации [38] или за счет эффекта Холла [39].

Радиальный профиль плазменного параметра $\beta $ показывает, что магнитное поле во всем диске является кинематическим, $\beta \gg 1$, т.е. электромагнитная сила не влияет на структуру диска. Отметим, что величина плазменного параметра меняется вдоль радиуса диска, от $\beta \sim 100$ вблизи внутренней границы диска до $\beta \sim {{(10}^{3}}{\kern 1pt} - {\kern 1pt} {{10}^{5}})$ в “мертвой” зоне и $\beta \to 10$ на периферии диска.

4.2.2 Динамика. Наиболее интенсивная генерация магнитного поля происходит в областях с высокой степенью ионизации, т.е. вне “мертвой” зоны. Для исследования условий генерации динамически сильного магнитного поля рассмотрим предельный случай, когда в диске отсутствует “мертвая” зона. Как показали Дудоров и Хайбрахманов [38], этот случай реализуется в аккреционных дисках с высоким темпом аккреции, $\dot {M} \geqslant {{10}^{{ - 7}}}$ ${{M}_{ \odot }}$/год, и/или в случаях, когда пылинки в диске отсутствуют или имеют крупные размеры.

На рис. 2 показаны радиальные профили степени ионизации и компонент магнитного поля в диске с теми же параметрами, что и на рис. 1, но для случая пылинок размером $1$ мм.

Рис. 2.

То же, что на рис. 1(в) и (г), но для случая пылинок размером ${{a}_{d}} = 1$ мм.

Согласно рис. 2(а), радиальный профиль степени ионизации является немонотонным, как и в случае ${{a}_{d}} = 0.1$ мкм. Отличие заключается в том, что минимальное значение $x$ составляет $ \sim {\kern 1pt} {{10}^{{ - 11}}}$, что на пять порядков больше, чем в случае, рассмотренном в предыдущем разделе. Это объясняется тем, что в рассматриваемом диапазоне плотностей основным типом рекомбинаций являются рекомбинации на пылинках, и в этом случае $x \propto {{a}_{d}}$ (см. [38]). Таким образом, “мертвая” зона отсутствует в случае ${{a}_{d}} \gtrsim 1$ мм.

В силу более высокой, чем в случае мелких пылинок, степени ионизации, на всем протяжении диска происходит интенсивная генерация магнитного поля. Компонента ${{B}_{z}}$ в этом случае пропорциональна поверхностной плотности диска $\Sigma $. Как показывает рис. 2(б), интенсивность ${{B}_{z}}$ уменьшается от примерно 500 Гс на внутренней границе диска до 25 Гс на $r = 1$ а.е. и 0.06 Гс на внешней границе диска, ${{r}_{{{\text{out}}}}} = 165$ а.е. Рисунок показывает, что магнитное поле является квазиазимутальным, ${{B}_{\varphi }} \sim {{B}_{z}}$, во всем диске. Интенсивность радиальной компоненты магнитного поля примерно на порядок меньше интенсивности ${{B}_{z}}$ в области $r > 1$ а.е. и на два порядка – в области минимальной степени ионизации, $r < 1$ а.е.

Радиальный профиль плазменного параметра показывает, что магнитное поле является динамически сильным на периферии диска: $\beta \sim 1$ для $r > 30$ а.е. Во внутренней области диска, $r < 10$ а.е., плазменный параметр увеличивается при приближении к звезде и достигает $\beta \sim 50$ на внутренней границе диске.

4.2.3. Отклонение от кеплеровского вращения. Результаты, приведенные в предыдущем разделе на рис. 2, показали, что если пылинки в аккреционном диски являются крупными, ${{a}_{d}} \gtrsim 1$ мм, то в диске генерируется динамически сильное магнитное поле. В этом случае можно ожидать заметного влияния магнитных натяжений на угловую скорость вращения газа в диске. Это влияние описывается вторым слагаемым под знаком корня в уравнении (10). Рассмотрим вклад магнитных натяжений в отклонение скорости газа от кеплеровской, и сравним этот вклад с отклонением, вызванным градиентом давления. Если учитываются оба эффекта, то из уравнения центробежного баланса (6) можно получить следующее выражение для азимутальной скорости газа в диске:

(30)
${{v}_{\varphi }} = \sqrt {\frac{{GM}}{r}{{{\left( {1 + \frac{{{{z}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{ - 3/2}}} - \frac{r}{\rho }\frac{{\partial p}}{{\partial r}} - \frac{{r{{B}_{r}}{{B}_{z}}}}{{2\pi \Sigma }}} {\kern 1pt} {\kern 1pt} .$
Эту формулу можно переписать в следующем виде:
(31)
${{v}_{\varphi }} = {{v}_{{\text{k}}}}\sqrt {1 - \beta _{{\text{k}}}^{{{\text{GD}}}} - \beta _{{\text{k}}}^{{{\text{MGD}}}}} ,$
где
(32)
$\beta _{{\text{k}}}^{{{\text{GD}}}} = \left( {\frac{r}{\rho }\frac{{\partial p}}{{\partial r}}} \right)\frac{1}{{{{g}_{r}}}},\quad \beta _{{\text{k}}}^{{{\text{MGD}}}} = \left( {\frac{{r{{B}_{r}}{{B}_{z}}}}{{2\pi \Sigma }}} \right)\frac{1}{{{{g}_{r}}}}$
– степени отклонения скорости газа от кеплеровской, обусловленные действием градиента газового давления и магнитными натяжениями соответственно. Из формулы (31) следует, что разница между кеплеровской скоростью и скоростью ${{v}_{\varphi }}$ определяется как $\Delta v \approx 1{\text{/}}2 \cdot {{\beta }_{{\text{k}}}}{{v}_{{\text{k}}}}$, где ${{\beta }_{{\text{k}}}}$ – одна или обе из величин в (32). Например, при ${{\beta }_{{\text{k}}}} = 0.02$ получим $\Delta v \approx 1\% {\kern 1pt} {{v}_{{\text{k}}}}$.

На рис. 3(а) изображены радиальные профили величин (32) для расчета со стандартными параметрами при ${{a}_{d}} = 1$ мм. На рис. 3(б) показаны аналогичные профили для расчета с теми же параметрами, но для темпа аккреции ${{10}^{{ - 7}}}$ ${{M}_{ \odot }}$/год. Производная газового давления по $r$ в выражении $\beta _{{\text{k}}}^{{{\text{GD}}}}$ вычислена с помощью формулы правых прямоугольников по радиальному профилю давления, полученному в результате численного решения уравнений радиальной структуры диска.

Рис. 3.

Радиальные профили степеней отклонения азимутальной скорости газа от кеплеровской, вычисленные согласно (32). Черной линией (GD) показано отклонение, обусловленное градиентом газового давления, желтой линией (MGD) – магнитными натяжениями. Расчеты проведены для радиуса пылинок ${{a}_{d}} = 1$ мм и темпов аккреции ${{10}^{{ - 8}}}{\kern 1pt} {{M}_{ \odot }}$/год (а) (соответствует рис. 2), и ${{10}^{{ - 7}}}{\kern 1pt} {{M}_{ \odot }}$/год (б).

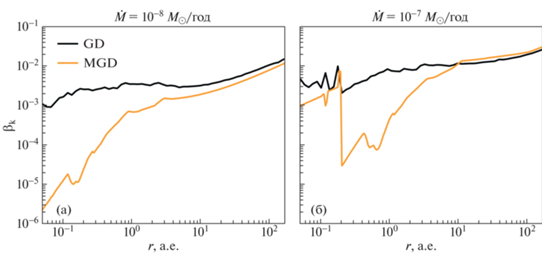
Рисунок 3(а) показывает, что “газодинамическая” степень отклонения угловой скорости газа от кеплеровской, $\beta _{{\text{k}}}^{{{\text{GD}}}}$, мало меняется с расстоянием, и ее значение лежит в диапазоне от ${{10}^{{ - 3}}}$ вблизи внутренней границы диска до $2 \times {{10}^{{ - 2}}}$ ($\Delta v \approx 1\% {\kern 1pt} {{v}_{{\text{k}}}}$) на внешней границе диска. Характерное значение $\beta _{{\text{k}}}^{{{\text{GD}}}}$ в области $r \in [1,{\kern 1pt} 50]$ а.е. составляет $(3{\kern 1pt} - {\kern 1pt} 4) \times {{10}^{{ - 3}}}$ ($\Delta v \approx 0.15{\kern 1pt} - {\kern 1pt} 0.20\% {\kern 1pt} {{v}_{{\text{k}}}}$). “Магнитогазодинамическое” отклонение, описываемое величиной $\beta _{{\text{k}}}^{{{\text{MGD}}}}$, меняется в более широких пределах. Величина $\beta _{{\text{k}}}^{{{\text{MGD}}}}$ в целом практически монотонно увеличивается с радиальным расстоянием $r$ от $2 \times {{10}^{{ - 6}}}$ на внутренней границе диска до ${{10}^{{ - 2}}}$ ($\Delta v \approx 0.5\% {\kern 1pt} {{v}_{{\text{k}}}}$) на внешней границе. В области $r \lesssim (3{\kern 1pt} - {\kern 1pt} 10)$ а.е. величина $\beta _{{\text{k}}}^{{{\text{MGD}}}}$ значительно меньше $\beta _{{\text{k}}}^{{{\text{GD}}}}$, т.е. вклад магнитных натяжений в центробежное равновесие мал по сравнению с вкладом градиента газового давления. Это обусловлено тем, что в этой области магнитное поле является динамически слабым, $\beta > 1$, как показывает рис. 2. Во внешней части диска, где магнитное поле играет динамически важную роль, $\beta \sim 1$, “магнитогазодинамическое” отклонение от кеплеровского вращения близко по величине к “газодинамическому”, $\beta _{{\text{k}}}^{{{\text{GD}}}}{\text{/}}\beta _{{\text{k}}}^{{{\text{MGD}}}} \approx (1{\kern 1pt} - {\kern 1pt} 2)$.

Расчеты, проведенные для более высокого темпа аккреции, $\dot {M} = {{10}^{{ - 7}}}$ ${{M}_{ \odot }}$/год (рис. 3(б)), показывают, что в таком случае магнитное поле является динамически сильным не только во внешней, но и во внутренней области диска. В этом случае степень “газодинамического” отклонения составляет от ${{10}^{{ - 3}}}$ до $3 \times {{10}^{{ - 2}}}$ ($\Delta v \approx 1.5\% {\kern 1pt} {{v}_{{\text{k}}}}$), т.е. несколько выше, чем в случае $\dot {M}{{ = 10}^{{ - 8}}}$ ${{M}_{ \odot }}$/год. “Магнитогазодинамическое” отклонение, $\beta _{{\text{k}}}^{{{\text{MGD}}}}$, оказывается сравнимо с “газодинамическим” как во внутренней области диска, $r < 0.2$ а.е., так и во внешней, $r > 10$ а.е.

4.3. Вертикальная структура диска

Как следует из системы уравнений магнитостатического равновесия (19)–(22), влияние магнитного поля на вертикальную структуру диска определяется вертикальным градиентом магнитного давления. Хайбрахманов и Дудоров [43] показали, что уравнение (22) для доминирующей азимутальной компоненты магнитного поля может быть решено аналитически. В случае граничного условия Дирихле (28), когда интенсивность магнитного поля на поверхности диска фиксирована,

(33)
${{B}_{\varphi }}(r,z) = {{B}_{{{\text{ext}}}}}\frac{z}{{{{z}_{{\text{s}}}}}} + \frac{1}{4}\frac{{{{v}_{k}}z}}{\eta }{{B}_{z}}\left[ {{{{\left( {\frac{z}{r}} \right)}}^{2}} - {{{\left( {\frac{{{{z}_{{\text{s}}}}}}{r}} \right)}}^{2}}} \right].$
В этом случае вертикальный профиль ${{B}_{\varphi }}$ является, вообще говоря, немонотонным, так что максимальное значение достигается внутри диска.

В случае граничного условия Неймана (29)

(34)
${{B}_{\varphi }}(r,z) = {{B}_{z}}\frac{{{{v}_{{\text{k}}}}z}}{\eta }{{\left( {\frac{{{{z}_{{\text{s}}}}}}{r}} \right)}^{2}}\left[ {\frac{1}{4}{{{\left( {\frac{z}{{{{z}_{{\text{s}}}}}}} \right)}}^{2}} - \frac{3}{4}} \right],$
т.е. ${{B}_{\varphi }}$ монотонно увеличивается от нуля в экваториальной плоскости до максимального значения на поверхности диска.

Выбор подходящего граничного условия на поверхности диска определяется моделью среды над диском. В данной работе анализируются оба случая.

4.3.1. Вертикальная структура на различных расстояниях. Рассмотрим вертикальную структуру диска, рассчитанную при типичных параметрах на радиальных расстояниях $r = 0.2$, $1$ и $50$ а.е. В табл. 1 показаны магнитное число Рейнольдса ${{R}_{{\text{m}}}}$, интенсивность вертикальной компоненты магнитного поля ${{B}_{z}}$, плотность и температура в экваториальной плоскости на выбранных расстояниях. Магнитное число Рейнольдса определено как ${{R}_{{\text{m}}}} = {{v}_{{\text{k}}}}H{\text{/}}{{\nu }_{{\text{m}}}}$. Расстояние $r = 0.2$ а.е. соответствует области тепловой ионизации вблизи звезды, $r = 1$ а.е. – “мертвой” зоне, $r = 50$ а.е. – внешней по отношению к “мертвой” зоне области диска. Как показывает табл. 1, вне “мертвой зоны”, $r = 0.2$ и 50 а.е., магнитное поле вморожено в газ, ${{R}_{{\text{m}}}} \gg 1$, внутри нее – эффективно развивается диффузия магнитного поля, ${{R}_{{\text{m}}}} \sim 1$.

Таблица 1.  

Параметры расчетов вертикальной структуры диска

$r$, а.е. ${{R}_{{\text{m}}}}$ ${{B}_{z}}$, Гс ${{\rho }_{0}}$, г/см3 ${{T}_{0}}$, К
(1) (2) (3) (4) (5)
0.2 194 7.2 $2.79 \times {{10}^{{ - 9}}}$ 1230
1 3 $5.5 \times {{10}^{{ - 2}}}$ $1.43 \times {{10}^{{ - 9}}}$ 350
50 5400 $4.9 \times {{10}^{{ - 3}}}$ $2.13 \times {{10}^{{ - 13}}}$ 13

На рис. 4 показаны вертикальные профили азимутальной компоненты магнитного поля, плазменного параметра, плотности и температуры на выбранных расстояниях. Для удобства сравнения все величины изображены в безразмерном виде. В качестве масштабов интенсивности магнитного поля выбрана величина ${{B}_{z}}$ (столбец 3 в табл. 1), масштабов плотности и температуры – соответствующие значения в экваториальной плоскости (столбцы 4 и 5 в табл. 1).

Рис. 4.

Вертикальная структура диска на радиальных расстояниях $r = 0.2$ а.е. (левый столбец панелей), $r = 1$ а.е. (средний столбец), $r = 50$ а.е. (правый столбец). Верхний ряд панелей: вертикальные профили азимутальной компоненты магнитного поля, рассчитанные для граничных условий первого рода (штриховая лиловая линия, помеченная символом “I”) и второго рода (сплошная желтая линия, помеченная “II”). Второй, третий и нижний ряды панелей показывают соответствующие вертикальные профили плазменного параметра, плотности и температуры. Тонкими черными линиями приведены вертикальные профили плотности и температуры для гидростатического случая (${{B}_{\varphi }} = 0$).

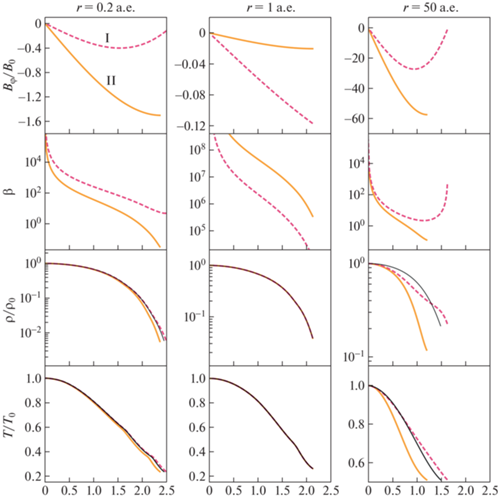
Рисунок 4 показывает, что характер профилей ${{B}_{\varphi }}(z)$ зависит от граничных условий на поверхности и от расстояния $r$. В случае граничных условий первого рода профиль ${{B}_{\varphi }}(z)$ является немонотонным вне “мертвой” зоны, $r = 0.2$ и 50 а.е. Например, на $r = 0.2$ а.е. интенсивность ${{B}_{\varphi }}$ меняется от 0 в экваториальной плоскости до $0.1{\kern 1pt} {{B}_{z}} \approx 0.7$ Гс на поверхности, и принимает максимальное значение $ \approx 0.4{\kern 1pt} {{B}_{z}} \approx 0.28$ Гс на высоте $z \sim 1.5{\kern 1pt} H$. Во внешней части диска, $r = 50$ а.е. максимальное значение ${\text{|}}{{B}_{\varphi }}{\kern 1pt} {\text{|}}$ составляет $ \approx {\kern 1pt} 20{\kern 1pt} {{B}_{z}}$, т.е. в этой области наиболее эффективно генерируется квазиазимутальное магнитное поле, ${\text{|}}{{B}_{\varphi }}{\kern 1pt} {\text{|}} \gg {{B}_{z}}$. Внутри “мертвой” зоны генерации магнитного поля практически не происходит из-за эффективной омической диффузии, и ${{B}_{\varphi }}$ почти линейно увеличивается до максимального значения $0.1{\kern 1pt} {{B}_{z}} = 5.5 \times {{10}^{{ - 3}}}$ Гс на поверхности диска.

В случае граничных условий второго рода, интенсивность ${{B}_{\varphi }}$ монотонно увеличивается от экваториальной плоскости к поверхности диска. Вне “мертвой” зоны, $r = 0.2$ и 50 а.е., генерация магнитного поля происходит наиболее эффективно так, что интенсивность ${{B}_{\varphi }}$ превосходит интенсивность начального поля ${{B}_{z}}$. Внутри “мертвой” зоны генерации магнитного поля практически не происходит, ${\text{|}}{{B}_{\varphi }}{\kern 1pt} {\text{|}} \lesssim 0.02{\kern 1pt} {{B}_{z}}$.

Вертикальные профили плазменного параметра, изображенные во втором ряду панелей на рис. 4, показывают, что во всех рассмотренных случаях магнитное поле является динамически слабым, $\beta \gg 1$, вблизи экваториальной плоскости, $z \lesssim (0.5{\kern 1pt} - {\kern 1pt} 1){\kern 1pt} H$. При удалении от экваториальной плоскости плазменный параметр уменьшается во всех случаях, кроме варианта с граничными условиями второго рода на $r = 50$ а.е. – в последнем случае уменьшение $\beta $ с высотой сменяется увеличением вблизи поверхности диска. Вне “мертвой” зоны, $r = 0.2$ и 50 а.е., магнитное поле является динамически сильным вблизи поверхности, $\beta \approx (0.1{\kern 1pt} - {\kern 1pt} 10)$ на $z \gtrsim (1{\kern 1pt} - {\kern 1pt} 1.5){\kern 1pt} H$. Внутри “мертвой” зоны $\beta \gg 1$ вплоть до поверхности диска, т.е. магнитное поле является кинематическим.

Рассмотрим влияние магнитного поля на структуру диска. Вертикальные профили плотности на выбранных расстояниях (третий ряд панелей на рис. 4) показывают, что вне “мертвой” зоны, $r = 0.2$ и 50 а.е., распределения плотности, рассчитанные с учетом влияния магнитного поля, отличаются от гидростатического. Внутри “мертвой” зоны, $r = 1$ а.е., отличий нет. Изменение характера профилей $\rho (z)$ связано с действием градиента магнитного давления в областях, где магнитное поле является динамически сильным. Знак градиента магнитного давления зависит от граничного условия на поверхности.

В случае граничных условий первого рода профили плотности становятся более пологими вблизи поверхности диска и наблюдается увеличение характерной полутолщины диска ($z$-координаты фотосферы) вне “мертвой” зоны, $r = 0.2$ и 50 а.е. Как показывает рис. 4, увеличение полутолщины диска является небольшим на $r = 0.2$ а.е. и существенным – на $r = 50$ а.е. В последнем случае не только увеличивается полутолщина диска, но и меняется характерный наклон профиля $\rho (z)$ внутри диска. Увеличение полутолщины диска обусловлено тем, что в данном случае в поверхностных слоях интенсивность магнитного поля растет с высотой, так что сила, обусловленная градиентом магнитного давления, действует против $z$-компоненты силы гравитации звезды и приводит к “расширению” диска в областях с $\beta \sim 1$.

В случае граничных условий второго рода профиль плотности вблизи поверхности диска является более крутым, чем гидростатический, а соответствующая полутолщина диска меньше. Этот эффект наиболее выражен на $r = 50$ а.е., где ${{z}_{{\text{s}}}} \approx 1.5{\kern 1pt} H$ в гидростатическом случае, и ${{z}_{{\text{s}}}} \approx 1.2{\kern 1pt} H$ – в магнитостатическом. Уменьшение характерной полутолщины диска связано с тем, что интенсивность магнитного поля монотонно увеличивается к поверхности диска, так что $z$-компонента электромагнитной силы сонаправлена с $z$-компонентной силы гравитации звезды и приводит к “поджатию” диска в областях с $\beta \sim 1$.

4.3.2. Влияние магнитного поля на толщину диска. В предыдущем разделе показано, что магнитное давление может приводить к изменению толщины аккреционного диска. Рассмотрим этот эффект в приложении к аккреционному диску молодой звезды типа Т Тельца солнечной массы при типичных параметрах, соответствующих рис. 1.

На верхней панели рис. 5 показаны зависимости координаты фотосферы диска от радиального расстояния, определенные на основе проведенных расчетов вертикальной структуры на $r = 0.2$, 0.4, 1, 10, 30 и 50 а.е. Для каждого $r$ проведено три расчета: без учета магнитного поля (расчет “ГД”), с учетом магнитного поля и омической диффузии для граничных условий типа I и II (расчеты “ОД, I” и “ОД, II”). Значения магнитного числа Рейнольдса на каждом радиусе $r$ приведены на нижней панели рисунка.

Рис. 5.

(а) – зависимость вертикальной координаты фотосферы диска, ${{z}_{{\text{s}}}}$, от радиального расстояния $r$. Розовой линией с маркерами показан профиль, полученный с использованием граничных условий первого рода для ${{B}_{\varphi }}(z)$, желтой линией с маркерами – для граничных условий второго рода, синей линией – без учета влияния магнитного поля на вертикальную структуру диска. Расчеты проведены с учетом омической диффузии; (б) – соответствующий профиль магнитного числа Рейнольдса. Рассмотрен случай стандартных параметров, соответствующая радиальная структура диска показана на рис. 1.

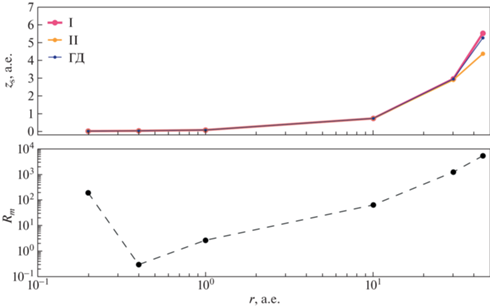
Рисунок 5 показывает, что в расчете без магнитного поля координата фотосферы увеличивается с радиусом от ${{z}_{{\text{s}}}} \approx 0.015$ а.е. на $r = 0.2$ а.е. до ${{z}_{{\text{s}}}} \approx 5.5$ а.е. на $r = 50$ а.е., т.е. толщина диска увеличивается с расстоянием, но он является геометрически тонким, ${{z}_{{\text{s}}}} \ll r$.

В расчетах с магнитным полем отличия профилей ${{z}_{{\text{s}}}}(r)$ от расчета “ГД” проявляются только во внешней области диска, $r > 30$ а.е., где магнитное число Рейнольдса ${{R}_{{\text{m}}}} \gtrsim {{10}^{3}}$. В случае граничных условий первого рода, как было показано в предыдущем разделе, градиент магнитного давления приводит к утолщению диска, что проявляется в том, что фотосфера в этой области диска находится выше, чем в случае без магнитного поля. В случае граничных условий типа II, наоборот, градиент магнитного поля приводит к поджатию диска, и фотосфера располагается ниже, чем в расчете “ГД”. Отличия толщины диска с магнитным полем от гидростатической во внутренней области диска, $r \sim 0.2$ а.е., где ${{R}_{{\text{m}}}} \sim 200$, малозначительны и незаметны в масштабе рисунка.

В области $r \in [0.3,30]$ а.е., соответствующей “мертвой” зоне (см. раздел 4.2 и рис. 1), профили ${{z}_{{\text{s}}}}(r)$ в расчетах “ГД” и “ОД” совпадают, т.е. магнитное поле не влияет на вертикальную структуру диска. Внутри “мертвой” зоны магнитное число Рейнольдса ${{R}_{{\text{m}}}}$ мало, т.е. эффективная омическая диффузия препятствует генерации динамически сильного магнитного поля.

В рассматриваемом случае максимальная степень утолщения диска в случае граничных условий типа I и поджатия в случае граничных условий типа II составляет примерно 5 и 20% соответственно.

5. ВЫВОДЫ И ОБСУЖДЕНИЕ

В данной работе выполнено развитие авторской МГД-модели аккреционных дисков молодых звезд для учета динамического влияния остаточного крупномасштабного магнитного поля диска на структуру диска. Уравнения, описывающие радиальную структуру диска, записаны с учетом влияния магнитных натяжений на вращение газа. Вертикальная структура диска определяется из уравнений магнитостатического равновесия с учетом градиента магнитного давления. Полагается, что поверхность диска лежит в области его фотосферы.

С помощью развиваемой модели проведены расчеты структуры аккреционнного диска звезды типа Т Тельца солнечной массы при различных значениях темпа аккреции $\dot {M}$ и радиуса пылинок ${{a}_{d}}$. Моделирование радиальной структуры проводилось в предположении, что интенсивность магнитного поля в диске ограничена величиной, соответствующей равнораспределению тепловой энергии газа и магнитной энергии. Вертикальная структура диска рассчитывалась для граничных условий первого и второго рода.

Расчеты радиальной структуры диска показывают, что при типичных параметрах, $\dot {M} = $ = 10‒8 ${{M}_{ \odot }}$/год и ${{a}_{d}} = 0.1$ мкм, магнитное поле в диске является кинематическим: плазменный параметр $\beta \gg 1$, и электромагнитная сила не влияет на центробежное равновесие газа в диске. Отметим, что плазменный параметр меняется в широких пределах: от $ \sim {\kern 1pt} 100$ вблизи внутренней границы диска, до $ \sim {\kern 1pt} {{10}^{3}}{\kern 1pt} - {\kern 1pt} {{10}^{5}}$ внутри “мертвой” зоны и $ \sim {\kern 1pt} 10$ на периферии диска.

В случае стандартного темпа аккреции, $\dot {M} = {{10}^{{ - 8}}}$ ${{M}_{ \odot }}$/год, и крупных пылинок, ${{a}_{d}} \gtrsim 1$ мм, “мертвая” зона отсутствует, т.е. магнитное поле вморожено в газ на всем протяжении диска. В этом случае во внешней области диска, $r \gtrsim 30$ а.е., генерируется динамическим сильное магнитное поле с $\beta \sim 1$. Натяжения остаточного крупномасштабного магнитного поля в этой области приводят к уменьшению скорости вращения газа по сравнению с кеплеровской. Степень отклонения от кеплеровской скорости составляет $ \sim {\kern 1pt} {{10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 2}}}$, что соответствует $\Delta v = {{v}_{{\text{k}}}} - {{v}_{\varphi }} \approx $ $ \approx 0.15{\kern 1pt} - {\kern 1pt} 0.5\% {{v}_{{\text{k}}}}$. Эта величина сравнима с величиной, обусловленной градиентом газового давления. При более высоком темпе аккреции, $\dot {M} = {{10}^{{ - 7}}}$ ${{M}_{ \odot }}$/год, магнитное поле является динамически сильным не только во внешней, $r \gtrsim 10$ а.е., но и во внутренней области диска, $r \lesssim 0.2$ а.е. Степень “магнитогазодинамического” отклонения от кеплеровского вращения в этом случае составляет до $ \sim {\kern 1pt} 3 \times {{10}^{{ - 2}}}$ ($\Delta v \approx 1.5\% {{v}_{{\text{k}}}}$), что превышает степень “газодинамического” отклонения при выбранных параметрах. Современные наблюдения нескольких протопланетных дисков указывают на субкеплеровское вращение во внешних областях исследуемых дисков с максимальным отклонением $\Delta {v}$ до нескольких процентов от ${{v}_{{\text{k}}}}$ [6, 7, 51]. Полученные в настоящей работе результаты показывают, что этот наблюдаемый эффект может быть вызван не только градиентом газового давления, но и магнитными натяжениями.

Отклонение азимутальной скорости газа от кеплеровской является основной причиной радиального дрейфа пылинок и малых тел в протопланентных дисках [44]. Согласно полученным результатам, в областях с динамически сильным магнитным полем радиальный дрейф пылинок будет происходить с большей скоростью, чем предсказывают газодинамические расчеты. Этот эффект может иметь важное значение с точки зрения условий образования и динамики планетезималей и зародышей планет в протопланетных дисках. Задача о радиальном дрейфе с учетом влияния остаточного магнитного поля требует дальнейшего детального исследования.

Расчеты вертикальной структуры аккреционного диска при стандартных параметрах показывают, что характер профилей азимутальной компоненты магнитного поля зависит от типа граничных условий и от радиального расстояния $r$.

В случае граничных условий первого рода, соответствующих заданной интенсивности ${{B}_{{{\text{ext}}}}}$ магнитного поля на поверхности диска, профиль ${{B}_{\varphi }}$ является немонотонным вне “мертвой” зоны, и максимальная интенсивность магнитного поля достигается внутри диска. Наиболее интенсивная генерация магнитного поля происходит во внешней по отношению к “мертвой” зоне части диска, где ${\text{|}}{{B}_{\varphi }}{\kern 1pt} {\text{|}} \sim 20{\kern 1pt} {{B}_{z}}$. Расчеты показывают, что в этой области максимальная интенсивность магнитного поля мало зависит от ${{B}_{{{\text{ext}}}}}$. Внутри “мертвой” зоны генерации магнитного поля практически не происходит, и ${{B}_{\varphi }}$ практически линейно растет с высотой, оставаясь пренебрежимо малой по сравнению с ${{B}_{z}}$.

В случае граничных условий второго рода, интенсивность магнитного поля монотонно увеличивается от экваториальной плоскости и достигает максимального значения у поверхности диска. Во внутренней области, $r < 1$ а.е., ${\text{|}}{{B}_{\varphi }}{\kern 1pt} {\text{|}} \sim {{B}_{z}}$, т.е. магнитное поле является квазиазимутальным. Во внешней области диска, $r \gtrsim 30$ а.е., магнитное поле также является квазиазимутальным, причем ${\text{|}}{{B}_{\varphi }}{\kern 1pt} {\text{|}} \gg {{B}_{z}}$. Внутри “мертвой” зоны генерации магнитного поля не происходит даже вблизи поверхности диска, ${\text{|}}{{B}_{\varphi }}{\kern 1pt} {\text{|}} \ll {{B}_{z}}$.

В обоих случаях магнитное поле является кинематическим, $\beta \gg 1$, вблизи экваториальной плоскости, $z \lesssim (1{\kern 1pt} - {\kern 1pt} 1.5){\kern 1pt} H$, и динамическим, $\beta = $ = 0.1–10, в поверхностных слоях диска вне “мертвой” зоны. В случае граничных условий первого рода градиент магнитного давления проводит к увеличению характерной толщины диска вне “мертвой” зоны, второго рода – к уменьшению толщины диска, т.е. к его “поджатию”. Вообще говоря, возможны оба случая в зависимости от условий над диском. При характерных параметрах отклонение толщины диска от гидростатической составляет 5–20% во внешней области, $r > 30$ а.е. Для детального исследования этого эффекта необходимо дальнейшее развитие модели и дополнение ее моделью среды над диском.

Следует отметить, что генерация интенсивного тороидального магнитного поля в поверхностных слоях аккреционного диска неизбежно должна приводить к развитию неустойчивости магнитной плавучести (известной также как неустойчивость Паркера [52] или магнитная неустойчивость Рэлея–Тэйлора). Для развития перестановочной моды неустойчивости достаточно, чтобы магнитное поле уменьшалось с высотой медленнее, чем плотность [53, 54]. Возможно также развитие изгибной моды, если интенсивность магнитного поля уменьшается с высотой. Как показывают расчеты настоящей работы, оба случая реализуются в поверхностных слоях диска вне “мертвой” зоны. Детальное исследование неустойчивости магнитной плавучести в аккреционных дисках молодых звезд планируется в одной из наших следующих работ.

Дальнейшее развитие модели предполагает разработку полностью самосогласованной двумерной МГД-модели диска, учитывающей перенос углового момента крупномасштабным магнитным полем, а также неоднородность коэффициентов диффузии и плавучесть магнитного поля в уравнениях магнитостатики. Разработка такой модели позволит учесть эффекты, связанные с образованием истечений из диска, и определить относительную роль различных механизмов переноса углового момента в аккреционных и протопланетных дисках молодых звезд.

Список литературы

  1. J. P. Williams and L. A. Cieza, Ann. Rev. Astron. Astrophys. 49, 67 (2011).

  2. A. Boccaletti, E. Di Folco, E. Pantin, A. Dutrey, et. al., Astron. and Astrophys. 637, id. 5 (2020).

  3. S. Nayakshin, T. Tsukagoshi, C. Hall, A. Vazan, et al., Monthly Not. Roy. Astron. Soc. 495, 285 (2020).

  4. C. L. Brogan, L. M. Pérez, T. R. Hunter, W. R. F. Dent, et al., Astrophys. J. Suppl. 808, id. L3 (2015).

  5. S. M. Andrews, J. Huang, L. M. Pérez, A. Isella, et al., Astrophys. J. Lett. 869, id. L41 (2018).

  6. C. Pinte, F. Ménard, G. Duchêne, T. Hill, et al., Astron. and Astrophys. 609, id. A47 (2018).

  7. R. Teague, J. Bae, Y. Aikawa, S. M. Andrews, et al., Astrophys. J. Suppl. 257, id. 18 (2021).

  8. M. Tamura and S. Sato, Astron. J. 98, 1368 (1989).

  9. D. Li, C. M. Telesco, H. Zhang, C. M. Wright, E. Pantin, P. J. Barnes, and C. Packham, Monthly Not. Roy. Astron. Soc. 473, 1427 (2018).

  10. A. Frank, T. P. Ray, S. Cabrit, P. Hartigan, et al. in: Jets and Outflows from Star to Cloud: Observations Confront Theory, edited by H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning (University of Arizona Press, Tucson, 2019), Ch. 2, p. 451.

  11. J.-F. Donati, F. Paletou, J. Bouvier, and J. Ferreira, Nature 438, 466 (2005).

  12. С. А. Хайбрахманов, А. Е. Дудоров, А. И. Васюнин, М. Ю. Кискин, Краткие сообщения по физике ФИАН 48, 29 (2021).

  13. R. E. Harrison, L. W. Looney, I. W. Stephens, Zhi-Yun Li, et al., Astrophys. J. 908, id. 141 (2021).

  14. W. H. T. Vlemmings, B. Lankhaar, P. Cazzoletti, C. Ceccobello, et al., Astron. and Astrophys. 624, 7 (2019).

  15. R. R. Fu, B. P. Weiss, E. A. Lima, R. J. Harrison, Xue-Ning Bai, et al., Science, 346(6213), 1089 (2014).

  16. E. H. Levy, Nature 276, 481 (1978).

  17. А. Е. Дудоров, Астрон. журн. 72, 884 (1995).

  18. A. E. Dudorov and S. A. Khaibrakhmanov, Adv. Space Research 55, 843 (2015).

  19. D. Moss, D. D. Sokoloff, and V. Suleimanov, Astron. and Astrophys. 588, id. A18 (2016).

  20. D. D. Sokoloff, Astron. Rep. 65, 1054 (2021).

  21. V. Agapitou and J. C. B. Papaloizou, Astrophys. Letters and Commun. 34, 363 (1996).

  22. S. H. Lubow, J. C. B. Papaloizou, and J. E. Pringle, Monthly Not. Roy. Astron. Soc. 267, 235 (1994).

  23. M. Reyes-Ruiz and T. F. Stepinski, Astrophys. J. 459, 653 (1996).

  24. F. Shu, D. Galli, S. Lizano, A. E. Glassgold, and P. H. Diamond, Astrophys. J. 665, 535 (2007).

  25. R. V. E. Lovelace, D. M. Rothstein, and G. S. Bisnovatyi-Kogan, Astrophys. J. 701, 885 (2009).

  26. J. Guilet and G. I. Ogilvie, Monthly Not. Roy. Astron. Soc. 441, 852 (2014).

  27. S. Okuzumi, T. Takeuchi, and T. Muto, Astrophys. J. 785, id. 127 (2014).

  28. S. Lizano, C. Tapia, Y. Boehler, and P. D’Alessio, Astrophys. J. 817, id. 35 (2016).

  29. J. B. Simon, Xue-Ning Bai, P. J. Armitage, J. M. Stone, and K. Beckwith, Astrophys. J. 775, id. 73 (2013).

  30. G. Lesur, M. W. Kunz, and S. Fromang, Astron. and Astrophys. 566, id. A56 (2014).

  31. O. Gressel, N. J. Turner, R. P. Nelson, and C. P. McNally, Astrophys. J. 801, id. 84 (2015).

  32. W. Bethune, G. Lesur, and J. Ferreira, Astron. and Astrophys. 600, id. A75 (2017).

  33. O. Gressel, J. P. Ramsey, C. Brinch, R. P. Nelson, N. J. Tur-ner, and S. Bruderer, Astrophys. J. 896, id. 126 (2020).

  34. S. Suriano, Z.-Y. Li, R. Krasnopolsky, and S. Hsien, Monthly Not. Roy. Astron. Soc. 477, 1239 (2018).

  35. A. Riols, G. Lesur, and F. Menard, Astron. and Astrophys. 639, id. A95 (2020).

  36. А. Е. Дудоров, С. А. Хайбрахманов, Вестник Челяб. гос. ун-та № 9(300). Физика 16, 27 (2013).

  37. А. Е. Дудоров, С. А. Хайбрахманов, Вестник Челяб. гос. ун-та, № 9(300), Физика 16, 40 (2013).

  38. A. E. Dudorov and S. A. Khaibrakhmanov, Astrophys. Space Sci. 351(1), 103 (2014).

  39. S. A. Khaibrakhmanov, A. E. Dudorov, S. Yu. Parfenov, and A. M. Sobolev, Monthly Not. Roy. Astron. Soc. 464, 586 (2017).

  40. Н. И. Шакура, Астрон. журн. 49, 921 (1972).

  41. N. I. Shakura and R. A. Sunyaev, Astron. and Astrophys. 24, 337 (1973).

  42. S. A. Khaibrakhmanov and A. E. Dudorov, Magnetohydrodynamics 55, 65 (2019).

  43. С. А. Хайбрахманов, А. Е. Дудоров, Челяб. физ.-мат. журн. 6, 53 (2021).

  44. S. J. Weidenschilling, Monthly Not. Roy. Astron. Soc., 180, 57 (1977).

  45. А. Е. Дудоров, Ю. В. Сазонов, Научные информации 63, 68 (1987).

  46. Н. И. Шакура, Аккреционные процессы в астрофизике (М: Физматлит, 2016).

  47. T. Kudoh and K. Shibata, Astrophys. J. 474, 362 (1997).

  48. R. D. Blandford and D. G. Payne, Monthly Not. Roy. Astron. Soc. 199, 883 (1982).

  49. D. Semenov, T. Henning, C. Helling, M. Ilgner, and E. Sedlmayr, Astron. and Astrophys. 410, 611 (2003).

  50. C. A. Iglesias and F. J. Rogers, Astrophys. J. 464, 943 (1996).

  51. C. P. Dullemond, A. Isella, S. M. Andrews, I. Skobleva, and N. Dzyurkevich, Astron. and Astrophys. 633, id. A137 (2020).

  52. E. Parker, Cosmical magnetic fields: Their origin and their activity (New York: Oxford, Clarendon Press, 1979).

  53. Ю. А. Церковников, Докл. АН СССР 130, 295 (1960).

  54. D. W. Hughes, Geophys. and Astrophys. Fluid Dyn. 32, 273 (1985).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал