1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 99, № 10, 2022

Астрономический журнал, 2022, T. 99, № 10, стр. 795-804

Силуэты кротовых нор, проходимых для излучения

С. В. Репин 1, *, М. А. Бугаев 2, И. Д. Новиков 1, 3, 4, И. Д. Новиков мл. 1

1 Физический институт им. П.Н. Лебедева РАН, Астрокосмический центр
Москва, Россия

2 Московский физико-технический институт
Долгопрудный, Московская область, Россия

3 The Niels Bohr International Academy, The Niels Bohr Institute
Copenhagen, Denmark

4 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

* E-mail: sergerepin1@gmail.com

Поступила в редакцию 20.05.2022
После доработки 11.08.2022
Принята к публикации 30.08.2022

Полный текст (PDF)

Аннотация

Рассматриваются задачи о прохождении света сквозь горловину кротовой норы нулевой массы и возможность наблюдения объектов из другого асимптотически плоского пространства сквозь горловину кротовой норы. Показано, что отдельная звезда может иметь несколько изображений и отмечен тот факт, что изображение плоского ламбертовского экрана имеет сложное распределение яркости для наблюдателя, находящегося с ним по разные стороны горловины. Построены изображения двух таких экранов, видимых внутри силуэта безмассовой кротовой норы, и распределение интенсивности излучения в их изображениях.

Ключевые слова: кротовые норы, черные дыры, общая теория относительности

1. ВВЕДЕНИЕ

В работах [1–4] мы начали программу систематического сравнения особенностей силуэтов11 – темных пятен, возникающих при наблюдении излучения, взаимодействующего с черными дырами (ЧД) и кротовыми норами (КН). Для выяснения и интерпретации этих особенностей целесообразно начинать с простейших моделей источников излучения и простейших моделей КН. В таком подходе будут наиболее ярко проявляться особенности, связанные именно с разной природой этих объектов, а не с добавочными эффектами, вызванными сложностями более реалистических моделей.

В данной работе мы продолжим использовать этот подход. В работе [1] мы использовали модель КН Эллиса–Бронникова–Морриса–Торна [10–13], предполагая, что КН заполнена непрозрачным веществом и рассматривая только лучи, движущиеся в нашем пространстве вокруг входа в КН, расположенного вблизи наблюдателя. В данной работе мы учтем свет, проходящий сквозь КН из другого пространства, т.е. считаем КН свободно проходимой для света. Ссылки на предыдущие работы см. в работе [1]. Там же выведены уравнения движения (способ см. в [14]) и дано описание наших численных методов.

Метрика кротовой норы, которую мы рассматриваем, может быть записана в виде:

(1)
$d{{s}^{2}} = {{c}^{2}}d{{t}^{2}} - d{{R}^{2}} - \left( {{{R}^{2}} + {{q}^{2}}} \right)\left( {d{{\theta }^{2}} + {{{\sin }}^{2}}\theta d{{\varphi }^{2}}} \right).$
Здесь $c$ – скорость света. В дальнейшем положим $c = 1$. Для наших целей эту же метрику удобно записывать в координатах $(t,r,\vartheta ,\varphi )$:
(2)
$d{{s}^{2}} = d{{t}^{2}} - \frac{{{{r}^{2}}}}{{{{r}^{2}} - {{q}^{2}}}}{\kern 1pt} d{{r}^{2}} - {{r}^{2}}\left( {d{{\vartheta }^{2}} + {{{\sin }}^{2}}\vartheta {\kern 1pt} d{{\varphi }^{2}}} \right),$
где координата $r$ выбрана так, чтобы длина окружности была равна $2\pi r$.

2. ПОСТАНОВКА ЗАДАЧИ

Прежде всего мы рассмотрим изображения и силуэты (тени), которые создают лучи, прошедшие сквозь КН.

Подчеркнем, что в метрике сферической КН, так же как и в метрике сферической ЧД, пространственные траектории лучей света всегда плоские. Поэтому нам достаточно будет рассматривать только одно плоское сечение пространственной метрики, например, экваториальное. Для вычисления траекторий световых лучей надо получить уравнения движения кванта света в метрике (1) сферически симметричной кротовой норы. Эти уравнения получаются разделением переменных в уравнении Гамильтона–Якоби для метрики (1):

(3)
$\begin{gathered} {{\left( {\frac{{\partial S}}{{\partial t}}} \right)}^{2}} - \frac{{{{r}^{2}} - {{q}^{2}}}}{{{{r}^{2}}}}{{\left( {\frac{{\partial S}}{{\partial r}}} \right)}^{2}} - \frac{1}{{{{r}^{2}}}}{{\left( {\frac{{\partial S}}{{\partial \vartheta }}} \right)}^{2}} - \\ \, - \frac{1}{{{{r}^{2}}\mathop {\sin }\nolimits^2 \vartheta }}{{\left( {\frac{{\partial S}}{{\partial \varphi }}} \right)}^{2}} - {{m}^{2}} = 0, \\ \end{gathered} $
и в безразмерных переменных преобразуются к системе шести обыкновенных дифференциальных уравнений:
(4)
$\frac{{dt}}{{d\sigma }} = \frac{1}{{{{r}^{2}}}},$
(5)
$\frac{{dr}}{{d\sigma }} = {{r}_{1}},$
(6)
$\frac{{d{{r}_{1}}}}{{d\sigma }} = 2\left( {\eta - {{\xi }^{2}}} \right){{r}^{3}} - \left( {1 + \eta + {{\xi }^{2}}} \right)r,$
(7)
$\frac{{d\theta }}{{d\sigma }} = {{\theta }_{1}},$
(8)
$\frac{{d{{\theta }_{1}}}}{{d\sigma }} = \frac{{{{\xi }^{2}}\cos \theta }}{{{{{\sin }}^{3}}\theta }},$
(9)
$\frac{{d\varphi }}{{d\sigma }} = \frac{\xi }{{{{{\sin }}^{2}}\theta }},$
где $(t,1{\text{/}}r,\theta ,\phi )$ – координаты Бойера–Линдквиста, ${{r}_{1}}$ и ${{\theta }_{1}}$ – вспомогательные переменные, $\eta $ и $\xi $ – константы Чандрасекара, которые определяются начальными условиями. Численное интегрирование системы (4)–(9) позволяет построить траектории квантов в поле кротовой норы.

Для наблюдателя, находящегося достаточно далеко от входа КН, лучи, приходящие к нему от входа и его окрестностей, почти параллельны. Заметим, что траектории нулевых геодезических в метрике (1) при $\left| R \right| \gg 1$ быстро становятся практически прямыми линиями. На рис. 1 изображено внешнее пространство наблюдателя в экваториальном сечении $\theta {{ = 90}^{ \circ }}$ (в координатах формулы (1)). Окружность – это горловина КН, где $R = 0$. Наблюдатель находится в точке на $R \to \infty $, $\varphi = 0$. Будем называть пространство $0 < R < + \infty $ пространством-1. Параллельный пучок нулевых геодезических уходит из района КН к наблюдателю. Назовем его пучком $A$.

Рис. 1.

Сечение пространства наблюдателя (пространства-1) на экваторе (θ = 90°), $0 < R < \infty $, $0 < \varphi < 2\pi $. Изображены траектории нулевых геодезических (лучей света) в этом пространстве. Эти траектории простираются от наблюдателя, находящегося справа на бесконечности $R \to \infty $, $\varphi = 0$ к району входа в КН. Траектории имеют прицельные параметры $b = 0$, 0.2, 0.4, 0.6, 0.8, 0.9, 1.1, 1.2, 1.4, 1.6, 1.8. Окружность – горловина КН. Координаты системы соответствуют формуле (1). Расстояния по вертикальной и горизонтальной осям отложены в единицах размера радиуса горловины.

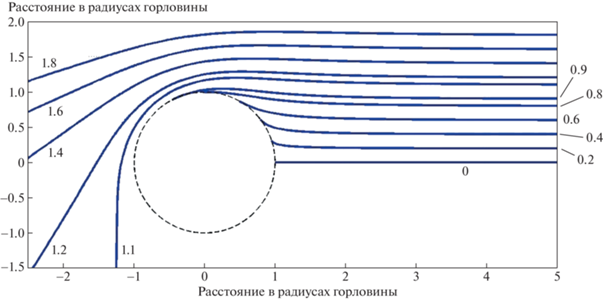
На рис. 1 изображены траектории нулевых геодезических, имеющих разный прицельный параметр $b$ по отношению к наблюдателю. Параметр $b$ измеряется в единицах радиуса горловины. Нулевые геодезические с $b > 1$ – это лучи в пространстве-1 наблюдателя. Траектории с $b < 1$ доходят до горловины КН и уходят в другое пространство, будем называть его “пространство-2”, где $R$ меняется от $R = 0$ до $R \to - \infty $.

На рис. 1 показаны траектории с прицельным параметром $b$ выше горизонтали $b = 0$, т.е. движущиеся против часовой стрелки. Разумеется, аналогичная картина должна повторяться для прицельного параметра $b$ ниже $b = 0$, т.е. движущиеся по часовой стрелке.

На рис. 2 изображено пространство-2. Здесь показаны нулевые геодезические, которые пришли из пространства-1, пересекая горловину. Соответствующие прицельные параметры $b < 1$ указаны рядом с траекториями. При значениях $b < 1$, но очень близких к 1 (т.е. $(1 - b) \ll 1$) траектории много раз оборачиваются по координате $\varphi $ прежде, чем уходят к $R \to - \infty $. Это показано на рис. 3.

Рис. 2.

Пространство-2. Продолжение траекторий с прицельными параметрами: 0, 0.2, 0.4, 0.6, 0.8 и 0.9 в пространстве-2 после пересечения горловины. Расстояния по осям координат измеряются в единицах радиуса горловины.

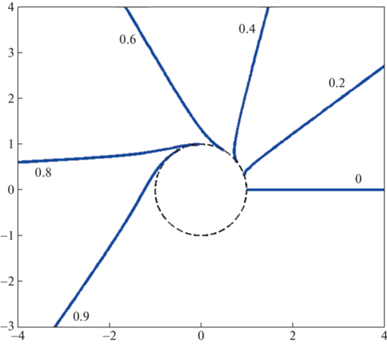
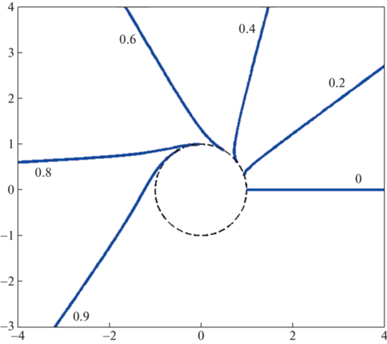
Рис. 3.

Траектории нулевых геодезических в пространстве-2, сильно искривляющиеся вокруг горловины. Прицельный параметр указан рядом с траекторией. Горизонтальная траектория рядом со стрелкой – это сливающиеся при данном разрешении входяшие траектории в пространстве-1 для всех приведенных на рисунке траекторий.

Траектории с $b < 1$ являются объектом нашего внимания в этой статье. Именно они используются для построения изображений и силуэтов, видимых наблюдателем сквозь КН.

3. ИЗОБРАЖЕНИЯ ОТДЕЛЬНЫХ ЗВЕЗД, ВИДИМЫХ СКВОЗЬ КН

Приступим теперь к нашей основной задаче – построению изображений отдельных объектов и силуэтов, видимых наблюдателем сквозь КН. Начнем с изображения отдельных звезд.

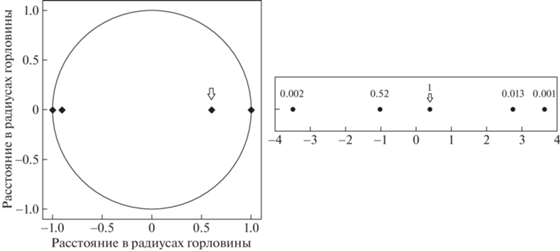
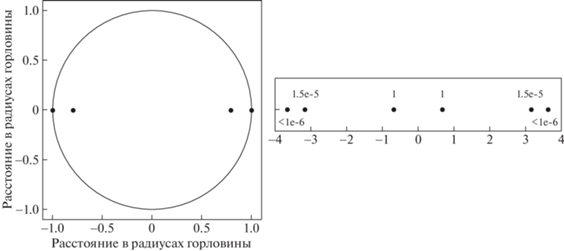
Пусть в пространстве-2 имеется далекий точечный источник (звезда), расположенный в нашем $R - \theta $ сечении с координатой $\theta $. Как ее увидит наблюдатель? От далекой звезды лучи света (нулевые геодезические) падают на вход КН в пространстве-2 параллельным пучком. Назовем его пучком $B$. К наблюдателю придет луч света, асимптотика которого при $R \to - \infty $ соответствует координате $\theta $. Его прицельный параметр ${{b}_{1}}$ и будет соответствовать положению изображения звезды для наблюдателя. Но изображение будет не единственным. Луч из пучка $B$, идущий вблизи горловины и сделавший полный оборот вблизи нее, может попасть в пучок $A$ и прийти к наблюдателю. Так возникает второе изображение звезды ${{b}_{2}}$ ближе к окружности горловины и т.д. Изображений будет бесконечно много все ближе и ближе к окружности, соответствующей горловине. Луч из пучка $B$ может также совершать полные обороты и в противоположную сторону. Такие изображения будут наблюдаться тоже вблизи окружности горловины, но с ее противоположной стороны. Множественные изображения отдельной звезды показаны на рис. 4 слева. Справа показаны те же изображения, но в качестве горизонтальной координаты использована величина $\lg (1 - \left| b \right|)$. Это сделано для того, чтобы различить отдельные сливающиеся изображения вблизи края горловины. Вблизи каждого изображения указана его относительная яркость для наблюдателя в пространстве-1. Эти значения можно получить после численного интегрирования системы (4)–(9) и сравнения телесных углов для конуса одних и тех же лучей в пространствах-1 и 2.

Рис. 4.

Слева – множественные изображения одной и той же звезды, находящейся в пространстве-2. Изображение, отмеченное стрелкой, можно условно назвать “главным”. Справа – для тех же изображений использована горизонтальная координата $\lg (1 - \left| {b{\kern 1pt} } \right|{\kern 1pt} )$. Числа у точек указывают яркость соответствующего изображения.

Характер самого изображения звезды и его повторения, разумеется, зависит от ее положения на небе пространства-2.

Будем считать, что меридиан сечения φ = 90°, вдоль которого мы рассматриваем разные положения звезд, соответствует горизонтальной линии в поле зрения наблюдателя изображения кротовой норы. Тогда схематически картина с повторяющимися изображениями показана на рис. 5. В районе полюса первое изображение звезды отсутствует. Лучи от нее прямо не попадают к наблюдателю. При этом самые внешние точки в поле зрения на левой панели состоят из двух слившихся изображений, которые в таком масштабе разделить невозможно. На правой панели с горизонтальной координатой $\lg (1 - \left| {b{\kern 1pt} } \right|{\kern 1pt} )$ они хорошо видны.

Рис. 5.

Слева – множественные изображения одной и той же звезды, находящейся в пространстве-2 и расположенные симметрично в поле зрения наблюдателя. Числа указывают яркость соответствующего изображения. Справа – для тех же изображений использована горизонтальная координата $\lg (1 - \left| {b{\kern 1pt} } \right|{\kern 1pt} )$. Числа у точек указывают яркость соответствующего изображения.

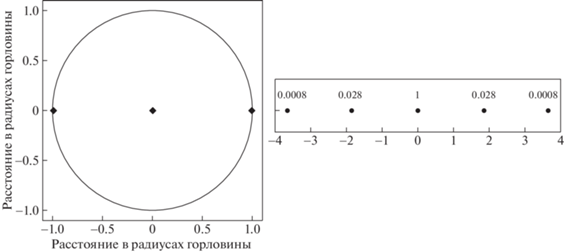
На рис. 6 показана еще одна симметричная ситуация, когда звезда из пространства-2 видна в центре поля зрения.

Рис. 6.

Слева – множественные изображения одной и той же звезды, находящейся в пространстве-2 и расположенные симметрично в поле зрения наблюдателя. Числа указывают яркость соответствующего изображения. “Главное” изображение находится в центре поля зрения. Справа – для тех же изображений использована горизонтальная координата $\lg (1 - \left| {b{\kern 1pt} } \right|{\kern 1pt} )$. Числа у точек указывают яркость соответствующего изображения.

4. ВНУТРЕННИЕ СИЛУЭТЫ (ТЕНИ) КРОТОВОЙ НОРЫ

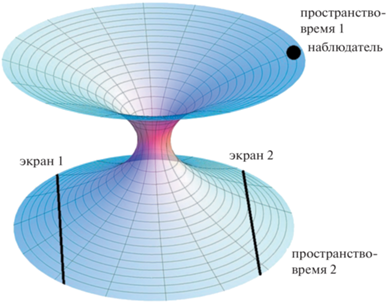
Рассмотрим теперь изображения, создаваемые для наблюдателя в нашем пространстве-1 протяженными светящимися экранами, расположенными в пространстве-2. Как и в работах [1–3], будем считать интенсивность свечения экрана во всех направлениях одинаковой (ламбертовский источник). Прежде всего рассмотрим экран, расположенный в пространстве-2 в направлении полюса, φ = 180°, перпендикулярно радиальному направлению и находящемуся достаточно далеко, $R \to - \infty $. На рис. 7 схематически показано положение наблюдателя в пространстве-1 и два экрана, находящиеся в пространстве-2. По рисунку можно понять, что луч света, идущий от наблюдателя точно в центр кротовой норы (т.е. с нулевым прицельным параметром), приходит в экран-2 перпендикулярно ему и поэтому в экран-1 не попадает. А для того, чтобы попасть в экран-1, луч света должен двигаться с отличным от нуля прицельным параметром $b$ и, значит, повернуть в пространстве-2 (вблизи горловины) на угол, больший 90°. Взглянув снова на рис. 2, можно увидеть, что прицельный параметр такого луча приблизительно равен $b \approx 0.5$.

Рис. 7.

Схема расположения наблюдателя в пространстве-1 и протяженных ламбертовских экранов в пространстве-2.

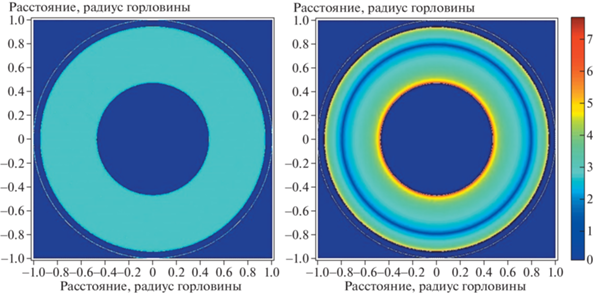
В первую очередь мы рассмотрим, как выглядит изображение экрана-1 с точки зрения наблюдателя, находящегося в пространстве-1. Размеры экрана считаем неограниченно большими, способы построения изображений аналогичны описанным в работе [1]. Изображение, которое видит наблюдатель в пространстве-1, показано на рис. 8. На левой панели показана форма изображения, которое видит наблюдатель, а справа – распределение интенсивности излучения в том же изображении, показанное в логарифмическом масштабе. Внутренний радиус светлой области, как сказано выше, соответствует повороту луча в пространстве-2 на угол $90^\circ $, а внешняя граница соответствует повороту на 270°. Точные значения прицельных параметров для этих значений угла поворота можно получить только численным интегрированием уравнений нулевых геодезических. Эти значения получились равными:

(10)
$\begin{gathered} {{b}_{{90}}} = 0.4704q, \\ {{b}_{{270}}} = 0.94008q. \\ \end{gathered} $
Луч, однако, может достигнуть экрана и более сложным путем: он может совершить несколько оборотов вблизи горловины кротовой норы и только после этого попасть в экран. Так, при повороте луча на углы от 450° до 630° луч достигнет экрана, сделав один полный оборот, а при повороте на углы от 810° до 990° – два полных оборота и т.д. Эти лучи должны проходить горловину кротовой норы с прицельными параметрами, очень близкими к единице, и образовывать бесконечное количество тонких колец. Для первого такого кольца прицельные параметры внутренней и внешней границ равны, соответственно:
(11)
$\begin{gathered} {{b}_{{450}}} = 0.9969445q, \\ {{b}_{{630}}} = 0.9998713q, \\ {{b}_{{630}}} - {{b}_{{450}}} \approx 0.003q. \\ \end{gathered} $
Точность этих значений составляет четыре–пять единиц последнего знака. Для второго и последующих колец для определения этих параметров требуется интегрирование с чрезвычайно высокой точностью, поскольку система уравнений становится слишком жесткой для стандартных численных методов.

Рис. 8.

Изображение плоского ламбертовского экрана-1, которое наблюдатель видит сквозь горловину кротовой норы. Слева показан силуэт этого экрана, а справа – распределение интенсивности излучения изображения в логарифмической шкале.

В работе [15] не учитывалось возникновение кольцевых структур в изображении.

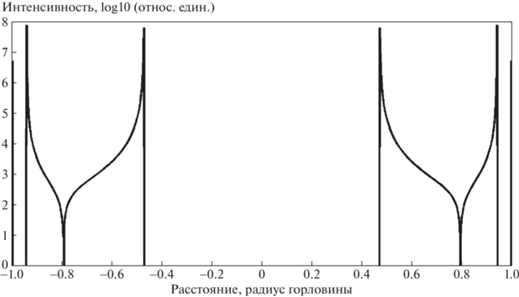
Распределение интенсивности вдоль диаметра изображения показано в виде графика на рис. 9. Локальный минимум интенсивности приходится на значение прицельного параметра $b = 0.793$, который соответствует повороту луча на 180°. Появление этого минимума можно легко понять и из общефизических соображений. Дело в том, что лучи, выпущенные от наблюдателя с прицельным параметром $b = 0.793$, попадают в одну и ту же точку экрана-1 в пространстве-2 и, следовательно, эту точку наблюдатель и видит, регистрируя любой луч с прицельным параметром $b = 0.793$.

Рис. 9.

Распределение интенсивности излучения вдоль диаметра горловины кротовой норы для первого экрана.

Рассмотрим теперь экран-2 (рис. 7), расположенный в пространстве-2 при φ = 0°, $R \to - \infty $. В этом случае луч, идущий с нулевым прицельным параметром, попадает в центр экрана и, значит, центр экрана должен быть виден светлым. Более того, луч, который попадает в экран-2, не может попасть в экран-1 и наоборот. Условно можно сказать, что изображение экрана-2 должно быть “дополнительным” к изображению экрана-1, показанному на рис. 8.

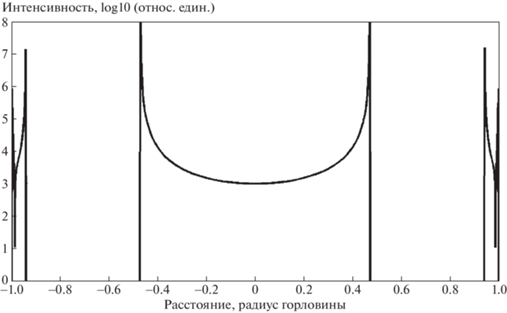
Изображение экрана-2 для наблюдателя в пространстве-1 показано на рис. 10. Аналогично рис. 8, на левой панели показан лишь силуэт изображения, которое видит наблюдатель, а справа в логарифмическом масштабе показано распределение интенсивности излучения в том же изображении. Как и следовало ожидать, центр экрана оказывается светлым, но распределение яркости отличается от рис. 8. В центре экрана интенсивность имеет минимум и увеличивается к краю яркого диска. Кроме того, мы видим яркое кольцо, образованное лучами, которые совершили полный оборот в горловине кротовой норы. В этом случае ширина кольца такова, что мы может построить внутри него распределение интенсивности излучения по радиальной координате. В увеличенном масштабе распределение интенсивности в кольце показано на рис. 11, где можно рассмотреть его детали. Например, хорошо виден минимум интенсивности, причем этот минимум расположен несимметрично и сильно смещен к внешнему краю кольца. Интенсивность излучения возрастает к краям кольца. Как и в первом случае, минимум возникает из-за того, что все лучи с этим прицельным параметром, совершив оборот, попадают в одну и ту же точку экрана. Значение прицельного параметра для минимума интенсивности в кольце составляет

(12)
$b = 0.985q.$
График распределения интенсивности излучения вдоль экваториального сечения силуэта кротовой норы показан на рис. 12.

Рис. 10.

Изображение плоского ламбертовского экрана-2, которое наблюдатель видит сквозь горловину кротовой норы. Слева показан силуэт этого экрана, а справа – распределение интенсивности излучения изображения в логарифмической шкале.

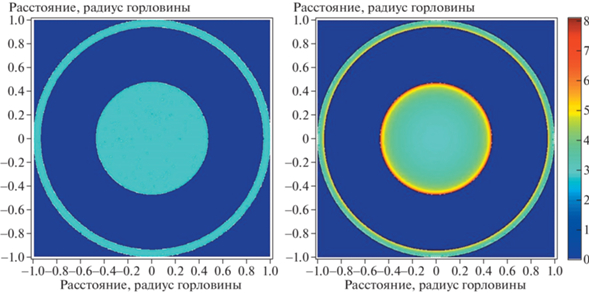
Рис. 11.

Детали распределения интенсивности излучения в первом кольце, т.е. квантами, совершившими один полный оборот в горловине кротовой норы.

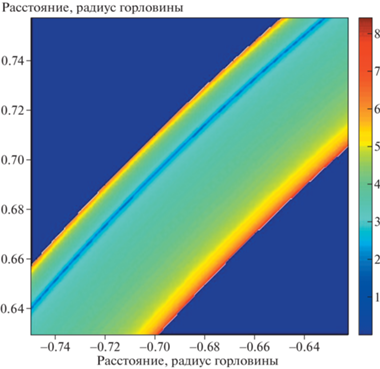
Рис. 12.

Распределение интенсивности излучения вдоль диаметра горловины кротовой норы для второго экрана.

Разумеется, наблюдатель в пространстве-1 будет видеть и лучи, прошедшие в его пространстве вокруг входа в КН, и лучи, прошедшие сквозь КН. Первую категорию лучей мы рассмотрели в работах [1–3]. Полная картина для наблюдателя складывается суммированием картины, рассмотренной в [1–3] и рассмотренной в данной работе.

5. ЗАКЛЮЧЕНИЕ

В рассмотренной модели силуэта проходимой кротовой норы существуют характерные детали изображения, которые можно использовать для идентификации этих объектов в интерферометрических наблюдениях [7]. Так, в отличие от черных дыр внутри силуэта кротовой норы могут наблюдаться достаточно сложные кольцевые структуры с изменяющейся яркостью изображения. Сами кротовые норы, как и сверхмассивные черные дыры, возможно, могут существовать в центрах галактик [16]. Для поиска и наблюдения таких объектов можно использовать каталог сверхмассивных черных дыр [17], в котором можно найти достаточное количество кандидатов для проведения наблюдений с помощью наземных интерферометров.

Еще более широкие возможности для наблюдений кротовых нор дает наземно-космический интерферометр, в котором одна из приемных антенн расположена на спутнике, находящемся в космосе на расстоянии от единиц до сотен радиусов Земли. Одним из объектов для установки такой антенны могла бы стать Луна. Другую возможность дает российский проект Миллиметрон [18, 19] с десятиметровой охлаждаемой антенной. Разрешающая способность Миллиметрона в режиме интерферометра может достигать десятков наносекунд дуги. Столь высокого разрешения достаточно, чтобы детально исследовать силуэты черных дыр и, возможно, кротовых нор в большом количестве галактик. Открытие таких объектов безусловно даст новый импульс развитию астрофизики.

БЛАГОДАРНОСТИ

С.В. Репин выражает свою благодарность О.Н. Суменковой, Р.Е. Бересневой и О.А. Косаревой за возможность плодотворно работать над настоящей задачей.

Список литературы

  1. M. A. Bugaev, I. D. Novikov, S. V. Repin, and A. A. Shel-kovnikova, Astron. Rep. 98(12), 1 (2021).

  2. M. A. Bugaev, I. D. Novikov, S. V. Repin, and A. A. Shel-kovnikova, Astronomy at the epoch of multimessenger studies, Proc. VAK-2021 Conference, p. 271 (2022).

  3. M. A. Bugaev, I. D. Novikov, S. V. Repin, and A. A. Shel-kovnikova, Astronomy at the epoch of multimessenger studies, Proc. VAK-2021 Conference, p. 272 (2022).

  4. И. Д. Новиков, С. В. Репин, Астрон. журн. 98, 3 (2021).

  5. Event Horizon Telescope Collaboration, Astrophys. J. Letters 875, id. L1 (2019), arXiv:1906.11238 [astro-ph.GA].

  6. R. Roy and S. Chakrabarti, Phys. Rev. D 102(2), id. 024059 (2020), arXiv:2003.14107 [gr-qc].

  7. E. V. Mikheeva, S. V. Repin, and V. N. Lukash, Astron. Rep. 64, 578 (2020), arXiv:2004.10429 [astro-ph.GA].

  8. T. Lacroix, M. Karami, A. E. Broderick, J. Silk, and C. Boehm, Phys. Rev. D 96, id. 063008 (2017), arXiv:1611.01961 [astro-ph.GA].

  9. T. Vetsov, G. Gyulchev, and S. Yazadjiev, arXiv:1801.04592 [gr-qc] (2018).

  10. H. Ellis, J. Math. Phys. 14, 104 (1973).

  11. K. A. Bronnikov, Acta Phys. Pol. 84, 251 (1973).

  12. M. S. Morris and K. S. Thorne, American J. Physics 56, 395 (1988).

  13. M. S. Morris, K. S. Thorne, and U. Yurtsever, Phys. Rev. Lett. 61, 1446 (1988).

  14. A. F. Zakharov and S. V. Repin, Astron. Rep. 43, 705 (1999).

  15. И. Д. Новиков, Н. С. Кардашев, А. А. Шацкий, Успехи физ. наук 177, 1017 (2007).

  16. N. S. Kardashev, I. D. Novikov, and S. V. Repin, Physics Uspekhi 63, 617 (2020).

  17. E. V. Mikheeva, V. N. Lukash, S. V. Repin, and A. M. Ma-linovskii, Astron. Rep. 63, 343 (2019), arXiv:1811.00808 [astro-ph.GA].

  18. Н. С. Кардашев, И. Д. Новиков, А. А. Шацкий, Астрон. журн. 83(8), 675 (2006).

  19. И. Д. Новиков, С. Ф. Лихачёв, Ю. А. Щекинов, А. С. Андрианов и др., Успехи физ. наук 191, 404 (2021).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал