Астрономический журнал, 2022, T. 99, № 2, стр. 91-99

1. ВВЕДЕНИЕ

В работах [1, 2] рассмотрена задача о пространственном движении пассивно-гравитирующего тела (ПГТ) в гравитационном поле эллиптической галактики (ЭГ) согласно моделям 1 и 2. Аналогичная задача о движении ПГТ внутри (вблизи) шарового скопления (ШС), принадлежащего ЭГ, исследуется в [3].

Полученные в работах [1–3] результаты применены к модельным эллиптическим галактикам с параметрами, точно совпадающими с параметрами эллиптических галактик NGC 4472 (M 49), NGC 4697 и NGC 4374 (М 84) и приведены в виде рисунков и таблицы.

В работе [4] рассмотрены три новые модели ЭГ (Модели 3, 4 и 5). Наибольший интерес представляет Модель 5, согласно которой ЭГ вместе с гало (вариант 1) или без него (вариант 2) представляет собой неоднородный эллипсоид вращения – вытянутый сфероид, состоящий из БМ и ТМ. В качестве модели трехосной ЭГ выбран именно такой сфероид потому, что его динамические свойства весьма близки к свойствам трехосного эллипсоида [5]. Кроме того, в Модели 5 не следует рассматривать выполнение условий сшивки потенциалов, так как граница раздела между БМ и ТМ в галактике отсутствует. Полученные в [4] результаты применены к шестидесяти ЭГ и приведены в виде таблиц для десяти из них.

Упомянутые выше модели предназначены для решения задач небесной механики и частично астрофизики. В рамках этих моделей сделана еще одна попытка исследовать влияние ТМ на кинематику и динамику ПГТ. Эти модели не могут претендовать на полноту охвата проблемы ТМ в целом. Тем более, по мнению одних авторов [6] основная часть ТМ находится вне светящейся части эллиптической галактики, а по мнению других [7, 8] – содержание ТМ во внутренних областях ЭГ сравнимо с содержанием БМ.

В настоящей работе на основе Модели 5 рассмотрена задача о пространственном движении ПГТ в гравитационном поле СНЭГ, имеющей форму вытянутого сфероида. Найден аналог интеграла Якоби, определена область возможного движения ПГТ, и построены поверхности нулевой скорости. Установлена устойчивость в смысле Ляпунова найденных стационарных решений – точек либрации.

Вопрос о равновесии и устойчивости динамической системы, исследованной в Модели 5, будет рассмотрен отдельно в другой работе автора.

2. ПОСТАНОВКА ЗАДАЧИ. УРАВНЕНИЯ ДВИЖЕНИЯ

Рассмотрим задачу о пространственном движении ПГТ в поле притяжения СНЭГ, согласно Модели 5 в системе координат $OXYZ$. Условные границы такой галактики определим по значениям величин ${{D}_{{25}}}$ и ${{R}_{{25}}}$ [9]. При этом $OXYZ$ является системой координат с началом в центре ЭГ, вращающейся с постоянной угловой скоростью $\Omega $ вокруг полярной оси $OZ$ и с осями, направленными по соответствующим главным осям ЭГ. Прямоугольные координаты ($x$, $y$, $z$) ПГТ в этой системе координат определяются из системы уравнений [10]

Здесь силовая функция $U = U(x,y,z)$ определяется равенством где первое слагаемое представляет собой потенциал центробежной силы, $V = V(x,y,z)$ – потенциал силы притяжения, а функцию $U$ можно считать потенциалом силы тяжести. $U{\kern 1pt} * = U{\kern 1pt} *{\kern 1pt} (x,y,z)$ и ${{U}_{G}} = {{U}_{G}}(x,y,z)$ – потенциалы БМ и ТМ СНЭГ соответственно, явный вид которых приведен в следующих разделах.

Для существования неоднородной ЭГ как фигуры равновесия должно удовлетворяться необходимое условие – неравенство Пуанкаре для угловой скорости вращения [11]:

Здесь $G$ – гравитационная постоянная, а $\bar {\rho }$ – средняя плотность неоднородной эллиптической галактики. Выполнение неравенства Пуанкаре гарантирует направление полной силы тяжести внутрь и неотрицательность давления. В скобках указаны более строгие неравенства Крудели и Кондратьева [12]. В неравенстве Крудели ${{\rho }_{0}}$ – плотность в центре галактики и она убывает от центра к периферии. Кроме того, о направлении силы тяжести речь не идет.

Очевидно, что cистема уравнений (1) допускает аналог интеграла Якоби в виде [1, 2, 10]:

из которого легко получаются поверхности нулевой скорости и область возможности движения ПГТ, соответственно, где $C$ – аналог постоянной Якоби.

3. ПОТЕНЦИАЛ БАРИОННОЙ МАССЫ СЛОИСТО-НЕОДНОРОДНОЙ ЭЛЛИПТИЧЕСКОЙ ГАЛАКТИКИ

Будем считать, что СНЭГ имеет форму неоднородного вытянутого сфероида, ограниченного сфероидальной поверхностью,

где значение параметра семейства $m = 0$ соответствует центру СНЭГ, а $m = 1$ – ее внешней границе. Законы распределения плотности $\rho (m)$ и поверхностной яркости $I(m)$ барионной массы определяются выражениями [3, 13, 14] соответственно. Здесь ${{\rho }_{0}}$ – плотность центра (ядра) эллиптической галактики, $m$ – параметр семейства эллипсоидальных поверхностей (5), из которых состоит ее светящаяся часть, а параметр $\beta \gg 1$ для каждой ЭГ выбирается отдельно [13] и находится выравниванием данных фотометрии [12, 13]. ${{I}_{0}}$ – центральная поверхностная яркость.

Профиль в виде (5) согласно [12] назовем “астрофизическим”, он согласуется с современными представлениями о строении ЭГ [13, 14].

Потенциал притяжения БМ СНЭГ с плотностью $\rho (m)$ на внешнюю точку $P = P(x,y,z)$ и его производные по координатным осям определяются равенствами [10, 12]

где $R$ – одна из координат ($x,y,z$), ${{A}^{2}} = \{ {{a}^{2}},{{c}^{2}}\} $. Если профиль БМ определяется равенством (5), то причем выполнение условия ${{m}^{2}}(0) > 1$ для координат внешней точки $P$ СЧ ЭГ является обязательным. Параметр $\lambda $ является положительным корнем квадратного уравнения ${{m}^{2}}(\lambda ) = 1$: где В силу (7) имеем для $p > 0$

Очевидно, что потенциал $U{\kern 1pt} *$ является функцией параметра $\lambda $, который, в свою очередь, зависит от координат внешней точки $P = P(x,y,z)$. После вычисления интеграла в (6) для внешнего потенциала получим:

где Здесь причем Аргумент $\alpha $ и модуль $n$ неполного эллиптического интеграла 1-го рода $F(\alpha ,n)$ равны

Очевидно, что в начале координат (в центре галактики) значение потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$ с учетом следующих равенств:

будет равно функция $\varphi (\lambda )$ определена выше.

Последнее равенство можно получить и из выражения (8) потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$, положив в нем ${{U}_{2}}(\lambda ) = {{U}_{1}}(\lambda )$ и $\lambda = 0$.

Положив $z = 0$, $x \ne 0$, $w = y \ne 0$ в соответствующие выражения, определяем параметр $\lambda $, корни ${{v}_{1}}$, ${{v}_{2}}$, затем значения функций ${{U}_{1}}(\lambda )$ и ${{U}_{2}}(\lambda )$. После чего находим выражение потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$ в плоскости $OXY$. Аналогично, при $y = 0$, $x \ne 0$, $w = z \ne 0$ находим выражение потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$ в плоскости $OXZ$.

Далее, в плоскости $OYZ$ имеем

Тогда потенциал $U{\kern 1pt} *{\kern 1pt} (\lambda )$ будет определяться точно таким же равенством, что и (8), но лишь с той разницей, что параметр $\lambda $ и функция ${{U}_{2}}(\lambda )$ определяются иначе: Здесь ${{\alpha }_{0}}$ и ${{n}_{0}}$ – аргумент и модуль неполного эллиптического интеграла 1-го рода $F({{\alpha }_{0}},{{n}_{0}})$.

Производная от потенциала $U{\kern 1pt} *(\lambda )$ по $w$ согласно (6) равна

где $F({{\alpha }_{0}},{{n}_{0}})$, $E({{\alpha }_{0}},{{n}_{0}})$ – неполные эллиптические интегралы 1-го и 2-го рода соответственно. Величины ${{\alpha }_{0}},{{n}_{0}}$, а также ${{h}^{2}}$ определены выше. Положив в этих формулах $z = 0$, или $y = 0$ получим выражения потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$ и его производной на координатных осях $OY$ или $OZ$ соответственно. Здесь учтено, что $x = 0$.

Наконец, на координатной оси $OX$ имеем

В этом случае в выражении (8) потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$ следует учесть где

Производная от потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$ по $x$ имеет вид

Функция ${{\varphi }_{1}}(\lambda )$ и параметр ${{p}^{2}}$ определены выше.

Теперь вычислим производные от потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$ по координатам в общем случае:

где Здесь где корни ${{v}_{1}}$, ${{v}_{2}}$, а также аргумент $\alpha $ и модуль $n$ эллиптических интегралов 1-го и 2-го рода $F(\alpha ,n)$ и $E(\alpha ,n)$ приведены выше.

Далее можно установить, что потенциал $U{\kern 1pt} *{\kern 1pt} (\lambda )$, определяемый формулой (7) или (8), обладает всеми характеристическими свойствами силовой функции:

1) является непрерывной функцией от координат $x,y,z$ во всем пространстве;

2) имеет всюду в пространстве непрерывные первые частные производные; эти производные не имеют разрыва на границе эллипсоида, что следует из выражения (7), в котором для получения внутреннего потенциала следует положить $\lambda = 0$;

3) на бесконечности вместе со своими первыми частными производными обращаются в нуль;

4) удовлетворяет уравнению Лапласа вне притягивающего тела СНЭГ, а внутри ($\lambda = 0$) – уравнению Пуассона.

Доказательство этих свойств вытекает, в том числе, из характеристик профиля $\rho (m)$, который является положительной, конечной, непрерывной функцией и обладает непрерывными производными первого и второго порядков. Такой же функцией является и $\delta ({{m}^{2}}(u))$. Следовательно, несобственные интегралы в формуле (7) сходятся, а потенциал $U{\kern 1pt} *{\kern 1pt} (\lambda )$ и его первые производные по координатам являются конечными, непрерывными функциями от своих аргументов. Кроме того, если ПГТ удаляется в бесконечность, то $\lambda $ тоже стремится к бесконечности. Поэтому силовая функция $U{\kern 1pt} *{\kern 1pt} (\lambda )$ и ее первые частные производные в бесконечности обращаются в нуль. Удовлетворение уравнений Лапласа и Пуассона проверяется вычислением частных производных от потенциала $U{\kern 1pt} *{\kern 1pt} (\lambda )$ второго порядка. Доказательство этого для краткости не приводится.

4. ПОТЕНЦИАЛ ТЕМНОЙ МАТЕРИИ СЛОИСТО-НЕОДНОРОДНОЙ ЭЛЛИПТИЧЕСКОЙ ГАЛАКТИКИ

Для краткости и удобства рассмотрим только вариант 2 Модели 5, из которого элементарной подстановкой получим результаты варианта 1. В этом случае внешний потенциал такой галактики определится равенством $\tilde {U}(\lambda ) = U{\kern 1pt} *{\kern 1pt} (\lambda ) + {{U}_{G}}(\lambda )$. Здесь $U{\kern 1pt} *{\kern 1pt} (\lambda )$ представляет собой потенциал БМ с профилем $\rho (m)$ из (5) и определяется равенством (8), а ${{U}_{G}}(\lambda )$ – потенциал ТМ с аналогом профиля ${{\rho }_{G}}(m)$ NFW [4, 15]

где ${{r}_{s}}$ – радиус-шкала галактики, а функции ${{m}^{2}}(u)$ и $\Delta (u)$ определяются равенством (7). Следовательно, Здесь величины ${{A}^{2}},\;\lambda $ и функция $\Delta (u)$ определены выше (см. раздел 3), а $\chi (u)$ есть Таким образом, потенциал ${{U}_{G}}(\lambda )$ примет вид где После интегрирования получим где

В плоскости $OZY$ имеем

В этом случае потенциал ${{U}_{G}}(\lambda )$ выражается равенством (12), в котором функция ${{J}_{1}}(\lambda )$ точно такая же, но функция ${{J}_{2}}(\lambda )$ определяется иначе: где

Положив $w = y$ или $w = z$ в функциях ${{J}_{1}}(\lambda )$ и ${{J}_{2}}(\lambda )$, получим выражения потенциала ${{U}_{G}}(\lambda )$ на координатных осях $OY$, или $OZ$ соответственно.

На координатной оси $OX$ имеем

Тогда для функции ${{J}_{2}}(\lambda )$ находим Здесь функция $\varphi (\lambda )$ определена выше. Потенциал ${{U}_{G}}(\lambda )$ при этом выражается равенством (12), в котором выражение функции ${{J}_{1}}(\lambda )$ остается точно таким же, а ${{J}_{2}}(\lambda )$ определяется равенством (16).

Наконец, значение потенциала в начале координат (в центре галактики) равно

где функция $\varphi (\lambda )$ определена выше.

Заметим, что согласно варианту 1 Модели 5 ЭГ рассматривается как неоднородный вытянутый сфероид, состоящий из БМ и ТМ с соответствующими профилями $\rho (m)$ и ${{\rho }_{G}}(m)$ вместе с гало. Если считать, что СНЭГ вместе с гало ограничена вытянутой сфероидальной поверхностью с полуосями $\tilde {a} > \tilde {b} = \tilde {c}$, то в этом случае в выражениях (8) и (12) потенциалов $U{\kern 1pt} *{\kern 1pt} (\lambda )$ и ${{U}_{G}}(\lambda )$ и их производных следует произвести замену $a$, $c$ на $\tilde {a}$, $\tilde {c}$. После чего получим и явное выражение для общего потенциала $\tilde {U}(\lambda ) = U{\kern 1pt} *{\kern 1pt} (\lambda ) + {{U}_{G}}(\lambda )$ согласно этому варианту Модели 5, которое для краткости не приведено. Кроме того, в этом варианте также не существует границы раздела между БМ и ТМ, т.е. нет необходимости определять условия сшивания потенциалов $U{\kern 1pt} *(\lambda )$ и ${{\tilde {U}}_{G}}(\lambda )$.

5. СТАЦИОНАРНЫЕ РЕШЕНИЯ. ТОЧКИ ЛИБРАЦИИ

Для нахождения стационарных решений системы уравнений (1) в ней положим

Это нам даст систему алгебраических уравнений для нахождения стационарных решений в виде При решении системы уравнений (18) будем рассматривать варианты 1 с гало и 2 без него Модели 5. Нулевое решение ${{x}_{0}} = 0$, ${{y}_{0}} = 0$ и ${{z}_{0}} = 0$ системы уравнений (18) соответствует центральной точке либрации, которую обозначим через ${{L}_{1}} = {{L}_{1}}(0,0,0)$. На оси $OX$ и $OY$ имеются по две точки либрации, а именно ${{L}_{2}} = {{L}_{2}}({{x}_{0}},0,0)$ и ${{L}_{3}} = {{L}_{3}}( - {{x}_{0}},0,0)$ на оси $OX$, ${{L}_{4}} = {{L}_{4}}(0,{{y}_{0}},0)$ и ${{L}_{5}} = {{L}_{5}}(0, - {{y}_{0}},0)$ на оси $OY$.

В табл. 1 приведены значения координат (в кпк) коллинеарных ${{L}_{2}},{{L}_{3}}$ и треугольных ${{L}_{4}},\;{{L}_{5}}$ точек либрации, вычисленные по вариантам 1 и 2 Моделям 5 для трех ЭГ: NGC 4374, NGC 4472 и NGC 4697, считающихся слоисто-неоднородными вытянутыми сфероидами.

6. ТИП И УСТОЙЧИВОСТЬ ОСОБЫХ ТОЧЕК

Особыми точками семейства $U = C$ являются точки, в которых невозможно построить единственную касательную плоскость. Для определения таких точек получим систему алгебраических уравнений, точно совпадающую с системой (18) для определения точек либрации. Следовательно, точки либрации ${{L}_{n}}$ являются особыми точками.

Для исследования типа и установления устойчивости особых точек – точек либрации – силовая функция $U$ разлагается в ряд Тейлора в окрестности ${{L}_{n}}$ $(n = 1,2, \cdots ,5)$ и записывается семейство поверхностей нулевой скорости $U = C$ (см. раздел 2). Затем рассматривается движение ПГТ вблизи этих точек, которое выражается системой дифференциальных уравнений в вариациях. После чего записывается характеристическое уравнение этой системы и в зависимости от значений корней этого уравнения, согласно известной теореме Ляпунова, устанавливается устойчивость точек либрации ${{L}_{n}}$ в смысле Ляпунова в первом приближении (или в линейной постановке). Вся эта процедура подробно описана в работах автора [2, 3], поэтому здесь для краткости она не приведена.

Тип и устойчивость центральной точки либрации ${{L}_{1}}(0,0,0)$ одинаковы во всех моделях: это изолированная особая точка, устойчивая в смысле Ляпунова в первом приближении и в нелинейной постановке. Найденные согласно Моделям 3, 4 и 5 в данной работе коллинеарные точки либрации ${{L}_{2}}$ и ${{L}_{3}}$ являются коническими особыми точками с осью конуса $OX$ и неустойчивы в смысле Ляпунова в первом приближении, а треугольные точки либрации ${{L}_{4}}$ и ${{L}_{5}}$ являются особыми точками с осью конуса $OZ$ и они устойчивы. Следовательно, если ПГТ (например, звезда) окажется очень близко к треугольным точкам либрации ${{L}_{4}}$ или ${{L}_{5}}$, то она будет там находиться вечно, т.е. имеет место устойчивость по Хиллу.

Заметим, что в работах [16–18] также показана неустойчивость точек либрации ${{L}_{2}}$, ${{L}_{3}}$ и устойчивость ${{L}_{4}}$ и ${{L}_{5}}$ в смысле Ляпунова. Кроме того, нелинейный анализ показал, что ${{L}_{4}}$ и ${{L}_{5}}$ устойчивы для большинства начальных условий в смысле меры Лебега, исключая лишь некоторые резонансные случаи, когда имеет место неустойчивость [18].

7. ПРИМЕРЫ ПОСТРОЕНИЯ ПОВЕРХНОСТЕЙ НУЛЕВОЙ СКОРОСТИ

Процедура и метод построения поверхностей нулевой скорости, или поверхностей Хилла, подробно описаны в работе автора [3] Поэтому здесь на них останавливаться не будем. В качестве примера возьмем эллиптические галактики NGC 4374 типа Е1, NGC 4472 типа Е2 и NGC 4697 типа Е4, которые мы считаем слоисто-неоднородными вытянутыми сфероидами с полуосями $a > b = c$. Ниже приведены значения ключевых параметров этих галактик: звездной массы $M{\kern 1pt} *$ и массы ${{M}_{h}}$ гало (в массах Солнца), радиус-шкалы ${{r}_{s}}$ в кпк, угловой скорости вращения галактик $\Omega $ в радианах на млн. лет, параметров $\beta $ и $K$ (в массах Солнца на кубический парсек), вычисленных по известной формуле, а также значения полуосей $a,\;b = c$ в кпк и плотности ${{\rho }_{0}}$ в центре галактики, выраженной в массах Солнца на кубический парсек:

• NGC 4374: $M{\kern 1pt} * = 3.38844 \times {{10}^{{11}}}{{M}_{ \odot }}$, ${{M}_{h}} = $ $ = \,1.5674 \times {{10}^{{13}}}{{M}_{ \odot }}$, $\Omega \, = \,0.01386$, $\beta \, = \,1815$, ${{r}_{s}}\, = \,168.80$, $a = 19.947$, $b = c = 17.373$, $K = 0.167 \times {{10}^{{ - 3}}}$, ${{\rho }_{0}} = $ $ = 132.71$;

• NGC 4472: $M{\kern 1pt} * = 4.67735 \times {{10}^{{11}}}{{M}_{ \odot }}$, ${{M}_{h}} = $ $ = 2.172 \times {{10}^{{13}}}{{M}_{ \odot }}$, $\Omega = 0.0139$, $\beta = 858$, ${{r}_{s}} = 197.0$, $a = 22.166$, $b = c = 18.437$, $K = 0.1467 \times {{10}^{{ - 3}}}$, ${{\rho }_{0}} = $ $ = 50.844$;

• NGC 4697: $M{\kern 1pt} * = 1.4125 \times {{10}^{{11}}}{{M}_{ \odot }}$, ${{M}_{h}} = $ $ = 6.494 \times {{10}^{{12}}}{{M}_{ \odot }}$, $\Omega = 0.02524$, $\beta = 650$, ${{r}_{s}} = 130.5$, $a = 9.991$, $b = c = 6.304$, $K = 0.3459 \times {{10}^{{ - 3}}}$, ${{\rho }_{0}} = $ $ = 194.589$.

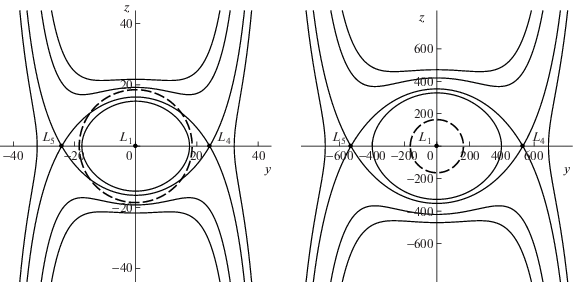
На рис. 1 приведены построенные поверхности нулевой скорости с коллинеарными ${{L}_{1}}$ (${{L}_{2}}$, ${{L}_{3}}$) и треугольными ${{L}_{4}}$, ${{L}_{5}}$ точками либрации для ЭГ NGC 4472 по Модели 5 в плоскости $x = 0$. Слева по варианту 2 без гало, а справа по варианту 1 вместе с гало галактики. Координаты указаны в килопарсеках.

8. ЗАКЛЮЧЕНИЕ

На основе созданной новой Модели 5 для решения задач небесной механики и астрофизики рассмотрено пространственное движение пассивно-гравитирующего тела (ПГТ) в гравитационном поле слоисто-неоднородной эллиптической галактики (СНЭГ). Согласно Модели 5, ЭГ вместе с гало (вариант 1) или без него (вариант 2) представляет собой слоисто-неоднородный вытянутый сфероид, состоящий из БМ и ТМ. Выбор вытянутого сфероида в качестве модели трехосной ЭГ объясняется тем, что его динамические свойства оказываются весьма близкими к свойствам трехосного эллипсоида. В этой модели не существует границы раздела между БМ и ТМ, поэтому определение условий сшивки потенциалов не рассматривается.

В качестве профиля БМ взят так называемый “астрофизический закон”, основанный на законе распределения поверхностной яркости Хаббла и хорошо моделирующий распределение плотности в ЭГ. Для ТМ берется аналог профиля NFW.

Найден аналог интеграла Якоби, определена область возможности движения пассивно-гравитирующего тела и построены поверхности нулевой скорости. Установлена устойчивость в смысле Ляпунова найденных стационарных решений – точек либрации. Найденные согласно Моделям 3, 4 и 5 в данной работе коллинеарные точки либрации ${{L}_{2}}$ и ${{L}_{3}}$ являются коническими особыми точками с осью конуса $OX$ и неустойчивы в смысле Ляпунова в первом приближении, а треугольные точки либрации ${{L}_{4}}$ и ${{L}_{5}}$ являются особыми точками с осью конуса $OZ$ и устойчивы. Определена поверхность вокруг СЧ ЭГ, внутри которой движения звезд или центра масс ШС оказываются устойчивыми по Хиллу.

Полученные результаты применены к эллиптическим галактикам NGC 4374, NGC 4472 (M 49) и NGC 4697 и приведены в виде рисунка и таблицы. Показано, что для получения точных результатов при нахождении точек либрации и исследовании их на устойчивость, вместо приближенных выражений потенциалов БМ и ТМ следует пользоваться их точными выражениями.

Исследование равновесия и устойчивости рассмотренных динамических систем по этим двум моделям будет проведено автором отдельно.