Астрономический журнал, 2022, T. 99, № 6, стр. 506-519

1. ВВЕДЕНИЕ

В настоящее время человечество осознало реальность угрозы столкновения Земли с малыми телами Солнечной системы. Для предотвращения этой угрозы необходимо выявить потенциально опасные объекты, определить их орбиты и оценить вероятность их столкновения или тесного сближения с Землей. Для повышения точности прогнозирования движения тела необходимо учитывать негравитационные эффекты, в частности эффект Ярковского. Этот эффект возникает вследствие теплового излучения вращающегося тела, имеющего ненулевую тепловую инерцию, и вызывает вековые изменения эксцентриситета, большой полуоси и, прежде всего, средней аномалии, изменение которой квадратично растет со временем. Таким образом, эффект Ярковского играет существенную роль в эволюции орбит малых тел, поэтому определение величины этого эффекта и изучение его влияния на астероиды, сближающиеся с Землей (AСЗ), являются необходимой составляющей для расчета их орбит и оценки их потенциальной опасности для Земли. Также эффект Ярковского считается одной из причин миграции астероидов в резонансные зоны Главного пояса, после чего они могут пополнить популяцию АСЗ. Кроме того, покрытие объекта специальным веществом для изменения орбиты с помощью эффекта Ярковского предлагается как один из способов воздействия на космические объекты, угрожающие столкновением с Землей.

Для учета эффекта Ярковского и изучения его влияния на долгосрочную эволюцию орбиты малого тела необходимо знать значения компонентов возмущающего ускорения, возникающего благодаря этому эффекту. В настоящее время наиболее распространенным методом оценки величины эффекта Ярковского является дифференциальная коррекция орбиты [1–4]. Поскольку эффект Ярковского приводит к вековым возмущениям большой полуоси, используется трансверсальное ускорение в виде

где $r$ – гелиоцентрическое расстояние до астероида, ${{r}_{0}} = 1$ а.е, ${{A}_{2}}$ – динамический параметр, определяемый в орбитальной подгонке вместе с элементами орбиты. Далее оценивается дрейф большой полуоси орбиты, и этот дрейф учитывается при прогнозировании движения астероида. Тем не менее значительная часть эффекта при определении его этим способом остается неучтенной, что может вызвать заметные ошибки при прогнозировании движения тела на основе найденной орбиты [5].

Более точным, на наш взгляд, является вычисление компонентов ускорения на основе какой-либо модели силы Ярковского. В настоящее время ведется обширная работа по определению теплофизических характеристик малых тел с помощью наблюдений, получаемых в наземных и орбитальных обсерваториях, например, определение формы и параметров вращения астероидов по их фотометрии [6, 7], определение диаметра и геометрического альбедо по общему тепловому излучению тел, полученному в результате 4-полосной тепловой инфракрасной съемки всего неба, проведенной находящимся на околоземной орбите инфракрасным телескопом (проект N-EOWISE) [8], уточнение тепловых характеристик поверхности при лабораторных исследованиях образцов метеоритного и астероидного вещества [9], а также в результате космических миссий к астероидам [10–12]. В будущем, при расширении знаний о свойствах малых тел явный учет эффекта Ярковского станет более предпочтительным.

Как упоминалось выше, при оценке дрейфа большой полуоси вследствие эффекта Ярковского возмущающее ускорение обычно моделируют трансверсальным компонентом. Однако тангенциальный компонент ускорения оказывает более непосредственное влияние на изменение скорости объекта и, как следствие, на дрейфы большой полуоси и средней аномалии. Это не принципиально для круговых орбит и при малых эксцентриситетах, когда трансверсальная и тангенциальная составляющие практически совпадают. Но для высокоэллиптических орбит это не так. Очевидно также, что величина изменения элементов орбиты не должна зависеть от выбора системы отсчета. Далее мы определим дрейфы элементов и смещение относительно невозмущенного положения за 1000 орбитальных оборотов для модельных астероидов с теплофизическими характеристиками как у астероида 101 955 Bennu, но с различными эксцентриситетами орбит в двух орбитальных системах и сравним их.

Для этого рассмотрим движение точки нулевой массы $\mathcal{A}$ (Aстероида) под действием притяжения к центральному телу $\mathcal{S}$ (Солнцу) и возмущающего ускорения ${\mathbf{P}}{\kern 1pt} '$, обратно пропорционального квадрату расстояния до $\mathcal{S}$, т.е. ${\mathbf{P}}{\kern 1pt} ' = {\mathbf{P}}{\text{/}}{{r}^{2}}$, и малого по сравнению с основным ускорением ${{\varkappa }^{2}}{\text{/}}{{r}^{2}}$:

Здесь ${\mathbf{r}} = \mathcal{S}\mathcal{A}$, $r = {\text{|}}{\mathbf{r}}{\text{|}}$, ${{\varkappa }^{2}}$ – произведение постоянной тяготения на массу $\mathcal{S}$, $\mu $ – малый параметр. Пусть ускорение ${\mathbf{P}}{\kern 1pt} {\text{'}}$ обязано эффекту Ярковского. В этом случае удовлетворяется условие (1), так как для АСЗ диаметром менее $1$ км типичное значение трансверсального параметра ${{A}_{2}} \sim {{10}^{{ - 15}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 13}}}$ а.е./сут², и для расстояния 1 а.е. $\mu \approx {{10}^{{ - 9}}} \ll 1$. Компоненты вектора ${\mathbf{P}}$ – постоянные и малые порядка $\mu $ величины. Для этой задачи в статье [13] получены эволюционные уравнения движения в средних элементах в первом порядке малости по $\mu $ для различных систем отсчета. В [14, 15] эти уравнения проинтегрированы для двух орбитальных систем отсчета: ${{\mathcal{O}}_{1}}$, связанной с радиусом-вектором, и ${{\mathcal{O}}_{2}}$, связанной с вектором скорости. В разделе 2 приведены частные решения, необходимые для исследования долгосрочной эволюции большой полуоси и средней аномалии.

Рассмотрим две системы отсчета с началом в $\mathcal{S}$: ${{\mathcal{O}}_{1}}$ с осями, направленными по радиусу-вектору, трансверсали (перпендикуляру к радиусу-вектору в плоскости оскулирующей орбиты в сторону движения) и бинормали (направленной по вектору площадей) и ${{\mathcal{O}}_{2}}$ с осями по вектору скорости, нормали к нему в плоскости оскулирующей орбиты и бинормали. Пусть вектор ${\mathbf{P}}$ имеет компоненты ${{P}_{r}},\;{{P}_{t}},\;{{P}_{n}}$ в системе ${{\mathcal{O}}_{1}}$ и ${{P}_{\mathfrak{T}}},\;{{P}_{\mathfrak{N}}},\;{{P}_{n}}$ в ${{\mathcal{O}}_{2}}$. Обозначим средние за орбитальный период значения компонентов вектора ${\mathbf{P}}$ следующим образом: $S = {{\bar {P}}_{r}}$, $T = {{\bar {P}}_{t}}$, $\mathfrak{T} = {{\bar {P}}_{\mathfrak{T}}}$, $\mathfrak{N} = {{\bar {P}}_{\mathfrak{N}}}$, $W = {{\bar {P}}_{n}}$ и будем называть их радиальным, трансверсальным, тангенциальным, нормальным и бинормальным параметрами соответственно. В статье [16] выведены соответствующие выражения для параметров $S$, $T$, $W$ на основе формул для составляющих ускорения Ярковского в проекции на оси системы ${{\mathcal{O}}_{1}}$, полученных в рамках линейной теплофизической модели силы Ярковского для сферических астероидов [17] и опубликованных в [18]. В настоящей статье выведены тангенциальный $\mathfrak{T}$ и нормальный $\mathfrak{N}$ параметры (см. раздел 3).

В разделе 4 для модельных астероидов в двух орбитальных системах отсчета найдены дрейфы большой полуоси и средней аномалии, а также смещение относительно невозмущенного положения за счет эффекта Ярковского и проведено их сравнение.

2. УРАВНЕНИЯ ДВИЖЕНИЯ

Как показано в [16], бинормальный компонент P_n в среднем за орбитальный период равен нулю (W = 0), поэтому используем частные аналитические решения.

Для системы отсчета ${{\mathcal{O}}_{1}}$ [14]:

и для ${{\mathcal{O}}_{2}}$ [15]: Здесь и далее индексом $0$ отмечены значения переменных в начальную эпоху $t = 0$, $e$ – эксцентриситет, $a$ – большая полуось, $n = \varkappa {{a}^{{ - 3/2}}}$ – среднее движение, $\eta = \sqrt {1 - {{e}^{2}}} $, $i$ – наклон, $\Omega $ – долгота восходящего узла, $\omega $ – аргумент перицентра, $M$ – средняя аномалия, а также использованы стандартные обозначения для полных эллиптических интегралов в нормальной тригонометрической форме [19]:

Решение (3) содержит определенные интегралы от комбинаций полных эллиптических интегралов, которые можно найти численными методами.

Первое выражение в системах (2), (3) представляет собой кинематическое уравнение, с помощью которого можно найти время, за которое произойдет заданное изменение эксцентриситета, и, наоборот, решая кинематическое уравнение $t(e) = \Delta t$ относительно $e$, найти изменение эксцентриситета за время $\Delta t$.

Область определения решений (2), (3) указана в [14, 15]. Там же даны представления этих решений в виде разложений в ряд по степеням эксцентриситета. Согласно [16] в случае решения (2) для системы отсчета ${{\mathcal{O}}_{1}}$ при $e \leqslant 0.8$ необходимо использовать степенн${\text{ы}}\prime $е ряды, поэтому приведем их здесь:

Приведем также решение для круговой орбиты, которое предпочтительнее использовать вместо (2), (3) при $e \approx 0$:

где средняя долгота $\lambda = \Omega + \omega + M$. Это решение справедливо и в системе отсчета ${{\mathcal{O}}_{1}}$ при замене $\mathfrak{T} \to T$, $\mathfrak{N} \to - S$.

3. МОДЕЛЬ УСКОРЕНИЯ ЯРКОВСКОГО

В рамках линейной теплофизической модели ускорения Ярковского для сферических астероидов [17] радиальный, трансверсальный и бинормальный компоненты этого ускорения в системе отсчета ${{\mathcal{O}}_{1}}$ имеют вид [18, ф-лы (12)]:

где индекс $s$ соответствует сезонному эффекту Ярковского, $d$ – суточному. В (5) $\gamma $ – наклон оси вращения астероида относительно нормали к плоскости его орбиты, $\lambda = {{\omega }_{{{\text{rev}}}}}(t - {{t}_{0}})$ – средняя долгота, ${{\omega }_{{{\text{rev}}}}}$ – среднее движение, $t$ – время, ${{t}_{0}}$ – момент начала отсчета времени, $\alpha = 1 - A$ – коэффициент оптического поглощения, $A$ – альбедо Бонда, $\Gamma $ – тепловая инерция поверхности, ${{T}_{ \star }}$ – температура подсолнечной точки, ${{\mathcal{E}}_{ \star }} = {{L}_{ \odot }}{\text{/}}(4\pi {{a}^{2}})$ – поток излучения Солнца на гелиоцентрическом расстоянии $a$, ${{L}_{ \odot }} = 3.86 \times {{10}^{{26}}}$ Вт – светимость Солнца, $c = 299792458$ м/с – скорость света, $\sigma = 5.670374419 \times {{10}^{{ - 8}}}$ Вт м^–2 К^–4 – постоянная Стефана–Больцмана, $m$, $R$, $\rho $, $\epsilon $, $K$, $C$ – масса, радиус, объемная плотность, тепловая излучательная способность, теплопроводность и удельная теплоемкость астероида соответственно. Далее, где ${{P}_{{{\text{rev}}}}}$ – период обращения астероида вокруг Солнца, ${{P}_{{{\text{rot}}}}}$ – период его вращения вокруг оси. Кроме того, в (5) амплитуда ${{E}_{{R'}}} = E(\sqrt 2 R{\kern 1pt} ')$ и фаза ${{\delta }_{{R'}}} = \delta (\sqrt 2 R{\kern 1pt} ')$ определены, как и в [17], соотношениями где $i = \sqrt { - 1} $, $x = \sqrt 2 R{\kern 1pt} '$ и вспомогательные функции

С учетом (6) получим

Линейная теплофизическая модель [17] разработана в рамках упрощающих предположений: круговая орбита вокруг Солнца и сферическая форма астероида. Для эллиптической орбиты коэффициент $\Phi $ будет зависеть от гелиоцентрического расстояния $r$ как $\Phi = ({{\Phi }_{0}}r_{0}^{2}){\text{/}}{{r}^{2}}$, где ${{r}_{0}} = 1$ а.е., ${{\Phi }_{0}}$ – это $\Phi $, вычисленное для расстояния 1 а.е. Эта обратная пропорциональность квадрату расстояния уже заложена в наши уравнения движения (2), (3) согласно поставленной во Введении задаче. Далее, заменим среднюю долготу $\lambda $, описывающую положение тела на орбите, на среднюю аномалию $M$ и проведем осреднение по средней аномалии за орбитальный период выражений для тангенциального ${{P}_{\mathfrak{T}}}$ и нормального ${{P}_{\mathfrak{N}}}$ компонентов вектора P, при этом учтем, что

где ${{P}_{r}}$, ${{P}_{t}}$ – радиальная и трансверсальная составляющие вектора P, $f$ – угол, на который надо повернуть вектор скорости до совмещения с трансверсалью (рис. 1), $E$ – эксцентрическая аномалия, $M = E - e\sin E$.

При осреднении мы предположим, что ориентация оси вращения астероида и периоды ${{P}_{{{\text{rev}}}}}$, ${{P}_{{{\text{rot}}}}}$ не изменяются со временем.

Учитывая в (5), что $\Phi = ({{\Phi }_{0}}r_{0}^{2}){\text{/}}{{r}^{2}}$, запишем выражения для ${{P}_{r}}$ и ${{P}_{t}}$ в виде:

Подставим (10) в (8) и приведем подобные слагаемые:

Проведем осредняющую процедуру выражений (11), (12):

и, учитывая результаты, приведенные в Приложении А (ф-лы (A14)), получим тангенциальный и нормальный параметры: где ${{E}_{{R{\kern 1pt} '}}}\cos {{\delta }_{{R{\kern 1pt} '}}}$, ${{E}_{{R{\kern 1pt} '}}}\sin {{\delta }_{{R{\kern 1pt} '}}}$ определены формула-ми (7), ${{I}_{k}}$ выражены рекуррентной формулой: коэффициенты ${{g}_{{1k}}}$, ${{g}_{{2k}}}$ даны в Приложении А (ф‑лы (A7)), их значения при $k = 0{\kern 1pt} - {\kern 1pt} 15$ приведены в таблице 4 Приложения А.

Выражения для радиального, трансверсального и бинормального параметров получены в статье [16]. Запишем их в виде:

Сравнивая (13), (14) c (15), увидим, что тангенциальный и нормальный параметры отличаются от трансверсального и радиального умножением суточного и сезонного компонентов на коэффициенты, зависящие от эксцентриситета. Учитывая выражение (A15) в Приложении, при $e = 0$ получим $ - \mathfrak{N} = S$, $\mathfrak{T} = T$, т.е. для круговых орбит триэдр ($S,\;T,\;W$) совпадает с триэдром ($ - \mathfrak{N},\;\mathfrak{T},\;W$), как и должно быть. При $e = 1$ эллиптическая орбита вырождается в прямолинейное движение и процедура осреднения за орбитальный период теряет смысл, поэтому формулы (13)–(15) неприменимы при $e = 1$.

Замечание 1. Радиальный $S$, трансверсальный T и бинормальный $W$ параметры являются аналогами негравитационных параметров ${{A}_{1}}$, ${{A}_{2}}$ и ${{A}_{3}}$ [20]. Они связаны соотношениями ${{A}_{1}} = S{\text{/}}r_{0}^{2}$, ${{A}_{2}} = T{\text{/}}r_{0}^{2}$, ${{A}_{3}} = W{\text{/}}r_{0}^{2}$, где ${{r}_{0}} = 1$ а.е.

Замечание 2. Выражения (13)–(15) позволяют оценить величину эффекта Ярковского, но требуют знания таких характеристик тела, как диаметр, объемная плотность, скорость вращения, наклон оси вращения к плоскости орбиты, альбедо Бонда, тепловая инерция поверхности, удельная теплоемкость, тепловая излучательная способность.

4. ЭВОЛЮЦИЯ ОРБИТ МОДЕЛЬНЫХ АСТЕРОИДОВ

Рассмотрим модельные объекты с различными эксцентриситетами орбит от 0 до 0.99, при этом все остальные орбитальные и теплофизические характеристики соответствуют астероиду 101 955 Bennu (табл. 1). Найдем для них средние по орбите значения компонентов вектора P, дрейфы элементов и смещение относительно невозмущенного положения в двух системах отсчета. Отметим дрейфы элементов и смещение нижним индексом “1”, если они определены в системе отсчета ${{\mathcal{O}}_{1}}$, и “2” в системе ${{\mathcal{O}}_{2}}$.

Для сравнения также вычислим дрейф средней аномалии и смещение по оценочным формулам, приведенным в [21]:

где $\Delta M$ – изменение средней аномалии в угловых секундах; $\Delta \rho $ – смещение в километрах; ${{\dot {a}}_{4}}$ – дрейф большой полуоси за счет эффекта Ярковского в единицах ${{10}^{{ - 4}}}$ а.е./млн. лет (значения приведены в 8-м столбце табл. 2); ${{\Delta }_{{10}}}t = 119.5479063961725$ – период времени, за который производится оценка, в десятках лет; ${{a}_{{AU}}}$ – большая полуось в астрономических единицах (табл. 1). Оценки (16), (17) получены в системе отсчета ${{\mathcal{O}}_{1}}$, пренебрегая членами четвертого порядка по эксцентриситету.

В табл. 2 приведены тангенциальный $\mathfrak{T}$ и нормальный $\mathfrak{N}$ параметры для различных значений начального эксцентриситета ${{e}_{0}}$. Согласно (15) радиальный $S$ и трансверсальный $T$ параметры не зависят от эксцентриситета, $S = 9.91079 \times $ $ \times \;{{10}^{{ - 14}}}$ а.е.³/сут², $T = - 5.10168 \times {{10}^{{ - 14}}}$ а.е.³/сут² для всех ${{e}_{0}}$. На рис. 2 показано отличие $T$ от $\mathfrak{T}$ в процентном соотношении при ${{e}_{0}} > 0.7$: при ${{e}_{0}} \in (0.7,0.9)$ $T$ превышает $\mathfrak{T}$ на величину от 19 до 58%, а в интервале ${{e}_{0}} \in (0.9,0.99)$ это отличие составляет от 58 до 230%. Аналогично поведение отличия $S$ от $\mathfrak{N}$.

Используя значения компонентов ускорения и формулы (2), (3), найдем изменения средней аномалии $d{{M}_{1}}$, $d{{M}_{2}}$ и большой полуоси $d{{a}_{1}}$, $d{{a}_{2}}$ за 1000 оборотов вокруг Солнца ($ \approx {\kern 1pt} 1195.48$ лет) при различных начальных эксцентриситетах ${{e}_{0}}$ (см. табл. 2). Отличие $d{{M}_{1}}$ от $d{{M}_{2}}$ и $d{{a}_{1}}$ от $d{{a}_{2}}$ менее $1\% $ при малых эксцентриситетах (до 0.5). При ${{e}_{0}}$ от 0.5 до 0.7 их отличие не превышает $6\% $, постепенно увеличиваясь с ростом ${{e}_{0}}$. При ${{e}_{0}} > 0.7$ эти отличия растут экспоненциально от 6 до 160%. В последнем столбце табл. 2 приведено изменение средней аномалии, вычисленное по формуле (16). Сравнение столбцов $d{{M}_{1}}$ и $\Delta M$ дает хорошее согласие этих величин (расхождение не превышает $3\% $).

По известным формулам небесной механики [24] определим смещение $d$ малого тела относительно невозмущенного положения, которое произойдет за счет эффекта Ярковского. Для этого вычислим прямоугольные координаты тела по невозмущенным и возмущенным элементам орбиты, а затем найдем расстояние между этими положениями. В табл. 3 приведены значения смещений ${{d}_{1}}$, ${{d}_{2}}$ за 1000 орбитальных оборотов ($ \approx {\kern 1pt} 1195.48$ лет) при различных ${{e}_{0}}$, а на рис. 3 показано отличие ${{d}_{1}}$ от ${{d}_{2}}$ в процентном соотношении при ${{e}_{0}} > 0.7$. При увеличении начального эксцентриситета от 0.7 до 0.9 превышение смещения ${{d}_{1}}$ над ${{d}_{2}}$ изменяется от 6 до 30%, а при ${{e}_{0}}$ от 0.9 до 0.99 отличие составляет от 30 до 127%.

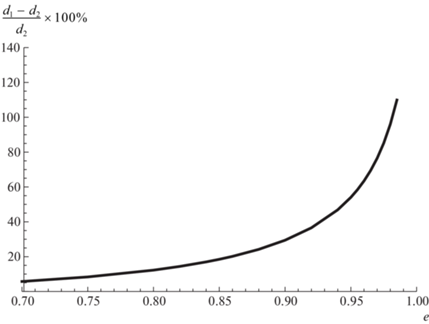
При вычислении смещения ${{d}_{2}}$ учтено также изменение аргумента перицентра $d{{\omega }_{2}}$, но за рассматриваемый период времени оно невелико, менее угловой секунды, и мало зависит от эксцентриситета орбиты. Также малы изменения эксцентриситета $d{{e}_{1}}$, $d{{e}_{2}}$. Если их не учитывать, то смещения ${{d}_{1}}$, ${{d}_{2}}$ изменятся не более, чем на 0.01%. В табл. 3 приведены разности ${{d}_{1}} - d_{1}^{'}$, ${{d}_{2}} - d_{2}^{'}$, где $d_{1}^{'}$, $d_{2}^{'}$ – смещения, вычисленные без учета $d{{e}_{1}}$, $d{{e}_{2}}$. Если же не учитывать также и изменение средней аномалии, то за счет только изменения большой полуоси смещение относительно невозмущенного положения будет незначительным (столбцы $d_{1}^{{''}}$, $d_{2}^{{''}}$ в табл. 3). Также для сравнения в пятом столбце табл. 3 приведено смещение $\Delta \rho $, вычисленное по формуле (17). При ${{e}_{0}} > 0.7$ оценка $\Delta \rho $ превышает ${{d}_{1}}$ в $1.65{\kern 1pt} - {\kern 1pt} 3.2$ раза, а ${{d}_{2}}$ в $1.75{\kern 1pt} - {\kern 1pt} 7.3$ раза, что говорит о том, что оценка смещения, вычисленная по формуле (17), может быть значительно завышена. Это, возможно, объясняет низкое обнаружение эффекта Ярковского непосредственно из астрометрических наблюдений: в базе малых тел JPL среди АСЗ диаметром менее 5 км параметр ${{A}_{2}}$ определен у 45 из 588 объектов с эксцентриситетами орбит до 0.5, и лишь у 18 из 640 объектов с $e > 0.5$, хотя оценочное значение смещения при таких эксцентриситетах больше при прочих равных условиях.

В системе ${{\mathcal{O}}_{2}}$ параметры $\mathfrak{T}$ и $\mathfrak{N}$ постепенно уменьшаются с ростом ${{e}_{0}}$, но несмотря на это уменьшение дрейфы элементов и смещение относительно невозмущенного положения увеличиваются. В системе ${{\mathcal{O}}_{1}}$ рост дрейфов элементов и смещения с ростом ${{e}_{0}}$ значительно больше, чем в ${{\mathcal{O}}_{2}}$, при одинаковых $T$ и $S$ для всех ${{e}_{0}}$. Таким образом, при моделировании эффекта Ярковского радиальным и трансверсальным ускорением оценки дрейфов элементов и смещения относительно невозмущенного положения для объектов с высокоэллиптическими орбитами могут оказаться завышенными. Для таких объектов необходима разработка специальных методов учета эффекта Ярковского.

5. ЗАКЛЮЧЕНИЕ

Выведены выражения для средних за орбитальный период значений тангенциального и нормального компонентов ускорения Ярковского на основе параметров вращения и теплофизических характеристик астероида в рамках линейной теплофизической модели силы Ярковского для сферических астероидов. При $e \to 0$ $\mathfrak{T} \to T$, $\mathfrak{N} \to - S$, как и должно быть. Для эллиптической орбиты тангенциальный и нормальный параметры по абсолютной величине всегда меньше, чем трансверсальный и радиальный, и их отличие растет с ростом эксцентричности орбиты. Дрейфы большой полуоси и средней аномалии, а также смещения относительно невозмущенного положения, вычисленные для двух орбитальных систем отсчета, при малых эксцентриситетах (${{e}_{0}} < 0.5$) почти одинаковые. При ${{e}_{0}} > 0.5$ величины, найденные в системе ${{\mathcal{O}}_{1}}$, всегда больше тех же величин в системе ${{\mathcal{O}}_{2}}$. При ${{e}_{0}}$ от 0.5 до 0.7 отличие умеренное ($ < {\kern 1pt} 6\% $), но постепенно увеличивается, а при $e > 0.7$ наблюдается экспоненциальный рост отличия дрейфов и смещения. Таким образом, при моделировании эффекта Ярковского радиальным и трансверсальным ускорением оценки дрейфов элементов и смещения относительно невозмущенного положения для объектов с высокоэллиптическими орбитами могут оказаться завышенными. Для таких объектов необходима разработка специальных методов учета эффекта Ярковского.