Астрономический журнал, 2022, T. 99, № 8, стр. 619-627
Либрации в двойных барах галактик
Б. П. Кондратьев 1, 2, *, Е. Н. Киреева 1, В. С. Корноухов 1, Н. Г. Трубицына 3
1 Государственный астрономический институт им. П.К. Штернберга
Московский государственный университет им. М.В. Ломоносова
Москва, Россия
2 Главная (Пулковская) Астрономическая обсерватория
Санкт-Петербург, Россия
3 Удмуртский государственный университет
Ижевск, Россия
* E-mail: kond@boris-kondratyev.ru
Поступила в редакцию 19.04.2022
После доработки 09.06.2022
Принята к публикации 21.06.2022
- EDN: EHIUVT
- DOI: 10.31857/S0004629922090067
Аннотация
Разработан новый аналитический метод исследования взаимных поворотных колебаний (либраций) гравитирующих звездных эллипсоидов, образующих двойные бары в дисковых галактиках. Модель двойного бара представлена суперпозицией двух концентрических несоосных эллипсоидов (бар 1 и бар 2), имеющих разные масштабы и массы. Рассмотрены два варианта моделей: с однородными барами и со слоисто-неоднородным внешним баром 2. Для каждой модели получены выражения взаимной гравитационной энергии эллипсоидов и рассчитан момент сил между ними, построены лагранжианы и выводятся дифференциальные уравнения нелинейных либраций баров относительно “срединной” плоскости. Найдены решения этих уравнений, вычислены частоты и периоды либраций как в общем нелинейном случае, так и в приближении гармонических колебаний. Обсуждается приложение метода к изучению динамики других подсистем галактик.
1. ВВЕДЕНИЕ
Бары (перемычки) являются неотъемлемой частью многих дисковых галактик [1, 2]. Как известно, более половины плоских галактик имеют бар, и чем ближе находятся к нам галактики при $z < 1,$ тем чаще они имеют бар [3]. Бары играют важную роль в динамике галактик, и интерес к ним еще более возрос после открытия их сложной структуры; оказалось, что в среднем каждый третий бар может состоять из двух вложенных друг в друга звездных баров, см., например, [4]. В частности, бар в нашей Галактике также имеет сложную структуру [5]. Динамика и устойчивость двойных баров пока полностью не изучены, и их исследование является актуальной задачей [6–8].
В работе [9] была построена фазовая модель звездного цилиндра, вложенного во вращающееся звездное гало. В этой модели было установлено существование сдвиговых течений центроидов вдоль внутренней “трубы”, вследствие чего масса модели могла теряться. В русле этих исследований находится и задача построения модели двойного бара с постоянными массами компонентов.
При постановке задач об эволюции баров важен выбор подходящего метода исследования. Построить нестационарную самосогласованную фазовую модель бара пока не удается из-за значительных математических трудностей. Однако некоторые важные результаты могут быть получены и более простыми методами. В данной работе, как первый шаг к решению проблемы, разработан метод изучения вращательных колебаний (либраций), вложенных друг в друга гравитирующих трехосных звездных баров. Задача сводится к построению лагранжиана, где в качестве потенциального члена используется взаимная гравитационная энергия компонентов двойного бара. Этот метод хорош тем, что производная от взаимной энергии по углу либрации сразу дает момент сил, действующих на внутренний бар со стороны внешнего (справедливо и обратное!). Это позволяет простым и надежным способом выводить дифференциальное уравнение либраций баров относительно друг друга.
В разделе 2 дана постановка задачи, в разделе 3 найдена взаимная гравитационная энергия однородных баров. Лагранжиан для этой задачи получен в разделе 4, где вводится понятие “срединной” плоскости, получено и решено уравнение нелинейных поворотных колебаний баров. В разделе 5 рассматривается задача о взаимной энергии и либрациях баров относительно “срединной” плоскости в случае, когда внешний бар представлен неоднородным эллипсоидом. В разделе 6 результаты обсуждаются.
2. ПОСТАНОВКА ЗАДАЧИ
Бар (перемычка, рукав) состоит в основном из звезд и моделируется вытянутым вдоль главной оси однородным трехосным эллипсоидом. Мы рассматриваем модель двойного бара и полагаем, что меньший по размерам бар 1 имеет границу
(1)
$\frac{{x_{1}^{2}}}{{a_{1}^{2}}} + \frac{{x_{2}^{2}}}{{a_{2}^{2}}} + \frac{{x_{3}^{2}}}{{a_{3}^{2}}} = 1,\quad \left( {{{a}_{1}} > {{a}_{2}} > {{a}_{3}}} \right),$Бар на стадии вековой эволюции находится в слабо неравновесном состоянии. Нас интересует, прежде всего, крупномасштабная нестационарность системы из двух баров в виде их поворотных колебаний относительно друг друга.
Пусть система декартовых координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ связана с главными (штрихованными) полуосями внешнего бара 2, а система $O{{X}_{1}}{{X}_{2}}{{x}_{3}}$ – с полуосями внутреннего бара 1. Ориентация бара 1 относительно осей бара 2 задается углом $\theta \left( t \right)$ (рис. 1).
Рис. 1.
Схема двойного бара, оба компонента которого имеют форму трехосных эллипсоидов с общим центром $O$. Показаны две системы декартовых координат и угол наклона $\theta {\kern 1pt} (t)$ баров друг к другу. Ось $O{{x}_{3}}$ нормальна к плоскости рисунка. Штрихами намечена “срединная линия” и показаны вспомогательные углы наклонов баров ${{\theta }_{1}}(t)$ и ${{\theta }_{2}}(t)$.
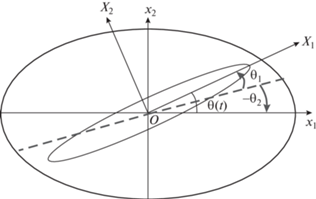
Введенные системы координат связаны соотношениями:
(2)
$\begin{gathered} {{x}_{1}} = {{X}_{1}}\cos \theta - {{X}_{2}}\sin \theta ; \\ {{X}_{1}} = {{x}_{1}}\cos \theta + {{x}_{2}}\sin \theta ; \\ {{x}_{2}} = {{X}_{1}}\sin \theta + {{X}_{2}}\cos \theta ; \\ {{X}_{2}} = {{x}_{2}}\cos \theta - {{x}_{1}}\sin \theta . \\ \end{gathered} $Для проверки формул (2) заметим, что квадрат длины отрезка $x_{1}^{2} + x_{2}^{2} = X_{1}^{2} + X_{2}^{2}$ одинаков в обеих системах координат.
3. ВЗАИМНАЯ ГРАВИТАЦИОННАЯ ЭНЕРГИЯ ДВУХ БАРОВ С ЕДИНЫМ ЦЕНТРОМ
Для решения задачи о либрациях компонентов двойного бара, находящихся в суперпозиции их гравитационных полей, применим метод, основанный на вычислении взаимной гравитационной энергии ${{W}_{{{\text{mut}}}}}$ внутреннего бара 1 (плотность которого ${{\rho }_{1}}$) и внешнего бара 2 плотности ${{\rho }_{2}}.$ В случае однородности обоих компонентов их взаимную энергию можно находить по формуле [10, 11]
(3)
${{W}_{{{\text{mut}}}}} = - {{\rho }_{1}}\iiint\limits_{{{V}_{1}}} {{{\varphi }_{2}}}\left( {{{x}_{i}}} \right)dV,$(4)
${{\varphi }_{2}} = \pi G{{\rho }_{2}}(I{\kern 1pt} '\; - A_{1}^{'}x_{1}^{2} - A_{2}^{'}x_{2}^{2} - A_{3}^{'}x_{3}^{2}),$(5)
$\begin{gathered} I{\kern 1pt} ' = a_{1}^{'}a_{2}^{'}a_{3}^{'}\int\limits_0^\infty {\frac{{ds}}{{\Delta (s)}}} ;\quad A_{i}^{'} = a_{1}^{'}a_{2}^{'}a_{3}^{'}\int\limits_0^\infty {\frac{{ds}}{{(a_{i}^{{'2}} + s)\Delta (s)}}} ; \\ {{\Delta }^{2}}(s) = (a_{1}^{{'2}} + s)(a_{2}^{{'2}} + s)(a_{3}^{{'2}} + s). \\ \end{gathered} $Далее потенциал (4) запишем в системе координат $O{{X}_{1}}{{X}_{2}}{{x}_{3}},$ относящихся к бару 1. Используя формулы (2), получим выражение
(6)
$\begin{gathered} {{\varphi }_{2}} = \pi G{{\rho }_{2}}\left[ {I{\kern 1pt} '\; - A_{1}^{'}{{{\left( {{{X}_{1}}\cos \theta - {{X}_{2}}\sin \theta } \right)}}^{2}} - } \right. \\ \, - \left. {A_{2}^{'}{{{\left( {{{X}_{1}}\sin \theta + {{X}_{2}}\cos \theta } \right)}}^{2}} - A_{3}^{'}x_{3}^{2}} \right], \\ \end{gathered} $(7)
$\begin{gathered} {{\varphi }_{2}} = \pi G{{\rho }_{2}}\left[ {I - (A_{1}^{'}{{{\cos }}^{2}}\theta + A_{2}^{'}{{{\sin }}^{2}}\theta )X_{1}^{2} - } \right. \\ \, - (A_{1}^{'}{{\sin }^{2}}\theta + A_{2}^{'}{{\cos }^{2}}\theta )X_{2}^{2} - \\ \left. { - \;(A_{2}^{'} - A_{1}^{'})\sin 2\theta \cdot {{X}_{1}}{{X}_{2}} - A_{3}^{'}x_{3}^{2}} \right]. \\ \end{gathered} $Подставляя гравитационный потенциал (7) под знак интеграла в (3) и учитывая, что тензор инерции второго порядка однородного эллипсоида равен
(8)
${{I}_{{ij}}} = {{\rho }_{1}}\iiint\limits_{{{V}_{1}}} {{{X}_{i}}{{X}_{j}}}{\kern 1pt} dV = \frac{1}{5}{{M}_{1}}a_{i}^{2}{{\delta }_{{ij}}}$(9)
$\begin{gathered} {{W}_{{{\text{mut}}}}}(\theta ) = \frac{1}{5}\pi G{{\rho }_{2}}{{M}_{1}}\left[ {{\text{(}}A_{1}^{'}a_{1}^{2} + A_{2}^{'}a_{2}^{2}{\text{)}}{{{\cos }}^{2}}\theta + } \right. \\ \, + \left. {(A_{1}^{'}a_{2}^{2} + A_{2}^{'}a_{1}^{2}){{{\sin }}^{2}}\theta + A_{3}^{'}a_{3}^{2} - 5I{\kern 1pt} '} \right]. \\ \end{gathered} $В частности, для $\theta = 0,$ когда большая ось $O{{X}_{1}}$ бара 1 совпадает с осью $O{{x}_{1}}$ бара 2, взаимная энергия принимает свое минимальное (максимальное по модулю) значение
(10)
$W_{{{\text{mut}}}}^{0}(\theta ) = \frac{1}{5}\pi G{{\rho }_{2}}{{M}_{1}}{\kern 1pt} \left[ {A_{1}^{'}a_{1}^{2} + A_{2}^{'}a_{2}^{2} + A_{3}^{'}a_{3}^{2} - 5I{\kern 1pt} '} \right].$Далее примем $W_{{{\text{mut}}}}^{0}(\theta )$ за точку отсчета взаимной энергии и составим разность
(11)
${{\tilde {W}}_{{{\text{mut}}}}}(\theta ) = {{W}_{{{\text{mut}}}}}(\theta ) - W_{{{\text{mut}}}}^{0}.$После простых преобразований в (11) находим
(12)
${{\tilde {W}}_{{{\text{mut}}}}}(\theta ) = \frac{1}{5}\pi G{{\rho }_{2}}{{M}_{1}}(A_{2}^{'} - A_{1}^{'})(a_{1}^{2} - a_{2}^{2}){{\sin }^{2}}\theta .$Отметим, что в формуле (12) присутствует только член, зависящий от угла $\theta ,$ причем коэффициент при ${{\sin }^{2}}\theta $ обращается в нуль в двух случаях: (i) при осевой симметрии внешнего бара 2 (когда $A_{1}^{'} = A_{2}^{'}$), а также (ii), когда бар 1 имеет круговую симметрию ${{a}_{1}} = {{a}_{2}}.$ Очевидно, в обоих случаях либрации компонентов бара отсутствуют.
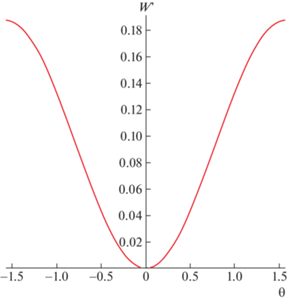
График формулы (12) показан на рис. 2. Из него видно, что минимум взаимной энергии достигается, когда большие оси обоих баров совпадают. Из этого рисунка также следует, что в интервале углов $ - \frac{\pi }{2} < \theta < \frac{\pi }{2}$ система баров находится в потенциальной яме, причем нормированная взаимная энергия имеет свой локальный минимум при $\theta = 0.$ Это означает, что либрацию бара 1 можно представить как колебания материальной точки, перекатывающейся в поле тяжести внутри вогнутой чаши. Такие поворотные колебания бара являются устойчивыми.
Рис. 2.
Зависимость нормированной взаимной гравитационной энергии $W{\kern 1pt} ' = \frac{{{{{\tilde {W}}}_{{{\text{mut}}}}}(\theta )}}{{\frac{1}{5}\pi G{{\rho }_{2}}{{M}_{1}}a_{1}^{2}}}$ двух баров от угла ориентации $\theta .$ Для расчетов взяты значения $A_{1}^{'} = 0.15;$ $A_{2}^{'} = 0.4;$ $n = \frac{{{{a}_{2}}}}{{{{a}_{1}}}} = 0.5$.
Рассмотрим подробнее поворотные либрации баров 1 и 2 друг относительно друга.
4. МОМЕНТ СИЛ И УРАВНЕНИЯ ЛИБРАЦИИ КОМПОНЕНТОВ В ДВОЙНОМ БАРЕ
При изучении взаимных либраций баров 1 и 2 применим метод, разработанный в работе Кондратьева [13]. Согласно этому методу, момент сил ${\mathbf{M}}$, действующих на бар 1 со стороны бара 2, мы находим через вычисление производной от функции взаимной энергии компонентов баров по углу либрации $\theta $. В нашем случае единственный отличный от нуля третий компонент момента сил будет равен:
где ${{\tilde {W}}_{{{\text{mut}}}}}$ из (12).Далее исходим из того, что в процессе поворотных колебаний баров 1 и 2 относительно оси $O{{x}_{3}}$ их суммарный угловой момент сохраняется
(14)
$\begin{gathered} I_{3}^{{\left( 1 \right)}}{{{\dot {\theta }}}_{1}} + I_{3}^{{\left( 2 \right)}}{{{\dot {\theta }}}_{2}} = 0;\quad I_{3}^{{\left( 1 \right)}} = \frac{1}{5}{{M}_{1}}(a_{1}^{2} + a_{2}^{2}), \\ I_{3}^{{\left( 2 \right)}} = \frac{1}{5}{{M}_{2}}(a_{1}^{{'2}} + a_{2}^{{'2}}). \\ \end{gathered} $Интегрируя (14), получим
По условию задачи, при ${{\theta }_{1}} = 0$ должно быть и ${{\theta }_{2}} = 0$, поэтому в (15) следует положить $C = 0.$ Таким образом, для вспомогательных углов ${{\theta }_{1}}(t)$ и ${{\theta }_{2}}(t)$ имеем два уравнения
(16)
$\begin{gathered} {{\theta }_{1}} - {{\theta }_{2}} = \theta , \\ I_{3}^{{\left( 1 \right)}}{{\theta }_{1}} + I_{3}^{{\left( 2 \right)}}{{\theta }_{2}} = 0, \\ \end{gathered} $(17)
${{\theta }_{1}} = \frac{\theta }{{1 + \frac{{I_{3}^{{\left( 1 \right)}}}}{{I_{3}^{{\left( 2 \right)}}}}}},\quad - {{\theta }_{2}} = \frac{\theta }{{1 + \frac{{I_{3}^{{\left( 2 \right)}}}}{{I_{3}^{{\left( 1 \right)}}}}}}.$Для нахождения периода колебаний баров составим лагранжиан
где $K$ – кинетическая энергия колебаний, а ${{W}_{{{\text{mut}}}}}$ – потенциальная энергия системы двух баров. Кинетическая энергия будет равна(19)
$K = \frac{1}{2}I_{3}^{{\left( 1 \right)}}\dot {\theta }_{1}^{2} + \frac{1}{2}I_{3}^{{\left( 2 \right)}}\dot {\theta }_{2}^{2} = \frac{1}{2}{{\dot {\theta }}^{2}}\frac{{I_{3}^{{\left( 1 \right)}} \cdot I_{3}^{{\left( 2 \right)}}}}{{I_{3}^{{\left( 1 \right)}} + I_{3}^{{\left( 2 \right)}}}},$Таким образом, оставляя для системы баров только ту часть лагранжиана $L\left( \theta \right),$ которая зависит от угла $\theta ,$ имеем редуцированный лагранжиан в виде
(20)
$\begin{gathered} L(\theta ) = K - {{{\tilde {W}}}_{{{\text{mut}}}}} = \frac{1}{2}{{{\tilde {I}}}_{3}}{{\left( {\frac{{d\theta }}{{dt}}} \right)}^{2}} - \\ - \;\frac{1}{5}\pi G{{\rho }_{2}}{{M}_{1}}\left[ {(A_{2}^{'} - A_{1}^{'})(a_{1}^{2} - a_{2}^{2}){{{\sin }}^{2}}\theta } \right], \\ \end{gathered} $(21)
${{\tilde {I}}_{3}} = \frac{{I_{3}^{{\left( 1 \right)}} \cdot I_{3}^{{\left( 2 \right)}}}}{{I_{3}^{{\left( 1 \right)}} + I_{3}^{{\left( 2 \right)}}}}.$Обратимся теперь ко второму уравнению движения Лагранжа
где член $\frac{{dL}}{{d\theta }}$ равен моменту сил в левой части (13). Подставляя в (22) лагранжиан из (20), в итоге получим искомое дифференциальное уравнение колебаний для угла $\theta {\kern 1pt} (t)$:Входящая в (23) величина ${{\omega }^{2}}$ имеет размерность квадрата частоты колебаний и связана с характеристиками обоих баров
(24)
${{\omega }^{2}} = \pi G{{\rho }_{2}}\frac{{a_{1}^{2} - a_{2}^{2}}}{{a_{1}^{2} + a_{2}^{2}}}(A_{2}^{'} - A_{1}^{'})\left( {1 + \frac{{{{M}_{1}}}}{{{{M}_{2}}}}\frac{{a_{1}^{2} + a_{2}^{2}}}{{a{{{_{1}^{'}}}^{2}} + a{{{_{2}^{'}}}^{2}}}}} \right).$Дифференциальное уравнение (23) дает решение поставленной задачи о нелинейных либрациях в двойном однородном баре.
В частности, при малых $\theta $ либрации бара описываются уравнением гармонических колебаний
Замечание 1. В данной работе вначале рассмотрим случай малых (гармонических) вращательных колебаний компонентов двойного бара. Общий случай нелинейных вращательных колебаний, представленных уравнением (23), будет рассмотрен в разделе 5.
Частота указанных малых колебаний есть
(26)
$\begin{gathered} \kappa = \sqrt 2 \omega = \\ = \sqrt {2\pi G{{\rho }_{2}}\frac{{a_{1}^{2} - a_{2}^{2}}}{{a_{1}^{2} + a_{2}^{2}}}(A_{2}^{'} - A_{1}^{'})\left( {1 + \frac{{{{M}_{1}}}}{{{{M}_{2}}}}\frac{{a_{1}^{2} + a_{2}^{2}}}{{a{{{_{1}^{'}}}^{2}} + a{{{_{2}^{'}}}^{2}}}}} \right)} , \\ \end{gathered} $Решение уравнения (25) имеет вид
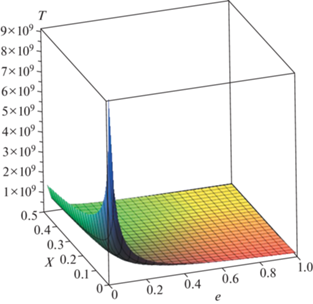
На рис. 3 показано $3D$ изображение формулы (27).
Рис. 3.
3D изображение периода ${{T}_{0}}$ (в земных годах) гармонических либраций компонентов двойного бара. Здесь $e = \sqrt {1 - \frac{{a_{2}^{2}}}{{a_{1}^{2}}}} $ есть эксцентриситет экваториального сечения внутреннего бара, а $x = A_{2}^{'} - A_{1}^{'}$ – разность коэффициентов потенциала для внешнего бара 2. Расчет сделан по формуле (27), в которой взято ${{\rho }_{2}} = 7.5\;{{M}_{ \odot }}\;{\text{п}}{{{\text{к}}}^{{ - 3}}} \approx 5 \times {{10}^{{ - 22}}}\;{\text{г/с}}{{{\text{м}}}^{3}}$ и $\frac{{I_{3}^{{\left( 1 \right)}}}}{{I_{3}^{{\left( 2 \right)}}}} = \frac{1}{3}$.
Для примера, возьмем следующие относительные размеры компонентов в двойном баре:
(29)
$a_{1}^{'} = {\text{\;3,}}\quad a_{2}^{'} = {\text{\;2,}}\quad a_{3}^{'} = {\text{\;1;}}\quad n = \frac{{{{a}_{2}}}}{{{{a}_{1}}}} = \frac{2}{3}.$Тогда коэффициенты внутреннего потенциала однородного гало, рассчитанные по формулам (5), будут равны
(30)
$A_{1}^{'} = {\text{0}}{\text{.3126014}};\quad A_{2}^{'} = {\text{0}}{\text{.5343081}}{\text{.}}$Среднюю плотность бара 2 возьмем равной ${{\rho }_{2}} \approx 5 \times {{10}^{{ - 22}}}\;\frac{{\text{г}}}{{{\text{с}}{{{\text{м}}}^{3}}}}.$ Тогда по формулам (26) и (27) находим период малых либраций
Найденный в (31) период малых либрационных колебаний бара равен примерно 44 млн. лет, что примерно в 5 раз меньше, чем вращение Солнца вокруг центра Галактики. Далее в разде-ле 5 мы покажем, что учет неоднородности бара 2 может заметно замедлить процесс колебаний компонентов двойного бара и увеличить период их либраций.
При больших амплитудах ${{\theta }_{0}}$ бар, согласно уравнению (23), совершает нелинейные колебания, частота и период которых равны
Здесь $K(\kappa )$ – стандартный полный эллиптический интеграл первого рода. С хорошей точностью период нелинейный колебаний с амплитудой ${{\theta }_{0}}$ может быть представлен формулой
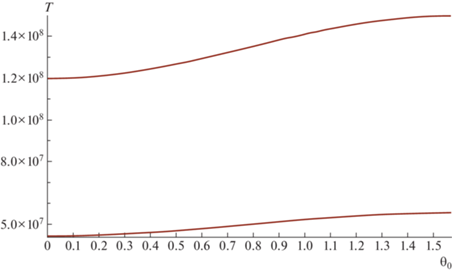
где ${{T}_{0}}$ дано в (27). Расчет периода нелинейных колебаний как функции от амплитуды показан на рис. 4.Рис. 4.
Период нелинейных колебаний $T$ компонентов двойного бара как функция от амплитуды ${{\theta }_{0}}$. Расчет по формуле (33). Нижняя кривая – для однородных баров 1 и 2 с коэффициентом ${{T}_{0}}$ из (31), верхняя кривая – для модели “однородный бар 1 – неоднородный бар 2” с коэффициентом ${{T}_{0}}$ из (57).
5. ЛИБРАЦИИ КОМПОНЕНТОВ ПРИ НЕОДНОРОДНОМ ВНЕШНЕМ БАРЕ 2
5.1. Плотность и внутренний потенциал в баре 2
В качестве другой модели бара 2 рассмотрим неоднородный трехосный эллипсоид с параболическим законом плотности $\rho \left( m \right)$ и массой ${{M}_{2}}$
(34)
$\begin{gathered} \rho = {{\rho }_{0}}(1 - {{m}^{2}}); \\ {{m}^{2}} = \frac{{x_{1}^{2}}}{{a{{{_{1}^{'}}}^{2}}}} + \frac{{x_{2}^{2}}}{{a{{{_{2}^{'}}}^{2}}}} + \frac{{x_{3}^{2}}}{{a{{{_{3}^{'}}}^{2}}}};\quad {{M}_{{\text{H}}}} = \frac{8}{{15}}\pi a_{1}^{'}a_{2}^{'}a_{3}^{'}{{\rho }_{0}}. \\ \end{gathered} $Замечание 2. Эллипсоид с параболическим законом плотности (34) является одним из самых простых после однородного. Мы рассмотрим его в качестве примера, чтобы оценить влияние неоднородности на взаимную энергию системы “бар 1–бар 2” и на период либраций компонентов бара. В техническом плане расчеты для этой модели более сложные, чем для модели с однородными компонентами.
Внутренний потенциал такого слоисто-неоднородного эллипсоида дается формулой (см. [14], а также [10, 11])
(35)
$\varphi (x) = \frac{1}{2}\pi G{{\rho }_{0}}a_{1}^{'}a_{2}^{'}a_{3}^{'}\int\limits_0^\infty {\frac{{ds}}{{\Delta (s)}}} {{\left( {1 - \sum\limits_1^3 {\frac{{x_{i}^{2}}}{{a_{i}^{{'2}} + s}}} } \right)}^{2}},$(36)
$\begin{gathered} {{\varphi }_{2}} = \frac{1}{2}\pi G{{\rho }_{0}}\left\{ {I{\kern 1pt} '\; - 2A_{1}^{'}x_{1}^{2} - 2A_{2}^{'}x_{2}^{2} - 2A_{3}^{'}x_{3}^{2}} \right. + \\ \, + A_{{11}}^{'}x_{1}^{4} + A_{{22}}^{'}x_{2}^{4} + A_{{33}}^{'}x_{3}^{4} + \\ \,\left. { + 2A_{{12}}^{'}x_{1}^{2}x_{2}^{2} + 2A_{{13}}^{'}x_{1}^{2}x_{3}^{2} + 2A_{{23}}^{'}x_{2}^{2}x_{3}^{2}} \right\}. \\ \end{gathered} $Напомним, что здесь ${{\varphi }_{2}}$ есть потенциал бара 2; коэффициенты $A_{i}^{'}$ даны в (5), а двойные индексы Чандрасекара [12] равны
(37)
$A_{{ij}}^{'} = a_{1}^{'}a_{2}^{'}a_{3}^{'}\int\limits_0^\infty {\frac{{ds}}{{(a_{i}^{{'2}} + s)(a_{j}^{{'2}} + s)\Delta (s)}}} .$Подставляя в (36) формулы (2), получим выражение потенциала внутри эллипсоида бара 2 в виде
(38)
$\begin{gathered} {{\varphi }_{{\text{H}}}} = \frac{1}{2}\pi G{{\rho }_{0}}\left\{ {I + A_{{33}}^{'}x_{3}^{4} + {{R}_{{1111}}}X_{1}^{4} + {{R}_{{2222}}}X_{2}^{4} + } \right. \\ \, + {{R}_{{1122}}}X_{1}^{2}X_{2}^{2} + {{R}_{{1133}}}X_{1}^{2}x_{3}^{2} + {{R}_{{2233}}}X_{2}^{2}x_{3}^{2} - \\ \left. {\, - {{R}_{{22}}}X_{2}^{2} - {{R}_{{11}}}X_{1}^{2} - 2A_{2}^{'}x_{3}^{2}} \right\}. \\ \end{gathered} $Входящие сюда коэффициенты равны
(39)
${{R}_{{2222}}} = ~A_{{11}}^{'}{{\sin }^{4}}\theta + 2A_{{12}}^{'}{{\cos }^{2}}\theta {{\sin }^{2}}\theta + A_{{22}}^{'}{{\cos }^{4}}\theta ;$Замечание 3. В (39) не включены три несимметричных члена ${{R}_{{{\text{1112}}}}}$, ${{R}_{{{\text{1222}}}}},$ ${{R}_{{{\text{1233}}}}},$ так как при последующем интегрировании по симметричному объему внутреннего эллипсоидального бара 1 эти члены дают ноль.
5.2. Взаимная энергия однородного бара 1 и неоднородного бара 2
Чтобы не усложнять объем выкладок, бар 1 по-прежнему считаем однородным. Для нахождения взаимной энергии системы “бар 1 – бар 2” подставим гравитационный потенциал (38) под знак интеграла в (3). Интегрируя по объему бара 1 и учитывая (8), а также формулы
(40)
$\begin{gathered} {{I}_{{iijj}}} = {{\rho }_{b}}\iiint\limits_{{{V}_{b}}} {X_{i}^{2}X_{j}^{2}dV} = \frac{1}{{35}}{{M}_{b}}a_{i}^{2}a_{j}^{2}, \\ ij = 1122,\;1133,\;2233; \\ \end{gathered} $(41)
$\begin{gathered} {{W}_{{{\text{mut}}}}} = - \frac{1}{{10}}\pi G{{\rho }_{0}}{{M}_{b}}\left\{ {5I - {{R}_{{11}}}a_{1}^{2} - {{R}_{{22}}}a_{2}^{2}\mathop - \limits_{_{{_{{}}}}} } \right. \\ \, - 2A_{3}^{'}a_{3}^{2} + \frac{3}{7}A_{{33}}^{'}a_{3}^{4} + \frac{3}{7}{{R}_{{1111}}}a_{1}^{4} + \frac{3}{7}{{R}_{{2222}}}a_{2}^{4} + \\ \, + \left. {\frac{1}{7}{{R}_{{1122}}}a_{1}^{2}a_{2}^{2} + \frac{1}{7}{{R}_{{1133}}}a_{1}^{2}a_{3}^{2} + \frac{1}{7}{{R}_{{2233}}}a_{2}^{2}a_{3}^{2}} \right\}. \\ \end{gathered} $Подставляя далее в (41) коэффициенты из (39), после преобразований находим
(42)
$\begin{gathered} {{W}_{{{\text{mut}}}}} = - \frac{1}{{10}}\pi G{{\rho }_{0}}{{M}_{b}}\left\{ {{{S}_{4}}{{{\sin }}^{4}}\theta + {{{\text{C}}}_{4}}{{{\cos }}^{4}}\theta + } \right. \\ + \;\left. {{\text{CS}}{{{\cos }}^{2}}\theta {{{\sin }}^{2}}\theta + {{{\text{S}}}_{2}}{{{\sin }}^{2}}\theta + {{{\text{C}}}_{2}}{{{\cos }}^{2}}\theta + R} \right\}. \\ \end{gathered} $Здесь для краткости введены следующие обозначения:
(43)
$\begin{gathered} CS = \frac{6}{7}A_{{12}}^{'}a_{1}^{4} + \frac{6}{7}A_{{12}}^{'}a_{2}^{4} + \frac{1}{7}(6A_{{11}}^{'} - 8A_{{12}}^{'} + 6A_{{22}}^{'})a_{1}^{2}a_{2}^{2}; \\ {{S}_{2}} = - 2A_{1}^{'}a_{2}^{2} + \frac{2}{7}A_{{13}}^{'}a_{2}^{2}a_{3}^{2} + \frac{2}{7}A_{{23}}^{'}a_{1}^{2}a_{3}^{2} - 2A_{2}^{'}a_{1}^{2}; \\ \end{gathered} $При $\theta = 0$ (см. также раздел 2), когда наибольшие оси баров $O{{x}_{1}}$ совпадают, взаимная энергия (42) принимает свое минимальное (максимальное по модулю) значение:
(44)
$W_{{{\text{mut}}}}^{0}(\theta = 0) = - \frac{1}{{10}}\pi G{{\rho }_{0}}{{M}_{b}}\left[ {{{C}_{4}} + {{C}_{2}} + R} \right].$Составляя по аналогии с разделом 2 разность
(45)
${{\tilde {W}}_{{{\text{mut}}}}}(\theta ) = {{W}_{{{\text{mut}}}}}(\theta ) - W_{{{\text{mut}}}}^{0},$(46)
${{\tilde {W}}_{{{\text{mut}}}}}(\theta ) = \frac{1}{{10}}\pi G{{\rho }_{0}}{{M}_{b}}\left\{ {{{D}_{4}}{{{\sin }}^{4}}\theta + {{D}_{2}}{{{\sin }}^{2}}\theta } \right\},$(47)
$\begin{gathered} {{D}_{2}} = 2{{C}_{4}} - CS + {{C}_{2}} - {{S}_{2}} \geqslant 0; \\ {{D}_{4}} = CS - {{S}_{4}} - {{C}_{4}} \geqslant 0. \\ \end{gathered} $Замечание 4. Проверка выражения (46) подтверждает: в случае круговой симметрии внутреннего бара ${{a}_{1}} = {{a}_{2}}$ действительно выполняются равенства
и тогда взаимные либрации баров исчезают. Но и в случае трехосного бара 1 ${{a}_{1}} \ne {{a}_{2}},$ помещенного в бар 2 с круговой симметрией, когда либраций также не будет.5.3. Лагранжиан и уравнение либраций
Момент сил, действующих со стороны внешнего бара на внутренний бар, согласно формуле (13), будет теперь равен:
(50)
$M = \frac{1}{{10}}\pi G{{\rho }_{0}}{{M}_{b}}\left( {{{D}_{2}} + 2{{D}_{4}}{{{\sin }}^{{\text{2}}}}\theta } \right)\sin 2\theta .$Кинетическая энергия колебательного движения системы баров (сравните с разделом 3) также изменится и будет теперь равна
(51)
$\begin{gathered} K = \frac{1}{2}I_{3}^{{\left( 1 \right)}}\dot {\theta }_{1}^{2} + \frac{1}{2}I_{3}^{{\left( 2 \right)}}\dot {\theta }_{2}^{2} = \frac{1}{2}{{{\dot {\theta }}}^{2}}\frac{{I_{3}^{{\left( 1 \right)}} \cdot I_{3}^{{\left( 2 \right)}}}}{{I_{3}^{{\left( 1 \right)}} + I_{3}^{{\left( 2 \right)}}}}, \\ I_{3}^{{\left( 1 \right)}} = \frac{1}{5}{{M}_{1}}(a_{1}^{2} + a_{2}^{2}),\quad ~I_{3}^{{\left( 2 \right)}} = \frac{1}{7}{{M}_{2}}(a_{1}^{{'2}} + a_{2}^{{'2}}). \\ \end{gathered} $Составим лагранжиан для системы $L(\theta )$:
(52)
$\begin{gathered} L(\theta ) = K - {{{\tilde {W}}}_{{{\text{mut}}}}} = \frac{1}{2}\frac{{I_{3}^{{\left( 1 \right)}} \cdot I_{3}^{{\left( 2 \right)}}}}{{I_{3}^{{\left( 1 \right)}} + I_{3}^{{\left( 2 \right)}}}}{{\left( {\frac{{d\theta }}{{dt}}} \right)}^{2}} - \\ - \;\frac{1}{{10}}\pi G{{\rho }_{0}}{{M}_{1}}\left[ {{{D}_{4}}{{{\sin }}^{4}}\theta + {{D}_{2}}si{{n}^{2}}\theta } \right]. \\ \end{gathered} $С учетом лагранжиана (52), второе уравнение движения Лагранжа (22) дает дифференциальное уравнение колебаний для угла $\theta {\kern 1pt} (t)$:
(53)
$\begin{gathered} \ddot {\theta } + \frac{{\pi G{{\rho }_{0}}}}{{2(a_{1}^{2} + a_{2}^{2})}}\left[ {1 + \frac{{I_{3}^{{\left( 1 \right)}}}}{{I_{3}^{{\left( 2 \right)}}}}} \right] \times \\ \times \;\left( {{{D}_{2}} + 2{{D}_{4}}{{{\sin }}^{2}}\theta } \right)\sin 2\theta = 0. \\ \end{gathered} $Новое уравнение нелинейных колебаний (53) отличается от полученного ранее уравнения для системы однородных баров (23).
Численные расчеты мы проведем для приемлемых относительных значений полуосей бара 2 и бара 1
(54)
$\begin{gathered} a_{1}^{'} = ~3,~\quad a_{2}^{'} = ~2,\quad a_{3}^{'} = ~1; \\ {{a}_{1}} = 1,\quad {{a}_{2}} = ~2{\text{/}}3,\quad {{a}_{3}} = ~1{\text{/}}3. \\ \end{gathered} $Соответствующие коэффициенты $A_{i}^{'},\;A_{{ij}}^{'},\;{{D}_{2}},\;{{D}_{4}}$ и другие приведены в табл. 1. Коэффициенты потенциала с двойными индексами из (37) были найдены численно.
Таблица 1.
Коэффициенты внутреннего потенциала однородного $(A_{1}^{'},A_{2}^{'},A_{3}^{'})$ и неоднородного (третий, четвертый и пятый столбцы) трехосного эллипсоидального бара 2. Также приводятся коэффициенты ${{D}_{2}}$ и ${{D}_{4}},$ используемые в уравнении нелинейных колебаний (53)
| $a_{1}^{'} = {\text{3,\;}}$$a_{2}^{'} = {\text{2,}}$$a_{3}^{'} = {\text{1;\;}}$${\text{\;}}{{a}_{1}} = {\text{1,}}$${{a}_{2}} = {\text{2/3,}}$${{a}_{3}} = {\text{1/3}}{\text{.}}$ | $A_{1}^{'} = {\text{0}}{\text{.3126014,}}$$A_{2}^{'} = {\text{0}}{\text{.5343081,}}$$A_{3}^{'} = {\text{1}}{\text{.1530905,}}$ | $A_{{11}}^{'} = {\text{0}}{\text{.0242733}}$$A_{{12}}^{'} = {\text{0}}{\text{.0443413}}$$A_{{13}}^{'} = {\text{0}}{\text{.1050611}}$$A_{{23}}^{'} = {\text{0}}{\text{.2062608}}$$A_{{22}}^{'} = {\text{0}}{\text{.0831326}}$$A_{{33}}^{'} = {\text{0}}{\text{.562893}}$ | ${\text{S4}} = {\text{0}}{\text{.0433138}}$${\text{C4}} = {\text{0}}{\text{.0205228}}$${\text{CS}} = {\text{0}}{\text{.063908}}$${\text{S2}} = - {\text{1}}{\text{.338454}}$${\text{C2}} = - {\text{1}}{\text{.093898}}$ | ${{D}_{2}} = {\text{0}}{\text{.2216933}}$${{D}_{4}} = {\text{0}}{\text{.0000717}}$ |
Выясняется, что $\frac{{2{{D}_{4}}}}{{{{D}_{2}}}} \sim {{10}^{{ - 3}}}$; поэтому, ввиду малости коэффициента ${{D}_{4}},$ членом $2{{D}_{4}}{{\sin }^{2}}\theta $ в правой части (53) можно пренебречь, и тогда с хорошим приближением уравнение нелинейных колебаний представим в виде
(55)
$\ddot {\theta } + \frac{{\pi G{{\rho }_{0}}{{D}_{2}}}}{{2(a_{1}^{2} + a_{2}^{2})}}\left[ {1 + \frac{{I_{3}^{{\left( 1 \right)}}}}{{I_{3}^{{\left( 2 \right)}}}}} \right]\sin 2\theta = 0.$В линейном приближении по $\theta $ уравнение (55) примет вид
(56)
$\ddot {\theta } + \frac{{\pi G{{\rho }_{0}}}}{{a_{1}^{2} + a_{2}^{2}}}{{D}_{2}}\left[ {1 + \frac{{I_{3}^{{\left( 1 \right)}}}}{{I_{3}^{{\left( 2 \right)}}}}} \right]\theta = 0.$Период малых либраций, согласно уравне-нию (56), равен
(57)
${{T}_{0}} = \frac{{2\pi }}{{\sqrt {\frac{{\pi G{{\rho }_{0}}}}{{a_{1}^{2} + a_{2}^{2}}}\left[ {1 + \frac{{I_{3}^{{\left( 1 \right)}}}}{{I_{3}^{{\left( 2 \right)}}}}} \right]{{D}_{2}}} }}.$Учитывая поправку за неоднородность (37), вместо прежней оценки $\frac{{I_{3}^{{\left( 1 \right)}}}}{{I_{3}^{{\left( 2 \right)}}}} = \frac{1}{3}$ теперь имеем
Тогда по формуле (57) получим период малых либраций
Заметим, найденный период малых либраций оказывается в 2.7 раза длиннее, чем период либраций однородных баров.
Период нелинейных либраций бара 1 в неоднородном баре 2 рассчитывается по найденной выше формуле (33), в которой ${{T}_{0}}$ из (57), см. рис. 4.
6. ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ
В данной работе разработан новый аналитический метод для изучения взаимных поворотных колебаний (либраций) гравитирующих звездных эллипсоидов, образующих двойные бары в дисковых галактиках. Модель двойного бара представлена суперпозицией двух концентрических несоосных эллипсоидов, вложенных друг в друга и имеющих разные размеры и массы. Отметим, что движение звезд в эллипсоидальных компонентах двойного бара является (в звездно-динамическом смысле) бесстолкновительным, вследствие чего бары не вытесняют материю друг друга и представляют собой взаимопроникающую суперпозицию компонентов. Такие модели с суперпозицией потенциалов нескольких компонентов (гало-бар-диск) часто используются в динамике звездных систем, см., например, [5, 15].
Мы рассмотрели два случая: модель с однородными эллипсоидами и технически более сложную модель с неоднородным внешним баром 2. Для каждой модели получены выражения взаимной гравитационной энергии эллипсоидальных компонентов и рассчитан момент сил между ними. Алгоритм вычисления момента сил в данном методе очень простой – для этого достаточно найти производную от взаимной энергии по углу либрации. Это заметно упрощает вывод дифференциальных уравнений нелинейных либраций баров относительно их “срединной” плоскости.
Так как колебания в общем случае нелинейные, то при изучении динамики двойных баров важным является вопрос правильной оценки из наблюдений взаимной ориентации составляющих его трехосных компонентов.
Изучение глобальных либраций в двойных барах актуально в связи с тем, что несмотря на заметный прогресс в изучении образования и эволюции плоских галактик, исследователи до сих пор не пришли к согласию в вопросе о доминирующем механизме образования баров, в том числе и двойных (о механизмах образования бар-мод см., например, [16]). Так как бар-мода является самой крупномасштабной, изучение динамики и эволюции галактик удобно начинать с изучения именно баров.
В данной работе найдены решения уравнений либрации компонентов двойного бара, причем как для нелинейного случая, так и в приближении гармонических колебаний. Были вычислены частоты и периоды либраций компонентов двойного бара. Установлено, что периоды либраций компонентов в двойном баре составляют десятки миллионов земных лет. С учетом неоднородности в распределении плотности у компонентов бара, периоды таких либраций могут, по-видимому, быть близкими к периодам движения звезд в окрестностях двойного бара. Весьма желательны поэтому прямая наблюдательная проверка данных эффектов и проведение дальнейших исследований с уточнением структуры компонентов в двойных барах.
Выше отмечалось, что кроме вращательных либраций существуют и другие механизмы взаимодействия бара с внешними подсистемами в галактиках. Так, эффект замедления вращения бара возможен как за счет передачи углового момента звездам [2], так и за счет влияния динамического трения между баром и гало [17]. Существует и так называемый “buckling” – эффект изменения формы бара [18], приводящий к округлению его формы и к дополнительному разогреву звездного диска. Предложенный в нашей работе метод расчета момента сил на бар указывает на существование еще одного механизма, влияющего на вращение (торможение или ускорение) бара через гравитационное влияние на него внешнего гало.
Список литературы
J. A. Sellwood and A. Wilkinson, Reports on Progress in Physics, 56, 173 (1993).
E. Athanassoula, Monthly Not. Roy. Astron. Soc. 341, 117903 (2003).
T. Kim, E. Athanassoula, K. Sheth, et al., Astrophys. J. 922, 196 (2021).
P. Erwin, Astron. and Astrophys. 415, 941 (2004).
M. C. Sormani, O. Gerhard, M. Portail, et al., Monthly Not. Roy. Astron. Soc. 514, L1 (2022).
K. Saha and W. Maciejewski, Monthly Not. Roy. A-stron. Soc. 433, L44 (2013).
H. Wozniak, Astron. and Astrophys. 575, A7 (2015).
A. de Lorenzo-Caceres, J. Mendez-Abreu, B. Thorne, and L. Costantin, Monthly Not. Roy. Astron. Soc. 484, 665 (2019).
B. P. Kondratyev and E. N. Kireeva, Baltic Astronomy 25, 247 (2016).
Б. П. Кондратьев, Динамика эллипсоидальных гравитирующих фигур (М.: Наука, 1989).
Б. П. Кондратьев, Теория потенциала. Новые методы и задачи с решениями (М.: Мир, 2007).
S. Chandrasekhar, Ellipsoidal Figures of Equilibrium (Yale University Press, New Haven, 1969).
B. P. Kondratyev, Solar System Research 46, 352 (2014).
B. P. Kondratyev, Soviet Astron. 26, 279 (1982).
A. T. Bajkova and V. V. Bobylev, Astron. Rep., 65, 737 (2021).
E. V. Polyachenko, Astron. Lett., 39, 72 (2013).
J. A. Sellwood, Astrophys. J., 637, 567 (2006).
R. Chiba and R. Schönrich, Monthly Not. Roy. Astron. Soc., 505, 2412 (2021).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


