1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 99, № 9, 2022

Астрономический журнал, 2022, T. 99, № 9, стр. 755-766

Моделирование тепловых поверхностных волн в протопланетном диске в двумерном приближении

Я. Н. Павлюченков 1, *, Л. А. Максимова 1, В. В. Акимкин 1

1 Институт астрономии Российской академии наук
Москва, Россия

* E-mail: pavyar@inasan.ru

Поступила в редакцию 10.06.2022
После доработки 11.08.2022
Принята к публикации 30.08.2022

Полный текст (PDF)

Аннотация

Теоретические модели предсказывают, что затенение звездного излучения неоднородностями на поверхности протопланетного диска может вызывать самозарождающиеся волны, бегущие по направлению к звезде. Однако при моделировании этого процесса обычно используется 1+1D подход, ключевые приближения которого – вертикальное гидростатическое равновесие диска и вертикальная диффузия ИК излучения – могут искажать картину. В данной статье представлена двумерная радиационная гидродинамическая модель эволюции аксиально-симметричного газопылевого диска. В рамках этой модели, но с использованием упрощенных предположений из 1+1D моделей, мы воспроизвели самопроизвольное зарождение и распространение тепловых поверхностных волн. Ключевым выводом нашей работы является то, что учет двумерной гидродинамики и диффузии ИК излучения подавляет самопроизвольное возникновение и развитие тепловых волн, наблюдавшихся в 1+1D приближении. Поиск возможности существования поверхностных тепловых волн необходимо продолжить, исследуя проблему для различных параметров протопланетных дисков.

Ключевые слова: физические процессы и неустойчивости в протопланетных дисках, численное моделирование газопылевых дисков у молодых звезд

1. ВВЕДЕНИЕ

В протопланетных дисках реализуются условия для возникновения самых разнообразных динамических неустойчивостей, развитие которых может влиять как на наблюдательные проявления, так и на общую эволюцию дисков [1–7]. Одной из них является неустойчивость, связанная с затенением звездного излучения поверхностными неоднородностями диска [8]. Эта неустойчивость обусловлена положительной обратной связью между углом вхождения излучения звезды в атмосферу диска и его прогревом. Многие теоретические модели показывают, что малое локальное искажение поверхности диска может провоцировать зарождение волн, бегущих к центральной звезде [9–11]. Подобные тепловые волны на поверхности диска предсказывались как во внутренних областях пассивных дисков, где характерное время установления теплового равновесия меньше динамического [8], так и на периферии дисков в обратной ситуации [12]. В нашей предыдущей работе [13] мы также воспроизвели картину формирования тепловых волн и нашли, что они могут затрагивать лишь верхние слои дисков без существенных колебаний температуры в экваториальной плоскости.

Однако в основе 1+1D подхода, использованного в нашей статье [13], как и в большинстве других работ по этой проблеме, лежит несколько ключевых приближений, которые могут существенно искажать реальную картину. Такими приближениями являются: 1) отсутствие диффузии теплового излучения в радиальном направлении; 2) гидростатическое равновесие в вертикальном направлении и отсутствие газодинамических эффектов в радиальном направлении. Постепенный отказ от этих предположений важен для обоснования реалистичности тепловых волн в реальных дисках.

Так, например, в недавней работе [11] была представлена двухслойная модель диска, в которой учтены двумерные ($R,z$) эффекты нагрева экваториальных слоев ИК излучением поверхностных слоев, и продемонстрировано развитие неустойчивости при различных параметрах численной модели. Однако еще более детальный учет диффузии ИК излучения в радиальном направлении может привести к широкому перераспределению тепловой энергии в окрестности возмущения, что может сгладить возникающие волны.

Уменьшить или даже полностью подавить первоначальное возмущение могут также и динамические эффекты. Действительно, повышенное в прогретом слое давление может идти не только на поднятие слоя (как в 1 + 1D модели), но и на расталкивание соседних радиальных слоев. Картина этих процессов схематично показана на рис. 1.

Рис. 1.

Схема, иллюстрирующая процессы при формировании горба на поверхности диска в 1+1D модели (левая панель) и в 2D модели (правая панель). Черными стрелками показаны силы, связанные с градиентом давления, красными сплошными стрелками показано ИК излучение, прогревающее внутренние слои диска, а красными пунктирными стрелками – выходящее ИК излучение.

Целью данной работы является учет процессов динамики газа и диффузии ИК излучения в возбуждении поверхностных тепловых волн. Это исследование мы проводим с помощью полностью двумерной радиационной гидродинамической модели. В рамках данной модели мы также реализовали упрощающие предположения 1+1D подходов с целью определения их обоснованности.

2. БАЗОВАЯ АКСИАЛЬНО-СИММЕТРИЧНАЯ МОДЕЛЬ ПРОТОПЛАНЕТНОГО ДИСКА

Для моделирования эволюции газопылевого диска мы используем комбинацию конечно-разностных методов для гидродинамики и переноса излучения, адаптированных для сферической системы координат (СК). Вся расчетная область разделена на ячейки, внутри которых значения физических величин предполагаются постоянными. Структура сетки показана на рис. 2. Сферическая СК представляется нам более удобной по сравнению с другими в связи с тем, что расчет нагрева среды УФ излучением звезды (трассировка в радиальном направлении) в сферической СК реализуется наиболее простым образом. Аксиальная симметрия в сферической СК реализуется введением единственной ячейки по координате φ. В своих расчетах мы используем неоднородную дискретную сетку, сгущающуюся к центру в радиальном ($r$) направлении и к экватору при разбиении по углу $\theta $ с разрешением 360 радиальных $ \times $ × 64 угловых ячеек. Протяженность ячеек по углу $\varphi $ выбрана равной одному градусу, что сопоставимо с разрешением по $\theta $ вблизи экватора. Такая сетка хорошо отражает структуру диска и позволяет отслеживать возникающие градиенты физических величин. Вычисление эволюции осуществляется в рамках расщепления по физическим процессам, т.е. за гидродинамическим шагом следует шаг расчета переноса излучения.

Рис. 2.

Структура расчетной сетки с обозначениями величин. Слева – индивидуальная ячейка в сферической СК. Справа – вертикальный срез сетки по углу $\varphi $.

2.1. Гидродинамический метод

Для описания динамической эволюции газопылевого диска мы используем стандартные уравнения газодинамики для невязкого газа, которые в дивергентной форме имеют вид:

(1)
$\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {\mathbf{U}}) = 0,$
(2)
$\frac{\partial }{{\partial t}}(\rho {\mathbf{U}}) + \nabla \cdot (\rho {\mathbf{UU}} + P) = \rho {\mathbf{f}},$
(3)
$\frac{{\partial E}}{{\partial t}} + \nabla \cdot ({\mathbf{U}}(E + P)) = \rho {\mathbf{f}} \cdot {\mathbf{U}},$
где $\rho $ – объемная плотность, ${\mathbf{U}}$ – скорость, $P$ – давление, ${\mathbf{f}}$ – гравитационная сила на единицу массы, $E = \frac{P}{{\gamma - 1}} + \frac{{\rho {{U}^{2}}}}{2}$ – полная энергия газа в единице объема, $\gamma $ – показатель адиабаты.

Для решения данной системы мы используем классический метод Годунова, подробное описание которого можно найти в [14, раздел 3]. В данном методе газодинамические потоки через границы ячеек находятся в результате решения задачи о распаде произвольного газодинамического разрыва. В используемой нами реализации задача о распаде разрыва решается точно с помощью метода бисекций для возникающего нелинейного уравнения. Найденные потоки между ячейками используются для вычисления физических величин в ячейках на новом временнóм слое. Конечно-разностная схема реализована нами в рамках формализма, изложенного в статье [15], где рассмотрены разностные схемы годуновского типа в криволинейных координатах, их применение в сферических координатах и тестовые примеры.

В конечном итоге реализованная нами разностная схема сводится к следующим вычислениям. Пусть ${\mathbf{q}} = (\rho ,\rho u,\rho v,\rho w,E{{)}^{T}}$ – вектор консервативных переменных, где $\rho $ – объемная плотность, $u$, $v$, $w$ – компоненты скорости в сферической системе координат. Для нахождения значения ${{{\mathbf{q}}}^{{n + 1}}}$ на новом временнóм слое производятся два шага – шаг адвекции и шаг учета гравитационных источников. Шаг адвекции сводится к нахождению промежуточных значений ${\mathbf{q}}{\kern 1pt} *$ следующим образом:

(4)
${\mathbf{q}}{\kern 1pt} * = {{{\mathbf{q}}}^{n}} + \frac{{\Delta t}}{{\Delta V}}\left( {\Delta {\mathbf{f}} + \Delta {\mathbf{G}} + \Delta {\mathbf{H}}} \right),$
где $\Delta t$ – временнóй шаг, $\Delta V$ – объем текущей ячейки, а $\Delta {\mathbf{f}}$, $\Delta {\mathbf{G}}$, $\Delta {\mathbf{H}}$ – потоки через соответствующие грани ячеек, компоненты которых приведены в Приложении A. После адвекционного шага следует шаг учета гравитационных источников, на котором вычисляется поправка к радиальной скорости:
(5)
${{u}^{{n + 1}}} = u{\kern 1pt} * - \frac{{GM}}{{{{r}^{2}}}}\Delta t,$
где $G$ – гравитационная постоянная, $M$ – масса центральной звезды, и пересчитываются зависимые от нее величины, формируя значения ${{{\mathbf{q}}}^{{n + 1}}}$ на новом временнóм слое:

(6)
${{{\mathbf{q}}}^{{n + 1}}} = (\rho {\kern 1pt} *,\rho {\kern 1pt} *{{u}^{{n + 1}}},\rho {\kern 1pt} *v{\kern 1pt} *,\rho {\kern 1pt} *w{\kern 1pt} *,E({{u}^{{n + 1}}},v{\kern 1pt} *,w{\kern 1pt} *{{))}^{T}}.$

Реализованный гидродинамический метод был тщательно нами протестирован. В частности, численное решение задачи о распаде разрыва хорошо согласуется с аналитическим решением для всех типов разрывов. Кроме того, мы убедились в том, что в рамках одномерной аксиально-симметричной геометрии использованный конечно-разностный подход показывает близкие результаты в сравнении с классическим подходом, при котором явно выделяются источниковые члены, связанные с криволинейностью системы координат.

2.2. Метод расчета переноса излучения

Для расчета тепловой структуры газопылевого диска мы используем обобщение нестационарной тепловой модели из работы [16] на двумерный случай. В модели учитываются нагрев среды прямым излучением звезды и диффузия теплового излучения. Соответствующая система уравнений имеет вид:

(7)
$\rho {{c}_{{\text{V}}}}\frac{{\partial T}}{{\partial t}} = c\rho {{\kappa }_{{\text{P}}}}\left( {{{E}_{{\text{r}}}} - a{{T}^{4}}} \right) + {{s}_{ \star }},$
(8)
$\frac{{\partial {{E}_{{\text{r}}}}}}{{\partial t}} = - c\rho {{\kappa }_{{\text{P}}}}\left( {{{E}_{{\text{r}}}} - a{{T}^{4}}} \right) + \hat {\Lambda }{{E}_{{\text{r}}}}{\kern 1pt} ,$
где $\rho $ – плотность газопылевой среды, ${{c}_{{\text{V}}}}$ – удельная теплоемкость среды [эрг г–1 K–1], $c$ – скорость света, ${{\kappa }_{{\text{P}}}}$ [см2 г–1] – истинный коэффициент поглощения ИК излучения, усредненный по Планку (без вклада рассеяния, на единицу массы газопылевой среды), ${{s}_{ \star }}$ [эрг см–3 с–1] – темп нагрева звездным излучением, $T$ – температура среды, ${{E}_{{\text{r}}}}$ – плотность энергии ИК излучения. Уравнение (7) описывает изменение объемной тепловой энергии среды в результате поглощения и переизлучения теплового ИК излучения (слагаемые $c\rho {{\kappa }_{{\text{P}}}}{{E}_{{\text{r}}}}$ и $c\rho {{\kappa }_{{\text{P}}}}a{{T}^{4}}$ соответственно), а также в результате поглощения прямого УФ излучения звезды (${{s}_{ \star }}$). Уравнение (8) представляет собой моментное уравнение переноса излучения в эддингтоновском приближении и описывает изменение плотности энергии ИК излучения в результате поглощения и переизлучения теплового ИК излучения, а также в результате пространственной диффузии ИК излучения, представленной оператором $\hat {\Lambda }{{E}_{{\text{r}}}}$:
(9)
$\hat {\Lambda }{{E}_{{\text{r}}}} = - \operatorname{div} {{{\mathbf{f}}}_{{\text{r}}}} = \operatorname{div} \left( {\frac{1}{\sigma }grad{{E}_{{\text{r}}}}} \right),$
где ${{{\mathbf{f}}}_{{\text{r}}}}$ – поток ИК излучения, $\sigma = 3\rho {{\kappa }_{{\text{r}}}}{\text{/}}c$, ${{\kappa }_{{\text{r}}}}$ [см2 г‒1] – коэффициент непрозрачности, усредненный по Росселанду (с учетом рассеяния, на единицу массы газопылевой среды).

Уравнения (7)–(9) формируют нелинейную систему уравнений в частных производных диффузионного типа. Для ее решения мы используем полностью неявный численный метод, в котором правые части уравнений (7), (8), а также дифференциальный оператор (9) зависят от значений функций на новом временнóм слое:

(10)
$\rho {{c}_{{\text{V}}}}\frac{{T - {{T}^{n}}}}{{\Delta t}} = c\rho {{\kappa }_{{\text{P}}}}\left( {{{E}_{{\text{r}}}} - a{{T}^{4}}} \right) + {{s}_{ \star }},$
(11)
$\frac{{{{E}_{{\text{r}}}} - E_{{\text{r}}}^{n}}}{{\Delta t}} = - c\rho {{\kappa }_{{\text{P}}}}\left( {{{E}_{{\text{r}}}} - a{{T}^{4}}} \right) + \hat {\Lambda }{{E}_{{\text{r}}}},$
где ${{T}^{n}}$ и $E_{{\text{r}}}^{n}$ – значения с $n$-го временнóго слоя, $T$ и ${{E}_{{\text{r}}}}$ – искомые значения на временнóм слое ($n$ + 1) для заданной пространственной ячейки. В уравнениях сверху для краткости мы опустили верхние индексы ($n$ + 1)-го временнóго слоя у $\rho ,\;T,\;{{\kappa }_{{\text{P}}}},\;{{s}_{ \star }}$ и ${{E}_{{\text{r}}}}$. Мы также опустили нижние пространственные индексы – для всех величин они соответствуют рассматриваемой ячейке $(i,j)$ за исключением значения ${{s}_{ \star }}$, связывающего три соседних ячейки по радиусу и оператора $\hat {\Lambda }$, связывающего ячейку $(i,j)$ с четырьмя примыкающими ячейками по радиусу и углу $\theta $. Алгоритм решения данной системы уравнений приведен в Приложении B.

Интенсивность ультрафиолетового излучения, необходимая для вычисления функции нагрева ${{s}_{ \star }}$, находится для каждой ячейки путем прямого интегрирования уравнения переноса излучения от звезды до рассматриваемого элемента среды вдоль радиального направления. Принципиальным моментом при вычислении функции нагрева звездным излучением в рамках нашей модели является учет радиального градиента плотности внутри ячейки. В нашей модели объемная функция нагрева $s{\kern 1pt} *$ [ эрг см–3 с–1] звездным излучением вычисляется аналогично тому, как предложено в работе [13]:

(12)
${{s}_{ \star }} = {{\rho }_{{\text{m}}}}{{\kappa }_{{{\text{UV}}}}}\frac{{L\exp ( - \tau )}}{{4\pi r_{a}^{2}}}{\kern 1pt} \left( {\frac{{1 - \exp ( - \Delta \tau )}}{{\Delta \tau }}} \right),$
где $L$ – светимость звезды, ${{\kappa }_{{{\text{UV}}}}} = {{\kappa }_{{\text{P}}}}({{T}_{ \star }})$ [см2 г–1] – коэффициент поглощения звездного излучения, ${{r}_{a}}$ – радиальное расстояние от звезды до внутренней границы ячейки, $\tau $ – полная оптическая толщина на луче зрения от звезды до внутренней границы ячейки, $\Delta \tau = \kappa {{\rho }_{{\text{m}}}}\Delta l$ – оптическая толщина самой ячейки вдоль луча, $\Delta l$ – длина отрезка луча внутри ячейки, ${{\rho }_{{\text{m}}}} = \frac{1}{4}\left( {{{\rho }_{{\text{L}}}} + 2{{\rho }_{i}} + {{\rho }_{{\text{R}}}}} \right)$ – усредненная плотность вдоль луча. При выводе формулы (12) из формального решения уравнения переноса излучения предполагалось, что плотность вдоль луча внутри ячейки линейно изменяется от ${{\rho }_{{\text{L}}}}$ до ${{\rho }_{i}}$ и от ${{\rho }_{i}}$ до ${{\rho }_{{\text{r}}}}$. Значения ${{\rho }_{{\text{L}}}}$ и ${{\rho }_{{\text{r}}}}$ на границах ячеек, в свою очередь, находятся нами с помощью линейной интерполяции плотности между центром текущей ячейки и центрами прилегающих в радиальном направлении ячеек.

В модели предполагается, что единственным источником непрозрачности является пыль, причем температуры газа и пыли равны. Отношение плотности пыли к плотности газа по всему диску предполагается постоянным и равным 0.01, т.е. пыль считается однородно перемешанной с газом. Особенностью тепловой модели является использование усредненных по Планку и Росселанду непрозрачностей, зависящих от температуры. Эти коэффициенты взяты нами из работы [17], где они подробно описаны. Отметим, что мы не используем более реалистичные коэффициенты, учитывающие, в частности, испарение пыли при высоких температурах (см., напр., [18]), чтобы ограничить число исследуемых эффектов.

2.3. Граничные и начальные условия

В качестве начального состояния задается гидростатический в вертикальном направлении кеплеровский диск с температурой 10 K и распределением полной $( - \infty ,\infty )$ поверхностной плотности со степенны́м обрезанием внутренней границы [13]:

(13)
$\Sigma (R) = {{\Sigma }_{0}}\left( {1 - \exp \left( { - {{{\left( {\frac{R}{{{{R}_{0}}}}} \right)}}^{p}}} \right)} \right){{\left( {\frac{R}{{1\;{\kern 1pt} {\text{a}}{\text{.u}}{\text{.}}}}} \right)}^{{ - 1}}},$
где ${{\Sigma }_{0}} = 200$ г см–2 – нормировка поверхностной плотности, ${{R}_{0}} = 3$ а.е., $p = 8$ – параметры сглаживания распределения плотности вблизи внутренней границы диска. Внутренняя и внешняя границы диска равны 1 и 20 а.е. Масса, температура и светимость центральной звезды равны соответственно $M = 1{\kern 1pt} \;{{M}_{ \odot }}$, ${{T}_{ \star }} = 6000$ K, $L = 5{\kern 1pt} \;{{L}_{ \odot }}$. Во внешней границе расчетной области задается фоновая плотность ${{10}^{{ - 19}}}$ г см–3, нулевые компоненты скорости и температура фонового ИК излучения, равная 10 K.

3. ПРИБЛИЖЕННЫЕ МОДЕЛИ ГАЗОПЫЛЕВОГО ДИСКА

Целью данной работы является исследование роли двумерных эффектов в генерации поверхностных тепловых волн. Для этого наряду с базовой двумерной моделью мы рассмотрели модели, в которых приближения, использованные нами в ранее представленной 1 + 1D модели [13], последовательно заменяются на более строгие. Наряду с полноценной 2D гидродинамикой (2D HD) мы рассмотрели модели, где газ находится в гидростатическом равновесии в $\theta $ направлении (1D static). Помимо двумерного приближения в переносе ИК излучения (2D RT) мы рассмотрели также модели, где ИК излучение может распространятся только в $\theta $ направлении (1D RT). На рис. 3 показаны рассмотренные нами комбинации моделей, а ниже мы кратко опишем реализацию используемых приближений.

Рис. 3.

Рассматриваемые модели газопылевого диска (static – гидростатика, HD – гидродинамика, RT – перенос излучения).

Отметим, что комбинация “1D static & 1D RT” наиболее схожа по постановке с моделью из нашей предыдущей работы [13]. В этой статье мы рассматриваем модель “1D static & 1D RT”, чтобы воспроизвести картину формирования поверхностных волн, полученную в [13] на декартовой сетке.

3.1. Гидростатическое приближение

Вычисление структуры диска в рамках данного приближения мы проводим на основе решения следующего уравнения:

(14)
$\frac{1}{\rho }{\kern 1pt} \frac{{d(\rho T)}}{{d\psi }} = - \beta \psi ,$
где $\psi = \pi {\text{/}}2 - \theta $ – угол, отсчитываемый от экваториальной плоскости диска, $\beta = \frac{{GM}}{{{{R}_{\mu }}{{r}_{c}}}}$, ${{R}_{\mu }} = \frac{{{{k}_{{\text{B}}}}}}{{\mu {{m}_{a}}}}$, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $\mu = 2.3$ – средний молекулярный вес, ${{m}_{a}}$ – атомная единица массы, ${{r}_{c}}$ – радиальное расстояние до центра ячейки. Уравнение (14) можно получить из уравнения для гидростатического в вертикальном направлении диска, предполагая, что отношение $z{\text{/}}r$ мало. Однако мы используем уравнение (14) для всех ячеек расчетной области. При численном интегрировании уравнения (14) мы предполагаем, что значения температуры в ячейках известны (определены после расчета переноса излучения). Дополнительным условием при интегрировании уравнения (14) является сохранение массы всей колонки ячеек по $\theta $. Таким образом, в рамках такого подхода мы позволяем перераспределяться веществу в $\theta $ направлении, подстраиваясь под текущую тепловую структуру. Такой диск, безусловно, не будет являться гидростатическим в физическом смысле, поскольку уравнение (14) является приближенным и некорректным для $z{\text{/}}r \sim 1$. Однако оно качественно верно отражает зависимость высоты диска от тепловой структуры и легко решается на сферической сетке, поэтому его удобно использовать для исследования неустойчивости диска.

3.2. Одномерная тепловая модель

В данном приближении мы предполагаем, что ИК излучение распространяется только в $\theta $ направлении, в то время как УФ излучение звезды прогревает диск только в радиальном направлении. В рамках описанных в разделе 2 и Приложении B уравнений это приближение реализуется занулением потоков ${{F}_{{{\text{r}},ra}}}$ и ${{F}_{{{\text{r}},rb}}}$ в выражении (B3), после чего нахождение тепловой структуры разбивается на ряд одномерных задач. Соответствующие конечно-разностные уравнения решаются нами методом прогонки. При этом важным моментом является задание граничных условий: если формально взять все ячейки по $\theta $ в полученной разностной схеме, то излучение внутри рассматриваемого массива по $\theta $ будет заперто, поскольку площади граней ячеек, соприкасающихся с полярной осью, равны нулю (${{S}_{{\theta a}}} = 0$ при $\theta = 0$, ${{S}_{{\theta b}}} = 0$ при $\theta = \pi $). Поэтому мы искусственно задаем плотность энергии излучения в приполярных ячейках равной межзвездному фону. Отметим, что это приближение, как и модель гидростатического равновесия по углу $\theta $, безусловно, является достаточно грубым и не может считаться полезным для практического использования. Мы используем его только как инструмент проверки приближений, лежащих в основе 1+1D аналитических моделей возникновения поверхностных волн.

4. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

В этом разделе мы описываем результаты численного моделирования поверхностных волн, начиная с моделей с самой простой трактовкой физических процессов (гидростатических и одрезультаты расчета эволюции экваториальной температуры диска в первые 300 лет для модели “1D static & 1D RT”. На распределении хорошо проявляются возмущения, зарождающиеся внутри 15 а.е. и распространяющиеся снаружи внутрь. Период возникновения и время распространения возмущений составляют ~50 лет, что сопоставимо с характерным тепловым временем ${{t}_{{{\text{th}}}}} = \frac{3}{8}{\kern 1pt} \frac{{{{c}_{{\text{V}}}}{{\Sigma }^{2}}{{\kappa }_{{\text{R}}}}({{T}_{{\text{m}}}})}}{{{{\sigma }_{{{\text{SB}}}}}T_{{\text{m}}}^{3}}}$, распределение которого показано белой линией для момента 300 лет. На данном распределении в волнах, бегущих снаружи внутрь, встречаются разрывы (см. напр., область в окрестности 6 а.е. на момент 150 лет). Эти разрывы связаны с формированием внутреннего горба на поверхности диска, который начинает затенять существующий в данный момент более внешний горб. После того как внутренний горб достигает внутренней границы диска, внешний горб восстанавливается и продолжает свое распространение с места, на котором он остановился в момент затмения (время затмения меньше времени остывания внешнего горба).

Рис. 4.

Результаты расчетов для модели “1D static & 1D RT”. Слева – эволюция экваториальной температуры в первые 300 лет. Белая линия показывает характерное тепловое время для всей толщи диска. Распределение вертикальной оптической толщины к собственному тепловому излучению показано черной линией. Справа – распределения плотности и температуры в полярном сечении диска на момент времени 200 лет.

На левой панели рис. 4 черной линией также показано распределение оптической толщины ${{\tau }_{{{\text{IR}}}}} = {{\kappa }_{{\text{P}}}}\Sigma (R)$ в вертикальном направлении к собственному тепловому излучению диска на момент времени 300 лет. Сильный пик в окрестности 6 а.е. связан с повышением температуры (и, соответственно, повышением ${{\kappa }_{{\text{P}}}}(T)$) в этой области вследствие зарождающегося теплового возмущения. Оптическая толщина превышает единицу в области 4–10 а.е., что оправдывает здесь использование приближения Эддингтона для расчета диффузии теплового излучения.

На правой панели рис. 4 приведены двумерные распределения плотности и температуры в полярном сечении диска на момент времени 200 лет. На распределениях отчетливо видны два возмущения в окрестности 5 и 12 а.е., имеющие форму арок. Такая форма возмущений связана с предположением гидростатической модели о том, что вещество перераспределяется только в $\theta $ направлении. Для каждого радиального положения в диске температура падает от атмосферы к экватору, что характерно для классического пассивного диска. Температура в области горбов, получающих бóльшую долю звездного излучения, повышена. Температура также повышена на протяжении ~2 а.е. за горбами, что связано с конечным временем охлаждения диска за счет собственного ИК излучения. Качественно описанная картина эволюции диска похожа на ту, что представлена нами в предыдущей работе [13] для модели диска с аналогичными начальными параметрами. Отметим, что ценность данной модели прежде всего методическая, т.к. нереалистичная (арочная) форма бегущих возмущений, связанная с одномерным описанием структуры диска и переноса излучения в $\theta $ направлении, не позволяет использовать ее для связи с какими-либо наблюдениями. Вместе с тем с помощью этой модели нам удалось воспроизвести формирование тепловых волн в рамках численного кода, реализованного в сферической системе координат. Эта модель служит отправной точкой для нашего последующего исследования двумерных эффектов.

Рис. 5.

Результаты расчетов для модели “2D HD & 1D RT”. Слева – эволюция экваториальной температуры в первые 300 лет. Белая линия показывает характерное тепловое время для всей толщи диска, красная линия – характерное динамическое (кеплеровское) время. Числовая шкала для этих времен совпадает со шкалой для времени эволюции. Справа – распределения плотности и температуры в полярном сечении диска на момент времени 200 лет.

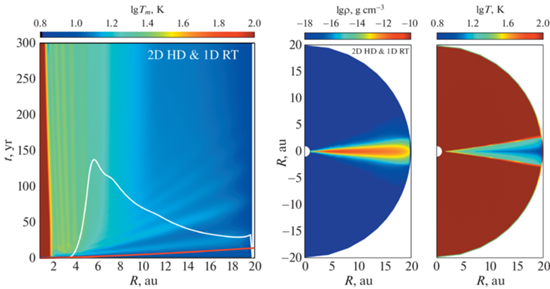
На рис. 5 приведены результаты расчета эволюции диска в рамках модели “2D HD & 1D RT”. Учет гидродинамических эффектов полностью изменяет картину эволюции диска. В отличие от модели “1D static & 1D RT”, где волны периодически зарождаются в области 6–15 а.е., возмущения в модели “2D HD & 1D RT” возникают только в начальные моменты времени внутри 4 а.е. и распространяются наружу. Мы полагаем, что эти возмущения связаны с сильной гидродинамической неравновесностью начального состояния диска. Данные волны со временем угасают и прослеживаются до времени ~150 лет. Во внутренней части диска ($r < 5$ а.е.) устанавливается стационарная кольцеобразная структура. Распределения плотности и температуры в полярном сечении диска выглядят гладкими, за исключением слабых кольцеобразных возмущений во внутренних областях диска. Тепловая структура диска является стандартной для пассивного диска: атмосфера диска теплее экваториальных областей, присутствует слабый радиальный градиент температуры в экваториальной плоскости.

На рис. 6 показана эволюция радиальной скорости $u$ в экваториальной плоскости, а также вдоль угловой координаты для ячеек на радиусе 10 а.е. Эти распределения иллюстрируют распространение и затухание гидродинамических возмущений, возникающих в начальный момент времени. Возмущения радиальных скоростей $\Delta u \sim 0.2$ км/c сопоставимы со звуковыми скоростями ${{c}_{{\text{s}}}} = {{\left( {{{k}_{{\text{B}}}}{{T}_{{\text{m}}}}{\text{/}}(\mu {{m}_{a}})} \right)}^{{1/2}}} \approx 0.19$ км/c для ${{T}_{{\text{m}}}} = 10$ K. Отметим, что возмущения скорости в поверхностных слоях ($\psi \approx \pm 0.3$ радиан) выше, чем в экваториальной плоскости ($\psi = 0$ радиан). Интересной особенностью данных распределений является то, что со временем в диске устанавливается меридиональная циркуляция – в поверхностных частях диска вещество течет на звезду, в то время как в экваториальной области вещество течет наружу. Сильные возмущения скоростей ~1 км/c на внешней границе расчетной области связаны с использованными граничными условиями.

Рис. 6.

Результаты расчетов для модели “2D HD & 1D RT”. Слева – эволюция распределения радиальной скорости $u(r)$ в экваториальной плоскости диска. В центре – эволюция широтного распределения радиальной скорости $u(\psi )$, где $\psi $ – угол, отсчитываемый от экватора, на радиусе 10 а.е. Справа – распределение радиальной скорости $u(r,\psi )$ в полярном сечении диска на момент времени 200 лет.

Тепловые волны, распространяющие снаружи внутрь, в данной модели не возникают. Мы считаем, что причиной этому является то, что возникающие поверхностные возмущения успевают разглаживаться динамически, прежде чем они успеют существенно прогреть нижележащие слои. Такое разглаживание аналогично описанному выше процессу релаксации первоначально неравновесного состояния. В пользу этого говорит сопоставление характерного теплового времени (продолжительность прогрева экваториальных слоев) и динамического времени ${{t}_{{\text{K}}}} = \sqrt {{{R}^{3}}{\text{/}}(GM)} $, показанных на левой панели рис. 5 белым и красным цветами соответственно. Действительно, в рассматриваемой области динамическое время короче теплового. Здесь важно отметить, что условие малости динамического времени по отношению к тепловому времени используется в качестве обоснования использования гидростатического равновесия в вертикальном направлении, являющегося ключевым приближением в современной картине формирования тепловых волн. Однако результаты нашего моделирования показывают, что это условие приводит к динамической релаксации возмущений в радиальном направлении. На основании данной модели мы делаем вывод, что гидродинамические эффекты могут подавлять поверхностные волны.

Рис. 7.

Результаты расчетов для модели “1D static & 2D RT”. Слева – эволюция экваториальной температуры в первые 300 лет. Справа – распределения плотности и температуры в полярном сечении диска на момент времени 200 лет.

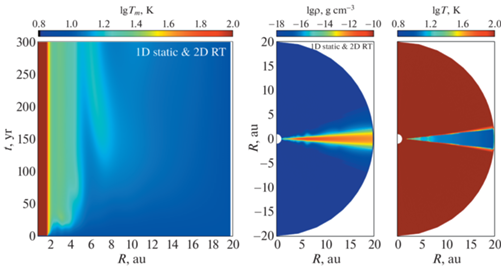
На рис. 7 показаны результаты расчета эволюции диска для модели “1D static & 2D RT”. Характер эволюции диска в этой модели существенно отличается от двух рассмотренных моделей. В данной модели не возникает периодических бегущих волн, однако в структуре диска можно выделить несколько горбов. Самый заметный формируется в области ~8 а.е. в момент $ \sim $120 лет и медленно движется внутрь, однако после 250 лет становится практически стационарным. Распределение температуры в полярном сечении диска на момент 200 лет более однородно по сравнению с моделью “2D HD & 1D RT”, в нем не так отчетливо проявляется вертикальная стратификация по температуре. Эту особенность мы связываем с эффектами затенения внешних слоев диска внутренними квазистационарными горбами, при этом тепловую структуру во многом определяет двумерный характер диффузии ИК излучения. Общий вывод по данной модели состоит в том, что двумерный перенос ИК излучения достаточно эффективно размывает тепловые неоднородности диска, тем самым подавляя (или многократно замедляя по сравнению с моделью “1D static & 1D RT”) периодическое возникновение и распространение поверхностных волн. Вместе с тем в данной модели наблюдаются внутренние квазистационарные возмущения, перехватывающие и перерабатывающие значительную долю излучения звезды, поступающего в диск.

Полученные в рамках данной модели выводы следует сопоставить с результатами работы [11], где в рамках гидростатического приближения также учитываются двумерные эффекты переноса излучения, но волны там образуются. Ключевым отличием между нашими моделями является то, что тепловая структура диска в работе [11] описывается в рамках двухзонного приближения, а характерная высота диска определяется значением экваториальной температуры. В нашей же модели гидростатическая структура диска выстраивается в соответствии с вертикальным профилем температуры. В статье [11] используется также другой метод расчета переноса теплового излучения на основе прямого интегрирования, в то время как в нашем подходе используется диффузионный метод. На основании этого можно предположить, что в рамках нашей модели релаксация тепловых неоднородностей более эффективна, что не приводит к их росту.

Рис. 8.

Результаты расчетов для модели “2D HD & 2D RT”. Слева – эволюция экваториальной температуры в первые 300 лет. Справа – распределения плотности и температуры в полярном сечении диска на момент времени 200 лет.

Наконец, на рис. 8 приведены результаты расчета эволюции диска для модели “2D HD & 2D RT”. Динамика и структура диска в рамках данной модели близки к тому, что наблюдалось в модели “2D HD & 1D RT”. Единственным существенным отличием от последней является то, что в модели “2D HD & 2D RT” внутренняя область диска ($r < 6$ а.е.) стала однородной, в ней отсутствует разбиение на кольца. Структура диска в плоскости $(r\theta )$ соответствует пассивному диску с выраженной тепловой стратификацией по вертикали. По результатам данной модели можно сделать глобальный вывод о том, что совместный учет двумерной гидродинамики и переноса теплового излучения подавляет формирование и распространение поверхностных тепловых волн в газопылевых дисках.

В связи с полученными нами результатами необходимо отметить статью [19], препринт которой появился на этапе рецензирования нашей работы. Fuksman & Klahr [19] независимо от нас с помощью своей численной модели также пришли к выводу о подавлении тепловых волн при учете гидродинамических эффектов и нестационарности теплопереноса.

5. ЗАКЛЮЧЕНИЕ

Данная работа – логическое продолжение исследования, представленного нами в статье [13]. Основной целью данной работы являлось изучение поверхностных тепловых волн в газопылевых дисках при более реалистичном описании процессов с учетом двумерных гидродинамических эффектов и двумерных эффектов переноса теплового излучения (в плоскости $(r\theta )$). Для этого мы разработали модель эволюции аксиально-симметричного диска, предназначенную для последовательного исключения приближений, лежащих в основе современной теории поверхностных тепловых волн. В данном двумерном численном коде мы также реализовали упрощенные подходы, используемые в 1+1D моделях – приближение вертикального гидростатического равновесия и вертикальной диффузии ИК излучения, и воспроизвели картину формирования бегущих поверхностных волн из статьи [13]. Затем мы показали, что замена приближения гидростатического равновесия на гидродинамическое моделирование приводит к исчезновению поверхностных тепловых волн. К такому же результату приводит и замена одномерного приближения для расчета теплового излучения на двумерное моделирование. Полученные результаты свидетельствуют о том, что совместный учет двумерных эффектов, связанных с гидродинамикой и переносом теплового излучения, подавляет развитие поверхностных тепловых волн, имеющих место в рамках 1+1D подхода.

Полученный здесь вывод нужно воспринимать с определенной осторожностью в связи с ограничениями нашей модели. Использованный нами метод расчета переноса излучения основан на эддингтоновском приближении, при котором предполагается изотропность поля ИК излучения. Это приближение преувеличивает диффузионный характер распространения излучения в оптически тонких и переходных областях, а значит приводит к более эффективному размыванию неоднородностей. Необходимо проверить полученные выводы с использованием более корректных методов расчета переноса излучения, таких как диффузионный метод с ограничителем потока (Flux Limited Diffusion) [20] или метод переменного тензора Эддингтона (Variable Eddington Tensor) [21]. В статье [11] отмечено, что подавлять развитие неустойчивости может также недостаточно высокое пространственное разрешение численной модели. В своих расчетах из-за высоких вычислительных затрат мы были ограничены относительно разреженной пространственной сеткой (${{N}_{r}} \times {{N}_{\theta }} = 360 \times 64$, однако она неоднородна). Поэтому необходим последующий анализ на более подробных сетках. Отметим, что полученные нами выводы не позволяют утверждать о принципиальной невозможности развития неустойчивости. Наши результаты лишь показывают отсутствие двумерных поверхностных волн в конкретных физических условиях, при которых они самопроизвольно формировались в 1+1D модели. Необходимо исследовать проблему для широкого интервала параметров газопылевых дисков, в частности, в случае когда характерные тепловые и динамические времена сопоставимы.

Список литературы

  1. E. P. Velikhov, Sov. J. Experim. Theoret. Phys. 36, 1398 (1959), http://jetp.ras.ru/cgi-bin/e/index/ e/9/5/p995?a=list .

  2. S. A. Balbus and J. F. Hawley, Astrophys. J. 376, 214 (1991).

  3. A. N. Youdin and J. Goodman, Astrophys. J. 620, 459 (2005), arXiv:astro-ph/0409263.

  4. R. P. Nelson, O. Gressel, and O. M. Umurhan, Monthly Not. Roy. Astron. Soc. 435, 2610 (2013), arXiv:1209.2753 [astro-ph.EP].

  5. H. Klahr and A. Hubbard, Astrophys. J. 788, id. 21 (2014), arXiv:1403.6721 [astro-ph.SR].

  6. G. R. J. Lesur and H. Latter, Monthly Not. Roy. Astron. Soc. 462, 4549 (2016), arXiv:1606.03012 [astro-ph.EP].

  7. V. V. Zhuravlev, Monthly Not. Roy. Astron. Soc. 512, 2636 (2022), arXiv:2203.04792 [astro-ph.EP].

  8. S.-I. Watanabe and D. N. C. Lin, Astrophys. J. 672, 1183 (2008), arXiv:0709.1760 [astro-ph].

  9. T. Ueda, M. Flock, and T. Birnstiel, Astrophys. J. Letters 914, id. L38 (2021), arXiv:2105.13852 [astro-ph.EP].

  10. Y. Wu and Y. Lithwick, Astrophys. J. 923, id. 123 (2021), arXiv:2105.02680 [astro-ph.EP].

  11. S. Okuzumi, T. Ueda, and N. J. Turner, arXiv:2201.09241 [astro-ph.EP] (2022).

  12. C. P. Dullemond, Astron. and Astrophys. 361, L17 (2000), arXiv:astro-ph/0007399.

  13. Y. N. Pavlyuchenkov, L. A. Maksimova, and V. V. Akimkin, Astron. Rep. 66, 321 (2022), arXiv:2203.06614 [astro-ph.EP].

  14. А. Г. Куликовский, Н. В. Погорелов, А. Ю. Семенов, Математические вопросы численного решения гиперболических систем уравнений (М.: Физматлит, 2012).

  15. M. В. Абакумов, Прикладная математика и информатика 45, 63 (2014). _. M. V. Abakumov, Prikladnaya matematika i informatika 45, 63 (2014).

  16. E. I. Vorobyov and Y. N. Pavlyuchenkov, Astron. and Astrophys. 606, id. A5 (2017), arXiv:1706.00401 [astro-ph.GA].

  17. Y. N. Pavlyuchenkov, A. V. Tutukov, L. A. Maksimova, and E. I. Vorobyov, Astron. Rep. 64, 1 (2020), arXiv:1912.08572 [astro-ph.SR].

  18. D. Semenov, T. Henning, C. Helling, M. Ilgner, and E. Sedlmayr, Astron. and Astrophys. 410, 611 (2003), arXiv:astro-ph/0308344.

  19. J. D. Melon Fuksman and H. Klahr, arXiv:2207.05106 [astro-ph.EP] (2022).

  20. C. D. Levermore and G. C. Pomraning, Astrophys. J. 248, 321 (1981).

  21. J. M. Stone, D. Mihalas, and M. L. Norman, Astrophys. J. Suppl. 80, 819 (1992).

  22. Y. Saad and M. H. Schultz, SIAM J. Sci. Stat. Comp. 7, 856 (1986), .https://doi.org/10.1137/0907058

  23. А. А. Самарский, Е. С. Николаев, Методы решения сеточных уравнений (М.: Наука, 1978).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал