Астрономический вестник, 2019, T. 53, № 2, стр. 125-132

Полуаналитический метод построения околоэкваториальных орбит гипотетических спутников астероидов почти сфероидальной формы

М. А. Вашковьяк^*

Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

Поступила в редакцию 07.06.2018
После доработки 12.09.2018
Принята к публикации 12.09.2018

DOI: 10.1134/S0320930X19020075

Аннотация

Рассматривается задача о движении материальной точки пренебрежимо малой массы (спутника) вблизи экваториальной плоскости сфероидального тела, в частности, астероида. Для малых наклонений орбиты спутника в первом приближении возможно разделение движений на экваториальную и широтную компоненты. Экваториальное центральное движение, когда силовая функция зависит лишь от расстояния спутника до начала координат (центра масс астероида), строится предложенным ранее полуаналитическим методом. Построение широтного движения предусматривает решение линеаризованной системы дифференциальных уравнений второго порядка с периодическими коэффициентами путем численного определения матрицы монодромии на периоде экваториального движения и его временное аналитическое продолжение. Рассмотрены модельные задачи о возмущенном движении гипотетических почти экваториальных спутников Цереры и Весты. Оценка методической точности получена путем сравнения с численным решением.

Ключевые слова: потенциал сфероида, околоэкваториальные орбиты, гипотетические спутники Цереры и Весты

ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ

Известную классическую задачу о движении пробной материальной точки пренебрежимо малой массы в поле притяжения произвольного твердого тела (или системы тел) в небесной механике терминологически иногда называют задачей Фату по имени французского ученого, систематически исследовавшего ее и выявившего в ней ряд динамических свойств (Fatou, 1931; Дубошин, 1964). В настоящей работе рассматривается частный случай этой задачи, когда притягивающее тело является однородным сфероидом, а движение пробной точки происходит вблизи его экваториальной плоскости.

Силовая функция притяжения однородного сфероида, зависящая от координат спутника, выражается известными формулами (Дубошин, 1961; Кондратьев, 2007). В дальнейшем будет использоваться система координат с началом в центре масс притягивающего тела O, а в качестве основной координатной плоскости xOy – плоскость экватора, нормальная к оси его вращения Oz. В силу осевой симметрии задачи направление оси Ox произвольно, а вместо пары прямоугольных координат x, y естественно и удобно использовать полярные координаты:

(1)

$\rho = \sqrt {{{x}^{2}} + {{y}^{2}}} ,\,\,\,\,\theta = {\text{arctg}}\left( {{y \mathord{\left/ {\vphantom {y x}} \right. \kern-0em} x}} \right).$

При этом силовая функция притяжения U(ρ, z) не зависит от полярного угла (или долготы) θ, а уравнения движения точки в выбранных цилиндрических координатах ρ, θ, z

(2)

$\begin{gathered} \frac{{{{d}^{2}}\rho }}{{d{{t}^{2}}}} - \rho {{\left( {\frac{{d\theta }}{{dt}}} \right)}^{2}} = \frac{{\partial U}}{{\partial \rho }}, \\ {{\rho }^{2}}\frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}} + 2\rho \frac{{d\rho }}{{dt}}\frac{{d\theta }}{{dt}} = \frac{{\partial U}}{{\partial \theta }}{\text{ = 0}},\,\,\,\,\frac{{{{d}^{2}}z}}{{d{{t}^{2}}}} = \frac{{\partial U}}{{\partial z}} \\ \end{gathered} $

допускают два первых интеграла (Дубошин, 1964)

(3)

${{\left( {\frac{{d\rho }}{{dt}}} \right)}^{2}} + {{\rho }^{2}}{{\left( {\frac{{d\theta }}{{dt}}} \right)}^{2}} + {{\left( {\frac{{dz}}{{dt}}} \right)}^{2}} = 2\left( {U + h} \right),\,\,\,\,{{\rho }^{2}}\frac{{d\theta }}{{dt}} = c.$

Постоянные c и h определяются начальными значениями координат и их производных по времени t при начальном значении t₀ = 0:

$\begin{gathered} {{\rho }_{0}},\,\,\,\,\frac{{d{{\rho }_{0}}}}{{dt}} = {{\left. {\frac{{d\rho }}{{dt}}} \right|}_{{{{t}_{0}} = 0}}},\,\,\,\,{{\theta }_{0}},\,\,\,\,\frac{{d{{\theta }_{0}}}}{{dt}} = {{\left. {\frac{{d\theta }}{{dt}}} \right|}_{{{{t}_{0}} = 0}}}, \\ {{z}_{0}},\,\,\,\,\frac{{d{{z}_{0}}}}{{dt}} = {{\left. {\frac{{dz}}{{dt}}} \right|}_{{{{t}_{0}} = 0}}}. \\ \end{gathered} $

Интегралы (3) оказываются полезными при контроле точности численного решения уравнений (2) с произвольной функцией U(ρ, z).

С использованием интеграла c уравнения (2), (3) принимают вид

(4)

$\frac{{{{d}^{2}}\rho }}{{d{{t}^{2}}}} = \frac{{\partial U}}{{\partial \rho }} + \frac{{{{c}^{2}}}}{{{{\rho }^{3}}}},\,\,\,\,\frac{{{{d}^{2}}z}}{{d{{t}^{2}}}} = \frac{{\partial U}}{{\partial z}},$

(5)

$\frac{1}{2}\left[ {{{{\left( {\frac{{d\rho }}{{dt}}} \right)}}^{2}} + {{{\left( {\frac{{dz}}{{dt}}} \right)}}^{2}}} \right] = U\left( {\rho ,z} \right) - \frac{{{{c}^{2}}}}{{2{{\rho }^{2}}}} + h.$

Угловая переменная θ после определения явной зависимости ρ от времени t может быть найдена вычислением интеграла

(6)

$\theta = {{\theta }_{0}} + c\int\limits_{{{t}_{0}}}^t {\frac{{d\tau }}{{{{\rho }^{2}}\left( \tau \right)}}} .$

Целью настоящей работы является построение приближенного полуаналитического решения системы уравнений (2) для ограниченного изменения ρ, а также малых значений z₀ и $\frac{{d{{z}_{0}}}}{{dt}}.$ Предполагается, что на рассматриваемом интервале времени остаются малыми наклонение орбиты спутника i и модуль его широты φ = = arctg(z/ρ). Предложенное решение может быть использовано в качестве первого (начального) приближения для описания орбитального движения околоэкваториальных спутников небесных тел, геометрические формы которых в известной степени близки к сжатым сфероидам, в том числе карликовой планеты Церера и астероида Веста. В действительности астероиды имеют достаточно сложную структуру гравитационного поля. Исследование, выполненное в ходе миссии Dawn, начавшейся в сентябре 2007 г., в частности, выявило наличие от 10 до 25 гармоник гравитационных полей Цереры и Весты. Оно детально описано в работе (Konopliv и др., 2011), содержащей и обзор исследований этих небесных тел, выполненных с помощью наземных средств. В дополнение к этому можно отметить, что при исследовании динамики перспективных искусственных спутников некоторых астероидов, в частности, Апофиса, используется модель вытянутого эллипсоида вращения (Ивашкин, Лан, 2018), а также трехосного эллипсоида (Гуо, Ивашкин, 2018).

СИЛОВАЯ ФУНКЦИЯ ПРИТЯЖЕНИЯ ОДНОРОДНОГО СФЕРОИДА И ЕЕ ПРОИЗВОДНЫЕ

Уравнение поверхности сфероида (эллипсоида вращения) имеет известный канонический вид

(7)

$\frac{{{{\rho }^{2}}}}{{a_{1}^{2}}} + \frac{{{{z}^{2}}}}{{a_{3}^{2}}} = 1.$

Для выражения силовой функции его притяжения на внешнюю точку мы воспользуемся формулами, приведенными в монографии (Кондратьев, 2007). В случае сжатого сфероида его полуоси удовлетворяют условиям а₁ = а₂ > а₃, а силовая функция имеет вид

(8)

$\begin{gathered} U\left( {\rho ,z,\lambda } \right) = \frac{{3\mu }}{{2\sqrt {a_{1}^{2} - a_{3}^{2}} }} \times \\ \times \,\,\left\{ {I\left( \lambda \right) - \frac{{{{\rho }^{2}}}}{{2\left( {a_{1}^{2} - a_{3}^{2}} \right)}}} \right.\left[ {I\left( \lambda \right) - \frac{{\sqrt {\left( {a_{1}^{2} - a_{3}^{2}} \right)\left( {a_{3}^{2} + \lambda } \right)} }}{{a_{1}^{2} + \lambda }}} \right] - \\ \left. { - \,\,\frac{{{{z}^{2}}}}{{a_{1}^{2} - a_{3}^{2}}}\left[ {\sqrt {\frac{{a_{1}^{2} - a_{3}^{2}}}{{a_{3}^{2} + \lambda }}} - I\left( \lambda \right)} \right]} \right\}. \\ \end{gathered} $

Здесь μ – произведение гравитационной постоянной на массу однородного сфероида,

(9)

$I\left( \lambda \right) = {\text{arctg}}\left( {\sqrt {\frac{{a_{1}^{2} - a_{3}^{2}}}{{a_{3}^{2} + \lambda }}} } \right).$

Параметр λ – это наибольший положительный корень уравнения

(10)

$\frac{{{{\rho }^{2}}}}{{a_{1}^{2} + \lambda }} + \frac{{{{z}^{2}}}}{{a_{3}^{2} + \lambda }} = 1,$

или ${{\lambda }^{2}} + \left( {a_{1}^{2} + a_{3}^{2} - {{\rho }^{2}} - {{z}^{2}}} \right)\lambda + a_{1}^{2}a_{3}^{2} - a_{3}^{2}{{\rho }^{2}} - a_{1}^{2}{{z}^{2}} = 0,$

т.е.

(11)

$\lambda = \frac{1}{2}\left( {\kappa - a_{1}^{2} - a_{3}^{2}} \right),$

(12)

где $\begin{gathered} \kappa = {{\rho }^{2}} + {{z}^{2}} + \\ + \,\,\sqrt {{{{\left( {{{\rho }^{2}} + {{z}^{2}}} \right)}}^{2}} + 2\left( {a_{1}^{2} - a_{3}^{2}} \right)\left( {{{z}^{2}} - {{\rho }^{2}}} \right) + {{{\left( {a_{1}^{2} - a_{3}^{2}} \right)}}^{2}}} . \\ \end{gathered} $

С введением упрощающих обозначений

(13)

$\begin{gathered} {{s}_{1}} = a_{1}^{2} + \lambda = \frac{1}{2}\left( {\kappa + {{b}^{2}}} \right), \\ {{s}_{2}} = a_{3}^{2} + \lambda = \frac{1}{2}\left( {\kappa - {{b}^{2}}} \right), \\ b = \sqrt {a_{1}^{2} - a_{3}^{2}} ,\,\,\,I\left( \lambda \right) = {\text{arctg}}\left( {\frac{b}{{\sqrt {{{s}_{2}}} }}} \right) \\ \end{gathered} $

выражение (8) принимает вид

(14)

$\begin{gathered} U\left( {\rho ,z,\lambda } \right) = \\ = \frac{{3\mu }}{{2b}}\left[ {\left( {1 + \frac{{2{{z}^{2}} - {{\rho }^{2}}}}{{2{{b}^{2}}}}} \right)I\left( \lambda \right) + \frac{{{{\rho }^{2}}\sqrt {{{s}_{2}}} }}{{2{{s}_{1}}b}} - \frac{{{{z}^{2}}}}{{b\sqrt {{{s}_{2}}} }}} \right]. \\ \end{gathered} $

Частные производные функции U по координатам, строго говоря, должны вычисляться дифференцированием по аргументам ρ и z, входящим в формулу (14) как явно, так и посредством $\lambda \left( {\rho ,z} \right).$ Частные производные первого порядка определяются относительно простыми формулами

(15)

$\begin{gathered} \frac{{\partial U}}{{\partial \rho }} = \frac{{3\mu \rho }}{{2{{b}^{3}}}}\left[ {\frac{{b\sqrt {{{s}_{2}}} }}{{{{s}_{1}}}} - I\left( \lambda \right)} \right], \\ \frac{{\partial U}}{{\partial z}} = \frac{{3\mu z}}{{{{b}^{3}}}}\left[ {I\left( \lambda \right) - \frac{b}{{\sqrt {{{s}_{2}}} }}} \right]. \\ \end{gathered} $

Нетрудно видеть, что знак производной $\frac{{\partial U}}{{\partial z}}$ противоположен знаку z. Как следствие общего свойства движения в задаче Фату (Fatou, 1931; Дубошин, 1964) это означает, что компонента ускорения $\frac{{{{d}^{2}}z}}{{d{{t}^{2}}}}$ постоянно направлена к основной (экваториальной) плоскости, а движение устойчиво относительно малых отклонений z от нуля.

В дальнейшем при анализе околоэкваториальных орбит и разделении движений на экваториальное и широтное будут также использоваться упрощенные выражения функции U и ее частных производных по ρ и z при z → 0, непосредственно следующие из формул (14), (15)

(16)

$\begin{gathered} U\left( {\rho ,0} \right) = \frac{{3\mu }}{{2b}}\left[ {\left( {1 - \frac{{{{\rho }^{2}}}}{{2{{b}^{2}}}}} \right){\text{arctg}}\left( \xi \right) + \frac{1}{{2\xi }}} \right], \\ {{\left. {\frac{{\partial U}}{{\partial \rho }}} \right|}_{{z = 0}}} = \frac{{3\mu \rho }}{{2{{b}^{3}}}}\left[ {\frac{{{{b}^{2}}}}{{\xi {{\rho }^{2}}}} - {\text{arctg}}\left( \xi \right)} \right], \\ {{\left. {\frac{{\partial U}}{{\partial z}}} \right|}_{{z \to 0}}} = \frac{{3\mu z}}{{{{b}^{3}}}}\left[ {{\text{arctg}}\left( \xi \right) - \xi } \right], \\ \end{gathered} $

${\text{г д е }}\,\,\,\,\xi = \frac{b}{{\sqrt {{{\rho }^{2}} - {{b}^{2}}} }}.$

РАЗДЕЛЕНИЕ ДВИЖЕНИЙ И ПРИБЛИЖЕННОЕ ПОСТРОЕНИЕ РЕШЕНИЯ

Экваториальное движение

Следуя методу последовательных приближений, для построения решения при малых значениях z/ρ пренебрежем в первом и втором уравнениях (4), соответственно, квадратом и кубом этого отношения. Рассмотрим вначале экваториальное движение, когда ${{z}_{0}} = 0,$ $\frac{{d{{z}_{0}}}}{{dt}} = 0.$ В этом приближении изменение ρ, определяемое первым интегралом (5), происходит в центральном поле и находится обращением квадратуры

(17)

$t = \pm \frac{1}{{\sqrt 2 }}\int\limits_{{{\rho }_{0}}}^\rho {\frac{{d\rho }}{{\sqrt {f\left( \rho \right)} }}} ,$

где

(18)

$f\left( \rho \right) = U\left( {\rho ,0} \right) - \frac{{{{c}^{2}}}}{{2{{\rho }^{2}}}} + h,$

причем для действительного движения должно быть выполнено условие

(19)

$h \geqslant \frac{{{{c}^{2}}}}{{2{{\rho }^{2}}}} - U\left( {\rho ,0} \right).$

В дальнейшем, не вводя существенных ограничений, будем считать, что

(20)

${{\rho }_{0}} = {{\rho }_{{{\text{min}}}}},\,\,\,\,\frac{{d{{\rho }_{0}}}}{{dt}} = 0,\,\,\,\,{{\theta }_{0}} = 0,\,\,\,\,\frac{{d{{\theta }_{0}}}}{{dt}} = \frac{c}{{\rho _{0}^{2}}}$

при t = 0.

Для нахождения зависимости ρ(t) в случае ее ограниченного (либрационного) изменения $\left( {0 < {{\rho }_{{{\text{min}}}}} < \rho < {{\rho }_{{{\text{max}}}}}} \right)$ мы применяем разработанный ранее приближенный полуаналитический метод (Вашковьяк, 2018), вкратце описываемый ниже.

Постоянные c и h заданием экстремальных значений ${{\rho }_{{{\text{min}}}}},$ ${{\rho }_{{{\text{max}}}}}$ однозначно определяются следующими формулами

(21)

$\begin{gathered} c = {{\rho }_{{\min }}}{{\rho }_{{\max }}}\sqrt {\frac{{2\left[ {U\left( {{{\rho }_{{\min }}},0} \right) - U\left( {{{\rho }_{{\max }}},0} \right)} \right]}}{{\rho _{{\max }}^{2} - \rho _{{\min }}^{2}}}} , \\ h = \frac{{\rho _{{\min }}^{2}U\left( {{{\rho }_{{\min }}},0} \right) - \rho _{{\max }}^{2}U\left( {{{\rho }_{{\max }}},0} \right)}}{{\rho _{{\max }}^{2} - \rho _{{\min }}^{2}}}. \\ \end{gathered} $

В предположении, что ρ_min и ρ_max являются простыми нулями функции f(ρ) она представима в виде

(22)

$f\left( \rho \right) = g\left( \rho \right)\left( {\rho - {{\rho }_{{{\text{min}}}}}} \right)\left( {{{\rho }_{{{\text{max}}}}} - \rho } \right),$

причем два последних множителя, очевидно, отражают главное качественное свойство ограниченного движения. При этом функция $g\left( \rho \right)$ вычисляется по известному выражению (18) и заданным экстремальным значениям ρ_min, ρ_max как

(23)

$g\left( \rho \right) = \frac{{f\left( \rho \right)}}{{\left( {\rho - {{\rho }_{{{\text{min}}}}}} \right)\left( {{{\rho }_{{{\text{max}}}}} - \rho } \right)}}.$

Далее для приведения интеграла (17) к эллиптическому виду применяется аппроксимация функции g(ρ) квадратичным полиномом

(24)

$\begin{gathered} P(\rho ){\text{ }} = {{p}_{1}}{{\rho }^{2}} + {{p}_{2}}\rho + {{p}_{3}} = \\ = {{p}_{1}}(\rho --{{\rho }_{1}}){\text{ }}(\rho --{{\rho }_{2}})\quad \approx \quad\,g(r). \\ \end{gathered} $

Таким образом, при фиксированных постоянных значениях с и h аналитическое решение для его построения требует предварительного вычисления коэффициентов аппроксимирующего полинома. Далее после замены f(ρ) на $Q\left( \rho \right) = P\left( \rho \right)\left( {\rho - {{\rho }_{{{\text{min}}}}}} \right)\left( {{{\rho }_{{{\text{max}}}}} - \rho } \right)$ в квадратуре (17) с помощью ее обращения находится зависимость ρ(t), а затем вычислением интеграла (6) определяется и θ(t). Эти зависимости, содержащие эллиптические функции и интегралы, описаны в работе (Вашковьяк, 2018), а здесь будет приведен лишь их общий вид, когда дискриминант квадратного уравнения P(ρ) = 0 отрицателен, а корни ρ₁ и ρ₂ – комплексно-сопряженные (именно этот случай реализуется в рассматриваемых далее конкретных численных примерах).

Зависимость расстояния от времени определяется формулами

(25)

$\begin{gathered} \rho \left( t \right) = \frac{{\alpha + \beta {\text{cn}}\nu t}}{{\gamma + \delta {\text{cn}}\nu t}},\,\,\,\,{{k}^{2}} = \frac{{{{{\left( {{{\rho }_{4}} - {{\rho }_{3}}} \right)}}^{2}} - {{\delta }^{2}}}}{{4pq}}, \\ \nu = \sqrt {2{{p}_{1}}pq} , \\ \end{gathered} $

где cn$\nu t$ – эллиптический косинус Якоби с модулем k, а постоянные величины α, β, γ, δ, p, q зависят от коэффициентов аппроксимирующего полинома P(ρ) и двух действительных (заданных) корней ${{\rho }_{{{\text{min}}}}},$ ${{\rho }_{{{\text{max}}}}}$ полинома Q(ρ).

Зависимость ρ(t) является периодической функцией времени с периодом

(26)

${{T}_{\rho }} = \frac{4}{\nu }{\mathbf{K}}\left( k \right),$

где K(k) – полный эллиптический интеграл 1-го рода с модулем k.

Зависимость от времени полярного угла θ определяется путем нахождения интеграла в формуле (6). Подстановка в его подынтегральное выражение зависимости ρ(τ), согласно формулам (25), дает

(27)

$\theta \left( t \right) = \frac{c}{\nu }{{\left( {\frac{\delta }{\beta }} \right)}^{2}}\left[ {\nu t + 2s{{I}_{1}}\left( t \right) + {{s}^{2}}{{I}_{2}}\left( t \right)} \right],$

где

$\begin{gathered} {{I}_{l}}\left( t \right) = \int\limits_0^{\nu t} {\frac{{dw}}{{{{{\left( {b + {\text{cn}}w} \right)}}^{l}}}}} ,\,\,\,\,\left( {l = 1,2} \right),\,\,\,\,b = \frac{\alpha }{\beta }, \\ s = \frac{\gamma }{\delta } - b. \\ \end{gathered} $

Интегралы I_l выражаются через тригонометрические функции и неполные эллиптические интегралы 1-го, 2-го и 3-го рода.

Широтное движение

При отличии величины $\frac{{d{{z}_{0}}}}{{dt}}$ от нуля в движении спутника будут присутствовать отклонения, связанные с изменением аппликаты z или широты $\varphi = {\text{arctg}}\left( {{z \mathord{\left/ {\vphantom {z \rho }} \right. \kern-0em} \rho }} \right).$ По аналогии с невозмущенным кеплеровским движением зададим начальные условия широтного движения в перицентре орбиты формулами

(28)

$\begin{gathered} {{z}_{0}} = {\text{ }}0,\,\,\,\,\frac{{d{{z}_{0}}}}{{dt}} = {{V}_{0}}{\kern 1pt} {\kern 1pt} {\text{sin}}{\kern 1pt} {\kern 1pt} {{i}_{0}},\,\,\,\,{{V}_{0}} = \sqrt {\frac{{\mu \left( {1 + e} \right)}}{{a\left( {1 - e} \right)}}} , \\ a = \frac{1}{2}\left( {{{\rho }_{{{\text{max}}}}} + {{\rho }_{{{\text{min}}}}}} \right),\,\,\,\,e = \frac{1}{{2a}}\left( {{{\rho }_{{{\text{max}}}}} - {{\rho }_{{{\text{min}}}}}} \right), \\ \end{gathered} $

где начальное наклонение орбиты i₀ будем предполагать достаточно малой величиной порядка нескольких градусов и $\left| \varphi \right| \leqslant {{i}_{0}}.$

При малых значениях z изменение этой координаты определяется линейным дифференциальным уравнением второго порядка

(29)

$\frac{{{{d}^{2}}z}}{{d{{t}^{2}}}} + R\left( t \right)z = 0.$

Здесь, согласно последней формуле (16) для производной ${{\left. {\frac{{\partial U}}{{\partial z}}} \right|}_{{z \to 0}}},$ функция

(30)

$R\left( t \right) = \frac{{3\mu }}{{{{b}^{3}}}}\left[ {\xi {\text{ - arctg}}\left( \xi \right)} \right] \geqslant 0.$

Она исходно зависит от расстояния ρ посредством ξ и фактически является функцией времени, поскольку в первом приближении ρ(t) определяется периодической зависимостью (25), так что

(31)

$R\left( {t + {{T}_{\rho }}} \right) = R\left( t \right),$

а период этой функции дается формулой (26).

Дифференциальное уравнение (29), известное как уравнение Хилла, в векторной форме имеет вид

(32)

$\frac{{d{\mathbf{x}}}}{{dt}} = A\left( t \right){\mathbf{x}},$

где

(33)

${\mathbf{x}} = {{\left( {z,\,\,\frac{{dz}}{{dt}}} \right)}^{{\text{т }}}},\,\,\,\,A\left( {t + {{T}_{\rho }}} \right) = A\left( t \right) = \left( {\begin{array}{*{20}{c}} 0&1 \\ { - R\left( t \right)}&0 \end{array}} \right),$

а верхний значок “т” означает транспонирование.

Согласно теории Ляпунова–Флоке (см., например, Якубович и Старжинский, 1972, гл. VII; Малкин, 1966, гл. V), решение дифференциального уравнения (32) с периодическими коэффициентами может быть получено путем вычисления фундаментальной матрицы (матрицанта) X(t), удовлетворяющей уравнению

(34)

$\frac{{dX}}{{dt}} = A\left( t \right)X,$

при начальном условии $X\left( 0 \right) = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right) = {{E}_{2}},$ а также матрицы монодромии M = X(T_ρ). При этом вектор x(t) находится по формуле

(35)

${\mathbf{x}}\left( t \right) = X\left( t \right){{{\mathbf{x}}}_{0}},$

где ${{{\mathbf{x}}}_{0}} = {{\left( {{{z}_{0}},{}^{{}}\frac{{d{{z}_{0}}}}{{dt}}} \right)}^{{\text{Т }}}}$ – вектор начальных данных. Матрицант X(t) для произвольного момента времени t > T_ρ определяется формулой

(36)

$\begin{gathered} X\left( {t > {{T}_{\rho }}} \right) = X\left( {0 \leqslant t \leqslant {{T}_{\rho }}} \right){{M}^{n}}, \\ n = {\text{Entier}}\left( {{t \mathord{\left/ {\vphantom {t {{{T}_{\rho }}}}} \right. \kern-0em} {{{T}_{\rho }}}}} \right). \\ \end{gathered} $

Таким образом, для построения широтного движения требуется нахождение матрицанта $X\left( t \right)$ лишь на ограниченном промежутке времени $\left[ {0 \leqslant t \leqslant {{T}_{\rho }}} \right],$ что без существенных вычислительных затрат может быть выполнено численным методом с контролем равенства ${\text{det}}X\left( t \right) \equiv 1.$

Свойства широтного движения существенно зависят от собственных чисел σ матрицы монодромии M (мультипликаторов), удовлетворяющих уравнению

(37)

${\text{det}}\left( {M - \sigma {{E}_{2}}} \right) = 0$

и от характеристических показателей $\alpha = \frac{1}{{{{T}_{\rho }}}}{\text{ln}}\sigma .$ Общее решение уравнения (32) представимо в виде произведений T_ρ – периодических функций на exp(αt), а σ определяются простейшими формулами

(38)

${{\sigma }_{{1,2}}} = B \pm \sqrt {{{B}^{2}} - 1} ,$

где $B = \frac{1}{2}{\text{Tr}}M$ – половина следа матрицы монодромии.

Если величина B > 1, то мультипликаторы и характеристические показатели положительны. В этом случае широтное движение описывается колебаниями периода T_ρ с экспоненциально возрастающей амплитудой, так что величина z выходит за пределы применимости линейного приближения (29).

Если B < 1, то комплексно сопряженные мультипликаторы лежат на единичной окружности $\left| {{{\sigma }_{1}}} \right| = \left| {{{\sigma }_{2}}} \right| = 1,$ а характеристические показатели чисто мнимы. Широтное движение ограниченно и описывается суперпозицией колебаний с ограниченными амплитудами и периодами T_ρ и T_α = = 2π/α.

МЕТОДИЧЕСКИЕ ПРИМЕРЫ РЕШЕНИЯ МОДЕЛЬНЫХ ЗАДАЧ

В данном разделе проводится сопоставление результатов, полученных двумя принципиально различными методами. Начальные параметры движения определяются формулами (20), (28), и этот полный набор начальных данных служит для расчета ограниченного движения вблизи экваториальной плоскости астероида как полуаналитическим методом, так и с помощью численного интегрирования уравнений (2) с контролем постоянства c и h вдоль решения. В качестве примеров рассматривается движение околоэкваториальных гипотетических спутников астероидов Цереры и Весты, которые предполагаются сжатыми сфероидами. В табл. 1 приведены их физические характеристики – гравитационные параметры μ, радиусы сфер Хилла R_H, геометрические размеры D₁ ≈ D₂ > D₃, периоды осевого вращения T_rot, а также начальное наклонение орбит спутников и их апсидальные расстояния.

Таблица 1.

Параметры астероидов и спутниковых орбит

Параметр	Церера	Веста
μ, км³ с^–2	62.6	17.8
R_H, км	223 500	125 500
D₁ = 2a₁, км	964.4	572.6
D₂ = 2a₂, км	964.2	557.2
D₃ = 2a₃, км	891.8	446.4
T_rot, час	9.074	5.342
i, град	3	3
ρ_min, км	800	400
ρ_max, км	1583.64	700.85

В принятой модели сфероида предполагается, что D₁ = D₂ (a₁ = a₂) для обоих астероидов, а их осевые вращения происходят вокруг меньших полуосей a₃.

Минимальные расстояния спутников Цереры и Весты считаются заданными, а высоты перицентров составляют примерно 318 и 114 км, соответственно. Максимальные расстояния приняты такими, чтобы они соответствовали кеплеровским орбитам спутников с периодами обращения, равными T_rot, т.е. – синхронным спутникам астероидов. Начальное малое наклонение спутниковых орбит принято равным 3°. Вычислительный временной интервал составляет два дня или примерно от 5–9 орбитальных периодов обращения спутников.

Предварительно для каждого из примеров по методу наименьших квадратов произведены аппроксимация функции g(ρ), определяемой формулой (23), квадратичным полиномом P(ρ) на отрезке ρ_min = ρ₃ ≤ ρ ≤ ρ₄ = ρ_max, вычисление его дискриминанта D и корней ρ₁, ρ₂.

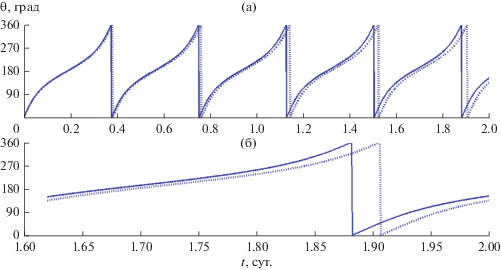
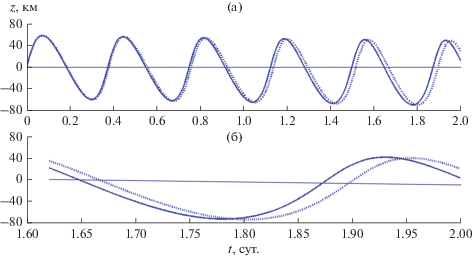
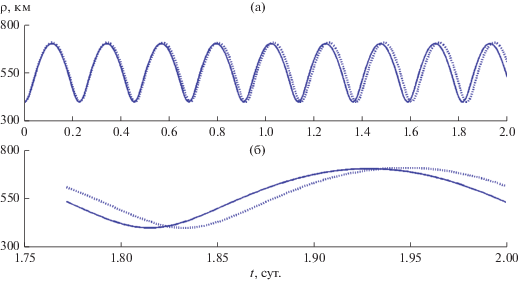
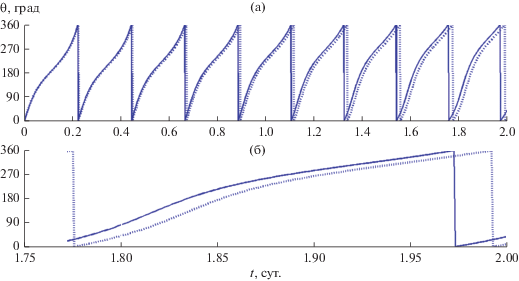
Сравнительные результаты расчетов зависимостей от времени расстояния полярного угла и аппликаты для спутника Цереры показаны на рис. 1–3 .

Рис. 1.

Зависимости от времени расстояния ρ для спутника Цереры (сплошные кривые – полуаналитическое решение, пунктирные кривые – численное решение).

Рис. 2.

То же самое, что и на рис. 1, но для полярного угла θ.

Рис. 3.

То же самое, что и на рис. 1, но для аппликаты z.

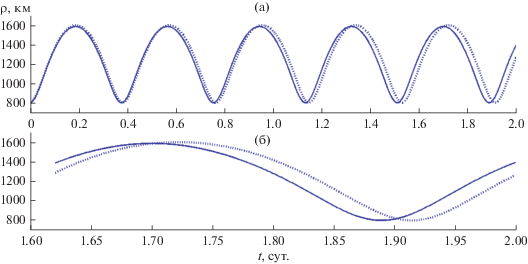
На фрагментах а этих рисунков представлен интервал времени два дня, а на фрагментах б – существенно меньший интервал, соответствующий последнему обороту спутника. Именно фрагменты б позволяют получить наглядную количественную оценку методической погрешности предлагаемого приближенного решения, обусловленной аппроксимацией функции g(ρ) (23) квадратичным полиномом Р(ρ) (24). На рис. 3а можно заметить слабое и кажущееся вековым изменение среднего и экстремальных значений z. В действительности это долгопериодическое изменение с периодом T_α, который здесь составляет примерно 22.5 дня и модулирует короткопериодическое изменение z с периодом T_ρ≈ T_rot = 9.074 ч.

Аналогичные зависимости для спутника Весты показаны рис. 4–6 .

Рис. 4.

То же самое, что и на рис. 1, но для спутника Весты.

Рис. 5.

То же самое, что и на рис. 2, но для спутника Весты.

Рис. 6.

То же самое, что и на рис. 3, но для спутника Весты.

На рис. 6а можно более отчетливо, чем на рис. 3а, заметить долгопериодическое изменение с периодом T_α, который здесь составляет примерно 2.6 дня и модулирует короткопериодическое изменение z с периодом T_ρ≈ T_rot = 5.034 ч.

ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

В данной работе предложен полуаналитический метод и описаны его возможности для нахождения приближенного решения задачи о движении спутника вблизи экваториальной плоскости однородного сжатого сфероида в виде зависимостей координат от времени. При построении экваториального движения спутника для принятых динамических и геометрических характеристик сфероида использование метода, вообще говоря, предусматривает либо предварительное нахождение экстремальных (апсидальных) значений расстояния с помощью численного решения строгих уравнений, либо априорное задание этих параметров. Получение аналитических зависимостей от времени расстояния и полярного угла выполняется с помощью разработанной ранее методики построения движения в центральном гравитационном поле. Для решения уравнения, описывающего широтное движение, требуется его численное интегрирование на относительно коротком интервале времени – периоде изменения расстояния в экваториальном движении. Продолжение этого решения для произвольного момента времени осуществляется с использованием матрицы монодромии.

На частных примерах орбит гипотетических спутников Цереры и Весты продемонстрировано качественное и приближенно количественное согласие результатов расчетов, выполненных предложенным методом и методом численного интегрирования уравнений движения в поле притяжения однородного сжатого сфероида.

Список литературы

Вашковьяк М.А. Метод построения ограниченного движения в центральном поле произвольного вида // Астрон. вестн. 2018. Т. 52. № 4. С. 364–376. (Vashkov’yak M.A. A method for construction of a restricted motion in an arbitrary central field // Sol. Syst. Res. 2018. V. 52. № 4. P. 359–370. doi 10.1134/ S003809461804007X
Гуо П., Ивашкин В.В. Методы вычисления потенциала однородного трехосного эллипсоида и их применение к анализу динамики спутника астероида // Препринт ИПМ им. М.В. Келдыша. 2018. № 94. 32 с. doi 10.20948/prepr-2018-94
URL: http://library.keldysh.ru/preprint.asp?id=2018-94.
Дубошин Г.Н. Теория притяжения. М.: Физматлит, 1961. 288 с.
Дубошин Г.Н. Небесная механика. Аналитические и качественные. М.: Физматлит, 1964. 560 с.
Ивашкин В.В., Лан А. Построение траекторий космического аппарата для экспедиции Земля-астероид-Земля с учетом выбора орбит пребывания у астероида // Препринт ИПМ им. М.В. Келдыша. 2018. № 90. 27 с. doi 10.20948/prepr-2018-90
URL: http://library.keldysh.ru/preprint.asp?id=2018-90.
Кондратьев Б.П. Теория потенциала. Новые методы и задачи с решениями. М.: Мир, 2007. 511 с.
Малкин И.Г. Теория устойчивости движения. М.: Наука, Физматлит, 1966. 530 с.
Якубович В.Я., Старжинский В.М. Линейные дифференциальные уравнения с периодическими коэффициентами и их приложения. М.: Наука, Физматлит, 1972. 718 с.
Konopliv A.S., Asmar S.W., Bills B.G., Mastrodemos N., Park R.S., Raymond C.A., Smith·D.E., Zuber M.T. The dawn gravity investigation at Vesta and Ceres // Space Sci. Rev. 2011. V. 163. P. 461–486. doi 10.1007/s11214-011-9794-8
Fatou P. Sur le mouvement d’un point materiel dans un champ de gravitation fixe (Memoire posthume) // Acta Astron. 1931. Ser. a. 2. P. 101.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал