Астрономический вестник, 2019, T. 53, № 6, стр. 467-474
Основное свойство интеграла Якоби для гравитационных маневров в Солнечной системе
Ю. Ф. Голубев a, *, А. В. Грушевский a, **, И. П. Киселева a, В. В. Корянов a, ***, А. Г. Тучин a, ****, Д. А. Тучин a, *****
a ИПМ им. М.В. Келдыша РАН
Москва, Россия
* E-mail: golubev@keldysh.ru
** E-mail: alexgrush@rambler.ru
*** E-mail: korianov@keldysh.ru
**** E-mail: tag@kiam1.rssi.ru
***** E-mail: den@kiam1.rssi.ru
Поступила в редакцию 22.05.2019
После доработки 06.06.2019
Принята к публикации 13.06.2019
Аннотация
В рамках круговой ограниченной задачи трех тел (ОЗТТ) поиск асимптотической скорости КА ${{V}_{\infty }}$ для гравитационных маневров (ГМ) может производиться с использованием интеграла Якоби $J$ и основного свойства постоянной интеграла Якоби для ГМ ${\text{const}} = J \approx 3 - V_{\infty }^{2}.$ В работе показано, что стандартный и громоздкий способ традиционного вывода этого свойства, применяемый в современной астродинамике, может быть значительно упрощен.
ВВЕДЕНИЕ
Проектирование современных космических миссий к телам Солнечной системы предполагает использование гравитационных маневров (Labunsky и др., 1998; Campagnola и др., 2009; Strange и др., 2007; Голубев и др., 2014; Тучин и др., 2018). Применение гравитационных маневров уменьшает расход характеристической скорости космического аппарата (КА) и обеспечивает тем самым возможность решения современных комплексных задач изучения космоса.
Каждый гравитационный маневр (ГМ, GAM – Gravity Assist Maneuver) можно рассматривать как составной элемент ограниченной задачи трех тел (ОЗТТ), поскольку, по определению, он предполагает прохождение пробной частицей (КА, кометой, астероидом) сферы действия “малого тела” (планеты, спутника планеты, малого тела Солнечной системы). В рамках метода сопряженных конических сечений (МсКС) КА пролетает сферу действия планеты по планетоцентрической гиперболе, а вне ее – движется по гелиоцентрическому коническому сечению (кеплеровой дуге). Время гиперболического прохождения сферы действия планеты считается пренебрежимо малым по сравнению со временем пролета гелиоцентрической дуги. Модули скорости КА относительно малого тела (планеты) при пересечении границ ее сферы действия приблизительно равны величине асимптотической скорости КА ${{V}_{\infty }}$ для планетоцентрической гиперболы.
В дальнейшем полученное с использованием МсКС решение используется в качестве первого приближения для последующего уточнения в соответствии с полной эфемеридной моделью движения небесных тел.
Таким образом, при поиске приближенного решения задачи перелета в рамках модели круговой ОЗТТ с использованием МсКС при переключении на границах сфер действия малых тел с гелиоцентрических дуг на планетоцентрические участки и обратно ${{V}_{\infty }}$ является “передаточным параметром” при переходе от одной модели движения к другой.
В рамках круговой ОЗТТ имеет место сохранение (инвариантность) величины ${{V}_{\infty }}$ асимптотической скорости КА относительно “малого тела” – “планеты” при неоднократном совершении около нее ГМ (Miller, Weeks, 2002), сохраняющих постоянную интеграла Якоби. В МсКС, являющейся, по сути, аппроксимацией круговой ОЗТТ с помощью последовательной склейки нескольких задач двух тел “текущий центр притяжения – пробная частица” с сингулярным переключением с одной на другую, указанное свойство, вообще говоря, очевидно в силу симметрии пролетной планетоцентрической гиперболы на одиночном гравитационном маневре. Вместе с тем, при активном маневрировании КА вне сферы действия малой планеты значение интеграла Якоби может изменяться. Отметим, что для случая плоской ограниченной круговой задачи трех тел в работе (Елькин и др., 2003) также показана инвариантность модуля планетоцентрической скорости как следствие интеграла Якоби с точностью до слагаемых, стремящихся к нулю вместе с отношением масс планеты и Солнца.
В рамках круговой ОЗТТ, с использованием ее интеграла Якоби J, возможно аналитическое вычисление ${{V}_{\infty }}$ с помощью основного свойства этого интеграла для серии ГМ: ${\text{const}} = J \approx 3 - V_{\infty }^{2}$ (в безразмерном виде как отношение к скорости планеты). Вывод этого свойства осуществляется в астродинамике достаточно громоздким способом (Себехей, 1982; Miller, Weeks, 2002; Campagnola, Russell, 2009): от канонической записи интеграла Якоби в синодической системе координат $J$ необходимо совершить переход к сидерической системе координат и его приближенной модификации при его записи через орбитальные оскулирующие элементы, которая становится идентичной параметру Тиссерана ${{T}_{{{\text{Ti}}}}}.$ Далее используются достаточно громоздкие геометрические соображения, позволяющие, тем не менее, приближенно получить основное свойство интеграла Якоби для серии ГМ в круговой ОЗТТ через связь интеграла Якоби, параметра Тиссерана и величины асимптотической скорости КА в виде: ${\text{const}} = J \approx {{T}_{{{\text{Ti}}}}} \approx 3 - V_{\infty }^{2}.$
В настоящей работе предлагается более короткий метод получения указанного основного свойства интеграла Якоби и представлена его геометрическая интерпретация для цепочек многократных ГМ с учетом динамических ограничений на угол разворота вектора асимптотической скорости при совершении элементарного ГМ.
КРУГОВАЯ ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
В рамках круговой ОЗТТ рассматриваются центральное тело с гравитационным параметром
μ1, малое тело с гравитационным параметром ${{\mu }_{2}} < {{\mu }_{1}}$ и пробная частица бесконечно малой массы (КА). Предполагается, что центральное и
малое тела взаимодействуют по закону всемирного тяготения и вращаются вокруг барицентра
с одинаковыми угловыми скоростями. Вводится вращающаяся (синодическая) барицентрическая
система координат $BXYZ,$ где ось BX проходит через центральное и малое тело и направлена в сторону малого тела, ось BY перпендикулярна к оси BX и сонаправлена относительной скорости малого тела, ось BZ дополняет их до правоориентированного репера. Пусть ${{a}_{p}}$ – расстояние между центральным и малым телами, $n = \sqrt {\left( {{{\mu }_{1}} + {{\mu }_{2}}} \right)/a_{p}^{3}} $ – угловая скорость вращения системы $BXYZ,$ ${{\tilde {R}}_{1}},$ ${{\tilde {R}}_{2}}$ – расстояния от пробной частицы (КА) до центрального и малого тел соответственно,
${{\tilde {V}}_{{{\text{sc\_rot}}}}}$ – скорость пробной частицы (КА) относительно вращающейся системы координат $BXYZ.$ Пробная частица не влияет на движения центрального и малого тел, но сама притягивается
к ним по закону притяжения Ньютона. При переходе к безразмерному времени τ = nt, безразмерным координатам КА X, Y, Z и расстояниям r1, r2 от КА до центрального и малого тел, нормированным по ap, безразмерная скорость $V$ пробной частицы (КА) во вращающейся системе координат $BXYZ$ запишется как $V = \frac{{{{{\tilde {V}}}_{{{\text{sc\_rot}}}}}}}{{{{{\tilde {V}}}_{{{\text{pl}}}}}}},$ где ${{\tilde {V}}_{{{\text{pl}}}}}$ – средняя орбитальная скорость планеты относительно центрального тела:
– угловая скорость вращения системы $BXYZ,$ ${{\tilde {R}}_{1}},$ ${{\tilde {R}}_{2}}$ – расстояния от пробной частицы (КА) до центрального и малого тел соответственно,
${{\tilde {V}}_{{{\text{sc\_rot}}}}}$ – скорость пробной частицы (КА) относительно вращающейся системы координат $BXYZ.$ Пробная частица не влияет на движения центрального и малого тел, но сама притягивается
к ним по закону притяжения Ньютона. При переходе к безразмерному времени τ = nt, безразмерным координатам КА X, Y, Z и расстояниям r1, r2 от КА до центрального и малого тел, нормированным по ap, безразмерная скорость $V$ пробной частицы (КА) во вращающейся системе координат $BXYZ$ запишется как $V = \frac{{{{{\tilde {V}}}_{{{\text{sc\_rot}}}}}}}{{{{{\tilde {V}}}_{{{\text{pl}}}}}}},$ где ${{\tilde {V}}_{{{\text{pl}}}}}$ – средняя орбитальная скорость планеты относительно центрального тела:
Здесь и далее размерные переменные будем отмечать тильдой.
Интеграл Якоби J является обобщенным интегралом энергии (Голубев и др., 2019), учитывающим действие центробежных сил, и единственным интегралом в круговой ОЗТТ (Murray, Dermot, 1999; Себехей, 1982). При этом не сохраняются ни энергия системы в обычном понимании, ни ее кинетический момент.
Выпишем выражения интеграла Якоби для ограниченной круговой задачи трех тел (в синодической и сидерической системах координат, в размерной и безразмерной форме).
ИНТЕГРАЛ ЯКОБИ
Интеграл Якоби $\tilde {J}$ для пробной частицы (КА) в синодической системе координат $BXYZ$ можно записать в виде (Jacobi, 1836; Себехей, 1982; Murray, Dermot, 1999):
В сидерической (инерциальной) системе координат $B\xi \eta \zeta ,$ для которой ось $B\zeta $ сонаправлена с осью BZ, с учетом того, что по теореме сложения скоростей (Голубев и др., 2019)
(1)
$\begin{gathered} {{{\tilde {V}}}^{2}} = {{{\dot {\tilde {X}}}}^{2}} + {{{\dot {\tilde {Y}}}}^{2}} + {{{\dot {\tilde {Z}}}}^{2}} = \\ = \,\,{{{{\tilde {v}}}}^{2}} + {{n}^{2}}({{{\tilde {\xi }}}^{2}} + {{{\tilde {\eta }}}^{2}}) - 2n(\tilde {\xi }\dot {\tilde {\eta }} - \tilde {\eta }\dot {\tilde {\xi }}), \\ \end{gathered} $В безразмерном виде обе формы интеграла Якоби соответственно примут вид
(2)
$J = ({{X}^{2}} + {{Y}^{2}}) + 2\frac{{1 - \mu }}{{{{r}_{1}}}} + 2\frac{\mu }{{{{r}_{2}}}} - {{V}^{2}},$(3)
$J = 2(\xi \dot {\eta } - \eta \dot {\xi }) + 2\frac{{1 - \mu }}{{{{r}_{1}}}} + 2\frac{\mu }{{{{r}_{2}}}} - {{{v}}^{2}},$КЛАССИЧЕСКИЙ ВЫВОД ОСНОВНОГО СВОЙСТВА СЕРИИ ГРАВИТАЦИОННЫХ МАНЕВРОВ: ${\text{const}} = J \approx {{T}_{{{\text{Ti}}}}} \approx 3 - V_{\infty }^{2}$
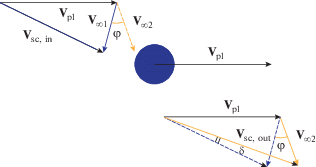
В классической постановке (Labunsky и др., 1998; Miller, Weeks, 2002; Голубев и др., 2017) гравитационный маневр описывается сингулярным прохождением КА сферы действия малого тела (планеты). Область проведения ГМ (с момента t1 входа в сферу действия второго тела до момента t2 выхода из нее) считается ничтожной по сравнению с участками гелиоцентрического движения и заменяется точкой склейки (рис. 1). На рисунке ${{{\mathbf{V}}}_{{{\text{sc,in}}}}}$ – вектор скорости КА относительно центрального тела до входа в сферу действия планеты, ${{{\mathbf{V}}}_{{{\text{sc,out}}}}}$ – соответствующий вектор скорости при выходе из сферы действия планеты (после проведения гравитационного маневра), ${{{\mathbf{V}}}_{{{\text{pl}}}}}$ – скорость планеты.
Угол $\delta $ излома вектора гелиоцентрической скорости КА определяется с помощью угла раствора $\varphi $ пролетной гиперболы относительно планеты. Модуль вектора асимптотической скорости КА ${{V}_{\infty }}$ относительно планеты-партнера при этом не меняется, $\left\| {{{{\mathbf{V}}}_{{\infty {\text{1}}}}}} \right\| = {{V}_{\infty }},$ однако сам вектор ${{{\mathbf{V}}}_{{\infty 1}}}$ поворачивается на угол $\varphi $ и переходит в ${{{\mathbf{V}}}_{{\infty 2}}},$ так что $\left\| {{{{\mathbf{V}}}_{{\infty {\text{1}}}}}} \right\| = \left\| {{{{\mathbf{V}}}_{{\infty 2}}}} \right\| = {{V}_{\infty }}.$
Основное свойство интеграла Якоби в круговой ОЗТТ для серии гравитационных маневров выводится в астродинамике достаточно громоздким способом (Себехей, 1982; Miller, Weeks, 2002; Campagnola, Russell, 2009). Рассматривается интеграл Якоби в сидерической системе координат. Приближенное представление этого интеграла через орбитальные оскулирующие элементы оказывается идентичным параметру Тиссерана (Tisserand, 1896). Далее, с использованием весьма громоздких геометрических соображений, становится возможным получить в приближенном виде основное свойство через связь интеграла Якоби, параметра Тиссерана и величины асимптотической скорости КА при совершении гравитационных маневров. Представим основные этапы традиционного получения в астродинамике основного свойства интеграла Якоби для гравитационных маневров ${\text{const}} = J \approx {{T}_{{{\text{Ti}}}}} \approx 3 - V_{\infty }^{2},$ сохраняющих модуль вектора асимптотической скорости КА (Miller, Weeks, 2002; Campagnola, Russell, 2009).
1. Выписывается выражение для интеграла Якоби J во вращающейся (синодической) барицентрической системе координат $BXYZ{\text{:}}$
2. С использованием теоремы сложения скоростей и интеграла площадей переходят к выражению интеграла Якоби в инерциальной (сидерической) системе координат $B\xi \eta \zeta {\text{:}}$
3. С использованием оскулирующих орбитальных элементов, при допущении верности предельного перехода $\frac{\mu }{{{{r}_{2}}}} \to 0$ (т.е. $\mu $ мало и КА находится за пределами сферы действия планеты), в качестве промежуточного вспомогательного результата выводится классический критерий Тиссерана:
(4)
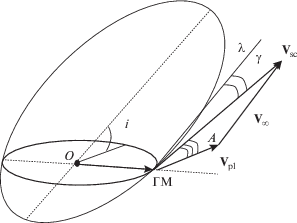
${\text{const}} = J \approx {{T}_{{{\text{Ti}}}}} \approx \frac{{1 - \mu }}{a} + 2\sqrt {(1 - \mu )a(1 - {{e}^{2}})} \cos i,$4. На этом, в рамках классической модели круговой ОЗТТ (Murray, Weeks, 1999; Себехей, 1982), ход традиционных преобразований заканчивается. Для вычисления ${{V}_{\infty }}$ и вывода основного свойства подключается непосредственно описанная выше модель ГМ, а формула для модуля асимптотической скорости КА относительно планеты ${{V}_{\infty }}$ выводится с помощью следующих геометрических рассуждений. Пусть $A$ – угол между скоростями планеты и КА в точке входа в сферу действия планеты при совершении ГМ. Согласно формулам (16), (19) из (Miller, Weeks, 2002), либо (39), (40) (Campagnola, Russell, 2009), с использованием формул (3) и (5) при ${{r}_{1}} \to 1,$ $\mu \to 0$ и теоремы косинусов для основного треугольника ГМ верно (рис. 2):
5. Введем γ – траекторный угол орбиты КА в точке пересечения сферы действия планеты (угол между вектором скорости КА ${{{\mathbf{V}}}_{{{\mathbf{sc}}}}}$ и вектором местной горизонтали ${\mathbf{\lambda }}$). Рассмотрим в точке совершения гравитационного маневра трехгранный угол с образующими – векторами орбитальных скоростей планеты, КА и ${\mathbf{\lambda }}$ (рис. 2). Из его свойств следует, что cos A = cos γ cos i и
6. Воспользовавшись соотношением $\cos \;\gamma = \;{h \mathord{\left/ {\vphantom {h {{{r}_{1}}{v}}}} \right. \kern-0em} {{{r}_{1}}{v}}}{\text{,}}$ выпишем выражения для $\frac{1}{a}$ и $h{\text{:}}$
7. В результате, с использованием (4) и выражения $h = \sqrt {(1 - \mu )a(1 - {{e}^{2}})} ,$ приходим, наконец, к получению основного свойства интеграла Якоби в круговой ОЗТТ для серии ГМ:
(5)
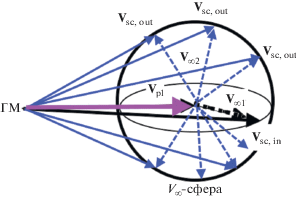
$\begin{gathered} {\text{const}} = J \approx {{T}_{{{\text{Ti}}}}} \approx \frac{1}{a} + 2h\cos i = \\ = 3 - 2h\cos i - V_{\infty }^{2} + 2h\cos i = 3 - V_{\infty }^{2}. \\ \end{gathered} $Формула (5) выражает важнейшее свойство серии ГМ в модели круговой ОЗТТ: ${{V}_{\infty }} = {\text{const}},$ что позволяет, в целях эффективного баллистического проектирования космических миссий с использованием ГМ, оперировать в ее рамках с такими геометрически прозрачными объектами, как ${{V}_{\infty }}$-сфера (сфера с радиусом ${{V}_{\infty }}$, центр которой находится на конце вектора скорости ${{{\mathbf{V}}}_{p}}$ планеты) и ее проекциями на плоскость Tour maps (Strange и др., 2007). Как при движении КА по гелиоцентрической дуге, так и при совершении им гравитационного маневра конец вектора асимптотической скорости ${{{\mathbf{V}}}_{\infty }}$ всегда будет оставаться на ${{V}_{\infty }}$-сфере (рис. 3). Отметим, что, в частности, непосредственно при совершении ГМ, в рамках ограниченной задачи двух тел, свойство ${{V}_{\infty }} = {\text{const}}$ следует из того, что КА движется относительно планеты в ее сфере действия по планетоцентрической гиперболе (Голубев и др., 2019, с. 267).
ЭКСПРЕСС-ВЫВОД ОСНОВНОГО СВОЙСТВА ИНТЕГРАЛА ЯКОБИ ДЛЯ ГРАВИТАЦИОННЫХ МАНЕВРОВ В КРУГОВОЙ ОЗТТ
Классический вывод в астродинамике основного свойства интеграла Якоби в круговой ОЗТТ представляется достаточно громоздким (Себехей, 1982; Miller, Weeks, 2002; Campagnola, Russell, 2009). Укажем на более короткий и наглядный вывод этого свойства с использованием модели МсКС, даже не выходя при этом из синодической системы координат.
1. Пусть в качестве центрального тела выбрано Солнце. Тогда для всех небесных тел Солнечной системы сфера действия малого небесного тела аппроксимируется эллипсоидом вращения с коэффициентом сжатия $\sqrt[5]{2} \approx 1.15$ и характерным безразмерным радиусом ${{\rho }_{2}} = {{\left( {\frac{\mu }{{1 - \mu }}} \right)}^{{\frac{2}{5}}}} \ll 1$ (Абалакин и др., 1976). Как следствие, при моделировании ГМ, для значений ${{r}_{2}} \leqslant {{\rho }_{2}}$ расстояние ${{\tilde {R}}_{1}}$ от КА до центрального тела можно в нулевом приближении заменить расстоянием ${{a}_{p}}$ от планеты до центрального тела, поскольку, очевидно, согласно неравенству треугольника, при проходе сферы действия планеты выполнено:
(6)
$\begin{gathered} {{a}_{p}} - {{\rho }_{2}}{{a}_{p}} \leqslant {{{\tilde {R}}}_{1}} \leqslant {{a}_{p}} + {{\rho }_{2}}{{a}_{p}}, \\ 1 - {{\left( {\frac{\mu }{{1 - \mu }}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0em} 5}}}} \leqslant {{r}_{1}} \leqslant 1 + {{\left( {\frac{\mu }{{1 - \mu }}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0em} 5}}}},\,\,\,\,{{\left. {{{r}_{1}}} \right|}_{{{\text{GAM}}}}} \approx 1. \\ \end{gathered} $2. Напомним, что в выражении интеграла Якоби (2) величина $V$ является скоростью пробной частицы относительно синодической системы координат. Однако при сближении с планетой и совершении около нее ГМ выполняется (6), и скорость КА относительно синодической системы координат $V$ приблизительно равна скорости КА относительно планеты, замороженной в этой системе координат.
3. Скорость КА относительно планеты на границе сферы действия этой планеты приблизительно равна входящей асимптотической скорости КА относительно этой планеты ${{V}_{\infty }}.$
4. С учетом (2) приходим к требуемому выражению интеграла Якоби при совершении ГМ:
(7)
$\begin{gathered} {{\left. J \right|}_{{{\text{GAM}}}}} = J \approx 1 + 2 - \\ - \,\,2\mu - V_{\infty }^{2} = 3 - V_{\infty }^{2},\,\,\,\,J \approx 3 - V_{\infty }^{2}. \\ \end{gathered} $Выражение (7) является хотя и приближенным, но общим для всех планет и планетных систем Солнечной системы. Оно очень удобно для предварительных оценочных расчетов эффективности гравитационных маневров.
5. В сидерической системе координат выражение интеграла Якоби при совершении GAM, двойственное (7), можно переписать в случае малости ${\mu \mathord{\left/ {\vphantom {\mu {{{r}_{2}}}}} \right. \kern-0em} {{{r}_{2}}}}$ в виде
(8)
$\begin{gathered} {{\left. J \right|}_{{{\text{GAM}}}}} = J \approx 2(\xi \dot {\eta } - \eta \dot {\xi }) + 2 - 2\mu + 2\frac{\mu }{{{{r}_{2}}}} - {{{v}}^{2}}, \\ J = 2U - {{{v}}^{2}} = \frac{{1 - \mu }}{a} + 2\frac{\mu }{{{{r}_{2}}}} + \\ + \,\,2\sqrt {(1 - \mu )a(1 - {{e}^{2}})} \cos i \approx {{T}_{{{\text{Ti}}}}}, \\ J \approx \frac{1}{a} + 2\sqrt {a(1 - {{e}^{2}})} \cos i = {{T}_{{{\text{Ti}}}}}, \\ \end{gathered} $Выражение (7) означает, что величина ${{V}_{\infty }}$ асимптотической скорости КА относительно малого тела, будучи связанной непосредственно с интегралом Якоби, останется постоянной для всех гравитационных маневров, выполняемых последовательно с этой планетой и сохраняющих константу интеграла Якоби, хотя само направление вектора асимптотической скорости может при этом существенно изменяться.
6. Представим также выражение для интеграла Якоби в размерных переменных, совпадающее с классическим (Субботин, 1968) при ${{\mu }_{2}} \to 0{\text{:}}$
(9)
$\begin{gathered} J = \tilde {J}\frac{{{{a}_{p}}}}{{{{\mu }_{1}} + {{\mu }_{2}}}} = \frac{{{{{{\mu }_{1}}} \mathord{\left/ {\vphantom {{{{\mu }_{1}}} {({{\mu }_{1}} + {{\mu }_{2}})}}} \right. \kern-0em} {({{\mu }_{1}} + {{\mu }_{2}})}}}}{{{{\tilde {a}} \mathord{\left/ {\vphantom {{\tilde {a}} {{{a}_{p}}}}} \right. \kern-0em} {{{a}_{p}}}}}} + \\ + \,\,2\frac{{{{{{\mu }_{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}} {({{\mu }_{1}} + {{\mu }_{2}})}}} \right. \kern-0em} {({{\mu }_{1}} + {{\mu }_{2}})}}}}{{{{{{{\tilde {r}}}_{2}}} \mathord{\left/ {\vphantom {{{{{\tilde {r}}}_{2}}} {{{a}_{p}}}}} \right. \kern-0em} {{{a}_{p}}}}}} + 2\sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{1}} + {{\mu }_{2}}}}} \sqrt {\frac{{\tilde {a}}}{{{{a}_{p}}}}(1 - {{e}^{2}})} \cos i. \\ \end{gathered} $7. В астрономии, помимо безразмерных выражений интеграла Якоби $J$ и параметра Тиссерана ${{T}_{{{\text{Ti}}}}},$ нормированных через угловую скорость планеты $n = \sqrt {{{\left( {{{\mu }_{1}} + {{\mu }_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\mu }_{1}} + {{\mu }_{2}}} \right)} {a_{p}^{3}}}} \right. \kern-0em} {a_{p}^{3}}}} $ (Себехей, 1982): ${{T}_{{{\text{Ti}}}}} = {{{{{\tilde {T}}}_{{{\text{Ti}}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {T}}}_{{{\text{Ti}}}}}} {({{n}^{2}}a_{p}^{2}),}}} \right. \kern-0em} {({{n}^{2}}a_{p}^{2}),}}$ используются также безразмерные выражения ${{J}_{{{\text{Astr}}}}},$ ${{T}_{{{\text{Ti\_Astr}}}}},$ нормированные через величину ${{n}_{1}} = \sqrt {{{{{\mu }_{1}}} \mathord{\left/ {\vphantom {{{{\mu }_{1}}} {a_{p}^{3}}}} \right. \kern-0em} {a_{p}^{3}}}} $ (Субботин, 1968): ${{J}_{{{\text{Astr}}}}} = {{\tilde {J}} \mathord{\left/ {\vphantom {{\tilde {J}} {(n_{1}^{2}a_{p}^{2})}}} \right. \kern-0em} {(n_{1}^{2}a_{p}^{2})}},$ ${{T}_{{{\text{Ti}}}}} = {{{{{\tilde {T}}}_{{{\text{Ti}}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {T}}}_{{{\text{Ti}}}}}} {(n_{1}^{2}a_{p}^{2})}}} \right. \kern-0em} {(n_{1}^{2}a_{p}^{2})}}.$ В таком случае можно использовать пересчет между этими безразмерными величинами с помощью правила $J = \frac{{{{\mu }_{1}}}}{{{{\mu }_{1}} + {{\mu }_{2}}}}{{J}_{{{\text{Astr}}}}},$ ${{T}_{{{\text{Ti}}}}} = \frac{{{{\mu }_{1}}}}{{{{\mu }_{1}} + {{\mu }_{2}}}}{{T}_{{{\text{Ti\_Astr}}}}}.$
Отметим, что в постановке круговой ОЗТТ теоретически возможен баллистический захват пробной частицы (КА) малым телом в случае достаточно большого значения отношения ${{{{\mu }_{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}}$ гравитационных параметров центрального тела и планеты (Голубев и др., 2019а). Анализ параметров всех планет Солнечной системы (Standish, 1998), когда большим телом служит Солнце, показывает, что пролетная траектория в сфере действия малой планеты будет гиперболической и баллистический захват в модели МсКС невозможен. Аналогичный результат вытекает и при анализе ОЗТТ для систем планет и их естественных спутников в Солнечной системе (Standish, 1998; JPL Planetary Satellite, 2019) (максимальными в Солнечной системе оказываются отношения гравитационных параметров спутника и планеты – “хозяина” для системы Земля–Луна, ${{{{\mu }_{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}} \approx 0.0123,$ и системы Плутон–Харон, ${{{{\mu }_{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}} \approx 0.0117$). Гигантские галилеевы луны Юпитера – Ио, Европа, Ганимед и Каллисто, так же, как и крупнейший естественный спутник Солнечной системы – Титан у Сатурна, имеют еще меньшее значение ${{{{\mu }_{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}}$ в силу значительной величины гравитационной постоянной их планет-хозяев: ${{{{\mu }_{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}} \leqslant 0.00008$ для галилеевых лун и ${{{{\mu }_{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}} \approx 0.00023$ для системы Сатурн–Титан. Таким образом, представленная в работе математическая небесномеханическая модель удобна для баллистического анализа последовательности гравитационных маневров, однако не позволяет проводить описание тонких эффектов баллистического захвата (Белбруно, 2011).
Представленные в работе рассуждения позволяют выделить прозрачную структуру трансформации основных параметров круговой ОЗТТ при рассмотрении ГМ и использовании модели МсКС.
1. Инвариантность интеграла Якоби глобальна и носит универсальный характер. Интеграл Якоби $J$ не меняет свою величину при проведении гравитационных маневров.
2. Значение параметра Тиссерана ${{T}_{{{\text{Ti}}}}}$ не меняется вдали от сферы действия планеты вплоть до совершения гравитационного маневра: ${{T}_{{{\text{Ti1}}}}} \approx {{\left. {{{T}_{{{\text{Ti0}}}}} \equiv {{T}_{{{\text{Ti}}}}}} \right|}_{{t = 0}}}.$
3. Параметр Тиссерана ${{T}_{{{\text{Ti}}}}}$ меняется сложным образом в процессе совершения гравитационного маневра около планеты.
4. После совершения гравитационного маневра значение ${{T}_{{{\text{Ti}}}}}$ принимает прежнее значение ${{T}_{{{\text{Ti0}}}}}$ и остается далее постоянным до момента совершения следующего гравитационного маневра: ${{T}_{{{\text{Ti2}}}}} \approx {{T}_{{{\text{Ti1}}}}} \approx {{T}_{{{\text{Ti0}}}}}.$
5. Вдали от сферы притяжения малого тела (планеты) параметр Тиссерана примерно равен значению интеграла Якоби: ${{T}_{{{\text{Ti}}}}} \approx J.$
6. Значение функции параметра Тиссерана от времени в рамках ОЗТТ равно константе интеграла Якоби за исключением конечного числа точек разрывов первого рода, соответствующих моментам проведения гравитационных маневров.
7. Полученные результаты представлены в виде таблицы трансформации интеграла Якоби и параметра Тиссерана в круговой ОЗТТ (табл. 1).
Таблица 1.
Трансформации интеграла Якоби и параметра Тиссерана в круговой ОЗТТ
| Конфигурация | Интеграл Якоби $J$ и его инвариантность | Параметр Тиссерана ${{T}_{{{\text{Ti}}}}}$ и его постоянство | Скорость в синодической (вращающейся) системе координат | Асимптоти-ческая скорость ${{{v}}_{\infty }}$ | ${{r}_{1}},$ согласно ОЗТТ | ${{r}_{2}},$ согласно ОЗТТ |
|---|---|---|---|---|---|---|
| В сфере действия центрального тела, вне сферы действия планеты | $\begin{gathered} \frac{{1 - \mu }}{a} + 2\frac{\mu }{{{{r}_{2}}}} + \\ + \,\,2\sqrt {(1 - \mu )\;a\;(1 - {{e}^{2}})} \cos i \\ \end{gathered} $ инвариантен |
$\begin{gathered} \frac{{1 - \mu }}{a} + \\ + \,\,2\sqrt {(1 - \mu )\;a\;(1 - {{e}^{2}})} \cos i \\ \end{gathered} $ постоянен |
v | Отсутствует | Произвольная конечная величина при условии невстречи | $ \sim 1$ |
| На границе сферы действия планеты (гравитационный маневр) | $\begin{gathered} \frac{{1 - \mu }}{a} + 2\;{{\mu }^{{\frac{3}{5}}}} + \\ + \,\,2\sqrt {(1 - \mu )\;a\;(1 - {{e}^{2}})} \cos i \\ \end{gathered} $ инвариантен |
$\begin{gathered} \frac{{1 - \mu }}{a} + \\ + \,\,2\sqrt {(1 - \mu )\;a\;(1 - {{e}^{2}})} \cos i \\ \end{gathered} $ постоянен |
${{V}_{\infty }}$ | ${{V}_{\infty }}$ | Отличается от 1 на малую, но конечную величину (при условии пролета) | ${{\left( {\frac{\mu }{{1 - \mu }}} \right)}^{{\frac{2}{5}}}}$ |
| В сфере действия планеты | $3 - V_{\infty }^{2}$ инвариантен |
Нет постоянства | $\sqrt {\frac{{2\mu }}{{{{r}_{2}}}} - V_{\infty }^{2}} $ | ${{V}_{\infty }}$ | Отличается от 1 на малую, но конечную величину (при условии пролета) | Малая конечная величина |
ЗАКЛЮЧЕНИЕ
Проектирование межпланетных траекторий с использованием серии гравитационных маневров начинается с построения баллистического облика. Соответствующее начальное приближение целесообразно строить методом сопряженных конических сечений в рамках модели круговой ограниченной задачи трех тел. При таком построении требуется вычисление “передаточного параметра” ${{V}_{\infty }}$ при переключении с гелиоцентрических дуг на планетоцентрические участки и обратно. В модели круговой ОЗТТ вычисление ${{V}_{\infty }}$ может производиться с использованием интеграла Якоби $J$ и основного свойства интеграла Якоби для гравитационных маневров в постановке круговой ОЗТТ: ${\text{const}} = J \approx {{T}_{{{\text{Ti}}}}} \approx 3 - V_{\infty }^{2}.$ Согласно этому свойству величина ${{V}_{\infty }}$ не изменяется при совершении многократных гравитационных маневров, сохраняющих константу интеграла Якоби. В астродинамике этот факт известен, но выводится достаточно громоздким способом (Miller, Weeks, 2002; Campagnola, Russell, 2009). В настоящей работе предложен более короткий метод его получения. Представлены модификации записи интеграла Якоби в круговой ограниченной задаче трех тел для различных конфигураций трех тел и таблица трансформации интеграла Якоби и параметра Тиссерана для всех случаев.
Список литературы
Абалакин В.К., Аксенов Е.П., Гребеников Е.А., Демин В.Г., Рябов Ю.А. Справочное руководство по небесной механике и астродинамике. Изд. 2-е, дополненное и переработанное / Ред. Дубошин Г.Н. М.: Наука, 1976. 864 с.
Белбруно Э. Динамика захвата и хаотические движения в небесной механике с приложениями к конструированию малоэнергетических перелетов. Ижевский институт компьютерных исследований, 2011. 264 с.
Боровин Г.К., Голубев Ю.Ф., Грушевский А.В., Заславский Г.С., Захваткин М.В., Корянов В.В., Лавренов С.М., Морской И.М., Симонов А.В., Степаньянц В.А., Тучин А.Г., Тучин Д.А., Ярошевский В.С. Баллистико-навигационное обеспечение полетов автоматических космических аппаратов к телам Солнечной системы / Ред. Тучин А.Г. Химки: НПО Лавочкина, 2018. 336 с.
Голубев Ю.Ф., Грушевский А.В., Корянов В.В., Тучин А.Г. Гравитационные маневры космического аппарата в системе Юпитера // Изв. РАН. Теория и системы управления. 2014. № 3. С. 149–167.
Голубев Ю.Ф., Грушевский А.В., Корянов В.В., Тучин А.Г., Тучин Д.А. Формирование орбит космического аппарата с большим наклонением к эклиптике посредством многократных гравитационных маневров // Изв. РАН. Теория и системы управления. 2017. № 2. С. 108–132.
Голубев Ю.Ф., Грушевский А.В., Корянов В.В., Тучин А.Г., Тучин Д.А. Основное свойство интеграла Якоби для гравитационных маневров в Солнечной системе // Препр. ИПМ им. М.В. Келдыша. 2019. № 34. 24 с.
Голубев Ю.Ф. Основы теоретической механики: Учебник. 3-е изд., переработанное и дополненное. М.: Изд-во Московского ун-та, 2019а. 728 с.
Елькин А.В., Соколов Л.Л., Титов В.Б., Шмыров А.С. Квазислучайные движения в гравитационном поле N-планет // Тр. Астрон. обсерватории СПбГУ. 2003. Т. 45. Вып. 436. С. 73–114.
Охоцимский Д.Е. Динамика космических полетов. М.: Изд-во Московского ун-та, 1968. 157 с.
Пуанкаре А. Избранные труды. Т.1. Новые методы небесной механики. М.: Наука, 1971. 772 с.
Себехей В. Теория орбит. Ограниченная задача трех тел. М.: Наука, 1982. 656 с.
Субботин М.Ф. Введение в теоретическую астрономию. М.: Наука, 1968. 800 с.
Campagnola S., Russell R.P. The Endgame problem part B: The Multi-Body Technique and the T-P Graph. Preprint AAS 09‑227. 2009. 20 c.
JPL Planetary Satellite Physical Parameters. URL: https://ssd.jpl.nasa.gov/?sat_phys_par
Labunsky A.V., Papkov O.V., Sukhanov K.G. Multiple Gravity Assist Interplanetary Trajectories // Earth Space Institute Book Series. L.: Gordon and Breach Publ., 1998. P. 292.
Miller J.K., Weeks C.J. Application of Tisserand’s Criterion to the Design of Gravity Assist Trajectories // AAS/AIAA Astrodynamics Specialist Conf. and Exhibit, Monterey, GA, 2002. AIAA 2002-4717. P. 7.
Murray C.D., Dermot S.F. Solar System Dynamics. Cambridge, England: Cambridge Univ. Press, 1999. P. 592. ISBN 0‑521-57597-4
Standish E.M. JPL Planetary and Lunar Ephemerides, DE405/LE405. 1998.
Strange N.J., Russell R., Buffington B. Mapping the V∞ Globe // AAS/AIAA Astrodynamics Specialist Conference and Exhibit. Mackinac Island, MI, 2007. AAS Paper 07‑277. P. 24.
Tisserand F.F. Traité de Mécanique Céleste. V. 4. Gauthier-Villars et fils. Paris, 1896. P. 548.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник