Астрономический вестник, 2020, T. 54, № 4, стр. 317-324
Точность анализа элементного и изотопного состава реголита методом лазерной времяпролетной масс-спектрометрии в ходе планируемых миссий Луна–Глоб и Луна–Ресурс-1
А. Е. Чумиков a, В. С. Чепцов a, b, *, Н. Г. Манагадзе a
a Институт космических исследований РАН
Москва, Россия
b Московский государственный университет им. М.В. Ломоносова
Москва, Россия
* E-mail: cheptcov.vladimir@gmail.com
Поступила в редакцию 26.08.2019
После доработки 25.11.2019
Принята к публикации 16.12.2019
Аннотация
Лазерная ионизационная масс-спектрометрия является одним из наиболее перспективных методов анализа элементного и изотопного состава твердых веществ в космических экспериментах в связи с высокой надежностью приборов и простотой их эксплуатации, отсутствием необходимости в пробоподготовке и высоким пространственным разрешением. С учетом указанных достоинств данного метода в состав миссий Луна–Глоб (Луна-25) и Луна–Ресурс-1 (Луна-27) включен лазерный ионизационный масс-спектрометр ЛАЗМА-ЛР с целью изучения элементного и изотопного состава реголита Луны в местах посадки космических аппаратов. Точность измерений с помощью масс-анализатора ЛАЗМА-ЛР существенно зависит от объема статистической выборки спектрального массива, что определяет временные параметры функционирования прибора в ходе космического эксперимента. Нами была снята серия спектров энстатита (минерала, входящего в состав лунного реголита) и проведена оценка приборной точности измерений при различных объемах спектрального массива. Показано, что 10% точность элементного анализа обеспечивается обработкой массива из 300 спектров, что соответствует времени непрерывной работы прибора ЛАЗМА-ЛР около 4 ч. За аналогичный 4-часовой период точность 1% измерения изотопных распределений достигается только для изотопов, находящихся в соотношении не более 10 : 1, в то время как измерение с точностью 1% изотопов с бо̀льшими соотношениями требует неоправданного увеличения длительности анализа.
ВВЕДЕНИЕ
Исследования молекулярного, элементного и изотопного состава реголита и пыли являются неотъемлемой частью практически всех посадочных космических миссий. Такие исследования необходимы для понимания процессов эволюции комических тел, для определения ряда их физико-химических характеристик, для оценки перспектив их освоения, а также для решения многих других фундаментальных и прикладных проблем. Одним из наиболее перспективных методов анализа элементного и изотопного состава твердых веществ в космических экспериментах является лазерная ионизационная масс-спектрометрия (ЛИМС), в связи с высокой надежностью приборов и простотой их эксплуатации, отсутствием необходимости в пробоподготовке и высоким пространственным разрешением (Tulej и др., 2012; 2015; Riedo и др., 2013a). ЛИМС для космических применений стремительно развивалась в течение последних десятилетий, и к настоящему времени был создан ряд прототипов и летных приборов (Tulej и др., 2015; Managadze и др., 2010; 2017). Один из них, ЛАЗМА, был установлен на борту космического аппарата Фобос-Грунт, и его модификация ЛАЗМА-ЛР включена в состав миссий Луна–Глоб (Луна-25) и Луна–Ресурс-1 (Луна-27) (Managadze и др., 2010; Mitrofanov и др., 2011).
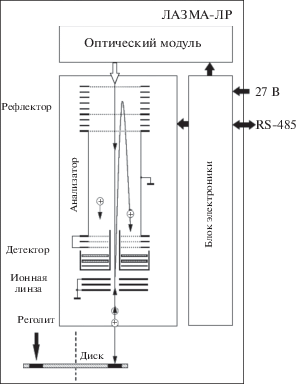
Анализ элементного и изотопного состава с помощью прибора ЛАЗМА-ЛР проводится следующим образом: образец реголита помещается на вращающийся диск на расстоянии, соответствующем фокусному расстоянию лазерного излучателя, затем Nd:YAG лазером с длиной волны 1.064 мкм производится импульсное воздействие длительностью 7 нс с плотностью мощности ~109 Вт/см2 (рис. 1). Такое воздействие вызывает полную атомизацию и ионизацию вещества образца, а сильный перегрев приводит к выбросу образованных ионов в виде плазменного факела.
Высокоскоростные ионы, эмитируемые из образовавшейся плазмы в режиме свободного разлета, попадают во времяпролетный масс-анализатор, где разделяются по времени пролета в соответствии с формулой:
где T – время пролета ионов с энергией Е и массой М бесполевого расстояния L. Разделенные во времени ионы, после их отражения в тормозящем поле электростатического рефлектора, регистрируются вторично-электронным умножителем. Далее сигнал поступает на быстродействующий аналого-цифровой преобразователь и сохраняется в памяти прибора в виде одиночного спектра. По времени пролета ионов и интенсивности сигнала можно определить массу ионов и их относительные концентрации с высокой точностью. По распределению и амплитуде изотопов можно отождествить химический элемент, и далее по интенсивности массовых пиков элементов определить химический, включая элементный и изотопный, состав исследуемого вещества (Managadze и др., 2010; 2017).Важно, что точность измерений с помощью масс-анализатора ЛАЗМА-ЛР существенно зависит от объема статистической выборки спектрального массива. От объема статистической выборки, требуемого для достижения заданной точности измерений, зависит время накопления спектров, которое, в свою очередь, задает временные параметры функционирования прибора в ходе космического эксперимента. В связи с этим целью настоящей работы являлось изучение зависимости точности определения элементного и изотопного состава от объема статистической выборки спектрального массива летного прибора ЛАЗМА-ЛР и определение необходимого количества спектров для получения данных об элементном и изотопном составе образца с точностью 10 и 1% соответственно. Данная точность достаточна для решения широкого круга задач планетологии, геохронологии и астробиологии, в частности, для предварительного анализа и отбора образцов для их доставки на Землю, для классификации космических тел, исследования процессов их формирования и изучения процессов выветривания их поверхности, для определения возраста пород, поиска редкоземельных элементов и др. (Brinckerhoff, 2005).
МАТЕРИАЛЫ И МЕТОДЫ
Объектом исследования являлся энстатит. Этот минерал входит в группу пироксенов, распространенных в лунном реголите и метеоритах (Reid и др., 1973; Rubin, 1997). Образец энстатита, отобранный в Норвегии, был получен нами из Музея естественной истории в Берлине, где его химический состав был исследован методом энергодисперсионной рентгеновской спектроскопии (ЭДС) с помощью полевого эмиссионного растрового электронного микроскопа JEOL 8500-F (JEOL USA Inc., США). Образец содержал в своем составе оксиды Аl2O3, Na2O, TiO2, Cr2O3, SiO2, MgO, MnO, CaO и FeO в концентрациях 0.09, 0.02, 0.04, 0.01, 57.15, 32.54, 0.04, 0.29 и 9.91 мас. % соответственно. Следовательно, содержание Al, Na, Ti, Cr, Si, Mg, Mn, Ca, Fe и O в образце составляло 0.037, 0.014, 0.105, 0.003, 19.93, 17.03, 0.012, 0.108, 2.88 и 59.98 ат. % соответственно. Микроскопические исследования показали, что образец однороден, что позволяет исключить влияние на точность анализа неоднородности мишени и обеспечивает определение именно приборной точности анализа.
Исследования точностных характеристик элементного и изотопного анализа проводились с помощью штатного образца прибора ЛАЗМА проекта Фобос-Грунт (Managadze и др., 2010), который является полным аналогом прибора ЛАЗМА-ЛР в аналитической части инструмента. Прибор помещался в вакуумную камеру, где производилась его откачка до рабочего давления 5 × 10–6 торр. Затем была снята серия из 135 спектров энстатита. Регистрация спектров осуществлялась в штатном режиме работы прибора. Частота получения спектров при этом определялась частотой работы лазера и составляла 0.1 Гц. Использование низкочастотного лазера обусловлено его низким средним энергопотреблением, отсутствием необходимости его активного охлаждения в ходе космического эксперимента и наличием отработанной технологии изготовления лазера для жестких условий эксплуатации. Диаметр пятна лазерного воздействия составлял около 30 мкм. Глубина образующегося при этом кратера существенно зависит от материала, из которого состоит мишень, и составляет порядка сотен нанометров.
Для обработки серий спектров в среде GNU Octave 3.4.3 было создано программное обеспечение, позволяющее определять процентное содержание элементов и изотопов в составе образца. Работа программы осуществлялась по следующему алгоритму: сшивка спектра на основе самого чувствительного канала; вычитание из спектра базовой линии; нахождение интегралов пиков отдельного спектра по методу трапеций; нормировка (приведение интегралов пиков к их процентному распределению); усреднение полученных значений содержания элементов и изотопов в образце в атомных процентах и вычисление стандартных отклонений среднего.
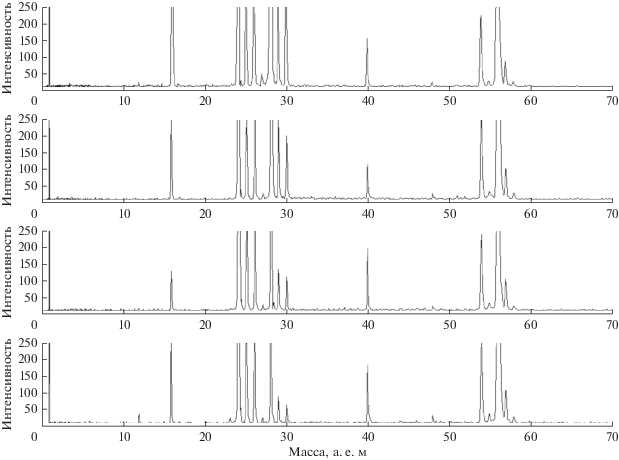
Важно, что точность измерения какой-либо величины определяется как случайной погрешностью измерения, так и систематической (влияние грубой ошибки в данной работе не рассматривается). При выполнении измерений с помощью прибора ЛАЗМА случайная ошибка определяется относительным разбросом интегралов спектральных пиков элементов в различных спектрах (рис. 2), а систематическая – постоянно заниженным или наоборот завышенным значением интеграла пика какого-либо элемента. Так, в приведенном спектре видно, что интеграл пика кислорода имеет существенно заниженное значение относительно указанных выше данных о составе образца, полученных методом рентгеноспектрального микроанализа. Влияние систематической погрешности на точность анализа элементного и изотопного состава лунного реголита будет компенсироваться введением соответствующих постоянных коэффициентов — коэффициентов относительной чувствительности (КОЧ) на этапе обработки полученных в ходе космического эксперимента научных данных, а также в ходе экспериментального анализа земных пород и грунтов, близких по составу к лунному реголиту. Поскольку введение данных коэффициентов планируется на этапе обработки научных данных, и они фактически не связаны со статистическим накоплением результатов измерения в ходе космического эксперимента, в настоящей работе все КОЧ приняты равными 1 и рассматривается влияние на точность измерений только случайной составляющей погрешности.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Результаты анализа элементного состава энстатита при обработке различных по объему выборок спектров приведены в табл. 1. Представленные данные демонстрируют, что точность определения концентрации элементов связана не только с объемом проанализированной выборки, что было ожидаемо, но и с величиной интеграла пика (концентрацией) элемента в спектре. Аналогичный эффект – снижение точности измерения концентрации элемента при уменьшении его содержания в образце – наблюдался ранее при исследовании характеристик ряда других лазерных ионизационных масс-спектрометров (Riedo и др., 2013b; 2013c).
Таблица 1.
Результаты определения элементного состава энстатита при анализе различных по объему выборок спектров
| Элемент | Объем выборки – 20 спектров | Объем выборки – 40 спектров | Объем выборки – 80 спектров | Объем выборки – 135 спектров | ||||
|---|---|---|---|---|---|---|---|---|
| (x ± σх), ат. % | Sr, % | (x ± σх), ат. % | Sr, % | (x ± σх), ат. % | Sr, % | (x ± σх), ат. % | Sr, % | |
| Si | 42.17 ± 3.95 | 9.3 | 44.09 ± 2.76 | 6.3 | 43.02 ± 1.87 | 4.3 | 42.40 ± 1.44 | 3.4 |
| Mg | 26.42 ± 1.66 | 6.3 | 25.36 ± 0.97 | 3.8 | 26.50 ± 0.87 | 3.3 | 26.99 ± 0.68 | 2.5 |
| Fe | 23.30 ± 3.27 | 14.0 | 23.47 ± 2.44 | 10.4 | 23.27 ± 1.70 | 7.3 | 23.85 ± 1.30 | 5.5 |
| O | 6.13 ± 2.31 | 37.6 | 5.39 ± 1.42 | 26.4 | 5.66 ± 1.13 | 20.0 | 5.23 ± 0.76 | 14.6 |
| Ca | 0.97 ± 0.19 | 20.3 | 0.86 ± 0.11 | 12.9 | 0.83 ± 0.07 | 8.3 | 0.80 ± 0.05 | 6.3 |
| Ti | 0.26 ± 0.10 | 38.4 | 0.26 ± 0.05 | 21.0 | 0.25 ± 0.03 | 12.7 | 0.28 ± 0.03 | 10.4 |
| Al | 0.42 ± 0.25 | 58.5 | 0.29 ± 0.12 | 43.0 | 0.22 ± 0.063 | 28.3 | 0.20 ± 0.038 | 18.3 |
| Mn | 0.11 ± 0.02 | 19.5 | 0.11 ± 0.014 | 13.0 | 0.10 ± 0.01 | 8.8 | 0.11 ± 0.008 | 7.0 |
| Na | 0.15 ± 0.05 | 34.5 | 0.11 ± 0.02 | 24.7 | 0.09 ± 0.015 | 16.8 | 0.08 ± 0.01 | 12.5 |
| Cr | 0.02 ± 0.01 | 44.0 | 0.02 ± 0.006 | 25.2 | 0.02 ± 0.004 | 18.2 | 0.02 ± 0.003 | 15.3 |
Большой статистический разброс элементов с малой концентрацией может быть вызван в первую очередь их негомогенным распределением в образце. Аналогичная картина наблюдалась бы очевидно и для пиков матричных элементов в случае сильно неоднородного образца. Таким образом, с высокой вероятностью приборная (не зависимая от характеристик исследуемого образца) точность анализа в данном случае определяется пиками матричных элементов (Mg, Si, Fe), а примесные элементы, такие как Na, Al, Cr, характеризуют уменьшение точности анализа вследствие неоднородности образца. Исключением является кислород – несмотря на его значительное содержание в образце, среднеквадратичное отклонение среднего для него сравнимо со среднеквадратичными отклонениями примесей. Очевидно, что такой разброс в результатах отдельных измерений не связан с неоднородностью распределения кислорода в образце, поскольку сам образец представляет собой смесь оксидов, а вызван физическими процессами спектрообразования кислорода, такими как смещение максимума энергетического распределения из рабочей зоны анализатора, близость порога энергии ионообразования к используемой интенсивности лазерного излучения и др. В целом, подобный эффект характерен для ЛИМС и наблюдается для всех элементов с атомной массой легче кислорода (Н, С, N и др.) (Tulej и др., 2012; 2015; Wurz и др., 2012).
Разобьем представленные в табл. 1 элементы на две группы. В первую группу включим матричные однородно распределенные элементы – Mg, Si и Fe, характеризующие приборную точность анализа, во вторую – все примесные элементы, а также кислород. Поскольку однородность распределения химических элементов в лунном реголите в местах посадки миссий Луна–Глоб и Луна–Ресурс-1 неизвестна, примем, что матричные элементы в лунном реголите имеют статистические распределения, близкие к статистическим распределениям примесей в энстатите. Таким образом, первая группа элементов определяет минимальное необходимое число спектров для получения заданной точности анализа в случае идеальной мишени, а вторая группа моделирует получаемую точность при негомогенном образце.
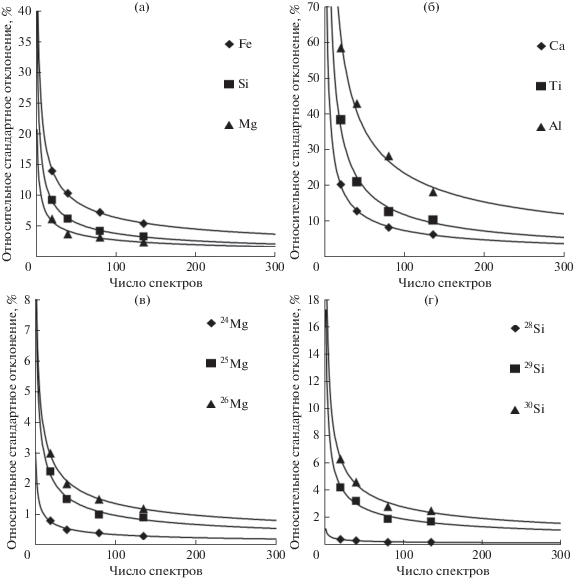
Согласно полученным зависимостям относительного стандартного отклонения среднего от числа проанализированных спектров, приборная относительная точность 10% для первой группы элементов достигалась при обработке 50 спектров, при анализе 135 спектров точность анализа составляла не менее 6% (рис. 3а). При экстраполяции полученных зависимостей с помощью степенной функции на статистические выборки бо̀льших объемов было установлено, что для элементов второй группы, за исключением Al, точность анализа 10% достигалась при увеличении спектрального массива до 300 спектров (рис. 3б), в то время как для Al относительное стандартное отклонение составляло 12%. При этом точность анализа для элементов первой группы возрастала до 4%. Для увеличения точности определения содержания Al в образце до 10% была необходима обработка массива из 400 спектров. Таким образом, полученные данные указывают, что для элементного анализа пробы лунного реголита с точностью 10% потребуется спектральный массив из ~300 одиночных спектров. Поскольку в условиях анализа сложного образца, к которым можно отнести пробу лунного реголита, отбраковывается до 80% спектров, для получения 300 полезных спектров потребуется около 1500 спектров. С учетом времени получения одного спектра (10 с), для накопления массива из 1500 спектров потребуется около 4.2 ч активной работы прибора. В связи с этим номинальное время элементного анализа единичной мишени составит около 4 ч.
Рис. 3.
Экспериментальные зависимости относительного стандартного отклонения среднего значения концентраций различных элементов и изотопов от объема проанализированной выборки спектров.
Следует отметить, что концентрации элементов, определенные с помощью прибора ЛАЗМА-ЛР (табл. 1), существенно отличаются от значений, полученных при анализе методом ЭДС. Это связано с влиянием на точность масс-спектрометрического анализа систематической погрешности, которое, как указано выше, будет компенсироваться введением КОЧ на дальнейших этапах работы.
Оценка точности изотопного анализа была проведена по тем же спектральным данным. В связи с тем, что элементы второй группы имеют малую концентрацию (не основные изотопы на уровне шума) или являются моноизотопными элементами, изотопные распределения определяли по элементам первой группы. Это оправдано еще и тем, что изотопные соотношения не зависят от гомогенности образца, т.е. проведенные статистические оценки будут действительны для любого надежно регистрируемого элемента.
Измеренные средние значения изотопной концентрации имели в ряде случаев значимое отличие от природной концентрации (табл. 2). Это означает, что для корректных измерений изотопных соотношений будет необходимо введение поправочных коэффициентов (изотопных КОЧ). Большой разброс данных по изотопу железа 58Fe, как и существенное отличие полученного значения от природной распространенности, обусловлен как малой концентрацией этого изотопа, так и наложением на данную атомную массу изотопа 58Ni. Согласно результатам измерений, точность определения концентрации изотопа напрямую зависит от его содержания в образце. Такая же зависимость характерна и для элементного анализа, как отмечалось выше. В связи с этим наиболее точно могут быть проанализированы изотопные распределения для матричных элементов, содержащих соизмеримые количества нескольких нуклидов; при увеличении изотопных соотношений точность их измерения будет снижаться.
Таблица 2.
Изотопные распределения элементов первой группы для различных объемов статистической выборки. Распространенность изотопов в природе приведена по данным (Rosman, Taylor, 1999)
| Изотоп | Распростра-ненность, % | Объем выборки – 20 спектров | Объем выборки – 40 спектров | Объем выборки – 80 спектров | Объем выборки – 135 спектров | ||||
|---|---|---|---|---|---|---|---|---|---|
| (x ± σх), ат. % | Sr, % | (x ± σх), ат. % | Sr, % | (x ± σх), ат. % | Sr, % | (x ± σх), ат. % | Sr, % | ||
| 24Mg | 78.99 | 76.68 ± 0.61 | 0.8 | 76.78 ± 0.37 | 0.5 | 76.34 ± 0.28 | 0.4 | 76.89 ± 0.22 | 0.3 |
| 25Mg | 10.00 | 10.55 ± 0.25 | 2.4 | 10.52 ± 0.16 | 1.5 | 10.58 ± 0.10 | 1.0 | 10.40 ± 0.09 | 0.9 |
| 26Mg | 11.01 | 12.76 ± 0.38 | 3.0 | 12.69 ± 0.25 | 2.0 | 13.06 ± 0.19 | 1.5 | 12.69 ± 0.15 | 1.2 |
| 28Si | 92.23 | 92.40 ± 0.36 | 0.4 | 91.69 ± 0.29 | 0.3 | 91.28 ± 0.18 | 0.2 | 91.88 ± 0.15 | 0.2 |
| 29Si | 4.68 | 4.30 ± 0.18 | 4.2 | 4.70 ± 0.15 | 3.2 | 4.87 ± 0.09 | 1.9 | 4.61 ± 0.07 | 1.7 |
| 30Si | 3.09 | 3.29 ± 0.21 | 6.3 | 3.60 ± 0.16 | 4.6 | 3.83 ± 0.10 | 2.8 | 3.50 ± 0.08 | 2.5 |
| 54Fe | 5.85 | 5.78 ± 0.19 | 3.3 | 5.67 ± 0.14 | 2.5 | 5.61 ± 0.08 | 1.6 | 5.59 ± 0.06 | 1.2 |
| 56Fe | 91.75 | 91.69 ± 0.27 | 0.3 | 91.58 ± 0.22 | 0.2 | 91.65 ± 0.20 | 0.2 | 91.70 ± 0.14 | 0.1 |
| 57Fe | 2.12 | 1.93 ± 0.11 | 5.7 | 2.15 ± 0.09 | 4.4 | 2.20 ± 0.07 | 3.5 | 2.16 ± 0.05 | 2.7 |
| 58Fe | 0.28 | 0.58 ± 0.10 | 17.4 | 0.59 ± 0.07 | 12.0 | 0.52 ± 0.06 | 12.7 | 0.53 ± 0.04 | 8.7 |
В частности, для всех изотопов магния точность 1% достигалась при обработке 200 спектров (рис. 3в), в то время как для определения всех изотопных соотношений кремния с такой же точностью требуется анализ массива объемом около 600 спектров (рис. 3г). Таким образом, с учетом приведенных выше временны̀х оценок для элементного анализа, заданная точность измерения содержаний изотопов, имеющих соотношение их распространенности в природе около 8 : 1 (изотопы 24Mg : 25Mg и 24Mg : 26Mg) будет достигнута через ~3 ч работы прибора, для изотопов с отношением около 30 : 1 (изотопы Si) потребуется около 9 ч, для изотопов же, имеющих бо̀льшие соотношения, время анализа становится неоправданно высоким. Так, для анализа концентраций изотопов с отношением около 50 : 1 (56Fe : 57Fe) потребуется накопление массива из 2000 полезных спектров (около 30 часов работы прибора), а для нуклидов с отношением около 300 : 1 (56Fe : 58Fe) – около 200 000 спектров (~12 сут непрерывной работы масс-анализатора). Итак, за 4 ч с точностью 1% будут определены изотопы, имеющие соотношения ~10 : 1 и менее. Такое время анализа представляется оптимальным, поскольку для изотопов с бо̀льшими соотношениями потребуется гораздо большее время, и, кроме того, данная величина хорошо согласуется с номинальным временем элементного анализа единичного образца. Принимая во внимание, что неоднородность изотопных отношений в пробах лунного реголита, взятых на небольшом расстоянии, должна отсутствовать, анализ изотопных распределений для изотопов с малой концентрацией предполагается проводить по суммарной статистике, полученной со всех загруженных проб. Конструкция грунтоприемного устройства прибора ЛАЗМА позволяет провести анализ 11 образцов реголита в ходе космического эксперимента (Managadze и др., 2010). В связи с этим возможно накопление суммарного массива объемом не менее 3300 полезных спектров, что позволит охарактеризовать с 1% точностью изотопные распределения для нуклидов с отношениями их распространенности в природе 50 : 1 и более.
Следует отметить, что на случайную составляющую погрешности влияет ряд факторов, таких как статистика дискретных событий, воспроизводимость плотности мощности лазерного излучения, флуктуации энергетических распределений элементов относительно диапазона допустимых энергий времяпролетного масс-анализатора и др., что в конечном итоге отражается на точности элементного и изотопного анализа. Более того, во многом эти факторы определяют и различную точность, как показано выше, получаемую для элементного и изотопного анализа. Однако в данной работе не ставилась цель изучения отдельного влияния каждого из этих факторов на конечные результаты. Проведенные измерения, по сути, отражают интегральное влияние всех случайных факторов на точность анализа конкретного бортового лазерного времяпролетного масс-спектрометра и позволяют определить номинальные условия его функционирования в рамках космического эксперимента, что и являлось основной целью данной работы.
ЗАКЛЮЧЕНИЕ
Проведенные экспериментальные исследования по определению величины спектрального массива и времени анализа единичного образца для достижения заданной точности измерений элементного и изотопного состава 10 и 1% соответственно показали, что:
− данная точность элементного анализа обеспечивается получением и обработкой массива из 300 спектров, что соответствует времени непрерывной работы прибора ЛАЗМА-ЛР около 4 ч;
− точность элементного анализа, а также точность определения изотопных распределений зависят не только от числа наблюдений, но и от их концентраций элементов и изотопов;
− за аналогичный 4-часовой период 1% точность измерения изотопных распределений достигается только для изотопов, находящихся в соотношении не более 10 : 1, в то время как измерение с точностью 1% распределений изотопов с бо̀льшими соотношениями требует неоправданного увеличения длительности анализа;
− в предположении однородности изотопного состава разных проб реголита Луны, взятых с одного места посадки, для измерения изотопных распределений предлагается совместно анализировать спектральные данные, полученные с различных образцов, что частично устранит ограничения, связанные с концентрацией изотопов, и позволит охарактеризовать с точностью 1% изотопные распределения для нуклидов с отношениями их концентраций в образце 50 : 1 и более.
Авторы благодарят главу департамента Космических исследований и планетологии Физического института Бернского университета Питера Вурца за предоставленный для анализа образец энстатита.
Список литературы
Brinckerhoff W.B. On the possible in situ elemental analysis of small bodies with laser ablation TOF-MS // Planet. and Space Sci. 2005. V. 53. № 8. P. 817–838.
Managadze G.G., Wurz P., Sagdeev R.Z., Chumikov A.E., Tuley M., Yakovleva M., Managadze N.G., Bondarenko A.L. Study of the main geochemical characteristics of Phobos’ regolith using laser time-of-flight mass spectrometry // Sol. Syst. Res. 2010. V. 44. P. 376–384.
Managadze G.G., Safronova A.A., Luchnikov K.A., Vorobyova E.A., Duxbury N.S., Wurz P., Managadze N.G., Chumikov A.E., Khamizov R.K. A new method and mass-spectrometric instrument for extraterrestrial microbial life detection using the elemental composition analyses of Martian regolith and permafrost/ice // Astrobiology. 2017. V. 17. № 5. P. 448–458.
Mitrofanov I.G., Zelenyi L.M., Tret’yakov V.I., Dolgopolov V.P. Science program of Lunar landers of “Luna-Glob” and “Luna-Resource” Missions // Lunar and Planet. Sci. Conf. 2011. V. 42. P. 1798.
Reid A.M., Warner J.L., Ridley W.I., Brown R.W. Luna 20 soil: Abundance and composition of phases in the 45–125 micron fraction // Geochim. et Cosmochim. Acta. 1973. V. 37. № 4. P. 1011–1030.
Riedo A., Bieler A., Neuland M., Tulej M., Wurz P. Performance evaluation of a miniature laser ablation time-of-flight mass spectrometer designed for in situ investigations in planetary space research // J. Mass Spectrometry. 2013a. V. 48. № 1. P. 1–15.
Riedo A., Meyer S., Heredia B., Neuland M.B., Bieler A., Tulej M., Leya I., Iakovleva M., Mezger K., Wurz P. Highly accurate isotope composition measurements by a miniature laser ablation mass spectrometer designed for in situ investigations on planetary surfaces // Planet. and Space Sci. 2013b. V. 87. P. 1–13.
Riedo A., Neuland M., Meye S., Tulej M., Wurz P. Coupling of LMS with a fs-laser ablation ion source: Elemental and isotope composition measurements // J. Analytical Atomic Spectrometry. 2013c. V. 28. № 8. P. 1256–1269.
Rosman K.J.R., Taylor P.D.P. Report of the IUPAC subcommittee for isotopic abundance measurements // Pure Appl. Chem. 1999. V. 71. P. 1593–1607.
Rubin A.E. The Hadley Rille enstatite chondrite and its agglutinate-like rim: Impact melting during accretion to the Moon // Meteoritics and Planet. Sci. 1997. V. 32. № 1. P. 135–141.
Tulej M., Riedo A., Iakovleva M., Wurz P. On applicability of a miniaturised laser ablation time of flight mass spectrometer for trace elements measurements // Int. J. Spectroscopy. 2012. Article ID 234949.
Tulej M., Neubeck A., Ivarsson M., Riedo A., Neuland M.B., Meyer S., Wurz P. Chemical composition of micrometer-sized filaments in an aragonite host by a miniature laser ablation/ionization mass spectrometer // Astrobiology. 2015. V. 15. № 8. P. 669–682.
Wurz P., Abplanalp D., Tulej M., Iakovleva M., Fernandes V.A., Chumikov A., Managadze G.G. Mass spectrometric analysis in planetary science: Investigation of the surface and the atmosphere // Sol. Syst. Res. 2012. V. 46. № 6. P. 408–422.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник