1. На главную
  2. Электронные версии
  3. Астрономический вестник
  4. T. 54, № 4, 2020

Астрономический вестник, 2020, T. 54, № 4, стр. 325-336

Определение глобальных плотностных неоднородностей и напряжений внутри Луны

Н. А. Чуйкова a, *, Л. П. Насонова a, **, Т. Г. Максимова a

a Государственный астрономический институт им. П.К. Штернберга, МГУ
Москва, Россия

* E-mail: chujkova@sai.msu.ru
** E-mail: nason@sai.msu.ru

Поступила в редакцию 19.08.2019
После доработки 16.01.2020
Принята к публикации 13.02.2020

Полный текст (PDF)

Аннотация

Определено возможное распределение аномалий плотности и напряжения в недрах Луны. Для этой цели применено разработанное нами новое решение некорректной обратной задачи гравиметрии, проверенное для Земли и Марса. Суть его заключается в том, что на основе только космических данных о гравитационном поле и рельефе планеты однозначно определяются глубины изостатической компенсации для ряда гармоник разложения высот рельефа по сферическим функциям. Показано, что возможная изостатическая компенсация рельефа осуществляется в диапазоне глубин 0–530 км. Определены наиболее вероятные глубины компенсации в этом диапазоне и найдено распределение компенсирующих масс на этих глубинах. Для остальных гармоник были выбраны два других варианта. 1) Компенсация на двух уровнях, первым из которых является средняя глубина коры в 2.7 км, соответствующая слою 0–10 км; возможные глубины для второго уровня определялись из анализа результатов, полученных для изостатически компенсированных гармоник. 2) Нескомпенсированные гармоники рельефа приводят к вертикальным напряжениям в литосфере Луны, достигающим в коре Луны по сжатию 16 МПа и по растяжению –15 МПа.

Ключевые слова: Луна, внутреннее строение, кора, мантия, аномалии плотности, напряжения, глубины изостатической компенсации, некорректная задача гравиметрии, квадратичное приближение

ВВЕДЕНИЕ

До сих пор о внутреннем строении планет мы можем получить информацию в основном из космических исследований гравитационного поля и рельефа. Для Луны имеется также ограниченный объем геохимических и сейсмическиx данных, соответствующий восьмилетнему сроку (1969–1977 гг.) работ шести сейсмографов на видимой стороне Луны, и результаты наблюдений теплового потока в местах посадок космических аппаратов. Однако попытки найти на основе анализа изменений скоростей сейсмических волн вклад латерально распределенных плотностных неоднородностей нельзя признать успешными, поскольку для глубинных недр Земли неизвестен даже знак зависимости между изменением скоростей и изменением плотности. Зависимость между аномалиями плотности и сейсмическими скоростями эмпирически исследована только для приповерхностных слоев Земли (соотношение Берча). Неизвестно, сохраняется ли эта закономерность при высоких давлениях и температурах, характерных для больших глубин. Об этом подробно сказано в книгах (Браун, Массет, 1984; Жарков, 2012). Тем не менее остаются вопросы по внутреннему плотностному строению всей Луны.

В работе (Чуйкова и др., 2019) были получены некоторые предварительные результаты о плотностном строении коры Луны. В настоящей работе, на основе разработанной авторами теории и комплекса программ для решения обратной задачи гравиметрии (Chujkova и др., 2014), определено возможное распределение плотности и напряжений в недрах Луны. Для этой цели применено новое решение некорректной обратной задачи гравиметрии (Chujkova и др., 2014; Чуйкова и др., 2018), проверенное нами для Земли и Марса (Чуйкова и др., 2014). Суть его заключается в том, что определяются возможные глубины изостатической компенсации для гармоник разложения высот рельефа относительно равновесной фигуры планеты для различных степеней и порядков гармоник. Поскольку каждая неоднородность рельефа характеризуется определенным набором гармоник, то максимальная концентрация компенсации этого набора в ограниченном диапазоне глубин может свидетельствовать о наиболее вероятных глубинах компенсации рассматриваемой неоднородности рельефа. Полученные таким образом глубины компенсации позволят решить поставленную задачу: найти латеральное распределение компенсирующих масс на выделенных глубинах. Прежде чем рассчитывать внутренние аномальные структуры Луны, из гравитационного поля Луны нужно вычесть вклад рельефа в квадратичном приближении. Формулы и программы, позволяющие решить эту задачу, были получены нами в ранних работах путем математического моделирования символьных вычислений в системах компьютерной алгебры (Насонова, Чуйкова, 2007).

Исследование решения как для Земли, так и для Марса (Чуйкова и др., 2014) показало, что компенсация масс рельефа на одном уровне возможна только для некоторого набора гармоник. Для остальных гармоник были выбраны два варианта компенсации, которые в наименьшей степени приводят к отклонениям внутреннего строения от равновесного.

Конечным результатом работы было полученное нами распределение аномалий плотности в различных слоях Луны (вплоть до нижней границы на глубине 528 км), а также распределение вертикальных напряжений сжатия и растяжения.

ТЕОРИЯ И МЕТОДИКА РАСЧЕТА АНОМАЛЬНЫХ СТРУКТУР НЕДР ЛУНЫ

Прежде чем рассчитывать аномальные структуры недр Луны, нужно из гармоник внешнего гравитационного поля вычесть вклад рельефа. Для определения вклада латерально распределенных аномальных масс рельефа в стоксовы постоянные гравитационного поля мы представляем эти массы в виде разложения по сферическим функциям слоя постоянной плотности, распределенного по высоте относительно сферической поверхности Луны с центром в центре масс.

В линейном приближении, когда слой аномальных масс распределен на сферической поверхности, между коэффициентами $a_{{nm}}^{{(s)}},b_{{nm}}^{{(s)}}$ разложения плотности простого слоя (s) по сферическим функциям и стоксовыми постоянными $\Delta C_{{nm}}^{{(s)}},{\text{ }}\Delta D_{{nm}}^{{(s)}}$, обусловленными вкладом этого слоя, существует линейная связь (Дубошин, 1961):

(1)
$\left\{ {\begin{array}{*{20}{c}} {\Delta C_{{nm}}^{{(s)}}} \\ {\Delta D_{{nm}}^{{(s)}}} \end{array}} \right\} = \frac{3}{{2n + 1}}{{\left( {\frac{{{{R}_{s}}}}{{{{R}_{0}}}}} \right)}^{3}}\frac{{\Delta {{\sigma }_{s}}}}{{\bar {\sigma }}}{{\left( {\frac{{{{R}_{s}}}}{a}} \right)}^{n}}\left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{(s)}}} \\ {b_{{nm}}^{{(s)}}} \end{array}} \right\},$
где ${{R}_{s}}$, Δσs – средний радиус и средняя плотность простого слоя, R0, $\bar {\sigma }$ – средний радиус и средняя плотность всей планеты, $a$ – принятый экваториальный радиус планетного эллипсоида (для Луны $a$ = ${{R}_{s}}$). Здесь для внешнего гравитационного потенциала Луны используется следующее представление:
$\begin{gathered} V(r,\varphi ,\lambda ) = \frac{{f{{M}_{0}}}}{r}\sum\limits_{n = 1}^N {{{{\left( {\frac{a}{r}} \right)}}^{n}}} \times \\ \times \,\,\sum\limits_{m = 0}^n {\left( {{{C}_{{nm}}}\cos (m\lambda ) + {{D}_{{nm}}}\sin (m\lambda )} \right)} {{P}_{{nm}}}\left( {\sin \varphi } \right), \\ \end{gathered} $
где М0 – масса Луны, f – гравитационная постоянная, $r,\varphi ,\lambda $ – сферические координаты точки наблюдения, ${{C}_{{nm}}},{{D}_{{nm}}}$ – стоксовы постоянные, ${{P}_{{nm}}}(\sin \varphi )$ – присоединенные функции Лежандра, N = 36. Относительные высоты ${{h}_{s}}\left( {\varphi ,\lambda } \right)$ (по отношению к среднему радиусу ${{R}_{s}}$) представлены в виде следующего разложения по сферическим функциям:

$\begin{gathered} {{h}_{s}}(\varphi ,\lambda ) = \\ = \sum\limits_{n = 1}^N {\sum\limits_{m = 0}^n {\left( {a_{{nm}}^{{(s)}}\cos (m\lambda ) + b_{{nm}}^{{(s)}}\sin (m\lambda )} \right)} } {{P}_{{nm}}}(\sin \varphi ). \\ \end{gathered} $

В реальности аномальные массы рельефа являются не простым сферическим слоем, а распределенными по высоте. В этом случае при учете квадратичных членов в формуле (1) для коэффициентов $a_{{nm}}^{{(s)}},b_{{nm}}^{{(s)}}$ нужно взять следующее выражение, содержащее дополнительные члены, а именно (Чуйкова и др., 2006; 2011):

(2)
$\begin{gathered} \left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{(s)}}} \\ {b_{{nm}}^{{(s)}}} \end{array}} \right\} = {{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{1}} + \frac{{n + 2}}{2}{{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{2}} + \\ + \,\,\alpha \left( {n + 2} \right){{\left\{ {\begin{array}{*{20}{c}} {{{a}_{{nm}}}} \\ {{{b}_{{nm}}}} \end{array}} \right\}}_{3}}, \\ \end{gathered} $
где первый член в сумме справа соответствует коэффициентам разложения относительных (по отношению к среднему радиусу слоя ${{R}_{s}}$) высот слоя ${{h}_{s}}$, член с индексом 2 – коэффициентам разложения функции ${{\left( {{{h}_{s}}} \right)}^{2}}$, а с индексом 3 – коэффициентам разложения функции ${{h}_{s}}{{\overline P }_{2}}\left( {\sin \varphi } \right)$, где $\alpha = {2 \mathord{\left/ {\vphantom {2 {3e}}} \right. \kern-0em} {3e}}$, $e$ – сжатие Луны, для Луны $e$ = 0.

Формулы, позволяющие выразить коэффициенты ${{\left\{ {{{a}_{{nm}}},{{b}_{{nm}}}} \right\}}_{2}}$, ${{\left\{ {{{a}_{{nm}}},{{b}_{{nm}}}} \right\}}_{3}}$ через ${{\left\{ {{{a}_{{nm}}},{\text{ }}{{b}_{{nm}}}} \right\}}_{1}}$, были получены нами в ранних работах путем математического моделирования символьных вычислений в системах компьютерной алгебры (Насонова, Чуйкова, 2007).

Чтобы определить глубину компенсации dnm для произвольной гармоники $a_{{nm}}^{{(s)}},b_{{nm}}^{{(s)}}$ разложения аномальных масс рельефа, нужно решить систему двух уравнений, одно из которых отражает соответствие наблюдениям вклада в гравитационное поле от масс слоя и компенсирующих масс, а другое – совпадение давлений с равновесной моделью ниже глубины компенсации. Полученное решение для глубины компенсации dnm для произвольной гармоники рельефа определяется в итоге соотношением:

(3)
${{d}_{{nm}}} = {{R}_{0}} - {{R}_{M}}{{\left( {{{a_{{nm}}^{{M1}}} \mathord{\left/ {\vphantom {{a_{{nm}}^{{M1}}} {a_{{nm}}^{{M2}}}}} \right. \kern-0em} {a_{{nm}}^{{M2}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}},$
где $a_{{nm}}^{{M1}},a_{{nm}}^{{M2}}$ – коэффициенты разложения по сферическим функциям высот поверхностей компенсации M1 (полученных на основе гравитационного поля после вычета вклада масс слоя в квадратичном приближении) и M2 (полученных на основе гипотезы изостатической компенсации аномальных масс относительно сферической поверхности при фиксированном значении радиуса RM).

Здесь $a_{{nm}}^{{M1}}$ определяются из уравнения

(4)
${{C}_{{nm}}} - \Delta C_{{nm}}^{{(s)}} = \frac{3}{{2n + 1}}{{\left( {\frac{{{{R}_{M}}}}{{{{R}_{0}}}}} \right)}^{3}}\frac{{\Delta {{\sigma }_{{com}}}}}{{\bar {\sigma }}}{{\left( {\frac{{{{R}_{M}}}}{a}} \right)}^{n}}a_{{nm}}^{{M1}},$
где $\Delta {{\sigma }_{{com}}}$ – средний скачок плотности на ${{R}_{M}}$.

С другой стороны, на глубине компенсации ${{R}_{{com}}}$ должно выполняться то же условие с заменой RM на ${{R}_{{com}}} = {{R}_{0}} - {{d}_{{nm}}},$ $a_{{nm}}^{{M1}}$ на $a_{{nm}}^{{com}}$

(5)
${{C}_{{nm}}} - \Delta C_{{nm}}^{{(s)}} = \frac{3}{{2n + 1}}{{\left( {\frac{{{{R}_{{com}}}}}{{{{R}_{0}}}}} \right)}^{3}}\frac{{\Delta {{\sigma }_{{com}}}}}{{\bar {\sigma }}}{{\left( {\frac{{{{R}_{{com}}}}}{a}} \right)}^{n}}a_{{nm}}^{{com}},$
где
(6)
$a_{{nm}}^{{com}}R_{{com}}^{3} = a_{{nm}}^{{M2}}R_{M}^{3},$
$a_{{nm}}^{{M2}}$ определяется условием выравнивания давлений от масс слоя s и компенсирующего слоя. Подставим (6) в (5), а уравнение (5) в уравнение (4), получим ${{\left( {{{R}_{{com}}}} \right)}^{n}}a_{{nm}}^{{M{{2}_{{}}}}} = {{\left( {{{R}_{M}}} \right)}^{n}}a_{{nm}}^{{M1}}.$

Отсюда следует уравнение (3). Для bnm – аналогичная формула с заменой anm на bnm, ${{C}_{{nm}}}$ на ${{D}_{{nm}}}$. Как мы видим, решение возможно, т.е. R0 ≥ dnm ≥ 0, если

(7)
$0 \leqslant {{a_{{nm}}^{{M1}}} \mathord{\left/ {\vphantom {{a_{{nm}}^{{M1}}} {a_{{nm}}^{{M2}}}}} \right. \kern-0em} {a_{{nm}}^{{M2}}}} \leqslant {{\left( {{{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{R}_{M}}}}} \right. \kern-0em} {{{R}_{M}}}}} \right)}^{n}}.$

Исследование решения для Земли и для Марса (Чуйкова и др., 2011; 2012; 2014) показало, что компенсация масс рельефа на одном уровне возможна только для некоторого набора гармоник. Для остальных гармоник были выбраны два варианта компенсации, которые в наименьшей степени приводят к отклонениям внутреннего строения от равновесного, а именно:

1) Компенсация осуществляется на двух уровнях, первым из которых является верхний слой коры, возможные глубины для второго уровня определялись из анализа результатов, полученных для гармоник, для которых существует решение (3). Окончательный выбор делался с учетом весовой функции, обратно пропорциональной отклонению внутреннего строения от равновесного.

2) Нескомпенсированные гармоники рельефа приводят к напряжениям в литосфере при условии, что напряжения не превосходят предела прочности литосферы.

После определения глубин компенсации были выделены основные диапазоны глубин компенсации. Карты распределения аномальных масс построены путем пересчета к плотности простого слоя на средней глубине для выделенных диапазонов. При этом для каждой гармоники должны выполняться условия равенства вклада во внешнее гравитационное поле от всех аномальных масс и совпадение давления с равновесной моделью в нижележащих слоях мантии. Пересчет выполнялся по формуле:

$\begin{gathered} \Delta m\left( {\bar {R},\varphi ,\lambda } \right) = \Delta {{\sigma }_{{com}}}\bar {R} \times \\ \times \,\,\sum\limits_{n = 1}^N {\sum\limits_{m = 0}^n {\left( {a_{{nm}}^{{(s)}}{{\alpha }_{{nm}}}\cos m\lambda + b_{{nm}}^{{(s)}}\beta _{{nm}}^{{}}\sin m\lambda } \right)} } P_{{nm}}^{{}}(\cos \varphi ), \\ \end{gathered} $
где ${{\alpha }_{{nm}}},{{\beta }_{{nm}}}$ – коэффициенты пересчета компенсирующих масс от глубины ${{d}_{{nm}}}$ на средний радиус $\bar {R}$ для каждого выделенного диапазона. Эти коэффициенты должны удовлетворять заданным условиям и считались отдельно для каждого диапазона и для каждой глубины ${{d}_{{nm}}}$.

Коэффициенты разложения вертикальных напряжений по сферическим функциям, то есть вертикальные компоненты тензора напряжений считались по формуле

(8)
$\left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{st}}} \\ {b_{{nm}}^{{st}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{M1}} - a_{{nm}}^{{M2}}} \\ {b_{{nm}}^{{M1}} - b_{{nm}}^{{M2}}} \end{array}} \right\} = \Delta {{\sigma }_{M}}{{g}_{0}}{{R}_{0}},$
где $\Delta {{\sigma }_{M}}$= $\Delta {{\sigma }_{{com}}}$ = 2.55 × ${{10}^{3}}$ кг/м3 (средняя плотность коры) , g0 = 1.62 м/c2, ${{R}_{0}}$ = 1737.15 × ${{10}^{3}}$ м. Формула (8) выписана для расчета напряжений в коре для сферически-симметричной коры с постоянной плотностью. Из формулы (8) видно, что напряжения отнесены к поверхности планеты радиуса $R_{M}^{{}} = {{R}_{0}}$. При пересчете в нижние слои радиуса r формула (8) меняется следующим образом:

(9)
${{\left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{st}}} \\ {b_{{nm}}^{{st}}} \end{array}} \right\}}_{r}} = \left\{ {\begin{array}{*{20}{c}} {a_{{nm}}^{{M1}}{{{\left( {\frac{{{{R}_{0}}}}{r}} \right)}}^{n}} - a_{{nm}}^{{M2}}} \\ {b_{{nm}}^{{M1}}{{{\left( {\frac{{{{R}_{0}}}}{r}} \right)}}^{n}} - b_{{nm}}^{{M2}}} \end{array}} \right\}\Delta {{\sigma }_{M}}{{g}_{0}}{{R}_{0}}{{\left( {\frac{{{{R}_{0}}}}{r}} \right)}^{2}}.$

Видно, что коэффициенты $a_{{nm}}^{{st}},b_{{nm}}^{{st}}$ возрастают пропорционально ${{\left( {\frac{{{{R}_{0}}}}{r}} \right)}^{2}}$, при этом $a_{{nm}}^{{M1}}$, $b_{{nm}}^{{M1}}$ увеличиваются пропорционально ${{\left( {\frac{{{{R}_{0}}}}{r}} \right)}^{n}}$.

Эти напряжения могут привести к тектоническим лунотрясениям в зонах максимальных градиентов напряжения на стыке положительных напряжений сжатия и отрицательных напряжений растяжения.

Некоторые результаты о плотностном строении коры Луны по данным миссии GRAIL были опубликованы в 2013 г. (Wieczorek и др., 2013). В работах других авторов для определения плотностного строения планет земной группы, в том числе Земли и Луны, обычно используется модель изостатической компенсации Эри, где глубины компенсации для различных неоднородностей рельефа определяются на основе аномалий Буге. Таким методом можно решить задачу определения внутреннего строения только при привлечении дополнительной информации о внутреннем строении, а также на основе некоторых теоретических выводов. Эти выводы опираются на космогонические сценарии формирования планет земной группы, на геофизическую и геохимическую информацию и на данные физики высоких энергий. Однако для Луны имеются только отдельные сейсмические наблюдения и измерения теплового потока и плотности образцов лунной коры в местах посадок космических аппаратов, соответствующие ограниченному времени проведения сейсмических наблюдений (1969–1977 гг.). По этим данным можно решить только ограниченные задачи определения внутреннего строения. Так, в работах (Matsuyama и др., 2016) решается задача уточнения границ внутреннего и внешнего ядра и переходного слоя ядро‒нижняя мантия. При этом эти результаты получены на основе известных параметров Луны: масса, моменты инерции, числа Лява для различных внутренних состояний Луны, а также при предположении о сферической симметрии модели рельефа. В работах (Besserer и др., 2014) и (Hemingway и др., 2017), на основе современных моделей гравитационного поля и рельефа и расчета вклада рельефа в гравитационное поле на основе аномалий Буге, найдено изменение толщины лунной коры для отдельных регионов видимого и обратного полушария, а также определено, как меняется толщина коры при разных принципах изостатической компенсации (по массе или по давлению). Подробный обзор современных результатов по анализу внутреннего строения Луны, основанный на сейсмических данных и на селенодезических данных о рельефе и гравитационном поле, приведен в (Matsumoto и др., 2015). Приведенные в нем данные о глубинах раздела внутри Луны (150, 192, 242, 290, 400, 500 км) говорят о противоречивости этих оценок в публикациях многочисленных авторов, хотя некоторые из них согласуются с нашими результатами о средних глубинах компенсации. Наиболее интересной работой на эту тему является статья (Кусков и др., 2018), где на основе совместной инверсии данных гравитационного поля, сейсмических и петрологических данных исследованы вариации валового состава силикатной Луны (кора + мантия).

ИСХОДНЫЕ ДАННЫЕ

В качестве исходных данных для гармонических коэффициентов гравитационного поля Луны была использована современная модель, полученная по данным слежения системы спутник–спутник (GRAIL mission) (Zuber и др., 2013).

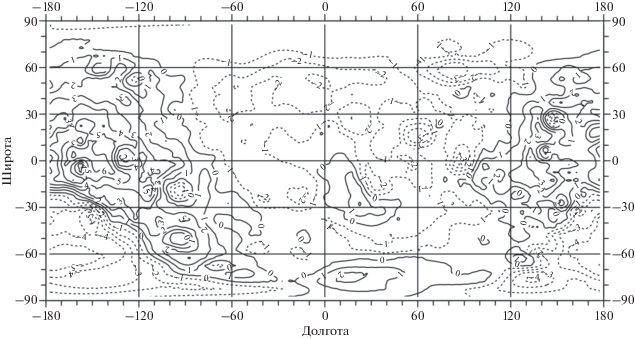
В качестве исходных данных для рельефа Луны (рис. 1) мы использовали полученное нами разложение высот по сферическим функциям до 36 степени на основе массива высот рельефа, осредненных нами по пятиградусным трапециям (Чуйкова и др., 2019). Осреднение выполнено на основе цифровой модели рельефа, построенной по данным лазерного альтиметра (LOLA) космического аппарата Lunar Reconnaissance Orbiter (LRO) с точностью 64 пикселя на градус (0.5 км на пиксель) (Smith и др., 2010) в программе ArcGIS. Осреднение по 5-градусным площадкам позволяет получить разложение высот рельефа по сферическим функциям до степени Nk = 180°/5° = 36. Нами была разработана методика и создана теория (Чуйкова, Максимова, 1996), которая позволяет получить для каждой степени N = 1–Nk наиболее хорошо обусловленное решение для коэффициентов разложения высот рельефа по сферическим функциям, не дающее при большой степени N накопления ошибок вычислений.

Рис. 1.

Высоты рельефа Луны для разложения до 36 степени относительно сферической поверхности с центром в центре масс. Сечение изолиний 1 км. Диапазон изменений (–5.5, 7.3) км.

РЕЗУЛЬТАТЫ И ОСНОВНЫЕ ВЫВОДЫ

Конечным результатом работы было полученное нами распределение аномалий плотности в различных слоях Луны (вплоть до нижней границы на глубине 528.2 км), а также распределение вертикальных напряжений сжатия и растяжения.

На рис. 2 представлена гистограмма распределения глубин компенсации гармоник рельефа на основе гипотезы изостатической компенсации. Гистограммы и средние глубины компенсации считались с учетом весов, соответствующих вкладу рассматриваемых гармоник в гравитационное поле (в %). Из рис. 2 видно, что основная компенсация рельефа осуществляется в коре и в верхах мантии (до глубин 280 км), а также на возможной границе верхней и средней мантии (на глубине 528 км). Впрочем, эту границу можно определить также как границу сейсмического разрыва в средней мантии (Gagnepain‒Beyneix и др., 2006). В статье (Кусков и др., 2018) также выделяется сейсмический разрыв на глубине 500 км как возможная глубина проплавления лунных недр.

Рис. 2.

Гистограмма распределения глубин изостатической компенсации для разложения высот рельефа Луны по сферическим функциям до 369 степени с шагом 10 км.

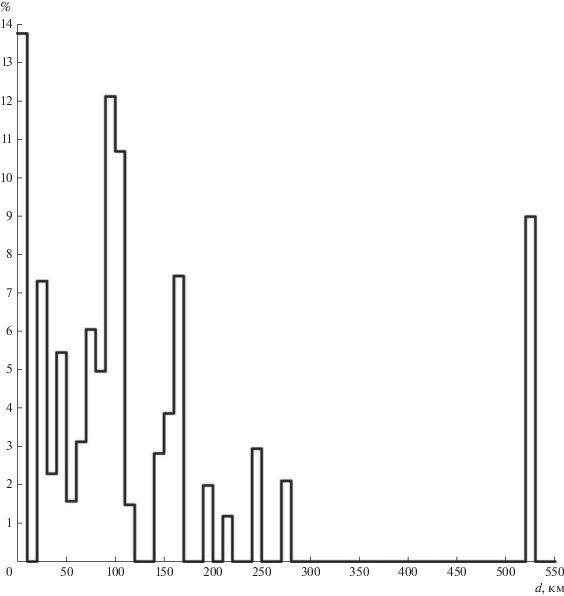
На рис. 2 четко прослеживаются основные слои компенсации (0–10, 20–50, 60–120, 140–170, 190–280, 520–530 км). На средних глубинах для каждого слоя (2.7, 32.7, 91.1, 156.8, 238.3, 528.2 км) были построены карты латеральных распределений аномалий плотности для простых слоев, учитывающие все три варианта компенсации (рис. 3–8), а также карта возможных напряжений в коре Луны (рис. 9). Средние глубины определяются для каждого слоя на основе весовой функции, соответствующей амплитудам гармоник рельефа, входящих в данный слой. Эти напряжения, по мнению авторов, могут привести к тектоническим лунотрясениям в зонах перехода от напряжений сжатия к напряжениям растяжения и наоборот. На картах (рис. 1, 3–9) горизонтальная ось соответствует долготам (нулевая долгота соответствует центру видимого полушария, долгота λ = ±180° соответствует центру обратного полушария). Вертикальная ось соответствует широтам (положительные широты соответствуют северному полушарию, отрицательные – южному). Из анализа карт видно, что основные аномалии плотности соответствуют верхнему слою коры (до глубины 10 км), для которого диапазон изменений плотности простого слоя составляет (–10.8–18.2) × 106 кг/м2 (рис. 3).

Рис. 3.

Распределение аномальных масс в коре на глубинах 0–10 км, приведенное к плотности простого слоя на средней глубине 2.7 км. Сечение изолиний 3 × 106 кг/м2. Диапазон измерений (–10.8, 18.2) × 106 кг/м2.

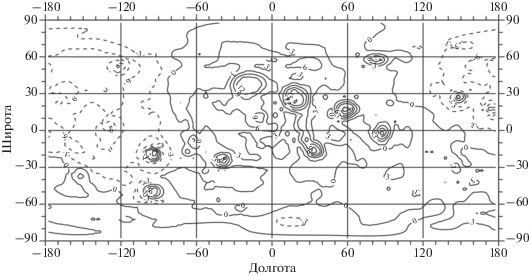
Рис. 4.

Распределение аномальных масс в коре на глубинах 20–50 км, приведенное к плотности простого слоя на средней глубине 32.7 км. Сечение изолиний 106 кг/м2. Диапазон измерений (–2.3, 2.7) × 106 кг/м2.

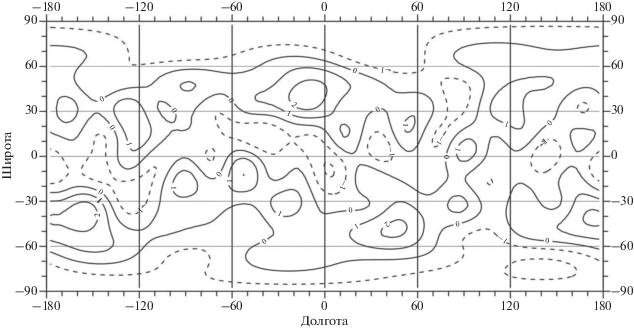
Рис. 5.

Распределение аномальных масс в верхней мантии на глубинах 60–120 км, приведенное к плотности простого слоя на средней глубине 91.1 км. Сечение изолиний 106 кг/м2. Диапазон измерений (–5.3, 4.9) × 106 кг/м2.

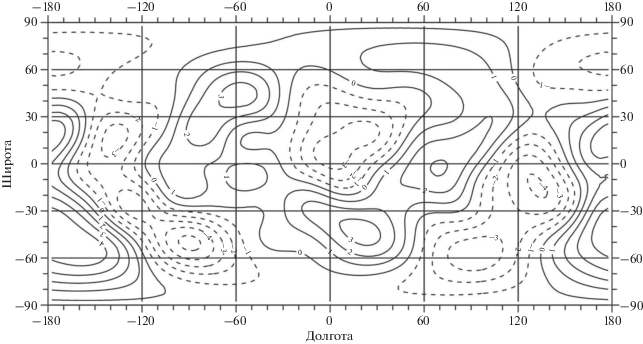
Рис. 6.

Распределение аномальных масс в верхней мантии на глубинах 140–170 км, приведенное к плотности простого слоя на средней глубине 156.8 км. Сечение изолиний 106 кг/м2. Диапазон измерений (–4.2, 4.9) × 106 кг/м2.

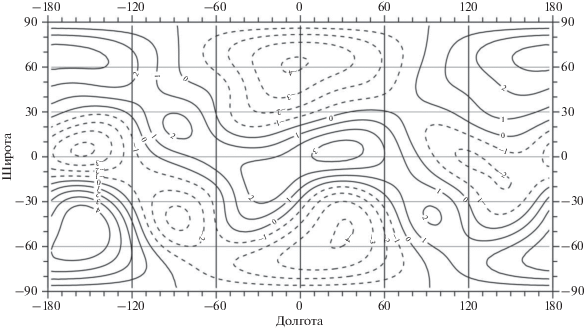
Рис. 7.

Распределение аномальных масс в переходном слое верхняя–средняя мантия на глубинах 190–280 км, приведенное к плотности простого слоя на средней глубине 238.3 км. Сечение изолиний 106 кг/м2. Диапазон измерений (–2.1, 1.9) × 106 кг/м2.

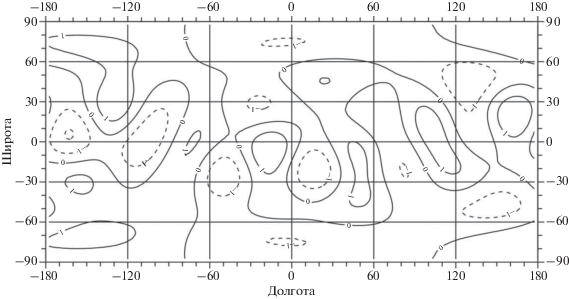
Рис. 8.

Распределение аномальных масс на границе средняя–нижняя мантия, приведенное к плотности простого слоя на глубине 528.2 км. Сечение изолиний 106 кг/м2. Диапазон изменений (–6.5, 7.8) × 106 кг/м2.

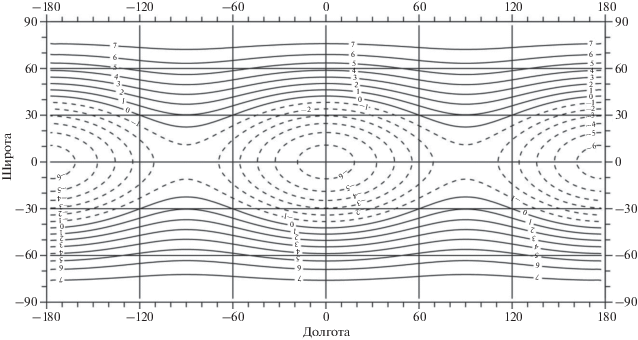
Рис. 9.

Изостатически невыравненные вертикальные напряжения в коре Луны. Сечение изолиний 3 МПа. Диапазон измерений (–15.1, 16.1) МПа.

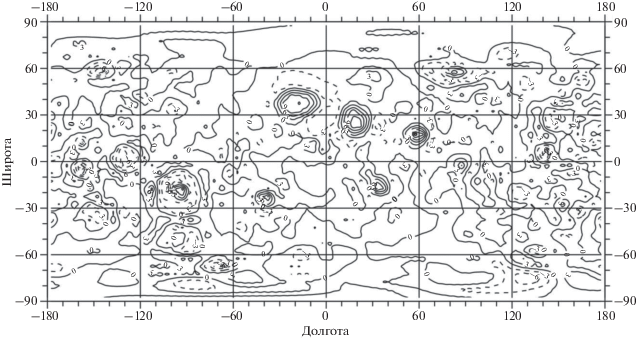
Максимальные вариации глубин относительно поверхности Луны меняются в диапазоне 1.6–6.5 км, средняя глубина d = (2.7 ± 1.3) км. Максимумы положительной плотности соответствуют лунным масконам (море Дождей, Ясности, Кризисов, Нектара, Смита, Гумбольдта – на видимой стороне Луны), причем некоторые из них окружены кольцом отрицательных аномалий (море Восточное, Ридберг, Москвы – на обратной стороне). Из карты также видно, что видимое полушарие коры соответствует в основном положительным аномалиям плотности, а обратное – отрицательным аномалиям, что, возможно, и вызывает сдвиг центра масс Луны по направлению к Земле. По-видимому, именно в коре на обратной стороне Луны могут быть сосредоточены основные запасы летучих (в том числе и воды), максимальные – в районе кратера Крылов.

Что же касается карт на других глубинах (рис. 4–8), то там аномалии плотности не превышают 7.8 × × 106 кг/м2. Однако вариации глубин весьма значительны. Так, для d = (32.7 ± 10.4) км глубины компенсации меняются в диапазоне (20.2–44.6) км; для d = (91.1 ± 14.1) км диапазон равен (70.3–106.2) км; для d = (156.8 ± 6.1) км диапазон равен (141.9–161.1) км. Особенно велик диапазон изменений (198.8–279.8) км в переходной зоне верхняя‒средняя мантия, где d = (238.3 ± 32.4) км. На основе анализа гистограммы можно также отметить значительные скачки плотности при d = 0, 20, 90, 160, 520 км, соответствующие глубинам 1.6, 20.2, 98.4, 161.1, 528.2 км и гармоникам рельефа a21, a43, a33, a31, a20 + a22, а также при d = 40, 70 км, соответствующие глубинам 44.6, 70.3 км и гармоникам рельефа a40, a42. Отсюда следует вывод, что основные скачки плотности в мантии Луны обусловлены компенсацией глобальных горизонтальных неоднородностей рельефа размерами 45° и больше, соответствующих гармоникам низких степеней (до n = 4). Отсутствие компенсации на глубинах (280–520) км для всех остальных гармоник, по-видимому, свидетельствует о том, что их компенсация произошла в более поздние времена для Луны, когда только верхняя мантия была в частично расплавленном состоянии. Отсутствие компенсации для всех гармоник рельефа на глубинах больше 530 км и меньше 1000 км, по-видимому, подтверждает вывод, что эта часть мантии соответствует наиболее древним, не подверженным плавлению слоям Луны (Nakamura, 1983; Хаббард, 1987). Тот вывод, что на глубинах, больших 530 км, находится средняя мантия первичного состава, есть в работе (Хаббард, 1987). Об этом же говорит и тот факт, что приливные лунотрясения сосредоточены в этой области до глубины порядка 1000 км, ниже которой как раз и расположены частично расплавленная нижняя мантия и ядро. В статьях (Weber и др., 2011; Williams и др., 2014; Раевский и др., 2015) как раз и говорится об этой частично расплавленной зоне. В статье (Кусков и др., 2018) также говорится о том, что граница на глубине 500 км может быть возможной глубиной проплавления лунных недр.

Полученные карты вертикальных напряжений (рис. 9), обусловленные давлением нескомпенсированных масс рельефа, пересчитанные к глубине 2.7 км для верхов коры, по-видимому, базальтового состава, приводят к диапазону изменений напряжений –(15.10–16.13) МПа. Эти напряжения не превосходят пределы прочности основных пород на сжатие (270–290) МПа и на растяжение 22 МПа (Рыжий, Начапкин, 2003). Положительные напряжения сжатия в основном характеризуют видимую сторону Луны и соответствуют лунным морям Дождей, Ясности, Кризисов, Нектара, Влажности (максимальное – морю Кризисов), а также есть в краевой зоне (море Восточное, Смита, Гумбольдта). Можно отметить, что почти все масконы с положительными значениями напряжений сжатия окружены кольцами отрицательных напряжений растяжения, особенно характерных для некоторых морей, окруженных горными областями (например, моря Дождей, Ясности, Восточное, Гумбольда, Нектара, Смита). А области с отрицательными аномалиями растяжения наиболее распространены на обратной стороне и в южном регионе (максимальное значение соответствует кратеру Королев) и окружены кольцами положительных аномалий сжатия (например, кратер Биркхоф, Королев, Герцшпрунг, Аполлон, Байи, Другальский, Шредингер, Менделеев, море Москвы).

Из анализа карт (рис. 4–7) видно, что компенсация бассейна Эйткин осуществляется в основном в верхней мантии на средней глубине 91.1 км (рис. 5) и на глубине 156.8 км (рис. 6), а также частично в коре на глубине 32.7 км (рис. 4) (северная часть бассейна) и в переходном слое верхняя‒средняя мантия на глубине 238.3 км (рис. 7) (юго-западная часть бассейна). А компенсация возвышенного региона на обратной стороне, окружающего бассейн, с максимальным значением высот рельефа вблизи вулкана Королев, также в основном осуществляется в верхней мантии на глубинах 91.1 и 156.8 км. Компенсация южной возвышенной части рельефа соответствует положительным аномалиям плотности на глубине 91.1 км (уступ Алтай) и на глубине 156.8 км. Интересно отметить, что, судя по рис. 4–7, плотностное строение коры и верхней мантии свидетельствует о блоковом строении верхней части Луны: области положительных аномалий плотности окружены кольцами отрицательных аномалий. Это может подтвеждать гипотезу, что Луна изначально сформировалась из отдельных кусков вещества: или протолун (Рускол, 1975), или кусков земной литосферы, оторванных от Земли в результате мегаимпакта (Cameron, Ward, 1976; Hartmann, Davis, 1975), или нескольких макроимпактов (Печерникова, 2015). Что же касается рис. 8, то он отражает глубину компенсации аномальных масс рельефа, соответствующих гармоникам a20+ a22, на границе средней и нижней мантии (528 км). Можно предположить, что рис. 8 отвечает компенсации на этой глубине для гармоник, соответствующих полярному и экваториальному сжатиям рельефа в более ранние времена, когда вся мантия Луны была в расплавленном состоянии. Из сравнения рис. 3 и рис. 9 можно заключить, что положительные аномалии плотности, соответствующие масконам, в основном не скомпенсированы и приводят к напряжениям в литосфере Луны. Есть только частичная компенация для морей Дождя, Ясности, Кризисов и Смита на глубине 238.3 км (рис. 7).

Из рис. 3 также видно, что смещение центра фигуры Луны относительно центра масс обусловлено отрицательными аномалиями плотности коры на обратной стороне Луны и положительными аномалиями на видимой стороне. Сравнение рис. 9 с данными об очагах тектонических лунотрясений (Nakamura, 1983; Галкин, 1988), по мнению авторов, может свидетельствовать о связи их расположения с максимальными градиентами напряжений в зонах перехода от напряжений сжатия к напряжениям растяжения и наоборот.

ЗАКЛЮЧЕНИЕ

Кора и верхняя мантия Луны характеризуются неоднородным распределением плотности вплоть до глубины 280 км и напряжений в коре. Нижние слои верхней мантии на глубинах 280–530 км, по-видимому, однородны и лишь на границе 530 км (согласно (Хаббард, 1987)) со средней мантией имеются глобальные плотностные неоднородности.

Впрочем, эти слои (280–530 км) можно назвать и средней мантией согласно (Кусков и др., 2018). Эти неоднородности на границе 530 км соответствуют изостатической компенсации гармоник рельефа a20 и a22 и особенно характерны для центральных частей видимой и обратной сторон Луны. Сделанные нами выводы о блоковом строении верхней части Луны хорошо коррелируют с гипотезой о первоначальном формировании Луны из отдельных блоков (Рускол, 1975; Печерникова, 2015). Наши результаты о глобальном внутреннем строении Луны хорошо согласуются с выводами, полученными на основе анализа современных сейсмологических и геофизических данных (Жарков, 1983; Галкин, 1988; Gusev и др., 2015; Хаббард, 1987; Zhao и др., 2008; 2012; Sakamaki и др., 2010), а также с данными об очагах тектонических лунотрясений (Галкин, 1988). Наличие значительных отрицательных аномалий плотности, простирающихся от верхов коры (рис. 3) и в мантии вплоть до переходного слоя верхняя-средняя мантия (рис. 4–7) может подтвердить вывод, сделанный в (Zhao и др., 2012; Sakamaki и др., 2010) о происхождении неоднородностей в лунной мантии и о возможности тепловой конвекции в недрах Луны (Zhao и др., 2012).

Разработанная методика определения внутреннего аномального плотностного строения для Луны на основе космических наблюдений гравитационного поля и рельефа, проверенная для Земли, дает хорошее модельное представление, на которое можно будет ориентироваться при будущих исследованиях на ее поверхности.

Список литературы

  1. Браун Д., Массет А. Недоступная Земля. М.: МИР, 1984. 262 с.

  2. Галкин И.Н. Внеземная сейсмология. М.: Наука, 1988. (Планета Земля и Вселенная), ISBN 5-02-005951-X. 195 с.

  3. Дубошин Г.Н. Теория притяжения. М., 1961. С. 258–261.

  4. Жарков В.Н. Внутреннее строение Земли и планет. М.: Наука, 1983. 416 с.

  5. Жарков В.Н. Физика земных недр. М.: Наука и образование, 2012. 383 с.

  6. Кусков О.Л., Кронрод Е.В., Кронрод В.А. Геохимические ограничения на “холодные” и “горячие” модели внутреннего строения Луны: 1. Валовый состав // Астрон. вестн. 2018. Т. 52. № 6. С. 481–494. (Kuskov O.L., Kronrod E.V., Kronrod V.A. Geochemical Constraints on the Cold and Hot Models of the Moon’s Interior: 1‑Bulk Composition // Sol. Syst. Res. 2018. V. 52. № 6. P. 467–479.) https://doi.org/10.1134/s0320930x1806004x

  7. Насонова Л.П., Чуйкова Н.А. Аномалии внешнего и внутреннего гравитационного поля изостатически уравновешенной коры Земли в квадратичном приближении // Вестн. Моск. ун-та. Сер. 3. Физ. Астрон. 2007. № 6. С. 61–68.

  8. Печерникова Г.В. Масса вещества, выброшенного при макроударах с растущей планеты, и проблема образования Луны // Сб. научных тр. ИДГ РАН. Вып. 7. М.: ГЕОС, 2015. С. 200–207.

  9. Раевский С.Н., Гудкова Т.В., Кусков О.Л., Кронрод В.А. О согласовании моделей внутреннего строения Луны с данными гравитационного поля // Физика Земли. 2015. № 1. С. 139–147.

  10. Рускол Е.Л. Происхождение Луны. М.: Наука, 1975. 185 с.

  11. Рыжий Б.П., Начапкин Н.И. О связи внутриплитной сейсмичности с вещественным составом земной коры и аномалиями гравитационного поля // Сб. тр. Четвертых геофизических чтений им. В.В. Федынского. М., 2003. С. 203–206.

  12. Хаббард У. Внутреннее строение планет. М.: МИР, 1987. 328 с.

  13. Чуйкова Н.А., Максимова Т.Г. Гармонический и статистический анализ глубин поверхности Мохоровичича // Тр. ГАИШ. 1996. Т. LXV. С. 33–50.

  14. Чуйкова Н.А., Насонова Л.П., Максимова Т.Г. Аномалии внутреннего гравитационного поля в коре и верхней мантии Земли // Вестн. Моск. ун-та. Сер. 3. Физ. Астрон. 2006. № 4. С. 48–56.

  15. Чуйкова Н.А., Насонова Л.П., Максимова Т.Г. Аномальное строение коры и мантии Марса // Вестн. Моск. ун-та. Сер. 3. Физ. Астрон. 2011. № 1. С. 63–69.

  16. Чуйкова Н.А., Насонова Л.П., Максимова Т.Г. Аномалии плотности, напряжений и гравитационного поля внутри Марса // Вестн. Моск. ун-та. Cер. 3. Физ. Астрон. 2012. № 2. С. 70–77.

  17. Чуйкова Н.А., Насонова Л.П., Максимова Т.Г. Аномалии плотности, напряжений и гравитационного поля внутри Земли и Марса и возможные геодинамические следствия: сравнительный анализ // Физика Земли. 2014. № 3. С. 127–143.

  18. Чуйкова Н.А., Насонова Л.П., Максимова Т.Г. Новое решение обратной задачи гравиметрии для планет земной группы и его проверка для Земли // Астрономия, геодезия и геофизика. Научно-технический сб. М.: Изд-во ФГБУ “Центр геодезии, картографии и ИПД”, 2018. С. 90–113.

  19. Чуйкова Н.А., Родионова Ж.Ф., Максимова Т.Г., Гришакина Е.А. Анализ высот рельефа Луны и корреляционной связи рельефа с гравитационным полем; предварительные выводы о глобальных плотностных неоднородностях коры Луны // Астрон. вестн. 2019. Т. 53. № 3. С. 174–184. (Chuikova N.A., Rodionova Zh.F., Maksimova T.G., Grishakina E.A. Analysis of Lunar Terrain Altitudes and Correlation Links between the Terrain and Gravitational Field; Preliminary Conclusions on the Global Density Inhomogeneities of the Lunar Crust // Sol. Syst. Res. 2019. V. 53. № 3. P. 161–171.)

  20. Besserer J., Nimmo1 F., Wieczorek M.A., Weber R.C., Kiefer W.S., McGovern P.J., Andrews-Hanna J.C., Smith D.E., Zuber M.T. GRAIL gravity constraints on the vertical and lateral density structure of the lunar crust // Geophys. Res. Lett. 2014. V. 41. P. 5771–5777. https://doi.org/10.1002/2014GL060240

  21. Cameron A.G.W., Ward W.R. The origin of the Moon // Lunar and Planet. Sci. Conf. VII. 1976. P. 120–122.

  22. Chujkova N.A., Nasonova L.P., Maximova T.G. The new method to fund the anomalous internal structute of terrestrial planets and its test on the Earth // IAG Symposia Series. 2014. V. 144. Chapter 195. P. 209–219. https://doi.org/10.1007/978-3-319-39820-4.

  23. Gagnepain-Beyneix J., Lognonn’e P., Chenet H., Lombardi D., Spohnd T. A seismic model of the lunar mantle and constraints on temperature and mineralogy // Phys. Earth and Planet. Interiors. 2006. V. 159. P. 140–166.

  24. Gusev A., Hanada H., Petrova N., Kosov A., Kuskov O., Kronrod E. Rotation, physical librations and interior structure of the active and multi-layer Moon. Monograph. Kazan: Kazan Univ. Publ. 2015. 328 p.

  25. Hartmann W.K., Davis D.R. Satellite-sized planetosimals and lunar origin // Icarus. 1975. V. 24. P. 504–515.

  26. Hemingway D.J., Matsuyama I. Isostatic equilibrium in spherical coordinates and implications for crustal thickness on the Moon, Mars, Enceladus, and elsewhere // Geophys. Res. Lett. 2017. V. 44. P. 7695–7705. https://doi.org/10.1002/2017GL073334

  27. Matsumoto K., Yamada R., Kikuchi F., Kamata S., Ishihara Y., Iwata T., Hanada H., Sasaki S. Internal structure of the Moon inferred from Apollo seismic data and selenodetic data from GRAIL and LLR // Geophys. Res. Lett. 2015. V. 42. P. 7351–7358. https://doi.org/10.1002/2015GL065335

  28. Matsuyama I., Nimmo F., Keanel J.T., Chan1 N.H., Taylor G.J., Wieczorek M.A., Kiefer W.S., Williams J.G. GRAIL, LLR, and LOLA constraints on the interior structure of the Moon // Geophys. Res. Lett. 2016. V. 43. P. 8365–8375. https://doi.org/10.1002/2016GL069952

  29. Nakamura Y. Seismic velocity structure of the lunar mantle // J. Geophys. Res. 1983. V. 88. P. 677–686.

  30. Sakamaki T., Ohtani E., Urakawa S., Suzuki A., Katayama Y., Zhao D. Density of high-Ti basalt magma at high pressure and origin of heterogeneities in the lunar mantle // Earth and Planet. Sci. Lett. 2010. V. 299. P. 285–289.

  31. Smith D.E., Zuber M.T., Jackson G.B., Cavanaugh J.F., Neumann G.A., Riris H., Sun X., Zellar R.S., Coltharp C., Connelly J., Katz R.B., Kleyner I., Liiva P., Matuszeski A., Mazarico E.M. The lunar orbiter laser altimeter investigation on the Lunar Reconnaissance Orbiter mission // Space Sci. Rev. 2010. V. 150. P. 209–241. https://doi.org/10.10 07/s11214-0 09-951

  32. Weber R.C., Lin P.-Y., Garnero E.J., Williams Q., Lognonné P. Seismic detection of the lunar core // Science. 2011. V. 331(6015). P. 309–312.

  33. Wieczorek M.A., Neumann G.A., Nimmo F., Kiefer W.S., Taylor G.J., Melosh H.J., Phillips R.J., Solomon S.C., Andrews-Hanna J.C., Asmar S.W., Konopliv A.S., Lemoine F.G., Smith D.E., Watkins M.M., Williams J.G., Zuber M.T. The crust of the Moon as seen by GRAIL // Science. 2013. V. 339(6120). P. 671–676. https://doi.org/10.1126/science.1231530

  34. Williams J.G., Konopliv A.S., Boggs D.H., Park R.S., Yuan D.-N., Lemoine F.G., Goossens S., Mazarico E., Nimmo F., Weber R.C., Asmar S.W., Melosh H.J., Neumann G.A., Phillips R.J., Smith D.E., Solomon S.C., Watkins M.M., Wieczorek M.A., Andrews-Hanna J.C., Head J.W., Kiefer W.S., Matsuyama I., McGovern P.J., Taylor G.J., Zuber M.T. Lunar interior properties from the GRAIL mission // J. Geophys. Res. Planets. 2014. V. 119. P. 1546–1578. https://doi.org/10.1002/2013JE004559

  35. Zhao D., Lei J., Liu L. Seismic tomography of the Moon // Chinese Sci. Bull. 2008. V. 53. P. 3897–3907.

  36. Zhao D., Arai T., Liu L., Ohtani E. Seismic tomography and geochemical evidence for lunar mantle heterogeneity: Comparing with Earth // J. Global and Planet. Change. 2012. V. 90–91. P. 29–36.

  37. Zuber M.T., Smith D.E., Watkins M.M., Asmar S.W., Konopliv A.S., Lemoine F.G., Melosh H.J., Neumann G.A., Phillips R.J., Solomon S.C., Wieczorek M.A., Williams J.G., Goossens S.J., Kruizinga G., Mazarico E. Gravity field of the Moon from the Gravity Recovery and Interior Laboratory (GRAIL) mission // Science. 2013. V. 339. № 6120. P. 668–671. https://doi.org/10.1126/science.1231507

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал