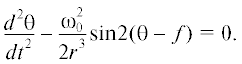Астрономический вестник, 2020, T. 54, № 5, стр. 458-467
ОРИЕНТАЦИЯ ФИГУР МАЛЫХ СПУТНИКОВ ПЛАНЕТ ПРИ ХАОТИЧЕСКОМ ВРАЩЕНИИ
А. В. Мельников *
Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия
* E-mail: melnikov@gaoran.ru
Поступила в редакцию 10.02.2020
После доработки 11.03.2020
Принята к публикации 29.04.2020
Аннотация
Посредством численных экспериментов рассмотрен эффект преимущественной ориентации наибольшей оси фигуры спутника по направлению на планету при его хаотическом вращении. Установлено, что данный эффект наиболее заметен в хаотической динамике малых спутников с величиной эксцентриситета орбиты e ≤ 0.005 и может затруднить идентификацию хаотического режима вращения спутника, если длина ряда наблюдений недостаточно велика. Показано, что рассмотренный эффект имеет место в возможной хаотической вращательной динамике 30% известных малых спутников планет Солнечной системы.
ВВЕДЕНИЕ
В настоящее время установлено, что в вековой динамике различных небесных тел (спутники планет, астероиды, кометы и пр.) имеет место хаотическое поведение (Морбиделли, 2014; Мюррей, Дермотт, 2009). Проявлением динамического хаоса (Лихтенберг, Либерманн, 1984) является экспоненциальная расходимость близких траекторий фазового пространства системы, поэтому ее динамика является непредсказуемой на временах больших чем т. н. ляпуновское время системы (Chirikov, 1979). Впервые возможность наличия хаоса во вращательной динамике спутников планет была показана в работе Wisdom и др. (1984), а в качестве наиболее вероятного кандидата на нахождение в хаотическом режиме вращения был указан Гиперион – седьмой спутник Сатурна. Численные моделирования вращательной динамики Гипериона и сопоставления его модельных кривых блеска с наблюдательными данными, проведенные в работах Klavetter (1989), Black и др. (1995), Девяткин и др. (2002) и Harbison и др. (2011), подтвердили хаотический режим вращения Гипериона в настоящее время. Ляпуновское время для хаотического вращения Гипериона согласно различным оценкам (Шевченко, 2002; Harbison и др., 2011) составляет всего 1–2 мес. (1.5–3 орбитальных периода). Поэтому хаотическую вращательную динамику Гипериона можно идентифицировать посредством анализа как длительных наземных наблюдений, так и относительно коротких (порядка месяца) наблюдений с борта межпланетных космических аппаратов. В работах Kouprianov и Shevchenko (2005) и Melnikov и Shevchenko (2008) показано, что еще два спутника Сатурна – Прометей (С16) и Пандора (С17) могут вращаться хаотически, поскольку их плоское синхронное вращательное движение (в этом режиме находятся подавляющее большинство спутников с установленными параметрами вращения) с большой долей вероятности является неустойчивым относительно наклона оси вращения. Ляпуновское время хаотического вращения этих спутников весьма мало – менее суток (Kouprianov, Shevchenko, 2005).
При хаотическом вращении спутника имеет место непредсказуемое изменение величины и направления вектора его угловой скорости вращения – наблюдается хаотичное “кувыркание” спутника. Посредством анализа информации, извлекаемой из снимков с межпланетных космических аппаратов, об изменении ориентации фигуры спутника в пространстве с течением времени определяют, в частности, угловую скорость вращения спутника. Например, в случае вращения спутника в точном синхронном спин-орбитальном резонансе наибольшая ось фигуры спутника в перицентре его орбиты параллельна радиус-вектору планета – спутник, а при движении по орбите должна быть ориентирована по направлению на планету, испытывая либрации (в частности из-за эксцентричности орбиты, см., например, Белецкий, 1965). В синхронном резонансе угловая скорость вращения спутника равна угловой скорости его обращения по орбите. Задача о том, существует ли преимущественная ориентация фигуры спутника в пространстве при его хаотическом вращении, или хаотическое кувыркание изотропно, имеет важное значение для определения характера вращения спутника из анализа наблюдательных данных.
Wisdom (1987) отметил, что в модельном хаотическом пространственном вращении Фобоса (М1) на относительно коротком интервале времени интегрирования в 75 орбитальных периодов (≈24 сут) наблюдается преимущественная ориентация наибольшей оси фигуры спутника по направлению на Марс, т.е. модельное хаотическое вращение Фобоса может быть схоже с регулярным. Под преимущественной ориентацией здесь и далее подразумевается, что относительное время нахождения наибольшей оси фигуры спутника в пределах конуса с углом раствора равным углу, под которым со спутника виден диск планеты, существенно превышает “изотропную норму” для случая, когда при хаотическом вращении спутника все направления ориентации его фигуры в пространстве равновероятны. При пространственном вращении величина изотропной нормы пропорциональна относительной площади на небесной сфере видимого со спутника диска планеты.
В работе Melnikov и Shevchenko (2008) было установлено, что в хаотической вращательной динамике Прометея и Пандоры на промежутке времени интегрирования в 10 тыс. орбитальных периодов (≈16 лет) для каждого спутника имеет место преимущественная ориентация наибольшей оси фигуры по направлению на Сатурн. Модельные численные эксперименты показали, что средние значения относительной величины времени ориентации наибольших осей фигур Прометея и Пандоры по направлению на Сатурн зависят от выбора начальных условий и находятся в интервале 20–30%. В случае, если бы ориентация фигур указанных спутников во время хаотического кувыркания являлась изотропной, это время должно было составлять 8–9%. Таким образом, можно ожидать, что эффект преимущественной ориентации типичен для спутников вытянутой формы, таких как Прометей и Пандора.
Теоретические исследования (см., например, Goldreich, Peale, 1966; Peale, 1977; 1999) показывают, что в ходе долговременной приливной эволюции вращательного движения спутник проходит через различные спин-орбитальные резонансные состояния, пока не будет захвачен в одно из них. Наиболее вероятным финальным режимом вращения спутника является синхронное с движением по орбите. В синхронном вращении находятся все большие (с радиусом более 500 км) спутники планет. Значительная часть (около 90%) из известных спутников планет представляют собой тела неправильной формы с размерами от единиц до нескольких сотен километров – так называемые малые спутники. Вращательные состояния большинства известных малых спутников планет не установлены. Melnikov и Shevchenko (2010) показали, что более 60% известных малых спутников с неустановленным в настоящее время режимом вращения находятся либо в регулярном (и более быстром, чем синхронное) вращении, либо вращаются хаотически. Хаотическое вращение должно наблюдаться у таких малых спутников, чья приливная эволюция уже завершена – в фазовом пространстве вращательного движения спутник приблизился к области, соответствующей синхронному вращению, однако синхронной резонанс является неустойчивым, либо вовсе не существует (см. подробнее Melnikov, Shevchenko, 2010). Следует ожидать, что в хаотической вращательной динамике малых спутников в окрестности синхронного резонанса может проявляться эффект преимущественной ориентации наибольшей оси фигуры спутника на планету. Далее нами подробно рассматривается возможность существования анизотропии в ориентации фигур малых спутников при нахождении их в хаотическом режиме вращения.
УРАВНЕНИЯ ДВИЖЕНИЯ
Динамика пространственного поступательно-вращательного движения спутника в гравитационном поле планеты определяется тремя параметрами – эксцентриситетом орбиты спутника e и отношением главных центральных моментов инерции A/C и B/C, где A < B < C. В случае плоского (в плоскости орбиты) вращения спутника динамика определяется величиной e и значением параметра ${{{\omega }}_{{\text{0}}}} = \sqrt {{{{\text{3(}}B - A{\text{)}}} \mathord{\left/ {\vphantom {{{\text{3(}}B - A{\text{)}}} C}} \right. \kern-0em} C}} ,$ характеризующего асимметрию фигуры спутника. Далее используем прямоугольную систему координат Oxyz, определенную исходно в перицентре орбиты следующим образом: ось x направлена по вектору “перицентр орбиты спутника – планета”, ось y параллельна вектору орбитальной скорости в перицентре, ось z ортогональна орбитальной плоскости и дополняет систему до “правой”. Ориентация спутника относительно осей системы координат Oxyz задается путем его воображаемых поворотов на углы Эйлера θ, φ, ψ из положения совпадения главных осей инерции спутника a > b > c с осями системы координат до их реального положения в пространстве в следующей последовательности (согласно Wisdom и др., 1984): сначала делаем поворот на угол θ вокруг оси c, затем на угол φ вокруг оси a и, наконец, на угол ψ вокруг оси b.
Вращательное движение спутника описывается динамическими и кинематическими уравнениями Эйлера. Выпишем динамические уравнения Эйлера (Белецкий, 1965; Мельников, Шевченко, 2007):
(1)
$\begin{gathered} A\frac{{d{{\omega }_{a}}}}{{dt}} - {{\omega }_{b}}{{\omega }_{c}}(B - C) = - 3\frac{{GM}}{{{{r}^{3}}}}\beta \gamma (B - C), \\ B\frac{{d{{\omega }_{b}}}}{{dt}} - {{\omega }_{c}}{{\omega }_{a}}(C - A) = - 3\frac{{GM}}{{{{r}^{3}}}}\gamma \alpha (C - A), \\ C\frac{{d{{\omega }_{c}}}}{{dt}} - {{\omega }_{a}}{{\omega }_{b}}(A - B) = - 3\frac{{GM}}{{{{r}^{3}}}}\alpha \beta (A - B), \\ \end{gathered} $r = as(1 – e2)/(1 + ecosf) – расстояние “спутник – планета”, где as – большая полуось орбиты, f – истинная аномалия; α, β, γ – направляющие косинусы главных осей инерции относительно направления на планету. Далее полагаем as = 1 и GM = 1. Таким образом, угловые скорости выражены в единицах среднего движения, расстояния – в единицах большой полуоси эллипса орбиты. Один орбитальный период соответствует 2π единицам времени.
Кинематические уравнения Эйлера и выражения для направляющих косинусов в принятой системе углов Эйлера имеют вид (Wisdom и др., 1984; Мельников, Шевченко, 2007):
(2)
$\begin{gathered} \frac{{d\theta }}{{dt}} = \frac{{{{\omega }_{c}}\cos \psi - {{\omega }_{a}}\sin \psi }}{{\cos \phi }}, \\ \frac{{d\phi }}{{dt}} = {{\omega }_{a}}\cos \psi + {{\omega }_{c}}\sin \psi , \\ \frac{{d\psi }}{{dt}} = {{\omega }_{b}} - ({{\omega }_{c}}\cos \psi - {{\omega }_{a}}\sin \psi ){\text{tg}}\phi , \\ \end{gathered} $α = cos(θ − f)cos ψ − sin(θ − f)sin φ sin ψ,
γ = cos(θ − f)sin ψ + sin(θ − f)sin φ cos ψ.
При пространственном вращении спутника, которое имеет место, например при его хаотическом кувыркании, в кинематических уравнениях Эйлера (2) присутствует сингулярность при φ = = ±π/2. Чтобы избавиться от сингулярности, при численном интегрировании вместо углов Эйлера нами использовались переменные Родрига–Гамильтона (λ0, λ1, λ2, λ3), связанные с углами Эйлера следующими соотношениями (Куприянов, 2014):
(4)
$\begin{gathered} {{\lambda }_{0}} = \cos \frac{\theta }{2}\cos \frac{\phi }{2}\cos \frac{\psi }{2} - \sin \frac{\theta }{2}\sin \frac{\phi }{2}\sin \frac{\psi }{2}, \\ {{\lambda }_{1}} = \cos \frac{\theta }{2}\sin \frac{\phi }{2}\cos \frac{\psi }{2} - \sin \frac{\theta }{2}\cos \frac{\phi }{2}\sin \frac{\psi }{2}, \\ {{\lambda }_{2}} = \cos \frac{\theta }{2}\cos \frac{\phi }{2}\sin \frac{\psi }{2} + \sin \frac{\theta }{2}\sin \frac{\phi }{2}\cos \frac{\psi }{2}, \\ {{\lambda }_{3}} = \cos \frac{\theta }{2}\sin \frac{\phi }{2}\sin \frac{\psi }{2} + \sin \frac{\theta }{2}\cos \frac{\phi }{2}\cos \frac{\psi }{2}. \\ \end{gathered} $Переменные Родрига–Гамильтона (Борисов, Мамаев, 2001; Whittaker, 1917) являются регулярными во всей области задания – 1≤ λi≤ 1, i = 0, …, 3. При использовании переменных Родрига–Гамильтона вместо кинематических уравнений Эйлера (2), представляющих собой систему из трех уравнений, мы имеем систему из четырех дифференциальных уравнений (Куприянов, 2014):
(5)
$\begin{gathered} \frac{{d{{\lambda }_{0}}}}{{dt}} = - \frac{1}{2}({{\lambda }_{1}}{{\omega }_{a}} + {{\lambda }_{2}}{{\omega }_{b}} + {{\lambda }_{3}}{{\omega }_{c}}), \\ \frac{{d{{\lambda }_{1}}}}{{dt}} = \frac{1}{2}({{\lambda }_{0}}{{\omega }_{a}} + {{\lambda }_{3}}{{\omega }_{b}} + {{\lambda }_{2}}{{\omega }_{c}}), \\ \frac{{d{{\lambda }_{2}}}}{{dt}} = \frac{1}{2}({{\lambda }_{3}}{{\omega }_{a}} + {{\lambda }_{0}}{{\omega }_{b}} + {{\lambda }_{1}}{{\omega }_{c}}), \\ \frac{{d{{\lambda }_{3}}}}{{dt}} = - \frac{1}{2}({{\lambda }_{2}}{{\omega }_{a}} + {{\lambda }_{1}}{{\omega }_{b}} + {{\lambda }_{0}}{{\omega }_{c}}). \\ \end{gathered} $Направляющие косинусы в параметрах Родрига–Гамильтона имеют вид (Куприянов, 2014):
(6)
$\begin{gathered} \alpha = \left( {\lambda _{0}^{2} + \lambda _{1}^{2} - \lambda _{2}^{2} - \lambda _{3}^{2}} \right)\cos f + \\ + \,\,2({{\lambda }_{0}}{{\lambda }_{3}} + {{\lambda }_{1}}{{\lambda }_{2}})\sin f, \\ \beta = 2({{\lambda }_{1}}{{\lambda }_{2}} + {{\lambda }_{0}}{{\lambda }_{3}})\cos f + \\ + \,\,\left( {\lambda _{0}^{2} - \lambda _{1}^{2} + \lambda _{2}^{2} - \lambda _{3}^{2}} \right)\sin f, \\ \gamma = 2({{\lambda }_{0}}{{\lambda }_{2}} + {{\lambda }_{1}}{{\lambda }_{3}})\cos f + ({{\lambda }_{2}}{{\lambda }_{3}} + {{\lambda }_{0}}{{\lambda }_{1}})\sin f. \\ \end{gathered} $При моделировании поступательно-вращательного движения спутника численно интегрировалась система уравнений (1) и (5). Ориентация фигуры спутника и скорость его вращения в начальный момент времени задавалась углами Эйлера и их производными по времени и переход к переменным Родрига–Гамильтона происходил непосредственно перед численным интегрированием уравнений движения.
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ХАОТИЧЕСКОГО ВРАЩЕНИЯ СПУТНИКА
Цель нашего численного моделирования состояла в выявлении анизотропии в ориентации фигуры малого спутника при его хаотическом вращении в окрестности синхронного резонанса. Для этого, посредством интегрирования уравнений вращательного движения спутника на длительном интервале проводилось определение σ – относительной величины времени, когда наибольшая ось фигуры спутника при хаотическом вращении ориентирована по направлению на планету (см. выше).
В качестве модельных тел были выбраны Прометей (С16) и Пандора (С17), вращательная динамика которых в синхронном резонансе близка к неустойчивой (Melnikov, Shevchenko, 2008), поэтому эти спутники являются наиболее вероятными кандидатами на нахождение в хаотическом режиме вращения. В табл. 1 приведены начальные значения орбитальных параметров и значения физических параметров Прометея и Пандоры, использовавшиеся в численных экспериментах. Значения отношений главных центральных моментов инерции спутников вычислены по формулам: A/C = (b2 + c2)/(a2 + b2), B/C = (a2 + + c2)/(a2 + b2), справедливым для случая, когда спутник представляет собой трехосный эллипсоид с однородной плотностью. Для численного интегрирования уравнений движения использовался интегратор DOP853 (Hairer и др., 1993), реализующий метод Рунге–Кутты 8-го порядка, с автоматически изменяемой величиной шага интегрирования. Интегрирование проводилось на промежутке времени t = 106 орбитальных периодов (около 1600 лет), точность интегрирования ε = 10–12, максимальный шаг интегрирования Δt = 10–3. Численные эксперименты показали, что при интегрировании на интервале времени t ≥ 106 среднеквадратичное отклонение величины σ, вычисленной для разных начальных данных, составляет Δσ ≤ 10%. При интегрировании на временах t = 104–105 величина Δσ достигает 30% (Melnikov, Shevchenko, 2008).
Плоское хаотическое вращение спутника
Рассмотрим сначала плоское вращение спутника, в этом случае его динамика может быть описана в рамках модели возмущенного математического маятника. Приняв φ = ψ = dφ/dt = = dψ/dt = 0 из уравнений (1) и (2), получим уравнение маятника:
При плоском вращении наибольшая ось фигуры спутника находится в плоскости орбиты, ось вращения совпадает с наименьшей осью инерции спутника и ортогональна плоскости орбиты. Ориентацию спутника определяет угол θ, представляющий собой угол между наибольшей осью фигуры спутника и радиус-вектором “центр масс спутника – планета”.
На рис. 1 приведен пример сечения фазового пространства, построенного для случая плоского вращения Прометея. Сечение определено в перицентре орбиты спутника – при численном интегрировании значения (θ, dθ/dt) фиксировались, когда t = 2πm, m = 0, 1, 2 … . В случае плоского вращения спутника для значений параметров e и ω0, соответствующих Прометею (см. табл. 1), существуют две моды синхронного резонанса (Мельников, Шевченко, 2007), их центрам на рис. 1 соответствуют координаты – (0, 1.01) и (0, 0.18). В качестве начальных значений θ и dθ/dt для численных экспериментов по определению величины σ выбирались координаты точек, принадлежащих на сечении фазового пространства хаотическому слою в окрестности сепаратрисы первой моды синхронного резонанса.
Рис. 1.
Сечение фазового пространства плоского вращательного движения спутника. e = 0.0023, ω0 = 1.1717 (“Прометей”). Заштрихованная область соответствует ориентации наибольшей оси фигуры Прометея на Сатурн.
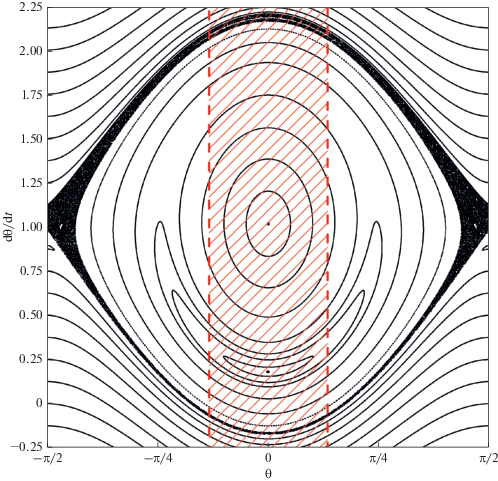
Таблица 1.
Орбитальные и физические параметры Прометея и Пандоры. Данные о величинах эксцентриситетов орбит и размерах спутников взяты из работ (Porco и др., 2005; Thomas, 2010)
| Прометей (С16) | Пандора (С17) | |
|---|---|---|
| e | 0.0023 | 0.0042 |
| a × b × c, км | 68.2 × 41.6 × 28.2 | 52.2 × 40.8 × 31.5 |
| A/C | 0.3958 | 0.6053 |
| B/C | 0.8534 | 0.8468 |
| ω0 | 1.1717 | 0.8512 |
На рис. 1 заштрихованная область по θ соответствует ориентации наибольшей оси фигуры Прометея на Сатурн. Вертикальные границы этой области θ = ±0.42 определены угловым размером Сатурна (средний радиус Сатурна – R = = 57 600 км) и расстоянием до него (средний радиус орбиты Прометея – r = 139 400 км). В случае изотропного плоского хаотического вращения спутника величина σ пропорциональна отношению площади хаотического слоя, заключенного в заштрихованной области на рис. 1 , к площади всего хаотического слоя на сечении и составляет в нашем случае σnorm = 11.9%. Определим величину σ для модельного хаотического вращения Прометея посредством численных экспериментов.
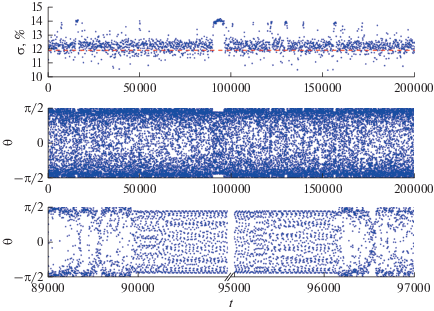
На рис. 2 приведены примеры зависимостей σ(t) и θ(t), построенные для хаотической траектории с начальными данными θ = –π/2, dθ/dt = 1. Интегрирование проводилось на временах до t = 106 орбитальных периодов. Для удобства дальнейшего анализа на рис. 2 приведены только начальные участки полученных зависимостей. Схожие зависимости были получены для других начальных данных (θ, dθ/dt) и параметров задачи (e, ω0). Из рис. 2 видно, что на зависимости σ(t) присутствуют относительно длинные промежутки времени (до 10 тыс. орбитальных периодов), где σ ≈ 14.2%, т.е. на 20% превышает изотропную норму. Анализ зависимости θ(t) показывает, что на промежутках времени, где изотропная норма превышена, характер вращательной динамики отличается от близлежащих участков – амплитуда колебаний угла θ меньше, на зависимости вместо хаотично расположенных точек присутствуют регулярные структуры. Такая динамика угла θ характерна для либрационного движения спутника на синхронном резонансе. Очевидно, имеет место “прилипание” хаотической траектории к границам областей с регулярным движением в фазовом пространстве (см., например, Shevchenko, Scholl, 1997; Shevchenko, 1998). Отметим также на зависимости θ(t), представленной на рис. 2, концентрацию точек в окрестности значений θ = ±π/2. Наблюдаемый эффект можно объяснить как большей толщиной хаотического слоя в этих областях фазового пространства (см. рис. 1 ), так и “зависаниями” возмущенного математического маятника в окрестности точек неустойчивого равновесия (Chirikov, 1979).
Рис. 2.
Примеры зависимостей от времени интегрирования для σ – относительной величины времени, когда фигура спутника ориентирована по направлению на Сатурн, и θ – угoл между наибольшей осью фигуры спутника и радиус-вектором “центр масс спутника – планета”. e = 0.0023, ω0 = 1.1717 (“Прометей”). Горизонтальная штриховая линия на верхней панели соответствует изотропной норме для плоского хаотического вращения Прометея – σnorm = 11.9%. На нижней панели представлен фрагмент зависимости θ(t) в увеличенном по горизонтальной оси масштабе. Время t указано в орбитальных периодах.
Пространственное хаотическое вращение спутника
Рассмотрим теперь случай пространственного хаотического вращения спутника в окрестности синхронного резонанса. Определение величины σ проводилось для множества заданных хаотических траекторий пространственного вращательного движения спутника. Для избранных значений e, A/C и B/C (табл. 1) хаотические траектории задавались начальными данными (θ, φ, ψ, dθ/dt, dφ/dt, dψ/dt), характеризующими ориентацию и скорость вращения спутника. Движение спутника начиналось в перицентре орбиты, т.е. в момент t = 0 принято f = 0. Начальные значения θ и dθ/dt выбирались так, чтобы они принадлежали хаотическому слою в окрестности сепаратрисы синхронного резонанса на сечении фазового пространства плоского вращательного движения спутника (см. рис. 1 ). Рассматривалось хаотическое пространственное вращение спутника, поэтому было принято: φ = 10–4 – ось вращения спутника в начальный момент времени отклонялась от нормали к плоскости орбиты на указанную величину. Для остальных начальных данных: ψ = dφ/dt = dψ/dt = 0, т.е. множество исследуемых хаотических траекторий определяется начальными значениями θ и dθ/dt.
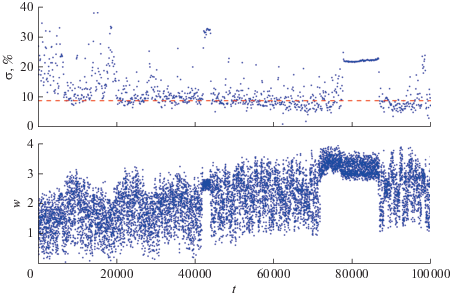
На рис. 3 для случая Прометея представлены типичные примеры полученных зависимостей от времени интегрирования для σ и w – величины модуля вектора угловой скорости вращения спутника. Зависимости получены для хаотической траектории с начальными данными θ =–π/2, dθ/dt = 1. Для удобства дальнейшего анализа на рис. 3 приведены только начальные участки полученных зависимостей. Из рис. 3 видно, что, как и в случае плоского хаотического вращения (см. рис. 2 ), в случае пространственного хаотического вращения на зависимости σ(t) присутствуют относительно длинные промежутки времени (до 10 тыс. орбитальных периодов), где величина σ в 2–3 раза превышает изотропную норму для пространственного хаотического вращения Прометея σnorm = 8.9%. На этих промежутках времени величина w колеблется почти периодически с малой амплитудой, т.е. скорость вращения спутника примерно постоянна, а не меняется непредсказуемым образом с большой амплитудой. Как и в случае плоского вращения, имеет место “прилипание” хаотической траектории к границам областей с регулярным движением в фазовом пространстве. Этот эффект, по всей вероятности, играет главную роль в проявлениях анизотропии в ориентации фигур малых спутников при их пространственном хаотическом вращении. В частности, на рис. 3 видно, что хаотическая траектория прилипает к областям фазового пространства, соответствующим резонансам 5 : 2 (при t = 40 000–45 000) и 3 : 1 (t = 70 000–85 000).
Рис. 3.
Примеры зависимостей от времени интегрирования для σ – относительной величины времени, когда фигура спутника ориентирована по направлению на Сатурн, и w – величины угловой скорости вращения спутника. e = 0.0023, A/C = 0.3958, B/C = 0.8534 (“Прометей”). Горизонтальная штриховая линия соответствует изотропной норме для пространственного хаотического вращения Прометея – σnorm = 8.9%. Время t указано в орбитальных периодах.
Для обоих спутников, Прометея и Пандоры, вычисленный в работе Shevchenko (1999, табл. 1) параметр адиабатичности (равный отношению частоты возмущения к частоте малых колебаний на резонансе, в данном случае (синхронном) λ ≈ 1, а “прилипания” эффективны при λ ~ 1 и λ > 1 (Shevchenko, 2010). Поэтому неудивительно, что режим прилипаний, обусловливающий наблюдаемую анизотропию ориентации, имеет место. Отметим значительное (на 200–300%) превышение изотропной нормы σnorm при пространственном хаотическом вращении, по сравнению с ее превышением на 20% в случае плоского хаотического вращения спутника. Эффект анизотропии выражен существенно сильнее при пространственном вращении малого спутника.
Чтобы учесть влияние выбора начальных данных на величину σ, для Прометея и Пандоры определялась средняя величина ${{{\sigma }}_{N}} = \frac{{\text{1}}}{N}\sum\nolimits_{k = {\text{0}}}^N {{{{\sigma }}_{k}}} ,$ где σk – вычислялось для хаотической траектории, заданной начальными данными (θk, dθk/dt). Для задания начальных данных проводилось разбиение интервала [–π/2, π/2] на N = 100 отрезков одинаковой длины. Затем для каждого значения θk = –π/2 + πk/N, k = 0, …, N – 1, выбиралась соответствующая величина dθk/dt так, чтобы начальные данные задавали траекторию, принадлежащую на сечении фазового пространства плоского вращательного движения (рис. 1 ) хаотическому слою в окрестности синхронного резонанса. Вычисленное нами значение σN для Прометея составило (29 ± 4)%, для Пандоры – (21 ± 3)%, что согласуется с оценками Melnikov и Shevchenko (2008), полученными на меньшей статистике.
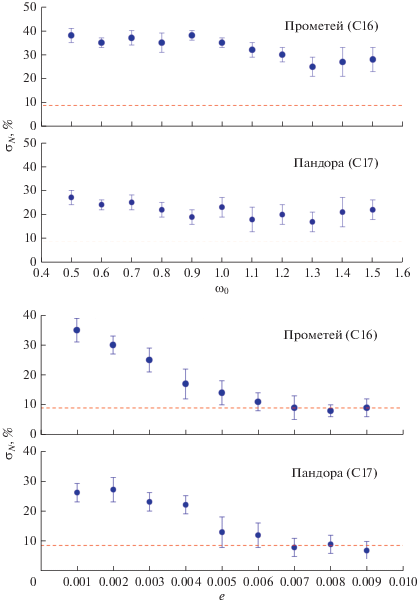
На рис. 4 представлены полученные для Прометея и Пандоры зависимости того, как изменение e и ω0 (формы спутника) влияет на величину σN. Зависимость σN (ω0) построена посредством вариации величины A/C при фиксированном значении B/C = 1. Из рис. 4 видно, что изменение формы спутника не оказывает существенного влияния на σN, в то же время при увеличении e более 0.005, наблюдается падение величины σN до значений, соответствующих изотропным нормам для пространственного хаотического вращения рассмотренных спутников. Полученные результаты говорят о том, что эффект анизотропии в ориентации фигуры спутника при его пространственном хаотическом вращении характерен для малых спутников с e ≤ 0.005. В динамике спутников с бóльшими эксцентриситетами орбит этот эффект не выражен – вращение таких малых спутников сугубо хаотическое.
Рис. 4.
Зависимости относительной величины времени, когда фигура спутника ориентирована по направлению на Сатурн, от ω0 при e = 0.0023 (Прометей), 0.0042 (Пандора) и e при ω0 = 1.1717 (Прометей), 0.8512 (Пандора). Горизонтальные штриховые линии соответствуют изотропным нормам для хаотического вращения Прометея и Пандоры.
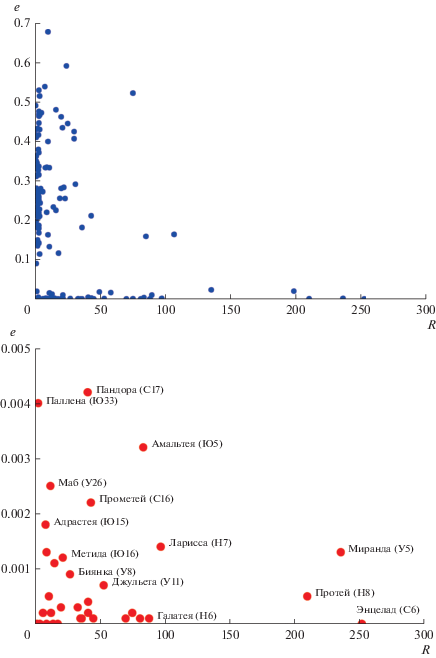
На рис. 5 представлена диаграмма “e–R”, где R – средний радиус фигуры спутника, на которой указано положение 92 известных малых спутников. Из более чем 200 известных в настоящее время спутников планет Солнечной системы (JPL Solar System Dynamics, 2020) были отобраны малые спутники, для которых: 1 км ≤ R ≤ 300 км. На нижней панели рис. 5 в увеличенном масштабе по e приведена часть диаграммы “e–R”, где указано положение 36 малых спутников для которых e ≤ 0.005. Для шести из этих спутников состояния вращения не установлены (спутники имеют R < 10 км и, скорее всего, весьма быстро вращаются), для 30 спутников принят (Archinal и др., 2018) синхронный режим вращения. Согласно нашим численным экспериментам в динамике этих спутников, составляющих 30% от всех известных малых спутников, присутствует эффект анизотропии в ориентации фигуры спутника при его хаотическом вращении в окрестности синхронного резонанса.
Рис. 5.
Диаграмма “e–R”, где R – средний радиус фигуры спутника в км. Точками указаны положения (JPL Solar System Dynamics, 2020) малых спутников для которых 1 км ≤ R ≤ 300 км. На нижней панели в увеличенном по e масштабе указаны малые спутники с e ≤ 0.005; в хаотической динамике таких спутников может иметь место эффект преимущественной ориентации наибольшей оси фигуры спутника на планету.
Как отмечено в Archinal и др. (2018), выводы о синхронном вращении спутника иногда основываются не на анализе наблюдательных данных, а на дополнительных предположениях, например, на теоретической оценке величины Tdespin – времени приливного замедления первоначально быстрого вращения спутника до синхронного (см. подробнее Peale, 1977; 1999). Если это время мало по сравнению с возрастом Солнечной системы (например, для Прометея и Пандоры Tdespin < 150 000 лет, Kouprianov, Shevchenko, 2005), то считается, что спутник завершил свою приливную вращательную эволюцию и находится в синхронном режиме вращения. Однако, если синхронное вращение неустойчиво (Kouprianov, Shevchenko, 2005; Melnikov, Shevchenko, 2008; 2010), то спутник может вращаться хаотически в настоящее время и в его динамике будет наблюдаться рассмотренный нами эффект анизотропии в ориентации фигуры.
Если у малого спутника e ≤ 0.005 и высока вероятность нахождения в хаотическом режиме вращения (например, вращение в синхронном резонансе неустойчиво), необходимо проводить детальное численное моделирование его возможной пространственной хаотической вращательной динамики. Моделирование позволит оценить длину ряда наблюдений, необходимую для достоверного определения режима вращения спутника. Для Прометея и Пандоры, согласно нашим численным экспериментам, длина такого ряда наблюдений должна составлять порядка 10 тыс. орбитальных периодов (≈16 лет). Численные эксперименты показывают, что интервал времени, на котором при хаотическом вращении наблюдается схожее с регулярным поведение в ориентации фигуры спутника со временем, может быть велик (тысячи орбитальных периодов). Поэтому нельзя исключать, что и уже определенный из анализа наблюдений синхронный режим вращения некоторых малых спутников является проявлением рассмотренного нами здесь эффекта анизотропии в ориентации фигуры спутника при его хаотическом вращении в окрестности синхронного резонанса.
ВЫВОДЫ
В настоящей работе проведено детальное исследование эффекта преимущественной ориентации (эффекта анизотропии) наибольшей оси фигуры спутника по направлению на планету, имеющего место при пространственной хаотической вращательной динамике малого спутника в окрестности синхронного резонанса. Под преимущественной ориентацией подразумевается, что относительное время нахождения наибольшей оси фигуры спутника в пределах конуса с углом раствора равным углу, под которым со спутника виден диск планеты, превышает изотропную норму, при которой все направления ориентации фигуры спутника в пространстве равновероятны.
Проведенные массовые численные эксперименты для различных значений параметров задачи (эксцентриситет орбиты и форма спутника) показали, что эффект анизотропии в ориентации фигуры спутника должен быть наиболее заметен в хаотической вращательной динамике малых спутников с эксцентриситетами орбит менее 0.005. Показано, что главную роль в наблюдаемом эффекте, вероятно, играет прилипание хаотической траектории к областям фазового пространства с регулярным вращением. Анализ данных об орбитальных параметрах и фигурах известных спутников планет Солнечной системы показал, что в возможной хаотической динамике 30% известных малых спутников присутствует рассмотренный нами эффект преимущественной ориентации наибольшей оси фигуры спутника на планету. Установлено, что наличие эффекта анизотропии в ориентации фигуры спутника может помешать идентификации хаотического режима его вращения, если длина ряда наблюдений недостаточно велика. Хаотическое вращательное движение спутника может быть схоже с регулярным (синхронным) на интервалах времени в тысячи орбитальных периодов. Численное моделирование возможной хаотической вращательной динамики малого спутника позволяет оценить длину ряда наблюдений, необходимую для достоверного определения режима вращения спутника.
Автор выражает признательность И.И. Шевченко за полезные замечания.
Работа поддержана Российским фондом фундаментальных исследований (проект № 19-02-00811).
Список литературы
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965. 416 с.
Борисов А.В., Мамаев И.С. Динамика твердого тела. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2001. 384 с.
Девяткин А.В., Горшанов Д.Л., Грицук А.Н., Мельников А.В., Сидоров М.Ю., Шевченко И.И. Наблюдения и теоретический анализ кривых блеска естественных спутников планет // Астрон. вестн. 2002. Т. 36. № 3. С. 269–281.
Куприянов В.В. Численно-экспериментальное исследование вращательной динамики спутников планет // Дис. канд. физ.-мат. наук. СПб: ГАО РАН, 2014. 148 с.
Лихтенберг А., Либерман М. Регулярная и стохастическая динамика. М.: Мир, 1984. 528 с.
Мельников А.В., Шевченко И.И. Необычные режимы вращения малых спутников планет // Астрон. вестн. 2007. Т. 41. № 6. С. 521–530.
Морбиделли А. Современная небесная механика. Аспекты динамики Солнечной системы. М.–Ижевск: Институт компьютерных исследований, 2014. 432 с.
Мюррей К., Дермотт С. Динамика Солнечной системы. М.: ФИЗМАТЛИТ, 2009. 588 с.
Шевченко И.И. О максимальных показателях Ляпунова хаотического вращения естественных спутников планет // Космич. исслед. 2002. Т. 40. № 3. С. 317–326.
Archinal B.A., Acton C.H., A’Hearn M.F., Conrad A., Consolmagno G.J., Duxbury T., Hestroffer D., Hilton J.L., Kirk R.L., Klioner S.A., McCarthy D., Meech K., Oberst J., Ping J., Seidelmann P.K., Tholen D.J., Thomas P.C., Williams I.P. Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2015 // Celest. Mech. Dyn. Astr. 2018. V. 130. № 22. P. 1–46.
Black G.J., Nicholson P.D., Thomas P.C. Hyperion: Rotational dynamics // Icarus. 1995. V. 117. № 1. P. 149–161.
Chirikov B.V. A universal instability of many-dimensional oscillator systems // Phys. Reports. 1979. V. 52. № 5. P. 263–379.
Goldreich P., Peale S. Spin-orbit coupling in the Solar system // Astron. J. 1966. V. 71. № 6. P. 425–438.
JPL Solar System Dynamics. http://ssd.jpl.nasa.gov/. Site manager: Park R.S. 2020.
Hairer E., Nørsett S.P., Wanner G. Solving Ordinary Differential Equations I. Nonstiff Problems. Berlin: Springer-Verlag, 1993. 528 p.
Harbison R.A., Thomas P.C., Nicholson P.C. Rotational modeling of Hyperion // Celest. Mech. and Dynam. Astron. 2011. V. 110. P. 1–16.
Klavetter J.J. Rotation of Hyperion. II – Dynamics // Astron. J. 1989. V. 98. P. 1946–1947.
Kouprianov V.V., Shevchenko I.I. Rotational dynamics of planetary satellites: A survey of regular and chaotic behavior // Icarus. 2005. V. 176. P. 224–234.
Melnikov A.V., Shevchenko I.I. On the rotational dynamics of Prometheus and Pandora // Celest. Mech. and Dynam. Astron. 2008. V. 101. № 1–2. P. 31–47.
Melnikov A.V., Shevchenko I.I. The rotation states predominant among the planetary satellites // Icarus. 2010. V. 209. P. 786–794.
Shevchenko I.I. On the recurrence and Lyapunov time scales of the motion near the chaos border // Phys. Letters A. 1998. V. 241. P. 53–60.
Shevchenko I.I. The separatrix algorithmic map: Application to the spin-orbit motion // Celest. Mech. and Dynam. Astron. 1999. V. 73. P. 259–268.
Shevchenko I.I. Hamiltonian intermittency and Lévy flights in the three-body problem // Phys. Rev. E. 2010. V. 81. P. 066216-1–066216-11.
Shevchenko I.I., Kouprianov V.V. On the chaotic rotation of planetary satellites: The Lyapunov spectra and the maximum Lyapunov exponents // Astron. and Astrophys. 2002. V. 394. P. 663–674.
Shevchenko I.I., Scholl H. Intermittent trajectories in the 3/1 Jovian resonance // Celest. Mech. and Dynam. Astron. 1997. V. 68. № 2. P. 163–175.
Peale S.J. Rotation histories of the natural satellites // Planetary satellites / Ed. J.A. Burns. Tucson: Univ. Arizona Press, 1977. P. 87–112.
Peale S.J. Origin and evolution of the natural satellites // Ann. Rev. Astron. and Astrophys. 1999. V. 37. P. 533–602.
Porco C.C., Baker E., Barbara J., Beurle K., Brahic A., Burns J.A., Charnoz S., Cooper N., Dawson D.D., Del Genio A.D., Denk T., Dones L., Dyudina U., Evans M.W., Giese B., Grazier K., Helfenstein P., Ingersoll A.P., Jacobson R.A., Johnson T.V., McEwen A., Murray C.D., Neukum G., Owen W.M., Perry J., Roatsch T., Spitale J., Squyres S., Thomas P.C., Tiscareno M., Turtle E., Vasavada A.R., Veverka J., Wagner R., West R. Cassini Imaging Science: Initial results on Phoebe and Iapetus // Science. 2005. V. 307. P. 1237–1242.
Thomas P.C. Sizes, shapes, and derived properties of the Saturnian satellites after the Cassini nominal mission // Icarus. 2010. V. 208. P. 395–401.
Whittaker E.T. A Treatise on the Analytical Dynamics of particles and rigid bodies. Cambridge: Cambridge Univ. Press, 1917. 432 p.
Wisdom J. Rotation dynamics of irregularly shaped natural satellites // Astron. J. 1987. V. 94. № 5. P. 1350–1360.
Wisdom J., Peale S.J., Mignard F. The chaotic rotation of Hyperion // Icarus. 1984. V. 58. № 2. P. 137–152.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник