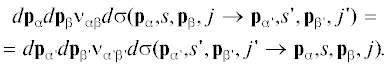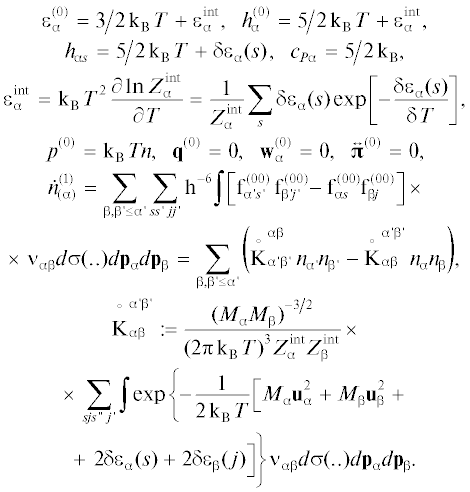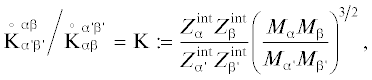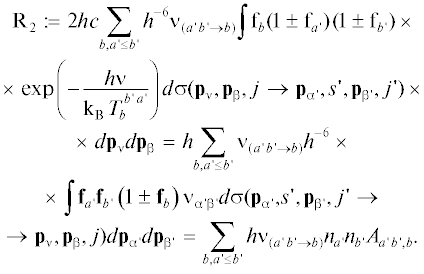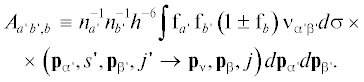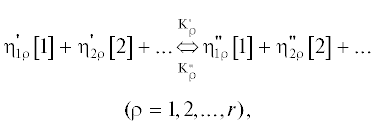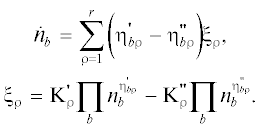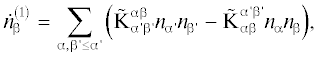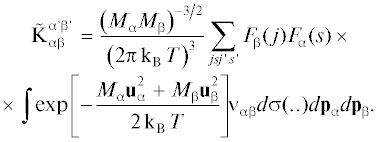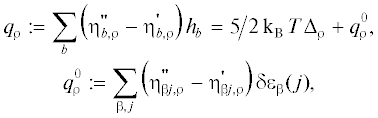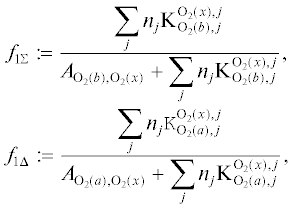Астрономический вестник, 2020, T. 54, № 6, стр. 542-559

ВВЕДЕНИЕ

Внешние газовые оболочки небесных тел (планет, комет) представляют собой разреженный многокомпонентный газ, подверженный прямому воздействию Солнечного электромагнитного и корпускулярного излучения. Структура и физико-химические свойства подобных сред, лежащих в пограничных областях между атмосферой и космосом и обычно называемых верхней атмосферой и/или околопланетным пространством, существенно различаются в зависимости от массы космического объекта, его расстояния от Солнца, наличия магнитного поля, условий формирования и эволюции. Общим для подобных оболочек небесных тел является наличие процессов фотолиза (сопровождаемых диссоциацией, ионизацией, многочисленными прямыми и обратными элементарными процессами и химическими реакциями), определяющих их динамику, тепловой режим и химическую структуру. Очевидно, в зависимости от характерных временных и пространственных масштабов изучаемых явлений, адекватное описание подобных сред возможно как в рамках газокинетического, так и гидродинамического подходов (см., например, Голицын, 1973; Уиттен, Поппов, 1977; Chamberlain, 1978; Кошелев и др., 1983; Vázquez, 2006; Marov, Kolesnichenko, 2001, 2015; Колесниченко, 2017). Вместе с тем, учет специфики изучения происходящих в верхних атмосферах физико-химических процессов сопряжен с необходимостью периодического пересмотра традиционных подходов моделирования, связанного с учетом новейших достижений в области космической физики, радиационной химической кинетики, электродинамики и т.п. Именно на этом пути открываются, по нашему мнению, широкие возможности создания современных математических моделей малодоступных областей околопланетного пространства (экспериментальные сведения о которых, как правило, крайне ограничены), включая прогнозирование их состояния и пространственно-временные вариации.

Отмеченные достижения стимулируют создание более продвинутых моделей верхних атмосфер, соответствующих алгоритмов и программных комплексов для их численной реализации (см., например, Четверушкин, Шильников, 2008; Мингалев и др., 2010). Новые подходы к моделированию стали возможны благодаря совершенствованию экспериментальных методов исследования ближайших окрестностей Земли и планет, а также бурному развитию вычислительной математики, которое расширило возможности создания адекватных математических моделей, учитывающих наличие многочисленных физико-химических явлений, таких как турбулентные, магнитогидродинамические и радиационные процессы, а также фазовые переходы, химические реакции и процессы коагуляции.

Усовершенствованные подходы теоретической аэрономии, основанные помимо традиционных методов химии верхних атмосфер, также и на совокупности газокинетических и гидродинамических методов, были развиты в монографиях (Маров, Колесниченко, 1987; Колесниченко, Маров, 1999; Колесниченко, 2017). В них, в частности, была продемонстрирована эффективность газокинетического подхода при изучении неравновесных аэрономических реакций, вызванных как электромагнитной, так и корпускулярной радиацией Солнца. При этом было показано, что кинетический поход эффективно работает на высотах верхней термосферы и экзосферы (где Kn > 0.1), а гидродинамический – на высотах нижней термосферы и мезосферы, где Kn < 0.1. Таким образом, в своей совокупности гидродинамические и кинетические подходы дают возможность значительно расширить класс решаемых климатических и аэрономических задач, что позволяет во многих случаях отказаться от использования в моделях эволюции планетных атмосфер так называемых параметров настройки, вводимых часто a posteriori для согласования получаемых численных результатов с новыми экспериментальными данными (см. Мингалев И.В., Мингалев В.С., 2005; Четверушкин и др., 2017).

Вместе с тем, одной из нерешенных проблем все еще остается корректное описание процессов взаимодействия верхней атмосферы планеты и солнечного излучения, в том числе в самом общем неравновесном случае, т.е. возможность детального учета вкладов многочисленных фотохимических и химических реакций от такого взаимодействия в энергетический баланс нижней термосферы и мезосферы. В частности, речь идет о получении так называемой функции нагревания верхней атмосферы, вызванного совокупностью эндо-и экзотермических аэрономических реакций, сопровождающих приток в атмосферу жесткого солнечного излучения.

Хорошо известно, что коротковолновая часть солнечного спектра (УФ и рентген) оказывает решающее влияние на энергетическое состояние внешних газовых оболочек Земли и планет, определяя свойства их верхних атмосфер и характер аэрономических процессов, хотя доля энергии, излучаемой Солнцем в этих диапазонах, составляет менее 10^–4 от полной энергии солнечного излучения. Поглощение в земной атмосфере на высотах выше ≈30 км энергии солнечного излучения во всем коротковолновом диапазоне (λ ≤ 3000 Å) имеет сложный характер. Это обусловлено сильными вариациями сечений поглощения основными атмосферными компонентами (N₂, О₂, О, а также О_з), их зависимостью от длины волны, а также наличием процессов фотолиза (диссоциация, ионизация), возбуждения и их различных комбинаций. При этом процессам диссоциации и ионизации отвечают соответствующие континуумы поглощения, в то время как процессы возбуждения молекул дают в соответствующем спектре молекулярные полосы поглощения или атомные линии. Промежуточным случаям процессов предиссоциации или ионизации соответствуют в спектрах диффузные полосы или линии. Можно, таким образом, рассматривать сечение поглощения как сумму парциальных сечений различных процессов, причем от величины парциального сечения зависит относительное содержание образующихся при поглощении конечных или промежуточных продуктов. Таким образом, только газокинетический подход может позволить повысить точность моделирования энергетического баланса атмосферной среды, зависящей от степени ее отклонения от ЛТР, и учесть большое число факторов, включая скорости и сечения химических реакций, константы элементарных (столкновительных и радиативных) процессов, ограниченное (по необходимости) число возбужденных уровней состояния и т.п.

Важно также иметь в виду, что тепловой баланс определенных областей планетных атмосфер (например, средней атмосферы Земли, атмосферы Марса, надоблачной атмосферы Венеры) существенно зависит не только от коротковолнового солнечного радиации, но и от длинноволнового излучения Солнца, планеты и приповерхностной атмосферы. Следует, однако, заметить, что вклады от всех видов радиации в тепловой баланс атмосферной среды возможно анализировать раздельно для коротковолнового и длинноволнового диапазонов длин волн (см. Гуди, 1966).

В представленной работе показано, как, при учете только жесткого солнечного излучения и в предположении термического равновесия¹¹ по поступательным степеням свободы, из системы обобщенных кинетических уравнений для многокомпонентных смесей многоатомных газов умеренной плотности с учетом химических реакций в интегралах столкновений, можно получить: уравнения радиационной гидродинамики, определяющие (замыкающие) соотношения, уравнениях химической кинетики (с учетом специфики неравновесных химических реакций и многочисленных элементарных процессов), а также функцию нагревания верхней атмосферы, позволяющую корректно учитывать эффективность тепловыделения, вызванного взаимодействием атмосферных частиц с солнечным коротковолновым излучением.

При конструировании функции нагревания атмосферы не учитывалось собственное излучением приповерхностной атмосферы в рентгеновском и ультрафиолетовом диапазонах, поскольку оно слишком мало при характерных температурах в термосферах (~1000 К). Большинство фотонов в эмиссиях, возникающих вследствие диссоциации с возбуждением или ионизации, рождаются в ближнем ультрафиолете и, обладая большими длинами пробега, уходят из термосферы. Рассеянное солнечное излучение также нами не учитывалось, поскольку сечение рэлеевского рассеяния имеет порядок ~10^–24 см², а сечение поглощения ~10^–17 см² в ионизационном континууме (40–1025.7 Å) и ~10^–19 см² в континууме Шумана–Рунге (1300–1750 Å). В качестве примера приведены конкретные функции нагревания термосферы и озоносферы солнечным УФ-излучением, оказывающим наиболее существенное влияние на тепловой режим, динамику и эмиссионные свойства этих областей земной атмосферы.

УРАВНЕНИЯ РАДИАЦИОННОЙ ГИДРОДИНАМИКИ ДЛЯ МОДЕЛИРОВАНИЯ ВЕРХНЕЙ АТМОСФЕРЫ

Проходя сквозь газовую оболочку небесного тела (планеты, кометы), солнечное излучение взаимодействует с веществом, многократно поглощаясь, переизлучаясь и рассеиваясь. Перенос энергии фотонами вызывает следующие радиативные процессы: 1) фотовозбуждение, или связанно-связанное поглощение, при котором фотон поглощается атомом (или молекулой), что приводит к переходу электрона между его дискретными квантовыми состояниями, и обратный процесс девозбуждения атома с испусканием фотона в результате столкновения его с другой частицей; 2) фотоионизация, или связанно-свободное поглощение, при котором происходит отрыв связанного электрона атома (молекулы) с одного из дискретных уровней и его переход с конечной кинетической энергией в состояние континуума с непрерывным энергетическим спектром, а также обратный процесс захвата свободного электрона на связанный уровень с рождением фотона (радиативная рекомбинация); 3) свободно-свободное поглощение, при котором фотон поглощается свободным электроном, движущимся в поле иона, в результате чего изменяется его кинетическая энергия относительно иона, в поле которого он движется, и обратный процесс, приводящий к излучению фотона (тормозное излучение); 4) рассеяние фотонов, в том числе когерентное рэлеевское рассеяние (связанными системами атомов и молекул), неупругое комбинационное рассеяние связанными системами и комптоновское рассеяние (свободными электронами), при которых фотон не исчезает, а только изменяет направление движения и, возможно, слегка смещается по частоте. Эти процессы определяют перенос излучения в атмосферном газе и околопланетном пространстве.

Описание указанных физико-химических процессов в верхней атмосфере удобно проводить в рамках кинетической теории многоатомных газов, исходя из системы обобщенных уравнений Больцмана для одночастичных функций распределения ${{f}_{{{\alpha }s}}}({\mathbf{r}},{{{\mathbf{p}}}_{{\alpha }}},s,t)$ для каждого сорта частиц вещества и фотонов. Для обозначения вещественных компонентов используем далее греческие буквы $\alpha ,\beta ,...$ $( = 1{\text{,}}2{\text{,}}...{\text{,}}N),$ для обозначения фотона используем его частоту $\nu ;$ $s = 0$ соответствует основному энергетическому уровню молекулы.

Система уравнений Больцмана для частиц сорта $\alpha $ в квантовом энергетическом состоянии s имеет вид:

где интегрирование производится по всем значениям импульсов ${{{\mathbf{p}}}_{{{\alpha }{\kern 1pt} '}}},{{{\mathbf{p}}}_{{{\beta }{\kern 1pt} '}}}$ и ${{{\mathbf{p}}}_{{\beta }}},$ совместным с условиями сохранения массы, импульса и энергии сталкивающихся частиц. Столкновительный член (2) представляет собой изменение функции распределения ${{f}_{{{\alpha }s}}}$ в единицу времени за счет как упругих столкновений, меняющих только скорость ${{{\mathbf{c}}}_{{\alpha }}}$ частиц, так и неупругих столкновений, которые ведут либо к изменению внутреннего состояния сталкивающихся частиц, либо к исчезновению или появлению частиц сорта $\alpha .$ Здесь $h$ − постоянная Планка; ${{{\mathbf{F}}}_{{\alpha }}} = {{{\mathbf{F}}}_{{\alpha }}}({\mathbf{r}}{\text{,}}{{{\mathbf{p}}}_{{\alpha }}},t)$ − макроскопическая сила, действующая на частицу $\alpha $-сорта (в случае излучения ${{{\mathbf{F}}}_{{\nu }}} \cong 0$); ${{\nu }_{{{\alpha \beta }}}} = \left| {{{{\mathbf{c}}}_{{\alpha }}} - {{{\mathbf{c}}}_{{\beta }}}} \right|$ − модуль относительной скорости частиц сортов $\alpha $ и $\beta ;$ ${{f}_{{{\alpha }s}}}: = {{f}_{{{\alpha }s}}}({\mathbf{r}}{\text{,}}{{{\mathbf{p}}}_{{\alpha }}},s,t),$ ${{f}_{{{\alpha }{\kern 1pt} 's{\kern 1pt} '}}}: = {{f}_{{{\alpha }{\kern 1pt} 's{\kern 1pt} '}}}({\mathbf{r}}{\text{,}}{{{\mathbf{p}}}_{{{\alpha }{\kern 1pt} {\text{'}}}}},s{\kern 1pt} ',t),$ где штрихованные и не штрихованные величины отмечают начальное и конечное состояния соответственно; $\sum\nolimits_{{\alpha }{\kern 1pt} ' \leqslant {\beta }{\kern 1pt} '} {: = \sum\nolimits_{{\beta }{\kern 1pt} '} {\sum\nolimits_{{\alpha }{\kern 1pt} ' = 1}^{{\beta }{\kern 1pt} {\text{'}}} , } } $ где ограничение $\alpha {\kern 1pt} ' \leqslant \beta {\kern 1pt} '$ при суммировании по сортам частиц сделано для того, чтобы не учитывать одни и те же аэрономические реакции дважды; $d\sigma ({{{\mathbf{p}}}_{{\alpha }}}{\text{,}}s,{{{\mathbf{p}}}_{{\beta }}},j \to {{{\mathbf{p}}}_{{{\alpha }{\kern 1pt} {\text{'}}}}}{\text{,}}s{\kern 1pt} ',{{{\mathbf{p}}}_{{{\beta }{\kern 1pt} {\text{'}}}}},j{\kern 1pt} ')$ − дифференциальное эффективное сечение бинарной реакции $\alpha (s) + \beta (j) \Leftrightarrow \alpha {\kern 1pt} '(s{\kern 1pt} ') + \beta {\kern 1pt} '(j{\kern 1pt} ')$ между частицами $\alpha $ и $\beta $ сортов в состояниях $s$ и $j,$ т.е. вероятность того, что в результате столкновения молекулы сорта $\alpha $ в состоянии $s{\text{,}}$ имеющей импульс ${{{\mathbf{p}}}_{{\alpha }}},$ с молекулой сорта $\beta $ в состоянии $j$ и импульсом ${{{\mathbf{p}}}_{{\beta }}}$ образуются молекулы сортов $\alpha {\kern 1pt} '$ и $\beta {\kern 1pt} ',$ импульсы и квантовые состояния которых будут, соответственно, $\left( {{{{\mathbf{p}}}_{{{\alpha }{\kern 1pt} {\text{'}}}}}{\text{,}}s{\kern 1pt} '} \right)$ и $\left( {{{{\mathbf{p}}}_{{{\beta }{\kern 1pt} '}}},j{\kern 1pt} '} \right),$ причем значения импульсов ${{{\mathbf{p}}}_{{{\alpha }{\kern 1pt} {\text{'}}}}}$ и ${{{\mathbf{p}}}_{{{\beta }{\kern 1pt} {\text{'}}}}}$ ограничены условиями сохранения массы, импульса и энергии при столкновении²²: $\Im $ − разность энергий связи систем частиц ($\alpha ,\beta $) и ($\alpha {\kern 1pt} ',\beta {\kern 1pt} '$), причем, когда $\Im > 0,$ то эта величина представляет собой пороговую энергию эндотермической реакции $\alpha (s) + \beta (j) \Rightarrow \alpha {\kern 1pt} '(s{\kern 1pt} ') + \beta {\kern 1pt} '(j{\kern 1pt} ').$ При написании столкновительного члена ${{\delta {{f}_{{{\alpha }s}}}} \mathord{\left/ {\vphantom {{\delta {{f}_{{{\alpha }s}}}} {\delta t}}} \right. \kern-0em} {\delta t}}$ в виде (2) предполагалось справедливость равенства ${{f}_{{{\alpha }s}}}({{{\mathbf{p}}}_{{\alpha }}},s)$ = ${{f}_{{{\alpha }s}}}({{{\mathbf{p}}}_{{\alpha }}},( - s))$ в случае, когда молекулы не обладают внутренним моментом импульса (спиновым, орбитальным, вращательным), и использовано соотношение взаимности Множители $\left[ {1 \pm {{f}_{{{\alpha }s}}}} \right]$ в выражении (2) для интеграла столкновений ${{\delta {{f}_{{{\alpha }s}}}} \mathord{\left/ {\vphantom {{\delta {{f}_{{{\alpha }s}}}} {\delta t}}} \right. \kern-0em} {\delta t}}$ учитывают зависимость вероятности столкновения частиц от функций распределения, получающихся после столкновения (принцип запрета Паули); при этом знаки “+” и “−” относятся соответственно к частицам бозевского и фермиевского типов. Для учета вкладов в интеграл столкновений (2) неупругих столкновений более общего типа (например, столкновений с участием более двух частиц, включая фотон в начальном состоянии, когда относительна скорость ${{\nu }_{{{\alpha \beta }}}}$ равна скорости света $с$) в выражении (2) следует считать, что некоторые или все символы $\beta ,\alpha {\kern 1pt} '$ и $\beta {\kern 1pt} '$ относятся к более чем одной частице. Способ для получения правой части уравнения Больцмана, явно выраженной через одночастичные функции распределения для каждого сорта частиц, для этого случая приведен, например, в работе (Сэмпсон, 1969).

Полумакроскопические уравнения радиационной гидродинамики. Анализ происходящих в верхней атмосфере физико-химических процессов на основе прямого использования системы интегро-дифференциальных уравнений (1) весьма сложен. Вместе с тем, с точки зрения макроскопических свойств термосферу часто можно рассматривать как континуальную среду и для ее адекватного описания использовать полумакроскопические уравнения многокомпонентной радиационной гидродинамики, к которым при ряде дополнительных допущений сводится система (1). Используя для этого функции распределения частиц вещества ${{f}_{{{\alpha }s}}}(\alpha = 1,2,...,N),$ определим гидродинамические структурные параметры среды, а также термодинамические потоки, характеризующие перенос массы, импульса и энергии в газе, следующим образом:

Здесь ${{n}_{{{\alpha }s}}}({\mathbf{r}},t)$ = ${{h}^{{ - 3}}}\int {{{f}_{{{\alpha }s}}}} d{{{\mathbf{p}}}_{{\alpha }}}$ − число частиц сорта $\alpha ,$ находящихся в состоянии $s{\text{;}}$ ${{M}_{{\alpha }}},$ ${{n}_{{\alpha }}}({\mathbf{r}},t),$ ${{\varepsilon }_{{\alpha }}}({\mathbf{r}},t)$ − соответственно масса молекулы, полное число частиц в единице объема и средняя внутренняя энергия на одну частицу сорта $\alpha ;$ ${{{\mathbf{w}}}_{{\alpha }}}({\mathbf{r}},t)$ − скорость диффузии $\alpha $-го компонента; ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {P} }}}_{{\alpha }}}({\mathbf{r}},t)$ – парциальный тензор давления вещества сорта $\alpha ;$ $\delta {{\varepsilon }_{{\alpha }}}(s)$ – внутренняя энергия молекулы $\alpha $-го сорта для состояния s; $p({\mathbf{r}},t),$ $\rho ({\mathbf{r}},t),$ ${\mathbf{V}}({\mathbf{r}},t){\text{,}}$ $\varepsilon ({\mathbf{r}},t)$ − соответственно давление, массовая плотность, полная среднемассовая скорость и средняя внутренняя энергия единицы массы газовой смеси; ${\mathbf{q}}({\mathbf{r}},t){\text{,}}$ ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\pi } }}({\mathbf{r}},t)$ − вектор полного потока тепла и тензор вязких напряжений газовой смеси; ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} }}$ − единичный тензор; $\langle ...\rangle $ − символ усреднения по пространству импульсов; $d{{{\mathbf{p}}}_{{\nu }}} = {\mathbf{p}}_{{\nu }}^{2}d\left| {{{{\mathbf{p}}}_{{\nu }}}} \right|d{\mathbf{\Omega }}$ − элемент объема в пространстве импульсов.

Используя функцию распределения фотонов ${{f}_{{{\nu }s}}}({\mathbf{r}}{\text{,}}{{{\mathbf{p}}}_{{\nu }}},s,t)$ (здесь ${{{\mathbf{p}}}_{{\nu }}} = {{h\nu {\mathbf{\Omega }}} \mathord{\left/ {\vphantom {{h\nu {\mathbf{\Omega }}} c}} \right. \kern-0em} c},$ ${\mathbf{\Omega }}$ – единичный вектор в направлении распространения фотонов) или полностью ей эквивалентную величину – спектральную интенсивность излучения

(множитель 2 появляется здесь в результате суммирования по поляризациям фотона $s$), введем следующие макроскопические характеристики поля излучения: Здесь ${{u}_{R}},{{{\mathbf{q}}}_{R}},{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} }}}_{R}}$ − объемная полная плотность энергии излучения, вектор потока радиации (вектор Пойнтинга) и тензор радиационного давления соответственно.

Гидродинамические уравнения сохранения массы, импульса и энергии для системы “вещество плюс излучение” получаются из системы кинетических уравнений (1) обычным образом − путем умножения каждого уравнения на аддитивные инварианты ${{h}^{{ - 3}}}\phi _{{\alpha }}^{{(i)}}$ $(i = 1,2,3)$ (здесь: $\phi _{{\alpha }}^{{(1)}} = {{M}_{{\alpha }}},$ $\phi _{{\alpha }}^{{(2)}} = {{{\mathbf{p}}}_{{\alpha }}},$ $\phi _{{\nu }}^{{(1)}} = {{M}_{{\nu }}} = 0;$ $\phi _{{\alpha }}^{{(3)}} = \Delta {{\varepsilon }_{{\alpha }}}(s)$ ≡ $\delta {{\varepsilon }_{{\alpha }}}(s) + \frac{{{\mathbf{p}}_{{\alpha }}^{2}}}{{2{{M}_{{\alpha }}}}},$ $\phi _{{\nu }}^{{(3)}} = \Delta {{\varepsilon }_{{\nu }}} = h\nu $), интегрирования полученного выражения по импульсам и суммирования по индексам $\alpha $ и $s$ (Ферцигер, Капер, 1976). В результате получим:

где ${{d(..)} \mathord{\left/ {\vphantom {{d(..)} {dt}}} \right. \kern-0em} {dt}}$ := ${{\partial (..)} \mathord{\left/ {\vphantom {{\partial (..)} {\partial t}}} \right. \kern-0em} {\partial t}} + {\mathbf{V}} \cdot \nabla (..)$ − оператор “полной производной по времени”. Кроме этого, из системы (1) могут быть получены следующие балансовые уравнения для плотности ${{n}_{{\alpha s}}}$ числа частиц сорта $\alpha {\text{:}}$где ${{\dot {n}}_{{({\alpha }s)}}}$ − скорость образования частиц сорта $\alpha $ в состоянии $s$ в результате всех аэрономических реакций. В “источниковом” члене ${{\dot {n}}_{{(\alpha s)}}}$ учтены столкновения следующих видов: 1) $\alpha \ne \alpha {\kern 1pt} ';$ $\beta \ne \beta {\kern 1pt} ';$ индексы $s,j,s{\kern 1pt} ',j{\kern 1pt} '$ − любые; 2) $\alpha = \alpha {\kern 1pt} ';$ $\beta = \beta {\kern 1pt} ';$ $s \ne s{\kern 1pt} ';$ индексы $j,j{\kern 1pt} '$ – любые. В случае, когда функции распределения ${{f}_{{\alpha s}}}$ не зависят от некоторых внутренних состояний s, естественно использовать, вместо соответствующих уравнений (5), кинетические уравнения для населенности ${{n}_{{{\alpha }l}}}$ $l$-го уровня (под уровнем здесь понимается набор вырожденных и неразличимых квантовых состояний с одинаковой энергией), получающиеся из (5) суммированием по вырожденным состояниям ${{s}_{l}}.$ В этом случае в выражениях для ${{\dot {n}}_{{\left( {{\alpha }l} \right)}}}\left( { \equiv \sum\nolimits_s {^{{(l)}}{{{\dot {n}}}_{{{\alpha }s}}}} } \right)$ будем считать, что сечения $d\sigma (..)$ уже просуммированы по конечным вырожденным состояниям (по соответствующим значениям индексов $s{\kern 1pt} ',j{\kern 1pt} '$) и усреднены по вырожденным начальным состояниям, т.е. по соответствующим $s$ и $j$ (Сэмпсон, 1969). Из системы кинетических уравнений (1) могут быть получены и некоторые другие уравнения переноса.

Пусть $L$ и ${{t}_{{{\text{гид}}}}}$ − характерный пространственный масштаб и характерное время макроскопических процессов в верхней атмосфере. Тогда

Если, кроме этого, движение излучающего газа происходит с нерелятивистскими скоростями, то имеет место неравенство ${L \mathord{\left/ {\vphantom {L {c{{t}_{{{\text{гид}}}}}}}} \right. \kern-0em} {c{{t}_{{{\text{гид}}}}}}} \ll 1$ – условие справедливое для всех атмосфер. В этом случае в гидродинамических уравнениях (4) можно пренебречь соответственно членами ${{c}^{{ - 2}}}{{{\mathbf{q}}}_{R}}$ и ${{u}_{R}}$ по сравнению с величинами, содержащими ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} }}}_{R}}$ и ${{{\mathbf{q}}}_{R}}.$ Пренебрежение слагаемыми $\partial {{u}_{R}}/\partial t$ и ${{{{c}^{{ - 2}}}\partial {{{\mathbf{q}}}_{R}}} \mathord{\left/ {\vphantom {{{{c}^{{ - 2}}}\partial {{{\mathbf{q}}}_{R}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ дает возможность не учитывать временную производную ${{\partial {{f}_{{\nu }}}} \mathord{\left/ {\vphantom {{\partial {{f}_{{\nu }}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ в уравнениях Больцмана (1). Заметим также, что во многих аэрономических задачах справедливы, неравенства ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} }}}_{R}} \ll \sum\nolimits_{\alpha } {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {P} }}}}_{{\alpha }}}} ,$ ${{u}_{R}} \ll \rho \varepsilon $ (Маров, Колесниченко, 1987); это обстоятельство позволяет параметры излучения, такие как ${{{\mathbf{q}}}_{R}},$ $\sigma _{b}^{{a{\kern 1pt} 'b{\kern 1pt} '}}$ и т.п., вычислять в сопутствующей системе координат, в которой частицы среды покоятся (в этой системе координат, например, параметры $\sigma _{b}^{{a{\kern 1pt} 'b{\kern 1pt} '}}(\nu )$ не зависят от вектора ${\mathbf{\Omega }}$).

Вместе тем, отсутствие локального термодинамического равновесия в верхней атмосфере планеты, выражающееся, в частности, в отношении поступательных степеней свободы в различие кинетических температур

для электронов, ионов и нейтральных частиц (см., например, Акасофу, Чепмен, 1974), не позволяет в общем случае ограничиться при вычислении теплового баланса термосферы одним лишь суммарным энергетическим уравнением (4), записанным через общую кинетическую температуру $T = {{T}_{{\alpha }}}$ смеси. Учет многотемпературности термосферной плазмы во многих случаях важен и может быть выполнен, в частности, на основе трех-жидкостной гидродинамики (Акасофу, Чепмен, 1974). Однако в данной работе мы, интересуясь главным образом определением радиационных и химических вкладов в энергетический баланс, будем предполагать термическое равновесие по поступательным степеням свободы для всех атмосферных компонентов.

Вводя удельную энтальпию вещества $H = {{\varepsilon + p} \mathord{\left/ {\vphantom {{\varepsilon + p} \rho }} \right. \kern-0em} \rho }$ = $\sum\nolimits_{\alpha } {{{{{h}_{{\alpha }}}{{n}_{{\alpha }}}} \mathord{\left/ {\vphantom {{{{h}_{{\alpha }}}{{n}_{{\alpha }}}} \rho }} \right. \kern-0em} \rho }} $ в энергетическое уравнение (4), перепишем его, с учетом (5), в переменных $T$ и $p$ в следующем удобном для гео- и астрофизических приложений виде

позволяющем, в частности, оценить воздействие аэрономических реакций на пространственное распределение кинетической температуры $T.$ Здесь ${{h}_{{{\alpha }s}}},{{c}_{{P{\alpha }s}}}$ ≡ ${{\partial {{h}_{{{\alpha }s}}}} \mathord{\left/ {\vphantom {{\partial {{h}_{{{\alpha }s}}}} {\partial T}}} \right. \kern-0em} {\partial T}}$ − соответственно энтальпия и теплоемкость на одну частицу сорта $\alpha ,$ находящуюся на $s$-м возбужденном уровне; ${{h}_{{\alpha }}} = \sum\nolimits_s {{{{{h}_{{{\alpha }s}}}{{n}_{{{\alpha }s}}}} \mathord{\left/ {\vphantom {{{{h}_{{{\alpha }s}}}{{n}_{{{\alpha }s}}}} {{{n}_{{\alpha }}}}}} \right. \kern-0em} {{{n}_{{\alpha }}}}}} $ − энтальпия на одну частицу сорта $\alpha ;$ ${{Q}_{d}}$ − возможные локальные источники нагрева.

Термодинамические функции. Для того чтобы гидродинамические уравнения, описывающие процессы переноса в многокомпонентном газе верхней атмосферы, были замкнуты, необходимы расчетные соотношения для определения термодинамических величин (таких как ${{\varepsilon }_{{\alpha }}}{\text{,}}{{h}_{{\alpha }}},{{c}_{{p{\alpha }}}},\varepsilon ,H$ и т.п.) как функций основных параметров системы $\rho ,{{n}_{{\alpha }}}$ и $T.$ Для полного решения этой задачи необходимо знание всех функций распределения ${{f}_{{{\alpha }s}}}.$ Если среда находится в состоянии локального термодинамического равновесия, то

где ${{\mu }_{{\alpha }}}$ − химический потенциал на одну частицу компоненты $\alpha $ в многокомпонентной смеси идеальных совершенных газов $({{\mu }_{{\nu }}} = 0);$ ${{k}_{B}}$ − постоянная Больцмана; знак “+” используется в случае фермионов, а знак “−” для бозонов; − статистическая сумма по внутренним степеням свободы для частиц сорта $\alpha ;$ ${{\varepsilon }_{{\alpha }}}(l)$ − энергия возбуждения $l$-го уровня молекулы сорта $\alpha $ (далее под уровнем понимается набор неразличимых − вырожденных квантовых состояний с одинаковой энергией); ${{g}_{{{\alpha l}}}}$ − кратность вырождения (статистический вес) уровня $l,$ т.е. число состояний, которые имеют одинаковую энергию ${{\varepsilon }_{{\alpha }}}(l).$ Если состояние вырождено, то для населенности $l$-го уровня (плотности частиц, находящихся на уровне $l$) необходимо использовать формулу связывающую ${{n}_{{{\alpha }l}}}$ с полным числом частиц данного сорта ${{n}_{{\alpha }}}$ (здесь суммирование производится по вырожденным состояниям уровня $l$). Из этой формулы следует, в частности, известное распределение Больцмана определяющее отношение плотности числа частиц типа ${{n}_{{{\alpha }l}}},$ находящихся на верхнем уровне $l,$ к их плотности ${{n}_{{{\alpha }s}}}$ на более низком уровне $s$ (здесь $h{{\nu }_{{sl}}}$ − энергия фотона, равная разности энергий этих уровней).

Для частиц с ненулевой массой покоя слагаемым $ \pm 1$ в выражении (7) часто можно пренебречь (см. Сэмпсон, 1969) (соответственно множитель $[1 \pm {{f}_{{{\alpha }s}}}]$ в (2) заменяется единицей, однако далее для общности множители $[1 \pm {{f}_{{\alpha s}}}]$ будем сохранять в некоторых случаях и для невырожденных абсорбентов). Тогда распределение (7) переходит в распределение Максвелла– Больцмана классических частиц

Отметим, что в случае, когда для частиц данного сорта $\alpha $ слагаемым $ \pm 1$ в (7) пренебречь нельзя при всех значениях энергии, такие частицы называются вырожденными. Наиболее легко вырождаются среди всех частиц с ненулевой массой покоя электроны, так как их масса мала. Поскольку фотоны – суть бозе-частицы с нулевым химическим потенциалом (${{\mu }_{{\nu }}} = 0$), то для них равновесное распределение (7) принимает вид:

Вычисленные с помощью равновесной функции распределения (8), термодинамические параметры для вещества, входящие в уравнения (5) и (6), можно записать следующим образом:

Здесь $\varepsilon _{{\alpha }}^{{\operatorname{int} }}$ – средняя энергия частицы, связанная с внутренними степенями свободы; $n = \sum\nolimits_{\alpha } {{{n}_{{\alpha }}}} $ = = $\sum\nolimits_{{\alpha },s} {{{n}_{{{\alpha }s}}}} $ − полная числовая плотность системы; $\dot {n}_{{(\alpha )}}^{{(1)}}$ – скорость образования (исчезновения) частиц сорта $\alpha $ в результате химических реакций в случае, когда столкновения не нарушают заметным образом распределения (9);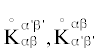 − коэффициенты скоростей прямых и обратных реакций, связанные с константой равновесия K соотношением справедливым только в равновесном случае (см. Полак, 1979). Заметим, что гидродинамические уравнения (4) для величин (10) принимают форму Эйлера.

Определяющие соотношения. Для замыкания системы уравнений (4) в случае, когда вещество находится в состоянии ЛТР, необходимы уравнения для величин ${{{\mathbf{q}}}_{R}}$ и ${{\dot {n}}_{{(\alpha s)}}},$ а также определяющие соотношения (линейные функции от градиентов макроскопических параметров), связывающие термодинамические потоки ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\pi } }},{{{\mathbf{w}}}_{{\alpha }}},{\mathbf{q}}$ с обобщенными термодинамическими силами. Эти соотношения можно получить путем решения системы уравнений (1) (см. Ферцигер, Капер, 1976). Вопрос получения приближенного решения системы (1) с учетом внутренних степеней свободы частиц и излучения оказался весьма сложным. До настоящего времени все еще получен лишь структурный вид соответствующих уравнений переноса, однако отсутствуют сколько-нибудь надежные расчеты кинетических коэффициентов переноса из решения обобщенных уравнений Больцмана (1). Именно, по этой причине в гидродинамических задачах аэрономии до последнего времени используются уравнения переноса, выведенные без учета взаимодействия вещества и излучения. Более того, в отношении кинетических коэффициентов переноса реагирующий газ часто рассматривается как нереагирующая смесь упругих молекул.

В рамках предположения, что вклад излучения в интегралы столкновений ${{\delta {{{\text{f}}}_{{{\alpha }s}}}} \mathord{\left/ {\vphantom {{\delta {{{\text{f}}}_{{{\alpha }s}}}} {\delta t}}} \right. \kern-0em} {\delta t}}$ для частиц вещества мал, т.е. переносные свойства среды определяются только взаимодействием молекул между собой, с помощью модификации метода Чепмена–Энскога были получены следующие определяющие соотношения для химически активных многоатомных газовых смесей в высших приближениях кинетических коэффициентов переноса (см., например, Колесниченко, 2017):

Здесь $p{\kern 1pt} '$ − вклад в давление, возникающий из-за наличия химических реакций; ${{k}_{{T{\alpha }}}},$ ${\text{D}}_{{{\alpha \beta }}}^{{(1)}},$ $\mu ,{{\mu }_{b}},\lambda $ − коэффициенты переноса, выражающиеся известным образом через коэффициенты разложения функций возмущения равновесных функций распределения $f_{{{\alpha }s}}^{{(00)}}$ в ряды по полиномам Сонина в методе Чепмена–Энскога, ${\text{g}}_{{{\alpha \beta }}}^{{\text{N}}}$ − поправочный множитель к бинарным коэффициентам диффузии ${\text{D}}_{{{\alpha \beta }}}^{{(1)}},$ зависящий от числа удерживаемых членов разложения функции ${{f}_{{{\alpha }s}}}$ в ряды.

Таким образом, разреженный газ внешних газовых оболочек планет и комет, расположенных в пограничных областях между атмосферой и космосом, во многих практически важных случаях моделирования может описываться макроскопическими методами многокомпонентной радиационной гидродинамики. Однако, с учетом специфики этих сред, необходима разработка подходов, позволяющих корректно учитывать вклад радиационных и химических источников нагрева, обусловленных прямым поглощением солнечной энергии и инициируемым ею многоканальным комплексом аэрономических процессов. Отклонение от ЛТР обуславливается неравновесностью падающего солнечного излучения по отношению к кинетическим параметрам газа верхних атмосфер. Заселенности возбужденных квантовых энергетических уровней, как правило, отклоняются от распределения Больцмана, и химические реакции, инициируемые нетермическим путем, имеют, по крайней мере на начальном участке, неравновесную стадию.

СТАЦИОНАРНОЕ УРАВНЕНИЕ ПЕРЕНОСА ИЗЛУЧЕНИЯ

Вклад радиации в тепловой баланс газовой среды, согласно энергетическому уравнению (6), имеет вид

Для определения спектральной интенсивности излучения ${{{\text{I}}}_{{\nu }}}$ будем использовать уравнение Больцмана (1) для фотонов без учета рассеяния, предполагая при этом стационарность поля излучения. Это справедливо для задач атмосферной радиации, поскольку время релаксации излучения с веществом $\tau $ (величина порядка времени свободного пробега фотона $\tau \approx {{(cn\sigma )}^{{ - 1}}},$ где $\sigma \approx {{10}^{{ - 17}}} - {{10}^{{ - 18}}}$ см², $n \geqslant {{10}^{8}}$ см^–3) в термосфере существенно меньше характерного времени макроскопических процессов переноса (${{t}_{{{\text{гид}}}}} > 1\,\,{\text{c}}$). Заметим попутно, что, даже будучи учтенными, томпсоновское и рэлеевское рассеяния не дают вклада в выражение (13) для дивергенции потока излучения (см., например, Бонд и др., 1968): именно по этой причине в гидродинамических задачах аэрономии рассеянием часто можно пренебречь. Уравнение Больцмана (1), записанное для фотонов, в этом случае упрощается и принимает вид:

Первое слагаемое в правой части (14) соответствует радиативным процессам, связанным либо с переходами между дискретными уровнями энергии атома или молекулы (фотовозбуждение на расположенные выше уровни, $j \to j{\kern 1pt} ';$ спонтанные и вынужденные переходы $j{\kern 1pt} ' \to j$), либо, в случае свободно-свободного поглощения, с переходами пар ион–электрон из одного энергетического состояния в другое. Второе слагаемое отвечает переходам, при которых одно из состояний принадлежит непрерывному энергетическому спектру, а другое − дискретному (фотодиссоциация с возбуждением, фотоионизация, спонтанные и вынужденные фоторекомбинации и т.п.). Индекс $b\,\,(b{\kern 1pt} '...)$ заменяет собой набор индексов $\beta ,j,\,\,(\beta {\kern 1pt} ',j{\kern 1pt} '...);$ $\beta ,\alpha ,\beta {\kern 1pt} ',\alpha {\kern 1pt} ' \in [1,N].$ При написании выражения (14) предполагалось, что сечения поглощения и испускания усреднены и просуммированы соответственно по двум вырожденным состояниям поляризации фотона, т.е. зависимостью сечений реакций от поляризации фотона пренебрегалось; предполагалось также, что можно пренебречь зависимостью сечения от импульса, т.е. справедливо тождество $d\sigma ({{{\mathbf{p}}}_{{\nu }}},{{{\mathbf{p}}}_{{\beta }}},j \to {{{\mathbf{p}}}_{{{\beta }{\kern 1pt} {\text{'}}}}},j{\kern 1pt} ')$ ≡ ≡ $d{{\sigma }_{{\beta }}}(\nu ,j \to j{\kern 1pt} '),$ поскольку при переходах с одного связанного уровня энергии на другой, импульс частицы, вообще говоря, не существенен. В этом случае уравнение (14) преобразуется к виду

Здесь введены следующие обозначения:

где $K_{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}(\nu ),$ $K_{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}}(\nu )$ – эффективные сечения поглощения фотона частоты $\nu $ (в расчете на одну частицу сорта $\beta ,$ находящуюся на уровне $j$) при переходах $\beta ,j \to \beta ,j{\kern 1pt} '$ (в линии) и $b \to b{\kern 1pt} ',a{\kern 1pt} '$ (в непрерывном спектре) соответственно (см. Бонд и др., 1968). Эти сечения определены здесь с учетом возможной вырожденности абсорбентов (например, электронов), при которой величины в скобках (16) и (17) не совпадают с единицей. В сечения поглощения в линиях $\sigma _{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}(\nu )$ и в сечения фотодиссоциации $\sigma _{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}}(\nu )$ включены множители, связанные с индуцированным испусканием излучения; $T_{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}}$ − так называемая внутренняя температура, характеризующая распределение энергии по внутренним состояниям системы и определяемая равенством (см. (7)) где окончательный вид правой части записан с учетом закона сохранения энергии $\Delta {{\varepsilon }_{b}} + h\nu $ = = $\Delta {{\varepsilon }_{{b{\kern 1pt} '}}} + \Delta {{\varepsilon }_{{a{\kern 1pt} '}}}$ и условия химического равновесия ${{\mu }_{b}} + {{\mu }_{{\nu }}}$ = ${{\mu }_{{b{\kern 1pt} '}}} + {{\mu }_{{a{\kern 1pt} '}}}$ (при температуре $T_{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}}$) для фотопроцесса $\beta (j) + h\nu $ → $\beta {\kern 1pt} '(j{\kern 1pt} ') + \alpha {\kern 1pt} '(s{\kern 1pt} ');$ $f_{{\nu }}^{{(0)}}\left( {T_{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}}} \right)$ − функция распределения для фотонов (7), соответствующая термическому равновесию при температуре $T_{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}};$ функция $f_{{\nu }}^{{(0)}}\left( {T_{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}} \right)$ и температура возбуждения $j{\kern 1pt} '$-го уровня относительно $j$-го $\left( {T_{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}} \right)$ определяются аналогично. Из соотношений (7) следует, что в случае термического равновесия все внутренние температуры равны между собой и совпадают с кинетической температурой газа $T$. Однако в общем неравновесном случае разности типа $\left( {T_{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}} - T} \right)$ при температурном описании состояния газа могут служить мерой отклонения отдельных равновесных поглощающих подсистем от термодинамического равновесия, а для определения параметров $T_{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}$ $\left( {T_{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}}} \right)$ (или соответствующих чисел заполнения) вместо соотношений статистической механики следует использовать уравнения физической кинетики (5) для “источниковых” членов ${{\dot {n}}_{{{\beta }j}}}.$

Таким образом, уравнение Больцмана (15) для фотонного газа, записанное относительно спектральной интенсивности ${{I}_{{\nu }}}({\mathbf{r}},{\mathbf{\Omega }},t),$ принимает вид уравнения переноса излучения (без учета рассеяния)

Здесь ${{\kappa }_{{{\nu }a}}}$ − массовый коэффициент поглощения (излучения) газовой смесью; ${{{\text{S}}}_{{\nu }}}$ − истинная функция внутренних источников излучения; – распределение интенсивности Планка при некоторой температуре $\tilde {T}$ (распределение по частотам поля излучения при термодинамическом равновесии). В случае локального термодинамического равновесия при температуре $T$ индексы у величин $T_{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}}$ и $T_{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}$ в соотношениях (18) могут быть опущены. В этом случае для истинной функции внутренних источников излучения будем иметь ${{{\text{S}}}_{{\nu }}} = {{B}_{{\nu }}}(T).$

В случае термодинамического равновесия удобна другая форма записи для истинного коэффициента поглощения излучения веществом ${{\kappa }_{{{\nu }a}}}$ и функции источников излучения ${{{\text{S}}}_{{\nu }}}.$ Используя распределение Больцмана (8) $\frac{{{{n}_{{{\beta }j{\kern 1pt} '}}}}}{{{{n}_{{{\beta }j}}}}}$ = $\frac{{{{{\text{g}}}_{{{\beta }j{\kern 1pt} '}}}}}{{{{{\text{g}}}_{{{\beta }j}}}}}\exp \left[ {{{ - h{{\nu }_{{j,j{\kern 1pt} '}}}} \mathord{\left/ {\vphantom {{ - h{{\nu }_{{j,j{\kern 1pt} '}}}} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right]$ при температуре $T$ для населенностей двух любых возбужденных уровней $j$ и $j{\kern 1pt} '$ частиц сорта $\beta $ ($h{{\nu }_{{j,j{\kern 1pt} '}}}$ − энергия возбуждения $j{\kern 1pt} '$-го уровня; ${{{\text{g}}}_{{{\beta }j}}}$ и ${{{\text{g}}}_{{{\beta }j{\text{'}}}}}$ − статистические веса, приписываемые соответственно уровням $j$ и $j{\kern 1pt} '$ для учета числа вырожденных состояний), а также закон действующих масс для перехода $b \to b{\kern 1pt} 'a{\kern 1pt} '$ при температуре $T,$ взятый в виде

(где $h{{\nu }_{{b \to b{\kern 1pt} 'a{\kern 1pt} '}}}$ − энергия перехода $b \to b{\kern 1pt} 'a{\kern 1pt} ';$ ${{g}_{{a{\kern 1pt} '}}},$ ${{g}_{{b{\kern 1pt} '}}}$ и ${{g}_{b}}$ − кратности вырождения состояний $a{\kern 1pt} ',b{\kern 1pt} '$ и $b$), можно получить следующие выражения для величин ${{\kappa }_{{{\nu }a}}}$ и ${{S}_{{\nu }}}{\text{:}}$

Таким образом, поле излучения зависит от населенностей уровней всех частиц газовой смеси через коэффициенты поглощения ${{\kappa }_{{{\nu }a}}}$ и излучения ${{\kappa }_{{{\nu }a}}}{{S}_{{\nu }}},$ влияющие на прохождение излучения через атмосферу. Поэтому в общем случае требуется полностью самосогласованное решение уравнений переноса излучения и уравнений физической кинетики для населенностей энергетических уровней частиц вещества. Уравнения физической кинетики должны описывать все возможные процессы (как радиативные, так и ударные), ведущие к изменению со временем плотности числа частиц любой химической составляющей $\beta ,$ находящихся в произвольном (связанном или свободном) состоянии $j.$

При постановке физически самосогласованных задач планетной аэрономии в приближении многокомпонентной радиационной гидродинамики возникает, как одна из важнейших, проблема точного учета вкладов от взаимодействия вещества и излучения в гидродинамические макроскопические уравнения. Получим теперь соотношения, позволяющие учесть эндотермические и экзотермические химические реакции (включая процессы фотолиза) в структуре энергетического уравнения и тем самым определим общий вид функции нагревания верхней атмосферы.

ВКЛАД ЖЕСТКОГО СОЛНЕЧНОГО ИЗЛУЧЕНИЯ В ЭНЕРГЕТИЧЕСКИЙ БАЛАНС ТЕРМОСФЕРЫ

Интегрирование стационарного уравнения переноса излучения (18) по всему спектру частот и по телесному углу ${\mathbf{\Omega }},$ приводит к следующему выражению для вклада радиации в тепловой баланс верхней атмосферы:

Здесь первый член A соответствует поглощаемой (исключая энергию индуцированного излучения), а второй член R − спонтанно излучаемой радиационной энергии в единице объема в единицу времени. Соотношение (19) может быть преобразовано к другому более удобному виду, в частности, при анализе влияния жесткого солнечного излучения на энергетический баланс верхней атмосферы. С учетом формул (18) для величин ${{\kappa }_{{{\nu }a}}},$ ${{S}_{{\nu }}},$ $f_{{\nu }}^{{(0)}}(\tilde {T}),$ а также соотношений (16) и (17) для эффективных сечений $\sigma _{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}(\nu )$ и $\sigma _{b}^{{b{\kern 1pt} 'a{\kern 1pt} '}}(\nu ),$ количество излучаемой радиационной энергии R может быть записано в следующем виде

Комбинируя выражения (16) и (3), можно показать, что сечения поглощения и испускания в газе $K_{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}(\nu )$ и $K_{{{\beta }j{\kern 1pt} '}}^{{{\beta }j}}(\nu )$ связаны соотношением $K_{{{\beta }j}}^{{{\beta }j{\kern 1pt} '}}(\nu ){{g}_{{{\beta }j}}}$ = $K_{{{\beta }j{\kern 1pt} '}}^{{{\beta }j}}(\nu ){{g}_{{{\beta }j{\kern 1pt} '}}},$в котором ${{g}_{{{\beta }j}}}$ и ${{g}_{{{\beta }j{\kern 1pt} '}}}$ − кратности вырождения возбужденных уровней $j$ и $j{\kern 1pt} '.$ Учитывая это соотношение, а также распределение Больцмана

для населенностей ${{n}_{{{\beta }j}}}$ и ${{n}_{{{\beta }j{\kern 1pt} '}}}$ уровней $j$ и $j{\kern 1pt} ',$ можно получить следующее выражение:

Два последних выражения для величины R₁ в (21) записаны здесь с использованием следующих известных соотношений (Гуди, 1966; Бонд и др., 1968)

Здесь ${{f}_{{{\beta }j,j{\kern 1pt} '}}}$ − сила осциллятора для поглощения при переходах $j \to j{\kern 1pt} '$ (являющаяся безразмерной величиной, лежащей в интервале от нуля до единицы, ${{f}_{{{\beta }j,j{\kern 1pt} '}}}$ = ${{ - {{f}_{{{\beta }j{\kern 1pt} ',j}}}{{g}_{{{\beta }j{\kern 1pt} '}}}} \mathord{\left/ {\vphantom {{ - {{f}_{{{\beta }j{\kern 1pt} ',j}}}{{g}_{{{\beta }j{\kern 1pt} '}}}} {{{g}_{{{\beta }j}}}}}} \right. \kern-0em} {{{g}_{{{\beta }j}}}}}$); ${{A}_{{{\beta }j{\kern 1pt} ',j}}}$ – атомный коэффициент Эйнштейна для спонтанного излучения (характеризующий вероятность спонтанного перехода $j' \to j$ и имеющий порядок 10⁸, 10 и 1 с^–1 для электронных, колебательных и вращательных переходов соответственно); ${{\nu }_{{{\beta }(j,j{\kern 1pt} ')}}}$ − средняя частота фотона, испускаемого в радиативном переходе с уровня $j{\kern 1pt} '$ на уровень $j;$ ${{P}_{{{\beta }j,j{\kern 1pt} '}}}(\nu )$ − функция формы линии поглощения, описывающая распределение поглощения внутри линии (имеет острый максимум при $\nu = {{\nu }_{{{\beta }(j,j{\kern 1pt} ')}}}$ и нормирована на единицу $\int_0^\infty {{{P}_{{{\beta }j,j{\kern 1pt} '}}}(\nu )d\nu } = 1$).

Выражение для второго слагаемого в формуле (20) может быть преобразовано с учетом соотношений взаимности (3), определения сечения фотодиссоциации (17) и формулы для дифференциала импульса $d{{{\mathbf{p}}}_{{\nu }}}$ = ${{h}^{3}}{{\nu }^{2}}{{c}^{{ - 3}}}d{\mathbf{\Omega }}d\nu $ (в сферических координатах) следующим образом

Здесь $h{{\nu }_{{(a{\kern 1pt} 'b{\kern 1pt} ' \to b)}}} = \Delta {{\varepsilon }_{{{\beta }{\kern 1pt} {\text{'}}}}}(j{\kern 1pt} ')$ + $\Delta {{\varepsilon }_{{{\alpha }{\kern 1pt} {\text{'}}}}}(s{\kern 1pt} ') - \Delta {{\varepsilon }_{{\beta }}}(j)$ − пороговая энергия (энергия диссоциации или потенциал ионизации) реакции $\beta (j) + h\nu $ → $\alpha {\kern 1pt} '(s{\kern 1pt} ') + \beta {\kern 1pt} '(j{\kern 1pt} ');$ ${{A}_{{a{\kern 1pt} 'b{\kern 1pt} ',b}}}$ − константа скорости для процесса спонтанной фоторекомбинации $\alpha {\kern 1pt} '(s{\kern 1pt} ') + \beta {\kern 1pt} '(j{\kern 1pt} ') \to \beta (j) + h\nu ,$ определяемая соотношением

Комбинируя (18), (19), (21) и (23), можно получить следующее “окончательное” выражение для вклада излучения ${{Q}_{R}}$ в уравнение энергии (4):

Здесь $h\nu {{\Phi }_{\nu }}: = \int_{\mathbf{\Omega }} {{{I}_{\nu }}d{\mathbf{\Omega }}} $ − спектральная интенсивность излучения, проинтегрированная по всему телесному углу ${\mathbf{\Omega }}.$ Поскольку величина ${{\Phi }_{\nu }}$ зависит в общем случае от испускания и поглощения собственного излучения средой, то при вычислении ${{Q}_{R}}$ по формуле (25) нужно учитывать перенос суммарной радиации. Для этого необходимо решать уравнение переноса излучения (18), что связано, как известно, с определенными трудностями (за исключением случая оптически тонкого (толстого) атмосферного слоя, часто используемого в расчетах (см., например, Гуди, 1966; Бонд и др., 1968). В случае переноса лишь коротковолновой радиации упрощение достигается за счет пренебрежения собственным излучением атмосферы в этой части энергетического спектра.

В качестве примера выпишем здесь общее выражение для величины поглощения солнечной (УФ и рентгеновской) радиации стратифицированной атмосферой планеты. Если направление на Солнце определяется вектором ${{{\mathbf{\Omega }}}_{ \odot }},$ то спектральный поток солнечной радиации может быть записан в виде:

где ${{{\mathbf{\Omega }}}_{ \odot }}{{\Phi }_{{{{{\nu }}_{ \odot }}}}}$ − спектральный поток солнечных фотонов (инсоляция), проходящих в единицу времени через единичную площадку с нормалью ${{{\mathbf{\Omega }}}_{ \odot }}.$ Для собственного УФ излучения верхняя атмосфера почти всегда прозрачна. Большинство фотонов в эмиссиях, возникающих вследствие диссоциации с возбуждением или ионизации, рождаются в мягком УФ диапазоне (Акасофу, Чепмен, 1974) и, обладая большими длинами пробега, уходят из термосферы. Поэтому можно пренебречь функцией источника ${{S}_{\nu }}$ в уравнении переноса излучения (18); тогда для ${{\Phi }_{{{{\nu }_{ \odot }}}}}$ будем иметь где $s$ – координата вдоль луча направления ${{{\mathbf{\Omega }}}_{ \odot }};$ ${{\Phi }_{{\nu \infty }}}$ − величина инсоляции на верхней границе атмосферы (экспериментально определяемая величина). Вторая форма записи в соотношении (26) справедлива для плоской модели атмосферы, когда $ds = \sec \theta dz$ ($\theta $ − зенитный угол Солнца; $z$ − высота). Учет кривизны атмосферных слоев приводит к тому, что в формуле (26) $\sec \theta $ заменяется на так называемую функцию Чепмена $Ch(\theta ,z)$ (см., например, Кошелев и др., 1983) (в случае, когда $\theta < 80^\circ ,$ функция $Сh(\theta ,z) \approx \sec \theta $). Комбинируя (19) и (26), получим выражение являющиеся основным при учете поглощения солнечной коротковолновой радиации в тепловом балансе термосферы.

СКОРОСТИ ЭЛЕМЕНТАРНЫХ ПРОЦЕССОВ

Как отмечалось выше, внутренние степени свободы частиц термосферы возбуждаются в основном под действием УФ и рентгеновских солнечных фотонов или выбитых ими фотоэлектронов. Населенности возбужденных квантовых энергетических уровней при этом, как правило, небольцмановы, химические реакции, инициируемые нетермическим путем, имеют, по крайней мере на начальном участке, неравновесную стадию. Отклонение от ЛТР в термосфере планеты обуславливается, в конечном счете, неравновесностью падающего солнечного излучения по отношению к кинетическим параметрам атмосферного газа. Наиболее полное описание аэрономических реакций в верхней атмосфере возможно только в рамках неравновесной химической кинетики.

Сложность и многочисленность химических и фотохимических реакций, происходящих в верхней атмосфере, обусловлена присутствием основных атмофильных элементов, входящих в состав исходных газов, и наличием агентов ионизации (диссоциации) в виде энергичных фотонов излучения и фотоэлектронов (продуктов фотолиза). Их поглощение приводит к диссоциации, ионизации, и/или возбуждению вращательных и колебательных уровней, причем каждая из этих реакций может протекать как в прямом, так и в обратном направлении (McElroy, 1976). Считая условно одни и те же частицы, находящиеся на разных уровнях возбуждения внутренних степеней свободы, различными компонентами газовой смеси, любую аэрономическую реакцию символически можно записать следующим образом:

где $\eta _{{b{\rho }}}^{'},$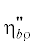 – стехиометрические коэффициенты компоненты $b$ по отношению к $\rho $-ой химической реакции; $\left[ b \right]$ – символ для обозначения частиц сортов $b$ ($b$ соответствует совокупности индексов $\alpha $ и $j$); $r$ − число реакций. Естественно, что при последовательном учете всех уровней возбуждения число компонент может возрастать до бесконечности. Однако при численном моделировании верхней атмосферы приходится довольствоваться, к сожалению, ограниченным комплексом аэрономических реакций, ответственных за приток и отток тепла в атмосферу на разных высотах.

Важнейшей задачей при моделировании химически активного газа является определение скорости ${{\xi }_{{\rho }}},$ с которой протекает каждая реакция в единице объема смеси. Если обозначить через ${\text{K}}_{\rho }^{{\text{'}}}$ и 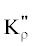постоянные скоростей прямой и обратной реакций соответственно, то общая скорость образования частиц сорта $b$ в результате всех реакций (28) задается cоотношением

Получим, исходя из системы уравнений Больцмана (1), конкретный вид “источниковых” членов ${{\dot {n}}_{{{\beta }j}}} = {{h}^{{ - 3}}}\int {{{(\delta {{f}_{{{\beta }j}}}} \mathord{\left/ {\vphantom {{(\delta {{f}_{{{\beta }j}}}} {\delta t)}}} \right. \kern-0em} {\delta t)}}} d{{{\mathbf{p}}}_{{\beta }}}$ в уравнениях баланса (5) для населенности энергетических состояний реагирующих частиц, обусловленных неравновесными химическими реакциями, элементарными процессами взаимодействия частиц вещества и радиативными процессами. Вклад бимолекулярных реакций $\beta (j) + \alpha (s) \Leftrightarrow \beta {\kern 1pt} '(j{\kern 1pt} ') + \alpha {\kern 1pt} '(s{\kern 1pt} ')$ (без участия фотонов) в правую часть (5), обозначаемый далее $\dot {n}_{{{\beta }j}}^{{\left( 1 \right)}},$ в случае максвелловского распределения по скоростям и произвольного распределения ${{F}_{{\beta }}}(j)$ реагирующих частиц по внутренним степеням свободы определяется соотношением где константы скоростей определены формулами

Источник $\dot {n}_{{{\beta }j}}^{{\left( 1 \right)}}$ в задачах моделирования верхней атмосферы связан, в частности, с химическими реакциями, с процессами возбуждения молекул (атомов) при неупругих столкновениях или с их диссоциацией, а также с противоположными процессами − девозбуждения и безызлучательной рекомбинации. Путем суммирования (31) по $j$ можно найти формулу для скорости образования (исчезновения) частиц химического элемента $\alpha $ в результате всех аэрономических реакций рассматриваемого типа:

Отметим, что при таком подходе и для “обыкновенной” химической реакции между химическими элементами константу скорости можно определить как статистически среднюю скорость по всем энергетически доступным каналам столкновений. Это согласуется с представлением о том, что химическая реакция “возмущает” статистическое распределение как по внутренним, так и по поступательным степеням свободы и позволяет, вообще говоря, рассчитать теоретически (при знании как сечений химической реакции для индивидуальных состояний, так и распределений реагирующих молекул по внутренним состояниям во время протекания реакций) константу скорости для неравновесных реакций.

Учет радиативных процессов в уравнениях для ${{n}_{{{\beta }j}}},$ согласно (1) , можно представить в виде суммы $\dot {n}_{{{\beta }j}}^{{\left( 2 \right)}} + \dot {n}_{{{\beta }j}}^{{\left( 3 \right)}}$ + $\dot {n}_{{{\beta }j}}^{{\left( 4 \right)}} + \dot {n}_{{{\beta }j}}^{{\left( 5 \right)}},$ где введены обозначения:

Величина $\dot {n}_{{{\beta }j}}^{{\left( 2 \right)}}$ обусловлена фотодиссоциацией (в том числе с возбуждением квантовых энергетических уровней образующихся частиц), фотоионизацией и процессами фоторекомбинации и радиативной ассоциации, приводящими, соответственно, к исчезновению и появлению частиц сорта $\beta ,j;$ величина $\dot {n}_{{{\beta }j}}^{{\left( 3 \right)}}$ связана с теми же фотопроцессами, приводящими, соответственно, к появлению и исчезновению частиц сорта $\beta ,j;$ величины $\dot {n}_{{{\beta }j}}^{{(4)}}$ и $\dot {n}_{{{\beta }j}}^{{(5)}}$ связаны с переходами межу дискретными уровнями энергии частиц сорта $\beta {\text{:}}$ фотовозбуждение с расположенных ниже уровней и радиативные переходы (спонтанные и вынужденные) с метастабильных уровней на уровни, расположенные ниже.

С учетом соотношений (4), (17) и (24), а также процедуры преобразования величины ${{{\text{R}}}_{{\text{2}}}}$ (ниже формулы (20)) перепишем (35) следующим образом:

Для дальнейшего преобразования выражения (36) используем соотношение взаимности (3). Так как получающаяся при этом подынтегральная величина при замене индексов $a$ и $b$ на индексы $a{\kern 1pt} '$ и $b{\kern 1pt} '$ отличается от аналогичной в (35) только знаком, то где величина есть константа скорости для процессов фоторекомбинации.

Поступая аналогичным образом при преобразовании выражений (37) и (38), получим

Здесь ${{A}_{{{\beta }j,j{\kern 1pt} '}}}$ − коэффициент Эйнштейна для спонтанного излучения при переходе в энергетически более низкое состояние $j \to j{\kern 1pt} '.$

С учетом (31), (35)−(38) уравнение непрерывности (5) для плотности числа частиц сорта $\beta $ в $j$‑ом внутреннем состоянии принимает вид

На практике при решении конкретных аэрономических задач почти всегда возможны различные упрощения уравнения (40): например, учет относительной величины констант различных столкновительных и радиативных процессов в условиях термосферы позволяет опустить некоторые члены; реальное число возбужденных уровней часто может быть аппроксимировано одним или несколькими уровнями, которым приписана фиктивная высокая степень вырождения; в тех случаях, когда скорости прямых и обратных аэрономических реакций достаточно велики (т.е. времена реакций много меньше характерного гидродинамического времени ${{t}_{{{\text{гид}}}}}$), второй член слева становится пренебрежимо малым и уравнение переходит в уравнение химической кинетики, и т.д.

РАДИАЦИОННЫЙ И ХИМИЧЕСКИЙ НАГРЕВ ТЕРМОСФЕРЫ

Все аэрономические реакции сопровождаются либо переходом внутренней энергии частиц в тепловую энергию или излучение – экзотермические реакции, либо переходом энергии движения молекул и излучения во внутреннюю энергию частиц при образовании новых компонентов – эндотермические реакции (Vázquez, Hanslmeier, 2006). При этом теплота $\rho $-ой реакции определяется выражением (см. (6))

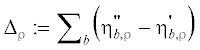в котором величина является энтальпией ${{h}_{{{\beta }j}}}$ частицы сорта $\beta $ в $j$-ом возбужденном состоянии, а величина есть алгебраическая сумма стехиометрических коэффициентов реакции (28).

В условиях верхней атмосферы, как правило, $q_{{\rho }}^{0} \gg {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}{{k}_{B}}T{{\Delta }_{{\rho }}};$ тогда в соответствии с (41) вклад всех аэрономических реакций ${{{\text{Q}}}_{{{\text{ch}}}}}$ в уравнение энергетического баланса (6) для кинетической температуры смеси может быть записан в следующем общем виде:

Конкретизируем теперь соотношение (43) для рассматриваемых бимолекулярных реакций общего типа. Введем обозначения ${\text{Q}}_{{{\text{ch}}}}^{{(i)}}: = - \sum\nolimits_b {\dot {n}_{b}^{{(i)}}{{h}_{b}}} ,$ $(i = 1,2,...,5);$ тогда ${{{\text{Q}}}_{{{\text{ch}}}}}: = \sum\nolimits_i^5 {{\text{Q}}_{{{\text{ch}}}}^{{(i)}}} .$ Преобразуем каждое слагаемое ${\text{Q}}_{{{\text{ch}}}}^{{(i)}}$ к виду (43). С учетом формул (31), (33)–(38), а также условия симметричности коэффициентов ${\text{K}}_{{ba}}^{{b{\kern 1pt} 'a{\kern 1pt} '}}$ по верхним и нижним индексам можно написать:

Здесь для теплот аэрономических реакций использованы обозначения

С учетом соотношений (25), (43)–(46) совместный вклад излучения и аэрономических реакций (так называемая функция нагревания верхней атмосферы) в энергетическое уравнение (6) может быть записан в следующем виде:

Это выражение особенно удобно использовать при расчете функции нагревания верхней атмосферы жестким солнечным излучением, поскольку в этом случае поток излучения ${{\Phi }_{\nu }}$ может быть с большой точностью заменен на поток солнечных фотонов ${{\Phi }_{{{{\nu }_{ \odot }}}}}$ (см. (26)).

Проиллюстрируем изложенный здесь подход на примере двух аэрономических процессов, протекающих в верхней атмосфере Земли.

Пример 1. Как известно, одним из основных источников нагрева нижней термосферы является диссоциативное поглощение молекулами ${{O}_{{\text{2}}}}$ излучения $1350 \leqslant \lambda \leqslant 2500\,\,{\AA}$ (см. Мак-Ивен, Филипс, 1978; Thuillier, 2000), причем в зависимости от энергии фотона могут возбуждаться различные электронные состояния продуктов диссоциации:

Энергия, затраченная на возбуждение одного из атомов кислорода до состояния ${}^{1}D{\text{,}}$ может, помимо спонтанного излучения, перейти в кинетическую энергию частиц вследствие ударной дезактивации либо пойти на возбуждение состояния $b{}^{1}\Sigma _{g}^{ + }$ молекул ${{O}_{{\text{2}}}}{\text{:}}$

Функция нагревания (46) для реакций (49)–(53) принимает вид

Здесь ${{D}_{{{{O}_{2}}}}} = 5.11$ эВ − энергия диссоциации ${{O}_{2}};$ ${{W}_{{1D}}} = 1.96$ эВ, ${{W}_{{1\Sigma }}} = 1.64$ эВ − соответственно энергия возбуждения уровня ${}^{1}D$ атома $O$ и уровня $b{}^{1}\Sigma _{g}^{ + }$ молекулы ${{O}_{2}}.$

Возможное упрощение выражения (54) основано на том, что времена релаксации ${{\tau }_{{O(D)}}}$ и ${{\tau }_{{{{O}_{2}}(b)}}}$ заселенностей возбужденных уровней ${}^{1}D$ и $b{}^{1}\Sigma _{g}^{ + }$ (${{\tau }_{{O(D)}}} \approx {{[{{{{{\dot {n}}}_{{O(D)}}}} \mathord{\left/ {\vphantom {{{{{\dot {n}}}_{{O(D)}}}} {{{n}_{{O(D)}}}}}} \right. \kern-0em} {{{n}_{{O(D)}}}}}]}^{{ - 1}}}$ ≈ 100 с, ${{\tau }_{{{{O}_{2}}(b)}}} \approx {{[{{{{{\dot {n}}}_{{{{O}_{2}}(b)}}}} \mathord{\left/ {\vphantom {{{{{\dot {n}}}_{{{{O}_{2}}(b)}}}} {{{n}_{{{{O}_{2}}(b)}}}}}} \right. \kern-0em} {{{n}_{{{{O}_{2}}(b)}}}}}]}^{{ - 1}}} \approx $ ≈ 140 с) намного больше соответствующих времен диссоциации и ассоциации. Поэтому можно считать, что числовые плотности ${{n}_{{O(D)}}}$ и ${{n}_{{{{O}_{2}}(b)}}}$ находятся в равновесии с мгновенными значениями плотностей ${{n}_{{O(P)}}}$ и ${{n}_{{{{O}_{2}}(x)}}},$ т.е.

Отсюда следует

Комбинируя теперь (54) и (57), получим следующую окончательную формулу для скорости нагревания атмосферы за счет фотодиссоциации ${{O}_{2}}$ с возбуждением:

где

Таким образом, если радиационные времена жизни $А_{{O(D),O(P)}}^{{ - 1}}$ и $А_{{{{O}_{2}}(b),{{O}_{2}}(x)}}^{{ - 1}}$ возбужденных компонентов $O({}^{1}D)$ и ${{O}_{2}}(b{}^{1}\Sigma _{g}^{ + })$ много больше соответствующих их столкновительных времен жизни ${1 \mathord{\left/ {\vphantom {1 {\sum\nolimits_j {{{n}_{j}}{\text{K}}_{{O(D)j}}^{{O(P)j}}} }}} \right. \kern-0em} {\sum\nolimits_j {{{n}_{j}}{\text{K}}_{{O(D)j}}^{{O(P)j}}} }}$ и ${1 \mathord{\left/ {\vphantom {1 {\sum\nolimits_j {{{n}_{j}}{\text{K}}_{{{{O}_{2}}(b)j}}^{{{{O}_{2}}(x)j}}} }}} \right. \kern-0em} {\sum\nolimits_j {{{n}_{j}}{\text{K}}_{{{{O}_{2}}(b)j}}^{{{{O}_{2}}(x)j}}} }},$ то ${\text{f}}_{{1D}}^{*} \cong 1,$ и в этом случае превышение фотонной энергии над энергией диссоциации в фотохимическом процессе реализуется как кинетическая энергия продуктов реакции, т.е. идет на нагревание термосферы − фотодиссоционное тепло. Остальная часть солнечной фотонной энергии реализуется как химическая энергия реакций рекомбинации. Однако в более общем случае, согласно (58), механизмом ударной дезактивации переводится в тепло лишь часть энергии солнечных фотонов, затраченной на возбуждение продуктов фотопроцесса, при этом остальная часть высвечивается в космическое пространство.

Пример 2. В качестве второго примера рассмотрим один из источников нагрева земной атмосферы в области озоносферы (≅30 км) – фотолиз озона (см. Haigh, 1999; Larkin и др., 2000). Фотодиссоциация озона солнечным излучением в диапазоне длин волн $2000 < \lambda < 3200\,\,{\AA}$

является источником метастабильных компонентов $O({}^{1}D),$ ${{O}_{2}}(a{}^{1}{{\Delta }_{g}}),$ ${{O}_{2}}\left( {b{}^{1}\Sigma _{g}^{ + }} \right),$ которые в связи с большим радиативным временем жизни (110 с, 12 с, 2.7 $ \times $ 10³ с) соответственно, способны испытать большое число соударений, прежде чем произойдет высвечивание энергии возбуждения (см. Мак-Ивен, Филипс, 1978): (${{А}_{{{{O}_{2}}(a),{{O}_{2}}(x)}}}$ = $3.7 \times {{10}^{{ - 4}}}\,\,{{{\text{c}}}^{{ - 1}}},$ инфракрасные атмосферные); (${\text{K}}_{{{{O}_{2}}(b)j}}^{{{{O}_{2}}(x)j}} = 2.0 \times {{10}^{{ - 14}}},$ $2.4 \times {{10}^{{ - 18}}},$ $ \leqslant 3 \times {{10}^{{ - 21}}},$ $ \leqslant 1.3 \times {{10}^{{ - 16}}}$ см³/с для ${{O}_{3}}{\text{,}}$ ${{O}_{2}},$$\;{{{\text{N}}}_{2}}$ и $O$ соответственно); (${\text{K}}_{{O(D),{{O}_{3}}}}^{{{{O}_{2}}(b),O(x)}}$ = $3 \times {{10}^{{ - 10}}}\,\,{{{\text{с}}{{{\text{м}}}^{{\text{3}}}}} \mathord{\left/ {\vphantom {{{\text{с}}{{{\text{м}}}^{{\text{3}}}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$).

Можно показать, что функция нагревания (47) озоносферы, с учетом комплекса реакций (48)–(53), в которых в качестве дезактивирующей частицы выступает озон, и реакций фотодиссоциации озона (60)–(63), принимает вид:

где введены обозначения Здесь ${{D}_{{{{O}_{3}}}}}$ − энергия диссоциации озона; ${{W}_{{1\Delta }}}$ (=0.98 эВ) − энергия возбуждения уровня $a{}^{1}{{\Delta }_{g}}$ молекулы ${{O}_{2}}.$

Приведенная здесь процедура легко применяется для оценки функции нагревания ионосферы солнечным ионизирующим излучением с учетом дополнительной ионизации, вызванной быстрыми фотоэлектронами.

ЗАКЛЮЧЕНИЕ

В работе развит подход, позволяющий корректно учитывать вклад в энергетический баланс газовых оболочек планет многоканального комплекса аэрономических реакций, обусловленных прямым поглощением жесткого солнечного излучения. Этот подход разработан с использованием системы обобщенных кинетических уравнений Больцмана для многокомпонентных смесей многоатомных газов умеренной плотности с учетом излучения и химических реакций в интегралах столкновений. На этой основе получены полумакроскопические уравнения радиационной многокомпонентной гидродинамики, пригодные для моделирования верхней атмосферы планеты, дополненные замыкающими соотношениями для термодинамических потоков, а также уравнениями химической кинетики для заселенностей энергетических уровней атмосферных частиц. Это позволяет, в частности, детально проанализировать источники нагрева и охлаждения атмосферных газов, как за счет столкновительных, так и радиативных процессов, вызванных солнечным ультрафиолетовым излучением, и конструировать так называемую функцию нагревания в уравнении энергетического баланса нижней термосферы и мезосферы в верхней атмосфере Земли.

Работа выполнена при поддержке гранта Минобрнауки России “Теоретические и экспериментальные исследования формирования и эволюции внесолнечных планетных систем и характеристик экзопланет”.