Астрономический вестник, 2021, T. 55, № 1, стр. 50-64

Динамика вращения внутренних спутников Юпитера

В. В. Пашкевич^a, *, А. Н. Вершков^a, А. В. Мельников^a

^a Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия

Поступила в редакцию 03.03.2020
После доработки 04.09.2020
Принята к публикации 08.09.2020

DOI: 10.31857/S0320930X20330038

Аннотация

В данной работе рассмотрены устойчивость синхронного вращения и наиболее существенные релятивистские эффекты во вращательной динамике внутренних спутников Юпитера – Метиды (J16), Адрастеи (J15), Амальтеи (J5) и Фивы (J14). Установлено, что плоское синхронное вращение всех внутренних спутников Юпитера для наиболее вероятных значений параметров их фигур является устойчивым относительно наклона оси вращения. Впервые определены наиболее существенные вековые, периодические и смешанные члены геодезического вращения внутренних спутников Юпитера в углах Эйлера относительно их собственных систем координат и в углах их вращения относительно неподвижного экватора Земли и точки весеннего равноденствия (на эпоху J2000.0). Показано, что в Солнечной системе есть объекты с существенным геодезическим вращением, обусловленным в первую очередь их близостью к возмущающему центральному телу, а не его массой. В частности, величина геодезической прецессии внутренних спутников Юпитера (для которых Юпитер является менее массивным возмущающим центральным телом, чем Солнце) в 10⁵ раз больше, чем у Юпитера вращающегося вокруг своего более массивного центрального тела (Солнца), и сопоставима с их прецессией в ньютоновом приближении.

Ключевые слова: спутники Юпитера, Амальтея, Фива, Адрастея, Метида, вращательная динамика, релятивистское вращение, геодезическая прецессия, геодезическая нутация

ВВЕДЕНИЕ

К внутренним спутника Юпитера (группа Амальтеи) относят Амальтею (Amalthea) (J5), Фиву (Thebe) (J14), Адрастею (Adrastea) (J15) и Метиду (Metis) (J16). Первый из этой группы спутников – Амальтея был открыт в 1892 г. Эдвардом Барнардом (Barnard, 1892) посредством визуальных наблюдений. В 1979 г. межпланетным космическим аппаратом (КА) Voyager-1 были получены первые детальные изображения Амальтеи, позволившие установить (Smith и др., 1979a), что она обладает весьма вытянутой (иррегулярной) формой и находится в режиме синхронного вращения. Три других малых внутренних спутника Юпитера были открыты в том же году из анализа изображений, полученных КА Voyager-2 (Smith и др., 1979b). Позднее Thomas и др. (1998) на основе изображений Метиды, Амальтеи и Фивы, полученных в 1997 г. КА Galileo, определили форму, цвет и отражающие свойства поверхностей указанных спутников и установили, что все спутники находятся в синхронном режиме вращения. В случае Адрастеи были получены только оценки ее размеров (средний радиус фигуры R ≈ 8.2 км). Наблюдения Метиды и Адрастеи, выполненные КА Cassini в 2000–2001 гг., позволили уточнить параметры их орбит (Porco и др., 2003).

Теоретические исследования показывают (см., например, Goldreich, Peale, 1966; Peale, 1977; 1999), что наиболее вероятным финальным режимом долговременной приливной эволюции вращательного движения спутника является его синхронное с движением по орбите вращение. В этом финальном режиме ось вращения спутника совпадает с наименьшей осью фигуры спутника (осью наибольшего момента инерции) и ортогональна плоскости орбиты, имеет место так называемое плоское вращение спутника. В случае плоского вращения спутника в точном синхронном спин-орбитальном резонансе наибольшая ось фигуры спутника в перицентре его орбиты параллельна радиус-вектору “центр масс спутника – планета”, а при движении по орбите ориентирована по направлению на планету, испытывая либрации (в частности, из-за эксцентричности орбиты, см., например, Белецкий, 1965).

В синхронном вращении находится подавляющее большинство спутников планет Солнечной системы, для которых режим вращения установлен из анализа наблюдений. Синхронный режим вращения Амальтеи был установлен Smith и др. (1979a) из анализа данных с КА Voyager-1, так же было отмечено, что наибольшая ось фигуры Амальтеи при ее движении по орбите ориентирована по направлению на Юпитер. Посредством анализа изображений, полученных с КА Galileo, Thomas и др. (1998) установили, что Метида, Амальтея и Фива находятся в режиме плоского синхронного вращения. Наибольшая ось фигуры каждого из перечисленных спутников (фигуры спутников аппроксимировались трехосными эллипсоидами с однородной плотностью) направлена на Юпитер, и ее ориентация испытывает либрации с амплитудой, не превышающей пяти градусов дуги. Низкое разрешение изображений, полученных КА Galileo, не позволило сделать вывод о режиме вращения Адрастеи. Однако Thomas и др. (1998) полагают, что Адрастея захвачена в синхронный спин-орбитальный резонанс. На это указывает теоретическая оценка величины времени приливного замедления первоначально быстрого вращения спутника до синхронного (см. подробнее Peale, 1977; 1999). Согласно Peale (1999), времена приливного замедления для внутренних спутников Юпитера составляют несколько тыс. лет, т.е. все спутники завершили свою приливную вращательную эволюцию и должны быть захвачены в синхронный резонанс, если вращение в нем является устойчивым. Исследование устойчивости плоского синхронного вращения внутренних спутников Юпитера является важным по причине того, что во вращательной динамике этих спутников присутствуют различные возмущающие факторы. Например, наличие на поверхностях Амальтеи и Фивы кратеров значительных размеров (Thomas и др., 1998) указывает на имевшие место столкновения спутников с массивными объектами. Столкновение помимо воздействия на форму спутника может привести к изменениям его ориентации в пространстве и скорости вращения; находящийся в неустойчивом плоском синхронном вращении спутник может быть захвачен в другой спин-орбитальный резонанс, либо перейти в режим хаотического вращения (Wisdom, 1987).

Поскольку Юпитер является вторым наибольшим по массе объектом в Солнечной системе, следует ожидать, что он будет вызывать релятивистские возмущения в динамике близких к нему тел. Наиболее существенными релятивистскими эффектами во вращении небесных тел являются эффекты геодезической прецессии и нутации, вместе составляющие геодезическое вращение. Эффект геодезической прецессии, впервые рассмотренный в 1916 г. Виллемом де Ситтером (De Sitter W., 1916), представляет собой систематическое изменение направления оси вращения небесного тела в результате параллельного переноса вектора углового момента тела вдоль его орбиты в искривленном пространстве-времени. Эффект геодезической нутации, введенный в 1991 г. Тошио Фукушимой (Fukushima, 1991), заключается в периодическом изменении направления оси вращения небесного тела, которое возникает по той же причине, что и геодезическая прецессия.

Систематическое или вековое изменение может быть представлено в виде полинома по степеням времени:

$\Delta {{x}_{{\text{I}}}} = \sum\limits_{n = 0}^N {\Delta {{x}_{n}}{{t}^{n}}} ,$

где t – время; $\Delta {{x}_{n}}$ – коэффициенты вековых членов; N – степень аппроксимирующего полинома.

В небесной механике традиционно нутационное движение оси вращения тела называют периодическим, хотя оно может описываться как периодическими рядами Фурье, так и дополнительно к ним смешанными по времени рядами Пуассона (см., например, Вулард, 1963; Абалакин, 1979; Brumberg, Bretagnon, 2000). Данная статья не является исключением. В ней эффект геодезической нутации будет представлен в виде суммы периодических членов Фурье и смешанных по времени Пуассоновских членов (которые далее в статье будут называться “периодическими” и “смешанными” членами):

$\begin{gathered} \Delta {{x}_{{{\text{II}}}}} = \sum\limits_j {\sum\limits_{k = 0}^M {(\Delta {{x}_{{Cjk}}}\cos ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)} } + \\ + \,\,\Delta {{x}_{{Sjk}}}\sin ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)){{t}^{k}}, \\ \end{gathered} $

где t – время; индекс суммирования j определяет количество суммируемых членов; $\Delta {{x}_{{Sjk}}}$, $\Delta {{x}_{{Cjk}}}$ – коэффициенты периодических членов и смешанных по времени Пуассоновских членов; ${{\nu }_{{j0}}}$, ${{\nu }_{{j1}}}$ – фазы и частоты исследуемого тела; M – параметр аппроксимации.

Отметим, что в данной статье под термином “величина геодезической прецессии” понимается, где это не отмечено особо, значение ее скорости.

Теоретические оценки величины геодезической прецессии двух спутников Юпитера – Ио (Io) (J1) и Метиды (Metis) (J16) были получены в работе Biscani и Carloni (2015). Рассматривалась упрощенная модель вращения спутников, а именно предполагалось, что спутники являются однородными сферами, а плоскости отсчета были выбраны перпендикулярно оси вращения планеты. В работе Melnikov и др. (2019) рассматривалась динамика вращения ряда малых спутников планет Солнечной системы, с установленными параметрами вращения. В частности, было установлено, что величина геодезической прецессии одного из ближайших спутников Юпитера – Амальтеи в 50 раз превосходит величину геодезической прецессии Меркурия. Согласно (Пашкевич, 2016) у Меркурия самая большая величина геодезической прецессии среди планет Солнечной системы, как ближайшей к Солнцу (самому массивному телу Солнечной системы) планеты. Таким образом, необходимо более подробное исследование релятивистских эффектов во вращении ближайших спутников Юпитера группы Амальтеи.

Целями данного исследования являлись изучение характера устойчивости синхронного вращения и определение наиболее существенных вековых и периодических членов геодезического вращения внутренних спутников Юпитера: Метиды, Адрастеи, Амальтеи и Фивы (спутники перечислены в порядке возрастания расстояния от Юпитера). Для исследования устойчивости вращения спутников использовались методы, разработанные Мельниковым и Шевченко (2000; 2007). Вычисления вековых и периодических членов геодезического вращения спутников производились с помощью метода для изучения геодезического вращения любых тел Солнечной системы (Пашкевич, 2016), имеющих долгосрочные эфемериды.

УСТОЙЧИВОСТЬ ПЛОСКОГО СИНХРОННОГО ВРАЩЕНИЯ

Динамика плоского (в плоскости орбиты) вращательного движения спутника в гравитационном поле планеты может быть описана в рамках модели возмущенного математического маятника. Далее предполагаем, что ось вращения спутника совпадает с наименьшей осью фигуры спутника и ортогональна плоскости орбиты. Определим угол φ, как угол между линией апсид и наибольшей осью фигуры спутника, тогда угол φ – f, где f – истинная аномалия, будет представлять собой угол между наибольшей осью фигуры спутника и направлением на планету. Уравнение плоского поступательно-вращательного движения спутника имеет вид (Goldreich, Peale, 1966; Wisdom, 1987):

(1)

$\frac{{{{d}^{2}}\varphi }}{{d{{t}^{2}}}} + \frac{{\omega _{0}^{2}}}{{2{{r}^{3}}}}\sin 2(\varphi - f) = 0,$

где параметр ${{\omega }_{0}} = \sqrt {3({{a}^{2}} - {{{{b}^{2}})} \mathord{\left/ {\vphantom {{{{b}^{2}})} {({{a}^{2}} + {{b}^{2}})}}} \right. \kern-0em} {({{a}^{2}} + {{b}^{2}})}}} $, характеризует асимметрию фигуры спутника, a > b > c – главные оси инерции трехосного эллипсоида с однородной плотностью, аппроксимирующего фигуру спутника; $r = {{a}_{{\text{s}}}}(1 - {{{{e}^{2}})} \mathord{\left/ {\vphantom {{{{e}^{2}})} {(1 + e\cos f)}}} \right. \kern-0em} {(1 + e\cos f)}}$ – расстояние “спутник–планета”, e – эксцентриситет орбиты спутника, a_s– большая полуось орбиты спутника. Согласно (1), динамика плоского вращательного движения спутника определяется величиной эксцентриситета орбиты e и значением параметра ω₀. Далее полагаем a_s = 1 и GM = 1, где G – универсальная гравитационная постоянная; M – масса планеты. Таким образом, один орбитальный период спутника соответствует 2π единицам времени.

При определенных значениях e и ω₀ уравнение плоского вращательного движения спутника имеет два устойчивых нечетных 2π-периодических решения (Торжевский и др., 1964) – в фазовом пространстве плоского вращательного движения спутника существует две моды синхронного резонанса. Одно из решений соответствует синхронному α-резонансу, другое – синхронному β-резонансу. Указанная терминология принята в (Мельников, Шевченко, 2000; 2007).

Проведенное Мельниковым и Шевченко (2000; 2007) исследование вращательной динамики малых спутников планет Солнечной системы показало, что несколько мод синхронного резонанса одновременно существуют в фазовом пространстве плоского вращательного движения ряда спутников, в частности, в случае Амальтеи. В ходе приливной эволюции вращательного движения Амальтея может быть захвачена в одну из мод синхронного резонанса, если плоское вращение в ней является устойчивым по Ляпунову относительно наклона оси вращения спутника к плоскости орбиты. В случае если плоское синхронное вращение спутника является неустойчивым, при наличии возмущений (например, столкновения/тесные сближения с другими телами), приводящих к смещению оси вращения от нормали, спутник может перейти в режим хаотического “кувыркания” (Wisdom, 1987). Исследование устойчивости вращательной динамики Амальтеи показало (Мельников, Шевченко, 2000), что синхронный α-резонанс является неустойчивым, а синхронный β-резонанс – устойчивым, т.е. в настоящее время Амальтея захвачена в синхронный β-резонанс. Это подтверждает малая (<5°) амплитуда наблюдаемых либраций (Thomas и др., 1998) ориентации наибольшей оси фигуры Амальтеи относительно направления на Юпитер при ее движении по орбите. В случае нахождения Амальтеи в синхронном α-резонансе амплитуда либраций могла бы достигать 30°.

В случаях Метиды и Фивы амплитуды наблюдаемых либраций (Thomas и др., 1998) также малы, а их периоды совпадают с периодами орбитального движения спутников. Выявить наличие либраций ориентации фигуры в случае Адрастеи не позволило низкое разрешение изображений, полученных КА Galileo. Отметим, что определение амплитуды либраций посредством анализа наблюдательных данных, получаемых с межпланетных космических аппаратов, позволяет уточнить динамические параметры спутников, в частности, значения моментов инерции (см., например, Tiscareno и др., 2009).

Далее рассмотрим устойчивость плоского синхронного вращения в случаях Метиды, Адрастеи и Фивы. Для исследования устойчивости вращательного движения спутников используем методы и алгоритмы, разработанные Мельниковым и Шевченко (2000; 2007).

В табл. 1 приведены значения орбитальных и физических параметров внутренних спутников Юпитера, использовавшиеся при анализе устойчивости. Согласно (Мельников, Шевченко, 2007), для значений параметров, представленных в табл. 1, в случаях Адрастеи и Фивы существует только синхронный α-резонанс, в случае Метиды и Амальтеи существуют синхронный α-резонанс и синхронный β-резонанс.

Таблица 1.

Орбитальные и физические параметры внутренних спутников Юпитера. Данные взяты из Burns и др. (2003), Thomas и др. (1998) и Porco и др. (2003)

	Метида (J16)	Адрастея (J15)	Амальтея (J5)	Фива (J14)
a_s, км	128 000	129 000	181 400	221 900
e	0.0002	0.0015	0.0031	0.0177
a × b × c, км	30 × 20 × 17	10 × 8 × 7	125 × 73 × 64	58 × 49 × 42
ω₀	1.0742	0.8115	1.2141	0.7079

Посредством численного интегрирования дифференциальных уравнений, описывающих пространственное вращение спутника (см. подробнее Мельников, Шевченко, 2000; 2007), и вычисления характеристических показателей Ляпунова (ХПЛ) для множества всех возможных значений параметров фигур спутников (c/b, b/a) и фиксированной величины e, был проведен анализ устойчивости по Ляпунову плоского синхронного вращения для случаев Метиды, Адрастеи и Фивы.

ХПЛ представляют собой среднюю скорость экспоненциальной расходимости близких (по начальным условиям) траекторий фазового пространства динамической системы (подробнее о ХПЛ см., например, Лихтенберг, Либерман, 1984). Гамильтонова система с N степенями свободы имеет 2N показателей Ляпунова: L_i ≥ L_{i +} ₁, i = 1, …, 2N – 1, образующие симметричные пары: L_j = –L_j ₊_N, j = 1, …, N. Ненулевая величина максимального ХПЛ – L₁ указывает на хаотический (неустойчивый), а нулевая – на регулярный (устойчивый) характер движения.

ХПЛ вычислялись для траекторий фазового пространства соответствующих вращению спутника в точном синхронном резонансе. Сначала для избранного значения e, на сечении фазового пространства (φ, dφ/dt), определенном в перицентре орбиты спутника (см. примеры сечений для различных спутников в работах Wisdom (1987), Shevchenko (1999), Мельников и Шевченко (2000; 2007), Melnikov и Shevchenko (2008)), определялись координаты центра синхронного резонанса (отдельно для α-резонанса и β-резонанса) в плоской задаче на множестве значений параметра b/a ∈ (0, 1]. При плоском вращении спутника с однородной плотностью эти координаты определяются только ${{\omega }_{0}} = \sqrt {3(1 - {{{{{({b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a})}}^{2}})} \mathord{\left/ {\vphantom {{{{{({b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a})}}^{2}})} {{{{(1 + {b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a})}}^{2}})}}} \right. \kern-0em} {{{{(1 + {b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a})}}^{2}})}}} $ и e. Затем вычислялись ХПЛ для разных значений параметров c/b ∈ (0, 1] и b/a ∈ (0, 1] на сетке с высоким разрешением. Шаг сетки на плоскости (c/b, b/a), в узлах которой вычислялись ХПЛ, был положен равным 0.001 по обеим осям. Вычисление всего спектра ХПЛ (в нашем случае N = 3, т.е. имеется шесть ХПЛ) проводилось на промежутке времени интегрирования 10⁶ орбитальных периодов посредством алгоритма, представленного в работе Kouprianov и Shevchenko (2003). На основе анализа вычисленных значений максимального ХПЛ (L₁) на плоскостях (c/b, b/a) определялись границы устойчивой (максимальный ХПЛ равен нулю) и неустойчивой динамики (максимальный ХПЛ больше нуля) вращательного движения спутника в точном синхронном резонансе.

Построенные таким образом для всех спутников диаграммы устойчивости представлены на рис. 1 и 2 . Анализ диаграмм устойчивости Адрастеи и Фивы, показал, что для наиболее вероятных параметров их фигур вращение обоих спутников в единственном возможном для них синхронном α-резонансе является устойчивым. На диаграммах устойчивости (см. рис. 1) Адрастея и Фива расположены далеко от областей с неустойчивой динамикой. Согласно рис. 2, для наиболее вероятных параметров фигуры Метиды ее вращение в синхронном α-резонансе является неустойчивым (на диаграмме устойчивости Метида расположена в области с неустойчивой динамикой), а синхронном β-резонансе – устойчивым.

Рис. 1.

Области устойчивости (светлый тон) и неустойчивости (темный тон) относительно наклона оси вращения спутника в центре синхронного α-резонанса: левая панель – e = 0.0015, ω₀ = 0.8115 (“Адрастея”); правая панель – e = 0.0177, ω₀ = 0.71079 (“Фива”). Положения спутников указаны точками с барами ошибок. Штриховые горизонтальные линии соответствуют приведенным справа значениям ω₀.

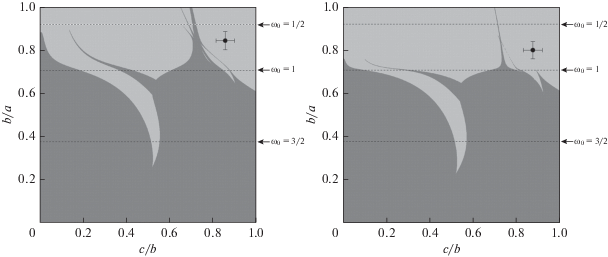
Рис. 2.

Области устойчивости (светлый тон) и неустойчивости (темный тон) относительно наклона оси вращения спутника в центре синхронного α-резонанса (слева) и синхронного β-резонанса (справа), e = 0.0002, ω₀ = 1.1717 (“Метида”). В белой области синхронный β-резонанс не существует. Положение Метиды (J16) указано точкой с барами ошибок. Штриховые горизонтальные линии соответствуют приведенным справа значениям ω₀.

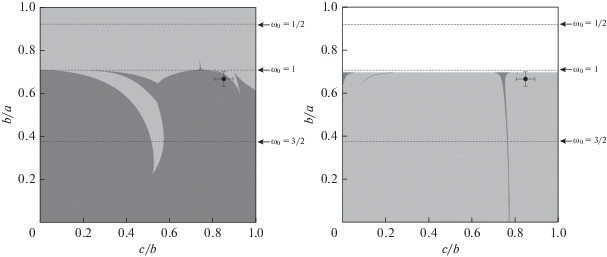
Таким образом, мы установили, что плоское синхронное вращение всех внутренних спутников Юпитера является устойчивым относительно наклона оси вращения к плоскости орбиты. Возмущения во вращательной динамике рассмотренных спутников, такие как столкновение/тесное сближение с другими телами и последующее несущественное изменение формы спутника (величины ω₀), либо величины и направления его вектора угловой скорости вращения, не приведут к выходу спутника из режима плоского синхронного вращения. Далее рассмотрим релятивистские эффекты во вращательной динамике внутренних спутников Юпитера.

РЕЛЯТИВИСТСКИЕ ЭФФЕКТЫ ВО ВРАЩЕНИИ СПУТНИКОВ

Изучение эффектов геодезического вращения внутренних спутников Юпитера производилось относительно кинематически невращающейся собственной координатной системы исследуемых тел (Kopeikin и др., 2011; Archinal и др., 2018). Положения, скорости и орбитальные элементы спутников брались из Horizons On-Line Ephemeris System (Giorgini и др., 2001) на всех интервалах времени существования эфемерид. В табл. 2 дана информация о шаге и интервале времени проводимых исследований. Для Солнца, больших планет, Луны и Плутона положения и скорости вычислялись с помощью фундаментальной эфемериды JPL DE431/LE431 (Folkner и др., 2014).

Таблица 2.

Интервал времени и шаг проводимых исследований

Спутник	Интервал времени производимых исследований	Шаг
Метида	400 лет (от AD1799 19 декабря до AD2200 13 января)	42 мин
Адрастея	400 лет (от AD1799 19 декабря до AD2200 13 января)	42 мин
Амальтея	1000 лет (от AD1600 07 февраля до AD2599 06 декабря)	60 мин
Фива	400 лет (от AD1799 19 декабря до AD2200 13 января)	90 мин

Вычисление скоростей геодезического вращения внутренних спутников Юпитера проводилось:

а) в углах вращения спутников $({{\alpha }_{0}},{{\delta }_{0}},W)$ относительно неподвижного экватора Земли эпохи J2000.0, определенного в международной системе координат (ICRF) (Ma и др., 1998), и точки весеннего равноденствия эпохи J2000.0;

б) в углах Эйлера (ψ, θ, φ) относительно систем координат этих спутников (Archinal и др., 2018), начало которых совпадает с их центрами масс.

Вид вектора угловой скорости геодезического вращения для любых тел Солнечной системы определяется следующей формулой (Eroshkin, Pashkevich, 2007; Pashkevich, Eroshkin, 2018):

(2)

${{\bar {\sigma }}_{i}} = \frac{1}{{{{c}^{2}}}}\sum\limits_{j \ne i} {\frac{{G{{m}_{j}}}}{{{{{\left| {{{{\bar {R}}}_{i}} - {{{\bar {R}}}_{j}}} \right|}}^{3}}}}} \left( {{{{\bar {R}}}_{i}} - {{{\bar {R}}}_{j}}} \right) \times \left( {\frac{3}{2}{{{\dot {\bar {R}}}}_{i}} - 2{{{\dot {\bar {R}}}}_{j}}} \right).$

Здесь c – скорость света в вакууме; G – гравитационная постоянная; индекс i соответствует исследуемым телам (внутренним спутникам Юпитера), а j – возмущающим телам; ${{\bar {R}}_{i}},{{\dot {\bar {R}}}_{i}},{{\bar {R}}_{j}},{{\dot {\bar {R}}}_{j}}$ – барицентрические векторы положений и скоростей i‑го и j-го тела, соответственно; m_j – масса j-го тела; символ × означает векторное произведение. Далее в формулах индекс i опущен. Как видно из формулы (2), величина вектора геодезического вращения спутника $\left| {\bar {\sigma }} \right| \sim \frac{M}{{{{r}^{{2.5}}}}}$, где ${{m}_{{j = M}}} = M$ – масса центрального тела (Юпитера), а $\left| {{{{\bar {R}}}_{i}} - {{{\bar {R}}}_{{j = M}}}} \right| = r$ – расстояние до него, т.е. существенным образом зависит от близости спутника к центральному телу. В частности, из формулы (2) следует, что геодезическое вращение тела зависит только от масс возмущающих тел и от расстояния до них, и не зависит от массы самого тела.

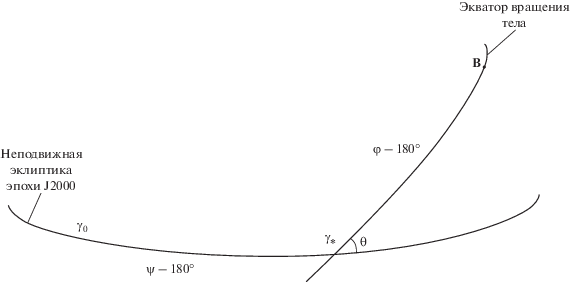
Скорости геодезического вращения внутренних спутников Юпитера определяются в углах Эйлера следующим образом (Пашкевич, Вершков, 2019):

(3)

$\left. \begin{gathered} \Delta \dot {\psi } = - \frac{{{{\sigma }_{1}}\sin \varphi + {{\sigma }_{2}}\cos \varphi }}{{\sin \theta }} \hfill \\ \Delta \dot {\theta } = - {{\sigma }_{1}}\cos \varphi + {{\sigma }_{2}}\sin \varphi \hfill \\ \Delta \dot {\varphi } = {{\sigma }_{3}} - \Delta \dot {\psi }\cos \theta \hfill \\ \end{gathered} \right\}.$

Здесь ψ – угол долготы нисходящего узла экватора тела на эклиптике эпохи J2000.0; θ – угол наклона экватора тела к неподвижной эклиптике эпохи J2000.0; φ – угол собственного вращения тела между нисходящим узлом эпохи J2000.0 и главной осью минимального момента инерции тела, проходящей через точку В, на экваторе вращения тела (рис. 3); $\Delta \dot {\psi } = {{\dot {\psi }}_{{\text{r}}}} - \dot {\psi },$ $\Delta \dot {\theta } = {{\dot {\theta }}_{{\text{r}}}} - \dot {\theta }$ и $\Delta \dot {\varphi } = {{\dot {\varphi }}_{{\text{r}}}} - \dot {\varphi }$ – разности релятивистских и ньютоновых углов Эйлера исследуемого тела, соответственно; точка означает дифференцирование по времени; σ₁, σ₂, σ₃– редуцированные (Пашкевич, 2016) компоненты вектора угловой скорости (2) геодезического вращения внутренних спутников Юпитера от геоцентрической системы координат (координатная система эфемериды DE431/LE431) к планетоцентрической координатной системе (Archinal и др., 2018).

Рис. 3.

Углы Эйлера (ψ, θ, φ), определяющие вращение тел Солнечной системы.

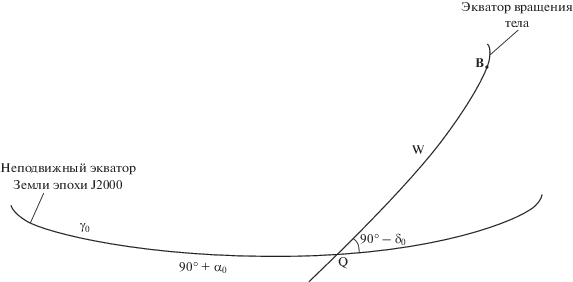
Представленная на рис. 4 конфигурация расположения углов вращения тел Солнечной системы (α₀, δ₀, W) аналогична конфигурации для углов Эйлера (см. рис. 3). Здесь α₀– прямое восхождение северного полюса вращения тела; δ₀– склонение северного полюса вращения тела; W = QB – угловое расстояние нулевого меридиана тела, отсчитываемое по экватору тела от неподвижного экватора Земли эпохи J2000.0. Посредством замены углов Эйлера на соответствующие углы вращения спутников (ψ → 270° + α₀, θ → 90° – δ₀, φ → 180° + W) из выражений (3) получаются выражения для скоростей геодезического вращения внутренних спутников Юпитера в углах их вращения:

(4)

$\left. \begin{gathered} \Delta {{{\dot {\alpha }}}_{0}} = \frac{{{{\sigma }_{1}}\sin {\text{W}} + {{\sigma }_{2}}\cos {\text{W}}}}{{\cos {{\delta }_{0}}}} \hfill \\ \Delta {{{\dot {\delta }}}_{0}} = - {{\sigma }_{1}}\cos {\text{W}} + {{\sigma }_{2}}\sin {\text{W}} \hfill \\ \Delta {\dot {W}} = {{\sigma }_{3}} - \Delta \dot {\alpha }\sin {{\delta }_{0}} \hfill \\ \end{gathered} \right\},$

где $\Delta {{\dot {\alpha }}_{0}} = {{\dot {\alpha }}_{{0{\text{r}}}}} - {{\dot {\alpha }}_{0}},$ $\Delta {{\dot {\delta }}_{0}} = {{\dot {\delta }}_{{0{\text{r}}}}} - {{\dot {\delta }}_{0}},$ и $\Delta {\dot {W}} = {{{\dot {W}}}_{{\text{r}}}} - {\dot {W}}$ – разности релятивистских и ньютоновых скоростей вращения исследуемого тела, соответственно; точка означает дифференцирование по времени.

Рис. 4.

Углы вращения тел Солнечной системы (α₀, δ₀, W).

Наиболее существенные составляющие скорости геодезического вращения исследуемого тела находились методами наименьших квадратов и спектрального анализа (Пашкевич, 2016). В результате вычисляются значения коэффициентов основных вековых, периодических и смешанных членов скорости геодезического вращения тела. Выражения, описывающие скорость геодезического вращения тела, представляются в следующем виде:

(5)

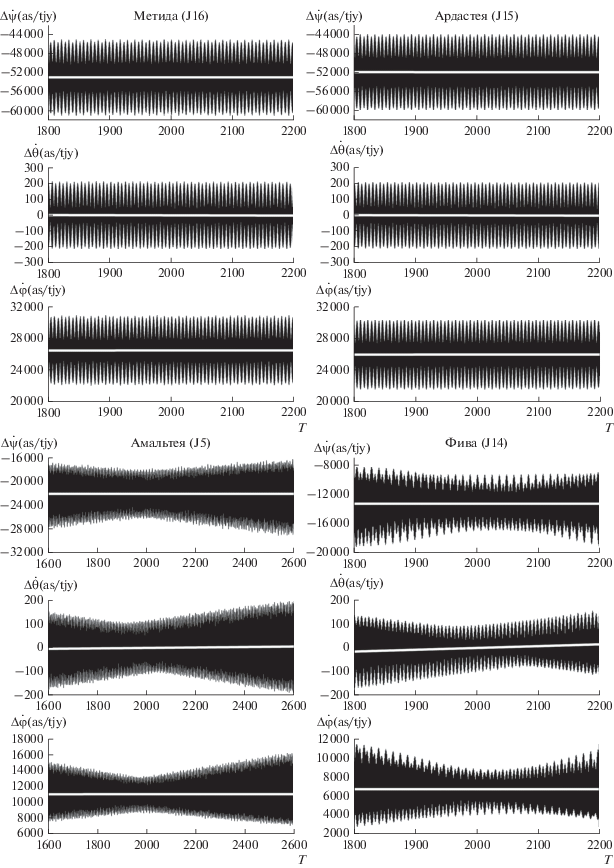
$\begin{gathered} \Delta \dot {x} = \Delta {{{\dot {x}}}_{{\text{I}}}} + \Delta {{{\dot {x}}}_{{{\text{II}}}}} = \sum\limits_{n = 1}^N {\Delta {{{\dot {x}}}_{n}}{{t}^{{n - 1}}}} + \\ + \,\,\sum\limits_j {\sum\limits_{k = 0}^M {(\Delta {{{\dot {x}}}_{{Cjk}}}\cos ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)} } + \\ + \,\,\Delta {{{\dot {x}}}_{{Sjk}}}\sin ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)){{t}^{k}}, \\ \end{gathered} $

где $\Delta {{\dot {x}}_{n}}$ – коэффициенты вековых членов; $\Delta {{\dot {x}}_{{Sjk}}}$, $\Delta {{\dot {x}}_{{Cjk}}}$ – коэффициенты периодических членов и смешанных членов; $\dot {x} = \dot {\psi },\dot {\theta },\dot {\varphi },{{\dot {\alpha }}_{0}},{{\dot {\delta }}_{0}},{\dot {W}}$; ${{\nu }_{{j0}}},{{\nu }_{{j1}}}$ – фазы и частоты исследуемого тела, являющиеся комбинациями соответствующих аргументов Делоне и средних долгот возмущающих тел; индекс суммирования j определяет количество суммируемых периодических членов и его значение изменяется для каждого исследуемого тела; t – время в юлианских днях; N и M – параметры аппроксимации.

На рис. 5 представлена вычисленная скорость геодезического вращения внутренних спутников Юпитера в углах Эйлера. Белая линия на графиках показывает вековой ход.

Рис. 5.

Скорость геодезического вращения внутренних спутников Юпитера в углах Эйлера (Т время в юлианских годах). Белая линия показывает вековой ход.

После аналитического интегрирования выражения (5) вычисляются вековые члены, периодические и смешанные члены геодезического вращения тела:

(6)

$\begin{gathered} \Delta x = \Delta {{x}_{{\text{I}}}} + \Delta {{x}_{{{\text{II}}}}} = \sum\limits_{n = 1}^N {\Delta {{x}_{n}}{{t}^{n}}} + \\ + \,\,\sum\limits_j {\sum\limits_{k = 0}^M {(\Delta {{x}_{{Cjk}}}\cos ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)} } + \\ + \,\,\Delta {{x}_{{Sjk}}}\sin ({{\nu }_{{j0}}} + {{\nu }_{{j1}}}t)){{t}^{k}}, \\ \end{gathered} $

где $\Delta {{x}_{n}} = \frac{{\Delta {{{\dot {x}}}_{n}}}}{n},$ $x = \psi ,\theta ,\varphi ,{{\alpha }_{0}},{{\delta }_{0}},{\text{W}},$ а коэффициенты при синусах и косинусах вычисляются следующим образом:

(7)

$\begin{gathered} \Delta {{x}_{{SjM}}} = \frac{{\Delta {{{\dot {x}}}_{{CjM}}}}}{{{{\nu }_{{j1}}}}},\,\,\,\,\Delta {{x}_{{CjM}}} = \frac{{ - \Delta {{{\dot {x}}}_{{SjM}}}}}{{{{\nu }_{{j1}}}}}, \\ \Delta {{x}_{{SjM - 1}}} = \frac{{\Delta {{{\dot {x}}}_{{CjM - 1}}} - m\Delta {{x}_{{CjM}}}}}{{{{\nu }_{{j1}}}}}, \\ \Delta {{x}_{{CjM - 1}}} = \frac{{m\Delta {{x}_{{SjM}}} - \Delta {{{\dot {x}}}_{{SjM - 1}}}}}{{{{\nu }_{{j1}}}}}, \\ ... \\ \Delta {{x}_{{Sj1}}} = \frac{{\Delta {{{\dot {x}}}_{{Cj1}}} - 2\Delta {{x}_{{Cj2}}}}}{{{{\nu }_{{j1}}}}},\,\,\,\,\Delta {{x}_{{Cj1}}} = \frac{{2\Delta {{x}_{{Sj2}}} - \Delta {{{\dot {x}}}_{{Sj1}}}}}{{{{\nu }_{{j1}}}}}, \\ \Delta {{x}_{{Sj0}}} = \frac{{\Delta {{{\dot {x}}}_{{Cj0}}} - \Delta {{x}_{{Cj1}}}}}{{{{\nu }_{{j1}}}}},\,\,\,\,\Delta {{x}_{{Cj0}}} = \frac{{\Delta {{x}_{{Sj1}}} - \Delta {{{\dot {x}}}_{{Sj0}}}}}{{{{\nu }_{{j1}}}}}. \\ \end{gathered} $

В результате исследований методом наименьших квадратов были определены значения величин N = 2 и M = 1, обеспечивающие наилучшую аппроксимацию параметров геодезического вращения.

В табл. 3–5 представлены вычисленные значения вековых (табл. 3 и 5 ), периодических и смешанных (табл. 4, 5 ) членов геодезического вращения внутренних спутников Юпитера. В табл. 3 и 4 : t – Динамическое Барицентрическое Время (Dynamical Barycentric Time) (TDB) измеряется в юлианских тысячелетиях (tjy) (365 250 суток) от эпохи J2000.

Таблица 3.

Вековые члены геодезического вращения Юпитера (Pashkevich, Vershkov, 2019) и его внутренних спутников, вычисленные для углов Эйлера

	Метида (J16)	Адрастея (J15)	Амальтея (J5)	Фива (J14)	Юпитер (J)
	Δψ_I ('')	Δψ_I ('')	Δψ_I ('')	Δψ_I ('')	Δψ_I ('')
t	– 52 957.2516	–51 932.8456	–22 118.2274	–13 372.5500	–0.2130
t²	– 20.0929	– 19.7509	–0.7460	–2.8287	0.0035
	Δθ_I ('')	Δθ_I ('')	Δθ_I ('')	Δθ_I ('')	Δθ_I ('')
t	– 0.4232	– 0.4151	–0.0923	–2.4703	–0.0060
t²	– 3.9838	– 3.9067	4.7351	37.7619	0.0001
	Δφ_I ('')	Δφ_I ('')	Δφ_I ('')	Δφ_I ('')	Δφ_I ('')
t	26 460.9380	25 949.0709	11 055.1784	6693.8317	–0.0987
t²	19.8858	19.5347	0.5755	2.8902	–0.0036

Таблица 4.

Периодические и смешанные члены геодезического вращения внутренних спутников Юпитера, вычисленные для углов Эйлера

Название тела	Угол	Период	Аргумент	Коэффициент при sin(Аргумент) ('' × 10^–6)	Коэффициент при cos(Аргумент) ('' × 10^–6)
Метида (J16)	Δψ_II	7.0752 ч	λ₅₁₆– λ₅	–491.02 + 66.84t	406.71 + 77.88t
	Δψ_II	7.0742 ч	λ₅₁₆+ λ₅	36.97 + 70.96t	326.50 – 3.60t
	Δθ_II	7.0752 ч	λ₅₁₆– λ₅	–12.11 – 0.68t	–4.19 + 1.84t
	Δθ_II	7.0742 ч	λ₅₁₆+ λ₅	12.68 – 0.25t	–1.43 – 2.68t
	Δφ_II	7.0752 ч	λ₅₁₆– λ₅	191.16 – 11.21t	–46.80 – 30.55t
	Δφ_II	7.0742 ч	λ₅₁₆+ λ₅	–36.99 – 70.18t	–326.96 + 3.90t
Адрастея (J15)	Δψ_II	7.1587 ч	λ₅₁₅– λ₅	–619.25 + 144.03t	–96.70 – 880.88t
	Δψ_II	7.1578 ч	λ₅₁₅+ λ₅	–216.77 – 332.46t	240.02 – 294.02t
	Δθ_II	7.1587 ч	λ₅₁₅– λ₅	–4.80 + 16.84t	–11.64 – 7.06t
	Δθ_II	7.1578 ч	λ₅₁₅+ λ₅	9.32 – 11.54t	8.41 + 12.88t
	Δφ_II	7.1587 ч	λ₅₁₅– λ₅	159.02 – 163.79t	110.20 + 221.18t
	Δφ_II	7.1578 ч	λ₅₁₅+ λ₅	217.02 + 333.29t	–240.32 + 295.24t
Амальтея (J5)	Δψ_II	143.7475 сут	Ω_L55	14788.07 – 20766.41t	–8065.69 – 240278.07t
		71.8737 сут	2Ω_L55	–705.83 + 8528.53t	1110.30 + 17772.11t
		11.9577 ч	λ₅₅– λ₅	428.18 – 518.50t	221.47 + 672.87t
		11.9549 ч	λ₅₅+ λ₅	215.16 +138.37t	–118.79 + 403.48t
	Δθ_II	143.7475 сут	Ω_L55	290.56 + 9211.87t	585.78 – 792.88t
		71.8737 сут	2Ω_L55	–16.61 – 340.18t	–27.57 + 162.20t
		11.9577 ч	λ₅₅– λ₅	0.57 – 17.16t	9.58 – 2.20t
		11.9549 ч	λ₅₅+ λ₅	–4.61 + 15.81t	–8.33 – 5.39t
	Δφ_II	143.7475 сут	Ω_L55	–14505.42 + 20809.18t	7964.79 + 240812.87t
		71.8737 сут	2Ω_L55	705.95 – 8528.58t	–1110.22 – 17772.10t
		11.9577 ч	λ₅₅– λ₅	–90.20 + 232.96t	–118.14 – 114.91t
		11.9549 ч	λ₅₅+ λ₅	–215.48 – 138.61t	118.75 – 404.03t
Фива (J14)	Δψ_II	291.3118 сут	Ω_L514	–20924.96 – 523207.02t	41738.74 – 1108462.06t
		145.6559 сут	2Ω_L514	871.19 + 180592.02t	–9582.70 + 175870.07t
		16.1914 ч	λ₅₁₄– λ₅	–463.338 + 113.40t	137.40 + 384.96t
		16.1863 ч	λ₅₁₄+ λ₅	–76.85 + 288.85t	205.30 + 55.46t
	Δθ_II	291.3118 сут	Ω_L514	–1560.60 + 39956.22t	–871.89 – 19067.79t
		145.6559 сут	2Ω_L514	170.03 – 3080.78t	11.00 + 3191.90t
		16.1914 ч	λ₅₁₄– λ₅	–7.24 – 3.94t	–6.81 + 4.93t
		16.1863 ч	λ₅₁₄+ λ₅	8.24 + 2.12t	2.76 – 9.20t
	Δφ_II	291.3118 сут	Ω_L514	21951.15 + 524366.28t	–42198.58 +1110937.40t
		145.6559 сут	2Ω_L514	–871.47 – 180591.77t	9582.78 – 175869.98t
		16.1914 ч	λ₅₁₄– λ₅	147.35 +19.52t	24.12 – 124.60t
		16.1863 ч	λ₅₁₄+ λ₅	77.02 – 288.66t	–205.62 – 55.10t

Таблица 5.

Углы вращения внутренних спутников Юпитера (α₀, δ₀, W) и их вековые, периодические и смешанные члены геодезического вращения

Метида (J16):	α₀ = 268.05 – 0.009T Δα₀ = 0.1241T – 0.00007T² – 8.590 × 10^–10 cos(J15) + 1.424 × 10^–9 sin(J15) – 2.068 × 10^–11T cos(J15) – 1.413 × 10^–11T sin(J15) – 7.330 × 10^–10 cos(J16) – 3.720 × 10^–10 sin(J16) + 8.023 × 10^–12T cos(J16) – 1.750 × 10^–11T sin(J16)
	δ₀ = 64.49 + 0.003T Δδ₀ = – 0.0199T – 0.00004 T ² + 2.620 × 10^–10 cos(J15) + 1.306 × 10^–10 sin(J15) – 1.233 × 10^–12T cos(J15) + 3.193 × 10^–12T sin(J15) + 1.600 × 10^–10 cos(J16) – 3.161 × 10^–10 sin(J16) + 7.374 × 10^–12T cos(J16) + 3.613 × 10^–12T sin(J16)
	W = 33.29 + 1206.9986602 d ΔW = – 0.0000232 d + 4×10^–14d ² + 1.076 × 10^–8 cos(J15) – 9.604 × 10^–9 sin(J15) + 1.500 × 10^–10T cos(J15) + 1.671 × 10^–10T sin(J15) + 6.420 × 10^–10 cos(J16) + 3.344 × 10^–10 sin(J16) – 6.380 × 10^–12T cos(J16) + 1.782 × 10^–11T sin(J16)
Адрастея (J15):	α₀ = 268.05 – 0.009T Δα₀ = 0.1217T – 0.00006T ² + 4.885 × 10^–10 cos(J13) + 1.559 × 10^–9 sin(J13) + 2.235 × 10^–10T cos(J13) – 7.292 × 10^–11T sin(J13) – 7.523 × 10^–10 cos(J14) + 2.984 × 10^–10 sin(J14) + 3.962 × 10^–11T cos(J14) + 1.021 × 10^–10T sin(J14)
	δ₀ = 64.49 + 0.003 T Δδ₀ = –0.0195 T – 0.00004 T ² + 2.665 × 10^–10 cos(J13) – 1.079 ×10^–10 sin(J13) – 1.513 × 10^–11T cos(J13) – 3.958 × 10^–11T sin(J13) – 1.288 × 10^–10 cos(J14) – 3.242 × 10^–10 sin(J14) – 4.402 × 10^–11T cos(J14) + 1.734 × 10^–11T sin(J14)
	W = 33.29 + 1206.9986602 d ΔW = –0.0000227 d + 4×10^–14d ² – 6.374 × 10^–11 cos(J13) – 1.418 × 10^–8 sin(J13) – 2.032 × 10^–9T cos(J13) + 1.056 × 10^–11T sin(J13) + 6.654 × 10^–10 cos(J14) – 2.579 × 10^–10 sin(J14) – 3.175 × 10^–11T cos(J14) – 8.922 × 10^–11T sin(J14)
Амальтея (J5):	α₀ = 268.05 – 0.009T – 0.84 sin(J1) + 0.01 sin(2 J1) Δα₀ = 0.0518T – 0.00003T ² – 1.091 × 10^–8 cos(J1) + 4.759 × 10^–7 sin(J1) + 5.759 × 10^–8T cos(J1) – 1.618 × 10^–8T sin(J1) + 1.424 × 10^–10 cos(2J1) – 2.774 × 10^–9 sin(2J1) – 3.866 × 10^–10T cos(2J1) + 1.040 × 10^–10T sin(2J1) – 7.333 × 10^–10 cos(J9) – 1.016 × 10^–9 sin(J9) – 1.531 × 10^–10T cos(J9) + 1.611 × 10^–10T sin(J9) + 4.740 × 10^–10 cos(J10) – 4.033 × 10^–10 sin(J10) – 8.403 × 10^–11T cos(J10) – 6.913 × 10^–11T sin(J10)
	δ₀ = 64.49 + 0.003T – 0.36 cos(J1) Δδ₀ = –0.0083T – 0.00002T ² +2.057 × 10^–7 cos(J1) – 1.972 × 10^–9 sin(J1) – 6.964 × 10^–9T cos(J1) – 2.489 × 10^–8T sin(J1) – 9.629 × 10^–10 cos(2J1) – 1.405 × 10^–11 sin(2J1) + 2.196 × 10^–11T cos(2J1) + 8.530 × 10^–11T sin(2J1) – 1.656 × 10^–10 cos(J9) + 1.449 × 10^–10 sin(J9) + 3.135 × 10^–11T cos(J9) + 2.542 × 10^–11T sin(J9) + 1.739 × 10^–10 cos(J10) + 2.039 × 10^–10 sin(J10) + 2.980 × 10^–11T cos(J10) – 3.628 × 10^–11T sin(J10)
	W = 231.67 + 722.6314560d + 0.76 sin(J1) – 0.01 sin(2 J1) ΔW = –0.0000097d + 2 × 10^–14d ² + 3.907 × 10^–9 cos(J1) – 4.044 × 10^–7 sin(J1) – 5.001 × 10^–8T cos(J1) + 1.474 × 10^–8T sin(J1) – 1.267 × 10^–10 cos(2J1) + 2.853 × 10^–9 sin(2J1) + 3.878 × 10^–10T cos(2J1) – 1.050 × 10^–10T sin(2J1) + 3.527 × 10^–9 cos(J9) + 1.030 × 10^–8 sin(J9) + 1.687 × 10^–9T cos(J9) – 9.374 × 10^–10T sin(J9) – 4.263 × 10^–10 cos(J10) + 3.506 × 10^–10 sin(J10) + 7.343 × 10^–11T cos(J10) + 6.139 × 10^–11T sin(J10)
Фива (J14):	α₀ = 268.05 – 0.009 T – 2.11 sin(J2) + 0.04 sin(2J2) Δα₀ = 0.0312 T – 0.00002 T ² – 1.284×10^–7 cos(J2) + 1.691×10^–6 sin(J2) + 3.038×10^–7T cos(J2) + 2.561×10^–8T sin(J2) + 2.417×10^–9 cos(2J2) – 2.937×10^–8 sin(2J2) – 5.145×10^–9T cos(2J2) – 4.619×10^–10T sin(2J2) – 1.736×10^–10 cos(J11) + 1.244×10^–9 sin(J11) – 1.025×10^–10T cos(J11) – 1.443×10^–11T sin(J11) – 6.169×10^–10 cos(J12) – 3.647×10^–11 sin(J12) + 4.938×10^–12T cos(J12) – 5.795×10^–11T sin(J12)
	δ₀ = 64.49 + 0.003T – 0.91cos(J2) + 0.01 cos(2J2) Δδ₀ = –0.0050T – 0.00002 T ² + 7.282 ×10^–7 cos(J2) + 3.502 ×10^–8 sin(J2) + 1.115 × 10^–8T cos(J2) – 1.311 ×10^–7T sin(J2) –6.510 × 10^–9 cos(2J2) – 4.351 ×10^–10 sin(2J2) – 1.171 × 10^–10T cos(2J2) + 1.131 ×10^–9T sin(2J2) + 2.223 × 10^–10 cos(J11) + 1.410 × 10^–11 sin(J11) – 7.947 × 10^–13T cos(J11) + 1.754 ×10^–11T sin(J11) + 1.612 × 10^–11 cos(J12) – 2.664 ×10^–10 sin(J12) + 2.429 × 10^–11Tcos(J12) + 1.468 × 10^–12T sin(J12)
	W = 8.56 + 533.7004100d + 1.91 sin(J2) – 0.04 sin(2J2) ΔW = –0.0000058d + 1×10^–14d ² + 9.219 × 10^–8 cos(J2) – 1.443 × 10^–6 sin(J2) – 2.651 × 10^–7T cos(J2) – 1.892 × 10^–8T sin(J2) – 2.387 × 10^–9 cos(2J2) + 2.933 × 10^–8 sin(2J2) + 5.164 × 10^–9T cos(2J2) + 4.613 × 10^–10T sin(2J2) + 4.639 × 10^–9 cos(J11) – 9.887 × 10^–9 sin(J11) + 8.151 × 10^–10T cos(J11) + 3.821 × 10^–10T sin(J11) + 5.425 × 10^–10 cos(J12) + 3.867 × 10^–11 sin(J12) – 3.672 × 10^–12T cos(J12) + 5.247 × 10^–11T sin(J12)
T – Динамическое Барицентрическое Время (Dynamical Barycentric Time) (TDB) измеряется в юлианских столетиях (сjy) (36525 дней) от эпохи J2000; d – Динамическое Барицентрическое Время (Dynamical Barycentric Time) (TDB) измеряется в юлианских днях (jd) от эпохи J2000; все величины углов (α₀, Δα₀, δ₀, Δδ₀, W, ΔW) приведены в градусах; J1 = Ω_L55 = 73°.32 + 91472°.9T, J2 = Ω_L514 = 24°.62 + 45137°.2T, J9 = λ₅₅– λ₅, J10 = λ₅₅+ λ₅, J11 = λ₅₁₄– λ₅, J12 = λ₅₁₄+ λ₅, J13 = λ₅₁₅– λ₅, J14 = λ₅₁₅+ λ₅, J15 = λ₅₁₆– λ₅, J16 = λ₅₁₆+ λ_5, λ₅ = 34°.35 + 3034°.9T = 0.59954632934 + 52.96909650946T, λ₅₅ = 722°.6314560d, λ₅₁₄ = 533°.7004100d, λ₅₁₅ = 1206°.9986602d, λ₅₁₆ = 1221°.2547301d.

Как видно из табл. 3, вычисленная величина линейного члена геодезической прецессии Метиды Δψ₁ = –1°.4710348 в столетие, что хорошо согласуется с теоретическим значением этой величины –1°.473 в столетие, полученной в работе (Biscani, Carloni, 2015) для упрощенной модели вращения спутника без квадратичного члена. Следует отметить, что присутствие квадратичного члена в табл. 3 указывает на изменение величины скорости геодезического вращения.

Следует отметить, что у Юпитера, вращающегося вокруг своего более массивного центрального тела (Солнца), величина геодезического вращения (Pashkevich, Vershkov, 2019) в 10⁵ раз меньше, чем у его ближайших спутников (см. табл. 3), для которых Юпитер является менее массивным центральным телом. Из данного обстоятельства следует, что в Солнечной системе есть объекты, у которых большая величина геодезического вращения обусловлена их близостью к возмущающему центральному телу, а не его массой.

В табл. 4 Ω_L55 , Ω_L514– долготы восходящих узлов (орбиты спутников Юпитера) на плоскости Лапласа для Амальтеи и Фивы, соответственно; λ₅– средняя долгота Юпитера; λ₅₅, λ₅₁₄, λ₅₁₅, λ₅₁₆– средние юпитероцентрические долготы Амальтеи, Фивы, Адрастеи и Метиды, соответственно. Средняя долгота Юпитера взята из работы (Brumberg, Bretagnon, 2000). Средние долготы и долготы восходящих узлов спутников Юпитера взяты из работы (Archinal и др., 2018).

В табл. 5 представлены углы вращения (α₀, δ₀, W) внутренних спутников Юпитера (Archinal и др., 2018) и вычисленные в настоящем исследовании наиболее существенные вековые, периодические и смешанные члены их геодезического вращения (Δα₀, Δδ₀, ΔW). Следует отметить, что используемые в модели для описания геодезического вращения смешанные по времени Пуассоновские члены в формуле (6) с коэффициентами из табл. 4 и 5 могут использоваться только на интервалах времени проводимых исследований (см. табл. 2). Эти члены очень хорошо описывают долгопериодические колебания с неполным периодом, представленные на рис. 5 в виде расходящихся амплитуд.

Как видно из табл. 3 и 5 значения величин геодезической прецессии спутников увеличиваются по мере уменьшения их расстояния до центрального тела – Юпитера, внося существенный вклад в величины прямых восхождений и склонений рассматриваемых спутников (см. табл. 5). Так, например, для Метиды (самого близкого на данный момент спутника Юпитера) величина геодезической прецессии в прямом восхождении Δα₀ в 13 раз по абсолютной величине превосходит результирующую величину его прямого восхождения α₀, а величина геодезической прецессии в склонении Δδ₀ в семь раз по абсолютной величине превосходит результирующую величину его склонения δ₀. Для Фивы (самого дальнего спутника из рассматриваемых спутников Юпитера) эти величины (Δα₀, Δδ₀) в три и в два раза по абсолютной величине превосходят его α₀ и δ₀, соответственно. Из данного обстоятельства следует, что в Солнечной системе есть объекты с существенным геодезическим вращением, так величина геодезической прецессии внутренних спутников Юпитера сопоставима с их прецессией в ньютоновом приближении (см. табл. 5).

ЗАКЛЮЧЕНИЕ

В настоящей работе была рассмотрена вращательная динамика внутренних спутников Юпитера – Метиды, Адрастеи, Амальтеи и Фивы. Исследование устойчивости плоского синхронного вращения показало, что теоретически ожидаемое (Goldreich, Peale, 1966; Peale, 1977; 1999) и наблюдаемое (Smith и др., 1979a; Thomas и др., 1998) плоское синхронное вращение всех внутренних спутников Юпитера для наиболее вероятных значений параметров их фигур является устойчивым относительно наклона оси вращения. На диаграммах устойчивости, построенных для всех теоретически возможных значений параметров фигур спутников, рассмотренные нами спутники расположены далеко от областей с неустойчивой динамикой. Возмущения во вращательной динамике спутников, вызванные, например, столкновениями (не приводящими к существенному изменению фигуры спутника) или тесными сближениями с другими телами, не приведут к выходу спутников из синхронного спин-орбитального резонанса. Возможная эволюция фигуры Амальтеи, обусловленная ее весьма вытянутой формой, также не приведет к ее выходу из наблюдаемого режима плоского синхронного вращения.

Исследование релятивистского вращения внутренних спутников Юпитера позволило определить, впервые в углах Эйлера и в углах их вращения относительно неподвижного экватора Земли эпохи J2000.0, наиболее существенные вековые, периодические и смешанные члены их геодезического вращения. Настоящее исследование показало, что величина геодезического вращения может быть существенной не только у объектов, которые вращаются вокруг сверхмассивных центральных тел (нейтронных звезд), но и у тел с малым расстоянием до менее массивного центрального тела, например, у близких спутников планет гигантов. Полученные аналитические значения для геодезического вращения внутренних спутников Юпитера могут быть использованы для численного исследования их вращения в релятивистском приближении.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-02-00811.

Список литературы

Абалакин В.К. Основы эфемеридной астрономии. М.: Наука, 1979. 448 с.
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965. 416 с.
Вулард Э. Теория вращения Земли вокруг центра масс. М.: Физматгиз, 1963.
Лихтенберг А., Либерман М. Регулярная и стохастическая динамика. М.: Мир, 1984. 528 с.
Мельников А.В., Шевченко И.И. Об устойчивости вращения несферических естественных спутников в синхронном резонансе // Астрон. вестн. 2000. Т. 34. № 5. С. 478–486. (Melnikov A.V., Shevchenko I.I. On the Stability of the Rotational Motion of Nonspherical Natural Satellites in a Synchronous Resonance // Sol. Syst. Res. 2000. V. 34. № 5. P. 434–442.)
Мельников А.В., Шевченко И.И. Необычные режимы вращения малых спутников планет // Астрон. вестн. 2007. Т. 41. № 6. С. 521–530. (Melnikov A.V., Shevchenko I.I. Unusual rotation modes of minor planetary satellites // Sol. Syst. Res. 2007. V. 41. № 6. P. 483–491.)https://doi.org/10.1134/S0038094607060032
Пашкевич В.В. Геодезическое (релятивистское) вращение тел Солнечной системы // Вестн. СПбГУ. 2016. Сер. 1. Т. 3(61). Вып. 3. С. 506–516.
Пашкевич В.В., Вершков А.Н. Учет релятивистских эффектов во вращении Марса и его спутников // Астрон. вестн. 2019. Т. 53. № 6. С. 423–427. (Pashkevich V.V., Vershkov A.N. Consideration of Relativistic Effects in the Rotation of Mars and its Satellites // Sol. Syst. Res. 2019. Vl. 53. № 6. P. 431–435. https://doi.org/10.1134/S0038094619060066)https://doi.org/10.1134/S0320930X19060069
Торжевский А.П. Периодические решения уравнения плоских колебаний спутника на эллиптической орбите // Космич. исслед. 1964. Т. 2. Вып. 5. С. 667–678.
Archinal B.A., Acton C.H., A’Hearn M.F. et al. Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2015 // Celest. Mech. Dyn. Astr. 2018. V. 130. № 22. P. 1–46.
Barnard E.E. Discovery and observations of a fifth satellite to Jupiter // Astron. J. 1892. V. 12. № 275. P. 81–85.
Biscani F., Carloni S. A first-order secular theory for the post-Newtonian two-body problem with spin – II. A complete solution for the angular coordinates in the restricted case // Mon. Notic. Roy. Astron. Soc. 2015. V. 446. P. 3062–3077.
Brumberg V.A., Bretagnon P. Kinematical Relativistic Corrections for Earth’s Rotation Parameters // Proc. of IAU Colloquium 180 /Eds. Johnston K., McCarthy D., Luzum B., Kaplan G. U.S. Naval Observatory. 2000. P. 293–302.
De Sitter W. On Einstein’s Theory of Gravitation and its Astronomical Consequences // Mon. Notic. Roy. Astron. Soc. 1916. № 77. P. 155–184.
Eroshkin G.I., Pashkevich V.V. Geodetic rotation of the Solar system bodies // Artificial Satellites. 2007. V. 42. № 1. P. 59–70.
Folkner W.M, Williams J.G., Boggs D.H., Park R.S., Kuchynka P. The Planetary and Lunar Ephemerides DE430 and DE431 // IPN Progress Report 42-196. 2014. P. 1–81.
Fukushima T. Geodesic Nutation // Astron. and Astrophys. 1991. V. 244. № 1. P. L11–L12.
Giorgini J.D., Chodas P.W., Yeomans D.K. Orbit Uncertainty and Close-Approach Analysis Capabilities of the Horizons On-Line Ephemeris System // 33rd AAS/DPS meeting in New Orleans. LA. Nov 26. 2001–Dec 01. 2001.
Goldreich P., Peale S. Spin-orbit coupling in the Solar system // Astron. J. 1966. V. 71. № 6. P. 425–438.
Kopeikin S., Efroimsky M., Kaplan G. Relativistic Celestial Mechanics in the Solar System. Hoboken, NY: John Wiley and Sons, 2011. 894 p.
Kouprianov V.V., Shevchenko I.I. On the chaotic rotation of planetary satellites: The Lyapunov exponents and the energy // Astron. and Astrophys. 2003. V. 410. P. 749–757.
Ma C., Arias E.F., Eubanks T.M. et al. The international celestial reference frame as realized by very long baseline interferometry // Astron. J. 1998. V. 116. P. 516–546.
Melnikov A., Pashkevich V., Vershkov A., Karelin G. Chaos and relativistic effects in the rotational dynamics of minor planetary satellites // Proc. Journées 2019 “Astrometry, Earth Rotation and Reference systems in the Gaia era”. Observatoire de Paris, Paris, France, 07–09 October 2019, Ed. C. Bizouard). P. 339–344. (Pub Date September 2020, Bibcode: 2020jsrs.conf.339M.)
Melnikov A.V., Shevchenko I.I. On the rotational dynamics of Prometheus and Pandora // Celest. Mech. Dynam. Astron. 2008. V. 101. № 1–2. P. 31–47.
Pashkevich V.V., Eroshkin G.I. Relativistic rotation of the rigid body in the Rodrigues–Hamilton parameters: Lagrange function and equations of motion // Artificial Satellites. 2018. V. 53, № 3. P. 89–115.https://doi.org/10.2478/arsa-2018-0008
Pashkevich V.V., Vershkov A.N. New High-Precision Values of the Geodetic Rotation of the Mars Satellites System, Major Planets, Pluto, the Moon and the Sun // Artificial Satellites. 2019. V. 54. № 2. P. 31–42. https://doi.org/10.2478/arsa-2019-0004
Peale S.J. Rotation histories of the natural satellites // Planetary satellites / Ed. Burns J.A. Tucson: Univ. Arizona Press, 1977. P. 87–112.
Peale S.J. Origin and evolution of the natural satellites // Ann. Rev. Astron. and Astrophys. 1999. V. 37. P. 533–602.
Porco C.C. and the Cassini imaging team. Cassini imaging of Jupiter’s atmosphere, satellites and rings // Science. 2003. V. 299. P. 1541–1547.
Shevchenko I.I. The separatrix algorithmic map: application to the spin-orbit motion // Celest. Mech. and Dynam. Astron. 1999. V. 73. P. 259–268.
Smith B.A. and the Voyager imaging team. Jupiter system through the eyes of Voyager-1 // Science. 1979a. V. 204. P. 951–972.
Smith B.A. and the Voyager imaging team. The Galilean satellites and Jupiter: Voyager-2 imaging results // Science. 1979b. V. 206. P. 927–950.
Thomas P.C., Burns J.A., Rossier L., Simonelli D. et al. The small inner satellites of Jupiter // Icarus 1998. V. 135. P. 360–371.
Tiscareno M.S., Thomas P.C., Burns J.A. The rotation of Janus and Epimetheus // Icarus. 2009. V. 204. P. 254–261.
Wisdom J. Rotation dynamics of irregularly shaped natural satellites // Astron. J. 1987. V. 94. № 5. P. 1350–1360.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал

Астрономический вестник, 2021, T. 55, № 1, стр. 50-64

Динамика вращения внутренних спутников Юпитера

ВВЕДЕНИЕ