Астрономический вестник, 2022, T. 56, № 4, стр. 254-265
Вращательная динамика сближающихся с планетами астероидов
А. В. Мельников *
Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия
* E-mail: melnikov@gaoran.ru
Поступила в редакцию 09.12.2021
После доработки 19.01.2022
Принята к публикации 09.02.2022
- EDN: DKSFEK
- DOI: 10.31857/S0320930X22040065
Аннотация
Посредством проведения массовых численных экспериментов рассмотрено влияние сближения астероида с планетой на его вращательную динамику. Для ряда астероидов, испытывающих последовательные сближения с несколькими планетами земной группы, получены характерные оценки изменения периода собственного вращения астероида из-за сближения с планетой. Рассмотрена вращательная динамика астероида (367 943) Duende при его весьма тесном сближении с Землей в 2013 г. и получены оценки возможной скорости вращения астероида до момента сближения.
ВВЕДЕНИЕ
Астероиды, испытывающие тесные сближения (ТС) с Землей и другими планетами Солнечной системы, представляют значительный интерес для детальных исследований из-за возможности оказать катастрофическое влияние на планету (при столкновении) и на сам астероид (возможно разрушение астероида из-за действия приливных сил). Кроме того, наблюдения ТС астероидов с планетами и последующее моделирование кривых блеска позволяют изучить физические свойства и вращательную динамику самого астероида. Посредством исследования вращательной динамики астероида при ТС с планетой можно получить информацию о его фигуре и внутреннем строении.
Задачу о влиянии прохождения астероида вблизи Земли на его вращательную динамику рассматривали Батраков и Медведев (1992), показавшие посредством численного моделирования, что при тесном сближении астероида с Землей “возникают большие гравитационные поворачивающие моменты”, приводящие к изменению вращения астероида. Richardson и др. (1998) при помощи численного моделирования рассмотрели задачу о деформации фигуры и распаде астероидов типа “rubble pile” (куча щебня; см. подробнее Walsh, 2018), представляющих собой тело с невысокой степенью жесткости либо груду обломков, из-за гравитационных моментов, возникающих при ТС астероида с Землей. Позднее Sharma и др. (2006) детально рассмотрели механизмы деформации тела астероида и его распада из-за приливных эффектов, действующих при ТС астероида с планетой. В недавно вышедшей работе Воропаевa и др. (2020) рассмотрено разрушение однородного вращающегося упругого астероида несферической формы при его ТС с Землей. Получены ограничения на минимальную дистанцию сближения, при которой возможен распад астероида с учетом его размеров, формы и ряда других физических параметров. Воропаев и др. (2020) отметили, что на напряжения и деформации, возникающие в теле астероида при ТС, влияют ориентация его фигуры относительно направления на Землю и ориентация в пространстве оси собственного вращения астероида.
Black и др. (1999) исследовали влияние ТС с Марсом на вращательную динамику астероида (433) Eros и показали, что в результате ТС могут возникнуть существенные либрации ориентации фигуры астероида в пространстве. Определив из наблюдений амплитуду либраций, можно оценить моменты инерции астероида. Scheeres и др. (2000), посредством проведения модельных численных экспериментов по сближению астероида (4179) Toutatis с Землей, показали, что малые возмущения, возникающие при многочисленных повторяющихся сближениях астероида с планетой, приводят к изменению его угловой скорости вращения. В то же время одиночное сильное гравитационное взаимодействие, имеющее место при весьма тесном сближении астероида с планетой, может изменить его режим вращения – астероид перейдет в режим “кувыркания” (tumbling). В режиме “кувыркания” ось собственного вращения астероида не совпадает с осью одного из трех главных центральных моментов инерции, такой режим характерен для астероидов малых размеров (см. подробнее о “кувыркающихся” астероидах Pravec и др., 2005). Динамика (4179) Toutatis была рассмотрена Takahashi и др. (2013), показавшими, что при каждом его сближении с Землей изменяется величина углового вращательного момента астероида, его относительное изменение за 20 лет может составить около 0.1%. Takahashi и др. (2013) определили параметры вращения астероида (4179) Toutatis и оценили его моменты инерции.
В работе Scheeres и др. (2004) проведено подробное статистическое исследование влияния ТС с Землей и с Венерой на вращательные состояния малых тел (астероидов и комет). Исследование вращательной динамики АСЗ (астероидов сближающихся с Землей) проведено в работе Boldrin и др. (2020), рассмотревших посредством модельных численных экспериментов изменение скорости вращения и ориентации фигур астероида при ТС с Землей. Scheeres и др. (2005) рассмотрели влияние предстоящего в 2029 г. ТС с Землей потенциально опасного астероида (99 942) Apophis и указали, что в результате сближения период вращения астероида может измениться почти в два раза. Отметим еще ряд работ (Pravec и др., 2014; Souchay и др., 2018; Lee и др., 2021), где детально рассмотрена вращательная динамика астероида (99 942) Apophis при его ТС с Землей.
Проведенный в работе (Devyatkin и др., 2016) анализ наблюдаемой кривой блеска астероида (367 943) Duende, полученной при ТС этого астероида с Землей 15 февраля 2013 г. на расстоянии около 27 700 км, показал, что периоды, наблюдаемые в изменении кривой блеска астероида до сближения с Землей и после, заметно отличаются. Моделирование кривых блеска и вращательной динамики (367 943) Duende в окрестности точки сближения позволило Devyatkin и др. (2016) получить информацию о физических параметрах астероида (оценить его размеры и моменты инерции) и параметрах его вращения. Devyatkin и др. (2016) сделали вывод, что ТС с Землей привело к изменению скорости собственного вращения астероида: период вращения астероида после прохождения перигея увеличился с ≈10.1 ч (вблизи точки сближения) до ≈10.9 ч (через трое суток после момента ТС). В недавно опубликованных работах (Benson и др., 2020; Moskovitz и др., 2020) была детально рассмотрена вращательная динамика астероида (367 943) Duende на основе большого массива наблюдательных данных. Посредством анализа наблюдаемых кривых блеска астероида, полученных после его сближения с Землей, Moskovitz и др. (2020) установили, что вращательную динамику (367 943) Duende можно описать вращением с двумя периодами: P1 = 8.71 ± 0.03 ч и P2 = 23.7 ± 0.2 ч (подробнее см. Pravec и др., 2005). Анализ на периодичность кривых блеска астероида показал, что после ТС величина периода прецессии P1 увеличилась с 8.37 до 8.71 ч, а величина P2 практически не изменилась. Проведенное Benson и др. (2020) моделирование вращательной динамики (367943) Duende подтвердило результаты, полученные Moskovitz и др. (2020). Таким образом, как анализ наблюдений, так и моделирование вращательной динамики астероида (367943) Duende при его ТС с Землей в 2013 г. показывают относительное изменение его скорости вращения на 5–8% (Devyatkin и др., 2016; Benson и др., 2020; Moskovitz и др., 2020). Численные эксперименты, проведенные Benson и др. (2020) по интегрированию вращательной динамики (367 943) Duende назад во времени от момента сближения, показали, что период вращения астероида в результате его ТС с Землей мог измениться почти на 30% (как увеличиться, так и уменьшиться).
Отметим, что на долговременную вращательную динамику астероидов могут оказывать влияние столкновения с другими астероидами (Asphaug, Scheeres, 1999; Henych, Pravec, 2013) и негравитационный YORP-эффект (Rubincam, 2000; Ershkov, Shamin, 2018). Эффект анизотропного переизлучения (YORP, Yarkovsky–O’Keefe–Radzievskii–Paddack) существенен в динамике малых астероидов (диаметр менее километра) неправильной формы и приводит к изменению угловой скорости вращения астероида и ориентации его оси вращения в пространстве. В пионерской работе (Lowry и др., 2007) установлено, что за четыре года наблюдений величина изменения угловой скорости вращения астероида (54 509) 2000 PH5 (позднее этот астероид получил наименование YORP) составила около 2 × 10–4 град/сут2 и не может быть объяснена его периодическими сближениями с Землей, а вызвана YORP-эффектом. В настоящее время величина YORP-эффекта определена менее чем у десятка астероидов (Zegmott и др., 2021).
В работе (Девяткин и др., 2022) выявлен ряд астероидов, которые в ходе долговременной орбитальной динамики испытывают сближения с двумя и более планетами земной группы. Если такие сближения будут достаточно тесными, то они должны найти свое отражение в эволюции вращения астероида. Актуальность исследования вращательной динамики астероидов, испытывающих ТС с планетами, обусловлена тем, что, зная степень влияния этих событий на эволюцию вращения конкретных астероидов, мы можем из анализа наблюдений и путем численного моделирования вращательной динамики определить моменты инерции астероида, величину YORP-эффекта, предположить наличие в истории астероида столкновений с другими малыми телами, оценить величину релятивистских эффектов (геодезическую прецессию, см. подробнее (Пашкевич, Вершков, 2022)).
В настоящей работе посредством проведения массовых численных экспериментов рассмотрено влияние сближения астероида с планетой на его вращательную динамику. Работа построена следующим образом: в первой ее части приведены основные уравнения, описывающие вращательную динамику астероида в окрестности точки сближения с планетой. Далее представлены результаты численных экспериментов по моделированию вращательной динамики избранных астероидов, испытывающих последовательные сближения с несколькими планетами земной группы, и результаты моделирования вращательной динамики астероида (367 943) Duende при его ТС с Землей в 2013 г. В конце работы приведены основные полученные результаты.
УРАВНЕНИЯ ДВИЖЕНИЯ
При изучении вращательной динамики астероида в окрестности точки сближения с планетой предполагалось, что движение астероида происходит по гиперболической орбите относительно планеты. Вращательную динамику астероида в задаче о его сближении с планетой определяют следующие параметры (Richardson и др., 1998; Sharma и др., 2006): фигура астероида, период собственного вращения астероида и ориентация оси вращения в пространстве, перицентрическое расстояние (дистанция между планетой и астероидом в точке сближения), орбитальная скорость астероида и его физические свойства, определяющие величину рассеяния энергии при деформации фигуры астероида из-за возникающих при ТС с планетой гравитационных моментов.
Фигура астероида аппроксимировалась трехосным эллипсоидом однородной плотности с главными полуосями инерции a > b > c. Планета считалась неподвижной гравитирующей точкой, масса астероида много меньше массы планеты. Использовалась прямоугольная система координат Oxyz, определенная исходно в перицентре орбиты астероида (в точке сближения) следующим образом: ось x направлена по вектору “перицентр орбиты астероида – планета”, ось y в перицентре орбиты параллельна вектору орбитальной скорости астероида, ось z ортогональна орбитальной плоскости астероида и дополняет систему до “правой”. Ориентация фигуры астероида относительно осей системы координат Oxyz задавалась путем его воображаемых поворотов на углы Эйлера (θ, φ, ψ) из положения совпадения главных осей инерции астероида с осями системы координат до их реального положения в пространстве в следующей последовательности (согласно Wisdom и др., 1984): сначала делаем поворот на угол θ вокруг оси c, затем на угол φ вокруг оси a и, наконец, на угол ψ вокруг оси b.
Вращательное движение астероида описывается динамическими и кинематическими уравнениями Эйлера. Выпишем динамические уравнения Эйлера (Белецкий, 1965):
(1)
$\begin{array}{*{20}{c}} {A\frac{{{\text{d}}{{{{\omega }}}_{a}}}}{{{\text{d}}t}} - {{{{\omega }}}_{b}}{{{{\omega }}}_{c}}\left( {B - C} \right) = - 3\frac{{GM}}{{{{r}^{3}}}}{{\beta \gamma }}\left( {B - C} \right),} \\ {B\frac{{{\text{d}}{{{{\omega }}}_{b}}}}{{{\text{d}}t}} - {{{{\omega }}}_{c}}{{{{\omega }}}_{a}}\left( {C - A} \right) = - 3\frac{{GM}}{{{{r}^{3}}}}{{\gamma \alpha }}\left( {C - A} \right),} \\ {C\frac{{{\text{d}}{{{{\omega }}}_{c}}}}{{{\text{d}}t}} - {{{{\omega }}}_{a}}{{{{\omega }}}_{b}}\left( {A - B} \right) = - 3\frac{{GM}}{{{{r}^{3}}}}{{\alpha \beta }}\left( {A - B} \right),} \end{array}$Кинематические уравнения Эйлера и выражения для направляющих косинусов в принятой системе углов Эйлера имеют вид (Wisdom и др., 1984; Мельников, 2020):
(3)
$\begin{gathered} \alpha = \cos (\theta - f)\cos \psi - \sin (\theta - f)\sin \varphi \sin \psi , \\ \beta = --\sin (\theta - f)\cos \varphi ,~ \\ ~\gamma = \cos (\theta - f)\sin \psi + \sin (\theta - f)\sin \varphi \cos \psi . \\ \end{gathered} $При пространственном вращении астероида в кинематических уравнениях Эйлера (2) присутствует сингулярность при φ = ±π/2. Чтобы избавиться от сингулярности, при численном интегрировании вместо углов Эйлера нами использовались переменные Родрига–Гамильтона (λ0, λ1, λ2, λ3), связанные с углами Эйлера следующими соотношениями (Куприянов, 2014; Мельников, 2020):
(4)
$\begin{gathered} {{\lambda }_{0}} = \cos \frac{\theta }{2}\cos \frac{\phi }{2}\cos \frac{\psi }{2} - \sin \frac{\theta }{2}\sin \frac{\phi }{2}\sin \frac{\psi }{2}, \\ {{\lambda }_{1}} = \cos \frac{\theta }{2}\sin \frac{\phi }{2}\cos \frac{\psi }{2} - \sin \frac{\theta }{2}\cos \frac{\phi }{2}\sin \frac{\psi }{2}, \\ {{\lambda }_{2}} = \cos \frac{\theta }{2}\cos \frac{\phi }{2}\sin \frac{\psi }{2} + \sin \frac{\theta }{2}\sin \frac{\phi }{2}\cos \frac{\psi }{2}, \\ {{\lambda }_{3}} = \cos \frac{\theta }{2}\sin \frac{\phi }{2}\sin \frac{\psi }{2} + \sin \frac{\theta }{2}\cos \frac{\phi }{2}\cos \frac{\psi }{2}. \\ \end{gathered} $Переменные Родрига–Гамильтона (Борисов, Мамаев, 2001; Whittaker, 1917) являются регулярными во всей области задания: 1 ≤ λi≤ 1, i = 0, …, 3. При использовании переменных Родрига–Гамильтона вместо кинематических уравнений Эйлера (2), представляющих собой систему из трех уравнений, мы имеем систему из четырех дифференциальных уравнений (Куприянов, 2014):
(5)
$\begin{array}{*{20}{c}} {\frac{{{\text{d}}{{{{\lambda }}}_{0}}}}{{{\text{d}}t}} = - \frac{1}{2}\left( {{{{{\lambda }}}_{1}}{{{{\omega }}}_{a}} + {{\lambda }_{2}}{{{{\omega }}}_{b}} + {{{{\lambda }}}_{3}}{{{{\omega }}}_{c}}} \right),} \\ {\frac{{{\text{d}}{{{{\lambda }}}_{1}}}}{{{\text{d}}t}} = \frac{1}{2}\left( {{{{{\lambda }}}_{0}}{{{{\omega }}}_{a}} + {{{{\lambda }}}_{3}}{{{{\omega }}}_{b}} + {{{{\lambda }}}_{2}}{{{{\omega }}}_{c}}} \right),} \\ {\frac{{{\text{d}}{{{{\lambda }}}_{2}}}}{{{\text{d}}t}} = \frac{1}{2}\left( {{{{{\lambda }}}_{3}}{{{{\omega }}}_{a}} + {{{{\lambda }}}_{0}}{{{{\omega }}}_{b}} + {{{{\lambda }}}_{1}}{{{{\omega }}}_{c}}} \right),} \\ {\frac{{{\text{d}}{{{{\lambda }}}_{3}}}}{{{\text{d}}t}} = - \frac{1}{2}\left( {{{{{\lambda }}}_{2}}{{{{\omega }}}_{a}} + {{{{\lambda }}}_{1}}{{{{\omega }}}_{b}} + {{{{\lambda }}}_{0}}{{{{\omega }}}_{c}}} \right){\text{.}}} \end{array}$Направляющие косинусы в параметрах Родрига–Гамильтона имеют вид (Куприянов, 2014):
(6)
$\begin{gathered} \alpha = (\lambda _{0}^{2} + \lambda _{2}^{2} - \lambda _{3}^{2})\cos f + 2({{\lambda }_{0}}{{\lambda }_{3}} + {{\lambda }_{1}}{{\lambda }_{2}})\sin f, \\ \beta = 2({{\lambda }_{1}}{{\lambda }_{2}} + {{\lambda }_{0}}{{\lambda }_{3}})\cos f + \\ + \,\,(\lambda _{0}^{2} - \lambda _{1}^{2} + \lambda _{2}^{2} - \lambda _{3}^{2})\sin f, \\ \gamma = 2({{\lambda }_{0}}{{\lambda }_{2}} + {{\lambda }_{1}}{{\lambda }_{3}})\cos f + ({{\lambda }_{2}}{{\lambda }_{3}} + {{\lambda }_{0}}{{\lambda }_{3}})\sin f. \\ \end{gathered} $При моделировании поступательно-вращательного движения астероида численно интегрировалась система уравнений (1) и (5). Ориентация фигуры астероида в начальный момент времени задавалась углами Эйлера, переход к переменным Родрига–Гамильтона проводился непосредственно перед численным интегрированием уравнений движения. Для численного интегрирования уравнений движения использовался интегратор DOP853 (Hairer и др., 1993), реализующий метод Рунге–Кутты 8-го порядка, с автоматически изменяемой величиной шага интегрирования. Локальная точность интегрирования составляла ε = 10–14, максимальный шаг интегрирования Δt = 10–3 ч. Переменные Родрига–Гамильтона обладают свойством (Борисов, Мамаев, 2001; Whittaker, 1917): $\lambda _{0}^{2} + \lambda _{1}^{2} + \lambda _{2}^{2} + \lambda _{3}^{2} = 1$, что позволяет при численном интегрировании дополнительно контролировать точность вычислений. В проведенных нами тестовых численных экспериментах по моделированию долговременной вращательной динамики астероида отклонение от единичной нормы не превышало 10–13.
Сближение астероида с планетой влияет не только на вращательную динамику астероида, но и на его орбиту, однако, как отметили Scheeres и др. (2000), тип орбиты (гиперболическая орбита относительно планеты) не меняется, хотя возмущения орбиты в дальнейшем отражаются и на вращательной динамике астероида. Интервал времени, на котором мы рассматривали вращательную динамику астероида, не превышает одного месяца, что существенно меньше орбитального периода, поэтому при численном моделировании мы считали орбиту астероида фиксированной. При исследовании вращательной динамики астероида мы также полагали, что астероид является твердым телом с однородной плотностью, деформации его фигуры из-за приливных моментов, вызванных Солнцем и Луной (в случае АСЗ), отсутствуют. Влияние на вращательную динамику несферичности планеты и YORP-эффекта также нами не учитывалось.
МОДЕЛИРОВАНИЕ СБЛИЖЕНИЙ АСТЕРОИДОВ С ПЛАНЕТАМИ
В работе Девяткина и др. (2022) установлена группа из 27 астероидов, испытывающих на промежутке времени 1500–2500 гг. сближения на расстояния менее 0.05 а. е. с планетами земной группы – Меркурием, Венерой, Землей и Марсом. Далее в нашей работе мы посредством численного моделирования оценим величину изменения скорости вращения для ряда астероидов из работы (Девяткин и др., 2022) при их сближениях с различными планетами. На основе полученных оценок сделаем выводы о возможности выявления таких изменений посредством анализа наблюдений. Также для оценки влияния очень тесного сближения астероида с планетой на его вращательную динамику проведем моделирование вращательной динамики астероида (367 943) Duende при его ТС с Землей 15 февраля 2013 г. на расстояние около 27 700 км.
Из перечня астероидов, приведенного в работе Девяткина и др. (2022), нами были отобраны объекты, сближающиеся с планетами на расстояния менее 100RE, где принято RE= 6370 км – радиус Земли. При сближении на данное расстояние астероид попадает в сферу действия планеты (за исключением случая Меркурия). Примерные радиусы сфер действия планет: Меркурий – 20RE, Венера – 100RE, Земля – 150RE, Марс – 90RE. В табл. 1 приведен список из шести отобранных нами астероидов, значения минимальной дистанции, (выраженной в RE) на которую они сближаются с планетой, и последовательность сближений с указанием их моментов времени. В табл. 1 для сравнения указаны имеющие место сближения с Юпитером. Информация о минимальных дистанциях и датах сближений астероидов с планетами на интервале времени 1900–2200 гг. получена с сайта https://ssd.jpl.nasa.gov/ (см. также https://cneos.jpl.nasa.gov/ca/). Траектории всех рассмотренных нами астероидов проходят достаточно далеко от планет и не попадают в сферу Роша планеты, поэтому их распад и столкновения с планетой маловероятны.
Таблица 1.
Минимальные дистанции сближений и последовательность сближений исследуемых астероидов с планетами на интервале времени 1900–2200 гг. Расстояния до планет указаны в радиусах Земли. Данные взяты с сайта https://ssd.jpl.nasa.gov/
| Астероид | Меркурий | Венера | Земля | Марс | Юпитер | Последовательность сближений: “Планета (день. месяц. год)” |
|---|---|---|---|---|---|---|
| 2008 FP | – | 2906.33 | 26.67 | – | 10 177.22 | Венера (01.06.2008) Земля (29.03.2008) Юпитер (29.11.2014) |
| 2009 WP6 | 576.27 | 402.64 | 40.84 | 455.52 | – | Марс (20.07.1970) Меркурий (02.03.1978) Венера (11.06.1979) Земля (15.11.2009) |
| 2010 JJ41 | 18.13 | 240.55 | 1164.89 | 645.62 | – | Венера (14.11.1985) Меркурий (13.01.2009) Земля (16.04.2010) Марс (22.12.2010) |
| 2015 EO61 | 246.07 | 582.17 | 277.40 | 65.08 | – | Венера (17.02.2047) Марс (17.08.2083) Меркурий (23.10.2169) Земля (25.11.2141) |
| 2015 TX24 | 43.33 | 941.67 | 416.57 | 56.34 | 27 955.26 | Земля (26.10.1900) Юпитер (07.06.1986) Венера (29.03.2002) Меркурий (24.02.2026) Марс (15.08.2039) |
| 2015 XG55 | 844.50 | 244.00 | 42.65 | 1629.35 | – | Марс (10.11.1964) Венера (24.03.2002) Меркурий (18.09.2061) Земля (01.12.2087) |
В табл. 2 приведены орбитальные параметры и диаметры отобранных астероидов. В табл. 3 даны орбитальные параметры и приблизительный диаметр астероида (367 943) Duende. Радарные наблюдения (Benner и др., 2013) и моделирование вращательной динамики (Devyatkin и др., 2016) указывают, что (367 943) Duende представляет собой сильно вытянутый объект с размерами сечения примерно 40 × 20 м.
Таблица 2.
Орбитальные параметры и диаметры фигур (D) исследуемых астероидов, сближающихся с планетами земной группы. Данные взяты из статьи (Девяткин и др., 2022)
| Астероид | a, а. е. | e | i, угл. град |
ω, угл. град |
Ω, угл. град |
M, угл. град |
D, м |
|---|---|---|---|---|---|---|---|
| 2008 FP | 2.5820417 | 0.897618 | 3.6053 | 152.3963 | 158.4591 | 314.7334 | 20 |
| 2009 WP6 | 1.1300877 | 0.740954 | 2.7620 | 228.0252 | 54.4203 | 316.4803 | 20 |
| 2010 JJ41 | 1.0726108 | 0.672689 | 3.2819 | 29.3474 | 50.1456 | 85.7767 | 150 |
| 2015 EO61 | 1.4551681 | 0.734409 | 1.9785 | 261.3447 | 43.6538 | 300.4765 | 170 |
| 2015 TX24 | 2.2660105 | 0.872083 | 6.0426 | 127.0568 | 32.9362 | 112.6511 | 250 |
| 2015 XG55 | 1.0294541 | 0.557679 | 2.3634 | 237.4629 | 70.3029 | 164.8940 | 10 |
Таблица 3.
Орбитальные параметры и диаметр фигуры (D) астероида (367 943) Duende. Параметры взяты с сайта https://ssd.jpl.nasa.gov, диаметр – из статьи (Moskovitz и др., 2020)
| a, а. е. | e | i, угл. град |
ω, угл. град |
Ω, угл. град |
M, угл. град |
Т, JD | D, м |
|---|---|---|---|---|---|---|---|
| 0.910140 | 0.089319 | 11.6090 | 195.5777 | 146.9281 | 262.7014 | 2 459 600.5 | 50 |
При проведении численных экспериментов по исследованию вращательной динамики сближающихся с планетами астероидов используют разные критерии для определения отрезка орбиты, на котором исследуется динамика. Richardson и др. (1998) в модельных численных экспериментах рассматривали динамику астероида на участке его траектории, начинающейся за 50RE до Земли и заканчивающейся на дистанции 60RE, при удалении астероида от Земли. Black и др. (1999) исследовали динамику астероида (433) Eros при его сближении с Марсом на отрезке орбиты, расположенном не далее 100 радиусов планеты. Boldrin и др. (2020) в модельных численных экспериментах по исследованию вращательного движения сближающихся с Землей астероидов рассматривали их динамику как на расстоянии, не превышающем 100RE от планеты, так и на отрезке орбиты, соответствующем интервалу времени в 10 суток (пять суток до точки сближения и пять после ее прохождения). В настоящей работе вращательная динамика астероидов рассматривалась на отрезках их орбит с началом на расстоянии 100RE от точки сближения и концом, находящимся на таком же расстоянии при удалении астероида от планеты. Величины интервалов времени, соответствующие определенным таким образом отрезкам орбит астероидов, составляли от 2 до 10 суток. Согласно табл. 2 и 3, наклонения орбит у всех астероидов малы, поэтому при определении начальной ориентации фигуры астероида в пространстве мы полагали, что на рассматриваемом участке траектории астероид движется в орбитальной плоскости планеты. При численном интегрировании гравитационные параметры для планет полагались равными (Folkner и др., 2014): GMMercury = 22 031.780 км3/с2, GMVenus = 324 858.592 км3/с2, GMEarth = 398 600.435 км3/с2, GMMars = 42 828.375 км3/с2.
Перед численным интегрированием уравнений поступательно-вращательного движения астероида при помощи системы JPL Horizons (https://ssd.jpl.nasa.gov/horizons/) на интервале времени, соответствующем отрезку рассматриваемой траектории астероида, определялись положения небесных тел (астероида и планеты) в прямоугольной системе координат с началом в барицентре Солнечной системы. На основе этих данных рассчитывалась величина расстояния между астероидом и планетой – определялась траектория астероида относительно планеты. Эфемериды строились с шагом в один час, при дальнейшем интегрировании уравнений движения координаты тел на нужный момент времени определялись посредством использования кубической сплайновой интерполяции.
Для моделирования вращательной динамики астероида в гравитационном поле планеты необходимо знать величины его главных центральных моментов инерции (достаточно знать их отношения A/C и B/C), определяемых фигурой астероида. В настоящее время параметры фигур известны для весьма малого количества астероидов (Ďurech и др., 2010). Обычно имеются только оценки диаметра астероида, полученные (см. подробнее Bowell и др., 1989) на основе его абсолютной звездной величины и предполагаемой величины альбедо его поверхности. Известно (см., например, Куприянов, Шевченко, 2006; Мельников, Шевченко, 2022), что чем меньше размер небесного тела, тем более неправильную форму он имеет. Согласно табл. 2, диаметры всех рассмотренных нами астероидов малы (менее 250 м), поэтому для полуосей трехосного эллипсоида, аппроксимирующего фигуру астероида, было выбрано соотношение: a : b : c = 4 : 2 : 1. Предполагая однородную плотность тела астероида для отношений его моментов инерции, имеем: A/C = (b2 + + c2)/(a2 + b2) = 0.25, B/C = (a2 + c2)/(a2 + b2) = 0.85. Указанные значения использовались при численном моделировании вращательной динамики всех отобранных астероидов. Полученные в работе (Devyatkin и др., 2016) посредством моделирования вращательной динамики оценки параметров фигуры астероида (367 943) Duende и его моментов инерции близки к указанным величинам (см. также Benner и др., 2013; Benson и др., 2020): A/C = 0.3, B/C = 0.8. Указанные значения использовались нами при моделировании вращательной динамики (367943) Duende.
Суть проведенных численных экспериментов состояла в следующем: в начальной точке траектории астероида, расположенной на расстоянии 100RE от точки сближения астероида с планетой, мы задавали вращательное состояние астероида – величину вектора угловой скорости ω и ориентацию фигуры астероида в пространстве, определяемую углами Эйлера (θ, φ, ψ). После этого проводилось численное интегрирование поступательно-вращательного движения астероида на отрезке орбиты от начальной точки траектории до расстояния 100RE удаления астероида от точки сближения. Вычислялась величина ΔP = Pfin – Pin, где Pin – начальное заданное значение периода вращения астероида, Pfin – установленное финальное значение периода вращения, которым обладал астероид в конечной точке рассмотренной нами траектории. Были взяты разные значения начальных угловых скоростей вращения астероида: |ω| = 2π/Pin, где Pin = 1, …, 30 ч с шагом 1 ч; для компонент вектора угловой скорости было принято: ωa = 0, ωb = 0, ωc = |ω|. Также были рассмотрены различные ориентации фигуры астероида в пространстве, для начальных значений углов Эйлера принято: θ = ψ = 0°, φ = 0°, …, 180° с шагом Δφ = 10°. Таким образом, угол φ в начальной точке траектории определял наклон оси вращения астероида к плоскости орбиты планеты. Случай φ = 0° соответствует вращению астероида вокруг оси, ортогональной плоскости орбиты планеты и совпадающей с осью наибольшего момента инерции астероида.
В табл. 4 приведены полученные нами в численных экспериментах на всей выборке начальных данных (Pin, φ) максимальные значения изменений периодов собственного вращения астероидов ΔP с указанием соответствующих им значений Pin и φ. На рис. 1 представлены примеры диаграмм распределения значений |ΔP| на плоскости (Pin, φ), построенные для астероидов (367 943) Duende и 2015 TX24. Диаграммы, построенные для других астероидов, имели схожий вид. Нас интересовала лишь абсолютная величина изменения периода вращения астероида, поскольку на ее основе можно прогнозировать возможность наблюдения/выявления изменения вращательного состояния астероида посредством анализа наблюдений. В численных экспериментах наблюдалось как замедление, так и ускорение первоначально заданного вращения астероида. В случаях, представленных на рис. 1, для астероида (367 943) Duende примерно 81% рассмотренных начальных данных приводил к замедлению вращения астероида (увеличению периода вращения) после ТС с Землей, а для астероида 2015 TX24 замедление вращения после его сближения с Марсом установлено для ≈93% начальных данных. На рис. 1 для каждого астероида отдельно приведены выявленные отрицательные значения ΔP, соответствующие ускорению вращения астероида после ТС. Видно, что множество начальных данных, приводящих к ускорению вращения астероида, мало.
Таблица 4.
Максимальное изменение периода собственного вращения астероида ΔP после его сближения с планетой и начальные значения Pin и φ, соответствующие ему. Прочерк означает отсутствие сближений астероида с планетой на интервале времени 1900–2200 гг. Жирным шрифтом выделены выявленные максимальные значения ΔP > 10–2 ч
| Астероид | Меркурий | Венера | Земля | Марс |
|---|---|---|---|---|
| 2008 FP | – | ΔP = 2 × 10–3 ч, φ = 30°, Pin = 13 ч |
ΔP = 7 × 10–3 ч, φ = 40°, Pin = 9 ч |
– |
| 2009 WP6 | ΔP = 3 × 10–4 ч, φ = 10°, Pin = 3 ч |
ΔP = 3 × 10–3ч, φ = 30°, Pin = 3 ч |
ΔP = 2 × 10–3 ч, φ = 20°, Pin = 5 ч |
ΔP = 9 × 10–4 ч, φ = 70°, Pin = 12 ч |
| 2010 JJ41 | ΔP = 2 × 10–4 ч, φ = 40°, Pin = 7 ч |
ΔP = 6 × 10–3 ч, φ = 60°, Pin = 11 ч |
ΔP = 4 × 10–3 ч, φ = 20°, Pin = 12 ч |
ΔP = 1 × 10–3 ч, φ = 20°, Pin = 5 ч |
| 2015 EO61 | ΔP = 2 × 10–3 ч, φ = 20°, Pin = 15 ч |
ΔP = 5 × 10–3 ч, φ = 10°, Pin = 6 ч |
ΔP = 8 × 10–3 ч, φ = 80°, Pin = 17 ч |
ΔP = 3 × 10–3 ч, φ = 40°, Pin = 14 ч |
| 2015 TX24 | ΔP = 4 × 10–3 ч, φ = 50°, Pin = 11 ч |
ΔP = 2 × 10–2 ч, φ = 60°, Pin = 19 ч |
ΔP = 9 × 10–2 ч, φ = 80°, Pin = 13 ч |
ΔP = 1 × 10–1 ч, φ = 130°, Pin = 13 ч |
| 2015 XG55 | ΔP = 8 × 10–3 ч, φ = 20°, Pin = 8 ч |
ΔP = 8 × 10–2 ч, φ = 10°, Pin = 8 ч |
ΔP = 2 × 10–1 ч, φ = 30°, Pin = 9 ч |
ΔP = 9 × 10–3 ч, φ = 10°, Pin = 12 ч |
Рис. 1.
На верхних рисунках приведены зависимости величины изменения периода собственного вращения астероида |ΔP| (в часах) при его тесном сближении с планетой от начальных значений периода вращения астероида Pin и угла φ между осью вращения астероида и нормалью к его плоскости орбиты. На нижних рисунках приведены зависимости только с отрицательными значениями ΔP, соответствующие ускорению вращения астероида после ТС. Левая колонка: тесное сближение астероида (367 943) Duende с Землей 15.02.2013; белый цвет соответствует |ΔP| < 0.5 ч. Правая колонка: сближение астероида 2015 TX24 с Марсом 15.08.2039; белый цвет соответствует |ΔP| < 0.0001 ч.
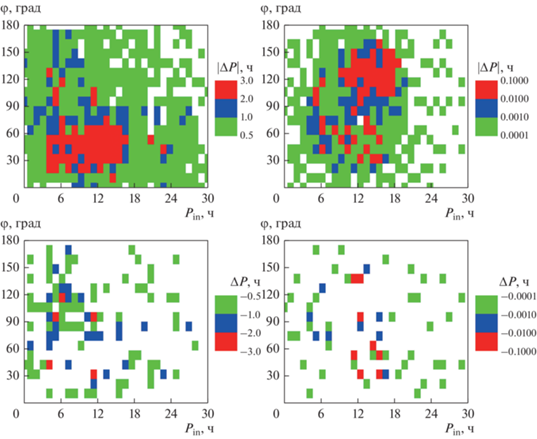
На рис. 2 для избранных начальных данных представлены примеры зависимостей изменения величины периода собственного вращения астероида от времени, построенные в окрестности точки сближения астероида с планетой. В случае астероида (367943) Duende приведено изменение P – текущей величины периода вращения. Поскольку величина P для астероида 2015 TX24 при его сближении с Марсом изменяется со временем мало (см. рис. 1), на рис. 2 приведено изменение относительной величины периода вращения: ΔPt = (P – Pin)/Pin. Для обоих астероидов полученные нами зависимости схожи с приведенными в работах других исследователей (Sharma и др., 2006; Benson и др., 2020; Boldrin и др., 2020).
Рис. 2.
Слева: Примеры зависимостей величины периода вращения P от времени t, полученные для астероида (367 943) Duende при его тесном сближении с Землей 15.02.2013, для разных начальных значений Pin и φ. Справа: Примеры зависимостей величины относительного изменения периода вращения от времени ΔPt= (P – Pin)/Pin, построенные для астероида 2015 TX24 при его сближении с Марсом 15.08.2039, для различных начальных значений Pin и φ. Момент времени t = 0 соответствует прохождению астероидом точки сближения.

На рис. 2 видно, что существенное изменение скорости вращения астероида происходит на интервале времени продолжительностью около суток в ближайшей окрестности от момента прохождения астероидом точки сближения.
Анализ примеров диаграмм, представленных на рис. 1, позволил выявить области начальных данных, которые соответствовали наибольшим изменениям скорости вращения астероида. Локальные максимумы значений ΔP, указанные в табл. 4, расположены именно в этих областях. В случае (367 943) Duende наибольшие установленные изменения скорости вращения астероида имели место для начальных данных, соответствующих прямому (с движением по орбите) вращению астероида: 10° <φ < 70° и 5 ч <Pin < 15 ч; максимальному изменению периода ΔP = 2.4 ч соответствовали начальные данные: φ = 40°, Pin = 12 ч. В представленном на рис. 1 случае сближения астероида 2015 TX24 с Марсом наибольшее изменение периода ΔP имело место для начальных данных, соответствующих обратному вращению астероида: 100° < φ < 150° и 9 ч <Pin < 18 ч. Максимальному изменению периода ΔP = 0.1 ч соответствовали начальные данные: φ = 130°, Pin = 13 ч. Анализ построенных нами диаграмм показал, что для всех рассмотренных астероидов начальное быстрое (Pin < 5 ч) и, напротив, медленное вращение (Pin > 18 ч) не приводили к существенному изменению скорости вращения астероида из-за его сближения с планетой (см. подробнее обсуждение в Sharma и др., 2006). Если рассмотреть направление вращения, то для всех астероидов и всех случаев сближений, за исключением сближения 2015 TX24 с Марсом 15.08.2039 (см. рис. 1), заметные изменения скорости вращения наблюдались только для случаев прямого вращения астероида (φ < 90°), что соответствует выводам других исследователей (Richardson и др., 1998; Scheeres, 2000; Sharma и др., 2006). Выявить закономерности среди начальных данных, для которых наблюдается ускорение вращения астероида после сближения с планетой (на рис. 1 этим данным соответствуют отрицательные значения ΔP), не представляется возможным.
Из результатов, представленных в табл. 4 и на рис. 1 и 2, следует, что скорости вращений рассмотренных астероидов при их сближениях с планетами изменяются незначительно. Это и следовало ожидать, поскольку траектории астероидов проходят довольно далеко от планет по сравнению, например, с траекторией астероида (367 943) Duende при его сближении с Землей в 2013 г. Величина изменения периода вращения астероида зависит также и от планеты, при сближении с Венерой период вращения изменяется на меньшую величину, чем при сближении с Землей или Марсом, что согласуется с выводами Scheeres и др. (2004). Современные методы и инструменты позволяют определять периоды вращения малых астероидов с точностью 10–4–10–6 ч (см., например, Lee и др., 2021; Podlewska‒Gaca и др., 2021; Zegmott и др., 2021). Поэтому выявленные нами величины изменений периодов вращения астероидов из-за их сближений с планетами можно определить посредством анализа даже современных наблюдений (в будущем их точность, несомненно, возрастет). Отметим, что для астероида (54 509) 2000 PH5, обладающего наибольшей известной величиной YORP-эффекта, скорость изменения периода вращения составляет около 10–5 ч/сут (Lowry и др., 2007). Поэтому даже далекое сближение астероида с планетой (на расстоянии порядка сотни радиусов Земли) оказывает влияние на скорость вращения астероида, сопоставимое с несколькими годами действия YORP-эффекта.
Итак, мы изучили влияние на вращательную динамику астероида при его сближении с планетой двух параметров – начального периода вращения астероида и наклона оси его вращения к плоскости орбиты. Варьируя другие параметры, при численном моделировании возможно найти более высокие, по сравнению с приведенными в табл. 4, значения ΔP. Данный вопрос был подробно рассмотрен нами на примере ТС астероида (367 943) Duende с Землей в 2013 г. Решалась обратная задача: посредством вариации установленных ранее (Devyatkin и др., 2016) значений параметров и начальных условий, характеризующих вращательную динамику астероида после ТС, определялся диапазон возможных значений P0 – периода вращения астероида до момента его ТС с Землей (схожая задача рассматривалась в работе (Benson и др., 2020)). Для этого было проведено интегрирование вращательной динамики (367 943) Duende назад во времени от момента задания параметров вращения астероида после ТС с Землей до момента времени за пять суток до ТС. В указанный момент времени дистанция между астероидом и Землей составляла около 3 × 106 км (≈490RE), т.е. астероид находился далеко за пределами сферы действия Земли. В качестве значений параметров и начальных условий, задающих вращательную динамику астероида, использовались (Devyatkin и др., 2016): A/C = 0.29 ± 0.09, B/C = 0.81 ± 0.14; θ = 1.82 ± 0.19, φ = 0.51 ± 0.16, ψ = 0.12 ± 0.06; ωa = (0.52 ± 0.10) ч–1, ωb = (0.19 ± 0.06) ч–1, ωc = (0.28 ± 0.04) ч–1, определенные на момент времени t0 = 16.62 ч после прохождения астероидом перигея его гиперболической относительно Земли орбиты. Приведенные значения соответствуют периоду вращения астероида P = 2π/|ω| ≈ 10.1 ч. При интегрировании в начальный момент времени мы варьировали значения одного из восьми указанных выше параметров в пределах его ошибки от минимальной до максимальной величины с шагом в 1/100 от величины интервала вариации, остальные значения параметров были фиксированы. В результате интегрирования на момент времени за пять суток до ТС определялась величина периода P0, которой астероид мог обладать до его сближения с Землей. Для каждого из варьируемых параметров определялись минимальное и максимальное возможные значения P0.
На рис. 3 представлены зависимости от параметров задачи и начальных условий размеров областей возможных значений периода вращения (367 943) Duende до момента его сближения с Землей. На рис. 3 видно, что на величину изменения периода вращения астероида из-за его тесного сближения с Землей существенным образом влияют значения моментов инерции и угловой скорости вращения астероида относительно оси, соответствующей максимальному моменту инерции. В большинстве случаев первоначальный период вращения астероида P0 отличается на два–три часа от периода, установленного из анализа наблюдений после момента ТС, что хорошо согласуется с результатами численного моделирования, проведенного Benson и др. (2020). Необходимо отметить, что результаты, представленные на рис. 3, позволяют сделать лишь предварительные выводы о возможной величине P0, поскольку при вариации значений параметров мы могли попасть на локальные минимумы/максимумы в пространстве возможных значений P0. Данный вопрос требует дополнительных трудоемких исследований, по моделированию вращательной динамики астероида на существенно большей выборке значений начальных данных и параметров.
Рис. 3.
Характерные размеры областей возможных значений P0 – периода собственного вращения астероида (367 943) Duende за пять суток до его тесного сближения с Землей 15.02.2013 в зависимости от вариаций значений параметров и начальных условий, характеризующих вращательную динамику астероида после сближения. Горизонтальная штриховая линия соответствует периоду вращения астероида P = 10.1 ч, установленному через ≈16 ч после момента сближения в работе (Devyatkin и др., 2016).

ВЫВОДЫ
В настоящей работе выполнено исследование вращательной динамики астероидов, сближающихся с планетами. Такое исследование, в частности, позволяет определить/уточнить физические параметры астероида (размеры, моменты инерции) и установить параметры его вращения (скорость вращения и ориентация оси вращения в пространстве). Проведены численные эксперименты по моделированию вращательной динамики шести астероидов, испытывающих последовательные сближения с несколькими планетами земной группы, и моделированию вращательной динамики АСЗ (367 943) Duende при его тесном сближении с Землей в 2013 г. Изучены зависимости величины изменения периода вращения астероида при его сближении с планетой от значения начальной скорости собственного вращения и ориентации оси вращения астероида в пространстве, заданных до момента сближения. Найденные максимальные изменения величины периода вращения для астероидов, сближающихся с несколькими планетами, составили 10–4–10–1 ч. Для случая АСЗ (367 943) Duende установленная максимальная величина изменения периода оказалась равной 2.4 ч. Полученные нами оценки изменения скорости вращения сближающихся с планетами астероидов позволяют в будущем посредством наблюдений и численного моделирования определить для них величину YORP-эффекта. Вероятно, у всех рассмотренных нами астероидов величина YORP-эффекта будет существенной. Результаты проведенного моделирования вращательной динамики АСЗ (367 943) Duende позволили сделать вывод о его скорости вращения до момента тесного сближения с Землей в 2013 г. Показано, что период собственного вращения (367 943) Duende за пять суток до тесного сближения с Землей отличался на 2–3 ч от величины периода, установленной из анализа полученных после момента сближения наблюдений (Devyatkin и др., 2016; Moskovitz и др., 2020).
Автор благодарит А.В. Девяткина и С.Н. Петрову за представленные данные об астероидах, сближающихся с планетами, и рецензентов за весьма полезные замечания.
Работа поддержана Российским фондом фундаментальных исследований (проект № 19-02-00811).
Список литературы
Батраков Ю.В., Медведев Ю.Д. О вращении астероида при его прохождении вблизи Земли // Тр. всесоюз. совещания “Астероидная опасность”. СПб: ИТА РАН, 1992. С. 129–133.
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965. 416 с.
Борисов А.В., Мамаев И.С. Динамика твердого тела. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2001. 384 с.
Воропаев С.А., Джианго Я., Барриот Ж.П. Разрыв вытянутого малого тела приливными силами Земли при подлете: возможные сценарии // Астрон. вестн. 2020. Т. 54. № 2. С. 171–182. (Voropaev S.A., Jianguo Y., Barriot J.P. Prolate body disruption by Earth at near flyby: Possible scenarios // Sol. Syst. Res. 2020. V. 54. № 2. P. 155–166.https://doi.org/10.1134/S003809462002008210.1134/S0038094620020082).https://doi.org/10.31857/S0320930X20020097
Девяткин А.В., Львов В.Н., Цекмейстер С.Д. Особые группы потенциально опасных астероидов // Астрон. вестн. 2022. Т. 56. № 1. С. 68–72. (Devyatkin A.V., Lvova V.N., Tsekmeister S.D. Special groups of potentially dangerous asteroids // Sol. Syst. Res. 2022. V. 56. № 1. P. 62–65.https://doi.org/10.1134/S003809462201002610.1134/S0038094622010026).https://doi.org/10.31857/S0320930X22010029
Куприянов В.В. Численно-экспериментальное исследование вращательной динамики спутников планет // Дисс. канд. физ.-мат. наук. СПб: ГАО РАН, 2014. 148 с.
Куприянов В.В., Шевченко И.И. О форме и вращательной динамике малых спутников планет // Астрон. вестн. 2006. Т. 40. № 5. С. 428–435. (Kouprianov V.V., Shevchenko I.I. The shapes and rotational dynamics of minor planetary satellites // Sol. Syst. Res. 2006. V. 40. № 5. P. 393–399).https://doi.org/10.1134/S0038094606050042
Мельников А.В. Ориентация фигур малых спутников планет при хаотическом вращении // Астрон. вестн. 2020. Т. 54. № 5. С. 458–467.(Melnikov A.V. Orientation of figures of small planetary satellites during chaotic rotation // Sol. Syst. Res. 2020. V. 54. № 5. P. 432–441. https://doi.org/10.1134/S003809462005006810.1134/S0038094620050068).https://doi.org/10.31857/S0320930X20050060
Мельников А.В., Шевченко И.И. Вращательная динамика и эволюция спутников планет Солнечной и экзопланетных систем // Астрон. вестн. 2022. Т. 56. № 1. С. 3–26. (Melnikov A.V., Shevchenko I.I. Rotational dynamics and evolution of planetary satellites in the Solar and exoplanetary systems // Sol. Syst. Res. 2022. V. 56. № 1. P. 1–22.https://doi.org/10.1134/S003809462201004X10.1134/S003809462201004X).https://doi.org/10.31857/S0320930X22010042
Пашкевич В.В., Вершков А.Н. Релятивистский эффект геодезической прецессии во вращении карликовых планет и астероидов Солнечной системы // Астрон. вестн. 2022. Т. 56. № 3. С. (в печати).
Asphaug E., Scheeres D.J. Deconstructing Castalia: Evaluating a postimpact state // Icarus. 1999. V. 139. № 2. P. 383–386.
Benner L., Brozovic M., Giorgini J.D., Jao J.S., Lee C.G., Busch M.W., Slade M.A. Goldstone Radar Images of Near-Earth Asteroid 2012 da14 (101.02) // Am. Astron. Soc. DPS meeting. № 45. 2013. id. 101.02.
Benson C.J., Scheeres D.J., Moskovitz N.A. Spin state evolution of asteroid (367943) Duende during its 2013 Earth flyby // Icarus. 2020. V. 340. id. 113518.
Black G.J., Nicholson P.D., Bottke W.F., Burns J.A., Harris A.W. NOTE: On a Possible Rotation State of (433) Eros // Icarus. 1999. V. 140. № 1. P. 239–242.
Boldrin L.A.G., Araujo R.A.N., Winter O.C. On the rotational motion of NEAs during close encounters with the Earth // European Phys. J. – Special Topics. 2020. V. 229. № 8. P. 1391–1403.
Bowell E., Hapke B., Domingue D., Lumme K., Peltoniemi J., Harris A.W. Application of photometric models to asteroids // Asteroids II. Proc. Conf. Tucson: Univ. Arizona Press, 1989. P. 524–553.
Devyatkin A.V., Gorshanov D.L., Yershov V.N., Melnikov A.V., Martyusheva A.A., Petrova S.N., L’vov V.N., Tsekmeister S.D., Naumov K.N. A study of the asteroid (367943) Duende at Pulkovo Observatory // Mon. Notic. Roy. Astron. Soc. 2016. V. 459. № 4. P. 3986–3997.
Ďurech J., Sidorin V., Kaasalainen M. DAMIT: a database of asteroid models // Astron. and Astrophys. 2010. V. 513. id. A46.
Ershkov S.V., Shamin R.V. The dynamics of asteroid rotation, governed by YORP effect: The kinematic ansatz // Acta Astronautica. 2018. V. 149. P. 47–54.
Folkner W.M., Williams J.G., Boggs D.H., Park R.S., Kuchynka P. The Planetary and Lunar Ephemerides DE430 and DE431 // IPN Progress Report 42-196. 2014. P. 1–81.
Hairer E., Nørsett S.P., Wanner G. Solving Ordinary Differential Equations I. Nonstiff Problems. Berlin: Springer-Verlag, 1993. 528 p.
Henych T., Pravec P. Asteroid rotation excitation by subcatastrophic impacts // Mon. Notic. Roy. Astron. Soc. 2013. V. 432. Iss. 4. P. 1623–1631.
Lee H.-J., Ďurech J., Vokrouhlický D., Pravec P., Moon H.-K., Ryan W., Kim M.-J., Kim C.-H., Choi Y.-J., Bacci P., Pollock J., Apitzsch R. Spin change of asteroid 2012 TC4 probably by R radiation torques // Astron. J. 2021. V. 161. № 3. id. 112.
Lowry S.C., Fitzsimmons A., Pravec P., Vokrouhlický D., Boehnhardt H., Taylor P.A., Margot J.-L., Galád A., Irwin M., Irwin J., Kusnirák P. Direct detection of the asteroidal YORP effect // Science. 2007. V. 316 (5822). P. 272–274.
Moskovitz N.A., Benson C.J., Scheeres D., Endicott T., Polishook D., Binzel R., DeMeo F., Ryan W., Ryan E., Willman M., Hergenrother C., Verveer A., Lister T., Birtwhistle P., Sickafoose A., Nagayama T., Gilmore A., Kilmartin P., Benecchi S., Sheppard S., Marchis F., Augusteijn T., Smirnova O. Observational investigation of the 2013 near-Earth encounter by asteroid (367943) Duende // Icarus. 2020. V. 340. id. 113519.
Podlewska‒Gaca E., Poleski R., Bartczak P., McDonald I., Pál A. Determination of rotation periods for a large sample of asteroids from the K2 campaign 9 // Astrophys. J. Suppl. Ser. 2021. V. 255. № 1. id. 4.
Pravec P., Harris A.W., Scheirich P., Kušnirák P., Šarounová L., Hergenrother C.W., Mottola S., Hicks M.D., Masi G., Krugly Yu.N., Shevchenko V.G., Nolan M.C., Howell E.S., Kaasalainen M., Galád A., Brown P., DeGraff D.R., Lambert J.V., Cooney W.R., Foglia S. Tumbling asteroids // Icarus. 2005. V. 173 (1). P. 108–131.
Pravec P., Scheirich P., Ďurech J., Pollock J., Kušnirák P., Hornoch K., Galád A., Vokrouhlický D., Harris A.W., Jehin E., Manfroid J., Opitom C., Gillon M., Colas F., Oey J., Vraštil J., Reichart D., Ivarsen K., Haislip J., LaCluyze A. The tumbling spin state of (99942) Apophis // Icarus. 2014. V. 233. P. 48–60.
Richardson D.C., Bottke W.F., Love S.G. Tidal distortion and disruption of Earth-crossing asteroids // Icarus. 1998. V. 134. P. 47–76.
Rubincam D.P. Radiative spin-up and spin-down of small asteroids // Icarus. 2000. V. 148. P. 2–11.
Scheeres D.J., Ostro S.J., Werner R.A., Asphaug E., Hudson R.S. Effects of gravitational interactions on asteroid spin states // Icarus. 2000. V. 147. P. 106–118.
Scheeres D.J., Marzari F., Rossi A. Evolution of NEO rotation rates due to close encounters with Earth and Venus // Icarus. 2004. V. 170. P. 312–323.
Scheeres D.J., Benner L.A.M., Ostro S.J., Rossi A., Marzari F., Washabaugh P. Abrupt alteration of Asteroid 2004 MN4's spin state during its 2029 Earth flyby // Icarus. 2005. V. 178. № 1. P. 281–283.
Sharma I., Jenkins J.T., Burns J.A. Tidal encounters of ellipsoidal granular asteroids with planets // Icarus. 2006. V. 183. № 2. P. 312–330.
Souchay J., Lhotka C., Heron G., Hervé Y., Puente V., Folgueira Lopez M. Changes of spin axis and rate of the asteroid (99942) Apophis during the 2029 close encounter with Earth: A constrained model // Astron. and Astrophys. 2018. V. 617. id. A74.
Takahashi Yu., Busch M.W., Scheeres D.J. Spin state and moment of inertia characterization of 4179 Toutatis // Astron. J. 2013. V. 146. № 4. id. 95.
Walsh K.J. Rubble Pile Asteroids // Ann. Rev. Astron. and Astrophys. 2018. V. 56. P. 593–624.
Whittaker E.T. A Treatise on the Analytical Dynamics of particles and rigid bodies. Cambridge: Cambridge Univ. Press, 1917. 432 p.
Wisdom J., Peale S.J., Mignard F. The chaotic rotation of Hyperion // Icarus. 1984. V. 58. № 2. P. 137–152.
Zegmott T.J., Lowry S.C., Rożek A., Rozitis B., Nolan M.C., Howell E.S., Green S.F., Snodgrass C., Fitzsimmons A., Weissman P.R. Detection of the YORP effect on the contact binary (68346) 2001 KZ66 from combined radar and optical observations // Mon. Notic. Roy. Astron. Soc. 2021. V. 507. № 4. P. 4914–4932.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник



