Астрономический вестник, 2022, T. 56, № 4, стр. 266-284
Численное моделирование динамики искусственных спутников Луны
Н. А. Попандопуло a, *, **, А. Г. Александрова a, ***, И. В. Томилова a, ****, В. А. Авдюшев a, *****, Т. В. Бордовицына a, ******
a Томский государственный университет
Томск, Россия
* E-mail: nikas.popandopulos@gmail.com
** E-mail: aleksann@sibmail.com
*** E-mail: aleksandrovaannag@mail.ru
**** E-mail: irisha_tom@mail.ru
***** E-mail: scharmn@mail.ru
****** E-mail: tvbord@sibmail.com
Поступила в редакцию 18.11.2021
После доработки 14.02.2022
Принята к публикации 14.02.2022
- EDN: CATLGU
- DOI: 10.31857/S0320930X22040077
Аннотация
В работе представлены описание численной модели движения искусственных спутников Луны (ИСЛ), разработанной авторами, и результаты исследования особенностей динамики объектов в окололунном пространстве. Было проведено численное моделирование движения 5180 объектов, равномерно распределенных в окололунном пространстве. Показано, что в ряде областей окололунного пространства время жизни ИСЛ на орбитах весьма мало в зависимости от выбора начального значения большой полуоси и наклонения, и выяснены причины этого явления. Данные результаты могут быть использованы при выборе стратегии размещения спутниковых систем долговременного использования в окололунном орбитальном пространстве.
ВВЕДЕНИЕ
Планируемое международным сообществом освоение Луны предполагает интенсивное исследование нашего естественного спутника с помощью космических аппаратов, а также создание окололунных спутниковых систем различного назначения. Одним из подготовительных этапов к созданию таких систем является детальное изучение динамической структуры окололунного пространства, т.е. выявление областей влияния различных возмущений на движение искусственных спутников Луны (ИСЛ). Это, в свою очередь, подразумевает создание программного математического обеспечения (ПМО) для прогнозирования и исследования движения ИСЛ. Такое ПМО может использоваться и в разнообразных практических целях, например, оценивания времени жизни моделируемого спутника на орбите; определения оптимальных начальных параметров орбиты космического аппарата и т.п.
Численные модели ИСЛ широко используются в исследованиях зарубежных авторов. Например, в статье (Song и др., 2010) авторы описали собственную численную модель и проведенные с ее помощью исследования особенностей орбитальной эволюции низколетящих спутников. В работе (Gupta, Sharma, 2011) исследуется влияние наклонения, аргумента перицентра и долготы восходящего узла круговой орбиты на продолжительность жизни объекта на орбите с помощью открытого ПМО “lprop”. Авторы статьи (Ramanan, Adimurthy, 2005) рассматривают особенности динамики окололунных спутников в зависимости от положения спутника, от порядка и степени гармоник селенопотенциала и т.д.
Представляемая здесь “Численная модель движения ИСЛ” (“ЧМД ИСЛ”) предназначена для исследования динамической структуры окололунного орбитального пространства, поэтому для повышения быстродействия в ней используется новый интегратор (Авдюшев, 2020), более эффективный по сравнению с предыдущей версией (Авдюшев, 2010). Совместно с уравнениями движения интегрируются уравнения для вычисления осредненного параметра MEGNO, позволяющего судить о хаотичности движения космических объектов (Александрова и др., 2017; Valk и др., 2009).
“ЧМД ИСЛ” позволяет учитывать возмущения от селенопотенциала до 1199-го порядка и степени (Spherical Harmonic ASCII Model, 2021), влияние приливных деформаций поверхности Луны, гравитационные влияния Земли и Солнца, а также возмущения от светового давления.
Для реализации полностью численного подхода к исследованию влияния вековых резонансов разработанная численная модель расширена возможностью вычисления вековых частот в движении ИСЛ с помощью точных формул (Александрова и др., 2020).
ЧИСЛЕННАЯ МОДЕЛЬ ДВИЖЕНИЯ ИСЛ
Уравнения движения ИСЛ и модель сил
Будем рассматривать движение искусственного спутника Луны как движение материальной точки бесконечно малой массы в поле тяготения центрального тела с массой M под действием сил, определенных потенциальными функциями U и R.
Дифференциальные уравнения движения ИСЛ в инерциальной прямоугольной системе координат, связанной с центром масс Луны, при сделанных предположениях имеют следующий вид:
(1)
$\frac{{{\text{d}}{\mathbf{x}}}}{{{\text{d}}t}} = {\mathbf{\dot {x}}},\,\,\,\,\frac{{{\text{d}}{\mathbf{\dot {x}}}}}{{{\text{d}}t}} = \frac{{\partial U}}{{\partial {\mathbf{x}}}} + \frac{{\partial R}}{{\partial {\mathbf{x}}}}$(2)
${{{\mathbf{x}}}_{0}} = {\mathbf{x}}({{t}_{0}}),\,\,\,\,{{{\mathbf{\dot {x}}}}_{0}} = {\mathbf{\dot {x}}}({{t}_{0}}),$В связи с тем, что потенциал гравитационного поля отнесен к вращающейся системе координат, жестко связанной с центральным телом, а уравнения (1) записаны в инерциальной системе координат, необходимо использовать преобразования, связывающие эти системы.
В программном комплексе дифференциальные уравнения движения интегрируются в инерциальной системе координат, связанной с экватором Земли на эпоху J2000.0. Данный выбор системы координат был сделан во избежание дополнительных переходов между системами при учете возмущений от третьих тел.
Для перехода из земной инерциальной системы координат в лунную вращающуюся систему используется следующее соотношение:
(3)
$\frac{{\partial U}}{{\partial {\mathbf{x}}}} = {{\left[ {{{R}_{Z}}\left( \alpha \right){{R}_{X}}\left( \beta \right){{R}_{Z}}\left( \gamma \right)} \right]}^{T}}\frac{{\partial V}}{{\partial {\mathbf{x}}{\kern 1pt} '}},$Потенциал притяжения Луны, действующий на внешнюю точку, будем представлять следующим образом (Аксенов, 1977):
(4)
$\begin{gathered} V = \frac{\mu }{{{{R}_{L}}}}\sum\limits_{n = 0}^\infty {\sum\limits_{m = 0}^n {{{{\left( {\frac{{{{R}_{L}}}}{r}} \right)}}^{{n + 1}}}{{{\bar {P}}}_{{n,m}}}\left( {\sin \varphi } \right)} \times } \\ \times \,\,\left( {{{{\bar {C}}}_{{n,m}}}\cos m\lambda + {{{\bar {S}}}_{{n,m}}}\sin m\lambda } \right), \\ \end{gathered} $Для вычисления потенциала и его производных в численной модели используется рекуррентный алгоритм, предложенный Cunningham (1970). Возмущения от приливных деформаций в теле Луны под действием притяжения Земли и Солнца вводятся как поправки в свободные от приливов коэффициенты ${{\bar {C}}_{{n,m}}},{\text{ }}{{\bar {S}}_{{n,m}}}$ разложения гравитационного поля Луны (4) и осуществляется только в рамках модели Лява (Petit, Luzum, 2010). Задача сводится к вычислению поправок, обусловленных частотно независимыми величинами ${{k}_{{nm}}}$, по формуле:
(5)
$\begin{gathered} \Delta {{{\bar {C}}}_{{n,m}}} - \Delta {{{\bar {S}}}_{{n,m}}} = \frac{{{{k}_{{nm}}}}}{{2n + 1}} \times \\ \times \,\,{{\sum\limits_{j = 2}^3 {\frac{{{{\mu }_{j}}}}{\mu }\left( {\frac{{{{R}_{L}}}}{{{{r}_{j}}}}} \right)} }^{{n + 1}}}{{{\bar {P}}}_{{nm}}}\left( {\sin {{\Phi }_{j}}} \right){{e}^{{ - im{{\Lambda }_{j}}}}}, \\ \end{gathered} $Для учета влияния третьего тела на движение ИСЛ используется известная формула (Дубошин, 1976):
(6)
$\frac{{\partial R}}{{\partial {{x}_{i}}}} = {{\mu }}{\kern 1pt} {\text{'}}\left( {\frac{{{{{\tilde {x}}}_{i}} - {{x}_{i}}}}{{{{\Delta }^{3}}}} - \frac{{{{{\tilde {x}}}_{i}}}}{{\tilde {r}{\kern 1pt} {{'}^{3}}}}} \right),$Возмущающие влияния третьих тел на движение спутника будем считать независимыми друг от друга. При одновременном учете возмущений от Земли и Солнца в правой части уравнений (1) будут присутствовать два слагаемых типа (6). Для вычисления координат возмущающих тел используется фонд DE438/LE438 (Folkner, Park, 2018), предназначенный для высокоточных вычислений на временном интервале (1550–2650 гг.).
Учет влияния светового давления и связанных с ним эффектов на движение околоземных объектов можно представить как (Авдюшев, 2015)
(7)
${\mathbf{P}} = L\frac{{\mathbf{x}}}{{\left| {\mathbf{x}} \right|}} - L\left( {\frac{{{\mathbf{\dot {x}}} \cdot {\mathbf{x}}}}{{c\left| {\mathbf{x}} \right|}}\frac{{\mathbf{x}}}{{\left| {\mathbf{x}} \right|}} + \frac{{\mathbf{x}}}{c}} \right),\,\,\,\,L = \kappa \theta \frac{{a_{{\text{E}}}^{2}}}{{{{{\left| {\mathbf{x}} \right|}}^{2}}}}\frac{\sigma }{m},$Влияние давления излучения на спутник будет не точным, если не учитывать периоды нахождения спутника в тени Луны или Земли. Поэтому формулу (7) нужно дополнить параметром функции тени $\Phi $.
Функция тени $\Phi $ для окололунного объекта при использовании “конусной” световой модели имеет вид
(8)
$\Phi = \left\{ \begin{gathered} 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{если }}\upsilon \leqslant \left| {{{r}_{{\text{S}}}} - {{r}_{{\text{E}}}}} \right|\,\,{\text{и}}\,\,{{r}_{{\text{E}}}} < {{r}_{{\text{S}}}} \hfill \\ 1 - \frac{{{{s}_{{{\text{SE}}}}}}}{s},\,\,\,{\text{если }}\upsilon > \left| {{{r}_{{\text{S}}}} - {{r}_{{\text{E}}}}} \right| \hfill \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{если }}\upsilon \leqslant \left| {{{r}_{{\text{S}}}} - {{r}_{{\text{E}}}}} \right|\,\,{\text{и}}\,\,{{r}_{{\text{E}}}} \geqslant {{r}_{{\text{S}}}} \hfill \\ \end{gathered} \right.,$(9)
$\begin{gathered} s = \pi r_{{\text{S}}}^{2},\,\,\,\,{{s}_{{{\text{SE}}}}} = \frac{{r_{{\text{S}}}^{2}}}{2}({{\varphi }_{{\text{S}}}} - sin{{\varphi }_{{\text{S}}}}) + \\ + \,\,\frac{{r_{{\text{E}}}^{2}}}{2}({{\varphi }_{{\text{E}}}} - sin{{\varphi }_{{\text{E}}}}). \\ \end{gathered} $Величины ${{\varphi }_{{\text{S}}}}$ и ${{\varphi }_{{\text{E}}}}$ – это углы между радиальным направлением из центров дисков в точки пересечения их границ и они определяются как
(10)
$\begin{gathered} {{\varphi }_{{\text{S}}}} = 2\arccos \left( {\frac{{{{r}^{2}} + r_{{\text{S}}}^{2} - r_{{\text{E}}}^{2}}}{{2r{{r}_{{\text{S}}}}}}} \right), \\ {{\varphi }_{{\text{E}}}} = 2\arccos \left( {\frac{{{{r}^{2}} + r_{{\text{E}}}^{2} - r_{{\text{S}}}^{2}}}{{2r{{r}_{{\text{E}}}}}}} \right). \\ \end{gathered} $Интегратор
Уравнения движения интегрируются с помощью колокационного интегратора Lobbie (Александрова и др., 2021a; Авдюшев, 2020) высокого порядка с переменным шагом, разработанного В.А. Авдюшевым и представляющего собой развитие интегратора Эверхарта (Авдюшев, 2010).
Интегрирование дифференциальных уравнений движения производится при переменном шаге, но есть возможность использовать постоянный шаг. Выбор шага интегрирования производится по следующей формуле:
(11)
$h* = h{{\left( {\frac{{{{{\left\| {\mathbf{e}} \right\|}}_{{tol}}}}}{{{{{\left\| {\mathbf{e}} \right\|}}_{{cal}}}}}} \right)}^{{\frac{1}{{p + 1}}}}},$Оценка точности интегратора была проведена путем сравнения с эталонной орбитой. Для оценки был выбран модельный низколетящий объект с высотой полета 100 км над поверхностью Луны, с круговой орбитой и нулевым наклонением. Прогнозирование движения для обоих методов осуществлялось на 1 год.
В программном комплексе для выбора шага интегрирования задается параметр LL, который связан с задаваемой точностью следующим образом: ${{\left\| {\mathbf{e}} \right\|}_{{tol}}} = {{10}^{{ - LL}}}$. В качестве эталонной орбиты была выбрана орбита, которая была получена интегрированием уравнений движения методом 16-го порядка и параметром LL, равным 10, на 64-битной разрядной сетке. При этом учитывались такие возмущающие факторы, как несферичность Луны до гармоник 50-го порядка и степени, приливные деформации в теле Луны, а также возмущения от притяжения Земли и Солнца. Результаты оценки точности, полученной вышеупомянутым способом, представлены на рис. 1.
Сравнение с результатами других авторов
ПМО “Численная модель движения ИСЛ” было протестировано на результатах, опубликованных другими авторами.
В статье (Gupta, Sharma, 2011) была проведена оценка влияния начальной эпохи на время жизни на круговой орбите (промежуток времени от начала движения спутника до его столкновения с поверхностью Луны) полярного спутника на высоте 100 км. Исследование проводилось на двух численных моделях движения – “lprop” и “STK”. В табл. 2 приведены данные, которые позволяют сравнить оценки, полученные указанными выше авторами, с оценками, полученными с использованием разработанного нами программного комплекса.
Таблица 2.
Сравнение оценок времени жизни на круговой полярной орбите с высотой 100 км над поверхностью в зависимости от начальной эпохи
| Начальная эпоха | Время жизни на орбите, сутки | ||
|---|---|---|---|
| модель “lprop” | модель “STK” | “ЧМД ИСЛ” | |
| 1 января 2010 | 219.04 | 219.24 | 219.19 |
| 1 января 2011 | 182.04 | 182.16 | 182.11 |
| 1 января 2012 | 172.00 | 172.06 | 172.01 |
| 1 января 2013 | 186.13 | 186.32 | 186.19 |
| 1 января 2014 | 178.71 | 178.78 | 178.73 |
| 1 января 2015 | 166.67 | 166.63 | 166.75 |
| 1 января 2016 | 186.08 | 186.28 | 186.23 |
Как видно из табл. 2, результаты очень близки между собой. Расхождение при сравнении с моделью “lprop” составляет в среднем 0.08%, а при сравнении с “STK” – 0.04%.
Кроме того, были проведены сравнения наших результатов с оценками, приведенными в (Song и др., 2010). Статья посвящена описанию возможностей модели движения окололунных объектов “YSPLOP”. В данной статье приведены полученные с помощью “YSPLOP” оценки влияния селенопотенциала на время жизни на круговой орбите полярного спутника с высотой полета 100 км. При получении оценок использовалась модель гравитационного поля Луны LP165P (Konopliv и др., 2001). Влияние Земли и Солнца не учитывалось. Результаты представлены в табл. 3.
Таблица 3.
Сравнение оценок времени жизни на круговой полярной орбите с высотой 100 км над поверхностью в зависимости от порядка и степени селенопотенциала
| Порядок × степень гравитационной модели LP165P | Время жизни на орбите, сутки | |
|---|---|---|
| Модель “YSPLOP” | “ЧМД ИСЛ” | |
| 70 × 70 | 161.12 | 161.06 |
| 65 × 65 | 163.36 | 163.51 |
| 60 × 60 | 163.42 | 163.43 |
| 55 × 55 | 161.20 | 161.30 |
| 50 × 50 | 163.42 | 163.43 |
| 45 × 45 | 146.17 | 146.17 |
| 40 × 40 | 146.00 | 146.00 |
| 35 × 35 | 146.15 | 146.17 |
| 30 × 30 | 131.46 | 131.73 |
| 25 × 25 | 198.75 | 199.11 |
| 20 × 20 | 221.58 | 221.28 |
| 15 × 15 | >2 лет | >2 лет |
| 10 × 10 | >2 лет | >2 лет |
Результаты, приведенные в табл. 3, показывают близость оценок, полученных в (Song и др., 2010) и в данном исследовании. Различие в среднем составляет 0.04%.
Данное исследование говорит о том, что при учете гравитационного поля, начиная с гармоник 50-го порядка и степени, время жизни объекта на орбите колеблется незначительно. Поэтому в нашей работе в качестве полного гравитационного поля Луны мы учитываем селенопотенциал до гармоник 50-го порядка и степени.
Было проведено еще одно сравнение с результатами тех же авторов: сравнивались графики зависимости высоты перицентра hp (величина отсчитывается от поверхности Луны) от времени прогнозирования при учете и без учета возмущений от третьих тел. Спутник, как и прежде полярный, и движется по круговой орбите на высоте 100 км над поверхностью Луны. Результат представлен на рис. 2. Полученный нами график имеет полное визуальное сходство с рис. 2 из работы (Song и др., 2010). Поскольку влияние Солнца мало, красная и синяя линии на рис. 2 почти полностью совпадают.
Рис. 2.
Зависимость высоты перицентра от времени для низколетящего полярного спутника на круговой орбите.

Таким образом, разработанный программный комплекс “Численная модель движения ИСЛ” дает результаты, либо совпадающие, либо близкие к оценкам, полученным другими авторами, что говорит о надежности решений, получаемых с помощью представленного здесь ПМО.
МЕТОДИКА ВЫЯВЛЕНИЯ И ИССЛЕДОВАНИЯ ВЕКОВЫХ РЕЗОНАНСОВ
Как и в наших последних работах по динамике ИСЗ (Александрова и др., 2021б; 2020) аналитический подход здесь используется для обозначения вековых резонансов, выявление которых осуществляется численно. С помощью этого подхода мы просто фиксируем те резонансы, влияние которых мы будем в дальнейшем исследовать путем численного моделирования с применением программного комплекса “ЧМД ИСЛ”.
Запишем аргумент возмущающей функции в виде
(12)
$\begin{gathered} \psi = \left( {l - 2p{\kern 1pt} '\,\, + q{\kern 1pt} '} \right)\lambda {\kern 1pt} '\,\, - \left( {l - 2p + q} \right)\lambda - \\ - \,\,q{\kern 1pt} '\varpi {\kern 1pt} '\,\, + q\varpi + \left( {\bar {m} - l + 2p{\kern 1pt} '} \right)\Omega {\kern 1pt} '\,\, - \left( {\bar {m} - l + 2p} \right)\Omega {\kern 1pt} \,. \\ \end{gathered} $Здесь $\lambda = \varpi + M$, $\lambda {\kern 1pt} ' = \varpi {\kern 1pt} '\,\, + M{\kern 1pt} '$ – средние долготы спутника и третьего тела, соответственно, $\varpi = \Omega + \omega $, $\varpi {\kern 1pt} ' = \Omega {\kern 1pt} '\,\, + \omega {\kern 1pt} '$ – долготы перицентра спутника и возмущающего тела. Элементы $i,\Omega ,i{\kern 1pt} ',\Omega {\kern 1pt} '$ отнесены к экватору Луны.
Будем полагать, что на спутник оказывают влияние следующие факторы: сжатие Луны, описываемое второй зональной гармоникой селенопотенциала, притяжение от Земли и Солнца, рассматриваемых как материальные точки, движущиеся по эллипсам с вращающимися линями апсид и узлов. При сделанных предположениях аргумент разложения возмущающей функции в ряд в однократно осредненной задаче запишется в виде:
(13)
$\begin{gathered} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } = (l - 2p{\kern 1pt} '\,\, + q{\kern 1pt} ')M{\kern 1pt} '\,\, - (l - 2p)\omega + \\ + \,\,(l - 2p{\kern 1pt} ')\omega {\kern 1pt} '\,\, - \bar {m}(\Omega - \Omega {\kern 1pt} '), \\ \end{gathered} $(14)
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = (l - 2p{\kern 1pt} ')\omega {\kern 1pt} '\,\, - (l - 2p)\omega - \bar {m}(\Omega - \Omega {\kern 1pt} '),$(15)
$\begin{gathered} M{\kern 1pt} ' = M_{0}^{'} + \bar {n}{\kern 1pt} '\left( {t - {{t}_{0}}} \right),\,\,\,\,\omega {\kern 1pt} ' = \omega _{0}^{'} + \dot {\omega }{\kern 1pt} '\left( {t - {{t}_{0}}} \right), \\ \Omega {\kern 1pt} ' = \Omega _{0}^{'} + \dot {\Omega }{\kern 1pt} '\left( {t - {{t}_{0}}} \right), \\ \omega = {{\omega }_{0}} + \dot {\omega }\left( {t - {{t}_{0}}} \right),\,\,\,\Omega = {{\Omega }_{0}} + \dot {\Omega }\left( {t - {{t}_{0}}} \right). \\ \end{gathered} $Условие возникновения резонанса может быть представлено следующими выражениями:
(16)
$\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } \approx 0,\,\,\,\,\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } } \approx 0.$Будем называть выражения (16) резонансными соотношениями, а соотношения (13) и (14) резонансными аргументами или критическими углами. Вековые частоты в движении спутника
(17)
$\dot {\Omega } = {{\dot {\Omega }}_{{{{J}_{2}}}}} + {{\dot {\Omega }}_{{\text{E}}}} + {{\dot {\Omega }}_{{\text{S}}}},\,\,\,\,\dot {\omega } = {{\dot {\omega }}_{{{{J}_{2}}}}} + {{\dot {\omega }}_{{\text{E}}}} + {{\dot {\omega }}_{{\text{S}}}}$Считая влияния Земли и Солнца аддитивными, с учетом формул (12)–(15) получим левые части резонансных соотношений (16), определяющие наличие вековых резонансов низких порядков для однократно и двукратно осредненных задач трех тел: Луна–спутник–Земля, Луна–спутник–Солнце. Для краткости будем называть левую часть резонансного соотношения (16) типом резонансного соотношения.
Принцип выявления того или иного резонанса в динамике орбитального движения объекта заключается в исследовании малости соотношений (16) для индексов l, p, $p{\kern 1pt} ',$ q, $q{\kern 1pt} '$ и $\bar {m}$ (Cook, 1962). Далее для тех же значений индексов рассматривается эволюция во времени критических аргументов, описываемых соотношениями (13) и (14) (Rossi, 2008; Александрова и др., 2021б; 2020). Это необходимо (Мюррей, Дермотт, 2010; Морбиделли, 2014), чтобы определить, какой характер имеют резонансные характеристики. При либрационном изменении соотношений (13) и (14) резонансные конфигурации имеют устойчивый характер, а при переходе от либрационного изменения к циркуляционному – неустойчивый. В случае чисто циркуляционного изменения критического аргумента считается, что резонанс отсутствует. Чтобы определить значения элементов орбиты спутника при исследовании долговременной эволюции во времени соотношений (16), (13) и (14), используется численное моделирование.
Вековые частоты $\dot {\omega },\,\,\dot {\Omega }$, входящие в формулу (17), определяются численно, с использованием уравнений Ньютона–Эйлера
(18)
$\begin{gathered} \frac{{{\text{d}}\Omega }}{{{\text{d}}t}} = \frac{r}{p}\frac{{\sin u}}{{\sin i}}W;\,\,\,\,\frac{{{\text{d}}\omega }}{{{\text{d}}t}} = - \frac{{\cos \upsilon }}{e}S + \\ + \,\,\frac{{\sin \upsilon }}{e}\left( {1 + \frac{r}{p}} \right)T - \frac{r}{p}\frac{{\sin u}}{{\operatorname{tg} i}}W, \\ \end{gathered} $(19)
$\begin{gathered} {{{\dot {\Omega }}}_{{{{J}_{2}}}}} = - \frac{3}{2}{{J}_{2}}\bar {n}{{\left( {\frac{{{{r}_{0}}}}{a}} \right)}^{2}}\cos i{{(1 - {{e}^{2}})}^{{ - 2}}}, \\ {{{\dot {\omega }}}_{{{{J}_{2}}}}} = \frac{3}{4}{{J}_{2}}\bar {n}{{\left( {\frac{{{{r}_{0}}}}{a}} \right)}^{2}}\frac{{5{{{\cos }}^{2}}i - 1}}{{{{{(1 - {{e}^{2}})}}^{2}}}}, \\ \end{gathered} $(20)
$\begin{gathered} {{{\dot {\Omega }}}_{{{\text{E,S}}}}} = - \frac{3}{{16}}\bar {n}\frac{{{{\mu }_{{{\text{E,S}}}}}}}{\mu }{{\left( {\frac{a}{{{{a}_{{{\text{E,S}}}}}}}} \right)}^{3}} \times \\ \times \,\,\frac{{2 + 3{{e}^{2}}}}{{\sqrt {1 - {{e}^{2}}} }}(2 - 3{{\sin }^{2}}{{i}_{{{\text{E,S}}}}})\cos i, \\ {{{\dot {\omega }}}_{{{\text{E,S}}}}} = \frac{3}{{16}}\bar {n}\frac{{{{\mu }_{{{\text{E,S}}}}}}}{\mu }{{\left( {\frac{a}{{{{a}_{{{\text{E,S}}}}}}}} \right)}^{3}} \times \\ \times \,\,\frac{{4 - 5{{{\sin }}^{2}}i + {{e}^{2}}}}{{\sqrt {1 - {{e}^{2}}} }}(2 - 3{{\sin }^{2}}{{i}_{{{\text{E,S}}}}}). \\ \end{gathered} $Вековые частоты возмущающих тел получаются численно из фонда координат больших планет по следующей схеме. Извлекаются из фонда координаты и скорости на 12 моментов времени с шагом 1 мин, затем эта сетка координат и скоростей преобразуется в сетки из элементов орбиты $q = \{ \Omega {\kern 1pt} ',\,\,\omega {\kern 1pt} '\} $ по формулам задачи двух тел. После чего величины $\dot {\Omega }{\kern 1pt} ',\,\,\dot {\omega }{\kern 1pt} '$ находятся с использованием производной от интерполяционного полинома Лагранжа 12-го порядка (Александрова и др., 2021б):
Далее мы будем рассматривать влияние только двух вековых резонансов наинизших порядков (табл. 4) путем численного моделирования движения ИСЛ с учетом влияния селенопотенциала, Земли и Солнца.
Таблица 4.
Типы рассматриваемых вековых резонансов
| № | Тип резонансного соотношения |
№ | Тип резонансного соотношения |
|---|---|---|---|
| 1 | $\dot {\omega }$ | 2 | $\left( {\dot {\Omega } - {{{\dot {\Omega '}}}_{{{\text{E,S}}}}}} \right)$ |
Соотношение 1 в табл. 4 является апсидальным резонансом первого порядка и представляет собой резонанс типа Лидова–Козаи, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \dot {\omega } \approx 0,$ трактуемый как $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \dot {\pi } \pm \dot {\Omega } = \dot {\omega } \approx 0$ (Shevchenko, 2017). Этот резонанс был открыт Лидовым (1961) в динамике ИСЗ и Kozai (1962) – в динамике астероидов в рамках двукратно осредненной круговой ограниченной задачи трех тел. Он является геометрическим резонансом, так как не связан с частотами движения возмущающих тел и зависит только от взаимного расположения объектов. Соотношение 2 в табл. 4 является чисто нодальным резонансом второго порядка.
В наших исследованиях мы используем численное моделирование без какого-либо осреднения. Поэтому рассматриваемые нами резонансы будут резонансами полной возмущенной задачи, содержащей влияние несферичности потенциала Луны, а также влияние притяжения Земли и Солнца.
ОБЩИЙ АНАЛИЗ СТРУКТУРЫ ВОЗМУЩЕНИЙ ИСЛ
С помощью ПМО “Численная модель движения ИСЛ” было проведено моделирование движения 5180 объектов на 10-летнем интервале времени. Начальное положение каждого спутника характеризовалось круговой орбитой и собственными значениями большой полуоси и наклонения. Элементы a и i варьировались в диапазонах $a \in [1.1{{R}_{L}},15{{R}_{L}}]$ с шагом $0.1{{R}_{L}}$ и $i \in [0,180^\circ ]$ с шагом 5° (${{R}_{L}}$ – экваториальный радиус Луны).
Рассмотрим зависимость величины влияния возмущающих факторов от начальных значений больших полуосей и наклонений орбит спутников. В качестве оценки величины влияния будем использовать модуль разности векторов положения объекта при учете влияния рассматриваемого возмущения и влияния только центральной силы. Оценки, полученные для таких возмущений как сжатие Луны, гравитационное поле Луны, разложение до 50-го порядка и степени, притяжение Земли и Солнца на конец интервала времени, равного 0.1 года, представлены на рис. 3.
Рис. 3.
Влияние возмущений от (а) сжатия Луны $\Delta {{r}_{{{{J}_{2}}}}}$, (б) селенопотенциала 50-го порядка и степени $\Delta {{r}_{{50 \times 50}}}$, (в) Земли $\Delta {{r}_{{\text{E}}}}$ и (г) Солнца $\Delta {{r}_{{\text{S}}}}$ на орбитальную эволюцию в зависимости от значений больших полуосей и наклонений орбит спутников.

Как показывают результаты, приведенные на рис. 3, существует зависимость величины влияния возмущений от наклонения и большой полуоси орбиты спутника в начальный момент времени. Воздействие сжатия Луны и полного ее гравитационного поля убывают с ростом большой полуоси, и примерно при $a \geqslant 5{{R}_{L}}$ их влияние становится едва заметным. При наклонении 90° влияние гравитационного поля минимально.
Графики влияния возмущений от Земли и Солнца (рис. 3в и 3г) имеют близкие по структуре карты распределения влияния в зависимости от начального положения объекта. Влияние и того, и другого объектов становится заметным, начиная с больших полуосей, равных $3{{R}_{L}}$, а максимальные значения оценок приходятся на наклонения 0°, 90° и 180°. В то же время величина влияния Земли примерно в 75 раз больше, чем Солнца.
Главной особенностью динамики окололунных объектов является рост эксцентриситетов их орбит. На рис. 4 представлены результаты, которые позволяют оценить зависимость величины роста эксцентриситета от начальных значений больших полуосей и наклонений орбит объектов для двух различных наборов возмущающих факторов. На рис. 4а оценки получены при учете влияния сжатия Луны, Земли и Солнца, а на рис. 4б с учетом влияния разложения селепотенциала до 50-го порядка и степени, Земли и Солнца.
Рис. 4.
Оценки роста эксцентриситетов в зависимости от начальных значений большой полуоси и наклонения объектов под влиянием возмущений от Земли, Солнца и (а) сжатия Луны, (б) селенопотенциала 50-го порядка и степени, (в) разница между вариантами (а) и (б).
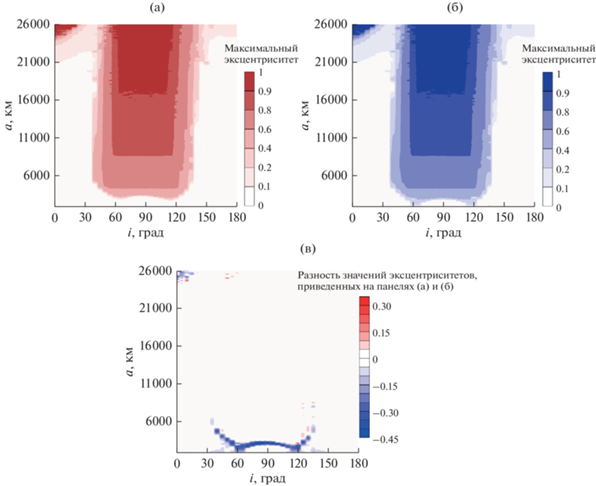
Как показывают приведенные на рис. 4 данные, значительный рост эксцентриситета наблюдается у объектов с начальными наклонениями в интервале от 60° до 120° и большой полуосью от 7500 км и выше. Рис. 4а и 4б отличаются только дополнительным ростом эксцентриситета для низколетящих объектов в случае учета возмущения от селенопотенциала 50-го порядка и степени.
Рост эксцентриситета может приводить к сокращению продолжительности жизни объекта на орбите. Влияние начальных положений спутников на время их жизни на орбите показывают графики, представленные на рис. 5. Продолжительностью жизни объекта на орбите мы называем промежуток времени от начала движения спутника до его столкновения с поверхностью Луны.
Рис. 5.
Продолжительность жизни объекта на орбите в зависимости от начальной высоты и наклонения объектов под влиянием возмущений от Земли и Солнца и (а) сжатия Луны, (б) селенопотенциала 50 порядка и степени (в) разница между вариантами (а) и (б).

Как и следовало ожидать, время жизни объектов тесно связано с ростом эксцентриситета. Эта взаимосвязь хорошо прослеживается при сопоставлении данных, приведенных на рис. 4 и 5. Начальным значением существенного уменьшения времени жизни, как и роста эксцентриситетов орбит спутников, является большая полуось, равная 7500 км. Диапазон наклонений орбит с малым временем жизни от 70° до 110° также хорошо согласуется с диапазоном наклонений орбит с быстро растущими эксцентриситетами. Графики на рис. 5а и 5б, как и на предыдущем рисунке, отличаются продолжительностью жизни на орбите для низколетящих спутников. При учете влияния селенопотенциала до 50-го порядка и степени объекты на низких орбитах имеют непродолжительное время жизни не только при наклонениях примерно от 60° до 120°, но и при ряде других наклонений. Рост эксцентриситета и соответственно короткая продолжительность жизни высоких околоэкваториальных объектов на рис. 4 и 5 объясняется прямым влиянием Земли. Особенности движения низколетящих объектов будут рассмотрены в следующем разделе.
АНАЛИЗ ОСОБЕННОСТЕЙ ДИНАМИКИ НИЗКОЛЕТЯЩИХ ИСЛ
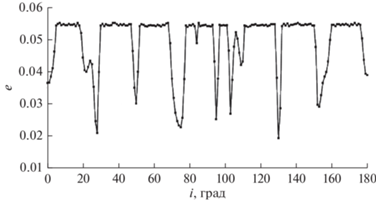
В предыдущем разделе исследование продолжительности жизни объекта на орбите и роста эксцентриситета в зависимости от начального положения спутника показало, что при учете полного поля Луны у низколетящих объектов при определенных значениях наклонения наблюдается короткая продолжительность жизни. На существование этой зависимости указывают многие авторы (Gupta, Sharma, 2011; Ramanan, Adimurthy, 2005). Мы также получили такую зависимость (рис. 6), график которой имеет визуальное сходство с результатами вышеупомянутых авторов. Высота полета моделируемого объекта составляет 100 км над поверхностью Луны, а в качестве возмущающих факторов учитывается только гравитационное поле Луны до 50-го порядка и степени.
Графики, приведенные на рис. 6, показывают, что на низкой высоте при различных наклонениях орбиты спутники имеют различное время жизни на орбите. Разница продолжительности жизни спутника на орбите при соседних наклонениях, как видим, может быть значительной. Например, при i = 4° время жизни спутника на орбите составляет более 10 лет, а при i = 5° – 38.5 сут. Для объяснения причины такой непродолжительной динамики объектов мы рассмотрели, как ведет себя эксцентриситет на низкой высоте при разных значениях наклонения орбиты. На рис. 7 показана зависимость роста эксцентриситета от начального значения наклонения орбиты.
Детальные данные по продолжительности жизни объектов на низких орбитах приведены на рис. 8.
Сопоставляя результаты, приведенные на рис. 6, 7 и 8, можно увидеть, что короткое время жизни спутника объясняется ростом эксцентриситета. Причем на самых низких орбитах достаточно роста эксцентриситета до 0.055. Поскольку объект низколетящий, такого роста эксцентриситета оказывается достаточно для столкновения объекта с поверхностью Луны. Покажем это. На рис. 9а сверху вниз отображена зависимость наклонения, эксцентриситета и высоты перицентра hp от времени, а на рис. 9б отображена эволюция аргумента перицентра и его скорости, полученная по точным формулам, для двух объектов с наклонением 4° (точечная линия) и 5° (сплошная линия). Эти характеристики у объектов практически совпадают.
Рис. 9.
Особенности орбитальной эволюции двух низколетящих объектов с наклонениями, отличающимися на 1°: (а) зависимость от времени наклонения, эксцентриситета и высоты перицентра; (б) изменения резонансных величин, полученных по точным и аналитическим формулам.
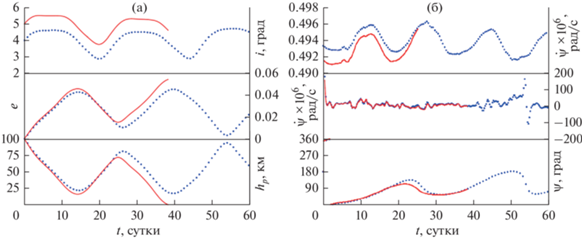
Здесь (рис. 9б) и далее на подобных графиках изображены сверху вниз: график изменения резонансного соотношения, полученного по приближенным аналитическим формулам (19)–(20), ниже график эволюции той же величины, полученной численно по формулам (18), и внизу график зависимости критического аргумента от времени. Напомним, что вариант эволюции резонансного соотношения, полученного с использованием приближенных формул, дается по причине возникновения неопределенностей в формулах (18) при нулевых значениях e и i.
Чтобы понять причину роста эксцентриситета низколетящих ИСЛ, мы сравнили особенности роста эксцентриситета при учете возмущений от сжатия Луны и под влиянием всего поля (рис. 10).
Рис. 10.
Особенности роста эксцентриситета при учете возмущений (а) только от сжатия Луны, (б) от всего гравитационного поля Луны до 50-го порядка и степени.

Как показывают данные, приведенные на рис. 10, сжатие Луны очень мало влияет на динамику ее объектов (рис. 10а), а влияние всего поля очень существенно (рис. 10б). Причем интересно отметить, что максимальный рост эксцентриситета наблюдается в окрестности так называемых критических наклонений, равных 60°.43 и 120°.43, получаемых в однократно осредненной задаче о движении спутника сжатой планеты (Дубошин, 1976).
Попытка установить связь для большого числа объектов между ростом эксцентриситета и резонансными характеристиками успехом не увенчалась. Наглядный пример – данные, приведенные на рис. 9б.
Таким образом, главным источником роста эксцентриситета на низких орбитах следует считать прямое действие сложного гравитационного поля Луны.
ВЛИЯНИЕ ВЕКОВЫХ РЕЗОНАНСОВ НАИНИЗШИХ ПОРЯДКОВ
Резонанс и эффект типа Лидова–Козаи в динамике окололунных объектов
Как показывают результаты, приведенные выше объекты на средних и больших высотах с начальными наклонениями в интервале от 60° до 120° имеют значительный рост эксцентриситета и малую продолжительность жизни. Такие особенности орбитальной эволюции, как правило (Lidov, 1962; Kozai, 1962; Прохоренко, 2002; Александрова и др., 2016; Shevchenko, 2017; Ito, Ohtsuka, 2019), являются следствием действия резонанса Лидова–Козаи, поэтому мы рассмотрели этот вопрос детально.
Эффект Лидова–Козаи, как было показано в (Shevchenko, 2017; Naoz, 2016), имеет резонансную природу. Характерными особенностями орбитальной эволюции объектов, подверженных действию эффекта Лидова–Козаи, является рост эксцентриситета орбиты, который при сохранении интеграла Моисеева–Лидова–Козаи ${{c}_{1}} = \sqrt {1 - {{е}^{2}}} \cos i,$ где е, i – эксцентриситет и наклонение орбиты спутника, приводит к возникновению взаимосвязанных колебаний эксцентриситета и наклонения орбиты: при росте эксцентриситета наклонение убывает и наоборот. Эти взаимосвязанные колебания и называют эффектом Лидова–Козаи.
Действие резонанса Лидова–Козаи зависит от величины наклонения орбиты объекта к орбите возмущающего тела.
Как утверждает теория (Лидов, 1961; Вашковьяк, 2016), острый резонанс, сопровождаемый быстрым ростом эксцентриситета, возникает, когда долгота перицентра от узла ${{\omega }} = 90^\circ ,$ при близости к нулю значения интеграла ${{c}_{1}}$ и при отрицательном значении интеграла Лидова ${{c}_{2}} = \left( {{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0em} 5} - {{{\sin }}^{2}}\omega {{{\sin }}^{2}}i} \right){{e}^{2}}$.
Сложность проявления этого механизма в динамике околопланетных объектов состоит в том, что помимо влияния внешних тел, которое приводит к появлению резонанса Лидова–Козаи, на эти объекты действует несферичность центрального тела, что может приводить к различным эффектам, которые в настоящее время мало изучены.
Особенно интересно исследовать это явление на примере динамики окололунных объектов, в движении которых сильны влияния Земли и гравитационного поля Луны.
Как показали наши исследования динамики околоземных объектов (Александрова и др., 2020; 2021), применяемая нами методика очень чувствительна к проявлению резонансных явлений и позволяет выявлять наличие резонанса типа Лидова–Козаи в динамике объектов, когда в орбитальной эволюции его влияние еще практически незаметно.
Используя результаты численного эксперимента, описанного выше, мы получили такую оценку области влияния резонанса типа Лидова–Козаи на динамику окололунных объектов (рис. 11).
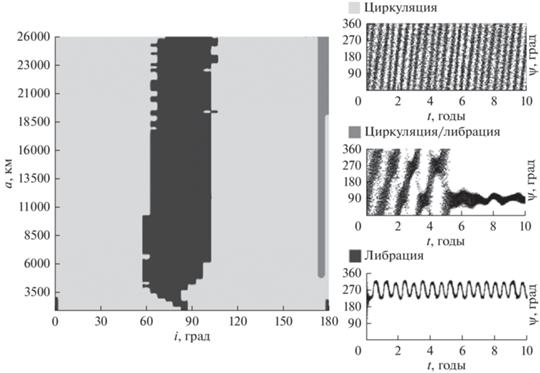
Рис. 11.
Области влияния резонанса типа Лидова–Козаи на динамику окололунных объектов и проявления эффекта типа Лидова–Козаи.

Оценки получены по анализу поведения критического аргумента в зависимости от большой полуоси и начального наклонения орбиты к экватору Луны. В качестве возмущений учитывались полное поле Луны до 50-го порядка и степени, влияние Земли и Солнца. На графике светло-серым цветом показана область циркуляции аргумента перицентра на всем промежутке прогнозирования, серым цветом – частичная либрация и циркуляция, а темно-серым цветом – либрация критического аргумента.
Результаты, приведенные на рис. 11, показывают, что область влияния резонанса типа Лидова–Козаи расширяется вдоль большой полуоси с 2500 до 4500 км и медленно смещается при прямом движении объектов вдоль наклонения с 30° до 50° с повышением высоты. Правая граница области влияния резонанса остается равной 140°. Неустойчивый резонанс высоких околоэкваториальных объектов объясняется прямым влиянием Земли.
Проанализировав орбитальную эволюцию модельных окололунных объектов на средних и больших высотах, мы обнаружили, что в динамике большинства из них присутствует эффект типа Лидова–Козаи. Граница области действия эффекта типа Лидова–Козаи представлена на рис. 11 (обозначена красной линией).
Как видно на рис. 11, область действия эффекта типа Лидова–Козаи покрывает большую часть области действия резонанса типа Лидова–Козаи на орбитальную эволюцию объектов. Как показывают оценки, в той части области действия резонанса типа Лидова–Козаи, где эффекта нет, данный резонанс не вполне устойчив и эксцентриситет растет очень медленно. Эффект типа Лидова–Козаи при этом не проявляется даже на больших интервалах времени, что продемонстрировано для объекта с начальными элементами: a = 6000 км, e = 0, i = 37° на рис. 12. Расположение графиков на рис. 12а и 12б подобно графикам на рис. 9а и 9б соответственно.
Рис. 12.
Орбитальная эволюция объекта, движущегося вне области действия эффекта Лидова–Козаи: (a) эволюция элементов орбиты; (б) резонансные характеристики, полученные по точным формулам и приближенным формулам; (в) сверху вниз изменение во времени интеграла Лидова ${{c}_{2}}$ и интеграла Моисеева–Лидова–Козаи ${{c}_{1}}.$
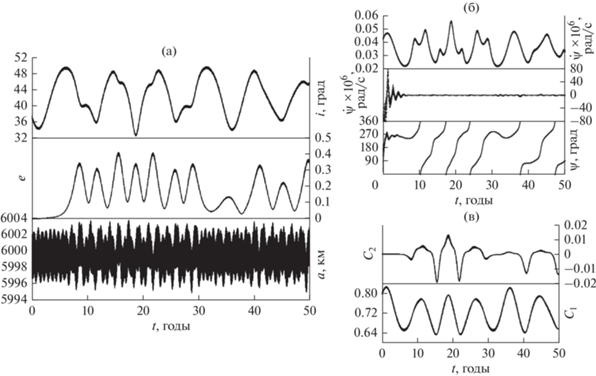
Остановимся на особенностях орбитальной эволюции объектов, подверженных действию резонанса типа Лидова–Козаи. Обратимся к рис. 3.
Сравнивая данные, приведенные на рис. 3 и 11, можно установить, что в динамике объектов, движущихся в интервале больших полуосей от 3000 до 8500 км, действие эффекта типа Лидова–Козаи будет проявляться в условиях наложения на него действия гравитационного поля Луны, а для объектов с большими полуосями от 8500 км и выше эффект будет проявляться в чистом виде.
На рис. 13 представлены результаты анализа орбитальной эволюции объекта со следующими начальными элементами: a = 5387.8 км, e = 0, i = 45°. Синим цветом выполнены графики, демонстриующие эволюцию орбит с учетом возмущений от полного гравитационного поля Луны, Земли и Солнца, а красным – с учетом возмущений только от Земли и Солнца. Расположение графиков на рис. 13 подобно графикам на рис. 12.
Рис. 13.
Проявление эффекта типа Лидова–Козаи для объекта с прямым движением и с высотой полета ниже 8500 км при учете возмущений от полного гравитационного поля Луны, Земли и Солнца (выполнено синим цветом) и только от Земли и Солнца (выполнено красным цветом): (a) эволюция элементов орбиты; (б) резонансные характеристики, полученные по точным формулам и приближенным формулам для соответствующих моделей (а); (в) сверху вниз изменение во времени интеграла Лидова ${{c}_{2}}$ и интеграла Моисеева–Лидова–Козаи ${{c}_{1}}$ для соответствующих моделей (а).

Графики, приведенные на рис. 13, показывают, что полное гравитационной поле Луны ускоряет проявление эффекта типа Лидова–Козаи для объектов с прямым движением. Острый резонанс типа Лидова–Козаи и максимальный рост эксцентриситета имеют место при достижении центром либрации величины ${{\omega = }}{{270}^{{\text{о}}}}.$
Приведем пример эволюции объекта с обратным движением и рассмотрим, как проявляется эффект типа Лидова–Козаи при наложении на него действия гравитационного поля Луны. На рис. 14 представлены изменения тех же характеристик, что и на рис. 13, для окололунного спутника с начальными элементами: a = 5387.8 км, e = 0, i = 125°.
Рис. 14.
То же, что и на рис. 13, но для объекта с обратным движением и с высотой полета ниже 8500 км.

Рис. 15.
То же, что и на рис. 13, но для объекта с обратным движением и с высотой полета выше 8500 км.

Из сопоставления рис. 13 и 14 видно, что для объектов с прямым и обратным движением и с большой полуосью ниже 8500 км гравитационное поле Луны ускоряет проявление эффекта типа Лидова–Козаи.
Теперь рассмотрим, как проявляется резонанс типа Лидова–Козаи на высотах, где влияние поля Луны незначительно. Для примера на рис. 15 приведены результаты для объекта с начальными элементами орбиты: a = 10949.4 км, e = 0, i = 125°. Расположение графиков совпадает с рис. 13 и 14.
Рис. 16.
Пример либрации аргумента перицентра с переносом центра для объекта с эволюцией элементов орбиты на рис. 14а: (а) эволюция элементов орбиты; (б) динамика резонансных характеристик, полученных по точным и приближенным формулам.
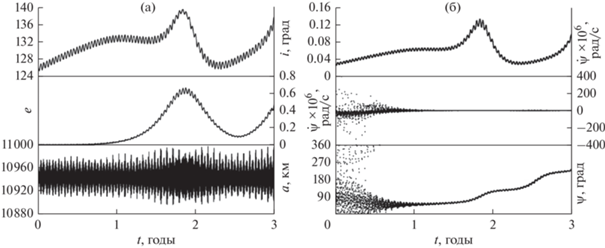
Как видно из графиков, приведенных на рис. 15, эффект типа Лидова–Козаи проявляется практически одинаково для обоих рассмотренных случаев учета возмущений.
Интерес представляют изменения резонансного аргумента, показанные на рис. 15б. С первого взгляда может показаться, что имеет место циркуляция аргумента перицентра, но при детальном рассмотрении оказывается, что это либрация с переносом центра. На рис. 16 показаны характеристики того же объекта на интервале времени 3 года, которые подтверждают это предположение.
Рис. 16б показывает, что аргумент перицентра либрирует на всем рассмотренном промежутке прогнозирования. Причем перенос центра либрации происходит примерно с шагом 90°. Это интересное дополнение численного моделирования к аналитической теории резонанса типа Лидова–Козаи.
Таким образом, исследование показывает, что причиной роста эксцентриситета и короткой жизни на орбите среднеорбитальных и высокорбитальных окололунных объектов является действие эффекта типа Лидова–Козаи.
Влияние нодального резонанса на динамику окололунных объектов
Как отмечалось выше (табл. 4) в данной работе мы рассмотрели влияние чисто апсидального и чисто нодального резонансов. Оценка области влияния нодального резонанса $\left( {\dot {\Omega } - \dot {\Omega }{{{_{{\text{E}}}^{'}}}_{{}}}} \right)$ на динамику ИСЛ представлена на рис. 16. Графики для нодального резонанса, связанного с прецессией Земли и Солнца, накладываются друг на друга, поэтому на рис. 16 показана оценка влияния нодального резонанса $\left( {\dot {\Omega } - \dot {\Omega }{{{_{{\text{E}}}^{'}}}_{{}}}} \right)$, связанного с прецессией орбиты Земли.
Рис. 17 показывает, что нодальный резонанс второго порядка сконцентрирован в окрестности наклонения, равного 90°. Сравнение рис. 11 и 17 показывает, что нодальный резонанс $\left( {\dot {\Omega } - \dot {\Omega }_{{{\text{E,S}}}}^{'}} \right)$ налагается на область влияния резонанса типа Лидова–Козаи, усиливая рост эксцентриситета и уменьшая продолжительность жизни объектов на приполярных орбитах.
ЗАКЛЮЧЕНИЕ
Представляемое в данной работе ПМО “Численная модель движения ИСЛ” позволяет прогнозировать долговременную орбитальную эволюцию окололунных объектов. Сравнение результатов, полученных с помощью данного программного комплекса, с результатами других авторов показало высокую степень совпадения, что говорит о том, что ПМО может быть использовано в различных задачах исследования динамики окололунных объектов.
Для анализа особенностей динамики окололунных объектов было проведено моделирование движения 5180 объектов на 10-летнем интервале времени. Начальное положение каждого спутника характеризовалось круговой орбитой и собственными значениями большой полуоси и наклонения.
Анализ влияния возмущений на орбитальную эволюцию ИСЛ показал, что влияния сжатия и несферичности полного гравитационного поля Луны становятся малозаметными, начиная с a = 8500 км, и минимальны для полярных спутников. При этом на орбитальную эволюцию низколетящих объектов влияние сжатия мало по сравнению с влиянием более высоких гармоник селенопотенциала. Что касается возмущений от Земли и Солнца, то их влияние начинает действовать приблизительно с a = 5000 км и максимально при i = 0°, 90° и 180°. При этом величина влияния Земли на вектор положения окололунного спутника примерно в 75 раз больше влияния Солнца.
Было обнаружено, что при начальных наклонениях окололунных спутников в диапазоне от 70° до 110° объекты имеют малую продолжительность жизни на орбите. Как выяснилось, это обусловлено значительным ростом эксцентриситета орбиты при наклонениях в интервале от 60° до 120°.
Для низколетящих ИСЛ была предпринята попытка установить связь между ростом эксцентриситета и изменением во времени некоторых резонансных характеристик. Результаты показали, что такой связи нет. Поэтому на данном этапе исследования рост эксцентриситета мы можем объяснить только прямым действием сложного гравитационного поля Луны.
Для среднеорбитальных и высокоорбитальных спутников было проведено исследование влияния резонанса типа Лидова–Козаи и нодального резонанса $\left( {\dot {\Omega } - \dot {\Omega }_{{{\text{E,S}}}}^{'}} \right)$ на динамику окололунных объектов. На основе анализа динамики 4995 объектов (без рассмотрения низколетящих объектов с высотой полета менее 2500 км) были построены карты областей влияния резонанса типа Лидова–Козаи и нодального резонанса на орбитальную эволюцию в зависимости от начальных значений большой полуоси и наклонения орбиты спутников. В ходе исследования эволюции элементов орбит объектов было выявлено, что в значительной части области влияния резонанса типа Лидова–Козаи имеет место эффект типа Лидова–Козаи. Область влияния резонанса типа Лидова–Козаи покрывает область значительного роста эксцентриситета орбит ИСЛ, а влиянию нодального резонанса подвержены приполярные окололунные орбиты. На основании полученных данных сделан вывод, что главной причиной роста эксцентриситета и, как следствие, малой продолжительности жизни объектов на средних и больших высотах является влияние резонанса типа Лидова–Козаи на орбитальную эволюцию ИСЛ, а нодальный резонанс дополнительно усиливает рост эксцентриситета приполярных окололунных орбит.
Было показано, что гравитационное поле Луны в области своего заметного влияния на динамику объектов ускоряет проявление резонанса типа Лидова–Козаи на орбитальную эволюцию ИСЛ. Еще одним интересным фактом было выявление случаев либрации аргумента перицентра с переносом центра. Причем перенос центра либрации совершается с шагом примерно 90°.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-72-10022).
Список литературы
Авдюшев В.А. Интегратор Гаусса–Эверхарта // Вычислит. технологии. 2010. Т. 15. № 4. С. 31–47.
Авдюшев В.А. Численное моделирование орбит небесных тел. Томск: Издательский дом Томск. ун-та, 2015. 336 с.
Авдюшев В.А. Новый коллокационный интегратор для решения задач динамики. I. Теоретические основы // Изв. вузов. Физика. 2020. Т. 63. №. 11. С. 131–140.
Александрова А.Г., Бордовицына Т.В., Томилова И.В. Резонанс Лидова–Козаи и его влияние на орбитальную эволюцию околоземных космических объектов // М.Л. Лидов – яркое имя в космической науке: сб. докладов / Ред. Вашковьяк М.А. М.: ИПМ им. М.В. Келдыша, 2016. С. 49–66.
Александрова А.Г., Бордовицына Т.В., Чувашов И.Н. Численное моделирование в задачах динамики околоземных объектов // Изв. вузов. Физика. 2017. Т. 60. № 1. С. 69–76.
Александрова А.Г., Бордовицына Т.В., Попандопуло Н.А., Томилова И.В. Новый подход к вычислению вековых частот в динамике околоземных объектов на орбитах с большими эксцентриситетами // Изв. вузов. Физика. 2020. Т. 63. № 1(745). С. 57–62.
Александрова А.Г., Авдюшев В.А., Попандопуло Н.А., Бордовицына Т.В. Численное моделирование движения околоземных объектов в среде параллельных вычислений // Изв. вузов. Физика. 2021a. Т. 64. № 8. С. 168–175.
Александрова А.Г., Блинкова Е.В., Бордовицына Т.В., Попандопуло Н.А., Томилова И.В. Вековые резонансы в динамике объектов, движущихся в областях LEO–MEO околоземного орбитального пространства // Астрон. вестн. 2021б. Т. 55. № 3. С. 272–287. (Aleksandrova A.G., Blinkova E.V., Bordovitsyna T.V., Popandopulo N.A., Tomilova I.V. Secular resonances in the dynamics of objects moving in LEO–MEO regions of near-Earth orbital space // Sol. Syst. Res. 2021. Т. 55. № 3. P. 266–281.)
Аксенов Е.П. Теория движения искусственных спутников Земли. М.: Наука, 1977. 360 с.
Вашковьяк М.А. Качественные особенности эволюции некоторых полярных спутниковых орбит // Астрон. вестн. 2016. Т. 50. № 1. С. 37. (Vashkov’yak M.A. Qualitative features of the evolution of some polar satellite orbits // Solar Syst. Res. 2016. Т. 50. № 1. P. 33–43.)
Дубошин Г.Н. Справочное руководство по небесной механике и астродинамике. М.: Наука, 1976. 864 с.
Дубошин Г.Н. Небесная механика. Основные задачи и методы. Физматгиз, 1963. 586 с.
Лидов М.Л. Эволюция орбит искусственных спутников под воздействием гравитационных возмущений внешних тел // Искусственные спутники Земли: журнал. 1961. Т. 8. С. 5–45.
Мюррей К., Дермотт С. Динамика Солнечной системы. М.: Физматлит, 2010. 588 с.
Морбиделли А. Современная небесная механика. Аспекты динамики Солнечной системы. М.–Ижевск: Институт компьютерных исследований, 2014. 432 с.
Прохоренко В.И. Исследование времени баллистического существования эллиптических орбит, эволюционирующих под влиянием гравитационных возмущений внешних тел // Космич. исслед. 2002. Т. 40. № 3. С. 285–294.
Тимошкова Е.И., Холшевников К.В. Лунно-солнечные возмущения в движении спутников планеты // Ученые записки Ленинградского государственного университета. 1974. № 373. С. 141–156.
Cook G.E. Luni–solar perturbations of the orbit of an Earth satellite // Geophys. J. 1962. V. 6. № 3. P. 271–291.
Cunningham L.E. On the computation of the spherical harmonic terms needed during the numerical integration of the orbital motion of an artificial satellite // Celest. Mech. 1970. V. 2. P. 207–216.
Folkner W.M., Park R.S. // Planetary ephemeris DE438 for Juno, Tech. Rep. IOM392R-18-004. Pasadena, CA: Jet Propulsion Laboratory, 2018.
Gupta S., Sharma R. Effect of altitude, right ascension of ascending node and inclination on lifetime of circular lunar orbits // Int. J. Astron. and Astrophys. 2011. V. 1. № 3. P. 155–163.
Ito T., Ohtsuka K. The Lidov-Kozai oscillation and Hugo von Zeipel // Monogr. Environ. Earth Planets. 2019. V. 7. № 1. P. 1–113.
Konopliv A.S., Asmar W., Carranza E., Sjogren W.L., Yuan D.N. Recent gravity models as a result of the lunar prospect mission // Icarus. 2001. V. 150. P. 1–18.
Kozai Y. Secular perturbations of asteroids with high inclination and eccentricity // Astron. J. 1962. V. 67. P. 591–598.
Lidov M.L. The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies // Planet. and Space Sci. 1962. V. 9. P. 719–759.
Naoz S. The eccentric Kozai–Lidov effect and its applications // Ann. Rev. Astron. and Astrophys. 2016. V. 54(1). P. 1–59.
Petit G., Luzum B. IERS Technical note 36. Frankfurt am Main, 2010. 179 p.
Ramanan R.V., Adimurthy V. An analysis of near circular lunar mapping orbits // J. Earth System Sci. 2005. V. 114. № 6. P. 619–626.
Rossi A. Resonant dynamics of Medium Earth Orbits: space debris // Celest. Mech. Dyn. Astr. 2008. V. 100. P. 267–286.
Shevchenko I.I. The Lidov–Kozai Effect – Applications in Exoplanet Research and Dynamical Astronomy. Springer, 2017. 198 p.
Song Y.J., Park S.Y., Kim H.D., Sim E.S. Development of precise lunar orbit propagator and lunar polar orbiter’s lifetime analysis // J. Astron. and Space Sci. 2010. V. 27. Iss. 2. P. 97–106.
Spherical Harmonic ASCII Model of the gravity fields of Earth’s Moon GRGM1200L 2021. URL: https://pds-geosciences.wustl.edu/grail/grail-l-lgrs-5-rdr-v1/grail_1001/shadr/gggrx_1200l_bouguer_sha.tab
Valk S., Delsate N., Lemaitre A., Carletti T. Global dynamics of high area-to-mass ratios GEO space debris by means of the MEGNO indicator // Adv. Space Res. 2009. V. 43. P. 1509–1526.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник