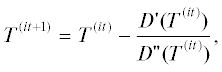Астрономический вестник, 2022, T. 56, № 5, стр. 335-343
Выявление столкновительных орбит астероидов при заметной нелинейности в задаче улучшения орбиты
А. П. Батурин *
* E-mail: alexbaturin@sibmail.com
Поступила в редакцию 10.01.2022
После доработки 29.01.2022
Принята к публикации 21.02.2022
- EDN: AINZCE
- DOI: 10.31857/S0320930X22040016
Аннотация
Разработан метод выявления столкновительных орбит астероидов в начальной доверительной области при заметной нелинейности в задаче улучшения их орбит. Метод заключается в условной минимизации расстояния от астероида до Земли в каком-либо его рассматриваемом сближении с Землей. В методе накладывается ограничение на функцию представления наблюдений астероида, определяющее уровенную поверхность, соответствующую некоторой доверительной вероятности. Разработан полуэмпирический способ определения соответствия уровенных поверхностей и доверительной вероятности. Метод протестирован при выявлении столкновительных орбит для четырех потенциально опасных астероидов.
ОПИСАНИЕ МЕТОДА
Данная работа продолжает исследования, опубликованные в работах автора (2016, 2020), и посвящена вопросу выявления столкновительных орбит потенциально опасных астероидов и оцениванию вероятности их столкновения с Землей. Этому вопросу посвящено множество работ, среди которых можно упомянуть: Milani (2006); Ivashkin, Stikhno (2007); Milani и др. (2009); Ивашкин, Стихно (2009); Железнов (2010); Прохоренко (2010); Соколов и др. (2012); Черницов и др. (2016); Ivashkin, Stikhno (2019).
Рассматриваемый в работе метод является обобщением метода, описанного в статье (Батурин, 2020), и предназначен для выявления начальных параметров движения, приводящих к столкновению какого-либо астероида с Землей (далее “столкновительных орбит”), в начальной доверительной области, определяемой в результате улучшения орбиты астероида по данным его наблюдений. Обобщение заключается в том, что поиск столкновительных орбит выполняется не в доверительном эллипсоиде, а в области, задаваемой уровенной поверхностью минимизируемой функции задачи улучшения орбиты. Как показано в работах (Черницов и др., 2014; 2017), при заметной нелинейности в задаче улучшения орбиты эта область может существенно отличаться от эллипсоидальной. Рассматриваемый метод заключается в условной минимизации квадрата расстояния от астероида до Земли в каком-либо его рассматриваемом сближении. В методе налагается ограничение на среднеквадратическую ошибку представления наблюдений, т.е. выполняется поиск столкновительных орбит, расположенных на одной и той же уровенной поверхности, соответствующей некоторой доверительной вероятности. Вопрос определения соответствия уровенных поверхностей и доверительной вероятности будет рассмотрен ниже.
Описываемый метод функционально является развитием методов, основанных на условной оптимизации, применяемых, например, в работе (Батурин, Черницов, 2001), а также в работах Ivashkin и Stikhno (2007; 2019).
Задачу поиска столкновительных орбит, расположенных на некоторой уровенной поверхности, можно представить в виде
где ${\mathbf{q}} = {{(x,y,z,\dot {x},\dot {y},\dot {z})}^{T}}$ – искомый вектор начальных параметров движения; T – момент наибольшего сближения с Землей; D – квадрат расстояния до Земли в момент T; $S({\mathbf{q}}) = \sum\nolimits_{i = 1}^n {\left( {\Delta \alpha _{i}^{2}{{{\cos }}^{2}}\delta _{i}^{{(O)}} + \Delta \delta _{i}^{2}} \right)} $ – функция представления наблюдений; K – заданное постоянное значение этой функции, определяющее ее уровенную поверхность; λ – множитель Лагранжа; $\Delta {{\alpha }_{i}} = {{\alpha }_{i}}({\mathbf{q}}) - \alpha _{i}^{{(O)}}$ и $\Delta {{\delta }_{i}} = {{\delta }_{i}}({\mathbf{q}}) - \delta _{i}^{{(O)}}$ – разности вычисленных и измеренных соответственно прямых восхождений и склонений объекта; n – число наблюдений.Параметр D определяется выражением
где $\Delta x = x({\mathbf{q}},T) - {{x}_{ \oplus }}(T),$ $\Delta y = y({\mathbf{q}},T) - {{y}_{ \oplus }}(T),$ $\Delta z = z({\mathbf{q}},T) - {{z}_{ \oplus }}(T).$ Здесь $x,y,z$ – гелиоцентрические координаты астероида и ${{x}_{ \oplus }},{{y}_{ \oplus }},{{z}_{ \oplus }}$ – гелиоцентрические координаты Земли.Условия минимума (1) можно записать в виде:
(2)
$\begin{gathered} {{F}_{j}} = \frac{1}{2}\frac{{\partial \Phi }}{{\partial {{q}_{j}}}} = \Delta x\frac{{\partial x}}{{\partial {{q}_{j}}}} + \Delta y\frac{{\partial y}}{{\partial {{q}_{j}}}} + \Delta z\frac{{\partial z}}{{\partial {{q}_{j}}}} + \\ + \,\,\lambda \sum\limits_{i = 1}^n {\left( {\Delta {{\alpha }_{i}}\frac{{\partial {{\alpha }_{i}}}}{{\partial {{q}_{j}}}}{{{\cos }}^{2}}\delta _{i}^{{(O)}} + \Delta {{\delta }_{j}}\frac{{\partial {{\delta }_{i}}}}{{\partial {{q}_{j}}}}} \right)} = 0 \\ (j = 1,...,6), \\ {{F}_{7}} = \frac{1}{2}\frac{{\partial \Phi }}{{\partial \lambda }} = \frac{1}{2}(S({\mathbf{q}}) - K) = 0, \\ \end{gathered} $Систему уравнений (2) можно решить, например, с помощью метода Ньютона или каких-либо его модификаций. При улучшении орбит для этого обычно применяется так называемый “метод дифференциальных поправок”, заключающийся в том, что в выражениях производных от левых частей системы (2) по определяемым параметрам отбрасываются слагаемые со вторыми изохронными производными. Итерации метода дифференциальных поправок можно, как и в случае метода Ньютона, записать в виде
(3)
${{{\mathbf{g}}}^{{(it + 1)}}} = {{{\mathbf{g}}}^{{(it)}}} - {{\left( {\frac{{\partial {\mathbf{F}}}}{{\partial {\mathbf{g}}}}} \right)}^{{ - 1}}}{\mathbf{F}}.$Однако элементы матрицы $\frac{{\partial {\mathbf{F}}}}{{\partial {\mathbf{g}}}}$ не содержат слагаемых со вторыми изохронными производными. Вектор g в (3) – это вектор q, расширенный путем добавления множителя Лагранжа λ, т.е. ${\mathbf{g}} = \left( {\begin{array}{*{20}{c}} {\mathbf{q}} \\ \lambda \end{array}} \right).$ Поэтому элементы матрицы $\frac{{\partial {\mathbf{F}}}}{{\partial {\mathbf{g}}}}$ имеют следующий вид:
Изохронные производные $\frac{{\partial x}}{{\partial {{q}_{i}}}},\frac{{\partial y}}{{\partial {{q}_{i}}}},\frac{{\partial z}}{{\partial {{q}_{i}}}}$ $(i = 1,...,6)$ вычисляются методом Мультона совместного интегрирования системы уравнений движения и уравнений в вариациях.
Поскольку расстояние в задаче (1) минимизируется для фиксированного момента сближения T, то в окрестности этого момента оно может быть еще меньшим. Поэтому далее квадрат расстояния до Земли минимизируется при фиксированном векторе g, найденном при решении задачи (1). В этом случае расстояние до Земли зависит только от времени $(D = D(T))$; поэтому для определения момента наибольшего сближения применяется метод Ньютона для нахождения нуля функции одной переменной:
где “it” – номер итерации; $D{\kern 1pt} '(T) = $ $ = 2(\Delta x\Delta \dot {x} + \Delta y\Delta \dot {y} + \Delta z\Delta \dot {z})$ – первая производная по моменту сближения от $D(T);$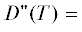 $ = 2(\Delta {{\dot {x}}^{2}} + \Delta {{\dot {y}}^{2}} + \Delta {{\dot {z}}^{2}}[ + \Delta x\Delta \ddot {x} + \Delta y\Delta \ddot {y} + \Delta z\Delta \ddot {z}])$ – вторая производная. Здесь выражение, взятое в квадратные скобки, при расчетах может
не учитываться. Момент сближения может исправляться по формуле (4) после каждой итерации процесса (3). В настоящей работе итерации процессов (3) и (4)
выполняются поочередно.
$ = 2(\Delta {{\dot {x}}^{2}} + \Delta {{\dot {y}}^{2}} + \Delta {{\dot {z}}^{2}}[ + \Delta x\Delta \ddot {x} + \Delta y\Delta \ddot {y} + \Delta z\Delta \ddot {z}])$ – вторая производная. Здесь выражение, взятое в квадратные скобки, при расчетах может
не учитываться. Момент сближения может исправляться по формуле (4) после каждой итерации процесса (3). В настоящей работе итерации процессов (3) и (4)
выполняются поочередно.
Рассмотрим теперь вопрос соответствия уровенных поверхностей функции $S({\mathbf{q}})$ доверительной вероятности при заметной нелинейности в задаче улучшения орбиты. Нелинейность этой задачи характеризуется так называемым коэффициентом нелинейности, который может определяться по-разному (Черницов и др., 2014). Здесь использован один из вариантов его определения, а именно коэффициент $\chi = 0.5({{\sigma }_{{\max }}} - {{{{\sigma }_{{\min }}})} \mathord{\left/ {\vphantom {{{{\sigma }_{{\min }}})} {({{\sigma }_{{\min }}}}}} \right. \kern-0em} {({{\sigma }_{{\min }}}}} - {{\sigma }_{0}}),$ где ${{\sigma }_{{\max }}}$ и ${{\sigma }_{{\min }}}$ – соответственно максимальная и минимальная среднеквадратическая ошибка представления наблюдений векторами начальных параметров, расположенными на концах двенадцати полуосей доверительного эллипсоида, причем коэффициент увеличения эллипсоида принимается равным 4.5 (поскольку такое его значение соответствует доверительной вероятности 0.997 в шестимерном случае); ${{\sigma }_{0}}$ – среднеквадратическая ошибка представления наблюдений МНК-оценкой начальных параметров, полученной в результате минимизации функции $S({\mathbf{q}}).$ Заметим, что среднеквадратическая ошибка $\sigma $ представления наблюдений каким-либо вектором q вычисляется как $\sqrt {{{S({\mathbf{q}})} \mathord{\left/ {\vphantom {{S({\mathbf{q}})} {(2n - 6)}}} \right. \kern-0em} {(2n - 6)}}} .$
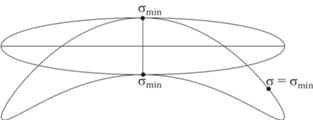
При сильной нелинейности коэффициент $\chi $ значительно превышает единицу, и в этом случае уровенные поверхности функции $S({\mathbf{q}})$ заметно отличаются от эллипсоидальных. Примерная картина расположения уровенной поверхности относительно эллипсоидальной приведена на рис. 1. Эти поверхности, как показано в работах (Черницов и др., 2014; 2017), практически совпадают на концах наименьшей оси эллипсоида, в этих точках (обозначенных знаком “•”) среднеквадратическая ошибка представления наблюдений минимальна для всей поверхности эллипсоида, что и отражено на рис. 1.
Рис. 1.
Примерное расположение уровенной поверхности относительно эллипсоидальной в двумерном случае.
Практическое совпадение уровенной и эллипсоидальной поверхности позволяет использовать значения функции $S({\mathbf{q}})$ в этих точках как значения, определяющие уровенную поверхность, соответствующую эллипсоидальной поверхности с заданной доверительной вероятностью. Зависимость же доверительной вероятности от размера эллипсоидальной поверхности, т.е. от коэффициента k увеличения доверительного эллипсоида, является взаимно-однозначной, формулы для ее вычисления выведены в работах (Черницов и др., 2007; Сюсина и др., 2012; Батурин, 2020). В табл. 1 приведен (с точностью до семи знаков после запятой) ряд значений доверительной вероятности для шестимерного пространства, вычисленной по этим формулам.
Таблица 1.
Доверительная вероятность p в зависимости от коэффициента k увеличения доверительного эллипсоида в шестимерном пространстве
| k | p | k | p | k | p | k | p |
|---|---|---|---|---|---|---|---|
| 0.1 | 0.0000000 | 1.9 | 0.2707182 | 3.7 | 0.9667026 | 5.5 | 0.9999648 |
| 0.2 | 0.0000013 | 2.0 | 0.3233236 | 3.8 | 0.9749107 | 5.6 | 0.9999784 |
| 0.3 | 0.0000147 | 2.1 | 0.3786267 | 3.9 | 0.9813152 | 5.7 | 0.9999869 |
| 0.4 | 0.0000804 | 2.2 | 0.4355078 | 4.0 | 0.9862460 | 5.8 | 0.9999921 |
| 0.5 | 0.0002965 | 2.3 | 0.4928079 | 4.1 | 0.9899925 | 5.9 | 0.9999953 |
| 0.6 | 0.0008498 | 2.4 | 0.5493950 | 4.2 | 0.9928023 | 6.0 | 0.9999972 |
| 0.7 | 0.0020419 | 2.5 | 0.6042243 | 4.3 | 0.9948825 | 6.1 | 0.9999984 |
| 0.8 | 0.0043044 | 2.6 | 0.6563863 | 4.4 | 0.9964031 | 6.2 | 0.9999991 |
| 0.9 | 0.0081971 | 2.7 | 0.7051412 | 4.5 | 0.9975006 | 6.3 | 0.9999995 |
| 1.0 | 0.0143877 | 2.8 | 0.7499387 | 4.6 | 0.9982830 | 6.4 | 0.9999997 |
| 1.1 | 0.0236121 | 2.9 | 0.7904225 | 4.7 | 0.9988338 | 6.5 | 0.9999998 |
| 1.2 | 0.0366199 | 3.0 | 0.8264219 | 4.8 | 0.9992168 | 6.6 | 0.9999999 |
| 1.3 | 0.0541093 | 3.1 | 0.8579341 | 4.9 | 0.9994799 | 6.7 | 1.0000000 |
| 1.4 | 0.0766596 | 3.2 | 0.8850978 | 5.0 | 0.9996585 | 6.8 | 1.0000000 |
| 1.5 | 0.1046694 | 3.3 | 0.9081638 | 5.1 | 0.9997783 | 6.9 | 1.0000000 |
| 1.6 | 0.1383068 | 3.4 | 0.9274640 | 5.2 | 0.9998577 | 7.0 | 1.0000000 |
| 1.7 | 0.1774790 | 3.5 | 0.9433816 | 5.3 | 0.9999096 | 7.1 | 1.0000000 |
| 1.8 | 0.2218227 | 3.6 | 0.9563244 | 5.4 | 0.9999433 | 7.2 | 1.0000000 |
Таким образом, в качестве значения K уровенной поверхности функции $S({\mathbf{q}}),$ соответствующего заданной доверительной вероятности, можно принять величину $(2n - 6)\,\sigma _{{\min }}^{2}.$
Для установления зависимости величины ${{\sigma }_{{\min }}}$ от k был решен ряд задач улучшения орбит астероидов с вычислением среднеквадратических ошибок на концах полуосей доверительного эллипсоида и последующим определением ${{\sigma }_{{\max }}},$ ${{\sigma }_{{\min }}}$ и коэффициента нелинейности$\chi .$ В качестве модельных объектов были выбраны четыре потенциально опасные астероида (на сайте https://cneos.jpl.nasa.gov/sentry/): 2012 QD8, 2021 EU, 2021 GX9 и 2021 QM1. Выбор объектов подчинялся двум требованиям: наличие достаточного числа наблюдений и не слишком удаленного в будущем сближения с Землей. Наблюдения астероидов были взяты с сайта Центра малых планет (https://minorplanetcenter.net/db_search). Эти астероиды имеют (в соответствии с порядком их перечисления выше): 42 наблюдения на дуге в 20 сут, 34 наблюдения на дуге в 13 сут, 41 наблюдение на дуге в 14 сут и 78 наблюдений на дуге в 8 сут. Коэффициент нелинейности $\chi $ для них получился, соответственно, равным 0.016, 0.086, 0.0043 и 0.023.
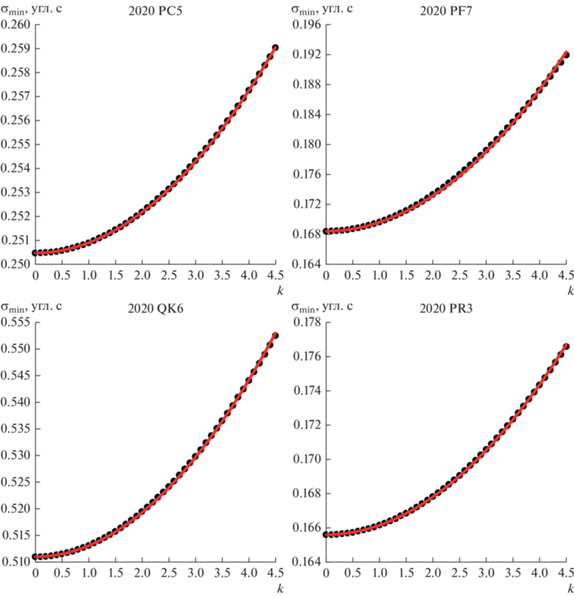
Кроме того, для большей достоверности результатов выполняемого исследования были взяты еще четыре объекта из числа астероидов, наблюдаемых на обсерватории в Терсколе, а именно: 2020 PC5 (76 наблюдений на дуге в 3 сут), 2020 PF7 (20 наблюдений на дуге в 4 сут), 2020 QK6 (33 наблюдения на дуге в 6 сут) и 2020 PR3 (40 наблюдений на дуге в 8 сут). Коэффициент нелинейности для этих четырех объектов оказался равным, соответственно, 5.37, 0.41, 1.53 и 1.32.
Коэффициент увеличения k для всех объектов варьировался от 0 до 4.5 с шагом 0.1. Для каждого значения k вычислялись среднеквадратические ошибки представления наблюдений на концах 12 полуосей доверительного эллипсоида и определялось их минимальное значение ${{\sigma }_{{\min }}}.$
Графики зависимости ${{\sigma }_{{\min }}}$ от k приведены на рис. 2 и 3, значения ${{\sigma }_{{\min }}}$ обозначены знаком “•”. На рис. 2 и 3 видно, что во всех случаях эта зависимость является почти точно квадратичной, поэтому была выполнена ее аппроксимация с помощью формулы ${{\sigma }_{{\min }}} = {{\sigma }_{0}} + b{{k}^{2}}$ с одним неизвестным коэффициентом b, определяемым методом наименьших квадратов. Графики аппроксимирующей кривой изображены красным цветом. Коэффициент детерминации (R-квадрат) значения b во всех восьми случаях оказался больше чем 0.9998.
Рис. 2.
Зависимость минимальной среднеквадратической ошибки на концах полуосей доверительного эллипсоида от коэффициента увеличения размеров эллипсоида для первых четырех астероидов.
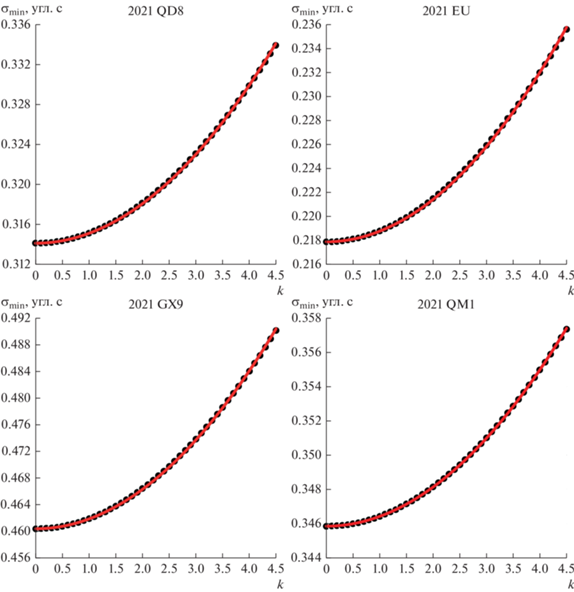
Рис. 3.
Зависимость минимальной среднеквадратической ошибки на концах полуосей доверительного эллипсоида от коэффициента увеличения размеров эллипсоида для вторых четырех астероидов (при заметной нелинейности в задаче улучшения орбиты).
Полученные значения среднеквадратической ошибки единицы веса ${{\sigma }_{0}}$ и коэффициента b для четырех астероидов приведены в табл. 2.
Таблица 2.
Значения ${{\sigma }_{0}}$ и b для рассматриваемых астероидов
| Астероид | ${{\sigma }_{0}}$ | b |
|---|---|---|
| 2012 QD8 | 0.314145255954″ | 0.000983958742038″ |
| 2021 EU | 0.217907172849″ | 0.000881464350620″ |
| 2021 GX9 | 0.460394069932″ | 0.001479070893158″ |
| 2021 QM1 | 0.345858661057″ | 0.000569358124535″ |
| 2020 PC5 | 0.250476040679″ | 0.000422040606227″ |
| 2020 PF7 | 0.168428513723″ | 0.001177743332847″ |
| 2020 QK6 | 0.511024051744″ | 0.002066964195520″ |
| 2020 PR3 | 0.165609273071″ | 0.000546075034815″ |
Таким образом, с помощью простейшей квадратичной аппроксимации устанавливается практически детерминированная зависимость значений ${{\sigma }_{{\min }}},$ задающих уровенные поверхности функции $S({\mathbf{q}}),$ от коэффициента увеличения размеров доверительного эллипсоида и, следовательно, от соответствующей ему доверительной вероятности.
ПРИМЕНЕНИЕ МЕТОДА
Описанный метод был апробирован при выявлении столкновительных орбит первых четырех выбранных астероидов в их предстоящих сближениях с Землей. Для этих астероидов были вычислены сближения с Землей, среди которых для каждого астероида было выбрано одно сближение, отстоящее не слишком далеко в будущем, а именно: 7 марта 2026 г. (0.013 а. е.) для 2012 QD8, 25 февраля 2024 г. (0.033 а. е.) для 2021 EU, 28 апреля 2032 г. (0.11 а. е.) для 2021 GX9 и 31 марта 2052 г. (0.033 а. е.) для 2021 QM1.
В качестве модели движения астероидов была использована возмущенная задача двух тел с учетом возмущений от восьми планет, Плутона и Луны, координаты которых при выполнении вычислений извлекались из последних на момент данной публикации эфемерид DE440 (ftp://ssd.jpl.nasa.gov/pub/eph/planets). Такой упрощенной модели вполне достаточно для демонстрации возможностей рассматриваемого способа выявления столкновительных орбит. При необходимости возможно более точного их выявления в модель движения следует включить учет более тонких эффектов, таких как возмущения от несферичности Земли, светового давления и т.п. Все вычисления выполнялись с использованием 80-битовых чисел с плавающей точкой, соответствующих 19-значной десятичной разрядности. Для компиляции программ был использован свободно распространяемый компилятор GNU-Fortran (https://sourceforge.net/projects/mingw-w64). Для численного интегрирования уравнений движения был применен метод Эверхарта (Everhart, 1985) 19-го порядка с переменным шагом интегрирования.
Поскольку метод позволяет получать столкновительные или близкие к ним орбиты с начальными параметрами движения, расположенными на какой-то уровенной поверхности, соответствующей заданному значению k, то вся начальная доверительная область была представлена как набор таких вложенных уровенных поверхностей, соответствующих значению коэффициента k, пробегающему с мелким шагом определенный интервал, а именно, интервал [0.1; 6.6] с шагом 0.1. Значение 6.6 выбрано в качестве конечного потому, что оно соответствует доверительной вероятности 0.9999999 (табл. 1 ) и, следовательно, позволяет получать верхнюю оценку вероятности столкновения величиной менее 1 × 10–7.
Начальные приближения для итерационных процессов (3) и (4) задавались как случайные равномерно распределенные точки, заполняющие шестимерный куб, описанный вблизи доверительного эллипсоида (сторона такого куба равна наибольшей полуоси эллипсоида). Выбор начальных приближений таким способом позволяет гарантированно “охватить” уровенную поверхность при заметной нелинейности в задаче улучшения орбиты. Для “крайних” случаев, соответствующих значениям k = 0.1 и k = 6.6, было использовано 100 и 1000 точек; число точек в остальных случаях (для k от 0.2 до 6.5 с шагом 0.1), изменялось по линейному закону между этими крайними значениями.
Результаты условной минимизации приведены на рис. 4–7 соответственно для объектов 2012 QD8, 2021 EU, 2021 GX5 и 2021 QM1. На этих рисунках для каждого значения k из интервала [0.1; 6.6] приводятся значения минимального расстояния dmin до центра Земли в рассматриваемых сближениях. Для каждого k вычислялись соответствующие ему величины ${{\sigma }_{{\min }}} = {{\sigma }_{0}} + b{{k}^{2}}$ (по значениям из табл. 2) и $K = (n - 6)\,\sigma _{{\min }}^{2},$ затем выполнялись процессы минимизации (3), (4). Значения dmin соответствуют всем начальным приближениям, задаваемым описанным выше способом. Сплошная линия на рисунках соответствует радиусу Земли, равному 4.26 × 10–5 а. е.
Рис. 4.
Результаты условной минимизации расстояния до Земли объекта 2012 QD8 вблизи его сближения с Землей 7 марта 2026 г.
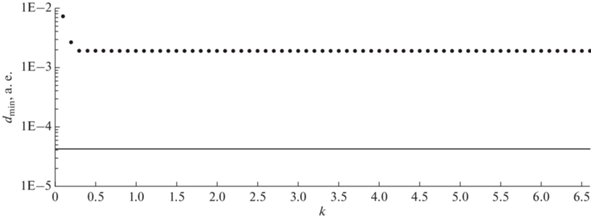
Рис. 5.
Результаты условной минимизации расстояния до Земли объекта 2021 EU вблизи его сближения с Землей 25 февраля 2024 г.
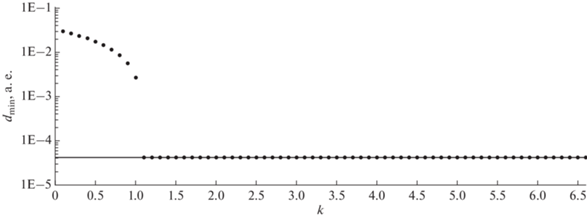
Рис. 6.
Результаты условной минимизации расстояния до Земли объекта 2021 GX9 вблизи его сближения с Землей 28 апреля 2032 г.
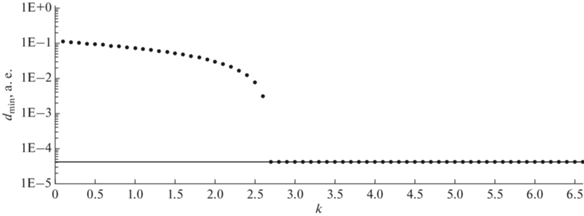
Рис. 7.
Результаты условной минимизации расстояния до Земли объекта 2021 QM1 вблизи его сближения с Землей 31 марта 2052 г.
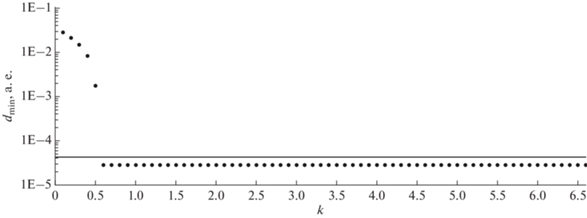
Как видно из рис. 4, процессы минимизации (3), (4) для всех точек каждой уровенной поверхности сходятся к практически сливающимся точкам, соответствующим минимальному расстоянию до центра Земли, равному 1.9 × 10–3 а. е. Поэтому можно сделать вывод, что для объекта 2012 QD8 в начальной доверительной области отсутствуют столкновительные орбиты и вероятность столкновения для этого объекта по крайней мере меньше чем 1 × 10–7, так как коэффициенту k = 6.6 соответствует доверительная вероятность 0.9999999 (табл. 1 ). Если продолжить поиск далее, то, как видно из рис. 4, скорее всего, минимальное значение 1.9 × 10–3 будет сохраняться очень долго, поэтому вероятность столкновения для этого объекта практически равна нулю.
Результаты, приведенные на рис. 5–7, качественно повторяют результаты, приведенные на рис. 4, однако отличаются тем, что минимальное расстояние до центра Земли оказывается меньше ее радиуса, т.е. что последние три астероида имеют столкновительные орбиты в начальной доверительной области. Так для объекта 2021 EU (рис. 5) минимальное расстояние в 4.25 × 10–5 а. е., практически совпадающее с радиусом Земли, достигается уже при k = 1.1; для объекта 2021 GX9 (рис. 6) минимальное расстояние в 4.0 × 10–5 а. е. достигается при k = 2.7; для объекта 2021 QM1 (рис. 7) минимальное расстояние в 2.8 × 10–5 а. е. достигается уже при k = 0.6.
Что касается вероятности столкновения, то ее “оценки сверху” на основе доверительной вероятности (табл. 1 ), для последних трех объектов получаются слишком завышенными: для 2021 EU вероятность столкновения оказывается меньше чем 0.976, для 2021 GX9 – меньше чем 0.295 и для 2021 QM1 – меньше чем 0.9992. Очевидно, что такие оценки являются слишком грубыми, так как реальная вероятность столкновения значительно меньше. Поэтому можно сделать вывод, что при наличии столкновительных орбит в начальной доверительной области для оценивания вероятности столкновения следует применять другие методы. В частности, поскольку область столкновительных орбит в фазовом пространстве обычно представляет собой узкую, практически прямолинейную в пределах рассматриваемой области трубку (Батурин, 2012), можно выявить множество столкновительных орбит, заполняющих эту трубку, и каким-то образом использовать полученные результаты для оценивания вероятности столкновения. Такие исследования автор планирует выполнить в дальнейшем.
Рассмотренный метод выявления столкновительных орбит в начальной доверительной области, прежде всего, может быть использован как первый этап в задаче оценивания вероятности столкновения. Метод позволяет выявлять столкновительные орбиты на каждой уровенной поверхности, и шаг перебора которых может быть сколь угодно малым. Если минимальное расстояние от астероида до Земли для всех уровенных поверхностей заметно превышает ее радиус, то можно сделать вывод, что вся начальная доверительная область не содержит приводящих к столкновению начальных параметров движения. Если же это минимальное расстояние на некоторых уровенных поверхностях окажется меньше радиуса Земли, то требуется более детальное исследование распределения столкновительных орбит в окрестностях найденных точек.
Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № FSWM-2020-0049).
Список литературы
Батурин А.П., Черницов А.М. Два алгоритма определения областей возможных движений космических объектов // Исследования по баллистике и смежным вопросам механики: Сб. статей. Томск: Изд-во Томск. ун-та, 2001. С. 86–88.
Батурин А.П. Выявление областей столкновительных орбит с помощью цилиндрических аппроксимаций и оценивание вероятности столкновения астероидов с Землей // Изв. вузов. Физика. 2012. Т. 55. № 10/2. С. 34–49.
Батурин А.П. Выявление столкновительных орбит астероидов с помощью представления начальной доверительной области в виде последовательности эллипсоидальных гиперповерхностей // Изв. вузов. Физика. 2016. Т. 59. № 10. С. 145–150.
Батурин А.П. Выявление столкновительных орбит астероидов с помощью условной минимизации расстояния до Земли // Астрон. вестн. 2020. Т. 54. № 6. С. 560–566. (Baturin A.P. Detection of asteroid impact orbits using conditional minimization of the distance to the Earth // Sol. Syst. Res. 2020. V. 54. № 6. P. 550–556.)
Железнов Н.Б. Влияние корреляционных связей между орбитальными параметрами астероида на определение вероятности его столкновения с планетой методом Монте-Карло // Астрон. вестн. 2010. Т. 44. № 2. С. 150–157. (Zheleznov N.B. The influence of the correlations between an asteroid’s orbital parameters on the estimation of the probability of planetary collision by the Monte Carlo method // Sol. Syst. Res. 2010. V. 44. № 2. P. 136–143.)
Ивашкин В.В., Стихно К.А. О предотвращении возможного столкновения астероида Апофис с Землей // Астрон. вестн. 2009. Т. 43. № 6. С. 502–516. (Ivashkin V.V., Stikhno C.A. On the prevention of a possible collision of asteroid Apophis with the Earth // Sol. Syst. Res. 2009. V. 43. № 6. P. 483–496.)
Прохоренко В.И. Об анализе тесных сближений двух космических тел на близких почти круговых орбитах // Космич. исслед. 2010. Т. 48. № 6. С. 541–548.
Соколов Л.Л., Башаков А.А., Борисова Т.П., Петров Н.А., Питьев Н.П., Шайдулин В.Ш. Траектории соударения астероида Апофис с Землей в XXI веке // Астрон. вестн. 2012. Т. 46. № 4. С. 311–320. (Sokolov L.L., Bashakov A.A., Borisova T.P., Petrov N.A., Pitjev N.P., Shaidulin V.S. Impact trajectories of the asteroid Apophis in the 21st century // Sol. Syst. Res. 2012. V. 46. № 4. P. 291–300.)
Сюсина О.М., Черницов А.М., Тамаров В.А. Построение доверительных областей в задаче вероятностного исследования движения малых тел Солнечной системы // Астрон. вестн. 2012. Т. 46. № 3. С. 209–222. (Syusina O.M., Chernitsov A.M., Tamarov V.A. Construction of confidence regions in problem on probabilistic study into motion of minor bodies of the Solar system // Sol. Syst. Res. 2012. V. 46. № 3. P. 195–207.)
Черницов А.М., Тамаров В.А., Авдюшев В.А., Баньщикова М.А., Дубас О.М. Особенности определения доверительных областей в пространстве начальных параметров движения Солнечной системы // Изв. вузов. Физика. 2007. Т. 50. № 12/2. С. 33–43.
Черницов А.М., Сюсина О.М., Тамаров В.А. Оценивание нелинейности в задаче построения доверительных областей движения потенциально опасных астероидов, наблюдаемых в одной оппозиции // Изв. вузов. Физика. 2014. Т. 57. № 12. С. 139–145.
Черницов А.М., Тамаров В.А., Баранников Е.А. Оценивание вероятности столкновения астероида с Землей методом Монте-Карло // Изв. вузов. Физика. 2016. Т. 59. № 5. С. 84–91.
Черницов А.М., Тамаров В.А., Баранников Е.А. Построение доверительных областей в задаче определения орбит астероидов // Астрон. вестн. 2017. Т. 51. № 5. С. 432–440. (Chernitsov A.M., Tamarov V.A., Barannikov Y.A. Сonstruction of confidence regions in the problem of asteroid orbit determination // Sol. Syst. Res. 2017. V. 51. № 5. P. 400–408.)
Everhart E. An efficient integrator that uses Gauss–Radauspacings // Proc. 83rd Colloq. Int. Astron. Union “Dynamics of Comets: Their Originand Evolution”, Rome, June 11–15, 1984 / Eds Carusi A., Valsecchi G.B. Dordrecht: D. Reidel, 1985. P. 185–202.
Ivashkin V.V., Stikhno C.A. A problem of the orbit correction for the near-Earth asteroid Apophis // Proc. 58th Int. Astronaut. Congress-2007, Hyderabad, India, September 24–28, 2007. ISSN 1995-6258), paper IAC-07-C1.7.08.
Ivashkin V.V., Stikhno C.A. Analysis of correction of asteroid Apophis’ orbit providing its collision with the Moon // Int. Meet. “Fundamental and applied problems of mechanics – 2018”. IOP Conf. Series: Journal of Physics: Conf. Series 1301 (2019) 012003 IOP Publishing, 2019.
Milani A. Asteroid impact monitoring // Serb. Astron. J. 2006. V. 172. P. 1–11.
Milani Andrea, Chesley Steven R., Sansaturio M.E., Bernardi F., Valsecchi G.B., Arratia O. Long term impact risk for (101955) 1999RQ36 // Icarus. 2009. V. 203. Iss. 2. P. 460–471.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник