Астрономический вестник, 2022, T. 56, № 5, стр. 344-355
Численное моделирование орбитального движения геосинхронных объектов по данным позиционных наблюдений
В. А. Авдюшев a, *, Т. В. Бордовицына a, **, А. П. Батурин a, ***, Н. С. Бахтигараев b, П. А. Левкина b, ****, Н. А. Попандопуло a, *****, К. В. Салейко a, И. В. Томилова a, ******, И. Н. Чувашов a
a Томский госуниверситет
Томск, Россия
b Институт астрономии РАН
Москва, Россия
* E-mail: sch@niipmm.tsu.ru
** E-mail: tvbord@sibmail.com
*** E-mail: nail@inasan.ru
**** E-mail: ayvazovskaya@inasan.ru
***** E-mail: nikas.popandopulos@gmail.com
****** E-mail: irisha_tom@mail.ru
Поступила в редакцию 28.12.2021
После доработки 22.03.2022
Принята к публикации 25.03.2022
- EDN: QNTTSV
- DOI: 10.31857/S0320930X22050012
Аннотация
Представлены результаты численного моделирования движения группы геосинхронных объектов по позиционным наблюдениям, полученным на уникальной научной установке Цейсс–2000 в ЦКП “Терскольская обсерватория” Института астрономии РАН. Дано описание усовершенствованного высокоточного программно-математического обеспечения (ПО), предназначенного для работы с позиционными наблюдениями ИСЗ, приведены результаты его апробации на наблюдениях околоземных объектов, выполненных на указанной выше установке Цейсс–2000. Модифицированное ПО позволяет определять вектор динамического состояния околоземного объекта и его параметр парусности. Апробация проводилась на наблюдениях геосинхронных объектов с номерами 90 008, 90 031, 90 214 и 97 149 (номера объектов даны в соответствии с нумерацией в динамической базе данных космических объектов Института прикладной математики им. М.В. Келдыша РАН). Полученные параметры использованы для исследования долговременной орбитальной эволюции объектов. Показано, что три объекта (90 008, 90 031, 90 214) захвачены в резонанс 1 : 1 со скоростью вращения Земли и имеют на интервале времени 10 лет устойчивое движение во вращающейся системе координат, близкое к гармоническому осциллятору. Объект 97149 не является резонансным, но его движение остается регулярным на интервале времени 10 лет.
ВВЕДЕНИЕ
По данным службы контроля околоземного космического пространства (ОКП) на околоземных орбитах находится в настоящее время более 500 тыс. объектов искусственного происхождения, причем 20 тысяч из них имеют размеры, большие 10 см, и доступны для позиционных наблюдений (Оголев, Морозов, 2019). Вся эта масса объектов создает угрозу действующим аппаратам (Klinkrad, 2006), что приводит к необходимости постоянного отслеживания большого количества объектов. А это, в свою очередь, требует постоянного совершенствования программно-математического обеспечения, предназначенного для обработки результатов оптических наблюдений, определения и улучшения орбит, а также высокоточного численного моделирования движения (Андрианов и др., 2019).
Коллектив авторов настоящей работы состоит из двух групп, одна из которых имеет большой опыт в разработке методов высокоточного численного прогнозирования движения ИСЗ (Александрова и др., 2017; Авдюшев, 2020), а вторая группа (Левкина и др., 2013) ведет позиционные наблюдения на уникальной научной установке Цейсс–2000 в ЦКП “Терскольская обсерватория” Института астрономии РАН.
Целью настоящей работы является создание высокоточного программно-математического обеспечения для определения, улучшения орбит и численного моделирования движения околоземных объектов, а также апробация и применение его при обработке высокоточных наблюдений околоземных объектов, полученных на установке Цейсс–2000.
Разработанный ранее программный комплекс “Численная модель движения систем ИСЗ” (Александрова и др., 2017) был усовершенствован для определения параметров движения и сил из обработки результатов высокоточных позиционных наблюдений. Были уточнены модели сил в соответствии с (IERS Conventions 2010), использован более эффективный интегратор (Авдюшев, 2020), введено точное вычисление изохронных производных путем численного интегрирования соответствующих уравнений. В новом программном комплексе совместно с параметрами орбиты определяется коэффициент парусности, представляющий собой отношение площади миделевого сечения объекта к его массе. Этот параметр определяет величину влияния светового давления на динамику объекта.
Начальное определение параметров орбит в рамках данного программного комплекса находится нетрадиционным способом, который в применении к астероидно-кометной задаче был описан в (Батурин, Чувашов, 2006). Как отмечается в работе (Андрианов и др., 2019), в связи с тем, что классические способы первоначального определения орбит мало приемлемы при обработке наблюдений объектов космического мусора, интерес к этой задаче в последнее время возрос (2009; Milani и др., 2004; Tommei и др., 2007; Maruskin и др., Kolessa и др., 2014; 2019).
Для апробации были выбраны объекты с номерами 90 008, 90 031, 90 214 и 97 149. Номера объектов даны в соответствии с нумерацией в динамической базе данных космических объектов Института прикладной математики им. М.В. Келдыша РАН (Молотов и др., 2020). Полученные параметры использованы для исследования долговременной орбитальной эволюции объектов.
ОПИСАНИЕ ПРОГРАММНОГО КОМПЛЕКСА “ЧИСЛЕННАЯ МОДЕЛЬ ДВИЖЕНИЯ ИСЗ”
Численную модель орбитального движения ИСЗ можно представить в виде
где ${{{\mathbf{p}}}^{{\text{C}}}}$–$2N$-мерный вектор модельных представлений наблюдений:(2)
${{{\mathbf{p}}}^{{\text{C}}}} = {{(\alpha _{1}^{{\text{C}}}\cos \delta _{1}^{{\text{C}}},\delta _{1}^{{\text{C}}}, \ldots ,\alpha _{N}^{{\text{C}}}\cos \delta _{N}^{{\text{C}}},\delta _{N}^{{\text{C}}})}^{T}},$Угловые координаты на каждый момент наблюдения вычисляются из топоцентрического вектора положения спутника ${{{\mathbf{x}}}_{{\text{T}}}} = {{({{x}_{{{\text{T}}1}}},{{x}_{{{\text{T}}2}}},{{x}_{{{\text{T}}3}}})}^{T}}$ как
(3)
$\alpha = \operatorname{arctg} \frac{{{{x}_{{{\text{T}}2}}}}}{{{{x}_{{{\text{T}}1}}}}},\,\,\,\,\delta = \arcsin \frac{{{{x}_{{{\text{T}}3}}}}}{{\left| {{{{\mathbf{x}}}_{{\text{T}}}}} \right|}}.$В свою очередь, топоцентрический вектор определяется как разность геоцентрических векторов положения спутника ${\mathbf{x}}$ и наблюдателя ${{{\mathbf{x}}}_{{\text{O}}}}$: ${{{\mathbf{x}}}_{{\text{T}}}} = {\mathbf{x}} - {{{\mathbf{x}}}_{{\text{O}}}}$. Положение наблюдателя корректируется за подвижку земной коры вследствие тектонических смещений и приливных деформаций, вызванных, главным образом, притяжением Луны и Солнца. В представлении наблюдений также учитывается эффект запаздывания света.
Движение спутника относительно геоцентра формализуется дифференциальными уравнениями 2-го порядка:
(4)
$\frac{{{{\operatorname{d} }^{2}}{\mathbf{x}}}}{{\operatorname{d} {{t}^{2}}}} = {\mathbf{P}}(t,{\mathbf{x}},{\mathbf{\dot {x}}},\gamma ),$Для приведения времени наблюдений UTC к эфемеридному времени ТТ ($t$), относительно которого формализуется движения ИСЗ (4), используется поправка
(5)
$\begin{gathered} {\text{UTC}} - {\text{TT}} = {\text{(UT1}} - {\text{UTC)}} - \\ - \,\,{\text{(UT1}} - {\text{TAI)}} + {\text{32}}.{\text{184}}\,\,{\text{(с)}}{\text{.}} \\ \end{gathered} $Поправки ${\text{UT1}} - {\text{UTC}}$ и ${\text{UT1}} - {\text{TAI}}$ ежедневно определяются в “Международной службе вращения Земли” (https://hpiers.obspm.fr/eop-pc/index.php), а 32.184 с – это разность между двумя эфемеридными временами ${\text{TAI}} - {\text{TT}}$.
Параметры модели ${\mathbf{q}}$ определяются из наблюдений спутника ${{{\mathbf{p}}}^{{\text{O}}}}$ в рамках задачи наименьших квадратов:
(6)
$S({\mathbf{\hat {q}}}) = {{\left\| {{{{\mathbf{p}}}^{{\text{O}}}} - {{{\mathbf{p}}}^{{\text{C}}}}({\mathbf{\hat {q}}})} \right\|}^{2}} \to \min ,$(7)
${{{\mathbf{q}}}_{{k{\kern 1pt} + {\kern 1pt} 1}}} = {{{\mathbf{q}}}_{k}} - {{({\mathbf{p}}_{{\mathbf{q}}}^{{'T}}{\mathbf{p}}_{{\mathbf{q}}}^{'})}^{{ - 1}}}{\mathbf{p}}_{{\mathbf{q}}}^{{'T}}({{{\mathbf{p}}}^{{\text{O}}}} - {{{\mathbf{p}}}^{{\text{C}}}}({{{\mathbf{q}}}_{k}})),$(8)
${{{\mathbf{p}}}^{{\text{O}}}} = {{(\alpha _{1}^{{\text{O}}}\cos \delta _{1}^{{\text{O}}},\delta _{1}^{{\text{O}}}, \ldots ,\alpha _{N}^{{\text{O}}}\cos \delta _{N}^{{\text{O}}},\delta _{N}^{{\text{O}}})}^{T}}.$(9)
${{({\mathbf{p}}_{{\mathbf{q}}}^{'})}_{i}} = \left( {\cos \delta _{{}}^{{\text{C}}}\frac{{\partial \alpha _{{}}^{{\text{C}}}}}{{\partial {{{\mathbf{x}}}_{{\text{T}}}}}}\frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{q}}}},\frac{{\partial \delta _{{}}^{{\text{C}}}}}{{\partial {{{\mathbf{x}}}_{{\text{T}}}}}}\frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{q}}}}} \right)_{i}^{T}.$Частные производные ${{\partial \alpha _{{}}^{{\text{C}}}} \mathord{\left/ {\vphantom {{\partial \alpha _{{}}^{{\text{C}}}} {\partial {{{\mathbf{x}}}_{T}}}}} \right. \kern-0em} {\partial {{{\mathbf{x}}}_{T}}}}$ и ${{\partial \delta _{{}}^{{\text{C}}}} \mathord{\left/ {\vphantom {{\partial \delta _{{}}^{{\text{C}}}} {\partial {{{\mathbf{x}}}_{T}}}}} \right. \kern-0em} {\partial {{{\mathbf{x}}}_{T}}}}$ получаются путем прямого дифференцирования формул (4). Частные производные ${{\partial {\mathbf{x}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{x}}} {\partial {\mathbf{q}}}}} \right. \kern-0em} {\partial {\mathbf{q}}}}$ определяются из дифференциальных уравнений
(10)
$\frac{{{{\operatorname{d} }^{2}}}}{{\operatorname{d} {{t}^{2}}}}\frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{q}}}} = \frac{{\partial {\mathbf{P}}}}{{\partial {\mathbf{x}}}}\frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{q}}}} + \frac{{\partial {\mathbf{P}}}}{{\partial {\mathbf{\dot {x}}}}}\frac{{\partial {\mathbf{\dot {x}}}}}{{\partial {\mathbf{q}}}} + \frac{{\partial {\mathbf{P}}}}{{\partial \gamma }}\frac{{\partial \gamma }}{{\partial {\mathbf{q}}}},$В результате обработки наблюдений формируется ковариационная матрица параметров ${\mathbf{q}},$ которая характеризует их неопределенность вследствие ошибок наблюдений:
(11)
${\mathbf{C}} = {{\sigma }^{2}}{{({\mathbf{p}}_{{\mathbf{q}}}^{{'T}}{\mathbf{p}}_{{\mathbf{q}}}^{'})}^{{ - 1}}},$Поскольку определяемые параметры ${\mathbf{q}}$ имеют разную размерность, целесообразно прибегать к их масштабированию (нормализации), что может улучшить обусловленность задачи и тем самым уменьшить вычислительные ошибки в поправках к параметрам в итерационной схеме Гаусса–Ньютона. Масштабирование предполагает умножение частных производных ${\mathbf{p}}_{{\mathbf{q}}}^{'}$ и поправок в итерационной схеме на диагональную матрицу $\operatorname{diag} ({{s}_{1}}, \ldots ,{{s}_{7}}).$ Оптимальный вариант масштабирования – ${{s}_{i}} = {{q}_{i}}$ $(i = 1, \ldots ,7)$. Обращение матрицы осуществляется методом SVD, что позволяет следить за обусловленностью процесса улучшения орбит.
Начальное приближение для итерационной схемы (7) определяется нетрадиционным способом (Батурин, Чувашов, 2006). Из двух наблюдений на соседние близкие моменты времени ${{t}_{i}}$ и ${{t}_{{i{\kern 1pt} + {\kern 1pt} 1}}}$ вычисляются топоцентрические векторы положения ${{({{{\mathbf{x}}}_{{\text{T}}}})}_{i}}$ и ${{({{{\mathbf{x}}}_{{\text{T}}}})}_{{i{\kern 1pt} + {\kern 1pt} 1}}}$ по формулам
(12)
${{{\mathbf{x}}}_{0}} = {{({{{\mathbf{x}}}_{{\text{T}}}})}_{i}} + {{({{{\mathbf{x}}}_{{\text{O}}}})}_{i}},\,\,\,\,{{{\mathbf{\dot {x}}}}_{0}} = {{{\mathbf{\dot {x}}}}_{{\text{T}}}} + {{({{{\mathbf{\dot {x}}}}_{{\text{O}}}})}_{i}}.$Поскольку начальные приближения (12) довольно грубые, для обеспечения сходимости итерационного процесса (7) его следует начинать с малым составом наблюдений на близкие к начальной эпохе моменты с последующим подключением других наблюдений и расширением мерного интервала, и так далее, пока в итерационный процесс не будет задействован весь наблюдательный материал.
Новая версия программного комплекса “Численная модель движения ИСЗ” написана на процедурном высокоуровневом языке программирования Fortran. Интерфейсом программного комплекса служит входной текстовый файл. В этом файле задаются следующие данные: положение наблюдателя; начальная эпоха; параметры движения объекта (при наличии); коэффициенты масштабирования определяемых параметров; выборка наблюдений (время наблюдения, прямое восхождение, склонение, блеск); параметры интегратора (шаг, порядок, доверительная точность); переключатели учета возмущающих факторов (порядок и степень гармоник геопотенциала и селенопотенциала, Луна, Солнце, планеты, световое давление, релятивистские эффекты, приливы, атмосфера); параметры спутника (масса, площадь миделевого сечения, коэффициенты лобового сопротивления и отражения).
Таким образом, новый программный комплекс существенно отличается от своего предшественника, он позволяет не только прогнозировать движение, но и определять параметры движения и сил из обработки высокоточных позиционных наблюдений. Кроме того, в нем уточнены модели сил в соответствии с (IERS Conventions 2010), использован новый более эффективный интегратор (Авдюшев, 2020), который позволяет работать с системой уравнений, состоящей из уравнений первого и второго порядка, что удобно при совместном интегрировании уравнений движения, уравнений в вариациях и уравнений параметров MEGNO, введено точное вычисление изохронных производных путем численного интегрирования соответствующих уравнений. В новом программном комплексе совместно с параметрами орбиты определяется коэффициент парусности объекта.
На данный момент программный комплекс не доступен для сторонних пользователей, но в дальнейшем планируется разработать версию для его опубликования на специальном сайте кафедры Астрономии и космической геодезии ТГУ.
РЕЗУЛЬТАТЫ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ПО ДАННЫМ ИЗМЕРЕНИЙ
В качестве объектов наблюдения была выбрана группа, состоящая из четырех неуправляемых геосинхронных спутников с номерами 90 008, 90 031, 90 214 и 97 149. Форма представления наблюдений показана в табл. 1.
Таблица 1.
Форма представления наблюдений
| Эпоха | Прямое восхождение, ч, мин, с |
Склонение, угл. град, угл. мин, угл. с |
Блеск, звездная величина |
|
|---|---|---|---|---|
| дата | время (UTC), ч, мин, с | |||
| 10 09 2020 | 22 59 23.50 | 05 23 07.44 | +02 28 45.27 | 17.1 |
С помощью описанной выше численной модели движения систем ИСЗ, содержащей блоки вычисления изохронных производных и определения параметров движения по данным измерений, было проведено определение и уточнение орбит перечисленных выше объектов. В процессе численного моделирования движения учитывались возмущения от гармоник геопотенциала до 20-го порядка и степени, возмущения от Луны и Солнца, рассматриваемых как материальные точки, а также световое давление. В табл. 2 приведены данные о процессе улучшения орбит по наблюдениям, полученным в сентябре 2020 г.
Таблица 2.
Данные о процессе улучшения орбит по наблюдениям в 2020 г.
| Номер объекта | Количество наблюдений | Период наблюдений, сутки | Ср. кв. ошибка, угл. с |
|---|---|---|---|
| 90 008 | 219 | 11–22.09.2021 | 0.480 |
| 90 031 | 344 | 11–25.09.2021 | 0.684 |
| 90 214 | 263 | 11–23.09.2021 | 3.740 |
| 97 149 | 224 | 15–25.09.2021 | 0.401 |
Далее в табл. 3–6 приведены координаты и скорости объектов, элементы их орбит на выбранные эпохи, а также средние квадратические ошибки процесса улучшения орбит и параметры парусности объектов, полученные по данным наблюдений. На рис. 1 и 2 показано изменение блеска объектов в процессе наблюдения и распределения невязок в сферических координатах.
Таблица 3.
Параметры объекта 90 008 по наблюдениям в сентябре 2020 г.
| Кол-во наблюдений | A/m, м2/кг | Ср. кв. ошибка, угл. с | Эпоха |
|---|---|---|---|
| 219 | 0.011727 | 0.480 | 17.09.2020 00:00:00 |
| координаты и скорости | элементы орбиты | ||
| ${{x}_{1}}$, км | –4405.2000101 | a | 42162.0071501 км |
| ${{x}_{2}}$, км | 41 739.3669507 | e | 0.0038175 |
| ${{x}_{3}}$, км | 4065.3397331 | i | 10°09′35″.287 |
| ${{\dot {x}}_{1}}$, км/с | –3.0268627233 | Ω | 308°44′33″.216 |
| ${{\dot {x}}_{2}}$, км/с | –0.2869651634 | ω | 239°05′00″.063 |
| ${{\dot {x}}_{3}}$, км/с | –0.4552572126 | М | 268°13′22″.280 |
Таблица 4.
Параметры объекта 90 031 по наблюдениям в сентябре 2020 г.
| Кол-во наблюдений | A/m, м2/кг | Ср. кв. ошибка, угл. с | Эпоха |
|---|---|---|---|
| 344 | 0.0081181 | 0.684 | 17.09.2020 00:00:00 |
| координаты и скорости | элементы орбиты | ||
| ${{x}_{1}}$, км | 18 901.7644368 | a | 42 147.2073162 км |
| ${{x}_{2}}$, км | 36 816.0003536 | e | 0.0019965 |
| ${{x}_{3}}$, км | 8142.2030811 | i | 11°25′41″.895 |
| ${{\dot {x}}_{1}}$, км/с | –2.7160495816 | Ω | 319°32′38″.249 |
| ${{\dot {x}}_{2}}$, км/с | 1.4310972256 | ω | 351°23′54″.007 |
| ${{\dot {x}}_{3}}$, км/с | –0.1361316100 | М | 111°24′51″.101 |
Таблица 5.
Параметры объекта 90 214 по наблюдениям в сентябре 2020 г.
| Кол-во наблюдений | A/m, м2/кг | Ср. кв. ошибка, угл. с | Эпоха |
|---|---|---|---|
| 263 | 0.10845 | 3.740 | 17.09.2020 00:00:00 |
| координаты и скорости | элементы орбиты | ||
| ${{x}_{1}}$, км | 34 646.6876473 | a | 42157.7890187 км |
| ${{x}_{2}}$, км | 23 765.4064407 | e | 0.014882 |
| ${{x}_{3}}$, км | –2090.0487432 | i | 4°20′3″.627 |
| ${{\dot {x}}_{1}}$, км/с | –1.6955198408 | Ω | 75°28′9″.131 |
| ${{\dot {x}}_{2}}$, км/с | 2.5673711145 | ω | 236°27′26″.176 |
| ${{\dot {x}}_{3}}$, км/с | 0.1732206676 | М | 80°45′6″.838 |
Таблица 6.
Параметры объекта 97 149 по наблюдениям в сентябре 2020 г.
| Кол-во наблюдений | A/m, м2/кг | Ср. кв. ошибка, угл. с | Эпоха |
|---|---|---|---|
| 224 | 0.014095 | 0.401 | 17.09.2020 00:00:00 |
| координаты и скорости | элементы орбиты | ||
| ${{x}_{1}}$, км | 32 744.5749188 | a | 42204.8022834 км |
| ${{x}_{2}}$, км | 26 445.0220050 | e | 0.016921 |
| ${{x}_{3}}$, км | 3186.42110713 | i | 4°19′47″.151 |
| ${{\dot {x}}_{1}}$, км/с | –1.8902143962 | Ω | 309°43′35″.287 |
| ${{\dot {x}}_{2}}$, км/с | 2.4226149179 | ω | 357°47′57″.965 |
| ${{\dot {x}}_{3}}$, км/с | 0.0071607046 | М | 89°27′44″.332 |
Рис. 1.
Распределение параметра блеска и невязок для объектов 90 008 (а) и 90 031 (б) по наблюдениям в сентябре 2020 г.
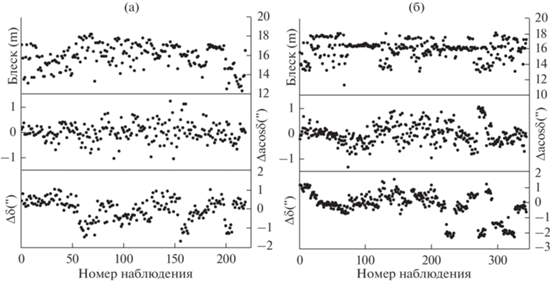
Рис. 2.
Распределение параметра блеска и невязок для объектов 90 214 (а) и 97 149 (б) по наблюдениям в сентябре 2020 г.
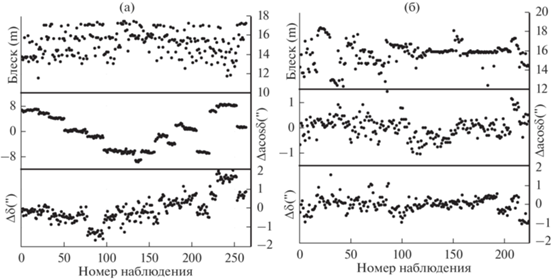
Как показывают приведенные результаты, орбиты объектов 90 008, 90 031 и 97 149 определяются с высокой точностью, а точность определения орбиты объекта 90 214 недостаточна. В то же время методическая точность прогнозирования движения всех объектов высокая. Данные приведены в табл. 7.
Таблица 7.
Оценки точности интегрирования
| Номер объекта | $\Delta {\mathbf{x}}$, м | Номер объекта | $\Delta {\mathbf{x}}$, м |
|---|---|---|---|
| 90 008 | 4.3 × 10–6 | 90 214 | 6.9 × 10–6 |
| 90 031 | 3.5 × 10–5 | 97 149 | 2.7 × 10–5 |
Здесь в качестве оценок точности $\Delta {\mathbf{x}}$ даны максимальные расхождения численных решений на интервале времени 1 год, полученные при двух соседних порядках задаваемой точности интегрирования ${{e}_{{{\text{tol}}}}} = 10$ и ${{e}_{{{\text{tol}}}}} = 11$. В процессе интегрирования учитывался полный набор возмущающих сил.
Наблюдения двух объектов 90 008 и 90 031 были продолжены в сентябре 2021 г. Данные о результатах улучшения орбит по этим измерениям приведены в табл. 7.
Приведенные в табл. 8 данные говорят о том, что наблюдения в сентябре 2021 г. не дают той точности, которая была получена по наблюдениям в 2020 г. Тем не менее была предпринята попытка объединить наблюдения объектов, выполненные в 2020 и 2021 годах, которая для объекта 90 031 увенчалась успехом.
Таблица 8.
Данные о процессе улучшения орбит по наблюдениям в 2021 г.
| Номер объекта | Количество наблюдений | Период наблюдений, сутки | Ср. кв. ошибка, угл. с |
|---|---|---|---|
| 90 008 | 1051 | 13–28.09.2021 | 1.308 |
| 90 031 | 354 | 13–28.09.2021 | 0.783 |
Таблица 9.
Параметры объекта 90 031 по всем объединенным наблюдениям: сентябрь 2020 г.–сентябрь 2021 г.
| Кол-во наблюдений | A/m, м2/кг | Ср. кв. ошибка, угл. с | Эпоха |
|---|---|---|---|
| 698 | 0.0028473 | 1.711 | 17.09.2021 00:00:00 |
| координаты и скорости | элементы орбиты | ||
| ${{x}_{1}}$, км | 2584.18827501 | a | 42 180.3274241 км |
| ${{x}_{2}}$, км | 41 717.9659702 | e | 0.0016904 |
| ${{x}_{3}}$, км | 5984.92635031 | i | 10°42′8″.290 |
| ${{\dot {x}}_{1}}$, км/с | –3.0388856164 | Ω | 315°42′39″.838 |
| ${{\dot {x}}_{2}}$, км/с | 0.24515726999 | ω | 2°9′45″.399 |
| ${{\dot {x}}_{3}}$, км/с | –0.3678748323 | М | 127°55′57″.430 |
В табл. 10 введены следующие обозначения: N – количество наблюдений, ON – отбраковано наблюдений, σ" – в конце процесса улучшения, контр. σ", во всех строках, кроме первой, – контрольное значение, полученное по 11 наблюдениям в октябре 2021 г., не участвовавших в улучшении орбиты, Т – число обусловленности Тодда.
Таблица 10.
Данные по улучшению и контролю орбиты объекта 90 031 по объединенным наблюдениям: сентябрь 2020 г.–сентябрь 2021 г. с отбраковкой
| N | ON | Способ отб-ки | σ, угл. с | контр. σ, угл. с | Т | Ошибки параметров, ${{x}_{1}}$… (м), ${{\dot {x}}_{1}}$… (м/с) и A/m… (м2/кг) |
|---|---|---|---|---|---|---|
| 344 | – | б/о | 0.68 | 50.51 | 1.7 × 105 | контр. σ" – первоначальное представление наблюдений в 2021 г. системой 2020 г. |
| 698 | – | б/о | 1.73 | 2.84 | 5.4 × 107 | ${{x}_{1}}$ ± 31.5, ${{x}_{2}}$ ± 26.9, ${{x}_{3}}$ ± 20.1; ${{\dot {x}}_{1}}$ ± 0.0022, ${{\dot {x}}_{2}}$ ± 0.0029, ${{\dot {x}}_{3}}$ ± 0.0014; A/m ± 0.00023 |
| 680 | 18 | 3σ | 1.65 | 2.77 | 5.6 × 107 | ${{x}_{1}}$ ± 30.8, ${{x}_{2}}$ ± 26.6, ${{x}_{3}}$ ± 19.7; ${{\dot {x}}_{1}}$ ± 0.0022, ${{\dot {x}}_{2}}$ ± 0.0028, ${{\dot {x}}_{3}}$ ± 0.0014; A/m ± 0.00023 |
| 585 | 113 | 2σ | 1.29 | 2.72 | 5.7 × 107 | ${{x}_{1}}$ ± 25.9, ${{x}_{2}}$ ± 24.3, ${{x}_{3}}$ ± 17.7; ${{\dot {x}}_{1}}$ ± 0.0020, ${{\dot {x}}_{2}}$ ± 0.0026, ${{\dot {x}}_{3}}$ ± 0.0013; A/m ± 0.00021 |
Результаты, полученные по новому ПО, сравнивались с результатами, полученными по разработанному ранее программному комплексу “Численная модель движения систем ИСЗ”. Модели показали хорошее согласие (до третьей значащей цифры) в невязках и среднеквадратических ошибках. Использование точных значений изохронных производных в новом ПО позволяет повысить точность сходимости итерационного процесса улучшения орбит на два порядка.
ИССЛЕДОВАНИЕ ОРБИТАЛЬНОЙ ЭВОЛЮЦИИ ОБЪЕКТОВ
Перейдем к рассмотрению долговременной орбитальной эволюции выбранных объектов. Для исследования орбитальной эволюции будем использовать разработанный пакет программ, дополненный интегрированием уравнений для вычисления текущего и усредненного параметров MEGNO (Cincotta, Simo, 2000; Cincotta и др., 2003). Эволюция во времени усредненного параметра MEGNO дает представление о характере движения объекта: для квазипериодических (регулярных) орбит параметр MEGNO осциллирует около 2, для таких орбит усредненное значение MEGNO всегда стремится к 2, а для устойчивых орбит типа гармонического осциллятора усредненное значение MEGNO равно нулю. При значении усредненного параметра MEGNO больше 2 имеет место хаотизация движения, что не позволяет точно прогнозировать эволюцию элементов орбиты. А для исследования резонансных характеристик объектов будем использовать методики и программы, разработанные ранее (Томилова и др., 2019; Александрова и др., 2020).
Представление о точности интегрирования на 10-летнем интервале времени дают графики, приведенные на рис. 3.
Рис. 3.
Оценка точности методом сравнения с эталонной орбитой для объектов 90 008 и 97 149 в конце 10‑летнего интервала прогнозирования.
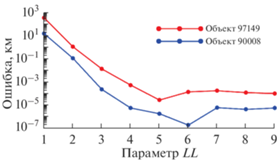
Оценка точности интегратора была проведена методом сравнения с эталонной орбитой. На графике представлены результаты для двух рассматриваемых в данной работе объектов. В программном комплексе для выбора шага интегрирования задается параметр LL, который связан с задаваемой точностью следующим образом: ${{\left\| {\mathbf{e}} \right\|}_{{{\text{tol}}}}} = {{10}^{{ - LL}}}$. В качестве эталонной орбиты была выбрана орбита, полученная интегрированием уравнений движения методом 16-го порядка и параметром LL, равным 10, на 128-битной разрядной сетке. Остальные расчеты были выполнены с помощью арифметики двойной точности. Прогнозирование движения осуществлялось на 10-летнем интервале времени. Как показывают оценки, субсантиметровую точность прогнозирования можно получить при значении параметра LL = 5. Дальнейшее увеличение параметра LL нецелесообразно на 64-битной разрядной сетке, поскольку приводит к ненужному дроблению шага и накоплению ошибки округления. Орбитальные характеристики объектов отличаются величинами больших полуосей. Как показали, приведенные ниже исследования, орбитальная эволюция объектов также очень различна: объект 90 008 захвачен в резонанс, и его движение обладает высокой устойчивостью, а объект 97 149 движется вне зоны устойчивого резонанса, имеет регулярное, но менее устойчивое движение.
Движение каждого из объектов было промоделировано численно на интервале времени 10 лет. В процессе моделирования учитывались возмущения от геопотенциала до V15,15, притяжение Луны, Солнца, влияние светового давления и приливных деформаций в теле Земли. Кроме того, был проведен анализ резонансных возмущений по методике Р. Алана (Allan, 1967a; 1967b), уточненной в работах (Кузнецов и др., 2012; Томилова и др., 2019).
Полученные из наблюдений значения больших полуосей говорят, что объекты находятся в окрестности резонанса 1 : 1 со скоростью вращения Земли. Указанная выше методика в этом случае дает следующие формулы для резонансных соотношений и резонансных (критических) аргументов:
Результаты исследования приведены на графиках ниже (рис. 4–7). Здесь в блоках (а) на единой временной шкале показаны изменения наклонения орбиты $i$, эксцентриситета $e$, большой полуоси $a$ и усредненного параметра MEGNO. В блоках (б) показана эволюция орбит объектов в плоскости $\left\{ {a,\,\,\lambda } \right\}$. В блоках (в) дана эволюция во времени долготы подспутниковой точки. На графиках, обозначенных (г), (д) и (е), показана эволюция во времени резонансных соотношений и критических аргументов компонент ${{\Phi }_{1}},$ ${{\Phi }_{4}},$ ${{\Phi }_{5}}$ мультиплета орбитального резонанса со скоростью вращения Земли. Влияние светового давления выделено красным цветом.
Рис. 4.
Особенности движения объекта 90 008: (а) орбитальная эволюция элементов орбиты и параметра MEGNO; (б) орбитальная эволюция объекта в фазовой плоскости $\left\{ {a,\,\,\lambda } \right\}$; (в) эволюция долготы подспутниковой точки; (г)–(е) компоненты ${{\Phi }_{1}},$ ${{\Phi }_{4}},$ ${{\Phi }_{5}}$ мультиплета орбитального резонанса со скоростью вращения Земли.
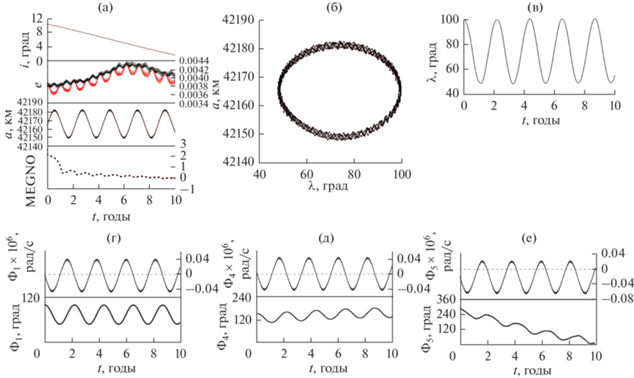
Рис. 5.
Особенности движения объекта 90 031: (а) орбитальная эволюция элементов орбиты и параметра MEGNO; (б) орбитальная эволюция объекта в фазовой плоскости $\left\{ {a,\,\,\lambda } \right\}$; (в) эволюция долготы подспутниковой точки; (г)–(е) компоненты ${{\Phi }_{1}},$ ${{\Phi }_{4}},$ ${{\Phi }_{5}}$ мультиплета орбитального резонанса со скоростью вращения Земли.
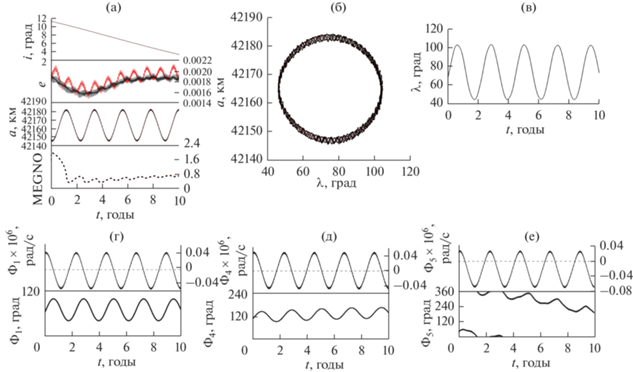
Рис. 6.
Особенности движения объекта 90 214: (а) орбитальная эволюция элементов орбиты и параметра MEGNO; (б) орбитальная эволюция объекта в фазовой плоскости $\left\{ {a,\,\,\lambda } \right\}$; (в) эволюция долготы подспутниковой точки; (г)–(е) компоненты ${{\Phi }_{1}},$ ${{\Phi }_{4}},$ ${{\Phi }_{5}}$ мультиплета орбитального резонанса со скоростью вращения Земли.
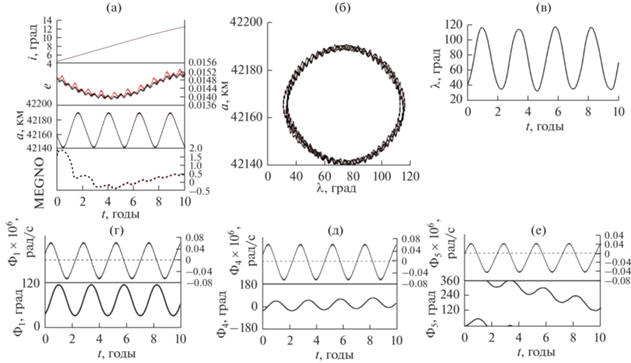
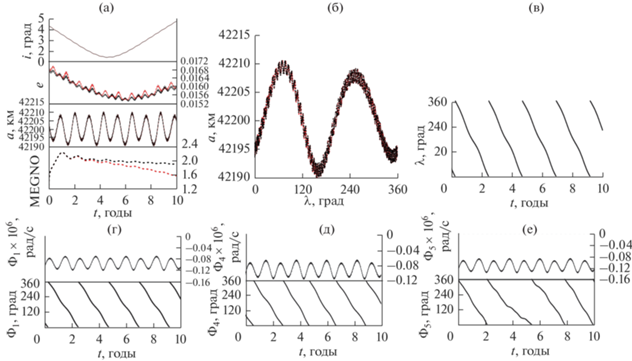
Рис. 7.
Особенности движения объекта 97 149: (а) орбитальная эволюция элементов орбиты и параметра MEGNO; (б) орбитальная эволюция объекта в фазовой плоскости $\left\{ {a,\,\,\lambda } \right\}$; (в) эволюция долготы подспутниковой точки; (г)–(е) компоненты ${{\Phi }_{1}},$ ${{\Phi }_{4}},$ ${{\Phi }_{5}}$ мультиплета орбитального резонанса со скоростью вращения Земли.
Кроме того, был проведен анализ наличия в динамике рассматриваемых вековых резонансов низких порядков по методике, изложенной в (Александрова и др., 2020). Анализ показал, что вековые резонансы низких порядков в динамике объектов отсутствуют.
Общий анализ результатов, приведенных на рис. 4–7, позволяет сделать ряд выводов о динамике исследуемых объектов:
− все изучаемые объекты принадлежат области геосинхронного движения; полученные результаты хорошо согласуются с результатами (Breiter и др., 2005);
− основными возмущающими факторами в движении объектов являются: влияние гармоник геопотенциала, гравитационное влияние Луны и Солнца, а также влияние светового давления;
− движение объектов 90 008, 90 031 и 90 214 является исключительно устойчивым, близко к гармоническому осциллятору, а движение объекта 97 149 является регулярным;
− объекты 90 008, 90 031 и 90 214 захвачены в резонанс 1 : 1 со скоростью вращения Земли (резонансные соотношения проходят через нулевые значения, а критические аргументы устойчиво либрируют);
− объект 97 149 не является резонансным;
− фазовые портреты в плоскости $\left\{ {a,\,\,\lambda } \right\}$ показывают, что во вращающейся системе координат объекты 90 008, 90 031, 90 214 либрируют около устойчивой точки либрации $\lambda $ = 75°;
− в плоскости $\left\{ {a,\,\,\lambda } \right\}$ во вращающейся системе координат объект 97149 находится в области регулярного движения;
− вековые резонансы низких порядков в движении объектов отсутствуют.
ЗАКЛЮЧЕНИЕ
Таким образом, в настоящей работе представлены результаты численного моделирования движения группы геосинхронных спутников, параметры которых получены по результатам позиционных наблюдений, выполненных на уникальной научной установке Цейсс–2000 в ЦКП “Терскольская обсерватория” Института астрономии РАН.
Моделирование выполнялось с помощью модифицированного программного комплекса “Численная модель движения ИСЗ”. Представлено описание программно-математического комплекса, который позволяет решать следующие задачи:
− численно с высокой точностью моделировать движение околоземных объектов;
− выполнять определение и улучшение орбит околоземных объектов по данным позиционных наблюдений;
− производить отбраковку наблюдений с контролем обусловленности задачи;
− определять из наблюдений параметр парусности объекта;
− проводить полное исследование долговременной орбитальной эволюции объекта с выявлением резонансных характеристик его динамики;
− использование точных значений изохронных производных позволяет повысить точность сходимости итерационного процесса на два порядка.
Использование данного программно-математического комплекса при обработке наблюдений группы геосинхронных спутников, полученных на телескопе Цейсс–2000, полностью подтвердило работоспособность и высокие характеристики точности программного комплекса.
Анализ орбитальной эволюции исследованных объектов позволил разделить объекты на захваченные в резонанс и нерезонансные.
Объекты 90 008, 90 031 и 90 214 захвачены в резонанс 1 : 1 со скоростью вращения Земли, их резонансные соотношения проходят через нулевые значения, а критические аргументы устойчиво либрируют. Фазовые портреты в плоскости $\left\{ {a,\,\,\lambda } \right\}$ показывают, что во вращающейся системе координат объекты 90 008, 90 031, 90 214 либрируют около устойчивой точки либрации $\lambda $ = 75°.
Объект 97 149 не является резонансным, в плоскости $\left\{ {a,\,\,\lambda } \right\}$ во вращающейся системе координат объект находится в области регулярного движения.
Вековые резонансы низких порядков в движении объектов отсутствуют.
Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № FSWM-2020-0049).
Список литературы
Авдюшев В.А. Новый коллокационный интегратор для решения задач динамики. I. Теоретические основы // Изв. вузов. Физика. 2020. Т. 63. №. 11. С. 131–140.
Александрова А.Г., Бордовицына Т.В., Чувашов И.Н. Численное моделирование в задачах динамики околоземных объектов // Изв. вузов. Физика. 2017. Т. 60. № 1. С. 69–76.
Александрова А.Г., Бордовицына Т.В., Попандопуло Н.А., Томилова И.В. Новый подход к вычислению вековых частот в динамике околоземных объектов на орбитах с большими эксцентриситетами // Изв. вузов. Физика. 2020. Т. 63. № 1 (745). С. 57–62.
Андрианов Н.Г., Иванов А.П., Иванов В.Н., Колесса А.Е., Лукьянов А.П., Радченко В.А. Новый комплекс программ планирования, обработки результатов оптических наблюдений и ведения базы данных космических объектов // Сб. тр. Всеросс. научн. конф. с международн. участием “Космический мусор: фундаментальные и практические аспекты угрозы”. М.: ИКИ РАН, 17–19 апреля 2019 г. С. 125–130.
Батурин А.П., Чувашов И.Н. Упрощенный способ определения начального приближения при улучшении орбит // Изв. вузов. Физика. 2006. Т. 49. № 2/2. С. 52–55.
Кузнецов Э.Д., Захарова П.Е., Гламазда Д.В., Шагабутдинов А.И., Кудрявцев С.О. О влиянии светового давления на орбитальную эволюцию объектов, движущихся в окрестности резонансов низких порядков // Астрон. вестн. 2012. Т. 46. № 6. С. 480–488. (Kuznetsov E.D., Zakharova P.E., Glamazda D.V., Shagabutdinov A.I., Kudryavtsev S.O. Light pressure effect on the orbital evolution of objects moving in the neighborhood of low-order resonances// Sol. Syst. Res. 2012. V. 46. № 6. P. 442–449.)
Левкина П.А., Бахтигараев Н.С., Сергеев А.В., Чазов В.В. Результаты фотометрических и позиционных наблюдений фрагментов космического мусора в обсерватории на пике Терскол // Изв. Главн. астрон. обсерватории в Пулкове. 2013. № 220. С. 47−52.
Молотов И.Е., Агапов В.М., Стрельцов А.И., Еленин Л.В., Шильдкнехт Т., Тунгалаг Н., Буянхишиг Р., Голиков А.Р., Капралов М.А., Сибиченкова М.А., Иванов Д.Е., Крылов А.Н., Жорниченко А.А., Позаненко А.С. Проблемы оптического мониторинга космического мусора // Препр. ИПМ им. М.В. Келдыша. 2020. № 7. 17 с. https://doi.org/10.20948/prepr-2020-7
Оголев А.В., Морозов С.В. Анализ засоренности околоземного космического пространства объектами техногенного происхождения и их влияние на функционирование космических аппаратов // Сб. тр. Всеросс. научн. конф. с международн. участием “Космический мусор: фундаментальные и практические аспекты угрозы”. М.: ИКИ РАН, 17–19 апреля 2019 г. С. 15–19.
Томилова И.В., Блинкова Е.В., Бордовицына Т.В. Особенности динамики объектов, движущихся в окрестности резонанса 1 : 3 с вращением Земли // Астрон. вестн. 2019. Т. 53. № 5. С. 323–338. (Tomilova I.V., Blinkova E.V., Bordovitsyna T.V. Features of the dynamics of objects moving in the neighborhood of the 1 : 3 resonance with the Earth’s rotation // Sol. Syst. Res. 2019. V. 53. № 5. P. 307–321.)
Allan R.R. Resonance effects due to the longitude dependence of the gravitational field of a rotating primary // Planet. and Space Sci. 1967a. V. 15. P. 53–76.
Allan R.R. Satellite’s resonance with the longitude dependent gravity. II. Effects involving the ec-centricity // Planet. and Space Sci. 1967b. V. 15. P. 1829–1845.
Breiter S., Wytrzyszczak I., Melendo B. Long-term predictability of orbits around the geosynchronous altitude // Adv. Space Res. 2005. V. 35. P. 1313–1317.
Cincotta P.M., Simo C. Simple tools to study global dynamics in non-axisymmetric galactic potentials – I // Astron. and Astrophys. Suppl. 2000. V. 147. P. 205–228.
Cincotta P.M., Girdano C.M., Simo C. Phase space structureof multi-dimensional systems by means of the mean exponential growth factor of nearby orbits // Physica D. 2003. V. 182. P. 151–178.
IERS Conventions 2010 – Gerard Petit and Brian Luzum // IERS Technical note 36. Frankfurt am Main, 2010. 179 p.
Klinkrad H. Space Debris. Models and Risk Analysis. Springer, 2006. 430 p.
Kolessa A.E., Ivanov V.N., Radchenko V.A. Searching of unknown Earth-orbiting object in the next observation session // Proc. Int. Conf. Engineering and Telecommunication. Moscow, 2014. P. 33–37.
Kolessa A.E., Tartakovsky A.G., Ivanov A.P., Ivanov A.P., Radchenko V.A. Nonlinear estimation and decision-making methods in short track identification and orbit determination problem // IEEE Trans. Aero- space and Electronic Systems. 2019. P. 301–312.
Maruskin J.M., Scheeres D.J., Alfriend K.T. Correlation of optical observations of objects in Earth orbit // J. Guidance, Control and Dynamics. 2009. V. 32. № 1. P. 194–209.
Milani A., Gronchi G., Vitturi M., Kneževic Z. Orbit determination with very short arcs. I. Admissible regions // Celest. Mech. and Dyn. Astron. 2004. V. 90. P. 57–85.
Tommei G., Milani A., Rossi A. Orbit determination of space debris: Admissible regions // Celest. Mech. and Dyn. Astron. 2007. V. 97. № 4. P. 289–304.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник


