Астрономический вестник, 2022, T. 56, № 6, стр. 389-409

ВВЕДЕНИЕ

Вопрос происхождения системы Земля–Луна является одной из самых актуальных проблем космогонии. Первая гипотеза формирования Луны была выдвинута еще в конце 19 века (Darwin, 1879). Впоследствии было выдвинуто множество гипотез формирования Луны, однако ни одна из них не подтвердилась. В настоящее время наиболее популярной среди них остается гипотеза мегаимпакта (Hartmann, Davis, 1975; Cameron, Ward, 1976). Согласно этому сценарию, Земля на поздней стадии своей аккумуляции столкнулась с крупным зародышем планеты размером с Марс. Часть выбросов вещества в результате такого столкновения была захвачена на околоземные орбиты и сформировала протолунный рой. Простой подбор параметров ударника позволяет получить массу и угловой момент Луны, соответствующие наблюдаемым. Однако эта гипотеза обладает рядом недостатков. Во-первых, такая модель формирования Луны предполагает наличие свободных параметров, таких как масса, скорость ударника, а также угол и время удара, которые подбираются исходя из современных параметров системы Земля–Луна. Такой подход в значительной степени снижает прогностическую ценность гипотезы. Формирование Луны в рамках сценария мегаимпакта становится случайным событием, которое не является наиболее вероятным следствием ныне общепринятой теории формирования планет земного типа (Сафронов, 1969). Во-вторых, гипотеза мегаимпакта противоречит современным геохимическим данным. Было показано (Melosh, 2000; Canup, 2004), что выброс, образующийся при столкновении с ударником, по большей части состоит из пород самого ударника. Это означает, что сходство в составе Земли и Луны маловероятно, поскольку ударник образовался независимо от Земли. Однако анализ лунного грунта показал, что в составе Луны и Земли существует одно сходство, которое нельзя отвергнуть. Соотношение изотопов некоторых элементов, например, кислорода (так называемая “кислородная подпись”), с хорошей точностью оказалось одинаковым для лунных и земных пород (Clayton, Mayeda, 1975). Для метеоритов эти соотношения совершенно иные (Clayton и др., 1973; 1976). Многие из последних работ, посвященных гипотезе мегаимпакта, направлены на разрешение проблемы “кислородной подписи”. В одной из таких работ (Belbruno, Gott III, 2005) предполагалось, что ударник сформировался в четырех или пяти точках Лагранжа, где космохимические условия должны быть теми же, что на Земле, потому что они находятся на том же расстоянии от Солнца, что и Земля. В недавней работе (Lock и др., 2018) авторы предположили, что удар был столь высокоэнергетический, что породы перешли в газообразное состояние, и Земля была окружена газовым облаком, названным авторами “синестией”, из которого потом сконденсировались частицы, сформировавшие Луну. В этой модели вещество будущих Земли и Луны хорошо перемешивается, что обеспечивает совпадение изотопного состава кислорода в земных и лунных породах. Оба упомянутых подхода к решению проблемы “кислородной подписи” предполагают наличие дополнительных условий, таких как наличие тела размером с Марс в точке Лагранжа (Belbruno, Gott III, 2005) или очень высокая энергия удара, достаточная для формирования газа из пород ударника и Земли (Lock и др., 2018), что, хотя и решает проблему “кислородной подписи”, но уменьшает вероятность осуществления таких сценариев по сравнению с первоначальной версией гипотезы мегаимпакта (Hartmann, Davis, 1975).

Данная работа посвящена развитию гипотезы коаккреции, которая также известна как “статистическая модель образования Луны” (Светцов и др., 2012). Согласно этой модели, так же как и в гипотезе мегаимпакта, Луна формируется из протолунного роя, однако механизм пополнения протолунного диска несколько иной. Околоземный рой постепенно формируется путем множества парных столкновений допланетных тел в сфере Хилла ранней Земли. Часть вещества в результате таких столкновений теряет свою скорость и оказывается захваченной в околоземный рой. В ранних вариантах этой гипотезы (Рускол, 1960; 1963; 1971; 1975; Harris, Kaula, 1975; Weidenschilling и др., 1986) учитывались только парные столкновения частиц из зоны питания Земли (свободно-свободные столкновения) или столкновения частиц из зоны питания Земли и тел из протолунного роя (свободно-связанные столкновения). Однако в такой модели масса протолунного диска получалась менее одной сотой массы современной Луны. Кроме того, было неясно, как объяснить существенную обедненность Луны железом по сравнению с Землей. Поэтому позднее модель коаккреции была расширена (Витязев, Печерникова, 1984; Печерникова, Витязев, 1984; Печерникова, 2014; 2015; Светцов и др., 2012; Горькавый, 2007) с учетом столкновений с частицами выбросов от ударов крупных тел (макроимпактов) по Земле. Учет вклада макроимпактов мог бы помочь решить проблему дефицита массы протолунного диска. Кроме того, поскольку выбросы преимущественно состоят из вещества мантии, то в протолунный рой поступает вещество, обедненное железом. В то же время рой, формирующийся за счет свободно-свободных и свободно-связанных столкновений, несмотря на свою малую массу, необходим как триггер (Горькавый, 2007) для начала аккумуляции роя за счет столкновений с выбросами. Важно отметить, что гипотеза коаккреции, в отличие от гипотезы мегаимпакта, не предполагает каких-либо маловероятных событий и содержит минимум свободных параметров. Гипотеза коаккреции является естественным следствием современной теории формирования планет из протопланетных дисков. Масса Луны и угловой момент системы Земля–Луна в рамках гипотезы коаккреции, в отличие от гипотезы мегаимпакта, не являются наперед заданными величинами, а прогнозируются исходя из параметров протопланетного диска. В перспективе теория, основанная на гипотезе коаккреции, могла бы объяснить, как сформировались спутниковые системы у других планет земного типа, а также у транснептуновых объектов (например, система Плутон–Харон) и двойных астероидов.

Также следует отметить, что недавно на основе численного моделирования ударов крупных тел по Земле была предложена модель множественных импактов (Rufu и др., 2017). Так же, как и в современной версии гипотезы коаккреции (Печерникова, 2014; Горькавый, 2007), в гипотезе множественных импактов учитывается вклад макроимпактов, однако фундаментальное различие этой модели с гипотезой коаккреции в том, что в гипотезе коаккреции захват вещества выбросов происходит в результате столкновений частиц выбросов с телами роя, а в модели (Rufu и др., 2017) захват происходит в результате движения выбросов в измененном потенциале Земли и выбросов, что достигается за счет очень большой (от массы Луны до массы Марса) массы ударников.

Кроме того, не так давно получила развитие гипотеза происхождения Луны (Galimov, Krivtsov, 2005), которая предполагает, что Земля и Луна сконденсировались из единого газопылевого облака, минуя стадию твердотельной аккреции. Ключевым фактором в этой модели является то, что вводится дополнительная сила отталкивания, возникающая из-за испарения газа с поверхности сконденсировавшихся частиц. В результате совместного действия этой силы с силой гравитации оказывается возможным формирование системы Земля–Луна.

В рамках гипотезы коаккреции столкновения между частицами являются основным процессом, обеспечивающим приток массы в протолунный рой. При этом, для корректности расчетов, необходимо знать, какая доля вещества оказывается захваченной на околоземные орбиты и при каких условиях происходит этот захват. В первом варианте гипотезы коаккреции, разработанном Рускол (1975), была определена величина, названная вероятностью захвата. В рамках модели Рускол при столкновении либо оба тела захватывались в протолунный рой, либо все осколки от столкновения этих тел уходили на гелиоцентрические орбиты. Вероятность захвата, согласно Рускол, – это вероятность того, что в результате столкновения оба тела окажутся захваченными при произвольных скоростях тел и углах между направлениями скоростей. Рускол (1975) дает оценку вероятности захвата, основанную на достаточно умозрительных предположениях. Кроме того, конечная формула для вероятности захвата не включает зависимости от отношения масс сталкивающихся тел. Поэтому оценка вероятности захвата вещества в рой требует более тщательного рассмотрения, что является целью нашего исследования.

Целью нашей работы является, во-первых, определение условий, при которых происходит захват при парных столкновениях тел в сфере Хилла Земли, во-вторых, корректная оценка вероятности захвата для свободно-свободных столкновений и, в-третьих, определение скорости прироста массы протолунного роя на единицу площади диска за счет свободно-свободных столкновений. В рамках модели коаккреции столкновения являются основным способом пополнения протолунного роя, поэтому корректная оценка вероятности захвата необходима для оценки массы и углового момента формирующейся Луны, основных параметров, которые могли бы дать возможность подтвердить истинность гипотезы коаккреции.

ПОСТАНОВКА ЗАДАЧИ И ИСПОЛЬЗУЕМЫЕ МОДЕЛИ

Прежде всего, отметим, что в нашем исследовании мы, в основном, будем использовать безразмерные величины расстояний и скоростей, которые определены следующим преобразованием:

где l – размерное расстояние от точки столкновения до центра Земли, u – размерная скорость, u_esc – размерная скорость убегания с поверхности Земли, М и R – переменные масса и радиус Земли, зависящие от времени и меняющиеся по мере роста Земли, а r и $v$ – безразмерные расстояние до центра Земли и скорость, в качестве которой могут быть ${{v}_{1}}$ или ${{v}_{2}}$ – безразмерные скорости планетезималей в момент столкновения, а также V_cm –безразмерная скорость центра масс сталкивающих тел, V_rel – безразмерная скорость одного тела относительно другого в момент удара, ${{\tilde {v}}_{1}}$ и ${{\tilde {v}}_{2}}$ – безразмерные скорости планетезималей относительно кеплеровского кругового движения на границе сферы Хилла Земли. Соответственно, для размерных величин тех же скоростей будут использоваться обозначения: u₁, u₂, U_cm, U_rel, ${{\tilde {u}}_{1}}$ и ${{\tilde {u}}_{2}}$.

Безразмерные величины r, ${{v}_{1}}$, ${{v}_{2}}$ и V_cm удобны тем, что вероятность захвата, выраженная через эти переменные, не зависит от рассматриваемого момента времени. Кроме того, радиус сферы Хилла Земли в единицах текущего радиуса Земли также остается постоянным по мере роста Земли. Это легко показать, разделив размерный радиус сферы Хилла растущей Земли R_H на текущий радиус Земли R:

где a – большая полуось земной орбиты, M_S – масса Солнца, M – масса растущей Земли, ρ – плотность Земли, а ρ* – “размазанная” плотность Солнца, то есть плотность, соответствующая массе Солнца, распределенной по объему сферы с радиусом, равным большой полуоси земной орбиты. Практически, в течение всего времени эволюции Земли ни большая полуось земной орбиты, ни плотность Земли существенно не менялись и потому величина радиуса сферы Хилла r_h, нормированная на радиус Земли, оставалась практически неизменной и равной приблизительно 235.

В рамках нашего исследования мы решаем три последовательно связанные задачи:

1. Определение критерия захвата. Два тела с заданными отношением масс k, геоцентрическими скоростями ${{v}_{1}}$ и ${{v}_{2}}$, углом между скоростями α и углом φ между направлением скорости центра масс сталкивающихся тел и направлением на центр Земли сталкиваются на расстоянии r от центра Земли. Безразмерная величина r_h радиуса сферы Хилла Земли задана и равна 235 в течение всего времени роста Земли. Необходимо определить, при каких условиях образующиеся при столкновении осколки будут захвачены на околоземную орбиту.

Движение облака осколков после столкновения мы будем рассматривать в рамках задачи двух тел: Земли и облака осколков, движущегося как материальная точка, со скоростью, равной скорости центра масс сталкивающихся тел. Такой подход небезоснователен, поскольку обычные скорости удара $U_{{{\text{rel}}}}^{2}$ ~ GM/R (Сафронов, 1969), как правило, много больше скоростей взаимного убегания $u_{{{\text{mut}}}}^{2}$ ~ 2G(m₁ + m₂)/(r₁ + r₂) двух сталкивающихся планетезималей с радиусами r₁ и r₂ (для оценок форму допланетных тел будем принимать сферической), так как $U_{{{\text{rel}}}}^{2}$/$u_{{{\text{mut}}}}^{2}$ ~ R²/(r₁ + r₂)²$ \gg $ 1 при R $ \gg $ r₁ + r₂. В этом случае из-за большой энергии удара наибольший осколок составляет очень малую долю общей массы (Leinhardt, Stewart, 2012) и распределение осколков по скоростям оказывается сферически симметричным относительно центра масс (Sevecek и др., 2017), а поскольку распределение масс осколков по скоростям относительно центра масс является показательной функцией (Leinhardt, Stewart, 2012), то значительная доля массы осколков в пространстве скоростей сосредоточена в некоторой окрестности точки, движущейся со скоростью центра масс, которую мы можем считать характерной скоростью облака осколков, пренебрегая скоростями осколков относительно скорости центра масс. В рамках такого подхода все осколки летят с одной геоцентрической скоростью, равной скорости центра масс относительно Земли.

При расчетах мы также будем пренебрегать гравитационными возмущениями со стороны Солнца и приливным возмущением со стороны Земли.

2. Расчет вероятности захвата. Два тела из зоны питания Земли с отношением масс k сталкиваются на заданном расстоянии r от центра Земли. Плотность сталкивающихся тел одинакова и постоянна, форму тел полагаем сферической. Безразмерная величина r_h радиуса сферы Хилла Земли определена и равна 235 в течение всего времени роста Земли. Необходимо вычислить вероятность захвата осколков на околоземную орбиту на множестве всех возможных геоцентрических скоростей ${{v}_{1}}$ и ${{v}_{2}}$, углов между скоростями α и углов φ между направлением скорости центра масс сталкивающихся тел и направлением на центр Земли.

Согласно (Витязев и др., 1990), распределение числа N допланетных тел по относительным скоростям $\tilde {u}$ (скорости планетезималей относительно кеплеровского кругового движения) на границе сферы Хилла Земли принимаем максвелловским:

где $\left\langle {{{{\tilde {u}}}^{2}}} \right\rangle $ – средний квадрат относительной скорости, который может быть выражен в виде: где M и R – масса и радиус растущей Земли, соответственно, а θ – параметр Сафронова, равный в зоне Земли θ ≈ 2.

Распределение числа N планетезималей по углу α между скоростями в момент столкновения будем считать однородным:

3. Определение скорости роста массы протолунного диска за счет свободно-свободных столкновений. Необходимо определить скорость прироста массы протолунного роя на единицу площади диска в результате парных столкновений тел из зоны питания Земли на расстоянии r от центра планеты в момент времени t от начала формирования Земли. Сталкивающиеся планетезимали считаем сферическими и равными по плотности ρ = 3000 кг/м³. Распределение числа планетезималей в протопланетном диске по скоростям и углам между скоростями принимаем согласно (3) и (5). Распределение числа N допланетных тел по массам m, согласно Сафронову (1969), считаем степенным:

где q ≈ 11/6, m_max – верхний предел массы тел в распределении, а ρ₀ – средняя объемная плотность протопланетного диска. Зависимость m_max, ρ₀, а также массы Земли M от времени t будем принимать в соответствии с моделью расширяющихся зон питания (Витязев и др., 1978; 1990), являющейся развитием теории Сафронова формирования планет земного типа (Сафронов, 1969).

ОПРЕДЕЛЕНИЕ КРИТЕРИЯ ЗАХВАТА

В простейшем приближении в результате столкновения образуется облако осколков, движущихся со скоростью, равной скорости центра масс сталкивающихся тел. В рамках такой модели возможны три варианта развития событий: все осколки окажутся на околоземной орбите, либо упадут на Землю, либо вернутся обратно в зону питания Земли. Характер развития событий определятся тремя условиями захвата.

Во-первых, столкновение должно произойти внутри сферы Хилла Земли, где возможно существование стационарных спутников. Таким образом, для захвата необходимо, чтобы расстояние от центра Земли до точки столкновения r было меньше, чем радиус сферы Хилла Земли:

Во-вторых, для захвата необходимо, чтобы осколки были гравитационно связаны с Землей. Для этого, помимо выполнения условия (7), необходимо, чтобы удельная энергия осколков была меньше нуля. В рамках задачи двух тел (облака осколков и Земли) это равносильно тому, что скорость облака осколков, равная скорости центра масс сталкивающихся тел, должна быть меньше второй космической скорости на заданном расстоянии r от Земли:

где V_cm – “обезразмеренная” согласно (1) скорость центра масс сталкивающихся тел, которая определяется формулой: где α – угол между геоцентрическими скоростями тел ${{v}_{1}}$ и ${{v}_{2}}$, а k – отношение масс сталкивающихся тел.

В-третьих, осколки не должны упасть на Землю. Исходя из законов сохранения энергии и момента импульса для облака осколков и условия, что орбита облака осколков не должна пересекаться с поверхностью Земли, были получены два условия, при которых осколки не выпадут на поверхность Земли. Рассмотрим систему двух тел: облако осколков и Земля. Нам известны начальная скорость облака осколков, равная скорости центра масс V_cm столкнувшихся планетезималей, расстояние до центра Земли r, а также угол φ между направлением движения облака осколков V_cm и направлением на центр Земли. Если при данной скорости V_cm в принципе возможен случай, когда осколки не падают на Землю, то существует критический угол φ_cr, при котором траектория облака осколков лишь касается поверхности Земли, и для любого другого угла φ должно быть выполнено неравенство sin φ > sin φ_cr для того, чтобы осколки не упали на поверхность Земли. В этом случае точка касания орбиты облака осколков будет ближайшей к центру Земли точкой орбиты, а значит, эта точка является перигеем орбиты осколка. Запишем законы сохранения энергии и момента импульса для облака осколков в безразмерных величинах (1) скорости V_cm и расстояния r (скорость убегания с поверхности планеты и текущий радиус Земли в этих величинах равны единице на любом этапе аккумуляции):

В этой системе $v$ – скорость облака осколков в момент касания их траектории поверхности Земли. Решая систему, получим:

При очень малых скоростях, однако, не найдется угла, при котором осколки не выпадут на Землю. Найдем предельное значение начальной скорости ${{v}_{{{\text{cr}}}}}$, при котором осколки не упадут на Землю, только если их начальная скорость перпендикулярна направлению из центра Земли на точку столкновения первоначальных тел. В этом случае начальная точка будет апогеем орбиты, а точка касания с поверхностью Земли – перигеем. Критическое значения угла здесь будет равно π/2, а значит, его синус будет равен единице. Воспользовавшись формулой (11), находим:

При скоростях V_cm < ${{v}_{{{\text{cr}}}}}$ облако осколков в любом случае упадет на Землю. Таким образом, для того чтобы облако осколков не упало на Землю, необходимы два условия. Первое: синус угла φ между направлением скорости облака осколков V_cm и направлением на центр Земли должен быть больше синуса критического значения φ_cr, при котором орбита облака осколков касается поверхности Земли. Второе: в случае, когда скорость облака осколков V_cm по модулю меньше критического значения ${{v}_{{{\text{cr}}}}}$, не найдется такого направления, при котором осколки останутся на околоземной орбите. Суммируя сказанное, запишем условие невыпадения осколков на поверхность Земли:

Объединяя условия (7), (8) и (13), получаем критерий захвата облака осколков на околоземную орбиту:

РАСЧЕТ ВЕРОЯТНОСТИ ЗАХВАТА

Вероятность захвата при заданном отношении масс сталкивающихся тел k и расстоянии r от точки столкновения до центра Земли может быть найдена как отношение числа столкновений N_cap, при которых происходит захват, к общему числу столкновений N_coll в интервалах времени dt, объема dΩ и отношений масс [k, k + dk] на расстоянии r от центра Земли при всевозможных геоцентрических скоростях сталкивающихся тел ${{v}_{1}}$ и ${{v}_{2}}$, углах между направлениями скоростей α и углах φ между направлением скорости облака осколков V_cm и направлением на центр Земли.

Для нахождения определенной таким образом вероятности захвата p = p(k, r) необходимо, во-первых, знание распределения числа планетезималей по скоростям ${{v}_{1}}$ и ${{v}_{2}}$, по углам α между направлениями скоростей ${{v}_{1}}$ и ${{v}_{2}}$, по углу φ между направлением скорости облака осколков V_cm и направлением на центр Земли, во-вторых, критерия захвата осколков и, в-третьих, знание частоты столкновений между телами.

Распределение числа N допланетных тел по относительным скоростям $\tilde {u}$, согласно (Витязев и др., 1990), принимаем максвелловским (3). Однако нам необходимо распределение по геоцентрическим скоростям ${{v}_{1}}$ и ${{v}_{2}}$ планетезималей в момент столкновения, а (3) определяет распределение по скоростям планетезималей на границе сферы Хилла Земли. Формула для преобразования скоростей была найдена, исходя из закона сохранения энергии в задаче двух тел:

Преобразуя скорости согласно (15), найдем распределение числа тел по геоцентрическим скоростям ${{v}_{1}}$ и ${{v}_{2}}$ в момент столкновения:

где C(r, θ) – безразмерный множитель, не зависящий от скоростей и не влияющий на результаты наших расчетов, θ – параметр Сафронова, как и в формуле (4).

Распределение числа N допланетных тел по углам α принимаем однородным (5), а распределение числа тел по углу φ мы учтем, рассчитав при заданных k, ${{v}_{1}}$, ${{v}_{2}}$, α и r, долю столкновений, при которых осколки не падают на поверхность Земли. Определим долю столкновений, при которых происходит захват осколков на околоземную орбиту при произвольном угле φ между направлением движения облака осколков и направлением на центр Земли и заданных k, ${{v}_{1}}$, ${{v}_{2}}$, α и r в предположении изотропного распределения скоростей V_cm по направлениям. Сначала для простоты предположим, что начальные параметры столкновения таковы, что условия захвата (7), (8), а также первое неравенство в условии (13) (V_cm > ${{v}_{{{\text{cr}}}}}$) выполнены. Если считать распределение числа столкновений по направлениям скоростей центра масс изотропным, то доля столкновений, при которых происходит захват, будет равна части сферы p_φ, которая соответствует условию sinφ > sinφ_cr:

В общем случае вероятность захвата при произвольном угле φ и заданных k, ${{v}_{1}}$, ${{v}_{2}}$, α и r была определена с учетом всех условий критерия захвата (14) облака осколков на околоземную орбиту и выражения (17):

Здесь Θ(x) – функция, равная единице при x > 0 и нулю при x < 0. Первый множитель учитывает условие захвата (7) – захвачены могут быть только те тела, столкновение которых произошло внутри сферы Хилла. Второй множитель учитывает энергетическое условие захвата (8). Третий множитель – первое неравенство в условии (13) (если скорость облака осколков меньше ${{v}_{{{\text{cr}}}}}$, то не найдется угла φ, при котором осколки не упадут на поверхность Земли). Последний множитель в (18) равен косинусу критического угла φ_cr и имеет смысл доли столкновений (17), при которых осколки оказываются захваченными на околоземную орбиту в случае, если первые три множителя равны единице.

Формула (18) выведена исходя из критерия захвата (14) и определяет вероятность захвата при произвольном угле φ и заданных k, ${{v}_{1}}$, ${{v}_{2}}$, α и r, однако для нахождения вероятности захвата p = p(k, r) необходимо знать частоту столкновений тел с массами, скоростями и углами между скоростями в интервалах: M₁ ∈ [m₁, m₁ + dm₁], M₂ ∈ [m₂, m₂ + + dm₂], V₁ ∈ [${{v}_{1}}$, ${{v}_{1}}$ + d${{v}_{1}}$], V₂ ∈ [${{v}_{2}}$, ${{v}_{2}}$ + d${{v}_{2}}$], α* ∈ ∈ [α, α +dα]. Мы будем считать, что k = m₂/m₁ > 1, и для определенности будем условно называть тела c массами и скоростями с индексом “2” мишенями, а с индексом “1” ударниками. Число столкновений мишеней и ударников в описанных выше интервалах можно выразить формулой:

Здесь dN₂ – количество мишеней в указанных интервалах масс и скоростей, находящихся в объеме dΩ, а dp – вероятность того, что за время dt одна мишень столкнется с ударником в заданных интервалах параметров. В правой части равенства dn₂ – объемная концентрация мишеней в заданных интервалах, а dω – плотность вероятности столкновения одной мишени с ударником в заданных интервалах. Концентрация dn₂ выражается через распределение (16) и объемную концентрацию dn_m2 мишеней в диапазоне масс [m₂, m₂ + dm₂]: где θ – параметр Сафронова, равный в зоне Земли θ ≈ 2, а С(r, θ) – безразмерный множитель, зависящий только от расстояния r и параметра Сафронова.

Вероятность dp столкновения одной мишени с ударником за время dt можно выразить как отношение этого интервала времени dt ко времени свободного пробега мишени τ, которое легко найти, если рассмотреть цилиндр с основанием, равным сечению столкновения мишени с ударниками σ и высотой, равной произведению размерной относительной скорости U_rel и времени dt:

Отметим, что здесь u_esc – текущая скорость убегания на поверхности Земли, равная (2GM/R)^1/2. Величина dn₁ это объемная концентрация ударников в интервалах масс, скоростей и углов между скоростями, которую аналогично (20) мы выразили по формуле:

где dn_m1 – объемная концентрация ударников в диапазоне масс [m₁, m₁ + dm₁], а С(r, θ) – тот же безразмерный множитель, что и в формуле (20).

Сечение столкновений σ может быть выражено по формуле (Сафронов, 1969):

Здесь r₁ и r₂ – радиусы мишени и ударника, которые мы предполагаем сферическими. Такое сечение столкновения не совпадает с геометрическим σ = π(r₁ + r₂)² из-за эффекта гравитационной фокусировки. Выясним, при каком условии сечение столкновения можно считать геометрическим. Это возможно, если последний множитель в (23) близок к единице, или, выражаясь иначе: Здесь ρ – плотность сталкивающихся планетезималей, ρ_E – плотность Земли, а V_rel – безразмерная относительная скорость согласно преобразованию (1). Средний квадрат безразмерной относительной скорости порядка единицы, поскольку $\left\langle {V_{{{\text{rel}}}}^{2}} \right\rangle $ = (2r + θ)/(θr) – величина порядка единицы. Отношение ρ/ρ_E ≈ 0.67 также порядка единицы. Так же, как правило, сталкивающиеся тела значительно меньше Земли: (r₁ + r₂)²$ \ll $ R². Это означает, что в большинстве столкновений условие (24) выполняется и сечение можно считать геометрическим, не зависящим от относительной скорости сталкивающихся тел:

Теперь, подставляя (20)–(22) и (25) в (19), получим величину, равную частоте столкновений в единице объема в заданных интервалах параметров m₁, m₂, ${{v}_{1}}$, ${{v}_{2}}$ и α:

где C* = С*(r, m₁, m₂, θ) – величина, имеющая размерность скорости роста объемной концентрации и не зависящая от скоростей ${{v}_{1}}$ и ${{v}_{2}}$ и угла между скоростями α. Значение этого множителя для нас не важно, поскольку число столкновений, при которых происходит захват, dN_cap = p_φ(k, ${{v}_{1}}$, ${{v}_{2}}$, α, r)dN_coll (p_φ – вероятность захвата согласно (18)) также пропорционально С* и при вычислении вероятности захвата p(k, r) по формуле: множитель C* сокращается, и мы получаем следующую формулу для расчета вероятности захвата: куда входит величина f(v_1,v_2, α, r): которую мы будем называть частотой столкновений. Эта величина пропорциональна частоте столкновений (26) в единице объема в заданных интервалах масс, скоростей и углов между скоростями с множителем, не зависящим от переменных ${{v}_{1}}$, ${{v}_{2}}$ и α. В (29) входит величина θ – параметр Сафронова, равный в зоне Земли θ ≈ 2.

Формула (28) дает возможность численно рассчитать вероятность захвата при заданных k и r. Интегрирование по скорости в формуле (28) выполняется от минимального значения $v_{{{\text{min}}}}^{2}$ = 1/r, которое достигается при нулевой относительной скорости планетезимали на границе сферы Хилла Земли, до бесконечности. Графики зависимости вероятности захвата p(k, r) (28) от отношения масс k и расстояния r представлены на рис. 1, 2 и 3.

На рис. 1 можно видеть, что зависимость (28) вероятности захвата от отношения масс k на заданном расстоянии r имеет максимум, который при увеличении расстояния r постепенно смещается в сторону меньших отношений масс. На расстоянии, равном 1.1 радиуса Земли вероятность захвата достигает максимума, когда сталкивающиеся тела различаются по массе в 6 раз, но уже на расстоянии, равном 5 земных радиусов, для достижения максимума необходимо, чтобы массы тел различались в 1.6 раз. На расстоянии r = 20 максимум все еще заметен, но уже при r = 50 он уже неразличим, как и на больших расстояниях. Кроме того, заметно, что значение вероятности захвата в максимуме по k растет при увеличении расстояния до r ≈ 2, а потом убывает. Было найдено, что вероятность захвата достигает глобального максимума при r ≈ 2.3 и k ≈ 2.5. В максимуме почти при каждом третьем столкновении (p ≈ 0.3) происходит захват планетезималей на околоземную орбиту.

На рис. 2 показаны графики для вероятности захвата в зависимости от расстояния r при не очень больших отношениях масс (k ≤ 3). Видно, что зависимость вероятности захвата от расстояния при заданном отношении масс также имеет максимум, который смещается к центру Земли при больших значениях k. Заметно, что при малых отношениях масс вероятность захвата остается существенной даже у границы сферы Хилла. Например, при равных массах сталкивающихся тел вероятность захвата равна 0.05 почти на границе сферы Хилла (r ≈ 220).

На рис. 3 изображены графики вероятности захвата от расстояния r при больших отношениях масс (k > 3). При увеличении отношения масс максимум вероятности захвата продолжает смещаться в сторону центра Земли от r ≈ 1.5 при k = 4 до r ≈ 1.05 при k = 20. Хотя при больших отношениях масс вероятность захвата довольно быстро падает с расстоянием (при k = 4 вероятность захвата оказывается равной 0.01 уже на расстоянии 2.8 земных радиусов), однако даже когда массы тел различаются по массе в 20 раз, в максимуме вероятность захвата остается весьма существенной (p_max≈ 0.05).

Для лучшего понимания характера зависимости и оптимизации дальнейших расчетов полезно найти аппроксимацию зависимости вероятности захвата (28) от отношения масс k и расстояния r. Аппроксимирующая функция P(k, r) должна удовлетворять следующим требованиям. Во-первых, P(k, r) → 0 при k → ∞ или r → ∞. Во-вторых, P(k, r) = 0 при r = 1. Кроме того, P(k, r) имеет максимум. Было показано, что вероятность захвата (28) может быть аппроксимирована формулой вида:

где a(k), n(k), с(k) и d(k) – коэффициенты, зависящие от отношения масс k. Для того, чтобы определить эти коэффициенты наложим на P(k, r) два условия: Здесь r_max(k) – функция, аппроксимирующая зависимость расстояния r_k, при котором достигается максимум вероятности захвата при заданном k согласно формуле (28), от отношения масс, f_max(k) – функция, аппроксимирующая зависимость максимального значения вероятности захвата p_max при заданном k согласно формуле (28) от отношения масс. Методом наименьших квадратов было найдено, что r_max(k) и f_max(k) определяются следующими формулами:

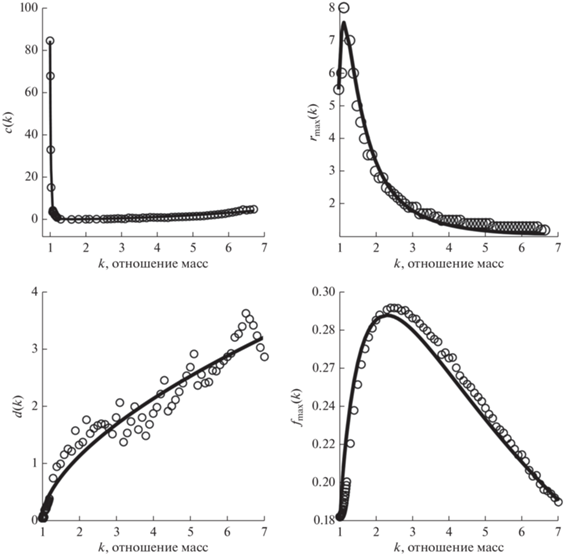
Справа на рис. 4 представлены графики зависимостей (32) и (33). Видно, что расстояние, на котором достигается максимум вероятности захвата (28) при одинаковых массах сталкивающихся тел, равно 5.5 земным радиусам. При увеличении отношения масс на коротком промежутке r_max(k) растет, достигая максимума r_max(k) ≈ 7.5 при отношении масс чуть большем единицы (k = 1.15), после чего r_max(k) падает по экспоненте, стремясь к r_max = 1 при больших k. Максимальное значение вероятности захвата f_max(k) также сначала растет при увеличении отношения масс до k = 2.5, где вероятность захвата достигает своего наибольшего значения 0.3, после чего f_max(k) медленно убывает. Даже при столкновениях тел, различающихся по массам в 7 раз, вероятность захвата f_max(k) ≈ 0.2 близка к максимальной вероятности захвата при k = 1.15.

Условия (31) позволяют определить значение a(k) и n(k), зная с(k), d(k), r_max(k) и f_max(k). При этом первое условие в (31) определяет a(k), а второе n(k):

Коэффициенты с(k) и d(k) могут быть найдены методом наименьших квадратов как аппроксимации зависимостей с_k и d_k от отношения масс k, определенных также по методу наименьших квадратов как коэффициенты в P(k, r) (30), обеспечивающие наилучшее приближение к p(k, r) (28) при заданном отношении масс k. Полученные аппроксимации с(k) и d(k) определяются формулами:

Графики зависимостей (36) и (37) представлены на рис. 4 слева. Коэффициент d(k) монотонно растет при увеличении k, начиная с d ≈ 0.05 при равных отношениях масс и достигая d ≈ 3 при массах, различающихся в 7 раз. Зависимость c(k) имеет два хорошо различимых участка. Начиная со значения c ≈ 85 при равных массах сталкивающихся тел, c(k) быстро падает и уже при k = 1.3 достигает значения с ≈ 0.2, после чего c(k) сравнительно медленно растет, достигая c ≈ 3.2 при массах, различающихся в шесть раз.

Отметим, что формула (30) для аппроксимации P(k, r), как и все входящие в нее коэффициенты, определены при k ≥ 1. При k ≤ 1 вероятность захвата определяется из соображений симметрии: P*(k, r)|_{k ≤1} = P(1/k, r), где P(1/k, r) задается формулой (30).

Также была найдена область применимости аппроксимации P(k, r) (30). На рис. 5 изображены изолинии вероятности захвата p(k, r) (28) и изолинии относительной ошибки аппроксимации err = = |P(k, r) – p(k, r)|/p(k, r). Заметно, что область со значениями расстояний и отношений масс, где вероятность захвата (28) больше 0.05 (слева от изолинии p(k, r) = 0.05), близка к области, где относительная ошибка аппроксимации меньше 0.5. Таким образом, в значительной доли области, где вероятность захвата (28) существенна, аппроксимация (30) позволяет с удовлетворительной точностью рассчитать вероятность захвата. Наибольшей точности аппроксимация достигает вблизи максимумов вероятности захвата при каждом k. Кроме того, из диаграммы на рис. 5 можно сделать вывод, что при отношениях масс k > 2 вероятность захвата (28) остается существенной только на расстояниях меньше восьми земных радиусов.

ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА ЗАХВАЧЕННОЙ МАССЫ ЗА СЧЕТ СВОБОДНО-СВОБОДНЫХ СТОЛКНОВЕНИЙ

Парные столкновения планетезималей из зоны питания происходят по всему объему сферы Хилла, где возможен захват осколков в протолунный рой. Определим скорость роста захваченной массы J(l, t) на расстоянии l от центра Земли (согласно (1) l – расстояние до центра Земли в размерных единицах) в околоземном пространстве, которая задается формулой:

где m_max – верхний предел в распределении допланетных тел по массе (6), q – показатель в распределении (6), а m₀ – нижний предел в распределении допланетных тел по массе. Например, в работе (Печерникова, Витязев, 1984) величина m₀ принималась равной массе межзвездной пыли (порядка 10^–17 кг). Здесь dM_cap – масса, захваченная в результате свободно-свободных столкновений в интервале времени [t, t + dt], в пределах сферического слоя с радиусом l и толщиной dl, а dM – масса, захваченная, кроме того, в интервале масс одного из тел [m, m + dm] и отношений масс [k, k + dk]. Величина dM может быть найдена как произведение массы одной пары сталкивающихся частиц m(1 + k) на число частиц dN_m с массой в интервале [m, m + dm] в сферическом слое с радиусом l и толщиной dl на вероятность столкновения p_coll одного тела с массой m в интервале времени [t, t + dt] с одной из планетезималей в интервале масс [mk, m(k + dk)] и на вероятность захвата p, определенную формулой (28):

Вероятность столкновения p_coll может быть определена как отношение рассматриваемого интервала времени dt ко времени свободного пробега τ частицы с массой m в среде частиц в интервале масс [mk, m(k + dk)], движущихся хаотично со среднеквадратичными относительными скоростями:

где dn_k – объемная концентрация тел в интервале масс [mk, m(k + dk)], σ – сечение столкновения, определяемое формулой (25) с подстановкой m вместо m₁, а ${{\left\langle {U_{{{\text{rel}}}}^{2}} \right\rangle }^{{1/2}}}$ – среднеквадратичная относительная скорость, равная: где θ – параметр Сафронова, равный 2 в зоне питания Земли, R – текущий радиус Земли, ρ_E – плотность Земли, а u_esc – скорость убегания на поверхности растущей Земли.

Согласно (40) для определения вероятности столкновения p_coll необходимо также знать объемную концентрацию тел dn_k в интервале масс [mk, m(k + dk)], которая определяется распределением (6) планетезималей по массам:

где ρ₀ – средняя объемная плотность протопланетного диска, m_max – верхний предел массы в распределении, а q = 11/6.

Кроме того, согласно (39), dM зависит от числа планетезималей dN_m в сферическом слое объемом 4πl²dl в интервале масс [m, m + dm]. Аналогично концентрации dn_k, это число определяется распределением (6):

Теперь подставив (25), (41) и (42) в формулу (40), получим вероятность столкновения p_coll. А подставив вероятность столкновения p_coll (40) и число планетезималей dN_m (43), в свою очередь, в (39), получим выражение для dM:

Эта формула записана для k > 1, поскольку вероятность захвата p(k, r) (28) определена при k > 1. Если мы рассматриваем случай k < 1, то из соображений симметрии p*(k, r)|_{k ≤1} = p(1/k, r). Подстановка дифференциала (44) в (38) с заменой l = Rr и интегрирование по отношению масс k от 0 до 1 и по массе m от m₀ до m_max дает формулу для J*(r, t) ≡ J(l, t):

где ρ_E, ρ и ρ₀ – плотности Земли, планетезималей и средняя плотность протопланетного диска, соответственно, а R – текущий радиус Земли, являющийся функцией времени. В формуле (45) размерное расстояние l заменено на безразмерное r = = l/R согласно (1). Функция j(r) в правой части формулы (45) является интегралом по k и зависит только от расстояния:

Поскольку вероятность захвата (28) определена только при k > 1, а в (46) интегрирование проводится по k от 0 до 1, то вероятность захвата p*(k, r)|_{k ≤1} = p(1/k, r). Для численного расчета интеграла (46) вместо формулы (28) была использована аппроксимация (30), для которой также P*(k, r)|_{k ≤1} = = P(1/k, r) из соображений симметрии.

Преимущество использования безразмерного расстояния r в формуле (45) в том, что функция J*(r, t) может быть разделена на множители, зависящие только от безразмерного расстояния r или только от времени t:

где С₀ – не зависящий от времени множитель, размерность которого в системе СИ: [С₀] = кг/(м с), а j_r(r) и j_t(t) – безразмерные функции. Физический смысл функции j_r(r) в том, что в заданный момент времени t скорость роста массы J*(r, t) захваченного вещества на единицу расстояния l пропорциональна j_r(r) с точностью до постоянного в данный момент множителя C₀j_t(t). Аналогично, J*(r, t) пропорционально j_t(t) на заданном расстоянии r с точностью до постоянного на данном расстоянии множителя C₀j_r(r). Функция j_r(r) может быть определена из (45)–(47) с точностью до безразмерного множителя, который мы принимаем равным единице:

Для того, чтобы определить j_t(t), необходимо знать зависимость входящих в (45) величин ρ₀, m_max, R и m₀ от времени. Как уже было упомянуто, нижний предел массы m₀ в более ранних работах по расчету J(l, t) (Печерникова, Витязев, 1984) принимался равным массе частицы межзвездной пыли (m₀~ 10^–17 кг), однако столь малые частицы имеют такую малую длину свободного пробега, что способны много раз столкнуться с частицами подобного размера во время пролета в сфере Хилла Земли, и в формуле (45) захват такой частицы может быть учтен несколько раз, что приведет к завышенной оценке J(l, t). Минимальный размер частицы m₀, при котором в среднем происходит только одно столкновение с частицами сравнимого размера в сфере Хилла Земли, равен:

что значительно больше массы межзвездной пыли. В этой формуле r_h – безразмерный радиус сферы Хилла (2). Однако необходимо отметить, что величина скорости роста массы J(l, t) очень слабо зависит от m₀, поскольку m₀ стоит под логарифмом ln(m_max/m₀), величина которого уменьшится всего в 1.5 раза при изменении m₀ на 16 порядков. Поэтому величину Λ = ln(m_max/m₀) для оценок будем принимать постоянной и равной 10². Выражение для зависимости текущего радиуса Земли R от времени t принимаем согласно модели растущих зон питания для планет земного типа (Витязев и др., 1978): где R_max – современный радиус Земли, а параметр a – постоянная, которая определяется выражением: Здесь σ₀ ≈ 100 кг/м² – поверхностная плотность вещества в протопланетном диске на момент начала аккреции, T – период обращения Земли вокруг Солнца, θ ≈ 2 – параметр Сафронова, а ρ_E – плотность Земли. Средняя объемная плотность протопланетного диска ρ₀ и верхний предел массы в распределении m_max, согласно стандартной модели формирования планет земной группы (Витязев и др., 1990), могут быть определены как: где M и R – текущие, а M_max и R_max – современные масса и радиус Земли, σ₀ ≈ 100 кг/м² – начальная поверхностная плотность в протопланетном диске, T – период обращения Земли вокруг Солнца, который предполагается неизменным и равным современному, а ${{\left\langle {{{{\tilde {u}}}^{2}}} \right\rangle }^{{1/2}}}$ – среднеквадратичная относительная скорость планетезималей, которая зависит от текущей массы и радиуса Земли и определяется формулой (4).

Тогда аналогично j_r(r), величина j_t(t) была определена из (45), (47) и (48) с подстановкой (50)–(52) с точностью до безразмерного множителя, который мы принимаем равным единице:

где a – постоянная, которая для зоны питания Земли равна 0.035 млн лет^–1 и определяется согласно (51). Выражения (48) и (53) для j_r(r) и j_t(t) позволяют определить С₀: где Λ = ln(m_max/m₀) ≈ 10², а ρ = 3000 кг/м³– плотность планетезималей.

Полученные формулы (47), (48) и (53), (54) позволяют получить полную массу, которая захватывается в результате свободно-свободных столкновений. Проинтегрировав (47) по пространству сферы Хилла и по времени от начала формирования Солнечной системы до момента накопления 97% массы Земли (около 100 млн лет согласно (Печерникова, 2005)), мы нашли массу захваченного в протолунный рой вещества, которая получается исключительно за счет свободно-свободных столкновений. Эта величина оказывается порядка 10^–5 современной массы Луны.

Мы будем считать протолунный диск достаточно уплощенным, поскольку согласно (Витязев и др., 1990) толщина диска во внутренней зоне сферы Хилла, на расстоянии l в промежутке 10–100 радиусов Земли, где вероятность захвата еще не очень мала, была порядка 10^–2–10^–1 расстояния l. При свободно-свободных столкновениях планетезимали захватываются по всему объему сферы Хилла, но пополнение основной, уплощенной части роя происходит при столкновениях захваченного вещества с телами уплощенного диска, поэтому для оценки поверхностной скорости прироста массы диска J₁(l, t) предположим, что захваченная в сферическом слое с объемом 4πl²dl масса пополнит уплощенную часть роя площадью 2πldl. Исходя из выражения (45) для скорости роста массы в сферическом слое, мы получили:

где j_1r(r) и j_1t(t) были определены как: На рис. 6 показаны графики зависимостей j_r(r), j_t(t), j_1r(r) и j_1t(t), которые выражаются формулами (48), (53), (56) и (57), соответственно. Поскольку J*(r, t) (45) с постоянным коэффициентом пропорционально j_r(r) в заданный момент времени t, то, можно сказать, что скорость роста массы протолунного роя J*(r, t) на единицу расстояния l в некоторый момент времени зависит от расстояния r так же, как и j_r(r) с точностью до постоянного коэффициента. Аналогично, поверхностная скорость прироста массы $J_{1}^{*}$(r, t) (55) в заданный момент времени зависит от расстояния r так же, как и j_1r(r) с точностью до постоянного коэффициента. Для j_t(t) и j_1t(t) также можно сказать, что поверхностная скорость прироста массы J*(r, t) (45) зависит от времени так же, как и j_t(t), а скорость роста массы $J_{1}^{*}$(r, t) (55) на единицу расстояния l зависит от времени так же, как и j_1t(t) при фиксированном расстоянии r. Таким образом, графики на рис. 6 дают представление о том, как зависят J*(r, t) и $J_{1}^{*}$(r, t) от расстояния r и времени t.

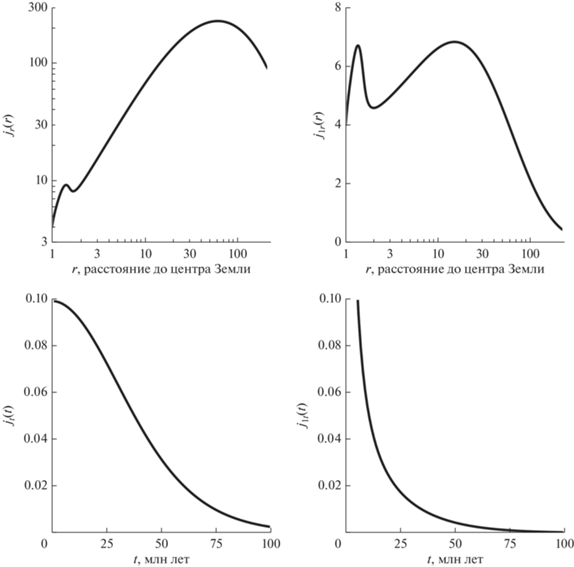
Из верхних графиков на рис. 6 видно, что j_r(r) и j_1r(r) имеют два максимума. Ближайшие к Земле максимумы j_r(r) и j_1r(r) достигаются почти на одном и том же расстоянии, равном полутора текущим радиусам Земли. Дальние максимумы j_r(r) и j_1r(r) достигаются на расстояниях, равных, соответственно, 64 и 15 текущим земным радиусам. Отношения значений дальних максимумов к ближним j_r(r) и j_1r(r) также сильно различаются. В случае j_1r(r) максимумы практически совпадают по величине, но для j_r(r) дальний максимум в 26 раз больше по своему значению. Кроме того, интересно отметить, что величина j_1r(r), пропорциональная поверхностной скорости притока массы, в промежутке между r ~ 1.5 и r ~ 60 меняется не очень сильно, в интервале между 5 и 7. По этой причине величина j_r(r) = rj_1r(r) в данном промежутке расстояний близка к линейной зависимости по r.

Графики зависимостей j_t(t) и j_1t(t) = j_t(t)R_max/R(t) близки по виду: обе функции падают со временем и имеют максимум при t = 0, однако j_t(0) ≈ 0.1, а j_1t(t) стремится к бесконечности при t → 0. Функция j_1t(t) с течением времени убывает быстрее, чем j_t(t): с 25 до 100 млн лет функция j_1t(t) убывает в 26 раз, а j_t(t) в 63 раза.

Для нас, в первую очередь, представляет интерес величина J₁(l, t) = $J_{1}^{*}$(r, t) (55) скорости притока массы за счет свободно-свободных столкновений на единицу площади роя, поскольку именно она входит в правую часть уравнения непрерывности для протолунного роя и определяет поверхностную плотность диска σ = σ(l, t):

Здесь J_k(l, t) – скорость притока массы на единицу площади извне за счет k-го способа пополнения роя. Помимо свободно-свободных столкновений, для которых скорость притока массы на единицу площади J₁(l, t) определяется выражением (55), существуют и другие пути пополнения протолунного роя, такие как столкновения между планетезималями из зоны питания Земли и телами, уже захваченными в протолунный рой (свободно-связанные столкновения), и столкновения между телами из роя или зоны питания и частицами выбросов от ударов крупных планетезималей по Земле. Каждый из этих четырех типов столкновений вносит свой вклад J_k(r, t), определение величины которого является предметом для будущих исследований. Отметим также, что величина ∑J_k(l, t) не совпадает со скоростью роста поверхностной плотности на данном расстоянии l и в момент времени t. Из-за наличия ненулевой радиальной скорости перемещения ${{v}_{l}}$ вещества роя реальная скорость роста поверхностной плотности ∂σ(l, t)/∂t на фиксированном расстоянии l от центра Земли отличается от ∑J_k(l, t). Существует несколько факторов, в результате которых скорость движения частиц в рое имеет ненулевую радиальную компоненту. Во-первых, с течением времени масса Земли увеличивается, но момент импульса тел в рое должен сохраняться, поэтому диск сжимается к центру Земли. Этот фактор оказывал существенное влияние на самом раннем этапе эволюции роя, когда масса Земли могла меняться в несколько раз, в результате чего большая часть захваченного в сферу Хилла вещества выпадала на поверхность Земли. Во-вторых, поскольку скорости захватываемых тел распределены хаотично по направлениям, средний удельный угловой момент сталкивающихся тел будет меньше удельного углового момента кеплеровского кругового движения диска, и суммарный угловой момент диска будет уменьшаться за счет притока вещества извне, что будет приводить к постепенному сжатию роя и выпадению части вещества на поверхность Земли. Подробно этот механизм был рассмотрен в работе (Печерникова, Витязев, 1984). Кроме того, протоспутниковый диск характеризуется дифференциальным вращением, что в случае вязкого диска приводит к переносу углового момента касательными напряжениями и смещению частиц роя в радиальном направлении. Однако целью нашего исследования является не решение уравнения (58) и поиск поверхностной плотности σ(l, t), а нахождение скорости притока массы на единицу поверхности диска J₁(l, t) за счет свободно-свободных столкновений, что необходимо для того, чтобы найти решение уравнения (58) в дальнейшем. Поэтому оценка вышеупомянутых факторов, приводящих к сжатию или расширению протолунного диска, остается за рамками данной работы.

Для большей наглядности полученных результатов построим также две диаграммы (рис. 7 и рис. 8), на которых изобразим изолинии $J_{1}^{*}$(r, t) и J₁(l, t). Диаграмма на рис. 7 для $J_{1}^{*}$(r, t) повторяет зависимости, ранее построенные для j_1r(r) и j_1t(t) на рис. 6. На некотором расстоянии r от Земли с течением времени $J_{1}^{*}$ монотонно убывает, а при t = const с ростом расстояния $J_{1}^{*}$ сначала растет до расстояния около 1.5 земных радиусов, потом до расстояния порядка 60 радиусов Земли испытывает незначительные колебания, а на больших расстояниях монотонно убывает. Несколько иной характер имеет диаграмма на рис. 8, где изображены изолинии J₁(l, t) в зависимости от расстояния l до центра Земли и времени t. Хотя $J_{1}^{*}$(r, t) ≡ J₁(l, t), но r = l/R(t), поэтому диаграмма изолиний для J₁(l, t) может быть получена из диаграммы на рис. 7 растяжением вдоль оси r в R(t)/R_max раз. В новых координатах значения радиуса Земли и границы сферы Хилла в единицах современного радиуса Земли растут со временем. На рис. 8 это две огибающие с J₁ = 0, поскольку у поверхности Земли (нижняя огибающая) вероятность захвата равна нулю и на границе сферы Хилла (верхняя огибающая) вероятность захвата скачком обращается в ноль. Зависимость J₁(l, t) от расстояния l в некоторый момент времени будет иметь тот же вид, что и j_1r(r), поскольку, если t = const, то и j_1r(l/R(t)) не будет зависеть от времени. Однако зависимость J₁(l, t) от времени на некотором расстоянии l будет качественно отличаться от j_1t(t) на рис. 6, поскольку j_1r(r) = j_1r(l/R(t)) теперь зависит от времени. По диаграмме на рис. 8 видно, что, например, прямая l = 50R_max, параллельная оси времени (изображена горизонтальными стрелками), дважды пересекает изолинию J₁ = 10^–3 кг/(м² млн лет), что свидетельствует о наличии экстремума J₁(l, t) для l = 50R_max. Аналогично, наличие экстремума (максимума) зависимости J₁(l, t) от времени при l = const может быть показано и для точек, находящихся на ином расстоянии l от Земли. На рис. 9 этот факт проиллюстрирован графиками зависимости J₁(l, t) от времени t для различных расстояний l от Земли, по которым видно, что зависимость скорости прироста массы на единицу площади J₁(l, t) от времени имеет максимум, который смещается в сторону больших времен при увеличении расстояния l до центра Земли. На расстоянии, равном 5 современным радиусам Земли (кривая l = 5R_max на верхнем графике), максимум достигается через 4 млн лет после начала формирования Земли, но для достижения максимума на расстоянии 50 земных радиусов (кривая l = 50R_max на нижнем графике) потребовалось уже 25 млн лет. Отметим, что кривые на рис. 9 начинаются не с t = 0, а с того момента, когда точка, находящаяся на заданном расстоянии l, окажется внутри сферы Хилла растущей Земли. Исходя из модели расширяющихся зон питания для планет земного типа (Витязев и др., 1978) мы получили, что это время выражается по формуле:

где a ≈ 0.035 млн лет^– согласно (51), r_h – радиус сферы Хилла в единицах текущего радиуса Земли, равный 235 согласно (7), а l/R_max – расстояние до центра Земли в единицах современного радиуса Земли. При времени, меньшем, чем t₀, скорость прироста массы роя на единицу площади равна нулю, поскольку за пределами сферы Хилла захват невозможен. Согласно формуле (59), чем больше выбранное расстояние l до центра Земли, тем позднее начинается захват в этой области. Графики на рис. 9 отчетливо иллюстрируют этот факт. Например, на расстоянии 30 современных радиусов Земли захват начинается через 10 млн лет с момента начала формирования Земли, а на расстоянии l = 100R_max захват в протолунный рой начинается только через 26 млн лет. Кроме того, в результате того, что захват на заданном расстоянии l начинается лишь спустя некоторое время, на расстояниях, больших чем 150 максимальных радиусов Земли, величина J₁(l, t) максимальна в момент, когда точка с заданным расстоянием оказывается в сфере Хилла, после чего скорость прироста массы на единицу площади диска монотонно убывает с течением времени.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

В нашей работе впервые после работы Рускол (1975) исследован столкновительный механизм захвата допланетных тел в протолунный рой, который является ключевым процессом при формировании Луны в рамках гипотезы коаккреции. Найдены условия (14), при которых происходит захват, а также вероятность захвата (18). Эти формулы применимы для любого типа столкновений, и это позволило вычислить вероятность захвата в случае свободно-свободных столкновений (28), (30), что в свою очередь, дало возможность уточнить оценку скорости прироста массы на единицу расстояния до центра Земли (45) и на единицу площади протолунного диска (55) за счет этого типа столкновений.

В наших формулах вероятности захвата (28) и (30) преодолены ограничения оценки Рускол (1975). Определена зависимость вероятности захвата не только от расстояния, но и от отношения масс сталкивающихся планетезималей и учтена возможность выпадения осколков на Землю. Благодаря учету последнего фактора, показано, что при заданном отношении масс вероятность захвата не плавно спадает до нуля у границ сферы Хилла, а имеет максимум (рис. 2 и рис. 3) на некотором расстоянии от Земли. Также было показано, что зависимость вероятности захвата от отношения масс на заданном расстоянии до центра Земли тоже имеет максимум (рис. 1). Кроме того, было обнаружено, что на расстоянии, равном 2.3 текущих радиусов Земли и при отношении масс 2.5 вероятность захвата принимает наибольшее значение и равна 0.3. Из графиков на рис. 1–3 и рис. 5 можно сделать вывод, что для столкновений тел с отношением масс, большим 2, вероятность захвата существенна (p > 0.05) на расстояниях, меньших восьми текущих земных радиусов. На больших расстояниях вероятность захвата существенна только для тел, различающихся по массе менее чем в 2 раза. Найденная нами аппроксимация (30) вероятности захвата позволяет сделать вывод о характере зависимости вероятности захвата от расстояния при заданном отношении масс. Согласно (30), по мере удаления от Земли вероятность захвата растет пропорционально степени расстояния до поверхности Земли, а во внешней зоне сферы Хилла экспоненциально убывает.

Найденная зависимость вероятности захвата от отношения масс (30) позволила оценить скорости прироста массы на единицу расстояния до центра Земли (45) и на единицу площади протолунного диска (55) за счет свободно-свободных столкновений. Последние оценки этой величины основывались на оценке вероятности захвата (Рускол, 1975), в которой отсутствовала зависимость от отношения масс, поэтому в работе (Печерникова, Витязев, 1984) принималось предположение, ограничивающее отношение масс. Выведенная нами зависимость (30), содержащая отношение масс сталкивающихся тел, позволила избавиться от этого ограничения и уточнить оценку скорости прироста массы J₁(l, t) на единицу площади протолунного диска. Отметим, что величина J₁(l, t) (55) отличается от скорости роста поверхностной плотности роя ∂σ(l, t)/∂t (первое слагаемое в уравнении непрерывности (58)), поскольку, во-первых, помимо свободно-свободных столкновений, имели место свободно-связанные столкновения и столкновения с веществом выбросов с Земли, а во-вторых, захваченные в рой частицы продолжают испытывать столкновения с телами роя, что приводит к выравниванию наклонений орбит, скоростей тел и постоянному сжатию диска (Safronov и др., 1986), в результате чего вещество диска в среднем имеет ненулевую компоненту радиальной скорости, направленную к центру Земли. Последнее, согласно (58), означает, что скорость роста поверхностной плотности роя не равна суммарной скорости притока массы на единицу площади диска.

Было обнаружено, что зависимость скорости притока массы (55) на единицу площади $J_{1}^{*}$(r, t), пропорциональная j_1r(r) (56) для любого заданного момента времени t, имеет два максимума (рис. 6). Дальний максимум на расстоянии 15 текущих земных радиусов обусловлен тем, что при увеличении расстояния от Земли растет объем сферического слоя с радиусом r, и, соответственно, растет число столкновений, но при этом падает вторая космическая скорость и все меньше частиц имеют возможность быть захваченными в протолунный рой. Второй, ближний максимум, на расстоянии примерно полутора текущих земных радиусов приблизительно соответствует значениям расстояний, при которых величина вероятности захвата (28) наибольшая. Максимум зависимости вероятности захвата (28) от расстояния при заданном отношении масс (рис. 2 и рис. 3) возникает из-за учета возможности выпадения осколков на поверхность Земли (13). С ростом расстояния все меньше осколков падает на Землю, что способствует росту вероятности захвата (28), но постепенное уменьшение скорости убегания (8) приводит сначала к прекращению роста вероятности захвата, а потом и к ее убыванию. Отметим также, что вещество протолунного диска, оказавшееся внутри предела Роша, в результате действия приливных сил со стороны Земли окажется раздробленным на мелкие осколки и не сможет сформировать крупные тела. Поэтому формирование крупных тел, необходимых для аккумуляции Луны, возможно только за пределом Роша, величина которого a_R≈ 1.44R примерно соответствует расстоянию до ближнего максимума скорости притока на единицу площади, равному 1.5R.

Также было показано, что зависимость скорости притока массы (55) на единицу площади диска $J_{1}^{*}$(r, t), пропорциональная j_1t(t) (57) для любого заданного расстояния в единицах текущего радиуса Земли, монотонно убывает с течением времени. Однако графики зависимости J₁(l, t) ≡ $J_{1}^{*}$(r, t) (рис. 9) от времени на заданном расстоянии l в метрах показывают, что скорость притока массы J₁(l, t) (55) на единицу площади достигала максимума в некоторый момент времени, что связано с наличием двух факторов. С одной стороны, с течением времени, по мере роста Земли точка, находящаяся на некотором расстоянии l, смещается внутрь сферы Хилла, где скорость притока массы (55) на единицу площади больше, но, с другой стороны, по мере роста Земли в зоне питания остается все меньше вещества, что сначала приводит к замедлению роста скорости притока массы на единицу площади, а потом и к его падению. С увеличением расстояния l максимум зависимости J₁(l, t) от времени смещается в сторону больших времен. Например, на расстоянии, равном 10 современным радиусам Земли (кривая l = 10R_max на рис. 9 сверху) максимум достигается через 8 млн лет после начала формирования Земли, но на расстоянии в 10 раз большем (кривая l = 100R_max на рис. 9 снизу) максимум достигается только спустя 34 млн лет. Необходимо отметить, что захват на заданном расстоянии l начинается не сразу, а только тогда, когда величина l оказывается меньше радиуса сферы Хилла R_H (2), поэтому кривые для скорости прироста массы на единицу площади на рис. 9 начинаются не с нулевого момента времени, а с t₀, которое определяется выражением (59). На диаграмме на рис. 8 эта особенность иллюстрируется верхней огибающей изолиний J₁(l, t) = const, где l ≈ 235R (R – текущий радиус Земли). Кроме того, на расстояниях l, меньших, чем современный радиус Земли R_max, захват заканчивается в момент, когда l = R_max, а все захваченное вещество выпадает на поверхность Земли. По диаграмме на рис. 8 видно, что при l < R_max захват заканчивается на нижней огибающей изолиний J₁(l, t) = const, которая фиксирует l = R (R – текущий радиус Земли).

Найденная в нашей работе величина скорости притока массы (55) на единицу площади диска J₁(l, t) за счет свободно-свободных столкновений входит в уравнение непрерывности (58) как один из источников пополнения протолунного роя и необходима для того, чтобы определить из уравнения (58) зависимость поверхностной плотности диска от расстояния и времени, что, в свою очередь, позволит найти конечную массу протолунного диска и формирующейся из него Луны. Необходимо отметить, что, поскольку в рамках нашего исследования мы рассматривали задачу двух тел (Земля и облако осколков), пренебрегая возмущениями гравитационного потенциала со стороны Солнца, то возможны такие столкновения, при которых начальная скорость облака осколков будет меньше второй космической скорости на данном расстоянии, но при этом орбита в своем апогее выходит за пределы сферы Хилла Земли. Согласно алгоритму, рассмотренному в статье, такие столкновения учитываются как приводящие к захвату, однако в действительности, из-за выхода осколков за пределы сферы Хилла, захват не произойдет. Поэтому оценка скорости притока массы (55) на единицу площади диска является несколько завышенной, в особенности во внешней зоне сферы Хилла.

Стоит также отметить универсальный характер формулы (45) для скорости роста, захваченной в результате свободно-свободных столкновений, массы. В (45) входят зависимости радиуса Земли R (50), плотности протопланетного диска ρ₀ и массы наибольшего тела m_max (52) от времени t с момента начала формирования Солнечной системы, которые в нашем исследовании мы принимали согласно модели расширяющихся зон питания (Витязев и др., 1978), однако выражение (45) допускает использование иных моделей роста Земли. В модели расширяющихся зон питания (Витязев и др., 1978) за 50 млн лет Земля набирает до 35% современной массы, что по порядку величины близко к оценке Сафронова (1969), согласно которой за 50 млн лет Земля набирала 55% современной массы. Согласно более поздней аналитической оценке (Печерникова, 2005), учитывающей вклад крупных планетезималей, за 50 млн лет Земля достигла около 70% своей массы. Последняя оценка (Woo и др., 2022), сделанная на основе численных расчетов, дает накопление массы Земли до 90% современной массы также за 50 млн лет. Отметим, что в случае более быстрого роста Земли, чем в модели расширяющихся зон питания (Витязев и др., 1978), следует ожидать более быстрого исчерпания тел зоны питания, что приведет к тому, что за время роста Земли в ее сфере Хилла произойдет меньшее число столкновений планетезималей и суммарная захваченная масса окажется меньше. При более быстром, чем в (Витязев и др., 1978), исчерпании тел зоны питания график зависимости величины j_t(t) (53) от времени t (рис. 6), пропорциональной c постоянным коэффициентом на заданном расстоянии r скорости роста массы протолунного роя J*(r, t) (45), сместится в сторону меньших времен. В то же время, график зависимости величины j_r(r) (48) от расстояния r до центра Земли (рис. 6), пропорциональной c постоянным коэффициентом в заданный момент времени t скорости роста массы протолунного роя J*(r, t) (45), останется неизменным, поскольку j_r(r) не зависит от массы Земли и плотности протопланетного диска в данный момент времени, а определяется распределением допланетных тел по массе (6) и вероятностью захвата (28), которая зависит от распределения числа тел по скоростям (3). Отметим также, что поскольку вероятность захвата (28) не зависит от массы Земли в данный момент времени, то графики зависимости вероятности захвата от отношения масс сталкивающихся тел (рис. 1) и от расстояния в единицах радиуса Земли (рис. 2 и рис. 3) останутся неизменными вне зависимости от рассматриваемой модели роста Земли.

Хотя свободно-свободные столкновения вносят незначительный вклад в массу Луны (порядка 10^–5 массы Луны, согласно нашим расчетам), именно они формируют протолунный рой на самых ранних этапах и служат триггером для дальнейшей аккреции путем свободно-связанных столкновений и столкновений с выбросами от ударов крупных тел по Земле. Без первичного роя, сформированного свободно-свободными столкновениями, невозможно дальнейшее накопление массы, поскольку в других типах столкновений, которые способны пополнить рой, одно из сталкивающихся тел должно быть гравитационно-связанным с Землей, что требует наличия протолунного диска с ненулевой массой. Поэтому оценка вклада свободно-свободных столкновений, проведенная в данной работе, является необходимой для построения теории формирования системы Земля–Луна в рамках гипотезы коаккреции.

Отметим, что гипотеза коаккреции является не произвольным допущением, а наиболее вероятным следствием общепринятой теории формирования планет земного типа (Сафронов, 1969; Витязев и др., 1990). Поэтому процессы, которые исследовались в нашей работе, и которые еще предстоит исследовать в рамках гипотезы коаккреции, с необходимостью присутствовали во время формирования протолунного роя. Основной вопрос заключается не в том, имели место эти процессы или нет, а в том, могли ли эти процессы обеспечить достаточный вклад, чтобы сформировать такой спутник, как Луна, или же необходимы дополнительные предположения, как, например, столкновение Земли с крупным телом, размером с Марс? Другими словами, необходимо выяснить, является ли Луна регулярным или нерегулярным спутником.

В заключение мы бы хотели выразить благодарность В.В. Светцову за ценное обсуждение и внимание к нашей работе.