Доклады Российской академии наук. Физика, технические науки, 2020, T. 490, № 1, стр. 29-32

Сопротивление высокоскоростному пластическому деформированию твердых тел при длительностях нагрузки порядка микросекунды или менее исследуется путем анализа эволюции профилей массовой скорости u_p(t) или напряжения сжатия σ_x(t) как функции времени t по мере распространения импульса ударного сжатия в исследуемом материале [1–6]. В данной работе предлагается простой способ оценки напряжения пластического течения ударно-сжатого материала по измеренному единичному профилю скорости свободной поверхности u_fs(t). Измерение u_fs(t) является наиболее доступным и точным способом регистрации волн сжатия и разрежения, пригодным также для экспериментов при повышенных температурах.

Предлагаемый способ оценки протестирован на примере показанного на рис. 1 профиля скорости свободной поверхности, который получен путем численного моделирования соударения алюминиевых пластин. Расчет проведен с использованием двухэлементной модели Мазинга [7], детали которой приведены в [8]. Модель Мазинга воспроизводит эффект Баушингера, расчеты ударно-волновых явлений с ее использованием дают хорошее согласие с экспериментальными данными. Показанный на рис. 1 профиль u_fs(t) демонстрирует четкое выделение упругого предвестника в волне сжатия, амплитуда которого равна динамическому пределу упругости (HEL, Hugoniot Elastic Llimit). Предел текучести σ_T связан с величиной динамического предела упругости σ_HEL соотношением

где c_l – продольная скорость звука, ${{c}_{b}} = \sqrt {{K \mathord{\left/ {\vphantom {K \rho }} \right. \kern-0em} \rho }} $ – объемная скорость звука, K – объемный модуль упругости, ρ – плотность. В идеальном упругопластическом теле упругий предвестник должен выделяться также в волне разгрузки, распространяющейся вслед за волной сжатия. Его амплитуда должна быть равна удвоенному значению HEL. На практике переход от упругой к пластической деформации обычно размыт из-за сильного эффекта Баушингера. Лидирующую часть волны разрежения в таких случаях часто называют квазиупругой волной.

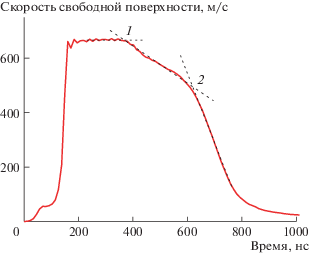
Будем анализировать квазиупругую волну разрежения в приближении простой волны. Согласно [9], разность в величинах сдвиговых напряжений, соответствующих двум значениям массовой скорости u_p1 и u_p2 в простой волне разрежения, выражается соотношением

Здесь фазовая скорость a и объемная скорость звука a_b взяты в координатах Лагранжа, напряжение σ_x(ε) и деформация ε принимаются положительными при сжатии. Так как при разгрузке из ударно-сжатого состояния сдвиговое напряжение переходит через нуль и выходит на напряжение пластического течения с обратным знаком, соотношение (2) фактически определяет предел текучести ударно-сжатого материала. Для простых оценок сделаем следующие допущения. Зависимость a_b(u_p) опишем соотношением, которое получается в предположении совпадения ударной адиабаты и римановой изэнтропы в координатах p–u_p [2, 10]:

где c₀, b – коэффициенты линейного выражения для ударной адиабаты, связывающего скорость ударной волны U_s и массовую скорость: U_s = c₀ + bu_p. Возьмем для оценки зависимость a(u_p) также в форме соотношения (3) с коэффициентами c_x и b_x. Тогда соотношение (2) принимает вид

Точность соотношения (4) оценена сопоставлением с непосредственными результатами компьютерного моделирования, в котором напряжение пластического течения перед началом разгрузки и после ее завершения составило σ_T = 0.215 ГПа. Квазиупругая часть волны разрежения на рассчитанном профиле скорости свободной поверхности аппроксимирована прямой линией 1–2 на рис. 1. Скорость фронта волны разрежения (точка 1) равна продольной скорости звука a_l, которую мы определяем в предположении постоянства коэффициента Пуассона как a_l(u_p1) = = a_b(u_p1)c_l/c₀.

Ранее было показано [2, 10], что это приближение хорошо согласуется с экспериментальными данными. В конце квазиупругого участка (точка 2) скорость волны разрежения равна объемной скорости звука a_b(u_p2). Величина массовой скорости определяется по измеренному профилю скорости свободной поверхности в соответствии с правилом удвоения как

где δ_ep – поправка, учитывающая гистерезис цикла упругопластического сжатия и разгрузки. Поправка к величине u_p1 равна δ_ep = $\frac{{{{\sigma }_{{{\text{HEL}}}}}}}{\rho }\left( {\frac{1}{{{{c}_{b}}}} - \frac{1}{{{{c}_{l}}}}} \right)$ [11] и в данном примере составляет 5.5 м/с. Поправка к величине u_p2 равна нулю вследствие взаимодействия падающей и отраженной волн разрежения. Линейная зависимость a(u_p) проведена через найденные значения a_l(u_p1) и a_b(u_p2). Подстановка этих данных в соотношение (4) дала величину τ(u_p1) – τ(u_p2) = 0.209 ГПа, т.е. весьма близко к реальному значению 0.215 ГПа, задаваемому использовавшейся в расчетах моделью.

Апробированный выше способ оценки предела текучести ударно-сжатого материала применен к результатам опытов с алюминием АД1, показанным на рис. 2. В проведенных экспериментах импульсы сжатия в плоских образцах толщиной 2.9 мм генерировались ударом пластины из алюминия А5М толщиной 0.72 мм, разогнанной до скорости 355 ± 10 м/с с помощью газовой пушки. Соотношение толщин ударника и образца специально выбрано таким малым, чтобы параметры волны разрежения, регистрируемой на профиле скорости свободной поверхности, определялись свойствами образца, а вклад материала ударника был незначителен. Для регистрации профилей скорости свободной поверхности u_fs(t) использовался лазерный интерферометрический измеритель скорости VISAR [12]. Эксперименты проведены при комнатной температуре и 498°С. Видно, что амплитуда упругого предвестника при высокой температуре в несколько раз выше, чем при комнатной, что объясняется большим вкладом фононной вязкости при высоких скоростях деформации [2, 3, 13]. Квазиупругие участки волн разрежения при нормальной и повышенной температурах зрительно примерно одинаковы. Второй подъем скорости свободной поверхности на представленных волновых профилях связан с откольным разрушением и вызванной им релаксацией растягивающих напряжений внутри образца [2].

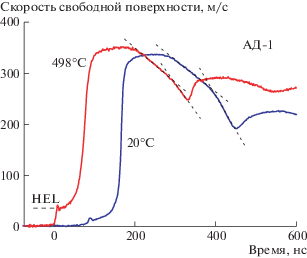
Оценки проведены с учетом температурных зависимостей плотности и модулей упругости алюминия по данным работы [14]. Ударная адиабата алюминия АД1 по данным работы [15] при комнатной температуре была взята в виде U_s = = 5.32 + 1.37u_p, ρ₀ = 2.71 г/см³, c_l = 6.4 км/с. Ударная адиабата алюминия при температуре ∼500°С и плотности ρ₀ = 2.59 г/см³ взята с использованием объемного модуля упругости из [14] в виде U_s = 5.05 + 1.37u_p км/с, c_l = 5.88 км/с. Коэффициент b при массовой скорости здесь тот же, что и при комнатной температуре; для ударных волн малой интенсивности его неточность не может привести к существенным погрешностям.

При комнатной температуре величина σ_HEL составила 0.12 ГПа, соответствующее значение σ_T = 0.056 ГПа. При 498°С величина σ_HEL составила 0.28 ГПа, σ_T = 0.11 ГПа. Квазиупругая часть волны разрежения определялась пересечением прямых, аппрокимирующих два режима деформации при разгрузке, как показано на рис. 2. При комнатной температуре она соответствует падению скорости свободной поверхности от 336 до 270 м/с. Оценка в описанном выше приближении дает величину динамического предела текучести ударно-сжатого алюминия 0.077 ГПа. Превышение начальной величины σ_T = 0.056 ГПа вполне объясняется деформационным упрочнением и влиянием высокого давления. Деформационное упрочнение проявляется также в нарастании параметров за фронтом упругого предвестника волны сжатия. При температуре 498°С квазиупругая часть волны разрежения соответствует уменьшению u_fs от 350 до 286 м/с, что дает величину предела текучести в ударно-сжатом состоянии 0.054 ГПа, т.е. в 5 раз ниже величины в упругом предвестнике сжатия и существенно меньше, чем при комнатной температуре.

Таким образом, впервые проведена экспериментальная оценка динамического предела текучести ударно-сжатого металла при высокой температуре. В то время, как параметры упругопластических волн сжатия демонстрируют аномальное возрастание напряжения высокоскоростного пластического течения увеличением температуры, подобная аномалия при разгрузке из ударно-сжатого состояния не зафиксирована. Полученный результат позволяет сделать некоторые предварительные заключения относительно динамики дислокаций. Скорость пластической деформации, как известно, пропорциональна произведению плотности подвижных дислокаций и их скорости, причем последняя возрастает с увеличением действующего напряжения. В процессе деформации происходит размножение дислокаций, вследствие чего высокая скорость деформации становится возможной при меньшей скорости дислокаций и, соответственно, меньшем напряжении. Сопоставление полученных результатов при 20 и 498°С дает основание для утверждения о более быстром размножении дислокаций при высоких температурах.