Доклады Российской академии наук. Физика, технические науки, 2020, T. 490, № 1, стр. 79-81

Изменение ориентации твердого тела при помощи вспомогательной массы

Академик РАН Ф. Л. Черноусько^*

Институт проблем механики им. А.Ю. Ишлинского Российской академии наук
Москва, Россия

Поступила в редакцию 30.05.2019
После доработки 30.05.2019
Принята к публикации 28.11.2019

DOI: 10.31857/S2686740020010113

Аннотация

Рассматривается задача об управлении ориентацией твердого тела в пространстве при помощи вспомогательной точечной массы. Построены движения этой массы, обеспечивающие заданное изменение ориентации тела.

Ключевые слова: динамика твердого тела, ориентация, управление движением

Управление пространственным движением твердого тела может осуществляться при помощи вспомогательной внутренней массы, снабженной актюатором и способной перемещаться относительно тела. В случае плоского движения при отсутствии внешних сил подобные задачи управления рассматривались в [1, 2], где построены оптимальные по быстродействию законы управления. Пространственным задачам переориентации посвящены статьи [3, 4]. В данной работе предложен простой способ управления, обеспечивающий при отсутствии внешних сил заданное изменение пространственной ориентации твердого тела при помощи подвижной массы.

ОСНОВНОЕ УРАВНЕНИЕ

Рассмотрим механическую систему, состоящую из твердого тела P массы M и материальной точки Q массы m. Точка Q может перемещаться относительно тела P при помощи актюатора. Предполагаем, что внешними силами, действующими на систему P + Q, можно пренебречь.

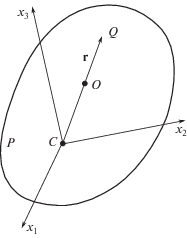
Обозначим через O центр масс системы P + Q, а через C – центр масс твердого тела P. Примем, что в начальный момент времени t = 0 система покоится. Тогда ее центр масс неподвижен во время движения. Обозначим через R_C и r векторы (см. рис. 1)

${{R}_{c}} = OC,\quad r = CQ.$

Рис. 1.

Механическая система.

Тогда условие неподвижности центра масс O системы P + Q запишется в виде

(1)

$M{{R}_{C}} + m({{R}_{C}} + r) = 0.$

Отсюда получим

(2)

${{R}_{C}} = - \mu r,$

где введено обозначение

(3)

$\mu = \frac{m}{{M + m}}.$

Так как по предположению внешние силы равны нулю, импульс системы P + Q и ее кинетический момент сохраняются и равны нулю. Условие сохранения импульса запишем в виде

(4)

$M{{v}_{C}} + m({{v}_{C}} + \omega \times r + v) = 0,$

где ω – угловая скорость твердого тела P, v_C – абсолютная скорость центра масс C тела P, v – скорость точки Q относительно твердого тела P. Для вектора v_C из соотношений (3), (4) получим

(5)

${{v}_{C}} = - \mu (\omega \times r + v).$

Закон сохранения кинетического момента запишется в виде

(6)

$\begin{gathered} M{{R}_{C}} \times {{v}_{C}} + J \cdot \omega + \\ + \,m({{R}_{C}} + r) \times ({{v}_{C}} + \omega \times r + v) = 0, \\ \end{gathered} $

где J – тензор инерции твердого тела P относительно его центра масс C, точкой обозначено произведение тензора на вектор. Подставляя в уравнение (6) выражение (2) для R_C и (5) для v_C, получим в результате уравнение

(7)

$J \cdot \omega + \mu Mr \times (\omega \times r + v) = 0,$

где μ введено соотношением (3).

ПЕРЕОРИЕНТАЦИЯ ТЕЛА

Введем декартову систему координат Cx₁x₂x₃, связанную с твердым телом P (рис. 1), оси которой Cx_i суть главные центральные оси инерции тела, i = 1, 2, 3. Пусть требуется перевести тело P из заданного начального состояния покоя в заданное конечное состояние покоя. При этом будем предполагать, что подвижная точка Q в начале и в конце движения совпадает с центром масс C тела P. Тогда центр масс C тела P в конце движения будет находиться в той же точке пространства, что и в начале движения. Таким образом, все движение сведется к изменению ориентации тела в пространстве.

Заданное движение можно осуществить при помощи трех последовательных плоских поворотов тела вокруг его главных центральных осей инерции Cx_i, i = 1, 2, 3 [4]. В результате поворота вокруг оси $C{{x}_{i}}$ твердое тело P должно повернуться на заданный угол $\Delta {{\varphi }_{i}}$, а подвижная масса Q должна начать движение в центре масс C тела P и окончить движение в той же точке C. В начале и в конце каждого плоского поворота тело P и точка Q должны находиться в состоянии покоя. Таким образом, для осуществления заданной пространственной переориентации тела P при сохранении положения его центра масс C в пространстве достаточно построить решение задачи о плоском повороте при условии, что точка Q начинает и заканчивает движение в точке C. Для построения требуемого движения точки Q можно воспользоваться результатами работ [1, 2], где построены решения, оптимальные по быстродействию, в случае ограничения на величину скорости точки Q относительно тела P. Ниже предлагается простое решение, в котором не наложено такого ограничения.

ПЛОСКИЙ ПОВОРОТ

Как показано в [1], оптимальные траектории точки Q в случае $\mu \ll 1$ оказываются дугами окружностей. Если же начальное и конечное положения точки Q относительно тела P совпадают, то эти траектории представляют собой окружности. Будем искать требуемое движение точки Q относительно тела P также в виде окружности.

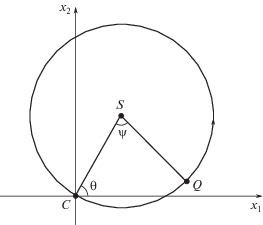
Рассматриваем плоский поворот тела P вокруг одной из осей Cx_i, i = 1, 2, 3. Пусть для определенности поворот происходит вокруг оси Cx₃. При этом точка Q движется в плоскости Cx₁x₂, начиная и заканчивая движение в точке C. Ее траекторию ищем в виде окружности некоторого радиуса R, проходящей через точку C (рис. 2). Пусть центр этой окружности расположен в точке S с координатами

$x_{1}^{S} = R\cos \theta ,\quad x_{2}^{S} = R\sin \theta ,$

где θ – произвольный угол, $\theta \in \left[ {0,{\text{ }}2\pi } \right)$.

Рис. 2.

Плоский поворот.

Точка Q движется по окружности, и ее текущее положение характеризуется углом ψ между текущим радиусом SQ и неподвижным радиусом CS (рис. 2). Тогда текущие координаты точки Q определяются формулами

(8)

$\begin{gathered} {{x}_{1}} = R\left[ {\cos \theta - \cos (\theta + \psi )} \right], \\ {{x}_{2}} = R\left[ {\sin \theta - \sin (\theta + \psi )} \right]. \\ \end{gathered} $

Запишем векторное уравнение (7) в проекции на ось Cx₃. Обозначая через I момент инерции тела P вокруг оси Cx₃, а через φ – угол поворота тела вокруг этой оси, получим

(9)

$I\dot {\varphi } + \mu M(\dot {\varphi }{{r}^{2}} + {{x}_{1}}{{\dot {x}}_{2}} - {{x}_{2}}{{\dot {x}}_{1}}) = 0.$

Подставим ${{r}^{2}} = x_{1}^{2} + x_{2}^{2}$, а также выражения (8) для x₁, x₂ в уравнение (9). Учитывая, что угол θ постоянен, а угол $\psi = \psi \left( t \right)$ зависит от времени, в результате получим

(10)

$\dot {\varphi } = - \frac{{\mu M{{R}^{2}}\left( {1 - \cos \psi } \right)}}{{I + 2\mu M{{R}^{2}}\left( {1 - \cos \psi } \right)}}\dot {\psi }.$

Интегрируя соотношение (10), найдем

(11)

$\varphi (t) = \frac{1}{a}Arctg\left( {a{\text{ }}tg\frac{\psi }{2}} \right) - \frac{\psi }{2},$

где введено обозначение

(12)

$a = {{(1 + 4\mu M{{R}^{2}}{{I}^{{ - 1}}})}^{{1/2}}}.$

В соотношении (11) нужно выбирать соответствующую ветвь функции Arctg: когда угол φ изменяется от 0 до 2π при движении точки Q по окружности, Arctg монотонно возрастает от 0 до π.

Соотношение (11) показывает, что угол φ поворота тела вокруг оси Cx₃ зависит только от угла ψ, т.е. от положения точки Q на окружности, и не зависит от закона ее движения вдоль этой окружности. Кроме того, угол φ не зависит от положения центра окружности (угла θ), что очевидно.

Полагая $\psi = 2\pi $ в равенстве (11), получим полный угол поворота Δφ тела P вокруг оси Cx₃ в виде

(13)

$\Delta \varphi = \frac{\pi }{a} - \pi ,$

где а определено равенством (12). Так как $a > 1$, имеем неравенства

(14)

$ - \pi < \Delta \varphi < 0.$

Следовательно, тело поворачивается вокруг оси Cx₃ в направлении, противоположном направлению вращения точки Q, которое выбрано положительным на рис. 2. Кроме того, из неравенств (14) следует, что угол поворота тела не может по величине превышать π. Если требуется повернуть тело в некотором направлении на угол, больший π, то этого можно добиться, вращая тело в противоположном направлении на угол, меньший π.

Возможности управления ориентацией тела P увеличатся, если точка Q совершит несколько оборотов по окружности радиуса R. В этом случае вместо формулы (13) будем иметь следующее выражение для величины угла поворота тела:

(15)

$\left| {\Delta \varphi } \right| = \frac{{n\pi (a - 1)}}{a}.$

Здесь n – число оборотов точки Q. Подставим формулу (12) в равенство (15) и разрешим его относительно радиуса окружности. Получим

(16)

$R = \sqrt {\frac{I}{M}} \frac{{\sqrt {\alpha \left( {1 - {\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}} \right)} }}{{\sqrt {2\mu } \left( {1 - \alpha } \right)}},\quad \alpha = \frac{{\left| {\Delta \varphi } \right|}}{{\pi n}}.$

Движение точки Q по окружности радиуса R, проходящей через центр масс C тела P, может осуществляться по произвольному закону. Требуется лишь, чтобы скорость точки Q при попадании ее в точку C обращалась в нуль. Если имеются те или иные ограничения, наложенные на движение точки Q относительно тела P, то можно реализовать, в частности, оптимальное движение в смысле того или иного критерия оптимальности.

Заметим, что согласно формуле (16) радиус окружности R убывает с ростом числа оборотов n точки Q по этой окружности. Это обстоятельство позволяет уменьшить область маневра массы Q в теле P.

Таким образом, дано описание движений подвижной точечной массы Q, обеспечивающих заданное изменение ориентации тела P в пространстве.

Список литературы

Черноусько Ф.Л. // ДАН. 2018. Т. 480. № 5. С. 528–532.
Шматков А.М. // ДАН. 2018. Т. 481. № 5. С. 498–502.
Черноусько Ф.Л. // ПМТФ. 2019. Т. 60. № 2. С. 107–112.
Наумов Н.Ю., Черноусько Ф.Л. // Известия РАН. Теория и системы управления. 2019. № 2. С. 106–113.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал