Доклады Российской академии наук. Физика, технические науки, 2020, T. 490, № 1, стр. 73-78

УСТОЙЧИВОСТЬ БАЛКИ БЕРНУЛЛИ–ЭЙЛЕРА ПОД ДЕЙСТВИЕМ ДВИЖУЩЕГОСЯ ТЕПЛОВОГО ИСТОЧНИКА

Академик РАН Н. Ф. Морозов^2, 3, член-корреспондент РАН Д. А. Индейцев^1, 2, А. В. Лукин^1, *, И. А. Попов¹, О. В. Привалова¹, Л. В. Штукин^1, 2

¹ Санкт-Петербургский политехнический университет Петра Великого
Санкт-Петербург, Россия

² Институт проблем машиноведения Российской академии наук
Санкт-Петербург, Россия

³ Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

^* E-mail: lukin_av@spbstu.ru

Поступила в редакцию 26.11.2019
После доработки 26.11.2019
Принята к публикации 06.12.2019

DOI: 10.31857/S2686740020010162

Полный текст (PDF)

Аннотация

В представленной работе решена задача о распространении волны прогиба в балке Бернулли–Эйлера при движении теплового источника и проведен анализ влияния тепловых изгибающего момента и продольной силы. Установлено, что сосредоточенный изгибающий момент, движущийся вместе с границей нагретой области, определяет форму волны прогиба, но не может привести к значительному росту ее амплитуды. Показано, что среднее значение продольной сжимающей силы линейно растет во времени при равномерном движении источника нагрева. Выявлены значения исходных параметров – скорости движения источника и температуры, при достижении которых возможна потеря устойчивости и значительный рост прогиба.

Ключевые слова: устойчивость, балка Бернулли–Эйлера, нестационарные упругие волны, температурные воздействия

В настоящее время растущую актуальность приобретают задачи динамики деформируемых элементов конструкций при лазерных термооптических воздействиях. Вот некоторые из областей техники и технологии, где такие задачи встречаются: задачи неразрушающего контроля оборудования и конструкций [1]; определение физико-механических свойств материалов [2]; изучение геометрических и физических параметров объектов и структур на нано- и микромасштабном уровне; биомедицина [3]; микромеханические актуаторы, использующие оптический метод сообщения упругому элементу температурных деформаций [5, 6]; влияние лазерного излучения на деформации поверхности микромеханических зеркал [7]; волоконно-оптические сенсоры, работающие в авторезонансном режиме при оптическом возбуждении [4]; метод лазерной термооптической частотной подстройки микромеханического резонатора и управления его нелинейной амплитудно-частотной характеристикой [8]; термооптическое возбуждение многомодового параметрического резонанса в графеновых мембранах [9].

В работе [10] показано, что в общем случае напряженно-деформированное состояние, вызванное нагревом, определяется продольной сжимающей силой P_T и изгибающим моментом M_T:

${{P}_{T}} = Eb{{\alpha }_{T}}\int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} {\theta dz,\quad } {{M}_{T}} = Eb{{\alpha }_{T}}\int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} {z\frac{{{{\partial }^{2}}\theta }}{{\partial {{x}^{2}}}}dz.} $

Рассмотрена задача об импульсном нагреве по всей поверхности балки, что позволяет учитывать только продольную сжимающую силу и не учитывать действие изгибающего момента.

В работе [11] показано, что при движении источника нагрева на границе нагретой и холодной частей стержня возникает сосредоточенный изгибающий момент, движущийся вместе с источником нагрева. Исследовано влияние изгибающего момента на динамику возникающей волны прогиба.

В настоящей работе рассмотрено одновременное влияние продольной силы и изгибающего момента на характер возникающей волны прогиба.

ПОСТАНОВКА ЗАДАЧИ

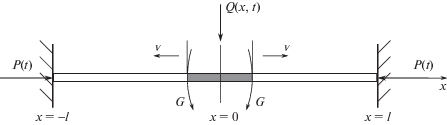
Два тепловых источника движутся вдоль балки от ее середины к концам со скоростью ${v}$ (рис. 1). Отсутствие отдачи тепла позволяет считать, что отрезок стержня длиной 2l_Θ = 2${v}$t остается нагретым до максимальной температуры достаточно длительное время. Полагаем, как и в [11], что действие движущегося теплового источника приводит к появлению сосредоточенных изгибающих моментов, движущихся вдоль стержня со скоростью движения источника нагрева. В отличие от [11], учтем изменение во времени продольной сжимающей нагрузки вследствие теплового расширения в нагретой области.

Рис. 1.

Балка при действии движущегося источника нагрева.

В работе [11] рассмотрена задача о нагреве тонкого стержня лазерным импульсом и показано, что прогрев по толщине происходит достаточно быстро по сравнению с характерным временем изменения прогиба. Это означает, что можно полагать распределение температуры по длине стержня

$\Theta (x,t) = \Theta {\text{*}}H(d + {{l}_{\theta }} - x),$

где Θ* – среднее значение температуры по толщине в прогретом участке стержня, l_Θ = ${v}$t – путь, пройденный источником нагрева, d – ширина пятна.

С другой стороны, в [11] показано, что наибольший градиент температуры будет вблизи движущейся границы нагретого и холодного участков. Это приводит к появлению сосредоточенных изгибающих моментов, приложенных на границе нагретого и холодного участков стержня, движущихся вдоль стержня вместе с этой границей.

Уравнения, описывающие динамическое поведение исследуемого стержня, состоят из системы уравнений продольных колебаний

(1)

$\begin{gathered} - \frac{{\partial N}}{{\partial x}} + \rho \ddot {u} = 0, \\ \frac{{\partial u}}{{\partial x}} = \frac{1}{{ES}}N\, + \propto \Theta (x,t), \\ \end{gathered} $

уравнения изгибных колебаний

(2)

$RJw{\kern 1pt} ''''\, - (N(x,t)w{\kern 1pt} '){\kern 1pt} '\, + \rho \ddot {w} + kw - F(x,t) = 0,$

граничных условий (на левом конце – середина стержня – условия симметрии, правый конец защемлен)

$\begin{gathered} u(0,t) = 0,\quad u(l,t) = 0,\quad w{\kern 1pt} '(0,t) = 0, \\ w{\kern 1pt} '''(0,t) = 0,\quad w(l,t) = 0,\quad w{\kern 1pt} '(l,t) = 0 \\ \end{gathered} $

и нулевых начальных условий:

$u(x,0) = 0,\quad \dot {u}(x,0) = 0;\quad w(x,0) = 0,\quad \dot {w}(x,0) = 0.$

В уравнениях колебаний Θ(x, t) = Θ*H(d + l_θ – x) – распределение температуры вдоль стержня, F(x, t) – распределенная поперечная нагрузка, связанная с изгибающим моментом G (считаем его постоянным).

Уравнения (1), описывающие продольные деформации, могут быть решены независимо от уравнений изгиба. Решение этой задачи может быть найдено методом двух аппроксимаций [14] в виде рядов по собственным формам. Полученное решение для продольной силы имеет вид

$N(x,t) = - \alpha {{\Theta }_{*}}ES\frac{{(d + {v}t)}}{l} + R(x,t),$

где R(x, t) – колебательная составляющая, содержащая гармоники с собственными частотами продольных колебаний.

РЕШЕНИЕ ЗАДАЧИ О РАСПРОСТРАНЕНИИ ВОЛНЫ ПРОГИБА

При нулевых начальных условиях наличие продольной силы не приведет к появлению прогиба. Однако, как это показано в [11], начальный прогиб появляется вследствие действия сосредоточенного изгибающего момента на границе прогретого и холодного участков стержня.

Высокочастотная составляющая продольной силы может привести к возникновению параметрического возбуждения поперечных колебаний. Однако значительные амплитуды параметрических колебаний возможны только при условии возникновения параметрического резонанса, что возможно только при весьма жестких условиях на соотношение между собственными частотами поперечных и продольных колебаний и, в конечном счете, на геометрию рассматриваемого стержня. Подробнее о возможности возбуждения параметрического резонанса в подобной ситуации указано в работе [12]. Исходя из этого, будем учитывать в продольной силе только ее медленную составляющую N(x, t) = –α$\Theta {\text{*}}ES\frac{{(d + {v}t)}}{l}$.

Зная зависимость продольной силы N(t) от времени, решаем далее задачу о распространении волны изгиба на ограниченном интервале времени.

Согласно [13], прогиб w(x, t) отыскиваем на переменном интервале l_w(t), 0 < x ≤ l_w < l, в виде

(5)

$\begin{gathered} w(x,t) = \beta (t){{w}_{1}}(x) = \\ = \beta (t)\left( {1 + \cos \frac{{\pi x}}{{{{l}_{w}}}}} \right)H({{l}_{w}} - x), \\ \end{gathered} $

выбрав в качестве формы функцию, удовлетворяющую граничным условиям. При этом считаем, что l_θ < l_w. Зависимость l_w(t) пока неизвестна и подлежит определению.

Применяя опять процедуру Галёркина, приходим к дифференциальному уравнению относительно амплитуды прогиба β(t):

(6)

$\begin{gathered} \ddot {\beta } + {{\Omega }^{2}}\beta = f(t), \\ \beta (0) = 0,\quad \dot {\beta }(0) = 0, \\ \end{gathered} $

где обозначено

Ω² = ${{\lambda }^{2}}\left( {{{{\left( {\frac{l}{{{{l}_{w}}}}} \right)}}^{4}} + \frac{k}{{\rho {{\lambda }^{2}}}} - {{P}_{0}}\frac{{(d + {v}t)}}{l}{{{\left( {\frac{l}{{{{l}_{w}}}}} \right)}}^{2}}} \right)$,

f(t) = D$\frac{1}{{l_{w}^{2}}}\sin \frac{{\pi (d + {v}t)}}{{{{l}_{w}}}}$, D = $\frac{2}{3}\frac{\pi }{\rho }$G, P₀ = $\frac{{\alpha {{\Theta }_{*}}ES}}{{{{P}_{{\text{э}}}}}}$,

λ² = $\frac{{EJ}}{{3\rho }}{{\left( {\frac{\pi }{l}} \right)}^{4}}$ – частота поперечных колебаний,

P_э = EJ${{\left( {\frac{\pi }{l}} \right)}^{2}}$ – критическая сила для защемленного по концам стержня длиной 2l.

Решение уравнения (6) при однородных начальных условиях принимает вид

(7)

$\beta (t) = D\frac{{(\Omega {\text{sin}}(\psi + \omega t) - \Omega {\text{sin}}\psi {\text{cos}}\Omega t - \omega {\text{cos}}\psi {\text{sin}}\Omega t)}}{{l_{w}^{2}\Omega ({{\Omega }^{2}} - {{\omega }^{2}})}},$

где ω = $\frac{{\pi {v}}}{{{{l}_{w}}}}$, ψ = $\frac{{\pi d}}{{{{l}_{w}}}}$.

В случае, когда Ω² – ω² = 0, решение для β(t) конечно и равно

$\beta (t) = D\frac{{(\Omega t\cos (\psi + \Omega t) - \cos \psi \sin \Omega t)}}{{ - 2l_{w}^{2}{{\Omega }^{2}}}}.$

Длину переменного интервала l_w(t) будем отыскивать, используя критерий максимальности энергии упругой деформации:

(8)

$\int\limits_0^{{{l}_{w}}} {EJ{{{(w{\kern 1pt} '')}}^{2}}dx = \max ,} $

что приводит к нелинейному уравнению относительно l_w и t

(9)

$\Phi ({{l}_{w}},t) = - 3\beta + 2{{l}_{w}}\frac{{\partial \beta }}{{\partial {{l}_{w}}}} = 0.$

Для удобства проведения вычислений введены безразмерные величины: τ = λt – безразмерное время, s(τ) = $\frac{{{{l}_{w}}(\tau )}}{l}$ – безразмерная длина переменного интервала, $\nu $ = $\frac{{v}}{{\lambda l}}$ – безразмерная скорость,

γ = $\frac{d}{l}$, ψ = $\frac{{\pi \gamma }}{s}$, r(t) = $\frac{{{v}t}}{l}$ = $\nu $τ

и безразмерные частоты

$\begin{gathered} \tilde {\Omega }(\tau ) = \frac{{\Omega (t)}}{\lambda } = \sqrt {\left( {\frac{1}{{{{s}^{4}}(\tau )}} + \frac{k}{{\rho {{\lambda }^{2}}}} - \frac{{{{P}_{0}}(\gamma + r(\tau ))}}{{{{s}^{2}}(\tau )}}} \right)} , \\ \tilde {\omega }(\tau ) = \frac{{\omega (t)}}{\lambda } = \frac{{\pi \nu }}{{s(\tau )}}. \\ \end{gathered} $

При этом получим

(10)

$\beta (\tau ) = C\frac{{(\tilde {\Omega }\sin (\psi + \tilde {\omega }\tau ) - \tilde {\Omega }\sin \psi \cos \tilde {\Omega }\tau - \tilde {\omega }\cos \psi \sin \tilde {\Omega }\tau )}}{{{{s}^{2}}\tilde {\Omega }({{{\tilde {\Omega }}}^{2}} - {{{\tilde {\omega }}}^{2}})}},$

где C = $\frac{D}{{{{l}^{2}}{{\lambda }^{2}}}}$.

Нелинейное уравнение Φ(s, τ) = 0 решаем численно следующим образом: фиксируем s = ${{s}_{*}}$ (0 < ${{s}_{*}}$ < 1, строим зависимость Φ(${{s}_{*}}$, τ) = 0 и отыскиваем первый корень этого уравнения τ = ${{\tau }_{*}}$. Таким образом, находим зависимость s = s(τ), а далее последовательно вычисляем $\tilde {\Omega }$(τ), $\tilde {\omega }$(τ), β(τ) и прогиб в любой момент времени τ и в любом сечении s.

На рис. 2 показаны зависимости длины интервала s(τ), полученные из условия (9) при различных значениях параметров.

Рис. 2.

Зависимость длины переменного интервала от времени. а – продольная сила P₀ = 0, б – продольная сила P₀ = 3. 1, 2, 3 – длины интервалов s(τ) при соответствующих скоростях ν = $\frac{{0.1}}{\pi }$, ν = $\frac{{0.25}}{\pi }$, ν = $\frac{{0.5}}{\pi }$, 4, 5, 6 – путь ντ, пройденный нагрузкой при тех же скоростях.

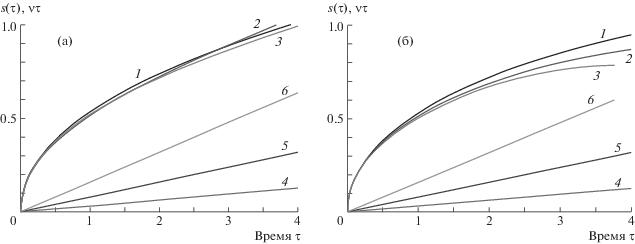
Из рис. 2 видно, что характер зависимости длины интервала от времени имеет вид $\sqrt t $, что соответствует известным результатам [13]. Температура (продольная сила) и скорость движения источника достаточно слабо влияют на зависимость длины переменного интервала от времени.

На рис. 3 представлены зависимости частот $\tilde {\Omega }$(τ) и $\tilde {\omega }$(τ) от времени для разных значений продольной силы и скорости движения.

Рис. 3.

Зависимости частот $\tilde {\Omega }$ и $\tilde {\omega }$ от времени τ. а – продольная сила P₀ = 0 , б – продольная сила P₀ = 3. 1, 2, 3 – частота $\tilde {\Omega }$(τ) при соответствующих скоростях ν = $\frac{{0.1}}{\pi }$, ν = $\frac{{0.25}}{\pi }$, ν = $\frac{{0.5}}{\pi }$, 4, 5, 6 – частота $\tilde {\omega }$(τ) при тех же значениях скорости.

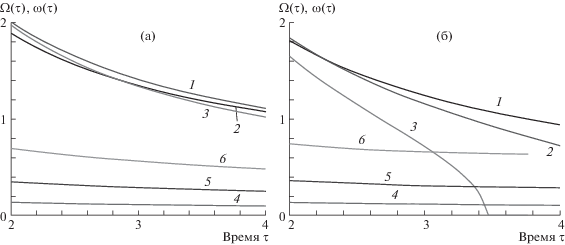
Видно, что при отсутствии продольной силы скорость движения нагрузки мало влияет на величину частоты $\tilde {\Omega }$(τ), однако наличие продольной силы может привести к ситуации, когда $\tilde {\Omega }$(τ) достигает нулевого значения.

На рис. 4 показано изменение во времени прогиба в центре балки при различных параметрах.

Рис. 4.

Изменение амплитуды прогиба в центре балки от времени. а – продольная сила P₀ = 0, б – продольная сила P₀ = 3. 1, 2, 3 – прогиб в центре балки при соответствующих скоростях ν = $\frac{{0.1}}{\pi }$, ν = $\frac{{0.25}}{\pi }$, ν = $\frac{{0.5}}{\pi }$.

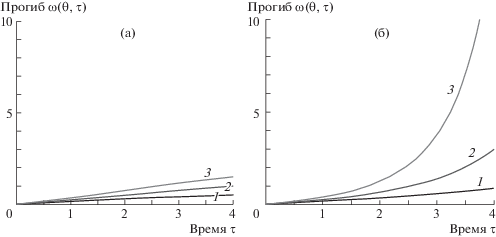
Наличие продольной силы, как следует из рис. 4, может привести к значительному росту прогиба, при этом наибольший рост прогиба наблюдается при тех же значениях параметров, для которых $\tilde {\Omega }$(τ) стремится к нулю.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ

Решена задача о распространении волны прогиба при движении теплового источника и проведен анализ влияния тепловых изгибающего момента и продольной силы.

Сосредоточенный изгибающий момент, движущийся вместе с границей нагретой области, определяет форму волны прогиба, но не может привести к значительному росту ее амплитуды.

В работе показано, что среднее значение продольной сжимающей силы линейно растет во времени при равномерном движении источника нагрева. Выявлены значения исходных параметров – скорости движения источника и температуры, при достижении которых возможна потеря устойчивости и значительный рост прогиба.

Для последующего анализа посткритической динамики следует учитывать нелинейное слагаемое в уравнении изгиба, обусловленное дополнительным растяжением, возникающим вследствие удлинения стержня при его изгибе.

Список литературы

Муратиков К.Л. Теория и методы лазерной диагностики материалов, основанные на генерации акустических и тепловых волн. Диссертация д.ф.-м.н. Физ.-техн. ин-т им. А.Ф. Иоффе РАН. 2008.
Pan Y., Rossignol C., Audoin B. Acoustic Waves Generated By a Laser Line Pulse in Cylinders; Application to the Elastic Constants Measurement // J. Acoust. Soc. Am. 2004. № 115.
Champion A., Bellouard Y. Direct Volume Variation Measurements in Fused Silica Specimens Exposed to Femtosecond Laser // Optical Materials Express. 2012. V. 2. № 6.
Zook J.D., et al. Optically Excited Self-Resonant Microbeams // Sensors and Actuators. A. 1996. № 52.
Phinney L.M., et al. Damage of MEMS Thermal Actuators Heated By Laser Irradiation / Proc. SPIE. 2005. V. 5716.
Serrano J.R., Phinney L.M. Displacement and Thermal Performance of Laser-Heated Asymmetric MEMS Actuators // J. Microelectromechanical Systems. 2008. V. 17. № 1.
Mai A., et al. In Situ Bow Change of Al-alloy MEMS Micromirrors During 248-nm Laser Irradiation // J. Micro/Nanolith. MEMS MOEMS. 2016. V. 15.
Yang T., Bellouard Y. Laser-Induced Transition between Nonlinear and Linear Resonant Behaviors of a Micromechanical Oscillator // Physical Review Applied. 2017. №. 7.
Dolleman R.J. Opto-thermally Excited Multimode Parametric Resonance in Graphene Membranes // Nature Scientific Reports. 2018. № 8.
Daining Fang, Soh A.K. Laser-induced Vibrations of Microbeams under Different Boundary Conditions // Intern. J. Solids and Structures 45 (2008) 1993–2013.
Морозов Н.Ф., Индейцев Д.А., Лукин А.В., Попов И.А., Привалова О.В., Штукин Л.В. Устойчивость балки Бернулли-Эйлера в связанных электрических и тепловых полях // ДАН. 2018. Т. 481. № 6. С. 619–624.
Морозов Н.Ф., Товстик П.Е. О динамической потере устойчивости стержня при продольной нагрузке, меньшей эйлеровой // ДАН. 2013. Т. 453. № 3. С. 282–285.
Слепян Л.И. Нестационарные упругие волны. Л.: Судостроение, 1972.
Фридман В.М. Теория упругих колебаний. Уравнения и методы. СПб.: Наука, 2014. 254 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал