1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Физика, технические науки
  4. T. 490, № 1, 2020

Доклады Российской академии наук. Физика, технические науки, 2020, T. 490, № 1, стр. 18-23

Модель адсорбции гелия и паров воды пористым композитным сорбентом на основе микросфер

А. С. Верещагин 1, 2, 3, *, В. Н. Зиновьев 1, И. В. Казанин 1, 2, А. Ю. Пак 1, В. А. Лебига 1, 2, 3, академик РАН В. М. Фомин 1, 2, 3

1 Институт теоретической и прикладной механики им. С.А. Христиановича Сибирского отделения Российской академии наук
Новосибирск, Россия

2 Новосибирский государственный университет
Новосибирск, Россия

3 Новосибирский государственный технический университет
Новосибирск, Россия

* E-mail: vereshchag@itam.nsc.ru

Поступила в редакцию 23.09.2019
После доработки 23.09.2019
Принята к публикации 11.11.2019

Полный текст (PDF)

Аннотация

В рамках подхода механики многофазных сред предложен вывод математической модели динамики смеси газов, включая гелий и пары воды, в слое покоящегося композитного сорбента на основе микросфер и пористой матрицы поглотителя влаги из оксида алюминия. Доказано, как можно согласовать течение в пористой среде адсорбера и диффузию газов в цилиндрической грануле адсорбента с учетом адсорбции гелия микросферами и паров воды пористой поверхностью адсорбента.

Ключевые слова: композитный сорбент, гелий, пары воды, микросферы, мембранно-сорбционный метод

ВВЕДЕНИЕ

В наши дни единственным практическим источником гелия является природный газ, выделения гелия из которого проводится преимущественно по криогенной технологии, которая является дорогой, материало- и энергоемкой и эффективна только при переработке больших объемов сырья. Альтернативные технологии – мембранная и адсорбционная – практически не применяются в промышленных установках, поскольку не могут обеспечить необходимую производительность.

Исключительно высокая селективность мембран из кварцевого стекла по гелию известна достаточно давно. Коэффициент проницаемости кварцевого стекла для гелия превышает таковой для метана на семь порядков (${{L}_{{{\text{He}}}}}\, = \,3.26\, \times \,{{10}^{{ - 15}}}$ моль м/(м2 ⋅ с ⋅ Па); ${{L}_{{{\text{C}}{{{\text{H}}}_{4}}}}} = 6.38 \times {{10}^{{ - 22}}}$ моль м/(м2 ⋅ с ⋅ Па)). Однако использованию кварца или других силикатных материалов в качестве привычных плоских, или капиллярно-трубчатых мембран проблематично из-за низкой скорости диффузии гелия, сложности в организации большой поверхности массообмена и эксплуатации мембран при большой разнице давления по разные их стороны.

Авторами был предложен пионерский подход в создании материалов, селективно поглощающих гелий, который совмещает одновременно мембранную и сорбционную технологии. В качестве мембранных элементов предлагается использовать полые стеклянные микросферы. Вследствие селективной проницаемости некоторых стекол гелий диффундирует в полость микросферы из-за разности парциальных давлений гелия внутри и снаружи микросферы. Размеры частиц позволяют создать большую поверхность массообмена, а сферическая форма обеспечивает высокую гидростатическую прочность.

1. КОМПОЗИТНЫЙ СОРБЕНТ

Для этой цели специально совместно с Центром новых химических технологий ИК СО РАН (Омский филиал) создается композитный сорбент. В качестве проницаемого для гелия компонента композитного сорбента используются синтетические стеклянные микросферы, связующим материалом служит гидроксид алюминия – псевдобемит. Синтез композитных сорбентов осуществляется методом формовки гидроксида алюминия с микросферами с использованием экструдера. Формованные образцы сначала проявляются на воздухе, затем сушатся и далее прокаливаются при более высокой температуре. При такой обработке гидроксид алюминия переходит в гамма-оксид алюминия (γ-Al2O3), иначе называемый активным оксидом алюминия, с развитой пористостью и большой удельной поверхностью, который находит широкое применение в качестве сорбента для осушки различных газовых и жидких сред [1]. Содержание микросфер в композитном сорбенте составляет 15% по массе, так как при такой массовой доле проницаемого компонента достигается оптимальное соотношение текстурных и прочностных характеристик сорбента. Гранулирование микросфер в цилиндрические гранулы из псевдобемита позволяет решить сразу несколько задач: во-первых, добиться оптимального размера гранул для засыпки в промышленный адсорбер, во-вторых, позволяет реализовать одновременно с удержанием гелия удаление паров воды из газовой смеси [2].

Динамика смеси газов через такой сорбент связана с прохождением газа между гранулами, а также диффузии внутрь гранул, адсорбции паров воды на влагопоглотителе и диффузии гелия внутрь микросфер (рис. 1). Такого рода течения можно описывать моделями с двойной пористостью, как, например, [3, 4], в которой имеется фильтрация газа сквозь гранулы в свободном объеме адсорбера 1 и свободном объеме гранулы 2 (рис. 1). Однако пористая структура композитного сорбента состоит в основном из мезопор с характерными размерами каналов до 200 нм [2], что обусловливает использование механизма кнудсеновской диффузии для описании течения газа внутри гранулы.

Рис. 1.

Структурные уровни при описании динамики смеси газов через адсорбер с композитным сорбентом: 1 – объем адсорбера, занятый цилиндрическими гранулами; 2 ' – объем, занятый цилиндрическими гранулами; 2 – свободное пространство внутри гранулы; 3 – внутренний объем полостей микросфер в грануле; 4 – объем, занятый пористой матрицей в грануле.

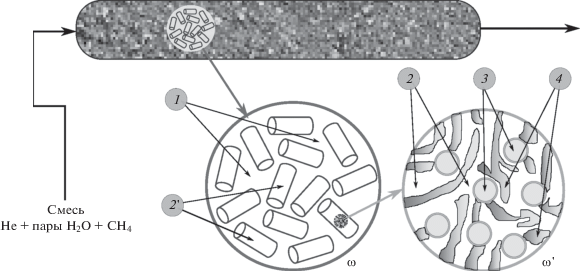
2. ОСНОВНЫЕ МЕХАНИЗМЫ МАССОПЕРЕНОСА В АДСОРБЕРЕ

Рассмотрим течение газовой смеси, состоящей из гелия, паров воды и метана (или любого другого газа, не взаимодействующего с сорбентом) через слой покоящихся гранул, распределенных равномерно в исследуемой области. Для описания такой среды воспользуемся методом взаимопроникающих континуумов, использующих осреднение по объему [5–7]. По аналогии с [8] будут осредняться по объему законы сохранения массы в исследуемых областях (рис. 1).

Будем рассматривать изотермическую модель, не учитывающую термические эффекты адсорбции, и влияние температуры на процесс диффузии, проницаемость микросфер и характер течения внутри адсорбера. Чтобы учесть все указанные явления, необходимо добавить к модели закон сохранения энергии и законы влияния температуры на указанные процессы, что будет сделано в дальнейшем.

Следуя работам [6, 7], определим “достаточно большой” макрообъем $\omega $ в окрестности произвольно выбранной точки $\xi $ внутри адсорбера (рис. 1). Пусть ${{\omega }_{1}}$ – свободный объем адсорбера, ${{\omega }_{2}}$ – объем цилиндрических гранул, ${{s}_{{12}}}$ – поверхность цилиндрических гранул сорбента внутри $\omega $. Введем объемные концентрации ${{m}_{1}}$, ${{m}_{2}}$ и удельную поверхность ${{\alpha }_{{12}}}$ в заданной точке по формулам

(1)
${{m}_{1}} = \frac{{{{\omega }_{1}}}}{\omega },\quad {{m}_{2}} = \frac{{{{\omega }_{2}}^{'}}}{\omega },\quad {{\alpha }_{{12}}} = \frac{{{{s}_{{12}}}}}{\omega }.$

Из геометрических соображений нетрудно установить следующие соотношения между величинами:

(2)
$\begin{gathered} {{m}_{2}} = 1 - {{m}_{1}} = \frac{{k{{V}_{p}}}}{\omega },\quad {{\alpha }_{{12}}} = \frac{{k{{S}_{p}}}}{\omega }, \\ {{V}_{p}} = \frac{{\pi d_{p}^{2}{{L}_{p}}}}{4},\quad {{S}_{p}} = \pi {{d}_{p}}\left( {\frac{{{{d}_{p}}}}{{2 + L}}} \right), \\ \end{gathered} $
где ${{V}_{p}}$, ${{S}_{p}}$ – объем и площадь поверхности цилиндрической гранулы длины ${{L}_{p}}$ и диаметра ${{d}_{p}}$; $k$ – число цилиндрических гранул в $\omega $.

В дальнейшем параметры ${{m}_{1}}$, $k$, ${{\alpha }_{{12}}}$, $L$, $d$ считаются постоянными, что вполне обосновано в большинстве приложений.

Динамика истинной плотности каждой из компонент газовой смеси в свободном объеме адсорбера описывается уравнением с граничными условиями

(3)
$\begin{gathered} \frac{{\partial {{\rho }_{{1i}}}}}{{\partial t}} + {\text{div}}{{\rho }_{{1i}}}{{{\mathbf{v}}}_{1}} = 0, \\ {{\rho }_{{1i}}}{{{\mathbf{v}}}_{i}} \cdot {\mathbf{n}}{{{\text{|}}}_{{{{\Gamma }_{{12}}}}}} = - {{D}_{i}}\nabla {{\rho }_{{2i}}} \cdot {\mathbf{n}}{{{\text{|}}}_{{{{\Gamma }_{{12}}}}}}\quad (i = 1,2,3), \\ \end{gathered} $
где ${{\rho }_{{1i}}}$, ${{\rho }_{{2i}}}$ – истинная плотность гелия, паров воды и метана в адсорбере и свободном объеме и гранулах соответственно ($i = 1,2,3$); ${{{\mathbf{v}}}_{1}}$ – истинная скорость компонент газа в адсорбере; Γ12 – межфазная поверхность между гранулами и свободным объемом; ${\mathbf{n}}$ – вектор внешней единичной нормали к Γ12; ${{D}_{i}}$ – коэффициент кнудсеновской диффузии i-й фазы. Последнее условие в (3) выражает тот факт, что поток газа в цилиндрическую частицу равен диффузионному потоку на фазовой границе.

Соотношение для скорости фильтрации может быть записано исходя из условий решаемой задачи. В самом простом случае при очень медленных течениях в коротких адсорберах ее можно положить константой. В более сложных ситуациях можно использовать соотношения для фильтрации Дарси, Форхгеймера или их нестационарные аналоги с учетом конвективного переноса.

После осреднения уравнения с граничными условиями (3) по пространству получим

(4)
$\begin{gathered} \frac{{\partial \mathop {\left\langle {{{\rho }_{{1i}}}} \right\rangle }\nolimits^1 }}{{\partial t}} + \mathop {{\text{div}}}\nolimits_\xi \mathop {\left\langle {{{\rho }_{{1i}}}{{{\mathbf{v}}}_{1}}} \right\rangle }\nolimits^1 = - {{\alpha }_{{12}}}\mathop {\left\langle {{{\rho }_{{1i}}}{{{\mathbf{v}}}_{i}} \cdot {\mathbf{n}}} \right\rangle }\nolimits_{{{s}_{{12}}}} \\ (i = 1,2,3), \\ \end{gathered} $
где
(5)
$\begin{gathered} \mathop {\left\langle {\varphi (t,{\mathbf{x}})} \right\rangle }\nolimits_i (t,\xi ) = \frac{1}{{{{\omega }_{i}}(\xi )}}\int\limits_{{{\omega }_{i}}(\xi )} \,\varphi (t,{\mathbf{x}})d{\mathbf{x}}, \\ \mathop {\left\langle {\varphi (t,{\mathbf{x}})} \right\rangle }\nolimits^i (t,\xi ) = \frac{1}{\omega }\int\limits_{{{\omega }_{i}}(\xi )} \,\varphi (t,{\mathbf{x}})d{\mathbf{x}}, \\ \end{gathered} $
(6)
$\mathop {\left\langle {\varphi (t,{\mathbf{x}})} \right\rangle }\nolimits_{{{s}_{{ij}}}} (t,\xi ) = \frac{1}{{{{s}_{{ij}}}(\xi )}}\int\limits_{{{s}_{{ij}}}(\xi )} \,\varphi (t,{\mathbf{x}})d{\mathbf{x}},$
где φ – скалярная, векторная или тензорная величина, определенная в исследуемой области ${{\omega }_{i}}$ и межфазной поверхности между i-й и j-й фазами ${{s}_{{ij}}}$. Первый интеграл соответствует среднему значению параметра $\varphi $ внутри объема ${{\omega }_{i}}$, второй – “размазанному значению” по всему $\omega $, а третий – среднему значению на межфазной границе ${{s}_{{ij}}}$.

Пренебрегая пульсациями ${{\rho }_{{1i}}}$ и ${{{\mathbf{v}}}_{1}}$ внутри ${{\omega }_{1}}$, получим

(7)
$\mathop {\left\langle {{{\rho }_{{1i}}}{{{\mathbf{v}}}_{1}}} \right\rangle }\nolimits^1 \approx \mathop {\left\langle {{{\rho }_{{1i}}}} \right\rangle }\nolimits^1 \mathop {\left\langle {{{{\mathbf{v}}}_{1}}} \right\rangle }\nolimits_1 ,$
а правую часть в (4) можно оценить, используя граничное условие из (3), как
(8)
${{\alpha }_{{12}}}\mathop {\left\langle {{{\rho }_{{1i}}}{{{\mathbf{v}}}_{i}} \cdot {\mathbf{n}}} \right\rangle }\nolimits_{{{s}_{{12}}}} \approx - \frac{k}{\omega }\int\limits_{{{S}_{g}}} {{{D}_{i}}\nabla {{\rho }_{{2i}}} \cdot {\mathbf{n}}dS} ,$
где Sg – поверхность некоторой гранулы, характеризующей состояние всех гранул в окрестности выбранной точки $\xi $ внутри объема $\omega $.

3. ОСНОВНЫЕ МЕХАНИЗМЫ МАССОПЕРЕНОСА ГАЗОВ В ГРАНУЛАХ

Рассмотрим диффузию газа внутри цилиндрической частицы с учетом его массообмена с внешней средой адсорбера и взаимодействия с внутренней структурой гранулы (для гелия это поглощение микросферами, для паров воды – адсорбция на поверхности пористой матрицы, для метана – отсутствие взаимодействия).

Диффузия истинной плотности газов в грануле в объеме 2 (рис. 1) описывается следующими уравнениями:

(9)
$\frac{{\partial {{\rho }_{{2i}}}}}{{\partial t}} = {{D}_{i}}\Delta {{\rho }_{{2i}}}\quad (i = 1,2,3).$

Проанализируем граничные условия для гелия, паров воды и метана.

Для гелия граничные условия имеют вид

(10)
$\begin{gathered} {{\rho }_{{21}}}{{{\text{|}}}_{{{{\Gamma }_{{12}}}}}} = {{\rho }_{{11}}}{{{\text{|}}}_{{{{\Gamma }_{{12}}}}}}, \\ - {{D}_{1}}\nabla {{\rho }_{{21}}} \cdot {\mathbf{n}}{{{\text{|}}}_{{{{\Gamma }_{{23}}}}}} = \frac{{{{C}_{m}}\beta }}{d}\left( {\mathop {\left\langle {{{p}_{{31}}}} \right\rangle }\nolimits_3 - \mathop {\left\langle {{{p}_{{21}}}} \right\rangle }\nolimits_2 } \right), \\ - {{D}_{1}}\nabla {{\rho }_{{21}}} \cdot {\mathbf{n}}{{|}_{{{{\Gamma }_{{24}}}}}} = 0, \\ \end{gathered} $
где Γ12 – граница между внутренним свободным объемом цилиндрической гранулы и внешним свободным объемом адсорбера; Γ23 – поверхность микросфер внутри гранулы; Γ24 – поверхность пористой матрицы гранулы; ${{C}_{m}}$ – коэффициент проницаемости стенки микросферы; $\beta = \frac{r}{R}$ – коэффициент структуры микросферы; $r$, $R$, $d$ – радиус полости, радиус и толщина стенки микросферы; $\mathop {\left\langle {{{p}_{{31}}}} \right\rangle }\nolimits_3 $, $\mathop {\left\langle {{{p}_{{21}}}} \right\rangle }\nolimits_2 $ – средние значения давления гелия внутри и снаружи микросфер в окрестности заданной точки в соответствии с определением (5).

Первое условие выражает то, что истинная плотность гелия на границе цилиндрической гранулы снаружи и внутри совпадают; второе условие – поток массы через поверхность микросфер пропорционален разности средних давлений внутри микросферы и снаружи; третье условие – гелий не адсорбируется на поверхности пористой ма-трицы.

Гелий, поглощенный микросферами, учитывается следующим образом:

(11)
$\frac{\partial }{{\partial t}}({{V}_{m}}{{\rho }_{{31}}}) = - \frac{{{{C}_{m}}{{S}_{m}}\beta }}{d}\left( {\mathop {\left\langle {{{p}_{{31}}}} \right\rangle }\nolimits_3 - \mathop {\left\langle {{{p}_{{21}}}} \right\rangle }\nolimits_2 } \right),$
где ${{\rho }_{{31}}}$ – истинная плотность гелия в выбранной микросфере; ${{V}_{m}} = \frac{4}{3}\pi {{r}^{3}}$ – объем полости микросферы; ${{S}_{m}} = 4\pi {{R}^{2}}$ – площадь поверхности микросферы.

Истинные давления гелия в ${{\omega }_{2}}$ и ${{\omega }_{{31}}}$ определяются из соотношений

${{p}_{{21}}} = {{\rho }_{{21}}}{{R}_{1}}T,\quad {{p}_{{31}}} = {{\rho }_{{31}}}{{R}_{1}}T,$
где $T$ – температура среды; ${{R}_{1}}$ – газовая постоянная для гелия.

Для паров воды граничные условия имеют вид

(12)
$\begin{gathered} {{\rho }_{{22}}}{{{\text{|}}}_{{{{\Gamma }_{{12}}}}}} = {{\rho }_{{12}}}{{{\text{|}}}_{{{{\Gamma }_{{12}}}}}},\quad - {{D}_{2}}\nabla {{\rho }_{{22}}} \cdot {\mathbf{n}}{{{\text{|}}}_{{{{\Gamma }_{{23}}}}}} = 0, \\ - {{D}_{2}}\nabla {{\rho }_{{22}}} \cdot {\mathbf{n}}{{{\text{|}}}_{{{{\Gamma }_{{24}}}}}} = {{\beta }_{w}}\left( {\mathop {\left\langle {{{\rho }_{{42}}}} \right\rangle }\nolimits_{{{s}_{{24}}}} - a\left( {\mathop {\left\langle {{{\rho }_{{22}}}} \right\rangle }\nolimits_2 ,T} \right)} \right), \\ \end{gathered} $
где βw – скорость установления равновесия между адсорбировавшимися и не адсорбировавшимися парами воды; $\mathop {\left\langle {{{\rho }_{{22}}}} \right\rangle }\nolimits_2 $ – среднее значение истинной плотности паров воды в окрестности точки в смысле определения (5); $a = a(\rho ,T)$ – изотерма адсорбции; $T$ – температура среды.

Первое условие выражает то, что истинная плотность паров воды на границе цилиндрической гранулы снаружи и внутри совпадают; второе условие – пары воды не проникают в микросферы; третье условие определяет закон адсорбции воды на пористой матрице адсорбента.

Масса адсорбировавшихся паров воды на поверхности сорбента ${{s}_{{24}}}$ внутри $\omega {\text{'}}$ учитывается в виде

$\frac{{\partial {{\rho }_{{42}}}}}{{\partial t}} = - {{\beta }_{w}}\left( {\mathop {\left\langle {{{\rho }_{{42}}}} \right\rangle }\nolimits_{{{s}_{{24}}}} - a\left( {\mathop {\left\langle {{{\rho }_{{22}}}} \right\rangle }\nolimits_2 ,T} \right)} \right).$

Для метана граничные условия имеют вид

(13)
$\begin{gathered} {{\rho }_{{22}}}{{{\text{|}}}_{{{{\Gamma }_{{12}}}}}} = {{\rho }_{{12}}}{{{\text{|}}}_{{{{\Gamma }_{{12}}}}}},\quad - {{D}_{3}}\nabla {{\rho }_{{22}}} \cdot {\mathbf{n}}{{{\text{|}}}_{{{{\Gamma }_{{23}}}}}} = 0, \\ - {{D}_{3}}\nabla {{\rho }_{{22}}} \cdot {\mathbf{n}}{{{\text{|}}}_{{{{\Gamma }_{{24}}}}}} = 0. \\ \end{gathered} $

Первое условие выражает то, что истинная плотность метана на границе цилиндрической гранулы снаружи и внутри совпадают; второе условие – метан не проникает в микросферы; третье условие – метан не адсорбируется гранулой.

4. ГЕОМЕТРИЧЕСКАЯ СТРУКТУРА И СРЕДНИЕ ПАРАМЕТРЫ КОМПОЗИТНОЙ ЧАСТИЦЫ

Основные геометрические параметры внутренней структуры композитного сорбента определяются методом осреднения по объему. Для выделенного объема $\omega {\text{'}}$ в окрестности выбранной точки $\xi $ в пористой среде адсорбента можно записать

$\omega {\text{'}} = {{\omega }_{2}} \cup {{\omega }_{3}} \cup {{\omega }_{4}},\quad {{\omega }_{3}} = {{\omega }_{{31}}} \cup {{\omega }_{{32}}},$
где ${{\omega }_{2}}$, ${{\omega }_{3}}$, ${{\omega }_{4}}$ – непересекающиеся части $\omega $, определяющие свободный, занятый микросферами, заполненный твердым материалом объемы; ${{\omega }_{{31}}}$, ${{\omega }_{{32}}}$ – непересекающиеся части ${{\omega }_{3}}$, соответствующие внутренней полости и твердой стенке микросфер соответственно.

Локальные объемные концентрации фаз и удельные межфазные поверхности определяются из соотношений

(14)
$\begin{gathered} {{l}_{2}} = \frac{{{{\omega }_{2}}}}{{\omega {\text{'}}}},\quad {{l}_{3}} = \frac{{{{\omega }_{3}}}}{{\omega {\text{'}}}},\quad {{l}_{{31}}} = \frac{{{{\omega }_{{31}}}}}{{\omega {\text{'}}}}, \\ {{l}_{{32}}} = \frac{{{{\omega }_{{32}}}}}{{\omega {\text{'}}}},\quad {{l}_{4}} = \frac{{{{\omega }_{4}}}}{{\omega {\text{'}}}}, \\ \end{gathered} $
(15)
${{\alpha }_{{23}}} = \frac{{{{s}_{{23}}}}}{{\omega {\text{'}}}},\quad {{\alpha }_{{24}}} = \frac{{{{s}_{{24}}}}}{{\omega {\text{'}}}},$
где ${{s}_{{23}}}$, ${{s}_{{24}}}$ – границы фаз между свободным объемом и микросферами и свободным объемом и пористой матрицей, лежащие внутри $\omega {\text{'}}$.

В предположении, что все микросферы одинаковые и равномерно распределены внутри гранул, из геометрических соображений следует, что ${{l}_{3}}$, ${{l}_{{31}}}$, ${{l}_{{32}}}$, ${{\alpha }_{{23}}}$ постоянны и

(16)
${{l}_{3}} = {{l}_{{31}}} + {{l}_{{32}}},\quad {{l}_{{31}}} = {{\beta }^{3}}{{l}_{3}},\quad {{l}_{{32}}} = (1 - {{\beta }^{3}}){{l}_{3}},$
(17)
${{\alpha }_{{23}}} = \frac{3}{R}{{l}_{3}},$
где $R$, $r$ – радиус микросферы и ее полости; $\beta = \frac{r}{R}$ – коэффициент структуры микросферы.

Считая пористую структуру сорбента распределенной равномерно, полагаем, что параметры ${{l}_{4}}$, ${{\alpha }_{{24}}}$, а тогда и ${{l}_{2}}$, являются постоянными величинами, что также обосновано в большом количестве приложений.

5. МАССОПЕРЕНОС В ГРАНУЛЕ В ТЕРМИНАХ ОСРЕДНЕННЫХ ПЕРЕМЕННЫХ

После осреднения уравнения диффузии (9) в бесконечной среде, состоящей из микросфер и пористой матрицы [8], получим

(18)
$\begin{gathered} \frac{{\partial \mathop {\left\langle {{{\rho }_{{2i}}}} \right\rangle }\nolimits^2 }}{{\partial t}} = {{D}_{i}}{{\Delta }_{\xi }}\mathop {\left\langle {{{\rho }_{{2i}}}} \right\rangle }\nolimits^2 + \\ \, + {{D}_{i}}{\text{di}}{{{\text{v}}}_{\xi }}[{{\alpha }_{{23}}}\mathop {\left\langle {{{\rho }_{{2i}}}{\mathbf{n}}} \right\rangle }\nolimits_{{{s}_{{23}}}} + {{\alpha }_{{24}}}\mathop {\left\langle {{{\rho }_{{2i}}}{\mathbf{n}}} \right\rangle }\nolimits_{{{s}_{{24}}}} ] + \\ \, + {{\alpha }_{{23}}}{{D}_{i}}\mathop {\left\langle {{{\nabla }_{{\mathbf{x}}}}{{\rho }_{{2i}}} \cdot {\mathbf{n}}} \right\rangle }\nolimits_{{{s}_{{23}}}} + {{\alpha }_{{24}}}{{D}_{i}}\mathop {\left\langle {{{\nabla }_{{\mathbf{x}}}}{{\rho }_{{2i}}} \cdot {\mathbf{n}}} \right\rangle }\nolimits_{{{s}_{{24}}}} \\ (i = 1,2,3). \\ \end{gathered} $

Показано [8], что выражения под оператором дивергенция во втором слагаемом в правой части (18) при разложении в ряд внутри $\omega {\text{'}}$ в первом приближении равен

(19)
${{\alpha }_{{23}}}\mathop {\left\langle {{{\rho }_{{2i}}}{\mathbf{n}}} \right\rangle }\nolimits_{{{s}_{{23}}}} + {{\alpha }_{{24}}}\mathop {\left\langle {{{\rho }_{{2i}}}{\mathbf{n}}} \right\rangle }\nolimits_{{{s}_{{24}}}} \approx - \mathop {\left\langle {{{\rho }_{{2i}}}} \right\rangle }\nolimits_2 \nabla {{l}_{2}}.$

Эти слагаемые описывают внутреннюю структуру распределения фаз внутри $\omega {\kern 1pt} '$. Учитывая постоянство объемной концентрации ${{l}_{2}}$, ими можно пренебречь.

Четвертое и пятое слагаемые в (18) определяются из условий массообмена между фазами (10), (12) и (13).

6. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Рассмотрим течение смеси гелия, метана и паров воды через пористую среду, созданную композитным сорбентом в некоторой области пространства $\Omega $ (адсорбер). Математическая модель с учетом сделанных выкладок будет записываться с использованием осредненных переменных. Для того чтобы не загромождать выкладки, введем следующие замены:

$\begin{gathered} \mathop {\left\langle {{{\rho }_{{1i}}}} \right\rangle }\nolimits^1 \to {{\rho }_{{1i}}},\quad \mathop {\left\langle {{{\rho }_{{2i}}}} \right\rangle }\nolimits^2 \to {{\rho }_{{2i}}},\quad \mathop {\left\langle {{{\rho }_{{31}}}} \right\rangle }\nolimits^3 \to {{\rho }_{{31}}}, \\ \mathop {\left\langle {{{\rho }_{{42}}}} \right\rangle }\nolimits_{{{s}_{{42}}}} \to {{\rho }_{{42}}},\quad \mathop {\left\langle {{{{\mathbf{v}}}_{1}}} \right\rangle }\nolimits_1 \to {{{\mathbf{v}}}_{1}}. \\ \end{gathered} $

Параметры ${{\rho }_{{1i}}}$, ${{{\mathbf{v}}}_{1}}$ являются функциями от $(t,{\mathbf{x}})$, где ${\mathbf{x}} \in \Omega $, $t > 0$ – время. В каждой точке пространства внутри макрообъема задается массообмен между свободным объемом адсорбера и адсорбентом. Таким образом, параметры ${{\rho }_{{2i}}}$ (i =1, 2, 3), ${{\rho }_{{31}}}$, ${{\rho }_{{42}}}$ являются функциями от $(t,{\mathbf{x}},\xi )$, где ${\mathbf{x}} \in \Omega $, $\xi \in G$, где $G$ – геометрическое место точек, ограниченное цилиндром ${{S}_{g}}$ длины ${{L}_{p}}$ и диаметром ${{d}_{p}}$.

Динамика смеси газов в адсорбере $\Omega $ имеет вид

(20)
$\begin{gathered} \frac{{\partial {{\rho }_{{1i}}}}}{{\partial t}} + {\text{di}}{{{\text{v}}}_{{\mathbf{x}}}}{{\rho }_{{1i}}}{{{\mathbf{v}}}_{1}} = {{K}_{{1i}}}, \\ {{K}_{{1i}}} = - {{D}_{i}}\frac{{{{m}_{2}}}}{{{{V}_{p}}}}\int\limits_{{{S}_{g}}} {{{\nabla }_{\xi }}{{\rho }_{{2i}}} \cdot {\mathbf{h}}ds} \quad (i = 1,2,3). \\ \end{gathered} $

Динамика гелия внутри композитного сорбента в области $G$ задается следующими соотношениями:

(21)
$\begin{gathered} \frac{{\partial {{\rho }_{{21}}}}}{{\partial t}} = {{D}_{1}}{{\Delta }_{\xi }}{{\rho }_{{21}}} + \frac{{3{{l}_{3}}{{C}_{m}}\beta }}{{Rd}}\left( {\frac{{{{\rho }_{{31}}}}}{{{{l}_{{31}}}}} - \frac{{{{\rho }_{{21}}}}}{{{{l}_{2}}}}} \right), \\ \frac{{\partial {{\rho }_{{31}}}}}{{\partial t}} = - \frac{{3{{l}_{3}}{{C}_{m}}\beta }}{{Rd}}\left( {\frac{{{{\rho }_{{31}}}}}{{{{l}_{{31}}}}} - \frac{{{{\rho }_{{21}}}}}{{{{l}_{2}}}}} \right), \\ \end{gathered} $
при этом

${{\rho }_{{21}}}{{{\text{|}}}_{{{{S}_{g}}}}} = \frac{{{{\rho }_{{11}}}{{l}_{2}}}}{{{{m}_{1}}}}.$

Динамика паров воды внутри композитного сорбента в области $G$ задается следующими соотношениями:

(22)
$\begin{gathered} \frac{{\partial {{\rho }_{{22}}}}}{{\partial t}} = {{D}_{2}}{{\Delta }_{\xi }}{{\rho }_{{22}}} + {{\alpha }_{{24}}}{{\beta }_{w}}\left( {{{\rho }_{{42}}} - a\left( {\frac{{{{\rho }_{{22}}}}}{{{{l}_{2}}}},T} \right)} \right), \\ \frac{{\partial {{\rho }_{{42}}}}}{{\partial t}} = - {{\beta }_{w}}\left( {{{\rho }_{{42}}} - a\left( {\frac{{{{\rho }_{{22}}}}}{{{{l}_{2}}}},T} \right)} \right), \\ \end{gathered} $
при этом

${{\rho }_{{22}}}{{{\text{|}}}_{{{{S}_{g}}}}} = \frac{{{{\rho }_{{12}}}{{l}_{2}}}}{{{{m}_{1}}}}.$

Динамика метана внутри композитного сорбента в области $G$ задается следующими соотношениями:

(23)
$\frac{{\partial {{\rho }_{{23}}}}}{{\partial t}} = {{D}_{3}}{{\Delta }_{\xi }}{{\rho }_{{23}}},$
при этом

${{\rho }_{{23}}}{{{\text{|}}}_{{{{S}_{g}}}}} = \frac{{{{\rho }_{{13}}}{{l}_{2}}}}{{{{m}_{1}}}}.$

ЗАКЛЮЧЕНИЕ

В рамках явлений, описанных в [2], показавших возможность создания технологии выделения гелия из природного газа на основе композитного адсорбента из микросфер, в работе получена математическая модель, описывающая динамику смеси газов гелия, метана и паров воды через пористую среду, состоящую из цилиндрических гранул композитного адсорбента, способного удерживать и впоследствии выделять гелий и пары воды.

Список литературы

  1. Кельцев Н.В. Основы адсорбционной техники. М.: Химия, 1984.

  2. Зиновьев В.Н. и др. О совместном выделении паров воды и гелия из природного газа // Теплофизика и аэромеханика. 2016. Т. 23. № 5. С. 771–777. https://doi.org/10.1134/S0869864316050127

  3. Лобковский Л.И., Рамазанов М.М. К теории фильтрации в среде с двойной пористостью // ДАН. 2019. Т. 484. № 3. С. 348–351. https://doi.org/10.31857/S0869-56524843348-351

  4. Баренблатт Г.И., Лобковский Л.И., Нигматулин Р.И. Математическая модель истечения газа из газонасыщенного льда и газогидратов // ДАН. 2016. Т. 470. № 4. С. 458–461. https://doi.org/10.7868/s0869565216280148

  5. Рахматулин Х.А. Основы газодинамики взаимопроникающих движений сжимаемых сред // ПММ. 1956. Т. 20. № 2. С. 184–195.

  6. Нигматулин Р.И. Динамика многофазных сред. Ч. I. М.: Наука. Гл. ред. физ.-мат. лит., 1987.

  7. Whitaker S. The Method of Volume Averaging. Dordrecht: Springer Science+Business Media, 1999. P. 220.

  8. Верещагин А.С., Фомин В.М. Математическая модель движения смеси газов и полых избирательно проницаемых микросфер // Прикладная механика и техническая физика. 2015. Т. 56. № 5. С. 5–17. https://doi.org/10.15372/PMTF20150501

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал