Доклады Российской академии наук. Физика, технические науки, 2020, T. 492, № 1, стр. 68-72

МЕТОДОЛОГИЯ И ФИЗИЧЕСКАЯ СИСТЕМА

В качестве физической системы рассматривались сферический кластер кремния Si и карбида кремния, имеющего структуру цинковой обманки (кубическая форма 3C-SiC). Диаметр кластеров изменялся в широком диапазоне значений (от 3 до 22 нм для карбида кремния и от 4 до 33 нм для кремния).

Кристаллический кластер, вписанный в сферу определенного радиуса, вырезался из идеального кубического образца, при этом диагональ этого куба, проходящая через начало координат, совпадала с направлением [1, 1, 1 ]. Полученная система имеет не совсем сферическую форму, но для простоты в дальнейшем мы будем использовать термин сферический кластер.

Интегрирование уравнения движения проводилось с использованием скоростной модификации схемы Верле второго порядка точности по временному шагу, а сам шаг по времени в численном расчете составлял 10^–16 с. Для численного моделирования был разработан и программно реализован параллельный алгоритм, позволяющий проводить расчеты с использованием графических процессоров (ГПУ) общего назначения компании NVIDIA, поддерживающих технологию CUDA (Compute Unified Device Architecture) [4].

Основным преимуществом метода молекулярной динамики (ММД) при моделировании процессов на микроуровне является то, что ММД не требует привлечения дополнительных моделей, как это делается в механике деформированного твердого тела. Таким образом, в основе предлагаемого подхода лежит закон Ньютона (или теория Гамильтона), при этом термодинамические и физические свойства материалов определяются потенциалом межатомного взаимодействия. Система охлаждалась при помощи метода искусственной вязкости, в результате чего ансамбль атомов в конце процесса охлаждения находился в минимуме потенциальной энергии [5]. При этом начальное состояние системы было близким к нулю (10^–7 К). В рамках классической механики при температуре системы, стремящейся к нулю, импульс также стремится к нулю. Метод молекулярной динамики не учитывает нулевые колебания системы.

В представленной работе для моделирования процесса деформирования кремния был использован потенциал Стиллинжера–Вебера [6], а для исследования свойств карбида кремния был использован потенциал, предложенный группой Вашишты [7]. Оба этих потенциала хорошо апробированы для моделирования различных ударно-волновых явлений в рассматриваемых веществах и корректно описывают процессы разрушения на микроуровне. И для кремния, и для карбида кремния потенциал межатомного взаимодействия состоит из суммы двухчастичной и трехчастичной частей:

где U – полная потенциальная энергия системы, а r_ij и r_ik – расстояние между атомами ij и ik.

В случае карбида кремния двухчастичная часть (1) включает в себя члены, отвечающие за пространственное влияние ионов, кулоновские взаимодействия, заряд диполя и ван-дер-ваальсовы взаимодействия:

константы потенциала H_ij, ${{\eta }_{{ij}}},$ Z_i, λ, ${{D}_{{ij}}},$ ξ, ${{W}_{{ij}}}$ приведены в статье [7].

Трехчастичная часть (1) ответственна за структурные трансформации под действием давления и процесс плавления:

где

Здесь B_ijk определяет прочность связи, ${{\theta }_{{ij}}}_{k}$ – угол, образованный векторами r_ij и r_ik, C_ijk ${{\bar {\theta }}_{{ijk}}},$ γ – константы, $\Theta \left( {{{r}_{0}} - r} \right)$ – функция Хевисайда, а r₀ = 2.9 Å. Значения констант, входящих в трехчастичную часть потенциала межатомного взаимодействия, приведены в статье [7].

С целью экономии вычислительных ресурсов была выполнена модификация двухчастичной части потенциала взаимодействия (2). Потенциал был обрезан на расстоянии r_c = 7.35 Å и сдвинут таким образом, чтобы и потенциал, и его производная обращались в нуль на расстоянии радиуса обрезания:

Для кремния двухчастичная часть потенциала межатомного взаимодействия (1) определяется следующим выражением:

где константы потенциала A, B, $\sigma ,\lambda ,$ $p,q,{{r}_{0}}$ можно найти в [6].

Трехчастичная часть потенциала (1) для кремния определяется как

где

Здесь ${{\theta }_{{ij}}}_{k}$ – угол, образованный векторами r_ij и r_ik, радиус обрезания r₀ = 3.77 Å, $\lambda ,$ ${{\bar {\theta }}_{{ijk}}},$ γ – константы [6].

Объемный модуль упругости является характеристикой, описывающей упругие свойства вещества под действием всестороннего сжатия, и определяется как

где V₀ – первоначальный объем, а ΔP, ΔV – изменение объема и давления.

В численном эксперименте проводилось квазистатическое сжатие первоначально охлажденного сферического кластера [4]. В качестве внешних параметров задавалось конечное сжимающее давление и величина приращения давления 0.0001 ГПа на каждом шаге (линейный рост внешнего давления).

При моделировании в рамках ММД необходимо оперировать такими характеристиками, как силы, действующие на атомы системы. Поэтому на каждом шаге интегрирования определялись силы, соответствующие прикладываемому сжимающему давлению и действующие на поверхностные атомы в направлении к центру масс кластера:

где S – площадь поверхности кластера, а N_S – число поверхностных атомов.

Поверхностные атомы кластера определялись при помощи анализа координационного числа всех атомов системы (у поверхностных атомов кремния и карбида кремния координационное число меньше четырех).

Во время всего процесса сжатия проводилось дополнительное охлаждение кластера при помощи метода искусственной вязкости. В проводимых численных экспериментах в качестве верхнего предельного значения была использована величина давления 1 ГПа. Выбор такой величины позволяет гарантированно вести речь об исследовании процессов в области упругих деформаций.

РАСЧЕТ ОБЪЕМНОГО МОДУЛЯ УПРУГОСТИ

На рис. 1 представлена временная динамика изменения объема кластера для кремния и для карбида кремния. Несмотря на то, что временной интервал приложения внешнего давления был всего 1 пс, последующее изменение объема кластера продолжалось несоизмеримо больший временной интервал.

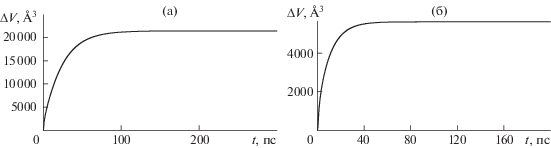
Видно, что объем кластера перестает изменяться и выходит на постоянные асимптотические значения к 80 пс для карбида кремния и в районе 200 пс для кремния. Значительную роль в установлении квазиравновесного состояния сжатого кластера играет его размер. Чем больше размер, тем больше времени требуется сжатой системе для установления конечного объема.

При определении объемного модуля упругости для маленьких кластеров принципиальное значение приобретает корректное определение объема рассматриваемой структуры. При определении объема условно больших кластеров (диаметр превышает 10 нм для карбида кремния и 15 нм для кремния) можно использовать обычное определение объема сферы. При этом радиус определяется как расстояние от центра масс системы до максимально удаленного атома, который, тем не менее, находится в пределах радиуса действия других атомов системы.

Однако по мере уменьшения диаметра кластера использование приближения сферы для определения его объема вносит значительные погрешности в определение объемного модуля упругости. По этой причине необходимо использовать более сложные подходы для определения объема кластера. В представленной работе был использован алгоритм, основанный на триангуляции Делоне и реализованный в свободно распространяемом пакете-анализаторе OVITO [9, 10 ] .

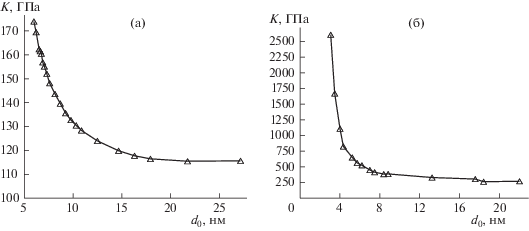
На рис. 2 представлены зависимости объемного модуля упругости от диаметра нанокластера. Зависимости для кремния и для карбида кремния показывают, что объемный модуль упругости K зависит от размера кластера и начиная с некоторого критического значения резко возрастает по мере уменьшения диаметра. Соответственно при увеличении размера значение K выходит на постоянные асимптотические значения, которые составляют: для кремния $K \approx 110$ ГПа, а для карбида кремния $K \approx 260$ ГПа. Полученные в результате молекулярно-динамического моделирования величины несколько превышают экспериментальные значения: для кремния K = 95 ГПа, а для карбида кремния K = 225 ГПа. Это связано с тем, что в качестве физической системы рассматривается идеальная бездефектная структура [6, 7].

ЗАКЛЮЧЕНИЕ

В работе предложена методология нахождения объемного модуля упругости на основании молекулярно-динамического моделирования. С помощью данной методологии были определены объемные модули упругости для кремния Si и для кубической формы карбида кремния 3C-SiC. Для обоих веществ было показано, что начиная с некоторого критического размера кластера объемный модуль упругости начинает возрастать по мере уменьшения объема структуры. Соответственно при увеличении размера структуры объемный модуль упругости стремится к постоянному асимптотическому значению, при этом отличие от экспериментальных данных находится в пределах 15–17%.