Доклады Российской академии наук. Физика, технические науки, 2020, T. 492, № 1, стр. 63-67

Очевидная тенденция в развитии физики нелинейных волн – переход от изучения эффектов слабой (W) к эффектам сильной (S) нелинейности. Это интересно, поскольку, повышая в экспериментах интенсивность волны, можно обнаружить и исследовать новые явления. Кроме того, изучение S-нелинейности важно для решения имеющихся актуальных проблем.

Прежде чем привести примеры конкретных задач, укажем на различное понимание термина S-нелинейность. На наш взгляд, ее нужно отличать от “сильно выраженной W-нелинейности” [1], которая уже много лет является основным объектом изучения в нелинейной акустике, нелинейной оптике и других разделах нелинейной физики.

Например, в акустике изучаются сигналы, для которых отношение приращения давления $p{\text{'}}$ в волне к внутреннему давлению среды ${{p}_{0}} = c_{0}^{2}{{\rho }_{0}}$ есть малая величина

Здесь c₀, ${{\rho }_{0}}$ – скорость звука и плотность среды. У воды, например, ${{p}_{0}}$ ~ 23 000 атм. Поэтому для ультразвуковых полей высокой интенсивности порядка I ~ 10 Вт/см², наиболее часто используемых в эксперименте, число $M\sim {{10}^{{ - 4}}}$ очень мало (см. [2, задачи 2.7–2.10]). Даже у весьма “сильных” одиночных импульсов, применяемых в аппаратах литотрипсии для разрушения почечных камней, давление в фокальной области насыщается на уровне порядка 1500 атм, т.е. M ~ 0.07 – нелинейность также слаба. Однако эффекты W-нелинейности могут накапливаться, если волна пробегает значительное расстояние, кратное большому числу (порядка M^–1) длин волн. При этом слабая нелинейность приводит к сильно выраженным нелинейным эффектам. Например, гладкая монохроматическая волна может трансформироваться в периодическую пилообразную волну, содержащую сотни гармоник; она, будучи слабой, сильно отличается по форме и спектральному составу от исходной волны.

Накопление может происходить не только в пространстве, но и во времени (например, в добротных резонаторах), и приводить к выраженной W-нелинейности по прошествии большого числа периодов колебаний.

В отличие от W-нелинейных эффектов, в S-волнах число M не является малым, т.е. M ~ 1 или даже M > 1. Такие значения реализуются при взрывах, а также в некоторых микронеоднородных природных или искусственных средах типа метаматериалов.

S-нелинейные волны существуют и в других физических системах. Простейший пример – волны на поверхности моря, для которых роль числа M выполняет отношение высоты гребня волны к глубине водоема. S-нелинейной может стать волна цунами при подходе к берегу, а также цунами, вызванное оползнем в мелководной бухте [3].

В последнее время большой интерес привлекают сверхсильные электромагнитные поля, создаваемые петаваттными лазерами [4]. Классическая нелинейная оптика обычно рассматривает лазерные поля, напряженность которых мала по сравнению с полем внутри атома и $M = \frac{E}{{{{E}_{{AT}}}}} \ll 1$, где ${{E}_{{AT}}}\sim \frac{e}{{r_{b}^{2}}}$ ~10¹¹ В/м, r_b – боровский радиус. В сильно нелинейных волнах поля сравнимы с внутренним полем $E\sim {{E}_{{AT}}}$. Но даже такая волна будет слабой при ее распространении в вакууме. Здесь сильной станет волна с напряженностью поля $E\sim {{E}_{{VAC}}}\sim \frac{{{{m}^{2}}{{c}^{3}}}}{{e\hbar }}\sim {{10}^{{18}}}$ В/м, в котором могут наблюдаться фундаментальные квантовые эффекты, например, рождение и аннигиляция электрон-позитронных пар.

Подведем итог: если форма (спектр) волны сравнивается со своей исходной формой (спектром) и при этом наблюдается большое различие, можно говорить о сильно выраженной W-нелинейности. Если же поле волны соотносится со значениями этого поля в среде и сравнимо с ним по величине, можно говорить об истинной S-нелинейности.

В статье [1] предложена классификация S-нелинейностей. Напомним, что в физике нелинейных волн чаще работают с W-нелинейностью, для которой “уравнения состояния” раскладываются (фактически по степеням малого M) в обычные степенные или функциональные ряды. Пример – разложение [2] адиабаты $\frac{p}{{{{p}_{0}}}} = {{\left( {\frac{\rho }{{{{\rho }_{0}}}}} \right)}^{\gamma }}$ по степеням возмущений плотности $\rho {\text{'}}$ и давления $p{\text{'}}$ в окрестности равновесного состояния $({{p}_{0}},{{\rho }_{0}})$:

В нелинейной оптике [5] рассматривают разложение вектора поляризации P по степеням отношения электрического поля к внутриатомному полю:

Здесь $\hat {\kappa }\left( \tau \right)$ – тензор линейной поляризуемости, ${{\hat {\chi }}^{{(2)}}}$, ${{\hat {\chi }}^{{(3)}}}$ – тензоры квадратичной и кубичной нелинейностей. Аналогичное (2) разложение в функциональный ряд использовал еще Вольтерра в нелинейной теории упругости.

Однако разложением в ряд неудобно пользоваться в трех случаях:

а) когда функциональные связи типа $p\left( \rho \right)$ или P(E) содержат особенности;

б) когда ряды (1), (2) расходятся в сильных полях;

в) когда в разложениях отсутствует линейный член, зато доминирует нелинейность высшего порядка. Приведем примеры таких систем первого, второго и третьего типа.

Системой 1-го типа (есть особенность) является уравнение Бюргерса с модульной ($\alpha \ne 0$, β = 0) и (или) квадратично-кубичной (α = 0, $\beta \ne 0$) нелинейностью:

Такие нелинейности встречаются во многих природных средах и метаматериалах [6]. Обратим внимание, что эффекты нелинейности не исчезают при V → 0, т.е. здесь нет перехода к линейной задаче.

Примером системы 2-го типа служит уравнение Ирншоу, описывающее (по Лагранжу) одномерное движение сжимаемой среды [2, (1.1)]:

Здесь ξ – смещение частиц сплошной среды. Приближение W-нелинейности соответствует малым деформациям $\left( {\left| {\,\frac{{\partial \xi }}{{\partial x}}\,} \right| \ll 1} \right)$. При больших отрицательных деформациях $\frac{{\partial \xi }}{{\partial x}} < - 1$ среда разрывается; это – проявление S-нелинейности. Если исходный сигнал гладкий, но усиливается, например, благодаря фокусировке, сингулярность может сформироваться при распространении волны. Аналогичное явление в жидкости называют кавитацией.

Примером системы 3-го типа служит уравнение

Оно описывает поперечные волны в системах со связями, а ранее использовалось Гейзенбергом в модели нелинейной теории поля [7].

Однако явления, связанные с S-нелинейностью, формально имеют место и в моделях, которые были получены при рассмотрении обычных W-нелинейных систем. Их изучение представляет интерес как с точки зрения математической физики, так и для анализа динамики формирования и разрушения сингулярностей различной природы.

Нетрудно проверить, что обычное уравнение Бюргерса (см., например, в обозначениях задачника [2]):

имеет точные решения с особенностями. Вот некоторые из них:

Первое решение (7) содержит единичную сингулярность в точке $\theta = {{\theta }_{0}}$. У второго решения (7) особенности расположены периодически при θ = = ${{\theta }_{0}} + \pi n$. Оба эти выражения не зависят от переменной z. Если придать решениям (7) физический смысл, сопоставив им бегущие волны, то эти волны, казалось бы, можно назвать стационарными. Это означает, что профили волн не изменяются при распространении (с увеличением расстояния z) благодаря тому, что конкурирующие между собой нелинейные и диссипативные эффекты уравновешивают друг друга. Существуют решения, которые не только содержат особенность, но и не являются ограниченными при $\left| \theta \right| \to \infty $ и зависят от расстояния z. Пример:

Существуют и другие подобные решения, которые практически не исследовались из-за их неясного физического содержания.

Возникает очевидный вопрос об устойчивости этих решений. В общем случае наиболее простой и очевидный путь – добавить к точному решению малое возмущение, например,

Затем нужно линеаризовать уравнение относительно возмущения $V{\kern 1pt} '$:

Решив (10), можно проследить за динамикой возмущения и понять, устойчиво ли изучаемое стационарное решение или нет. Однако этот приближенный подход не описывает полностью картину эволюции стационарной волны с особенностью. К счастью, уравнение (6) является исключительным; оно может быть решено точно, что позволяет полностью описать процесс разрушения сингулярности. Как показано ниже, “стационарные” волны (7) таковыми вовсе не являются.

Точное решение уравнения (6) для исходной (при z = 0) формы волны

имеет вид [2]

Здесь ${{\tilde {V}}_{0}}$ – первообразная функции V₀ (7), а G – функция Грина:

Для исходной “стационарной” формы

согласно (12), нужно вычислить интеграл

Решение получается таким:

Здесь ${\text{erf}}\left( \xi \right)$ – интеграл вероятности [8].

Форма профиля на различных пройденных волной расстояниях (для разных значений параметра $\sqrt {4\Gamma z} $) изображена на рис. 1. Штриховая кривая – это исходная форма (14).

Видно, что особенность в точке θ = 0 исчезает, причем возмущение (разность между исходной и текущей формами профиля) в окрестности особенности не может считаться ни малой, ни медленно изменяющейся. Волна (14), формально являющаяся точным решением уравнения (6), в действительности стационарной не является и эволюционирует так, как показано на рис. 1. Уже на малых расстояниях форма волны описывается решением (16), имеющим автомодельную форму.

Заметим, что автомодельные решения уравнений типа Бюргерса для волн плоской и цилиндрической симметрий найдены в работе [9]. Они приведены в справочнике [10]. Подобные решения для сред с квадратично-кубичной нелинейностью (3), допускающих существование ударных волн разрежения, изучены в работе [11].

Перейдем теперь ко второму “стационарному” решению (7), положив в нем для простоты ${{\theta }_{0}} = 0$. Для него аналог формулы (15) будет таким:

При вычислении удобно использовать разложение модуля под интегралом (17) в ряд Фурье. Результат таков:

При z = 0 ряд в формуле (18) суммируется (см. [8, задача 5.4.5 (1)]):

Подставляя (19) в (18), придем к правильному выражению

В другом предельном случае $z \gg 1$ преобладающим становится первый член ряда, и решение принимает вид затухающей гармонической волны:

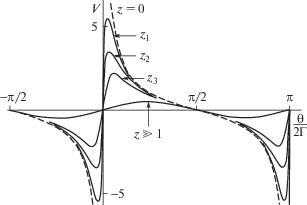
В промежуточной области расстояний волна содержит набор основной и высших гармоник. Ее профиль при различных z, $0 < {{z}_{1}} < {{z}_{2}} < {{z}_{3}} < \infty $, изображен на рис. 2. Как и для предыдущего случая (14), сингулярности в периодической “стационарной” волне быстро разрушаются при ее распространении через нелинейную диссипативную среду.

Заметим, что наличие источников энергии, усиливающих волну, может привести к обратному эффекту [12]. Исходная волна с гладким профилем искажается, в ней образуются ударные фронты. Затем, по мере усиления, фронты становятся более крутыми, “скачок” возмущения на фронте увеличивается и происходит “катастрофа” – образование сингулярности.

Решения с особенностями имеет не только уравнение (6), но и другие точно решаемые модели, например, (3). На рис. 3 изображен процесс столкновения двух импульсных сигналов одинаковой формы, но разной полярности, в среде с модульной нелинейностью (уравнение (3) для значений α = 1, $\beta = 0$) и слабой диссипацией ($\Gamma \ll 1$). Вначале положительный и отрицательный сигналы движутся навстречу друг другу, никак не взаимодействуя между собой (кривая 1). Взаимодействие начинается в момент их столкновения (кривая 2). Затем сигналы пересекаются; при этом происходит их взаимное поглощение (кривые 3–6). Особенность исчезает, а на ее месте появляется крутой фронт, как для квадратично-нелинейных волн на рис. 1 и рис. 2. В дальнейшем происходит “аннигиляция” импульсов – их исчезновение на конечном расстоянии.

Решения с сингулярностями имеют и другие известные нелинейные уравнения, например уравнение Кортевега-де Вриза, по форме аналогичное уравнению Бюргерса (6), но содержащее третью производную вместо второй. Одно из его решений

также имеет “стационарную” форму, однако процесс его разрушения более сложен и в данном сообщении не описан.