Доклады Российской академии наук. Физика, технические науки, 2020, T. 494, № 1, стр. 5-9
МЕТОД ЭФФЕКТИВНЫХ МОД ДЛЯ ОЦЕНКИ ТЕМПЕРАТУРЫ СЛАБОСВЯЗАННЫХ МОЛЕКУЛЯРНЫХ СИСТЕМ
Е. Д. Белега 1, *, Д. Н. Трубников 1, А. И. Чуличков 1
1 Московский государственный университет
имени М.В. Ломоносова
Москва, Россия
* E-mail: EDBelega@gmail.com
Поступила в редакцию 12.05.2020
После доработки 26.07.2020
Принята к публикации 27.07.2020
Аннотация
Предложен подход для оценки числа мод коллективного движения частиц в слабосвязанной молекулярной системе, основанный на методе главных компонент. На примере кластера молекул воды (H2O)8 показаны существенные различия оценок числа эффективных и нормальных мод и установлены энергетические и временные пороговые критерии применимости метода нормальных мод.
Описание термодинамических свойств конечномерных систем, таких как атомные и молекулярные кластеры, является фундаментальной проблемой. Применение подхода классической термодинамики к конечномерным системам в теории кластеров выявило особенности их термодинамических свойств [1]. При этом широко используются методы описания термодинамических свойств кластера, исходя из вероятностей его микроканонических состояний, связанных с координатами и импульсами всех частиц системы [2]. В частности, для невращающихся изолированных кластеров в теории кластеров принято определять температуру (параметр, используемый при описании фазовых переходов в конечномерных системах) как долю средней по траектории кинетической энергии, приходящуюся на одну колебательную степень свободы [3]. Однако слабосвязанные молекулярные кластеры, такие как кластеры молекул воды, описываются моделью с неквадратичным потенциалом взаимодействия, что приводит к нелинейным уравнениям движения, и число колебательных степеней свободы в таких системах должно изменяться в зависимости от энергии возбуждения [4]. В результате подход нормальных мод может быть существенно ограничен областью низких энергий системы. Цель работы – построение математической модели описания динамики конечномерных систем методом эффективных мод, который учитывает нелинейный вклад в динамику колебаний всех частиц, для оценки температуры слабосвязанного кластера как термодинамического параметра. Полученные численные результаты сравниваются с оценкой температуры, рассчитанной методом нормальных мод. Объектом исследования выбран октамер воды – наименьший кластер молекул воды, претерпевающий фазовые превращения [5], что должно отразиться на поведении температуры системы.
АППРОКСИМАЦИЯ ТРАЕКТОРИИ В ФАЗОВОМ ПРОСТРАНСТВЕ МЕТОДОМ ЭФФЕКТИВНЫХ МОД И ОЦЕНКА ТЕМПЕРАТУРЫ
По аналогии с классической термодинамикой, температура конечномерных систем, какими являются и кластеры, оценивается по следующей формуле [3]:
где E – средняя по траектории кинетическая энергии кластера, kB – константа Больцмана, Ndf – число внутренних степеней свободы. Для описания динамики кластера фазовую траекторию системы удобно представить как суперпозицию независимых (в некотором смысле) составляющих, каждая из которых описывает некоторое коллективное движение его атомов. Например, для системы из n частиц в приближении малых колебаний вблизи состояния равновесия фазовую траекторию можно представить в виде линейной комбинации нормальных мод. Динамика мод описывается системой независимых колебательных уравнений [6]. Каждая нормальная мода отражает коллективное колебание системы материальных точек с фиксированной частотой. В случае невращающегося кластера в системе центра масс число нормальных мод Nnm оценивается следующим образом: Nnm = 3n – Q – 6 (здесь n – число атомов, Q – число жестких связей в кластере). Для октамера воды с PIT4P потенциалом Nnm = 42 (в каждой молекуле воды зафиксированы 3 внутренние координаты: расстояния между атомами водорода и кислорода, а также угол между линиями ковалентных связей в молекуле).При росте полной энергии системы линеаризованная модель становится слишком грубым приближением. В этом случае мы используем подход, описанный в работе [7], представляющий собой модификацию метода главных компонент и состоящий в следующем.
Пусть $x(t) = (q(t),p(t)) \in {{R}^{{6n}}}$, $t \in [0,\tau ]$, – фазовая траектория кластера из n частиц. Метод главных компонент позволяет представить траекторию в виде разложения x(t) = $\sum\limits_{i = 1}^{6n} {(x(t),{{e}_{i}})} \,{{e}_{i}}$ по ортонормированному базису $\left\{ {{{e}_{i}}} \right\} \subset {{R}^{{6n}}}$, обладающему следующим экстремальным свойством: любая m-я частичная сумма
приближает траекторию x(t) в среднем по времени не хуже, чем m-я частичная сумма $x_{m}^{'}(t)$ = $\sum\limits_{i = 1}^m {(x(t),e_{i}^{'})\,e_{i}^{'}} $ в разложении по любому другому ортонормированному базису $\{ e_{i}^{'}\} \subset {{R}^{{6n}}}$. Векторы базиса {ei} есть собственные векторы линейного оператора X : R6n → → ${{R}^{{6n}}}$, определенного для любого $y \in {{R}^{{6n}}}$ равенствомОни соответствуют собственным числам оператора X, упорядоченным по невозрастанию: $X{{e}_{i}} = \alpha _{i}^{2}{{e}_{i}}$, i = 1, …, 6n, $\alpha _{1}^{2} \geqslant \alpha _{2}^{2} \geqslant \; \ldots \; \geqslant \alpha _{{6n}}^{2} \geqslant 0$. При этом
Таким образом, траектория x(t), $t \in [0,\tau ]$, может быть представлена в виде суммы эффективных мод $(x(t),{{e}_{i}})\,{{e}_{i}}$, векторы ${{e}_{1}},{{e}_{2}},\; \ldots ,\;{{e}_{{6n}}}$ представляют собой взаимно ортогональные в R6n коллективные моды движения кластера, а зависящие от времени скалярные произведения $(x(t),{{e}_{i}})$ – амплитуды эффективных мод. Средний квадрат i-й эффективной моды равен $\alpha _{i}^{2}$, i = 1, …, 6n, а его доля в величине среднего по времени квадрата нормы траектории x(t) равна $\frac{{\alpha _{i}^{2}}}{{\sum\limits_{i = 1}^{6n} {\alpha _{i}^{2}} }}$.
В настоящем сообщении вместо траектории $x(t) \in {{R}^{{6n}}}$, $t \in [0,\tau ]$, предлагается рассматривать функцию от фазовых координат ${{E}^{{1/2}}}(t) \in {{R}^{{3n}}}$, квадрат нормы которой в каждый момент времени равен кинетической энергии кластера. Если движение молекулярного кластера происходит в трехмерном декартовом пространстве, то эта функция получена путем деления каждой координаты импульса каждой частицы на квадратный корень из ее удвоенной массы, так что ее координаты запишутся в виде $\left( {\frac{{{{p}_{1}}(t)}}{{\sqrt {2{{m}_{1}}} }}} \right.,\frac{{{{p}_{2}}(t)}}{{\sqrt {2{{m}_{1}}} }},\frac{{{{p}_{3}}(t)}}{{\sqrt {2{{m}_{1}}} }},\frac{{{{p}_{4}}(t)}}{{\sqrt {2{{m}_{2}}} }},\; \ldots ,\;\left. {\frac{{{{p}_{{3n}}}(t)}}{{\sqrt {2{{m}_{n}}} }}} \right)$. Тогда, заменив в формулах (2), (3) $x(t) \in {{R}^{{6n}}}$ на E1/2(t) ∈ R3n, решив задачу $E{{g}_{i}} = \lambda _{i}^{2}{{g}_{i}}$ на собственные значения линейного оператора $E:{{R}^{{3n}}} \to {{R}^{{3n}}}$, такого, что
Траектория движения кластера как целого рассчитывалась методом молекулярной динамики с начальными условиями, полученными методом Монте-Карло [8]. Начальное состояние системы соответствовало энергии глобального минимума Н0 = –3.17 эВ и S4 – конфигурации кластера. Для описания взаимодействия между молекулами воды использовался аналитический потенциал жесткого типа TIP4P [9].
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
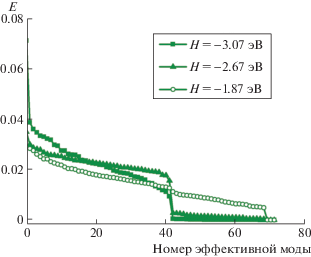
На рис. 1 показано, каким образом средняя по траектории кинетическая энергия E кластера распределяется по эффективным модам коллективного движения частиц системы. Три кривые отражают зависимость этого распределения от начальной полной энергии H кластера. На рис. 1 хорошо виден процесс активации эффективных мод с ростом энергии системы. Время наблюдения за системой составляло 100 пс в каждом из трех случаев.
Рис. 1.
Распределение средней по траектории кинетической энергии E кластера по эффективным модам в зависимости от полной энергии H.
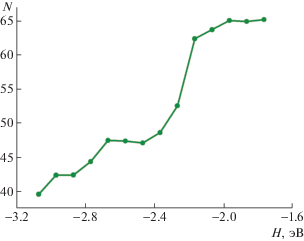
Имея распределение кинетической энергии кластера по эффективным модам (аналогичное рис. 1), можно получить энтропийную оценку числа эффективных мод по следующей формуле: N = $\exp \left( { - \sum\limits_{j = 1}^{3n} {{{\theta }_{j}} \times \ln ({{\theta }_{j}})} } \right)$. Здесь ${{\theta }_{j}} = \frac{{\left\langle {{{E}_{j}}} \right\rangle }}{E}$ – доля кинетической энергии в j-й моде: $\left\langle {{{E}_{j}}} \right\rangle $ = = $\frac{1}{\tau }\int\limits_0^\tau {{{{({{E}^{{1/2}}}(t),{{g}_{i}})}}^{2}}dt} $, нормированная на $E$. Для квантовых систем асимптотика энтропии представлена в [10]. На рис. 2 показаны результаты расчета числа эффективных мод N кластера с ростом полной энергии H. Видно, что число эффективных мод не превышает число нормальных мод Nnm, которое для октамера воды с жестким потенциалом взаимодействия равно 42, только в области низких энергий кластера.
Резкий скачок числа эффективных мод системы в области H ∼ –2.2 эВ приводит к падению температуры Teff, рассчитанной по формуле (1) с учетом N (рис. 3). Следует заметить, что аналогичное немонотонное поведение температуры было обнаружено и для других кластеров [11], и является характерным для нелинейных конечномерных систем в области фазового перехода.
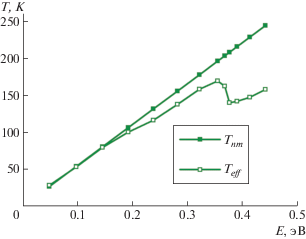
Рис. 3.
Зависимость температуры от кинетической энергии системы: температура Tnm оценена в приближении нормальных мод, Teff – методом эффективных мод.
На рис. 4 представлены зависимости числа эффективных мод от времени наблюдения за траекторией при разных значениях полной энергии кластера. Так как число эффективных мод октамера воды растет со временем, в отличие от числа нормальных мод, которое остается постоянным, система может рассматриваться как линейная только для малых значений t. C течением времени нелинейность системы становится более значимой, в результате траектория покидает линейное подпространство фазовой траектории, определенное линеаризацией.
ЗАКЛЮЧЕНИЕ
Результаты, представленные в данной работе, показывают, что
1) число эффективных мод коллективной динамики кластера в фазовом пространстве существенно зависит от полной энергии системы, в отличие от числа нормальных мод, которое остается неизменным при любой его энергии;
2) поведение температуры с ростом энергии, полученное двумя методами, позволяет оценить пороговое значение энергии кластера, ниже которого метод нормальных мод может быть использован;
3) зависимости числа эффективных мод кластера от времени наблюдения за траекторией в фазовом пространстве дают временн${\text{ы}}'$е оценки линейной динамики системы;
4) при энергиях системы, превышающих примерно пятую часть энергии глобального минимума, динамика система не может рассматриваться в предположении малых колебаний из-за сильной ее нелинейности.
Список литературы
Берри Р.С., Смирнов Б.М. Фазовые переходы в кластерах различных типов // Успехи физ. наук. 2009. Т. 179. С. 147–177.
Gross D.H.E., Votyakov E.V. Microcanonical Thermodynamics. Phase transitions in “small” systems // European Physics Journal B. 2000. V. 15. P. 115–126.
Plummer P.L.M., Chen T.S. A Molecular Dynamics Study of Water Clathrates // J. Physical Chemistry. 1983. V. 87. P. 4190–4197.
Белега Е.Д., Трубников Д.Н., Чуличков А.И. Моделирование фазовых переходов в слабосвязанных молекулярных кластерах // ДАН. 2018. Т. 483. № 4. С. 359–362. https://doi.org/10.31857/S086956520003265-4
Tsai C.J., Jordan K.D. Monte Carlo simulation of (H2O)8: Evidence for a lowenergy S4 structure and characterization of the solid ↔ liquid transition // J. Chemical Physics. 1991. V. 95. P. 3850–3853.
Landau L.D., Lifshitz E.M. Mechanics. V. 1 (3rd ed.). Butterworth-Heinemann. 1976. ISBN 978-0-7506-2896-9.
Belega E.D., Rybakov A.A., Trubnikov D.N. et al. Effective Dimension of a Phase Trajectory in the Visualization of Dynamical Systems // Computational Mathematics and Mathematical Physics. 2002. V. 42. № 12. P. 1817–1823.
Belega E.D., Tatarenko K.A., Trubnikov D.N., Cheremukhin E.A. The dynamics of water hexamer isomerization // Russ. J. Phys. Chem. B. 2009. V. 3. P. 404– 409.
Белега Е.Д., Трубников Д.Н. Молекулярная динамика кластеров воды и потенциалы взаимодействия // ДАН. 2019. Т. 484. № 6. С. 659–662. https://doi.org/10.31857/S0869-56524846659-662
Aptekarev A.I., Belega E.D. Asymptotic behaviour of the information entropy of hydrogen-like quantum systems // Russ. Math. Surv. 2018. V. 73. P. 922–924. https://doi.org/10.1070/RM9854
Schmidt M., Kusche R., Hippler T. et al. Negative Heat Capacity for a Cluster of 147 Sodium Atoms // Physical Review Letters. 2001. V. 86. № 7. P. 1191–1194.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Физика, технические науки