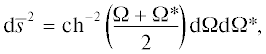Доклады Российской академии наук. Физика, технические науки, 2020, T. 494, № 1, стр. 10-12

В последние годы уравнения Янга–Миллса находят все более широкое применение в физике конденсированных сред [1]. При этом наибольший интерес представляют топологические и сингулярные структуры в этих средах. Функционал Янга–Миллса в евклидовом пространстве R⁴ c координатами (x₁, x₂, x₃, x₄) имеет вид

где тензор ${{{\mathbf{F}}}_{{\mu \nu }}}$ выражается через поле A_μ = = $(A_{\mu }^{1},A_{\mu }^{2},A_{\mu }^{3})$: зависящее от трех вещественных переменных (x₁, x₂, x₃). Здесь и далее греческие буквы пробегают значения 1, 2, 3, 4, а латинские – 1, 2, 3, подстрочный индекс обозначает знак дифференцирования по независимым переменным $\left( {{{A}_{{\mu ,\nu }}} = \frac{{\partial {{A}_{\mu }}}}{{\partial {{x}_{\nu }}}}} \right)$. Известно [2], что решения уравнений Янга–Миллса (минимизация функционала (1)) удовлетворяют уравнениям дуальности

Для решения этих уравнений были использованы различные подстановки (см., например, обзор [3]). В этой работе мы исследуем решения уравнений дуальности в трехмерном евклидовом пространстве с координатами переменных x_i = (x₁, x₂, x₃). Для этой цели удобно использовать представление Фаддеева–Ниеми [4, 5] для полей A_μ:

через вещественные поля C_μ, σ, K и единичный вектор n:

и положить C₄ = 0.

Задача поиска решений уравнения дуальности с использованием параметризации Фаддеева–Ниеми для калибровочного SU(2) поля Янга–Миллса сформулирована в статье [1]. Отметим также, что трехмерные структуры, в отличие от инстантонов, характеризуются бесконечным значением действия [1]. Установлено, что при решении уравнений дуальности удобно использовать замену

При этом в уравнения (2) входят только поля A, $~{\mathbf{W}} = {\mathbf{C}} + \nabla B$, Φ, θ и их производные. Эти поля инвариантны при калибровочном преобразовании матрицей U = exp[iαnσ] группы SU(2) [4, 5] с параметром α(x₁, x₂, x₃). Поля C, B преобразуются как

Приравнивая нулю все компоненты разложения по степеням exp[iB(x₁, x₂, x₃)] уравнений (2) (после подстановки (3), (4)), мы находим калибровочно инвариантные дифференциальные уравнения в простом виде

Здесь введены сокращенные обозначения: F = = $~\nabla \theta \, \times \,\nabla {\Phi }$. Из уравнений (6), (7) или дивергенции уравнения (8) сразу следует дополнительное уравнение ${\mathbf{F}} \cdot \nabla A = 0$ для поля A. Из теории дифференциальных уравнений первого порядка следует, что поле A зависит от двух независимых интегралов характеристической системы [6]. Нетрудно убедиться в том, что вследствие соотношений $(\nabla \theta \cdot {\mathbf{F}})$ = 0, $\left( {\nabla {\Phi } \cdot {\mathbf{F}}} \right) = 0$ эти интегралы являются произвольными функциями θ, Φ. Однако, как показано далее, наиболее простое уравнение для A получается при выборе

где

Тогда из (6), (7) поле W имеет простой вид:

Наконец, уравнение для поля T = lnA можно найти подстановкой уравнений (9)–(11) в (8). Тогда все три уравнения (8) приводятся к одному уравнению

Преобразованием T = TT + ln(cha) оно сводится к модифицированному уравнению Лиувилля:

В итоге решения (12) определяются произвольной аналитической функцией G[Ω], Ω = a + iΦ и комплексно сопряженной к ней G*[Ω]:

В общем случае структуры, определяемые этим уравнением, сингулярны. Представленные здесь решения зависят от произвольных функций, и их полный анализ будет изложен в другом месте. Отметим также, что они не описывают всех трехмерных решений уравнений дуальности в теории Янга–Миллса. Так, они, в частности, не приводят к сферически симметричным решениям уравнений дуальности в SU(2)-теории Янга–Миллса, найденным в работе [9]. Использованный в этой работе анзатц удовлетворяет уравнениям

и не совпадает с (3) ни при каких значениях полей. В нашем случае все поля зависят от параметров (a, Φ). Обсудим их выбор. Формула (4) представляет структуру “ежа” в сферической системе координат. В координатах (R, a, Φ) евклидова метрика имеет вид

Слагаемое ${\text{d}}{{\bar {s}}^{2}} = {\text{c}}{{{\text{h}}}^{{ - 2}}}a~({\text{d}}{{a}^{2}} + {\text{d}}{{{\Phi }}^{2}})$ в переменных (Ω = a + iΦ, Ω* = a − iΦ) имеет конформный вид

и, следовательно, координаты (a, Φ) являются конформными координатами [7]. Известно, что конформный вид метрики инвариантен относительно комплексно аналитических замен координат. Этот факт и отражает наличие G(Ω) и G*(Ω) в формуле (13). В итоге в качестве параметров (a, Φ) в формуле (12) можно выбрать любые две конформные координаты, которые параметризуют вектор r и классифицируют точные решения уравнения Янга–Миллса. Рассмотрим преобразование x_i = = x_i(y₁, y₂, y₃), где (y₁, y₂) = (a, Φ), при котором евклидова метрика ds² = d$x_{1}^{2}$ + d$x_{2}^{2}$ + d$x_{3}^{2}$ преобразуется к виду и определяет метрический тензор g_kj и обратный ему g^ik:

Тогда система криволинейных координат с ограничениями

приводит к конформным координатам. Системы ортогональных координат g_kj = 0 (k ≠ j) приведены во многих справочниках и монографиях (например, см. [8]). Наиболее интересными являются тороидальная (σ, τ, φ) и биполярная (σ, τ, φ) [8] системы координат. Положим σ = Φ, τ = a в тороидальной системе. Тогда

Здесь и далее $r = \sqrt {x_{1}^{2} + x_{2}^{2}} $. Структура (17) описывает вихревое кольцо, центр которого лежит в плоскости x₃ = 0 на окружности r = A, с топологическим зарядом

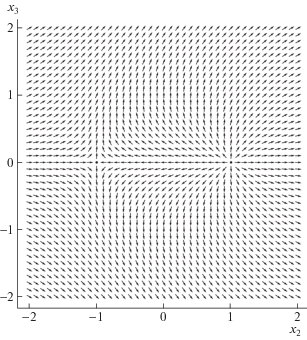
равным единице. Здесь γ – произвольный замкнутый контур, охватывающий центр кольца. Интегрирование производится против часовой стрелки. Наиболее простой вид формула (17) имеет на контуре γ вблизи центра вихря:

Тогда Φ → Ψ при p → 0. Структура вихрей более наглядна в распределении векторного поля Z = = (cosΦ, sinΦ). Это поле в плоскости x₁ = 0 при A = 1 изображено на рис. 1. Ясно видна структура вихря при x₃ = 0, x₂ = 1 и антивихря при x₃ = 0, x₂ = −1.

Отметим, что предложенная в этом сообщении процедура обобщается на точные решения в D = 4. Соответствующие результаты будут изложены в другом месте.