Доклады Российской академии наук. Физика, технические науки, 2020, T. 495, № 1, стр. 73-77
НОВЫЙ ПОДХОД К АНАЛИТИЧЕСКОМУ ОПИСАНИЮ РОСТА ПАРОВОГО ПУЗЫРЬКА В ПЕРЕГРЕТОЙ ЖИДКОСТИ
А. А. Чернов 1, 2, *, академик РАН М. А. Гузев 3, А. А. Пильник 1, 2, И. В. Владыко 1, 2, В. М. Чудновский 1
1 Новосибирский государственный университет
Новосибирск, Россия
2 Институт теплофизики им. С.С. Кутателадзе Сибирского отделения Российской академии наук
Новосибирск, Россия
3 Институт прикладной математики
Дальневосточного отделения Российской академии наук
Владивосток, Россия
* E-mail: chernov@itp.nsc.ru
Поступила в редакцию 28.08.2020
После доработки 13.10.2020
Принята к публикации 14.10.2020
Аннотация
Представлена математическая модель роста парового пузырька в перегретой жидкости, учитывающая как динамические, так и тепловые эффекты и включающая в себя известные классические уравнения – уравнение импульсов и уравнение теплопроводности, записываемые с учетом процесса испарения жидкости. Найдено приближенное полуаналитическое решение задачи, построение которого основано на существовании квазистационарного состояния для процесса роста пузырька. Это позволяет редуцировать исходную краевую задачу с подвижной границей к системе обыкновенных дифференциальных уравнений первого порядка. Полученное решение справедливо на всех стадиях процесса и в широком диапазоне режимных параметров. Показано, что на больших временах решение становится точным автомодельным и в предельных случаях согласуется с известными решениями других авторов.
Детальное исследование всего многообразия процессов, происходящих при кипении жидкости, представляет собой как чисто научный, так и практический интерес и актуально по сей день. Элементарным актом процесса кипения является рост парового пузырька, описание которого представляет собой комплексную задачу, в которой следует совместно решать уравнения гидродинамики и теплообмена. Попытки получить закон роста парового пузырька имеют давнюю историю, начиная с классических работ [1–5] и заканчивая многочисленными современными исследованиями [6, 7].
Следует заметить, что при построении математических моделей для роста парового пузырька авторы предлагают учитывать различные факторы: динамические, кинетические, тепловые и другие, которые определяют этот процесс. Поскольку на той или иной стадии процесса происходит смена факторов в зависимости от свойств рассматриваемой двухфазной системы, то для решения задачи используются различные допущения, позволяющие построить упрощенные математические модели, в которых выделен какой-либо один основной управляющий процессом механизм. Основные наиболее распространенные из них [8]: динамическая инерционная модель, в которой рост пузырька происходит исключительно вследствие инерционных эффектов; динамическая вязкая модель, в которой рост пузырька лимитируется вязкими силами; энергетическая молекулярно-кинетическая модель, в которой предпринимается попытка учесть кинетику фазового перехода и энергетическая тепловая модель. Последняя наиболее распространена в литературе. В этой модели рост пузырька обусловлен подводом тепла к межфазной границе от внешних перегретых слоев жидкости; все тепло при этом расходуется на испарение. Зависимость радиуса пузырька от времени в данной модели имеет вид степенной функции с показателем степени 1/2. При этом коэффициент пропорциональности является функцией числа Якоба и находится различными авторами по-разному. Наиболее известной является формула Плессета–Цвика [1], справедливая для больших чисел Якоба. Достаточно полное аналитическое решение задачи в интегральном виде получено Скрайвеном [4]. Наряду с этим, большое распространение получили различные эмпирические зависимости [9].
Анализ энергетической тепловой модели показывает, что несмотря на ее широкую распространенность, она имеет ограниченную область применения. В частности, это проявляется в том, что ряд приближений, сделанных в ней, приводит к решению с бесконечной скоростью роста пузырька в начальный момент времени, что физически некорректно. В связи с этим, предпринимаются попытки создания различного рода гибридных моделей, одновременно учитывающих как динамические, так и тепловые эффекты [10–13], что, как показывает опыт, сопряжено со значительными трудностями. Целью настоящей работы является нахождение приближенного аналитического решения данной задачи, которое корректно бы описывало все стадии роста парового пузырька.
Пусть в начальный момент времени в однородно перегретой жидкости зародился и начал расти паровой пузырек. Система уравнений, описывающих данный процесс, включает известные классические уравнения, записываемые применительно к рассматриваемой задаче с учетом специфики, связанной с испарением жидкости. При решении задачи будем использовать приближение однородного равновесного пузырька, согласно которому пар в пузырьке находится в насыщенном состоянии, а температура и давление однородны [14].
Динамика пузырька описывается уравнением импульсов (модифицированным уравнением Рэлея):
(1)
$\frac{1}{R}~\frac{{\text{d}}}{{{\text{d}}t}}({{{v}}_{{lR}}}{{R}^{2}}) - \frac{{{v}_{{lR}}^{2}}}{2} = \frac{{{{p}_{{lR}}} - p_{l}^{i}}}{{{{\rho }_{l}}}},$Граничные условия, отражающие законы сохранения массы, импульса и энергии записываются следующим образом:
(3)
${{p}_{{lR}}} = {{p}_{{v}}} + j{{{v}}_{{lR}}} - \frac{{2\sigma }}{R} - 4{{\eta }_{l}}\frac{{{{{v}}_{{lR}}}}}{R};$(4)
${{j}_{{\text{L}}}} = {{\lambda }_{l}}{{\left( {\frac{{\partial {{T}_{l}}}}{{\partial r}}} \right)}_{{r = R}}}~,$Данную систему уравнений замыкает тепловая задача, в которой динамика температурного поля в жидкости описывается уравнением теплопроводности:
(5)
$\frac{{\partial \left( {{{\rho }_{l}}{{c}_{l}}{{T}_{l}}} \right)}}{{\partial t}} + {{{v}}_{l}}~\frac{{\partial \left( {{{\rho }_{l}}{{c}_{l}}{{T}_{l}}} \right)}}{{\partial r}} = \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}~\left( {{{\lambda }_{l}}{{r}^{2}}~\frac{{\partial {{T}_{l}}}}{{\partial r}}} \right),$В начальный момент времени температура жидкости однородна и больше температуры насыщения при давлении $p_{l}^{i}$ (давлении вдали от пузырька): ${{({{T}_{l}})}_{{t = 0}}} = {{T}^{i}} > {{T}^{s}}(p_{l}^{i})$. Вдали от пузырька температурное поле остается невозмущенным: ${{({{T}_{l}})}_{{r \to \infty }}}$ = T i. На поверхности пузырька выполняется условие локального термодинамического равновесия: ${{({{T}_{l}})}_{{r = R}}}$ = = ${{T}^{s}}({{p}_{{v}}})$. Здесь и далее верхний индекс s означает значение величины на линии насыщения.
Задачу следует дополнить уравнением состояния пара в пузырьке и зависимостью давления насыщения от температуры, которые в общем случае имеют следующий вид:
(7)
${{p}_{{v}}} = {{p}^{s}}\left( {{{T}_{{v}}}} \right)\quad {\text{или}}\quad {{T}_{{v}}} = {{T}^{s}}\left( {{{p}_{{v}}}} \right).$Это могут быть как модельные, так и более точные эмпирические зависимости. Как правило, в качестве уравнения состояния используют уравнение Менделеева–Клапейрона, считая пар идеальным газом, а для кривой равновесия – уравнение Клапейрона–Клаузиуса. Надо сказать, что это несколько сужает общность как самой постановки задачи, так и получаемых решений. Однако в большинстве случаев этого вполне достаточно, чтобы обеспечить приемлемую точность получаемого решения. Отметим также, что зависимости (6), (7) однозначно определяют функции ${{T}^{s}}({{p}_{{v}}})$ и ${{p}^{s}}({{\rho }_{{v}}})$, которые появятся ниже.
В общем случае сформулированную задачу (даже без учета инерционных эффектов) можно решить только численно. Однако можно предложить подход, на основе которого построить приближенное решение задачи почти во всем временном интервале эволюции пузырька. С математической точки зрения его удобно сконструировать, если перейти от переменных (t, r) к переменным $(t,\chi )$, где $\chi = \frac{r}{{R(t)}}$, тем самым сведя краевую задачу к задаче с неподвижными границами (аналогично тому, как это сделано в работе [15] при решении задачи о диффузионным росте газового пузырька).
Уравнение теплопроводности (5) примет следующий вид:
(8)
$\frac{{{{R}^{2}}}}{{{{a}_{l}}}}\frac{{\partial {{\Theta }_{l}}}}{{\partial t}} = \left( { - \frac{\alpha }{{{{\chi }^{2}}}} + \frac{2}{\chi } + \beta \chi } \right)\frac{{\partial {{\Theta }_{l}}}}{{\partial \chi }} + \frac{{{{\partial }^{2}}{{\Theta }_{l}}}}{{\partial {{\chi }^{2}}}},$Начальное и граничные условия запишутся следующим образом:
(9)
${{({{\Theta }_{l}})}_{{t = 0}}} = 0;\quad {{({{\Theta }_{l}})}_{{\chi = 1}}} = {{\Theta }^{s}}\left( {{{{\bar {\rho }}}_{{v}}}} \right);\quad {{({{\Theta }_{l}})}_{{\chi \to \infty }}} = 0,$Переходя к анализу уравнения (8), заметим, что структура решения зависит от поведения управляющих функций $\alpha = \alpha (t)$, $\beta = \beta (t)$. На начальном этапе эволюции пузырька скорость его роста мала, поэтому величины $\alpha ,\beta \ll 1$. Тогда член $\frac{2}{\chi }$ в круглых скобках в правой части (8) становится ведущим слагаемым по сравнению с остальными. В этом случае (8) редуцируется к известному для тепловой задачи уравнению, решение которого асимптотически убывает во времени. При дальнейшей эволюции системы структура решения изменяется из-за монотонного роста α, β. Но оно, по-прежнему, содержит асимптотически убывающее во времени слагаемое. Однако учет α, β приводит к распределению температуры, для которого начальная стадия процесса становится несущественной. Такое решение для температуры можно найти при условии обращения в нуль правой части (8), и с учетом условий (9) оно дается формулой
(10)
${{\Theta }_{l}}\left( {\tau ,\chi } \right) = {{\Theta }^{s}}\left( {{{{\bar {\rho }}}_{{v}}}} \right)\frac{{\int\limits_0^{1/\chi ~} {{\text{exp}}\{ - \alpha \zeta - \beta {{\zeta }^{{ - 2}}}{\text{/}}2\} d\zeta } }}{{\int\limits_0^1 {{\text{exp}}\{ - \alpha \zeta - \beta {{\zeta }^{{ - 2}}}{\text{/}}2\} d\zeta } }}.$Решение (10) не является стационарным с точки зрения математики, поскольку зависит от времени через $\alpha = \alpha (t)$, $\beta = \beta (t)$, поэтому его естественно называть квазистационарным. При этом численные расчеты для (8) показывают, что время установления квазистационарного состояния существенно меньше времени всего процесса эволюции пузырька. Это означает, что решение (10) с хорошей точностью описывает динамику температурного поля, формирующегося вокруг пузырька на протяжении всего его роста.
Модифицируя исходную систему уравнений (1)–(4) и подставляя найденный профиль температуры (10) в обезразмеренное уравнение (4), получим следующую систему дифференциальных уравнений первого порядка:
(12)
$\begin{gathered} (\beta - \alpha )\mathop \smallint \limits_0^1 {\text{exp}}\{ \{ \alpha (1 - \zeta ) + \beta (1 - {{\zeta }^{{ - 2}}}){\text{/}}2\} {\text{d}}\zeta = \\ = - \,{\text{K}}{{{\text{u}}}^{{ - 1}}}~{{\theta }^{s}}({{{\bar {\rho }}}_{{v}}}), \\ \end{gathered} $Таким образом, задача свелась к решению системы из трех обыкновенных дифференциальных уравнений вида $\frac{{{\text{d}}{\mathbf{y}}}}{{{\text{d}}t}} = {\mathbf{f}}({\mathbf{y}})$, где ${\mathbf{y}} = (\alpha ,{{\bar {\rho }}_{{v}}},R)$ – искомая векторная функция, а функция f(y) задана правой частью уравнений (11).
По мере роста пузырька давление в нем постепенно падает и асимптотически стремится к давлению окружающей жидкости; плотность пара в пузырьке и температура жидкости на межфазной границе при этом стремятся к постоянным значениям: ${{\rho }_{{v}}} \to \rho _{{v}}^{f};~{{({{\Theta }_{l}})}_{{\chi = 1}}} \to - 1$, где $\rho _{{v}}^{f}$ – плотность пара при давлении $p_{l}^{i}$. На этой стадии процесса, которая, к слову, может быть описана в рамках энергетической тепловой модели, рост пузырька определяется исключительно теплопередачей к межфазной границе, температурное поле в жидкости становится стационарным, функции α и β – константами, а решение краевой задачи – точным автомодельным:
(13)
$\begin{gathered} {{\Theta }_{l}}\left( \chi \right) = - \frac{{\int\limits_0^{1/\chi } {{\text{exp}}\{ - {{\beta }^{f}}(\zeta (1 - \bar {\rho }_{{v}}^{f}) + {{\zeta }^{{ - 2}}}{\text{/}}2)\} {\text{d}}\zeta } }}{{\int\limits_0^1 {{\text{exp}}\{ - {{\beta }^{f}}(\zeta (1 - \bar {\rho }_{{v}}^{f}) + {{\zeta }^{{ - 2}}}{\text{/}}2)\} {\text{d}}\zeta } }};~ \\ R = \sqrt {2{{\beta }^{f}}{{a}_{l}}t\,} . \\ \end{gathered} $Отметим, что аналогичное решение было получено Скрайвеном [4]. Коэффициент βf, фигурирующий в уравнении (13), на данной стадии является функцией только числа Якоба Ja = ${{(\bar {\rho }_{{v}}^{f}Ku)}^{{ - 1}}}$ = = $\frac{{{{\rho }_{l}}}}{{\rho _{{v}}^{f}}}\frac{{{{c}_{l}}\Delta T_{l}^{i}}}{{\text{L}}}$ и находится из следующего интегрального уравнения (которое напрямую следует из уравнения (12)):
(14)
${{\beta }^{f}}\mathop \smallint \limits_0^{1~{\text{\;}}} {\text{exp}}\left\{ {\left. {{{\beta }^{f}}\left( {\left( {1 - \zeta } \right)(1 - \bar {\rho }_{{v}}^{f}) + \frac{{1 - {{\zeta }^{{ - 2}}}}}{2}} \right)} \right\}} \right.{\text{d}}\zeta = {\text{Ja}}{\text{.}}$В случае малых и больших перегревов при $\bar {\rho }_{{v}}^{f} \ll 1$ уравнение (14) имеет следующие приближенные решения:
Последнее совпадает с известным решением Плессета–Цвика [1] (если не брать во внимание аддитивную поправку к числу Якоба, которая значительно улучшает данное асимптотическое приближение).
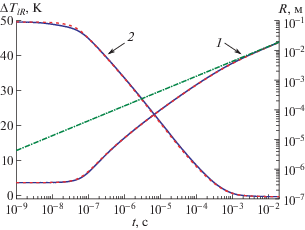
На рис. 1 представлены зависимости радиуса пузырька и температуры жидкости на межфазной границе от времени, построенные для воды при атмосферном давлении и начальном перегреве 50 K, наглядно иллюстрирующие механизм роста парового пузырька в перегретой жидкости, объединяющий в себе динамические и тепловые эффекты. Начальный размер пузырька полагался равным 1.1 Rcr, где Rcr = $\frac{{2\sigma }}{{~\Delta p_{{v}}^{i}}}$ – критический радиус, при начальной нулевой скорости роста и температуре пара, равной температуре окружающей жидкости. Как видно из рисунка, различие в результатах расчета, полученных в результате прямого численного моделирования исходной системы уравнений (1)–(7) и на основе найденного полуаналитического решения (11), (12), достаточно мало, что говорит о состоятельности последнего (это же наблюдалось в расчетах и для других перегревов, и для других жидкостей). Отметим также, что автомодельное решение (13), (14) справедливо лишь на больших временах, так как по сути является асимптотическим, что говорит о его ограниченности применительно к реальным системам, особенно в случае больших перегревов, где характерное время переходной стадии может оказаться много больше характерного времени наблюдения.
Рис. 1.
Зависимость радиуса пузырька $R$ (1) и перегрева жидкости на межфазной границе $\Delta {{T}_{{lR}}}$; (2) от времени: сплошная линия – полученное полуаналитическое решение (11), (12); штриховая линия – прямое численное моделирование; штрих-пунктирная линия – автомодельное решение (13), (14).
Таким образом, в работе найдено сравнительно простое полуаналитическое решение задачи о росте парового пузырька в изначально однородно перегретой жидкости, которое одновременно описывает как инерционные, так и тепловые эффекты, управляющие данным процессом, и которое может послужить хорошей альтернативой прямым численным расчетам.
Список литературы
Plesset M.S., Zwick S.A. The growth of vapor bubbles in superheated liquids // J. Appl. Phys. 1954. V. 25. № 4. P. 493–500.
Forster H.K., Zuber N. Growth of a vapor bubble in a superheated liquid // J. Appl. Phys. 1954. V. 25. № 4. P. 474–478.
Birkhoff G., Margulies R. S., Horning W.A Spherical bubble growth // The Physics of Fluids. 1958. V. 1. № 3. P. 493–500.
Scriven L.E. On the dynamics of phase growth // Chemical Engineering Science. 1959. V. 10. № 1. P. 1–13.
Mikic B.B., Rohsenow W.M., Griffith P. On bubble growth rates // Intern. J. Heat and Mass Transfer. 1970. V. 13. № 4. P. 657–666.
Prosperetti A. Vapor bubbles // Annual Review of Fluid Mechanics. 2017. V. 49. № 1. P. 221–248.
Zudin Y.B. Non-equilibrium Evaporation and Condensation Processes. Springer, 2019. 404 p.
Лабунцов Д.А. Физические основы энергетики. Избранные труды по теплообмену, гидродинамике, термодинамике. М.: Издательство МЭИ, 2000. 388 с.
Авдеев А.А. Закономерности роста парового пузыря в объеме перегретой жидкости (Тепловая энергетическая схема) // Теплофизика высоких температур. 2014. Т. 52. № 4. С. 617–632.
Lee H.S., Merte H. Spherical vapor bubble growth in uniformly superheated liquids // International J. Heat and Mass Transfer. 1996. V. 39. № 12. P. 2427–2447.
Robinson A.J., Judd R.L. The dynamics of spherical bubble growth // Intern. J. Heat and Mass Transfer. 2004. V. 47. № 23. P. 5101–5113.
Коледин В.В., Шагапов В.Ш. К динамике роста паровых пузырьков в перегретой жидкости // Прикладная математика и механика. 2013. Т. 77. № 5. С. 754–767.
Wang Q., Gu J., Li Z., Yao W. Dynamic modeling of bubble growth in vapor-liquid phase change covering a wide range of superheats and pressures // Chemical Engineering Science. 2017. V. 172. P. 169–181.
Нигматулин Р.И. Динамика многофазных сред. Т. 1. М.: Наука, 1987. 464 с.
Chernov A.A., Pil’nik A.A., Davydov M.N., Ermanyuk E.V., Pakhomov M.A. Gas nucleus growth in high-viscosity liquid under strongly non-equilibrium conditions // Intern. J. Heat and Mass Transfer. 2018. V. 123. P. 1101–1108.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Физика, технические науки


