Доклады Российской академии наук. Физика, технические науки, 2021, T. 499, № 1, стр. 58-65

ВВЕДЕНИЕ

Один из быстро развивающихся методов ультразвукового контроля – дифракционно-временной, или, в англоязычной литературе – метод TOFD (Time-of-Flight Diffraction) [1]. Если раньше в ультразвуковой дефектоскопии чаще всего ориентировались на прием максимального по амплитуде сигнала, зеркально отраженного от дефекта, то метод TOFD оперирует со слабыми сигналами от ребер (краев) дефектов. При этом неизбежно  приходится анализировать результат 3D-рассеяния ультразвука на локальных неоднородностях в упругой среде [2, 3]. Для рассмотрения этих тонких эффектов целесообразно обратиться к аналитическим решениям задачи рассеяния ультразвука на трещинах различной формы и размеров.

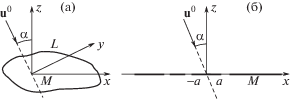
В общем виде геометрию задачи можно представить как на рис. 1: продольная или поперечная волна под углом α падает на локальную неоднородность в изотропной среде с коэффициентами Ламе λ и μ, плотностью ρ₀. Пусть u⁰ – вектор смещения в падающей волне, $\delta {\mathbf{u}}$ и u – рассеянное и результирующее поля, так что ${\mathbf{u}} = {{{\mathbf{u}}}^{0}} + \delta {\mathbf{u}}$. Тогда в пространстве вокруг неоднородности имеем:

где тензор напряжений ${{\sigma }_{{ij}}}\left( u \right) = {{c}_{{ijkl}}}\frac{{\partial {{u}_{l}}}}{{\partial {{x}_{k}}}}$ имеет вид

Здесь мы ограничимся рассеянием на трещинах M, под которыми будем понимать бесконечно тонкие препятствия в плоскости z = 0, у которых противоположные поверхности $z = \pm {\text{\;}}0{\text{\;}}(x,y \in M){\text{\;}}$ свободны от напряжений и не взаимодействуют между собой нигде, кроме разве точек кривой L, ограничивающей поверхность M. При этом граничные условия можно записать в виде

где n_j – внешняя нормаль к поверхности трещины.

Поверхностью M можно моделировать локальные или протяженные, сплошные или прерывистые трещины. В простейших случаях, можно говорить о таких моделях:

диск ${{x}^{2}} + {{y}^{2}} \leqslant {{a}^{2}}$ (или $r \leqslant a),{\text{\;}}z = \pm 0$ (L – окружность радиуса a на рис. 1а);

полуплоскость $x \geqslant 0, - \infty < y < \infty ,~~z = \pm 0$ (рис. 1б, правая сторона);

полоса $\left| x \right| \leqslant a, - {\kern 1pt} \infty < y < \infty ,z = \pm 0$ (рис. 1б в центре) или решетка из полос, расположенных регулярно или нерегулярно (рис. 1б).

Если, помимо граничных условий, учесть условия излучения и условия на ребре (ребрах) трещины, то известно, что для трещин простейшей формы задача о нахождении δu имеет единственное решение. Например, в [4, 5] это показано для 2D-рассеяния на полуплоскости, в [6, 7] и других работах – для 3D-рассеяния на круглом диске. Также многократно рассматривались различные приближенные решения, например, в [8, 9]. Однако если говорить о 3D-задачах в общем случае рассеяния упругой волны на трещинах произвольной формы, то они часто сводятся к численному решению интегральных уравнений различного типа. Для упрощения инженерных расчетов было бы целесообразно построить общее решение в квадратурах и выделить в явном виде отдельные составляющие рассеянных полей. Этой цели и посвящено данное сообщение.

1. ПОСТАНОВКА ЗАДАЧИ РАССЕЯНИЯ НА ПЛОСКОЙ ТРЕЩИНЕ

Имея в виду условия излучения для рассеянной волны, введем запаздывающую функцию Грина ${{G}_{{ij}}}$, которая подчиняется уравнению

Точную форму этой функции можно найти, например, в [5, 6, 10]:

где

Здесь $R\, = \,{\text{|}}x - x{\kern 1pt} '{\text{|}}$. Используя преобразование Фурье запаздывающей функции Грина G = = $\frac{1}{{2\pi }}\int {{{e}^{{ - i{{\omega }}(t - t{\kern 1pt} ')}}}{{G}^{{{\omega }}}}d\omega } $, где ω – круговая частота, для компонент Фурье получим

Видно, что для компонент Фурье волны ${\mathbf{u}}(\omega ,x$, y, z) условие излучения формулируются следующим образом: при $r = \sqrt {{{x}^{2}} + {{y}^{2}} + {{z}^{2}}} \to \infty $ вектор смещения пропорционален преобразованию Фурье запаздывающей функции Грина: $u({{\omega }})~\,\sim \,q({{\omega }}){{G}^{\omega }}{\text{(}}r{\text{)}}$, а множитель q(ω) зависит только от угловых переменных.

Условие на ребре трещины сформулируем позже. При этом задача будет поставлена полностью, и можно приступать к ее решению. В данной работе мы рассмотрим стационарный случай, когда зависимость переменных от времени монохроматическая $\sim ~{{e}^{{i{{\omega t}}}}}$. При этом волновое уравнение (1) можно заменить на уравнение Гельмгольца, которое запишем в виде интегрального уравнения, учитывающего все особенности поверхностей (граничные условия), по которым берутся интегралы:

Согласно [4, 10] первый интеграл описывает падающую волну u⁰. Второй интеграл берется по поверхности, состоящей из поверхности трещины и поверхности сферы с бесконечным радиусом $R \to \infty $. Нормаль к поверхности трещины направлена внутрь объема (т.е. наружу из трещины). Тогда, учитывая граничное условие (3), уравнение (4) перепишем в виде

Таким образом, поле, рассеиваемое трещиной, полностью определяется значениями этого поля на ее поверхности ${\mathbf{u}}{{{\text{|}}}_{M}}$. Как только мы получим решение на трещине, то найдем и общее решение задачи о рассеянии упругой волны.

Разобьем поверхность трещины M на две части: M⁺ – “освещенную”, или “верхнюю” с вектором нормали ${\mathbf{n}} = \left( {0,0,1} \right)$, и M^– – “теневую”, или “нижнюю” с вектором нормали ${\mathbf{n}} = \left( {0,0, - 1} \right)$. Тогда и поле смещения u можно разбить на две части: u⁺ – решение на поверхности M⁺ и u^– − решение на поверхности M^–. Из (5) получим

где интегрирование проводится только по освещенной стороне, а [u] обозначает разность смещения на разных сторонах трещины:

2. ПОТЕНЦИАЛЫ ПОЛЯ, ГРАНИЧНЫЕ УСЛОВИЯ, УСЛОВИЯ НА РЕБРЕ

Поскольку смещения ищем на поверхности трещины, то вблизи нее удобно использовать специальную систему координат. Введем вместо z координату ${{\zeta }} = \left| z \right|$, так что $x,y \in M,{{\zeta }} = 0$ соответствует обеим сторонам трещины $z = \pm 0$. Например, поверхность трещины в виде диска в новых координатах $(x,y,{{\zeta }}){\text{\;}}$ имеет вид $r = \sqrt {{{x}^{2}} + {{y}^{2}}} \leqslant a$, ζ = 0.

Разложим вектор u на нормальную u_n и тангенциальную u_τ к поверхности трещины составляющие: ${{u}_{n}} = {{u}_{{{\zeta }}}}$, ${{u}_{\tau }} = \left( {{{u}_{x}},{{u}_{y}}} \right)$, и введем параметризацию искомого поля δu:

где введен антисимметричный тензор Леви–Чивиты ${{e}_{{ab}}} = - {{e}_{{ba}}},{{e}_{{12}}} = 1$, а x^a – координаты, выбранные на поверхности трещины. Отметим, что такая параметризация возможна для вектора смещения также и на любой искривленной поверхности.

Функции ψ и τ содержат как продольную, так и поперечную компоненты упругой волны, а χ – только поперечную. Компоненты тензора напряжений в (3) принимают вид

Выражение (10) в случае плоской поверхности трещины сводится к двум независимым комбинациям:

Выразим ${\text{div}}\,\delta {\mathbf{u}}$ через новые параметры: div δu = = ${{\partial }_{\zeta }}\psi + {{\Delta }_{2}}\tau ,$ где ${{\Delta }_{2}}\tau = {{{{\delta }}}_{{ab}}}{{\partial }_{a}}{{\partial }_{b}}\tau = \partial _{a}^{2}\tau $. Тогда из (3), (9), (10) получим:

Поскольку метрика вблизи ребра трещины не сводится к простой евклидовой форме, то уравнения (11)–(13) следует дополнить условиями на ребре, в простейшем случае – требованием непрерывности на ребре функций ψ, τ и χ и их производных. Это соответствует предельному случаю сжатия в диск полости с гладкой границей в виде сплюснутого эллипсоида вращения. В более общем случае производные или комбинация функций и их производных испытывают разрыв, и ребро будет содержать дополнительный дельта-источник, что соответствует дополнительным напряжениям на ребре.

Разделим смещение u на продольную и поперечную части: ${\mathbf{u}} = {{{\mathbf{u}}}^{l}} + {{{\mathbf{u}}}^{t}},{\text{div}}\,{{{\mathbf{u}}}^{t}} = 0,$ так что ${{{\mathbf{u}}}^{l}}\, = \,\nabla f$, ${{{\mathbf{u}}}^{t}} = {\mathbf{u}} - \nabla f.$ Тогда из (1) приходим к уравнениям Гельмгольца:

где ${{K}^{2}} = \frac{{{{\omega }^{2}}}}{{c_{l}^{2}}},{{{{\unicode{230} }}}^{2}} = \frac{{{{\omega }^{2}}}}{{c_{t}^{2}}}$ , т.е. ${{K}^{2}}\left( {\lambda + 2\mu } \right) = {{{{\unicode{230} }}}^{2}}\mu $.

Далее используем дополнительную параметризацию, вводя скалярную функцию h:

Необходимо отметить, что аналогичная параметризация введена в [11], но там она охватывала только плоские поверхности. Выполненная здесь поэтапная параметризация позволяет сделать обобщение сразу на случай любых кривых поверхностей.

Далее, поскольку ${\text{div}}\,{\mathbf{u}} = \Delta f = - {{K}^{2}}f$, то через h и f можно выразить и функцию ψ:

Последнее выражение с точностью до произвольной функции от (x, y) дает искомую связь¹¹:

Подставляя выражения для ψ и τ в систему уравнений (11)–(13), приведем граничные условия на поверхности трещины к окончательному виду: при ζ = 0

Здесь функции в правых частях задаются падающей волной ${{g}_{1}} = \left( {\frac{\lambda }{{2\mu }}{\text{div}}\,{{{\mathbf{u}}}^{0}} + {{\partial }_{\zeta }}u_{\zeta }^{0}{\text{\;}}} \right)$, Δ₂g₂ = = $ - \frac{1}{2}\left[ {\frac{\partial }{{\partial \zeta }}\left( {\frac{{\partial u_{x}^{0}}}{{\partial x}}\, + \,\frac{{\partial u_{y}^{0}}}{{\partial y}}} \right)\, + \,{{\Delta }_{2}}u_{\zeta }^{0}} \right]$ и ${{g}_{3}} = - {{\partial }_{\zeta }}({{\partial }_{y}}u_{x}^{0} - {{\partial }_{x}}u_{y}^{0}).$ Таким образом, в задаче о рассеянии объемной волны (продольной или поперечной с любой поляризацией) на плоской трещине любой формы граничные условия сведены к системе уравнений (17), (18) для скалярных функций f и h и независимому от них уравнению (19) для скалярной функции χ. Эти функции можно назвать потенциалами, причем f соответствует продольной волне, а h и χ – поперечным волнам, поляризованным во взаимно перпендикулярных плоскостях.

В 2D-случае, как на рис. 1б, получаем $\frac{{\partial f}}{{\partial y}} = \frac{{\partial h}}{{\partial y}}$ = 0, и потенциалы f и h определяют смещения в продольной и вертикально (SV) поляризованной поперечной волнах, соответственно, а потенциал χ – смещения в горизонтально (SH) поляризованной поперечной волне. В 3D-случае $\frac{{\partial f}}{{\partial y}} \ne 0$, $\frac{{\partial h}}{{\partial y}} \ne 0$, $\frac{{\partial \chi }}{{\partial y}} \ne 0$, и все три потенциала f, h и χ определяют смещения, которые могут происходить как в плоскости падения, так и в плоскости трещины. Последнее имеет место, например, при рассеянии упругой волны на диске при произвольной ориентации волнового вектора падающей волны.

При отсутствии падающей волны ${{{\mathbf{u}}}^{0}} = 0$ (т.е. ${{g}_{1}} = {{g}_{2}} = {{g}_{3}} = 0$) уравнение (19) имеет только тривиальное решение χ = 0, а система уравнений (17), (18), как будет показано ниже, имеет решение, соответствующее волнам Рэлея, которые распространяются вдоль трещины и затухают внутри объема.

3. ОБЩЕЕ РЕШЕНИЕ ДЛЯ РАССЕЯННОГО ПОЛЯ

Рассматриваемая задача допускает точное решение в случае, когда поверхность трещины позволяет построить в явном виде базис собственных функций оператора Лапласа (скалярные гармоники трещины):

Например, это возможно для трещины в виде диска.

Разложим скалярные функции f, h и χ по гармоникам типа $\chi = \Sigma {{\chi }_{k}}{{\Psi }_{k}}$. Уравнения (14), (15) вблизи трещины имеют вид

Отсюда следуют зависимости от ζ вида f_k(ζ) = = ${{e}^{{ - {{p}_{l}}\zeta }}}{{f}_{k}}$, ${{h}_{k}}(\zeta ) = {{e}^{{ - {{p}_{t}}\zeta }}}{{h}_{k}},{{\chi }_{k}}(\zeta ) = {{e}^{{ - {{p}_{t}}\zeta }}}{{\chi }_{k}}$, где коэффициенты в показателях экспонент определяются из соотношений

Данный выбор комплексных значений для p_l и p_t соответствует условию излучения, а действительных значений – затуханию внутрь объема. В итоге получим систему алгебраических уравнений

Теперь из уравнений (17)–(19) легко получить явный вид потенциалов f, h и χ в окрестности поверхности трещины:

где введено обозначение

Здесь интеграл берется по всей поверхности трещины.

4. СКАЛЯРНЫЕ ГАРМОНИКИ ДЛЯ ТРЕЩИНЫ В ВИДЕ ДИСКА

Рассмотрим для определенности рассеяние упругой волны на трещине в виде диска. Чтобы найти скалярные гармоники, удобно сначала отобразить поверхность трещины на всю плоскость Oxy. Это можно сделать, если ввести метрику [12]

где масштабная функция

В области r < a имеем стандартную плоскую метрику, которая соответствует стороне диска $z = + 0$, тогда как метрика в области r > a при замене $\tilde {r} = \frac{{{{a}^{2}}}}{r}$ переходит в метрику

которая снова соответствует плоской области $\tilde {r} < a$, т.е. стороне диска $z = - 0$. На ребре r = a метрика содержит положительную дельта-подобную кривизну.

Сначала найдем собственные значения. С учетом представленной метрики решение уравнения вида $ - {{\Delta }_{2}}{{\Psi }_{j}} = k_{j}^{2}{{\Psi }_{j}}$ удобно искать в полярной системе координат:

где $n = 0,1,2,...$ Подставляя собственные значения ${{\lambda }_{n}} = {{n}^{2}}$, получаем уравнение

В области $r < a$ имеем ρ = 1 и приведенное выше уравнение заменой $x = {{x}^{ + }} = kr$ сводится к уравнению Бесселя порядка n. Его решением являются либо функции Бесселя J_n(x) и функции Неймана N_n(x), либо функции Ханкеля первого и второго рода $H_{n}^{ \pm }(x)$. В области $r < a$ запишем это решение в виде

В области $r > a$ имеем $\rho = \frac{{{{a}^{2}}}}{{{{r}^{2}}}}$ и уравнение на собственные функции сводится к уравнению Бесселя заменой $x = {{x}^{ - }} = \frac{{k{{a}^{2}}}}{r}$, а решение запишем в виде

Имея в виду дельта-подобную кривизну на ребре, в общем случае гармоники можно строить для оператора Лапласа–Бельтрами $({{\Delta }_{2}} + cP)\Psi $ = = k²Ψ, где c – произвольная константа, а P – скалярная кривизна поверхности. Однако при c ≠ 0 производные на ребре будут содержать разрыв, что приведет к появлению дельта-источников на ребре (8), (16). Требование ограниченности поля смещения приводит к условию c = 0. Следует также сделать еще одно важное замечание. В используемой параметризации потенциалы и поле смещения являются непрерывными вместе со своими производными. При этом можно осуществить непрерывный предельный переход от некоторой гладкой поверхности к поверхности с ребром (в частности, выбирая семейство функций ρ(r) в приведенной выше метрике). Однако в терминах декартовых координат x, y, z в результате предельного перехода компоненты поля смещения δu будут испытывать конечный разрыв на ребре. Это легко увидеть, используя связь $\zeta = \left| z \right|$, что приводит к соотношению $\delta {{u}_{z}} = \pm \psi $, где знак зависит от знака z. Непрерывность ψ соответствует появлению конечного скачка в δu_z. Аналогичный конечный скачок появляется и в компонентах δu_x и δu_y.

Итак, условия на ребре сводятся к непрерывности потенциалов и их производных на ребре. Это означает, что они должны совпадать при r = a:

Здесь знаки ± относятся к областям r < a и r > a соответственно. Минус в последнем уравнении означает, что когда r растет, мы получаем вторую теневую поверхность трещины, при этом ${{\left. {\frac{{dx}}{{dr}}} \right|}_{a}}$ = –k $\left( {\frac{{^{{}}}}{{}}} \right.$при $r > a$ мы имеем $x = {{x}^{ - }} = \left. {\frac{{k{{a}^{2}}}}{r}} \right)$.

Теперь необходимо потребовать, чтобы решение было конечным. Поэтому $B_{n}^{ \pm } = 0$ и с учетом (27), (28), получим

Здесь $J_{n}^{'}\left( {ka} \right) = \frac{d}{{d\left( {kx} \right)}}{{J}_{n}}\left( {kx} \right){{{\text{|}}}_{a}}$.

Эти соотношения определяют спектр (собственные значения) оператора Лапласа и формы основных скалярных гармоник на трещине. Собственные значения k_j разделяются на две серии. Первая соответствует собственным значениям k_s, заданным уравнением $J_{n}^{'}\left( {{{k}_{s}}a} \right)$ = 0, и собственные функции принимают вид

Вторая серия соответствует собственным значениям k_a, заданным уравнением ${{J}_{n}}\left( {{{k}_{a}}a} \right) = 0$, и собственные функции принимают вид

Коэффициенты A_n определяются из условий нормировки

и дают

5. ПРИМЕР: РАССЕЯНИЕ SH-ВОЛНЫ НА ДИСКЕ

Итак, любая скалярная функция на трещине M может быть разложена по базису Ψ_nj(r, ϕ) = = ${{Y}_{{nj}}}(r){{{{\Phi }}}_{n}}(\phi )$ следующим образом:

где

Приведенные выражения позволяют записать общее решения для всех трех потенциалов. В явном виде оно представляет собой довольно громоздкую конструкцию. Поэтому здесь для примера рассмотрим рассеяние на дискообразной трещине поперечной SH-волны вида

Здесь $s = \sqrt {{{\kappa }^{2}} - k_{z}^{2}} ~$, а r_< и r_> обозначают большую и меньшую величину из r и r₀. Тогда из (26) χ = = $\sum\nolimits_k^{} {{{e}^{{ - {{p}_{t}}\zeta }}}{{\chi }_{k}}{{\Psi }_{k}}(x),} $ и разложение по гармоникам диска ${{\chi }_{k}} = {{\chi }_{{nj}}}$ принимает вид

где ${{n}_{z}} = \pm 1$. Будем полагать ${{r}_{0}} > a > r.$ Тогда получим где ${{C}_{n}}\left( {{{k}_{a}},s} \right) = \mathop \smallint \limits_0^a {{J}_{n}}\left( {{{k}_{a}}r} \right){{J}_{n}}\left( {sr} \right)rdr~$ – коэффициенты разложения падающей волны, а поле в окрестности трещины имеет вид

Заметим, что здесь количество слагаемых конечно: учтены только члены с комплексными показателями, поскольку только они описывают поток энергии от трещины. Все остальные члены затухают внутри объема.

Далее, из (6) для рассеянной волны во всем объеме получим выражение

или где коэффициенты разложения имеют вид

Здесь $r_{ < }^{'}$ и $r_{ > }^{'}$ соответствуют наибольшей и наименьшей из $r,r'$. Полагая в точке наблюдения $r > a$, получим окончательно в явном виде выражение для коэффициентов разложения:

где $s = \sqrt {{{\kappa }^{2}} - k_{z}^{2}} $ и $s{\kern 1pt} ' = \sqrt {{{\kappa }^{2}} - k_{z}^{{'2}}} .$

ЗАКЛЮЧЕНИЕ

Таким образом, соотношения (24)–(26) вместе с (6) полностью определяют потенциалы $f,~h,\chi $ и смещение в рассеянной волне δu в зависимости от параметров падающей волны (в рассмотренном примере (29) – сферической). Расчеты по этим соотношениям сводятся к вычислениям в квадратурах. Выражения (24)–(26) представляют собой вынужденные колебания трещины под воздействием внешней падающей волны u⁰. Эти колебания, вообще говоря, не всегда приводят к излучению волн, т.е. наличию потока энергии от трещины. Для получения дифракционной картины на достаточном удалении от трещины следует учитывать не все члены суммы (24)–(26), а только первые члены, соответствующие комплексным значениям показателей ${{p}_{l}}$ и ${{p}_{t}}~$ в (20), т.е. ограничивая суммы максимальным значением ${{k}^{2}} < {{K}^{2}},{{{{\unicode{230} }}}^{2}}$. Члены с действительными значениями показателей затухают в направлении нормали и не дают вклада в поток энергии внутрь объема от трещины. Часть подобных членов в (24), (25) отвечает возбуждению волн Рэлея [13, 14], которые для рассеянного поля не дают вклада в дифракционную картину, хотя и поглощают часть падающей на трещину энергии. В самом деле, при ${{k}^{2}} > {{K}^{2}}$ оба корня в (20) действительные, и знаменатель в (24), (25) обращается в нуль ${{\Lambda }}\left( {{{\omega }},k} \right) = 0$ при ${{\omega }} = ck$, где скорость соответствующей поверхностной волны определяется уравнением

Раскладывая знаменатель Λ(ω, k) в ряд, получим

где ${{\Lambda '}} = {{\left. {\frac{{d{{\Lambda }}\left( {{{\omega }},k} \right)}}{{d({{{{\omega }}}^{2}})}}} \right|}_{{\omega = ck}}}$.

Здесь первый член соответствует интегралу в смысле главного значения, а второй, содержащий дельта-функцию, соответствует волнам Рэлея. Для диска конечного радиуса спектр возможных значений $k_{j}^{2}$ является дискретным. Это означает, что резонансные члены будут возникать только на дискретном наборе частот.