Доклады Российской академии наук. Физика, технические науки, 2021, T. 499, № 1, стр. 22-24

Рассмотрим вопрос об высокочастотных эффективных магнитных параметрах композитной среды, в которой магнитные частицы помещены в матрицу из немагнитного материала. Обзор результатов для случая, когда внешнее магнитное поле отсутствует, дан в работе [1]. В магнитном поле динамическая магнитная проницаемость – это тензорная величина, и для описания резонансных явлений важны как диагональные, так и недиагональные компоненты этого тензора. Если магнитные частицы по форме отличаются от сферы, то для описания ширины и формы линии необходим учет пространственной ориентации частиц. Эти проблемы решаются в данном сообщении. Рассмотрены частицы в форме эллипсоида, параметры которого изменяются в широких пределах, и предложенный метод позволяет выполнить расчет проницаемости композитов с частицами различной формы, в том числе далекой от сферической.

Будем рассматривать среду, магнитные свойства любого элементарного объема которой будут считаться одинаковыми. Размеры этого объема много меньше таких характерных пространственных масштабов задачи, как длина распространяющейся в среде электромагнитной волны и размеры образца, но много больше размера любой содержащейся в нем магнитной частицы. Намагниченность композитной среды характеризуется количеством магнитного вещества, т.е. его объемной долей ${{\theta }_{{v}}}$, которая предполагается одинаковой для любого элементарного объема среды. Для такого вида композитной среды могут быть введены определенные усредненные или эффективные параметры.

Предположим, что свойства ферромагнитных частиц в композитной среде описываются тензором магнитной проницаемости ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }}$. Для определения тензора магнитной проницаемости композитной среды ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }}}^{m}}$ используем одну из моделей смешения на основе приближения степенными законами. Простейшее из таких приближений основано на использовании линейного закона или формулы Зильберштейна [2], что приводит к соотношению

где ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} }} = {{\delta }_{{ij}}}$ – единичный тензор, ${{\delta }_{{ij}}}$ – дельта-функция Кронекера. Формула (1) справедлива при ${{\theta }_{{v}}} \ll 1$, а при учете изменений среднего поля из-за присутствия магнитных частиц, область ее применения может быть расширена в сторону бóльших концентраций, как это показано ниже.

Для частиц в виде эллипсоидов вращения общего вида тензор ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }}$ имеет следующий вид [3]:

Здесь используются обозначения: ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {N} }}$ – тензор размагничивания с элементами N_ij, $tr{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {N} }} = 1$; ${{\omega }_{H}}$ = = γH_z, ${{\omega }_{M}} = 4\pi \gamma {{M}_{z}}$, где $\alpha $ – параметр диссипации, $\omega $ – круговая частота, $\gamma $ – гиромагнитное отношение для электрона, H_z – постоянное поле намагничивания, направленное вдоль оси z, M_z – проекция постоянного поля намагничивания на ось z. Заметим, что модуль вектора ${\mathbf{M}}$ равен намагниченности насыщения материала.

Тензор размагничивания для некоторой магнитной частицы определяет отличие магнитного поля внутри нее от заданного внешнего магнитного поля в окружающей частицу немагнитной среде. Магнитное поле в элементарном объеме однородной композитной среды фактически является результатом усреднения полей внутри и вне магнитных частиц, располагающихся в этом объеме. Если ${{\theta }_{{v}}} \ll 1$, то среднее поле мало отличается от поля в немагнитной среде. Однако по мере увеличения ${{\theta }_{{v}}}$ отличие этих полей становится все больше. Такого рода изменения в композитной среде при различных значениях объемной доли ${{\theta }_{{v}}}$ должны учитываться посредством введения эффективного тензора размагничивания ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {L} }}$, который зависит от ${{\theta }_{{v}}}$ следующим образом: при ${{\theta }_{{v}}} \to 0$ используется тензор ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {L} }} \approx {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {N} }}$, где тензор ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {N} }}$ определен для единственной частицы заданной формы, в то время как при ${{\theta }_{{v}}} \to 1$ выполняется равенство ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {L} }} \approx {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {0} }}$, что соответствует неограниченной магнитной среде. Согласно [4], соответствующий эффективный тензор размагничивания может быть определен как

Подставляя (1) в (3) и пренебрегая, в первом приближении, влиянием тензора ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }}$ на ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {L} }}$, получаем, что

Таким образом, тензор магнитной проницаемости композитной среды ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }}}^{m}}$ будет определяться выражением (1), в котором элементы тензора ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }}$ соответствуют формулам (2), но с заменой соответствующих элементов тензора ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {N} }}$ на ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {L} }}$, согласно соотношению (4). Окончательно можно записать, что

При анализе распространения электромагнитных волн в поперечно намагниченной среде, когда поле намагничивания направлено перпендикулярно и переменному магнитному полю, и волновому вектору электромагнитной волны, необходимо использовать скалярную величину – эффективную магнитную проницаемость ${{\mu }_{{eff}}}$ [3]. Если мы рассматриваем композитную среду, характеризуемую тензором магнитной проницаемости вида (5), то можно показать, что

Для получения усредненного тензора магнитной проницаемости композитной среды $\left\langle {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }}}}^{m}}} \right\rangle $ в случае произвольно ориентированных эллипсоидальных частиц нужно провести статистическое усреднение его элементов с учетом различной пространственной ориентации ферромагнитных частиц, которая может быть определена введением параметров ${\mathbf{\Theta }} = \left( {\begin{array}{*{20}{c}} \alpha &\beta &\gamma \end{array}} \right)$ – векторов углов поворота ферромагнитных частиц относительно осей x, y, z на углы α, $\beta $, $\gamma $ соответственно. Он обусловливает, во-первых, изменение тензора размагничивания частицы ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {N} }}\left( {\mathbf{\Theta }} \right)$ при изменении ее ориентации в пространстве, во-вторых, изменение величины M_z, а следовательно, и ${{\omega }_{M}}\left( {\mathbf{\Theta }} \right)$, при таком изменении. Усредненное значение эффективной магнитной проницаемости $\left\langle {{{\mu }_{{eff}}}} \right\rangle $ композитной среды находится путем усреднения выражения (6) по всем возможным значениям углов ориентации магнитных частиц α, $\beta $, $\gamma $.

Результаты расчетов для нескольких значений ${{\theta }_{{v}}}$ и различной формы частиц (с разными отношениями длин полуосей эллипсоидов a, b, c) показаны на рис. 1. Использованные при расчетах формулы для тензоров размагничивания частиц в форме эллипсоидов вращения общего вида приведены в [5]. Расчет эффективной магнитной проницаемости намагниченного композита был выполнен для ансамбля из 10 000 частиц из материала с намагниченностью насыщения 4πM_s = = 7.04 кГс и постоянной магнитного затухания α = 0.05, частота f = 30 ГГц. Наблюдаются изменения эффективной магнитной проницаемости, связанные с ферромагнитным резонансом.

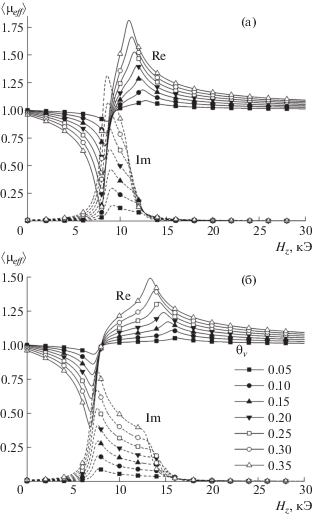
Из рис. 1 видно, что резонанс занимает широкую область магнитных полей, несмотря на малое значение постоянной α. Рассмотренный метод определения эффективной проницаемости использован при анализе прохождения микроволн через композитную среду, содержащую чешуйки из сплава Fe–Si–Nb–Cu–B [6, 7].