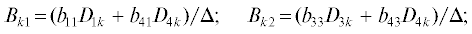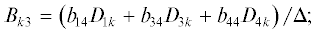Доклады Российской академии наук. Физика, технические науки, 2022, T. 505, № 1, стр. 59-65

ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС ТРЕХСЛОЙНОЙ ЦИЛИНДРИЧЕСКОЙ КОМПОЗИТНОЙ ОБОЛОЧКИ, ПОДКРЕПЛЕННОЙ ПРОДОЛЬНЫМИ РЕБРАМИ И ЦИЛИНДРОМ, ПРИ ДЕЙСТВИИ ИЗМЕНЯЮЩЕЙСЯ ВО ВРЕМЕНИ ОСЕВОЙ СИЛЫ

В. Н. Бакулин^1, *, А. Я. Недбай²

¹ Институт прикладной механики Российской академии наук
Москва, Россия

² АО Корпорация “Московский институт теплотехники”
Москва, Россия

^* E-mail: vbak@yandex.ru

Поступила в редакцию 30.12.2021
После доработки 30.12.2021
Принята к публикации 28.01.2022

EDN: CNTZYR
DOI: 10.31857/S2686740022030026

Полный текст (PDF)

Аннотация

Предложена модель для исследования параметрического резонанса подкрепленной продольными ребрами трехслойной композитной цилиндрической оболочки с несимметричным пакетом слоев, по внутренней поверхности скрепленной с упругим пустотелым цилиндром, при действии внешнего давления и изменяющихся во времени осевых сил. Получены уравнения и рассмотрены основные этапы решения задачи c помощью предложенной комбинации методов. Впервые построены зависимости критических частот главных областей неустойчивости и исследовано влияние на них жесткости внутреннего цилиндра, количества продольных ребер, жесткости заполнителя трехслойной цилиндрической оболочки. Разработанная математическая модель значительно расширяет круг решаемых актуальных научных и прикладных задач и позволяет впервые провести исследования одновременного влияния продольных ребер и внутреннего цилиндра на границы областей неустойчивости для трехслойных цилиндрических оболочек, являющихся перспективными элементами конструкций ракетно-космической и другой современной техники.

Ключевые слова: трехслойная цилиндрическая оболочка, несимметричный пакет слоев, продольные ребра, параметрический резонанс, изменяющиеся во времени осевые силы

ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧИ

Трехслойные композитные оболочки являются перспективными элементами конструкций ракетно-космической техники (РКТ), в том числе твердотопливных двигателей (РДТТ) [1–3]. Это объясняется высокими показателями весовой эффективности, изгибной жесткости, тепловой защиты, а также возможностями регулирования этих и многих других важных характеристик.

На трехслойный корпус воздействуют осевые силы (в виде тяги двигателей, лобового сопротивления воздуха и инерционных сил), изменяющиеся во времени, а также внешнее давление воздушных потоков [4]. При определенных значениях и сочетаниях этих нагрузок возможно возникновение параметрического резонанса [5] и разрушение конструкции.

Три вида потери устойчивости трехслойных оболочек в зависимости от жесткости заполнителя при действии осевой сжимающей силы рассмотрено в работе [6].

Для повышения критической нагрузки потери устойчивости трехслойные оболочки могут быть усилены продольными ребрами (стрингерами).

Установка в трехслойной оболочке продольных ребер позволяет решить сразу несколько следующих важных задач:

– дает возможность использовать широкий класс легких заполнителей, что приводит к уменьшению массы конструкции;

– допускает установку бортовой кабельной сети внутри ребер, что значительно повышает устойчивость этой сети к электромагнитному и рентгеновскому излучению;

– значительно увеличить критическую силу потери устойчивости при незначительном увеличении массы;

– в случае повреждения наружной оболочки твердыми частицами или мощным тепловым излучением продольные ребра принимают на себя действие осевой силы.

Проблеме динамической устойчивости посвящен ряд работ [7–9 и др.], в том числе для гладких [10–12] и подкрепленных [7, 13–15] оболочек. Однако параметрический резонанс трехслойных оболочек, подкрепленных продольными ребрами жесткости, остается практически не исследованным.

В представленном сообщении предложена математическая модель, впервые получены уравнения и рассмотрены основные этапы решения задачи c помощью предложенной комбинации методов для исследования параметрического резонанса подкрепленной продольными ребрами трехслойной композитной цилиндрической оболочки с несимметричным пакетом слоев, по внутренней поверхности скрепленной с упругим пустотелым цилиндром, при действии внешнего давления и изменяющихся во времени осевых сил.

С помощью разработанной математической модели определяется возникновение параметрического резонанса, который может привести к разрушению конструкции.

Рассматриваемая математическая модель значительно расширяет круг решаемых актуальных научных и прикладных задач и позволяет впервые провести исследования одновременного влияния продольных ребер и внутреннего цилиндра на границы областей неустойчивости трехслойных цилиндрических оболочек, являющихся перспективными элементами конструкций ракетно-космической и другой современной техники.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Рассмотрим трехслойную цилиндрическую оболочку с несимметричным пакетом слоев и легким заполнителем, подкрепленную продольными ребрами и упругим пустотелым цилиндром, при действии внешнего давления и осевой силы, изменяющейся во времени по гармоническому закону. Торцы оболочки шарнирно оперты, а внешняя поверхность нагружена постоянным давлением. Будем считать, что ребра связывают оба несущих слоя в осевом и радиальном направлениях и расположены сравнительно редко. При этом взаимным влиянием тангенциальных контактных усилий и радиальных инерционных сил можно пренебречь. Цилиндр представляется безинерционным упругим основанием Винклера, коэффициент постели которого определяется из уравнений трехмерной теории упругости [15].

Введем безразмерную систему цилиндрических координат, в которой за координатную поверхность принята срединная поверхность заполнителя. Тогда уравнения движения оболочки можно представить в виде [15]

${{L}_{{i1}}}{{u}_{\alpha }} + {{L}_{{i2}}}{{{v}}_{\alpha }} + {{L}_{{i3}}}w + {{L}_{{i4}}}{{u}_{\beta }} + {{L}_{{i5}}}{{{v}}_{\beta }} + $

(1)

$\begin{gathered} + \,({{\delta }_{{i1}}} + {{\delta }_{{i3}}} + {{\delta }_{{i4}}}) \times \\ \times \,\mathop \sum \limits_{j = 1}^M \left[ {l_{{i1}}^{{\left( j \right)}}{{u}_{{\alpha j}}} + l_{{i3}}^{{\left( j \right)}}{{w}_{j}} + l_{{i4}}^{{\left( j \right)}}{{u}_{{\beta j}}}} \right]\delta \left( {\beta - {{\beta }_{j}}} \right) = 0 \\ \end{gathered} $

(i = 1, 2, …, 5),

где ${{u}_{\alpha }}\, = \,\frac{{{{u}_{1}} + {{u}_{2}}}}{2}$, ${{u}_{\beta }}\, = \,\frac{{{{u}_{1}} - {{u}_{2}}}}{2}$, ${{{v}}_{\alpha }} = \frac{{{{{v}}_{1}} + {{{v}}_{2}}}}{2}$, ${{{v}}_{\beta }} = \frac{{{{{v}}_{1}} - {{{v}}_{2}}}}{2},$ ${{u}_{1}},{{u}_{2}},{{{v}}_{1}},{{{v}}_{2}}$ – осевые и тангенциальные перемещения срединных поверхностей верхнего (индекс 1) и нижнего (индекс 2) несущих слоев соответственно, w – прогиб трехслойной оболочки; ${{L}_{{ij}}}$, ${{l}_{{ij}}}$ – дифференциальные операторы, имеющие вид (вид других операторов и обозначений аналогичен приведенным в работе [15])

$\begin{gathered} {{L}_{{33}}} = \frac{{{{D}_{{11}}}}}{{{{R}^{2}}}}\frac{{{{\partial }^{4}}}}{{\partial {{\alpha }^{4}}}} + \frac{{2\left( {{{D}_{{12}}} + {{D}_{{33}}}} \right)}}{{{{R}^{2}}}}\frac{{{{\partial }^{4}}}}{{\partial {{\alpha }^{2}}\partial {{\beta }^{2}}}} + \\ + \frac{{{{D}_{{22}}}}}{{{{R}^{2}}}}\frac{{{{\partial }^{4}}}}{{\partial {{\beta }^{4}}}} - \frac{{h_{0}^{2}}}{h}\left( {{{G}_{{13}}}\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}} + {{G}_{{23}}}\frac{{{{\partial }^{2}}}}{{\partial {{\beta }^{2}}}}} \right) + \\ \end{gathered} $

$\begin{gathered} + \,{{\theta }_{1}}\left( {{{T}_{0}} + {{T}_{1}}{\text{cos}}\omega t} \right)\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}} + \Pi {{R}^{2}} + \\ + \,{{B}_{{22}}} + {{F}_{0}}{{R}^{2}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + PR\frac{{{{\partial }^{2}}}}{{\partial {{\beta }^{2}}}}; \\ \end{gathered} $

$l_{{11}}^{{\left( j \right)}} = \frac{{{{E}_{j}}{{F}_{j}}}}{R}\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}};\quad l_{{13}}^{{\left( j \right)}} = l_{{31}}^{{\left( j \right)}} = 0;$

$l_{{14}}^{{\left( j \right)}} = l_{{41}}^{{\left( j \right)}} = - 2\frac{{{{\varepsilon }_{j}}{{E}_{j}}{{F}_{j}}}}{{R{{h}_{0}}}}\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}};$

$l_{{33}}^{{\left( j \right)}} = - \frac{{{{a}_{j}}}}{R}\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}} + {{\rho }_{j}}{{F}_{j}}R\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + \frac{{{{\theta }_{2}}}}{R}\left( {{{T}_{0}} + {{T}_{1}}\cos \omega t} \right)\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}};$

$\begin{gathered} l_{{34}}^{{\left( j \right)}} = l_{{43}}^{{\left( j \right)}} = - \frac{{2{{a}_{j}}}}{{{{h}_{0}}}}\frac{\partial }{{\partial \alpha }};~ \\ l_{{44}}^{{\left( j \right)}} = - \frac{4}{{Rh_{0}^{2}}}\left[ {{{a}_{j}}{{R}^{2}} - {{E}_{j}}(\varepsilon _{j}^{2}{{F}_{j}} + {{I}_{j}})\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}}} \right]; \\ \end{gathered} $

${{\theta }_{1}}~ = \frac{{E_{1}^{В}{{h}_{1}} + E_{1}^{Н}{{h}_{2}}}}{{2\pi R(E_{1}^{В}{{h}_{1}} + E_{1}^{Н}{{h}_{2}}) + \sum\limits_{j = 1}^M {{{E}_{j}}{{F}_{j}}} }};$

${{\theta }_{2}} = \frac{{\sum\limits_{j = 1}^M {{{E}_{j}}{{F}_{j}}} }}{{2\pi R(E_{1}^{В}{{h}_{1}} + E_{1}^{Н}{{h}_{2}}) + \sum\limits_{j = 1}^M {{{E}_{j}}{{F}_{j}}} }};$

$\begin{gathered} ~{{B}_{{ss}}} = B_{s}^{B} + B_{s}^{H};\quad {{D}_{{ss}}} = D_{s}^{B} + D_{s}^{H}\quad (s = 1,{\text{\;}}2,{\text{\;}}3); \\ B_{1}^{B} = \frac{{E_{1}^{B}{{h}_{1}}}}{{{{\eta }^{B}}}};\quad B_{2}^{B} = E_{2}^{B}{{h}_{1}}{\text{/}}{{\eta }^{B}}; \\ \end{gathered} $

$\begin{gathered} B_{3}^{B} = G_{{12}}^{B}{{h}_{1}};\quad {{D}_{{12}}} = D_{1}^{B}\nu _{2}^{B} + D_{1}^{H}\nu _{2}^{H}; \\ D_{1}^{В} = E_{1}^{В}h_{1}^{3}{\text{/}}(12{{\eta }^{В}});\quad D_{2}^{B} = E_{2}^{B}h_{1}^{3}{\text{/}}(12{{\eta }^{B}}); \\ \end{gathered} $

$\begin{gathered} ~D_{3}^{B} = G_{{12}}^{B}h_{1}^{3}{\text{/}}6;\quad {{z}_{0}} = {{R}_{0}}{\text{/}}R; \\ {{a}_{i}} = 5{{G}_{j}}{{F}_{j}}{\text{/}}6;~\quad {{F}_{0}} = {{\rho }^{B}}{{h}_{1}} + {{\rho }^{H}}{{h}_{2}} + h{{\rho }_{0}}; \\ \end{gathered} $

${{\eta }^{B}} = 1 - \nu _{1}^{B}\nu _{2}^{B};$

${{h}_{0}} = h + \left( {{{h}_{1}} + {{h}_{2}}} \right){\text{/}}2;\quad 2{{\varepsilon }_{i}} = r_{j}^{B} + r_{j}^{H};$

$\alpha ,\,~\beta $ – безразмерные координаты вдоль образующей и в окружном направлении срединной поверхности заполнителя, принятой за координатную поверхность; $R,~{{R}_{0}}$ – радиусы срединной поверхности заполнителя и внутренний радиус цилиндра (радиус канала цилиндра) соответственно; ${{h}_{1}},~{{h}_{2}},~h$ – соответственно толщина верхнего, нижнего и среднего слоев; $E_{1}^{B},~E_{2}^{B},~G_{{12}}^{B},~\nu _{1}^{B},~\nu _{2}^{B}$ – соответственно осевой и окружной модули упругости, модуль сдвига и коэффициенты Пуассона верхнего слоя (обозначения для нижнего слоя с индексом “Н” имеют аналогичный смысл); ${{G}_{{13}}},~{{G}_{{23}}}$ – модули поперечного сдвига заполнителя; ${{\rho }^{B}},~{{\rho }^{H}},~{{\rho }_{0}}$ – плотности материалов верхнего, нижнего и среднего слоев; ${{E}_{j}},~{{G}_{j}},~{{\rho }_{j}}$ – модуль упругости, модуль сдвига и плотность материала j-го ребра; ${{F}_{j}},~{{I}_{j}}$ – площадь и момент инерции ребра; M – количество ребер; П – коэффициент постели; T₀ – постоянная составляющая осевой силы; T₁ – амплитуда переменной составляющей осевой силы; $\delta \left( \beta \right)$ – дельта-функция; ${{\delta }_{{kj}}}$ – символ Кронекера; $r_{j}^{B},~r_{j}^{H}$ – соответственно расстояния от оси ребра до срединной поверхности верхнего и нижнего слоев, причем эта величина считается положительной, если ось ребра лежит ниже срединной поверхности несущего слоя; P – внешнее давление.

Решение уравнений (1) будем искать в виде

$\left\{ {{{u}_{\alpha }},~{{u}_{\beta }}} \right\} = \cos \gamma \alpha \mathop \sum \limits_{n = 0}^\infty \left\{ {{{f}_{{1n}}}\left( t \right),~{{f}_{{4n}}}\left( t \right)} \right\}\cos n\beta ;$

$\left\{ {{{{v}}_{\alpha }},~{{{v}}_{\beta }}} \right\} = \sin \gamma \alpha \mathop \sum \limits_{n = 0}^\infty \left\{ {{{f}_{{2n}}}\left( t \right),~{{f}_{{5n}}}\left( t \right)} \right\}\sin n\beta ;$

(2)

$w = \sin \gamma \alpha \mathop \sum \limits_{n = 0}^\infty {{f}_{{3n}}}\left( t \right)\cos n\beta ,$

где $\gamma = m\pi {\text{/}}{{\alpha }_{0}}$; ${{\alpha }_{0}} = L{\text{/}}R$; L – длина оболочки; f_jn(t) – неизвестные функции времени (в дальнейшем аргумент t опускается); m – количество полуволн в осевом направлении; n – количество волн в окружном направлении.

Раскладывая дельта-функцию в тригонометрический ряд

$\delta \left( {\beta - {{\beta }_{j}}} \right) = \frac{1}{\pi }\left[ {\frac{1}{2} + \mathop \sum \limits_{n = 1}^\infty \cos n\left( {\beta - {{\beta }_{j}}} \right)} \right]$

и подставляя (2) в (1), получим неоднородную систему дифференциальных уравнений типа Матье–Хилла:

${{a}_{{11}}}{{f}_{{1n}}} + {{a}_{{12}}}{{f}_{{2n}}} + {{a}_{{13}}}{{f}_{{3n}}} + {{a}_{{14}}}{{f}_{{4n}}} + {{a}_{{15}}}{{f}_{{5n}}} = $

$ = - \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\mathop \sum \limits_{j = 1}^M ({{b}_{{11}}}{{f}_{{1j}}} + {{b}_{{14}}}{{f}_{{4j}}})\cos n{{\beta }_{j}};$

${{a}_{{21}}}{{f}_{{1n}}} + {{a}_{{22}}}{{f}_{{2n}}} + {{a}_{{23}}}{{f}_{{3n}}} + {{a}_{{24}}}{{f}_{{4n}}} + {{a}_{{25}}}{{f}_{{5n}}} = 0;$

${{a}_{{31}}}{{f}_{{1n}}} + {{a}_{{32}}}{{f}_{{2n}}} + a_{{33}}^{0}{{f}_{{3n}}} - {{\theta }_{1}}{{\gamma }^{2}}{{T}_{1}}\cos \omega t{{f}_{{3n}}} + $

$\begin{gathered} + {{R}^{2}}{{F}_{0}}\frac{{{{d}^{2}}{{f}_{{3n}}}}}{{d{{t}^{2}}}} + {{a}_{{34}}}{{f}_{{4n}}} + {{a}_{{35}}}{{f}_{{5n}}} = \\ = - \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\mathop \sum \limits_{j = 1}^M \left( {b_{{33}}^{0}{{f}_{{3j}}} + {{\rho }_{j}}{{F}_{j}}R\frac{{{{d}^{2}}{{f}_{{3j}}}}}{{d{{t}^{2}}}}} \right. - \\ \end{gathered} $

$\left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}} - \,{{\theta }_{2}}{{T}_{1}}{{\gamma }^{2}}\cos \omega t{{f}_{{3j}}} + {{b}_{{34}}}{{f}_{{4j}}}} \right)\cos n{{\beta }_{j}};$

${{a}_{{41}}}{{f}_{{1n}}} + {{a}_{{42}}}{{f}_{{2n}}} + {{a}_{{43}}}{{f}_{{3n}}} + {{a}_{{44}}}{{f}_{{4n}}} + {{a}_{{45}}}{{f}_{{5n}}} = $

$ = - \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\mathop \sum \limits_{j = 1}^M ({{b}_{{41}}}{{f}_{{1j}}} + {{b}_{{43}}}{{f}_{{3j}}} + {{b}_{{44}}}{{f}_{{4j}}})\cos n{{\beta }_{j}};$

(3)

${{a}_{{51}}}{{f}_{{1n}}} + {{a}_{{52}}}{{f}_{{2n}}} + {{a}_{{53}}}{{f}_{{3n}}} + {{a}_{{54}}}{{f}_{{4n}}} + {{a}_{{55}}}{{f}_{{5n}}} = 0,$

где

${{a}_{{11}}} = - {{B}_{{11}}}{{\gamma }^{2}} - {{B}_{{33}}}{{n}^{2}};$ ${{a}_{{12}}}\, = \,{{a}_{{21}}}\, = \,({{B}_{{12}}}\, + \,{{B}_{{33}}})\gamma n$;

a₁₃ = $ - {{a}_{{31}}} = {{B}_{{12}}}\gamma ;$ ${{a}_{{14}}} = {{a}_{{41}}} = - {{\bar {B}}_{{11}}}{{\gamma }^{2}} - {{\bar {B}}_{{33}}}{{n}^{2}};$

a₁₅ = a₅₁ = $({{\bar {B}}_{{12}}}\, + \,{{\bar {B}}_{{33}}})\gamma n;$ ${{a}_{{22}}} = - {{B}_{{33}}}{{\gamma }^{2}} - {{B}_{{22}}}{{n}^{2}};$ ${{a}_{{23}}} = - {{B}_{{22}}}n$;

a₂₄ = ${{a}_{{42}}} = ({{\bar {B}}_{{12}}} + {{\bar {B}}_{{33}}})\gamma n;$ ${{a}_{{25}}} = {{a}_{{52}}} = - {{\bar {B}}_{{33}}}{{\gamma }^{2}} - {{\bar {B}}_{{22}}}{{n}^{2}};$

a₃₂ = B₂₂n; $a_{{33}}^{0}\, = \,\frac{{{{D}_{{11}}}}}{{{{R}^{2}}}}{{\gamma }^{4}}\, + \,\frac{{2({{D}_{{12}}}\, + \,{{D}_{{33}}})}}{{{{R}^{2}}}}{{\gamma }^{2}}{{n}^{2}}$ + $\frac{{{{D}_{{22}}}}}{{{{R}^{2}}}}{{n}^{4}}$ + + $\frac{{h_{0}^{2}}}{h}({{G}_{{13}}}{{\gamma }^{2}}$ + G₃₃n₂) – $PR{{n}^{2}}\, - \,{{\theta }_{1}}{{T}_{0}}{{\gamma }^{2}}\, + \,{{B}_{{22}}}\, + \,{{R}^{2}}{{\Pi }_{n}};$

a₃₄ = –a₄₃ = $ - \left( {{{{\bar {B}}}_{{12}}} - \frac{{2R{{h}_{0}}}}{h}{{G}_{{13}}}} \right)\gamma ;$

a₃₅ = $\left( {{{{\bar {B}}}_{{22}}} - \frac{{2R{{h}_{0}}}}{h}{{G}_{{23}}}} \right)n;$

a₄₄ = –B₁₁γ₂ – ${{B}_{{33}}}{{n}^{2}} - \frac{{4{{R}^{2}}}}{h}{{G}_{{13}}};$

a₄₅ = a₅₄ = (B₁₂ + ${{B}_{{33}}})\gamma n;$ ${{a}_{{53}}} = - \left( {{{{\bar {B}}}_{{22}}} - \frac{{2R{{h}_{0}}}}{h}{{G}_{{23}}}} \right)n;$

a₅₅ = –B₃₃γ₂ – ${{B}_{{22}}}{{n}^{2}} - \frac{{4{{R}^{2}}}}{h}{{G}_{{23}}};$ ${{b}_{{11}}} = - {{E}_{j}}{{F}_{j}}{{\gamma }^{2}}{\text{/}}R;$

b₁₄ = b₄₁ = $\frac{{2{{\varepsilon }_{j}}}}{{R{{h}_{0}}}}{{E}_{j}}{{F}_{j}}{{\gamma }^{2}}$; $b_{{33}}^{0} = ({{a}_{j}}{{\gamma }^{2}} - {{\theta }_{2}}{{T}_{0}}{{\gamma }^{2}}){\text{/}}R;$

b₃₄ = –b₄₃ = $2{{a}_{j}}\gamma {\text{/}}{{h}_{0}};$

b₄₄ = $ - \frac{4}{{Rh_{0}^{2}}}[{{a}_{j}}{{R}^{2}} + {{E}_{j}}(\varepsilon _{j}^{2}{{F}_{j}} + {{I}_{j}}){{\gamma }^{2}}].$

Коэффициент постели ${{{\text{П}}}_{n}}$ будет иметь вид

${{{\text{П}}}_{n}} = \frac{{2\mu }}{R}\frac{{{{\Delta }_{n}}}}{\psi };\quad \psi = \mathop \sum \limits_{j = 1}^6 {{Ф}_{j}}D_{{6j}}^{{\left( n \right)}};\quad \xi = \gamma ;\quad x = {{z}_{0}}\gamma ;$

$\begin{gathered} {{\Phi }_{1}} = - \frac{{{{n}^{2}}}}{\xi }{{I}_{n}}\left( \xi \right); \\ {{\Phi }_{3}} = - \frac{{\left( {\lambda + \mu } \right)}}{{2\left( {\lambda + 2\mu } \right)}}\xi \left( {\frac{{{{n}^{2}}}}{{{{\xi }^{2}}}} + 1} \right){{I}_{n}}\left( \xi \right);\quad {{Ф}_{5}} = - I_{n}^{'}\left( \xi \right); \\ \end{gathered} $

$D_{{6j}}^{{\left( n \right)}}$, Δ_n – соответственно дополнение и определитель матрицы [15].

Решение уравнений (3) будем искать в виде

$\left\{ {{{f}_{{1n}}},~{{f}_{{2n}}},~{{f}_{{3n}}},~{{f}_{{4n}}},~{{f}_{{5n}}};~{{f}_{{1j}}},~{{f}_{{3j}}},~{{f}_{{4j}}}} \right\} = $

$ = \,\mathop \sum \limits_{q = 1,~3 \ldots }^\infty \left\{ {\left[ {A_{{1n}}^{{(q)}},~A_{{2n}}^{{(q)}},~A_{{3n}}^{{(q)}},~A_{{4n}}^{{(q)}},~A_{{5n}}^{{(q)}};~A_{{1j}}^{{(q)}},~A_{{3j}}^{{(q)}},~A_{{4j}}^{{(q)}}} \right]{\text{sin}}{\kern 1pt} \frac{{q\omega t}}{2}} \right\} + $

(4)

$\begin{gathered} + \sum\limits_{q = 1,3...}^\infty {\left\{ {\left[ {Н_{{1n}}^{{(q)}},} \right)Н_{{2n}}^{{(q)}},Н_{{3n}}^{{(q)}},Н_{{4n}}^{{(q)}}{{,}_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}} \right.} \\ \left. {Н_{{5n}}^{{(q)}};Н_{{1j}}^{{(q)}},Н_{{3j}}^{{(q)}},\left. {Н_{{4j}}^{{(q)}}} \right]{\text{cos}}\frac{{q\omega t}}{2}} \right\}. \\ \end{gathered} $

Подставляя первую сумму из (4) в (3) и приравнивая коэффициенты при одинаковых ${\text{sin}}(q\omega t{\text{/}}2)$, получим систему неоднородных алгебраических уравнений. Ограничимся первым членом ряда q = 1, который определяет границу главной области неустойчивости и, согласно [8], в большинстве случаев его достаточно для практических расчетов. В результате получим (индекс q в дальнейшем опускается)

$\mathop \sum \limits_{i = 1}^5 {{a}_{{2i}}}{{A}_{{in}}} = 0;~\quad \mathop \sum \limits_{i = 1}^5 {{a}_{{5i}}}{{A}_{{in}}} = 0;$

$\mathop \sum \limits_{i = 1}^5 {{a}_{{1i}}}{{A}_{{in}}} = - \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\mathop \sum \limits_{j = 1}^M \left( {{{b}_{{11}}}{{A}_{{1j}}} + {{b}_{{14}}}{{A}_{{4j}}}} \right)\cos n{{\beta }_{j}};$

$\mathop \sum \limits_{i = 1}^5 {{a}_{{3i}}}{{A}_{{in}}} = - \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\mathop \sum \limits_{j = 1}^M \left( {{{b}_{{33}}}{{A}_{{3j}}} + {{b}_{{34}}}{{A}_{{4j}}}} \right)\cos n{{\beta }_{j}};$

(5)

$\begin{gathered} \mathop \sum \limits_{i = 1}^5 {{a}_{{4i}}}{{A}_{{in}}} = \\ = - \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\mathop \sum \limits_{j = 1}^M ({{b}_{{41}}}{{A}_{{1j}}} + {{b}_{{43}}}{{A}_{{3j}}} + {{b}_{{44}}}{{A}_{{4j}}})\cos n{{\beta }_{j}}, \\ \end{gathered} $

где

a₃₃ = $a_{{33}}^{0} - {{R}^{2}}{{F}_{0}}{{\omega }^{2}}{\text{/}}4 \mp {{\theta }_{1}}{{T}_{1}}{{\gamma }^{2}}{\text{/}}2;$

b₃₃ = $b_{{33}}^{0}$ – ${{\rho }_{j}}{{F}_{j}}R{{\omega }^{2}}{\text{/}}4 \mp {{\theta }_{2}}{{T}_{1}}{{\gamma }^{2}}{\text{/}}2R.$

Решая систему (5), получим

${{A}_{{kn}}} = - \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\mathop \sum \limits_{j = 1}^M \left( {{{B}_{{k1}}}{{A}_{{1j}}} + {{B}_{{k2}}}{{A}_{{3j}}} + {{B}_{{k3}}}{{A}_{{4j}}}} \right)\cos n{{\beta }_{j}}$

(6)

(k = 1, 2, … 5),

где

${{\Delta }},~{{D}_{{jk}}}$ – определитель и дополнение элемента a_jk матрицы (5).

Так как в местах расположения продольных ребер справедливы соотношения

$\left( {{{A}_{{1r}}},~{{A}_{{3r}}},~{{A}_{{4r}}}} \right) = \mathop \sum \limits_{n = 0}^\infty \left( {{{A}_{{1n}}},~{{A}_{{3n}}},~{{A}_{{4n}}}} \right)\cos n{{\beta }_{r}},$

то, подставив в них выражение (6), получим систему 3M уравнений относительно A_ij:

$\begin{gathered} {{A}_{{1r}}} = - \mathop \sum \limits_{n = 0}^\infty \mathop \sum \limits_{j = 1}^M \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}({{B}_{{11}}}{{A}_{{1j}}} + {{B}_{{12}}}{{A}_{{3j}}} + {{B}_{{13}}}{{A}_{{4j}}}) \times \\ \times \cos n\,{{\beta }_{j}}\cos n\,{{\beta }_{r}}; \\ \end{gathered} $

$\begin{gathered} {{A}_{{3r}}} = - \mathop \sum \limits_{n = 0}^\infty \mathop \sum \limits_{j = 1}^M \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\left( {{{B}_{{31}}}{{A}_{{1j}}} + {{B}_{{32}}}{{A}_{{3j}}} + {{B}_{{33}}}{{A}_{{4j}}}} \right) \times \\ \times \cos n\,{{\beta }_{j}}\cos n\,{{\beta }_{r}}; \\ \end{gathered} $

$\begin{gathered} {{A}_{{4r}}} = - \mathop \sum \limits_{n = 0}^\infty \mathop \sum \limits_{j = 1}^M \frac{{2 - {{\delta }_{{0n}}}}}{{2\pi }}\left( {{{B}_{{41}}}{{A}_{{1j}}} + {{B}_{{42}}}{{A}_{{3j}}} + {{B}_{{43}}}{{A}_{{4j}}}} \right) \times \\ \times \cos n\,{{\beta }_{j}}\cos n\,{{\beta }_{r}} \\ \end{gathered} $

(7)

(r = 1, 2, …, М).

Равенство нулю определителя системы (7) представляет характеристическое уравнение критических частот.

Подставляя вторую сумму из (4) в (3), получим характеристическое уравнение типа (7), в котором коэффициенты ${{A}_{{jr}}}$ необходимо заменить на Н_jr соответственно, а в коэффициентах ${{a}_{{33}}}$ и ${{b}_{{33}}}$ принять знак “+”.

Для случая равномерно расположенных продольных ребер $\left( {{{\beta }_{j}} = 2\pi j{\text{/}}M} \right)$ коэффициенты перед A_ij не будут зависеть от индекса j и решение системы (7) можно представить в виде

(8)

$\begin{gathered} \left\{ {{{A}_{{1j}}},~{{A}_{{3j}}},~{{A}_{{4j}}}} \right\} = \left\{ {{{A}_{1}},~{{A}_{3}},~{{A}_{4}}} \right\}\cos \frac{{2\pi jN}}{M},~ \\ 0 \leqslant N \leqslant \frac{M}{2}, \\ \end{gathered} $

где N – целое число, характеризующее форму потери устойчивости.

Подставляя (8) в уравнение (7), получим однородную систему трех алгебраических уравнений

(9)

$\frac{M}{{2\pi }}\mathop \sum \limits_k \left( {{{B}_{{l1}}}{{A}_{1}} + {{B}_{{l2}}}{{A}_{3}} + {{B}_{{l3}}}{{A}_{4}}} \right) - {{A}_{l}} = 0\,~\left( {l = 1,~3,~4} \right),$

где суммирование производится по k, принимающим значения

$\begin{gathered} k = Ms + N~(s = 0,~1,~2, \ldots ), \\ k = Ms - N~\left( {s = 1,~2,~3, \ldots } \right)~. \\ \end{gathered} $

Характеристическое уравнение получим из условия равенства нулю определителя системы (9). Придавая m и N различные целочисленные значения, находим критическое значение частоты.

ЧИСЛЕННЫЙ ПРИМЕР

В качестве примера с помощью разработанной математической модели проведены исследования и анализ полученных критических частот колебаний трехслойных оболочек симметричной структуры, подкрепленных четырьмя равномерно расположенными одинаковыми продольными ребрами и внутренним цилиндром, при нагружении внешним давлением и осевой силой, изменяющейся во времени по гармоническому закону. Базовые параметры трехслойных оболочек, продольных ребер и цилиндра были следующие:

$\begin{gathered} L{\text{/}}R = 6;\quad \left( {{{h}_{1}},~{{h}_{2}}} \right){\text{/}}R = 0.004;\quad h{\text{/}}R = 0.01; \\ (E_{1}^{В},~E_{1}^{Н}){\text{/}}{{E}_{0}} = 1.5 \cdot {{10}^{4}}; \\ \end{gathered} $

$\begin{gathered} (E_{2}^{В},~E_{2}^{Н}){\text{/}}{{E}_{0}} = 2.3 \cdot {{10}^{4}};\quad (G_{{12}}^{В},~G_{{12}}^{Н}){\text{/}}{{E}_{0}} = 2.4 \cdot {{10}^{3}}; \\ \left( {{{G}_{{13}}},~{{G}_{{23}}}} \right){\text{/}}{{E}_{0}} = 30; \\ \end{gathered} $

$\begin{gathered} {{E}_{j}}{\text{/}}{{E}_{0}} = 2.3 \cdot {{10}^{4}};\quad {{G}_{j}}{\text{/}}{{E}_{0}} = 2.4 \cdot {{10}^{3}};~ \\ \nu _{1}^{В} = \nu _{1}^{Н} = 0.15;\quad \nu _{2}^{В} = \nu _{2}^{Н} = 0.23; \\ \end{gathered} $

$\begin{gathered} ~{{\nu }_{0}} = 0.49;\quad ({{\rho }^{В}},~{{\rho }^{Н}},~{{\rho }_{j}}){\text{/}}{{\rho }_{0}} = 5; \\ {{F}_{j}}{\text{/}}{{R}^{2}} = 8 \cdot {{10}^{{ - 4}}};\quad ~{{P}_{0}}{\text{/}}{{E}_{0}} = 0.05;~\quad {{z}_{0}} = 0.6; \\ \end{gathered} $

$\begin{gathered} ~r_{j}^{В}{\text{/}}R = - 0.006;\quad r_{j}^{Н}{\text{/}}R = - 0.02;~ \\ I{\text{/}}F{{R}^{2}} = 1.4 \cdot {{10}^{{ - 4}}};\quad M = 4;\quad {{T}_{0}}{\text{/}}{{E}_{0}}{{R}^{2}} = 5. \\ \end{gathered} $

На рис. 1 показаны области неустойчивости для подкрепленных продольными ребрами трехслойных цилиндрических оболочек:

Рис. 1.

Области неустойчивости трехслойной подкрепленной оболочки с базовыми параметрами (1) (${{z}_{0}} = 0.6$) (m – количество полуволн по оси; N – число, характеризующее форму потери устойчивости); при увеличенных в два раза: жесткостях заполнителя (2), цилиндра (3) и количестве ребер (4).

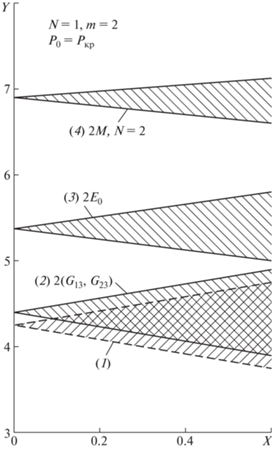
– имеющих базовые параметры (область 1),

– с увеличенной в два раза жесткостью заполнителя трехслойной оболочки (область 2),

– с увеличенным в два раза модулем упругости внутреннего цилиндра (область 3),

– с увеличенным в два раза количеством продольных ребер (область 4).

По оси ординат $Y = \omega {\text{/}}{{\omega }_{0}}~~$ откладывается отношение критической частоты колебаний к собственной частоте неподкрепленной трехслойной оболочки без внутреннего цилиндра, а по оси абсцисс $X = {{T}_{1}}{\text{/}}{{T}_{0}}$ – отношение амплитуды переменной составляющей к постоянной составляющей осевой силы, величина которой равна критической силе потери устойчивости трехслойной оболочки без подкрепления продольными ребрами и внутренним цилиндром.

Из анализа полученных результатов проведенных исследований трехслойных цилиндрических оболочек, подкрепленных продольными ребрами и внутренним цилиндром, при нагружении внешним давлением и осевой силой, изменяющейся во времени по гармоническому закону, следует, что:

– увеличение в два раза жесткости заполнителя рассматриваемой трехслойной цилиндрической оболочки увеличивает критическую частоту этой оболочки на 5%;

– увеличение модуля упругости внутреннего цилиндра в два раза увеличивает критическую частоту для трехслойной подкрепленной цилиндрической оболочки на 27% и снижает площадь области неустойчивости на 25%;

– увеличение количества продольных ребер в два раза увеличивает критическую частоту на 60% для трехслойной подкрепленной цилиндрической оболочки и уменьшает площадь области неустойчивости в 1.9 раза.

ЗАКЛЮЧЕНИЕ

Впервые представлена математическая модель для исследования параметрического резонанса подкрепленной продольными ребрами трехслойной цилиндрической оболочки с несимметричным пакетом слоев и легким заполнителем, по внутренней поверхности скрепленной с упругим пустотелым цилиндром, при действии внешнего давления и изменяющихся во времени осевых сил. Рассмотрены основные этапы решения указанной задачи c помощью предложенной комбинации методов.

На численном примере впервые построены зависимости критических частот главных областей неустойчивости и исследовано влияние на эти частоты жесткости внутреннего цилиндра, количества продольных ребер, жесткости заполнителя трехслойной цилиндрической оболочки. Разработанная математическая модель значительно расширяет круг решаемых актуальных научных и прикладных задач и позволяет впервые провести исследования одновременного влияния продольных ребер и внутреннего цилиндра на границы областей неустойчивости для трехслойных цилиндрических оболочек, являющихся перспективными элементами конструкций ракетно-космической и другой современной техники.

Получены приоритетные научные результаты, заключающиеся в разработке математической модели для исследования параметрического резонанса трехслойных цилиндрических оболочек и впервые построенных с помощью этой модели зависимостей, определяющих возникновение параметрического резонанса, который может привести к разрушению конструкции.

Список литературы

Bakulin V. N. Investigation of the Influence of the Cutout Dimensions on the Stress-strain State of Three-layer Shells with Load-bearing Layers of Composite Materials // Journal of Physics: Conference Series: Materials Science and Engineering. 2020. P. 714. 012002.
Бакулин В.Н., Недбай А.Я. Динамическая устойчивость трехслойной цилиндрической оболочки, подкрепленной кольцевыми ребрами и пустотелым цилиндром, при действии внешнего пульсирующего давления // Доклады РАН. Физика, технические науки. 2021. Т. 498. С. 46–52.
Bakulin V. N., Boitsova D. A., Nedbay A.Ya. Parametric Resonance of a Three-Layered Cylindrical Composite Rib-Stiffened Shell // Mechanics of Composite Materials. 2021. V. 57. № 5. P. 623–634.
Липанов А.М., Карсканов С.А., Чернышев С.Л., Липатов И.И. Теоретическое исследование условий возникновения скоростного бафтинга // Вестн. Удмурт. ун-та. Матем., мех., компьют. науки. 2019. Т. 29. № 3. С. 382–395.
Вольмир А.С. Оболочки в потоке жидкости и газа. Задачи аэроупругости. М.: Физматлит, 1976. 416 с.
Сухинин С.Н. Прикладные задачи устойчивости многослойных композитных оболочек. М.: Физматлит, 2010. 248 с.
Bakulin V.N., Volkov E.N., Nedbai A.Ya. Dynamic Stability of a Cylindrical Shell Reinforced by Longitudinal Ribs and a Hollow Cylinder Under the Action of Axial Forces // J. Engineering Physics and Thermophysics. 2016. V. 89. № 3. P. 747–753.
Болотин В.В. Динамическая устойчивость упругих систем. М.: ГИТТЛ, 1956. 600 с.
Майлыбаев А.А., Сейранян А.П. Многопараметрические задачи устойчивости. Теория и приложения в механике. М.: Физматлит, 2009. 400 с.
Bakulin V.N., Volkov E.N., Simonov A.I. Dynamic Stability of a Cylindrical Shell under Alternating Axial External Pressure // Russian Aeronautics. 2017. V. 60. № 4. P. 508–513.
Bakulin V.N., Nedbai A.Ya. Dynamic Stability of Composite Cylindrical Shell of Linear-Variable Thickness under the Action Pulsed External Pressure // J. Engineering Physics and Thermophysics. 2021. V. 93. № 2. P. 537–543.
Огибалов П.М., Колтунов М.А. Оболочки и пластины. М.: ГИТТЛ, 1971. 696 с.
Багдасарян В.В, Кузнецов О.В., Малютин И.С. О параметрическом резонансе цилиндрической оболочки, подкрепленной продольными ребрами // Вопросы мат. физики и теории колебаний. 1975. Вып. 3. С. 89–96.
Bakulin V.N., Nedbai A.Ya., Shepeleva I.O. Dynamic Stability of an Orthotropic Cylindrical Shell of Piecewise Constant Thickness under the Action of External Pulsating Pressure. Russian Aeronautics. 2019. V. 62. № 2. P. 192–198.
Соломонов Ю.С., Георгиевский В.П., Недбай А.Я., Андрюшин В.А. Прикладные задачи механики композитных цилиндрических оболочек. М.: Физматлит, 2014. 408 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал