Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 490, № 1, стр. 81-84

1. Теория управляемых систем с последействием изучалась многими авторами [1, 3, 6–8]. Обычно предполагалось, что функционально-дифференциальные уравнения, описывающие систему, имеют запаздывающий или нейтральный тип, при этом в случае нейтрального типа старшие члены с запазыванием имели достаточно малые коэффициенты. Задача об успокоении системы управления с последействием, описываемая системой дифференциально-разностных уравнений запаздывающего типа, рассматривалась Н.Н. Красовским [1]. В работах [4, 9] эта задача обобщалась на случай, когда уравнение, описывающее управляемую систему, содержит также старшие производные с запаздыванием. Многомерная система с постоянными матричными коэффициентами исследовалась в [2, 5].

2. В данной работе мы рассмотрим линейную нестационарную систему управления, описываемую системой дифференциально-разностных уравнений нейтрального типа

где $y(t) = {{({{y}_{1}}(t),\; \ldots ,\;{{y}_{n}}(t))}^{{\text{т}}}}$ – вектор-функция, описывающая состояние системы, u(t) = (u₁(t), ... ... ${{u}_{n}}(t){{)}^{{\text{т}}}}$ – вектор-функция управления, A_m(t) = = ${{{\text{\{ }}a_{{ij}}^{m}(t){\text{\} }}}_{{i,j = 1, \ldots ,n}}}$, ${{B}_{m}} = {{{\text{\{ }}b_{{ij}}^{m}(t){\text{\} }}}_{{i,j = 1, \ldots ,n}}}$ – матрицы порядка n × n с элементами $a_{{ij}}^{m}(t)$, $b_{{ij}}^{m}(t)$, которые являются непрерывно дифференцируемыми функциями, $\tau = {\text{const}} > 0$ – запаздывание.

Предыстория системы опеределяется начальным условием

где $\varphi (t) = {{({{\varphi }_{1}}(t),\; \ldots ,\;{{\varphi }_{n}}(t))}^{{\text{т}}}}$ – заданная вектор-функция.

Рассмотрим задачу о приведении системы (1)–(2) в положение равновесия при $t \geqslant T$. Найдем такое управление $u(t)$, $0 < t < T$, что

где $T > (M + 1)\tau $.

Из всевозможных управлений будем искать управление, доставляющее минимум функционалу $\int\limits_0^T {{{{\left| {u(t)} \right|}}^{2}}} dt \to {\text{min}}$, где | ⋅ | – евклидова норма в ${{\mathbb{R}}^{n}}$. Таким образом, мы получаем вариационную задачу о минимуме функционала энергии

3. Введем некоторые вещественные функциональные пространства.

Обозначим через $W_{2}^{k}(a,b)$ пространство абсолютно непрерывных на [a, b] функций, имеющих производную k-го порядка из ${{L}_{2}}(a,b)$ со скалярным произведением

Пусть $\mathop {W_{2}^{k}}\limits^ \circ (a,b) = {\text{\{ }}w \in W_{2}^{k}(a,b){\kern 1pt} :\;{{w}^{{(i)}}}(a) = {{w}^{{(i)}}}(b)$ = 0, $i = 0,1, \ldots ,k - 1{\text{\} }}.$

Введем пространства вектор-функций

со скалярными произведениями где ${v} = {{({{{v}}_{1}}, \ldots ,{{{v}}_{n}})}^{{\text{т}}}}$, $w = {{({{w}_{1}},\; \ldots ,\;{{w}_{n}})}^{{\text{т}}}}$.

4. Пусть $y \in W_{2}^{{1,n}}( - M\tau ,T)$ – решение вариационной задачи (2)–(4), где $\varphi \in W_{2}^{{1,n}}( - M\tau ,\;0)$.

Введем пространства $\tilde {W} = {\text{\{ }}{v} \in W_{2}^{{1,n}}( - M\tau ,T)$: ${v}(t)$ = 0, $t \in ( - M\tau ,0) \cup (T - M\tau ,T){\text{\} }}$ и $\tilde {L}$ = = ${\text{\{ }}{v}\, \in \,L_{2}^{n}( - M\tau $, T): ${v}(t)$ = 0, $t\, \in \,( - M\tau ,0)\, \cup \,(T\, - \,M\tau $, T)}.

В дальнейшем будем отождествлять пространство $\tilde {W}$ с $\mathop {W_{2}^{{1,n}}}\limits^ \circ (0,T - M\tau )$, не оговаривая этого специально. Пусть ${v} \in \tilde {W}$ – произвольная фиксированная функция. Тогда функция y + $s{v} \in W_{2}^{{1,n}}( - M\tau $, T) и удовлетворяет краевым условиям (2), (3) для каждого $s \in \mathbb{R}$. Обозначим $J(y + s{v})$ = F(s). Поскольку J(y + $s{v}) \geqslant J(y)(s \in \mathbb{R})$, мы имеем $\mathop {\left. {\tfrac{{dF}}{{ds}}} \right|}\nolimits_{s = 0} = 0$. Отсюда получим

В слагаемых, содержащих ${v}{\text{'}}(t - l\tau )$ или ${v}(t - l\tau )$, сделаем замену переменной $\xi = t - l\tau $, а затем положим t = ξ. Учитывая краевые условия ${v}(t) = 0$, $t \in ( - M\tau ,0) \cup (T - M\tau ,T)$ и интегрируя по частям, получим

Из (6) и определения обобщенной производной следует, что

В силу (7) мы можем проинтегрировать по частям в тождестве (6) члены, содержащие сомножитель ${v}{\text{'}}(t)$. Тогда мы получим

Определение 1. Вектор-функция y $ \in $ $ \in $ $W_{2}^{{1,n}}( - M\tau $, T) называется  обобщенным решением задачи (8), (2), (3), если выполняется условие (7) и y(t) удовлетворяет системе уравнений (8) почти всюду на $(0,T - M\tau ),$ а также краевым условиям (2), (3).

Вектор-функция $y \in W_{2}^{{1,n}}( - M\tau $, T) является обобщенным решением задачи (8), (2), (3) тогда и только тогда, когда она удовлетворяет интегральному тождеству (6) для всех ${v} \in \mathop {W_{2}^{{1,n}}}\limits^ \circ (0,T - M\tau )$ и краевым условиям (2), (3). Таким образом, было доказано, что если на функции $y \in W_{2}^{{1,n}}( - M\tau ,T)$ достигается минимум функционала (4) с краевыми условиями (2), (3), то она является обобщенным решением задачи (8), (2), (3).

С другой стороны, если $y \in W_{2}^{{1,n}}( - M\tau ,T)$ – обобщенное решение задачи (8), (2), (3), то для любых ${v} \in \tilde {W}$

Таким образом, доказана следующая

Теорема 1. Пусть $\varphi \in W_{2}^{{1,n}}( - M\tau ,0)$. Функция $y \in W_{2}^{{1,n}}( - M\tau ,T)$ доставляет минимум функционалу (4) с краевыми условиями (2), (3) тогда и только тогда, когда она является обобщенным решением краевой задачи (8), (2), (3).

5. Введем оператор ${{R}_{0}}{\kern 1pt} :\;\tilde {L} \to L_{2}^{n}(0,T - M\tau )$ по формуле

Рассмотрим функционал

Лемма 1. Пусть ${\text{det}}{{A}_{0}}(t) \ne 0$, $t \in \mathbb{R}$. Тогда для всех $w \in \tilde {W}$

где ${{c}_{0}} > 0$ – постоянная, не зависящая от $w$.

Доказательство. (i) Предположим противное: для любого $k \in \mathbb{N}$ существует ${{w}_{k}} \in \tilde {W}$ такое, что

Не ограничивая общности, будем считать, что

Тогда в силу компактности вложения $\tilde {W}$ в $L_{2}^{n}(0,T - M\tau )$ существует подпоследовательность ${\text{\{ }}{{w}_{{{{k}_{m}}}}}{\text{\} }} \subset \tilde {W}$, сходящаяся в $L_{2}^{n}(0,T - M\tau )$ при m → ∞ к некоторой вектор-функции ${{w}_{0}} \in L_{2}^{n}(0,T - M\tau )$. В силу предположения ${{\left\| {{{w}_{{{{k}_{m}}}}}} \right\|}_{{W_{2}^{{1,n}}(0,T - M\tau )}}}$ = 1 имеем ${{w}_{0}} \ne 0$.

(ii) Пусть $0 < t < \tau $. Тогда выражение $({{R}_{0}}w_{{{{k}_{m}}}}^{'})(t)$ примет вид

Следовательно, в силу невырожденности матрицы ${{A}_{0}}(t)$ и неравенства (12) получим $w_{{{{k}_{m}}}}^{'} \to 0$ в $L_{2}^{n}(0,\tau )$ при m → ∞.

(iii) Пусть теперь $\tau < t < 2\tau $. Тогда

Отсюда в силу неравенства (12) и (ii) имеем $({{R}_{0}}w_{{{{k}_{m}}}}^{'})(t) \to 0$ и ${{A}_{1}}(t)w_{{{{k}_{m}}}}^{'}(t - \tau ) \to 0$ в $L_{2}^{n}(\tau ,2\tau )$ при m → ∞. Следовательно, поскольку матрица ${{A}_{0}}(t)$ невырождена, то $w_{{{{k}_{m}}}}^{'}(t) \to 0$ в $L_{2}^{n}(\tau ,2\tau )$ при m → ∞.

(iv) Аналогично за конечное число шагов докажем, что $w_{{{{k}_{m}}}}^{'} \to 0$ в $L_{2}^{n}(l\tau ,L)$ для любого l ∈ $\mathbb{N}$ такого, что $2\tau \leqslant l\tau < L$, где $L = {\text{min\{ }}(l + 1)\tau ,T - M\tau {\text{\} }}$. Таким образом, w₀ ∈ $\mathop {W_{2}^{{1,n}}}\limits^ \circ (0,T - M\tau )$ и w₀ = ${\text{const}} \ne 0$. Полученное противоречие доказывает лемму 1.

Из леммы 1 вытекает следующий результат.

Лемма 2. Пусть ${\text{det}}{{A}_{0}}(t) \ne 0$, $t \in \mathbb{R}$. Тогда для всех $w \in \tilde {W}$

где ${{c}_{1}} > 0$ – постоянная, не зависящая от $w$.

Теорема 2. Пусть ${\text{det}}{{A}_{0}}(t) \ne 0$, $t \in \mathbb{R}$. Тогда для любого $\varphi \in W_{2}^{{1,n}}( - M\tau ,0)$ существует единственное обобщенное решение $y \in W_{2}^{{1,n}}( - M\tau ,T)$ краевой задачи (8), (2), (3), при этом

где $c > 0$ не зависит от φ.

Для доказательства теоремы 2 однородная система дифференциально-разностных уравнений (8) с неоднородными краевыми условиями (2), (3) сводится к неоднородной системе уравнений с однородными краевыми условиями. Затем в силу леммы 2 в пространстве $\mathop {W_{2}^{{1,n}}}\limits^ \circ (0,T - M\tau )$ вводится эквивалентое скалярное произведение по формуле 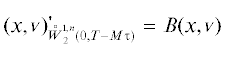и применяется теорема Рисса об общем виде функционала в гильбертовом пространстве.