Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 490, № 1, стр. 5-8

Понятие степенной $R$-группы, где $R$ – произвольное ассоциативное кольцо с единицей, введено Р. Линдоном в [1]. А.Г. Мясников и В.Н. Ремесленников в [2] уточнили понятие $R$-группы, введя дополнительную аксиому. В частности, новое понятие $R$-группы является непосредственным обобщением понятия $R$-модуля на случай некоммутативных групп. В честь А.Г. Мясникова $R$-группы с дополнительной аксиомой в статье М.Г. Амаглобели и В.Н. Ремесленникова [3] названы MR-группами ($R$-кольцо). Хорошо известна роль тензорного расширения кольца скаляров для модулей. Авторы работы [2] определили точный аналог этой конструкции для произвольной MR-группы – тензорное пополнение. В работе М.Г. Амаглобели [4] предложен конкретный способ построения тензорного пополнения данной MR-группы. Систематическое изучение MR-групп начато в работах [3–9]. Отметим, что результаты этих работ оказались весьма полезны при решении известных проблем Тарского.

В определении многообразия MR-групп мы следуем стандартной схеме. Существенное отличие изучаемого случая от классического в том, что, во-первых, понятие многообразия расслаивается в зависимости от кольца скаляров, во-вторых, вербальная подгруппа, вообще говоря, не порождается значениями слов, определяющих многообразие. К счастью, функтор тензорного пополнения связывает слои многообразий по различным кольцам скаляров.

Напомним основные определения и факты, следуя работе [2]. Зафиксируем произвольное ассоциативное кольцо $R$ с единицей 1, а также группу $G$. Результат действия $\alpha \in R$ на $g \in G$ будем записывать в виде ${{g}^{\alpha }}$. Рассмотрим аксиомы:

где $\left[ {g,h} \right] = {{g}^{{ - 1}}}{{h}^{{ - 1}}}gh$.

Определение 1 [2]. Группу $G$ будем называть степенной $R$-группой по Линдону, если выполнены аксиомы (1)–(3), и степенной MR-группой, если выполнены аксиомы (1)–(4).

Пусть ${{L}_{R}}$ и ${{M}_{R}}$ – классы всех степенных $R$‑групп по Линдону и всех MR-групп. Очевидно, что ${{L}_{R}} \supseteq {{M}_{R}}$. Существуют примеры, показывающие, что это включение строгое (см. [1]). Кроме того, выполнено свойство: каждая абелева MR‑группа является $R$-модулем и наоборот. Большинство естественных примеров $R$-групп лежат в классе ${{M}_{R}}$. Например, свободная $R$-группа по Линдону является MR-группой, унипотентная группа над полем $K$ нулевой характеристики является MK-группой, произвольная про-p-группа является $M{{\mathbb{Z}}_{p}}$-группой над кольцом целых $p$-адических чисел ${{\mathbb{Z}}_{p}}$ и т.д. (см. другие примеры в [2]).

Стандартным образом вводятся понятия MR‑подгруппы, MR-порождаемости, нормальной $MR$-подгруппы и т.д. Ясно, что этот класс является квазимногообразием в сигнатуре $\langle \left. { \cdot \;{{,}^{{ - 1}}},{{f}_{\alpha }}} \right|\alpha \, \in \,R\rangle $, где ${{f}_{\alpha }}$ – унарная операция возведения в степень α, т.е. ${{f}_{\alpha }}(g)$ = g^α и в нем есть понятие свободной MR-группы, R-гомоморфизма и т.д. В частности, гомоморфизм   R-групп   $\varphi {\kern 1pt} :\;G \to G{\text{*}}$   называется R-гомоморфизмом, если $\varphi ({{g}^{\alpha }}) = \varphi {{\left( g \right)}^{\alpha }}$ для любых $g \in G$, $\alpha \in R$. Ядра R-гомоморфизмов в категории ${{M}_{R}}$ могут быть охарактеризованы как так называемые ${{M}_{R}}$-идеалы. Для $g,h \in G$, $\alpha \in R$ элемент ${{\left( {g,h} \right)}_{\alpha }} = {{h}^{{ - \alpha }}}{{g}^{{ - \alpha }}}{{\left( {gh} \right)}^{\alpha }}$ назовем α-коммутатором элементов $g$и $h$. Очевидно, что α-коммутатор ${{\left( {g,h} \right)}_{\alpha }}$ при $\alpha = - 1$ совпадает с обычным коммутатором $[{{h}^{{ - 1}}},{{g}^{{ - 1}}}]$. Ясно, что (gh)^α = ${{g}^{\alpha }}{{h}^{\alpha }}{{(g,h)}_{\alpha }}$ и $G \in {{M}_{R}} \leftrightarrow ([g,h] = e \to {{(g,h)}_{\alpha }}$ = e). Последняя эк-вивалентность  приводит к определению M_R-идеала.

Определение 2 [2]. Нормальная MR-подгруппа $H\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \triangleleft } G$, $G \in {{L}_{R}}$, называется ${{M}_{R}}$-идеалом, если ${{\left( {g,h} \right)}_{\alpha }} \in H$ для любых $g,h \in G$, $\alpha \in R$.

В [2] показано, что если $\varphi {\kern 1pt} :\;G \to G{\text{*}}$ – $R$-гомоморфизм групп из ${{M}_{R}}$, то $Ker\;\varphi $ – ${{M}_{R}}$-идеал в G, и если $H$ – ${{M}_{R}}$-идеал в $G$, то ${G \mathord{\left/ {\vphantom {G H}} \right. \kern-0em} H} \in {{M}_{R}}$.

Многообразия $MR$-групп. Многообразия тесно связаны со свободными группами, поскольку тождества – это элементы свободных групп. Пусть $X = \left\{ {\left. {{{x}_{i}}} \right|\;i \in I} \right\}$ – бесконечный счетный алфавит, $R$ – кольцо с единицей, ${{F}_{R}}\left( X \right)$ – свободная $MR$-группа с базой X (см. [4]). Элемент $w(\bar {x}) = w({{x}_{1}}, \ldots ,{{x}_{n}}) \in {{F}_{R}}(X)$ будем называть $R$-словом в алфавите X. Если $G \in {{M}_{R}}$ и $\bar {g}$ = (g₁, ... ...,  ${{g}_{n}}) \in {{G}^{n}}$, то отображение ${{x}_{i}} \mapsto {{g}_{i}}$ продолжается до $R$-гомоморфизма $\varphi {\kern 1pt} :\;{{F}_{R}}\left( X \right) \to G$. Образ w(x₁, ..., x_n)^φ = $w({{g}_{1}}, \ldots ,{{g}_{n}}) \in G$ будем называть значением $R$-слова w при подстановке ${{x}_{1}} = {{g}_{1}}, \ldots ,{{x}_{n}}$ = g_n. Обозначим через w(G) = $\{ \left. {w\left( {\bar {g}} \right)} \right|\;\bar {g} \in {{G}^{n}}\} $. $R$-слово $w(\bar {g})$ будем называть тождеством в группе $G \in {{M}_{R}}$, если $w(G) = e$. Пусть W – произвольное множество $R$-слов в алфавите X. Тогда W определяет многообразие MR-групп N = N(W) = = $\{ \left. {G \in {{M}_{R}}} \right|w\left( G \right) = e\,\forall \;w \in W\} $. R-слово $u\left( {\bar {x}} \right)$ назовем следствием множества слов $W \subseteq {{F}_{R}}\left( X \right)$, если $u\left( G \right) = e$ для любой группы $G \in N\left( W \right)$. Множества $R$-слов W₁ и W₂ эквивалентны, если каждое R-слово из W₁ является следствием из W₂ и наоборот. В частности, два R-слова, получаемые одно из другого переименованием букв, эквивалентны.

Определение 3. ${{M}_{R}}$-идеал в G, порожденный множеством значений всех $R$-слов из множества W, будем называть W-вербальным идеалом в G. Далее W-вербальный идеал обозначается через $W\left( G \right)$.

Предложение 1. W-вербальный идеал в ${{F}_{R}}(X)$, порожденный множеством $R$-слов $W\, \subseteq \,{{F}_{R}}(X)$, состоит в точности из всех следствий множества W в ${{F}_{R}}\left( X \right)$.

В каждом многообразии $N\left( W \right)$ есть свободные относительно этого многообразия группы.

Теорема 1. Свободной группой в многообразии $MR$-групп $N\left( W \right)$ является группа

Теорема 2. Класс $MR$-групп $N$ является многообразием тогда и только тогда, когда $N$ замкнут относительно взятия MR-подгрупп, декартовых $R$-произведений и $R$-гомоморфных образов.

Доказательство этой теоремы аналогично доказательству классической теоремы Биркгофа для многообразий алгебраических систем.

Замечание 1. При определении многообразий MR-групп мы следуем монографии [10], где есть объяснение, как понимать многообразие групп внутри квазимногообразия групп. В подходящей сигнатуре класс L_R является многообразием $R$-групп, а класс ${{M}_{R}}$ – квазимногообразием $R$‑групп и включение ${{L}_{R}} \supseteq {{M}_{R}}$ строгое. Пусть $N$ – некоторое многообразие $R$-групп из L_R. Рассмотрим пересечение ${{N}_{R}} = N \cap {{M}_{R}}$. Согласно определению из [10, гл. 2, параграф 2.5] этот класс является биркгофовым классом, т.е. в нем справедливы известные теоремы Биркгофа. В частности, для этого класса существует теория определяющих соотношений, понятие MR-подгруппы и понятие MR-фактор-группы. Поэтому естественно класс N_R называть многообразием MR-групп внутри квазимногообразия групп ${{M}_{R}}$.

Тензорные пополнения. Пусть ${{N}_{R}}$ и ${{N}_{S}}$ – многообразия MR-групп и $MS$-групп, заданные множеством слов W.

Определение 4. Группу $G_{W}^{S}$ будем называть тензорным $S$-пополнением $G$ в многообразии ${{N}_{S}}$, если существует $R$-гомоморфизм $\lambda :G \to G_{W}^{S}$ такой, что $\lambda \left( G \right)$ S-порождает $G_{W}^{S}$, т.е. ${{\left\langle {\lambda \left( G \right)} \right\rangle }_{S}} = G_{W}^{S}$, и для любой группы H из ${{N}_{S}}$ и любого $R$-гомоморфизма $\varphi :G \to H$ существует S-гомоморфизм $\psi :G_{W}^{S} \to H$, замыкающий до коммутативной диаграмму

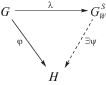
Отметим, что в отличие от [2] мы рассматриваем только ситуацию, когда $\mu :R \to S$ – вложение колец, а потому $\mu $ не участвует в определении и обозначениях. Это ограничение не по существу и сделано только ради упрощения обозначений.

Теорема 3. Пусть $G \in {{N}_{R}}$. Тогда тензорное S-пополнение $G_{W}^{S}$ относительно N_S существует, причем $G_{W}^{S} = {{{{G}^{S}}} \mathord{\left/ {\vphantom {{{{G}^{S}}} {W({{G}^{S}})}}} \right. \kern-0em} {W({{G}^{S}})}}$.

Теорема 4. Пусть $R \subseteq S$ – кольца, ${{F}_{{W,R}}}(X)$ – свободная группа в многообразии ${{N}_{R}}$. Тогда $({{F}_{{W,R}}}\left( X \right))_{W}^{S}$ – свободная группа в многообразии N_S, т.е. $({{F}_{{W,R}}}(X))_{W}^{S} \cong {{F}_{{W,S}}}(X)$.

$R$-коммутант и абелевы многообразия $MR$-групп. Пусть $G \in {{M}_{R}}$. $MR$-подгруппу (G, G)_R = ${{\left\langle {\left. {{{{(g,h)}}_{\alpha }}} \right|g,h \in G,\alpha \in R} \right\rangle }_{R}}$ будем называть $R$-коммутантом группы $G$.

Предложение 2. Для любой $MR$-группы $G$ $R$-коммутант является вербальной MR-подгруппой, определяемой словом $\left[ {x,y} \right] = {{x}^{{ - 1}}}{{y}^{{ - 1}}}xy$; $R$-коммутант – это наименьший ${{M}_{R}}$-идеал, фактор-группа по которому абелева.

Как мы уже отмечали, обычный коммутатор является (–1)-коммутатором. Какие еще $\alpha $-коммутаторы порождают $R$-коммутант как вербальную MR-подгруппу? Мы ответим на этот вопрос в случае, когда $R$ – поле.

Предложение 3.  Пусть $R$ – поле. Тогда $\alpha $-коммутатор ${{\left( {x,y} \right)}_{\alpha }}$ порождает $R$-коммутант как вербальную MR-подгруппу при условии $\alpha \ne 0,1$.

Теорема 5. Любое множество $R$-слов $V$ в алфавите $X = \left\{ {{{x}_{1}},{{x}_{2}},\; \ldots } \right\}$ эквивалентно множеству $R$-слов $W = \{ \left. {x_{1}^{{{{\alpha }_{i}}}},{{u}_{j}}} \right|\;{{\alpha }_{i}} \in R,\;i \in I,\;j \in J\} $, где ${{u}_{j}}$ – слова из $R$-коммутанта группы ${{F}_{R}}\left( X \right)$.

Следующие результаты характеризуют абелевы многообразия $MR$-групп.

Теорема 6. Свободная абелева MR-группа с базой X является свободным $R$-модулем и $R$-изоморфна фактор-группе свободной MR-группы с базой X по ее $R$-коммутанту.

Теорема 7. Существует взаимно-однозначное соответствие между решеткой двусторонних идеалов кольца $R$ и решеткой вербальных MR-подгрупп свободного $R$-модуля.

Следствие 1. При $R = \mathbb{Z}$ любое собственное подмногообразие абелевых групп есть многообразие абелевых групп периода $n \geqslant 2$.

Нильпотентные многообразия MR-групп. Выше было определено понятие $R$‑коммутанта группы $G \in {{M}_{R}}$. Будем называть его первым $R$-коммутантом и обозначать через ${{G}^{{\left( {1,R} \right)}}}$. $R$-коммутант ${{G}^{{\left( {2,R} \right)}}}$ от ${{G}^{{\left( {1,R} \right)}}}$ будем называть вторым $R$-коммутантом и т.д. Возникает убывающий ряд $R$-коммутантов

Степенную MR-группу будем называть $R$-разрешимой, если существует натуральное число $n$ такое, что ${{G}^{{\left( {n,R} \right)}}} = e$. Индукцией по $n$ нетрудно доказывается, что обычный $n$-й коммутант ${{G}^{{\left( n \right)}}}$ содержится в ${{G}^{{\left( {n,R} \right)}}}$. Поэтому $n$-ступенно разрешимая группа в категории ${{M}_{R}}$ является $n$-ступенно разрешимой в категории групп.

Перейдем к определению нижнего центрального ряда в категории ${{M}_{R}}$. Первым членом этого ряда будет $R$-коммутант группы $G$, который мы в этом случае обозначим через ${{G}_{{\left( {1,R} \right)}}}$. Пусть уже определен $n$-й член нижнего центрального ряда ${{G}_{{\left( {n,R} \right)}}}$. Тогда ${{G}_{{\left( {n + 1,R} \right)}}} = id([G,{{G}_{{\left( {n,R} \right)}}}])$, т.е. ${{G}_{{\left( {n + 1,R} \right)}}}$ – это ${{M}_{R}}$-идеал, порожденный взаимным коммутантом $G$ и ${{G}_{{\left( {n,R} \right)}}}$. Возникает нижний центральный ряд

Степенную MR-группу будем называть нижне-$R$-нильпотентной, если существует такое натуральное число $n$, что ${{G}_{{\left( {n,R} \right)}}} = e$. Наименьшее число $n$ с таким свойством называется ступенью нижней $R$-нильпотентности.

Так как обычный член нижнего центрального ряда ${{G}_{{\left( n \right)}}}$ содержится в ${{G}_{{\left( {n,R} \right)}}}$, то $n$-ступенно нижненильпотентная группа в категории ${{M}_{R}}$ является нильпотентной группой ступени $ \leqslant n$ в категории групп. Из определения рядов (5), (6) и определения вербальной $MR$-подгруппы непосредственно следует, что для любого натурального $n$ и кольца $R$ группы ${{G}^{{\left( {n,R} \right)}}}$ и ${{G}_{{\left( {n,R} \right)}}}$ являются вербальными MR-подгруппами. В связи с этими определениями возникают следующие вопросы.

Вопрос 1. Верно ли, что ${{G}^{{\left( {n,R} \right)}}} = id({{G}^{{\left( n \right)}}})$ и ${{G}_{{\left( {n,R} \right)}}} = id({{G}_{{\left( n \right)}}})$, т.е. порождается ли вербальная $MR$-подгруппа ${{G}^{{\left( {n,R} \right)}}}$ словом ${{{v}}_{n}} = \left[ {{{{v}}_{{n - 1}}}\left( {\bar {x}} \right),{{{v}}_{{n - 1}}}\left( {\bar {y}} \right)} \right]$, где ${{{v}}_{1}} = \left[ {x,y} \right]$,  и порождается ли вербальная $MR$-подгруппа ${{G}_{{\left( {n,R} \right)}}}$ коммутатором $\left[ {{{x}_{1}}, \ldots ,\;{{x}_{n}}} \right]$?

Вопрос 2. Будет ли $n$-ступенно разрешимая MR-группа $n$-ступенно $R$-разрешимой? Будет ли $n$-ступенно нильпотентная MR-группа $n$-ступенно нижне-$R$-нильпотентной?

Ряды (5), (6) можно продолжить для любого ординала $\alpha $. Если $\alpha $ не предельный ординал, то ${{G}^{{\left( {\alpha ,R} \right)}}}$ получается из ${{G}^{{\left( {\alpha - 1,R} \right)}}}$ описанным выше способом. Если же $\alpha $ – предельный ординал, то ${{G}^{{\left( {\alpha ,R} \right)}}} = \bigcap\limits_{\beta < \alpha } {{{G}^{{\left( {\beta ,R} \right)}}}} $, ${{G}_{{\left( {\alpha ,R} \right)}}} = \bigcap\limits_{\beta < \alpha } {{{G}_{{\left( {\beta ,R} \right)}}}} $.

Вопрос 3. Пусть $F = {{F}_{R}}\left( X \right)$ – свободная $MR$-группа с базой $X$. Для любого ли кольца $R$ существуют ординалы $\alpha $ и $\beta $, зависящие от $R$, такие что ${{F}^{{\left( {\alpha ,R} \right)}}} = e$ и ${{F}_{{\left( {\beta ,R} \right)}}} = e$?

Обозначим класс нижне-$R$-нильпотентных групп ступени $n$ через ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{N} }_{{n,R}}}$. Введем также и другие определения нильпотентности в категории $MR$‑групп. Для этого индукцией по $n$ определим понятие простого $\bar {\alpha }$-коммутатора веса $n$, где $\bar {\alpha } = ({{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - 1}}})$. Если $n = 2$, то $\bar {\alpha } = \left( \alpha \right)$ – это $\alpha $‑коммутатор ${{\left( {{{g}_{1}},{{g}_{2}}} \right)}_{\alpha }}$ элементов ${{g}_{1}}$, ${{g}_{2}}$ из $G$, определенный выше. Пусть при $n \geqslant 2$ простые $\bar {\alpha }$‑коммутаторы веса $n$ уже определены. Тогда простой $(\bar {\alpha },{{\alpha }_{n}})$-коммутатор есть элемент ${{(x,{{g}_{n}})}_{{{{\alpha }_{n}}}}}$, где $x$ – простой $\bar {\alpha }$-коммутатор. Далее, пусть X = = $\{ {{x}_{1}},{{x}_{2}}, \ldots \} $ – множество букв. Обозначим через ${{W}_{n}}$ множество $\{ {{( \cdots {{({{({{x}_{1}},{{x}_{2}})}_{{{{\alpha }_{1}}}}},{{x}_{3}})}_{{{{\alpha }_{2}}}}}, \ldots ,{{x}_{{n + 1}}})}_{{{{\alpha }_{n}}}}}$ | α₁, ..., ${{\alpha }_{n}} \in R\} $ всех простых $\bar {\alpha }$-коммутаторов веса $n + 1$ от букв ${{x}_{1}},\; \ldots ,\;{{x}_{{n + 1}}}$. Многообразие групп, определяемое множеством $R$-слов W_n, обозначим через ${{N}_{{n,R}}}$. Группы этого многообразия будем называть $R$-нильпотентными MR-группами ступени $n$. Введем еще одно определение нильпотентности. Обозначим через ${{\bar {N}}_{{n,R}}}$ многообразие MR-групп, определяемое словом ${{{v}}_{n}} = [ \cdots [[{{x}_{1}},{{x}_{2}}], \ldots ,{{x}_{3}}]$, ..., x_{n + 1}]. Группы этого многообразия будем называть верхне-R-нильпотентными ступени $n$. Ясно, что имеют место включения ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{N} }_{{n,R}}} \subseteq {{N}_{{n,R}}} \subseteq {{\bar {N}}_{{n,R}}}$.

Теорема 8. При $n = 1,\;2$ все три определения нильпотентности совпадают. Вопрос о совпадении этих понятий при n > 2 остается открытым.

В [2] отмечено, что тензорные пополнения абелевых MR-групп являются абелевыми MR-группами. В общем случае тензорное пополнение в категории всех MR-групп строится с помощью свободных конструкций (см. [4]), а потому, как правило, в некоммутативном случае содержит свободные подгруппы. Тем не менее справедлива

Теорема 9. Если G – нильпотентная MR‑группа ступени нильпотентности 2, то ее тензорное пополнение G^S также является нильпотентной MS-группой ступени 2.