Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 491, № 1, стр. 90-94

1. ОПИСАНИЕ МОДЕЛЕЙ ВЗАИМОДЕЙСТВИЯ ЧАСТИЦ

Рассмотрим систему взаимно гравитирующих тел, которые могут сталкиваться друг с другом в процессе движения. Для простоты тела будем предполагать однородными шарами. Взаимодействие частиц представляется силами притяжения и отталкивания. Притяжение описывается ньютоновскими гравитационными силами – сила ${\mathbf{F}}_{{ij}}^{a}$, действующая на частицу i со стороны частицы j, имеет вид

Здесь $\gamma $ – гравитационная постоянная, ${{{\mathbf{r}}}_{n}}$ и ${{m}_{n}}$ – радиус-вектор и масса частицы n, $n = i,j$.

Силы отталкивания возникают в процессе столкновения и контактного взаимодействия частиц. Этот процесс можно описать двумя моделями.

Первая из них – классическая модель жесткого неупругого столкновения шаров без учета касательного взаимодействия с использованием формулы с коэффициентом восстановления Ньютона $\kappa $ для относительной скорости соударяющихся тел.

Во второй модели допускается проникание шаров друг в друга, при этом сила отталкивания растет с увеличением глубины проникания существенно быстрее, чем сила гравитационного притяжения. Здесь, не обсуждая физики контактного взаимодействия, мы задаем силу отталкивания ${\mathbf{F}}_{{ij}}^{r}$, действующую на частицу i со стороны частицы j, формулой

Коэффициент ${{k}_{1}}$ выбирается так, чтобы на расстоянии между центрами шаров, равном сумме их радиусов, силы притяжения и отталкивания равнялись по величине:

Здесь ${{R}_{i}}$, ${{R}_{j}}$ – радиусы шаров i, j. Можно выбирать разные показатели степени p. Компьютерные эксперименты показывают, что величина p слабо влияет на качественное поведение системы.

Итак, в рамках предлагаемой модели, сила ${\mathbf{F}}_{{ij}}^{{}}$, действующая на частицу i со стороны частицы j, принимает вид силы Леннарда-Джонса:

Будем называть эти силы силами типа Леннарда-Джонса.

Соответствующий потенциал – “потенциал типа Леннарда-Джонса” V для частиц на расстоянии $\rho = {\text{|}}{{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}{\text{|}}$ имеет вид

Потенциал $V(\rho )$ ограничен снизу и $V(\rho ) \to + \infty $ при $\rho \to + 0$. Отсюда следует, что во второй модели, в силу диссипации энергии в процессе движения, расстояние между центрами шаров для любой пары шаров i и j не может стремиться к нулю. Действительно, допустим противоположное. Полная энергия системы может только убывать:

где $T \geqslant 0$ – полная кинетическая энергия системы, ${{T}_{0}}$ и ${{V}_{0}}$ – начальные значения функций T и $\sum {V({{\rho }_{{ij}}})} $. Тогда для любой пары шаров i и j величины $V({{\rho }_{{ij}}})$ должны быть ограничены сверху. Это противоречит предположению.

Это значит, что во второй модели для любых начальных относительных скоростей центры шаров никогда не совпадут. В таком случае диссипативная сила выбирается зависящей от скорости глубины проникновения. Компьютерные эксперименты показывают, что в обоих случаях: в случае жесткого удара и в случае сглаженного контактного взаимодействия – вследствие диссипации энергии движение системы эволюционирует, проходя газообразное и жидкое состояния, к движению в твердотельной фазе с образованием планет, двойных звезд и других космических объектов.

2. МОДЕЛЬ ДИССИПАЦИИ

Опишем модель диссипации. Пусть $0 < \varepsilon < 1$ – параметр, ${{\varphi }_{\varepsilon }}(s)$ – гладкая монотонно убывающая функция от $s \in R$, такая, что ${{\varphi }_{\varepsilon }}(s) = 1$ при $s < 1 - \varepsilon $ и ${{\varphi }_{\varepsilon }}(s) = 0$ при $s \geqslant 1$. Для пары частиц i, j будем считать, что происходит процесс диссипации, если расстояние между ними становится меньше определенной величины:

Введем единичный вектор e относительного расположения частиц

Скорости относительного сближения–отдаления частиц равны

В этом случае на частицы действуют диссипативные силы линейного вязкого трения, равные

Здесь $c > 0$ и $0 < \varepsilon < {{({{R}_{i}} + {{R}_{j}})}^{{ - 1}}}$ – параметры модели вязкого трения системы.

3. УСТОЙЧИВОСТЬ ПО ЯКОБИ

Для заданного движения системы будем говорить, что частицы не сталкиваются, если во все время движения ${\text{|}}{{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}}{\text{|}} > {{R}_{i}} + {{R}_{j}}$ для любой пары частиц i, j, $i \ne j$. В этом случае диссипация отсутствует, на частицы действуют только потенциальные силы типа Ленарда-Джонса и выполняется закон сохранения энергии:

где T – кинетическая энергия системы:

Потенциальная энергия $V$ всей системы частиц равна

Обозначим первую сумму через ${{V}_{1}}({{{\mathbf{r}}}_{1}}, \ldots ,{{{\mathbf{r}}}_{N}})$, а вторую сумму через ${{V}_{2}}({{{\mathbf{r}}}_{1}}, \ldots ,{{{\mathbf{r}}}_{N}})$. Тогда $V = {{V}_{1}} + {{V}_{2}}$. Заметим, что V₁ – однородная функция степени –1, а V₂ – однородная функция степени –p. Применяя теорему Эйлера об однородных функциях, получаем

Уравнения движения частиц имеют вид

поэтому

Перейдем к доказательству собственно теоремы Якоби, проводя его по стандартной схеме. Движение будем называть устойчивым по Якоби, если во все время движения частицы не сталкиваются и не разбегаются, т.е. расстояние между любой парой частиц не превышает некоторой положительной константы.

Будем рассматривать движение частиц в системе Кенига. Поскольку все силы, действующие в системе, являются внутренними, то эта система инерциальна.

Теорема Якоби. Если движение устойчиво по Якоби, то h < 0, где h – константа интеграла энергии, вычисленная в системе Кенига.

Доказательство. Пусть частицы не сталкиваются и $h \geqslant 0$. Покажем, что тогда частицы будут разбегаться. Обозначим $I = \sum\limits_{i = 1}^N \,{{m}_{i}}{\mathbf{r}}_{i}^{2}$. Поскольку $\dot {I} = 2\sum\limits_{i = 1}^N \,{{m}_{i}}({{{\mathbf{\dot {r}}}}_{i}},{{{\mathbf{r}}}_{i}})$, то

Значит, I(t) – строго выпуклая функция. Следовательно, либо $I \to + \infty $ при $t \to + \infty $, либо $I \to + \infty $ при $t \to - \infty $.

Введем обозначение $J = \sum\limits_{i,j}^N \,{{m}_{i}}{{({{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}})}^{2}}$. Тогда

Третье слагаемое неотрицательно, а второе слагаемое равно нулю, поскольку в кениговой системе центр масс находится в начале координат $\sum\limits_{i = 1}^N \,{{m}_{i}}{{{\mathbf{r}}}_{i}} = 0$, откуда

Поэтому

Следовательно, $J \to + \infty $ либо при $t \to + \infty $, либо при $t \to - \infty $. Но это означает, что найдется такая пара индексов i, j, для которой ${\text{|}}{{{\mathbf{r}}}_{i}},{{{\mathbf{r}}}_{j}}{\text{|}} \to + \infty $ либо при $t \to + \infty $, либо при $t \to - \infty $. В этом случае движение неустойчиво по Якоби.

4. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

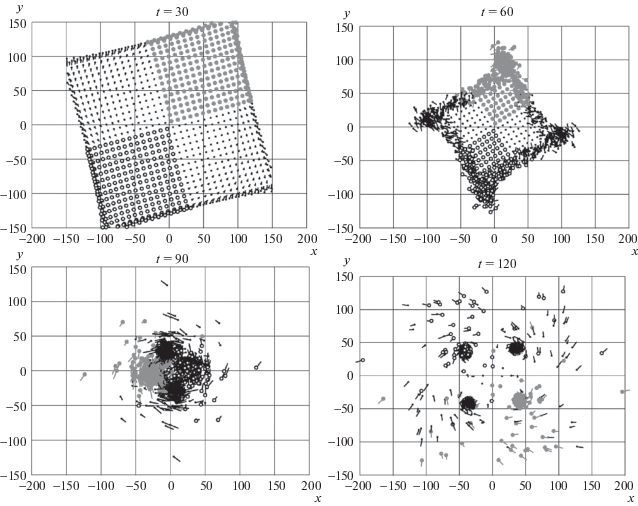
В качестве иллюстрации рассматривается эволюция плоского движения одинаковых шаров в модели жесткого удара (рис. 1). В начальный момент шары равномерно расположены внутри квадрата и имеют начальные скорости, соответствующие вращению квадрата, как твердого тела, вокруг оси симметрии, перпендикулярной плоскости квадрата. Расстояние между центрами соседних шаров равно 10 диаметрам шара. Короткие отрезки, выходящие из точек, показывают направления их скоростей. В наших вычислениях диаметр и масса шара выбраны за единицы длины L и массы $M$. Единица времени $T$ выбрана так, чтобы удов-летворялось   следующее   условие:   $\gamma = 6.6743$  × × 10^–11 м³/(кг ⋅ с²) = $1{{L}^{3}}{\text{/}}(M{{T}^{2}}).$ Если взять среднюю плотность астероида $\rho = 2000$ кг/м³ в качестве плотности шаров, то мы получим $T = 3783$ с, что примерно соответствует одному часу. Начальная угловая скорость и коэффициент восстановления взяты следующими: $\omega = 0.008$, $\kappa = 0.98$. Под действием гравитации система начинает сгущаться от периферии квадрата к центру. По мере того как фронт уплотнения движется к центру, возрастает интенсивность столкновений шаров и диссипация кинетической энергии, что приводит к полному разрушению первоначальной структуры и появлению стабильных образований. Скорость такого процесса в основном зависит от величины коэффициента восстановления Ньютона κ. В консервативном случае (κ = 1) шары не слипаются. При рассмотрении второй модели взаимодействия, описываемой силами типа Леннарда-Джонса, вместе с диссипативными силами во время фазы проникания, мы получаем сходные результаты.

ЗАКЛЮЧЕНИЕ

Многие важные разработки и концепции в математике начинаются с задачи $n$ тел, описывающей движение n материальных точек под влиянием их взаимного притяжения, согласно закону тяготения Ньютона. Задача существенно усложняется, если учитывать размеры гравитирующих частиц и их возможные столкновения. Предлагаемая в настоящем исследовании модель сглаженного столкновения, когда к гравитационному потенциалу добавляется потенциал силы отталкивания, позволяет учитывать размеры частиц и избежать сингулярностей, характерных для гравитационного потенциала.

Если число частиц стремится к бесконечности, то эволюция функции плотности распределения вероятности описывается кинетическими уравнениями [1]. Если допускаются столкновения гравитирующих частиц, то функция плотности эволюционирует в соответствии с системой уравнений Власова–Больцмана–Пуассона. Вместо использования этой системы с соответствующим функционалом столкновений Больцмана предлагается для исследования задач астрофизики использовать кинетическое уравнение Власова с потенциалом типа Леннарда-Джонса.