Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 493, № 1, стр. 95-98

УСЛОВИЯ ОПТИМАЛЬНОСТИ ТРАЕКТОРИЙ ПОДВИЖНОГО ОБЪЕКТА, ОБЛАДАЮЩЕГО НЕОДНОРОДНОЙ ИНДИКАТРИСОЙ ИЗЛУЧЕНИЯ

Член-корреспондент РАН А. А. Галяев^1, *, П. В. Лысенко^1, **, В. П. Яхно^1, ***

¹ Институт проблем управления им. В.А. Трапезникова Российской академии наук
Москва, Россия

^* E-mail: galaev@ipu.ru
^** E-mail: pashlys@yandex.ru
^*** E-mail: vic_iakhno@mail.ru

Поступила в редакцию 06.05.2020
После доработки 06.05.2020
Принята к публикации 16.05.2020

DOI: 10.31857/S2686954320040062

Аннотация

Рассмотрена и решена задача поиска оптимальных траекторий подвижного объекта с неоднородной индикатрисой излучения при уклонении от обнаружения как задача вариационного исчисления. Предложены необходимые и достаточные условия оптимальности траектории движения объекта, обладающего неоднородной индикатрисой излучения сигнала, по которому ведет обнаружение поисковая система, состоящая из единственного сенсора. Получены аналитические выражения для оптимальных траекторий, закона изменения скорости и значения интегрального риска обнаружения на оптимальных траекториях.

Ключевые слова: планирование траекторий, необходимые и достаточные условия оптимальности, индикатриса излучения

Обширный класс поиска-обнаружения подвижных объектов сводится к задачам оптимизации траекторий и законов скорости подвижных объектов с интегральным критерием-риском обнаружения, связанным с вероятностью обнаружения и предложенным в [1–3]. Математические постановки выражаются в терминах задач вариационного исчисления или оптимального управления, а решение этих задач оптимизации опирается на интегрирование уравнений Эйлера–Лагранжа или сопряженных уравнений с учетом условия максимума функции Понтрягина, как в [4, 5]. Большинство исследований посвящено разработке численных алгоритмов построения оптимальных траекторий движения. Обзор таких алгоритмов приведен в [6], и лишь незначительная часть работ, в силу нелинейности постановок, посвящена аналитическому выводу, нахождению и классификации решений, например [1, 4, 7]. Настоящее сообщение является продолжением работы [7] и обобщает постановку, рассмотренную в ней. Рассматривается задача поиска оптимальных траекторий подвижного объекта с неоднородной индикатрисой излучения в присутствии сенсора (обнаружителя). Предложена постановка в более общей форме, охватывающая различные типы физических полей, по которым ведется обнаружение объекта, что позволяет решать широкий класс задач поиска-уклонения.

1. ПОСТАНОВКА ЗАДАЧИ

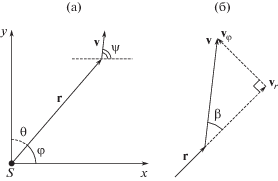
Подвижный объект движется в поле обнаружения поисковой системы, представляющей собой в простейшем случае одиночный сенсор, расположенный в начале координат. Поставим задачу нахождения оптимальных траекторий объекта как задачу классического вариационного исчисления с интегральным фунционалом риска, зависящим от уровня излучаемого объектом сигнала S(t).

Этот уровень сигнала зависит от различных постоянных характеристик подвижного объекта и сенсора, а также от мгновенного значения скорости объекта и расстояния до сенсора

(1)

$S = {{\left( {\frac{{v}}{r}} \right)}^{\mu }}G\left( \varphi \right)\gamma \left( {r,\varphi } \right)g\left( \beta \right),$

где множитель $G\left( \varphi \right)$ отвечает за диаграмму принимающей антенны сенсора, $g\left( \beta \right)$ – это индикатриса излучения подвижного объекта, r – текущее расстояние между сенсором и объектом, ${v}$ – мгновенная скорость объекта, $\gamma \left( {r,\varphi } \right)$ – коэффициент затухания сигнала в среде. Геометрический смысл углов ψ и φ пояснен на рис. 1a. Угол ψ – это угол поворота вектора скорости объекта, а φ – угол поворота радиус-вектора объекта. Угол $\psi - \varphi = \beta $ – это угол в прямоугольном треугольнике, построенном из радиальной ${{{v}}_{r}}$ и трансверсальной ${{{v}}_{\varphi }}$ проекций скоростей подвижного объекта, т.е. угол между скоростью объекта и ее проекцией на радиус-вектор, как показано на рис. 1б. Величина μ > 1 характеризует физическое поле, по которому ведется обнаружение. Это может быть магнитное, тепловое, акустическое или электромагнитное поле.

Рис. 1.

Расположение объекта на плоскости декартовых координат с сенсором S.

Таким образом, критерий оптимизации задачи – риск R как интегральный функционал сигнала S из (1) имеет вид

(2)

$R = \mathop \smallint \limits_0^T {{\left( {\frac{{v}}{r}} \right)}^{\mu }}G\left( \varphi \right)\gamma \left( {r,\varphi } \right)g\left( \beta \right)dt.$

Будем считать, что диаграмма принимающей антенны равномерна $G\left( \varphi \right) \equiv 1$ и сигнал в среде не затухает, т.е. $\gamma \left( {r,\varphi } \right) = 1$.

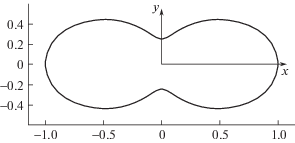
Пример индикатрисы излучения g(β) приведен на рис. 2.

Рис. 2.

Пример индикатрисы излучения подвижного объекта.

Таким образом, можно сформулировать постановку задачи нахождения оптимальных траекторий.

Задача 1. Требуется найти такую траекторию $(r{\text{*}}(t),\varphi {\text{*}}(t))$, которая минимизирует функ-ционал

(3)

$R = \mathop \smallint \limits_0^T {{\left( {\frac{{v}}{r}} \right)}^{\mu }}g\left( \beta \right)dt,$

где $v$ – это скорость объекта, а r – расстояние между сенсором и объектом. Краевые условия фиксированы:

$r\left( 0 \right) = {{r}_{A}},\quad r\left( T \right) = {{r}_{B}},\quad \varphi \left( 0 \right) = {{\varphi }_{A}},\quad \varphi \left( T \right) = {{\varphi }_{B}}.$

Время T движения по маршруту от точки A к точке B также фиксировано.

2. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ

Лемма 1. Подстановка переменной $\rho = {\text{ln}}r$ приводит функционал (3) к виду

(4)

$R\left( {\rho ( \cdot ),\varphi ( \cdot )} \right) = \mathop \smallint \limits_0^T {{({{\dot {\rho }}^{2}} + {{\dot {\varphi }}^{2}})}^{{\mu /2}}}g\left( {{\text{arctg}}\frac{{\dot {\varphi }}}{{\dot {\rho }}}} \right)dt.$

Из леммы 1 следует, что изначальная задача 1 эквивалентна двухточечной краевой вариационной задаче на минимум функционала (4).

Задача 2. Требуется найти траекторию $(\rho {\text{*}}(t)$, φ*(t)), которая минимизирует функционал

(5)

$\begin{gathered} R\left( {\rho \left( \cdot \right),\varphi \left( \cdot \right)} \right) = \mathop \smallint \limits_0^T S(\rho ,\dot {\rho },\varphi ,\dot {\varphi },t)dt = \\ = \int\limits_0^T {{{{({{{\dot {\rho }}}^{2}} + {{{\dot {\varphi }}}^{2}})}}^{{\mu /2}}}g\left( {{\text{arctg}}\frac{{\dot {\varphi }}}{{\dot {\rho }}}} \right)} dt \to \mathop {\min }\limits_{\rho ( \cdot ),\varphi ( \cdot )} . \\ \end{gathered} $

с краевыми условиями

$\rho \left( 0 \right) = {{\rho }_{A}},\quad \rho \left( T \right) = {{\rho }_{B}},\quad \varphi \left( 0 \right) = {{\varphi }_{A}},\quad \varphi \left( T \right) = {{\varphi }_{B}}.$

Вследствие вида функционала (5) он обладает рядом первых интегралов. Справедлива следующая

Лемма 2. Лагранжиан $S\left( {\rho ,\dot {\rho },\varphi ,\dot {\varphi },t} \right)$ имеет постоянное значение S* на экстремальной траектории $\left( {\rho {\text{*}}(t),\varphi {\text{*}}(t)} \right)$.

Следующая теорема дает необходимое условие оптимальности траектории, которая может являться решением задачи 2.

Теорема 1. Пусть $0 < {{g}_{1}} < g\left( \beta \right) < {{g}_{2}}$ для всех $\beta \in \left[ {0,2\pi } \right]$ – дважды дифференцируемая функция β, где g₁, g₂– некоторые константы, и $\ddot {\rho }(t)$, $\ddot {\varphi }(t)$ существуют и являются непрерывными функциями по t. Тогда экстремальная траектория задачи 2 удовлетворяет следующей системе уравнений:

(6)

$\begin{gathered} \dot {\rho } = {\text{const}}, \\ \dot {\varphi } = {\text{const}}. \\ \end{gathered} $

Следствие 1. Из теоремы 1 следует, что экстремальная траектория имеет форму логарифмической спирали

(7)

$\begin{gathered} r\left( t \right) = {{r}_{A}}{\text{exp}}\left( {\frac{t}{T}{\text{ln}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}}} \right), \\ \varphi \left( t \right) = {{\varphi }_{A}} + \frac{{{{\varphi }_{B}} - {{\varphi }_{A}}}}{T}t. \\ \end{gathered} $

Уравнение экстремальной траектории на полярной плоскости имеет вид

(8)

$r(\varphi ) = {{r}_{A}}{\text{exp}}\left( {\frac{{\varphi - {{\varphi }_{A}}}}{{{{\varphi }_{B}} - {{\varphi }_{A}}}}{\text{ln}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}}} \right).$

Следующие две леммы определяют скоростной режим объекта и значение риска обнаружения при движении по экстремальной траектории.

Лемма 3. Закон изменения скорости объекта на экстремальной траектории (8) имеет вид

(9)

${v}\left( t \right) = \frac{{{{r}_{A}}}}{T}{\text{exp}}\left( {\frac{t}{T}{\text{ln}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}}} \right)\sqrt {{\text{l}}{{{\text{n}}}^{2}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}} + {{{\left( {{{\varphi }_{B}} - {{\varphi }_{A}}} \right)}}^{2}}} .$

Лемма 4. Значение функционала (4) на экстремальной траектории (8) равно

(10)

$R{\text{*}} = \frac{{{{{({{{({{\rho }_{B}} - {{\rho }_{A}})}}^{2}} + {{{({{\varphi }_{B}} - {{\varphi }_{A}})}}^{2}})}}^{{\mu /2}}}}}{{{{T}^{{\mu - 1}}}}}g\left( {\beta {\text{*}}} \right),$

где $\beta {\text{*}} = {\text{arctg}}\frac{{{{\varphi }_{B}} - {{\varphi }_{A}}}}{{{{\rho }_{B}} - {{\rho }_{A}}}}$, и зависит только от краевых условий.

3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ

Теперь найдем условия, при которых полученная экстремальная траектория является оптимальным решением задачи 2, т.е. доставляет сильный минимум функционалу (4). Для этого обратимся к матрице Гессе.

Лемма 5. Пусть $S(\rho ,\dot {\rho },\varphi ,\dot {\varphi },t)$ = ${{({{\dot {\rho }}^{2}} + {{\dot {\varphi }}^{2}})}^{{\mu /2}}}$g(β), g(β) – трижды непрерывно дифференцируемая функция β, тогда матрица Гессе функции H имеет вид

(11)

${\mathbf{H}} = \left( {\begin{array}{*{20}{c}} {{{H}_{{11}}}}&{{{H}_{{12}}}} \\ {{{H}_{{21}}}}&{{{H}_{{22}}}} \end{array}} \right),$

где

$\begin{gathered} {{H}_{{11}}} = \frac{{{{\partial }^{2}}S}}{{\partial {{{\dot {\rho }}}^{2}}}} = ( - 2\dot {\varphi }\dot {\rho }(\mu - 1)g{\kern 1pt} '(\beta ) + \\ \, + \mu ({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}}(\mu - 1))g(\beta ) + g{\kern 1pt} ''(\beta ){{{\dot {\varphi }}}^{2}}){{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\frac{\mu }{2} - 2}}}, \\ \end{gathered} $

$\begin{gathered} {{H}_{{12}}} = \frac{{{{\partial }^{2}}S}}{{\partial{ \dot {\rho }}\partial{ \dot {\varphi }}}} = (({{{\dot {\rho }}}^{2}} - {{{\dot {\varphi }}}^{2}})(\mu - 1)g{\kern 1pt} '(\beta ) + \\ \, + \dot {\rho }\dot {\varphi }(({{\mu }^{2}} - 2\mu )g(\beta ) - g{\kern 1pt} ''(\beta ))){{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\frac{\mu }{2} - 2}}}, \\ \end{gathered} $

$\begin{gathered} {{H}_{{21}}} = \frac{{{{\partial }^{2}}S}}{{\partial{ \dot {\varphi }}\partial{ \dot {\rho }}}} = (({{{\dot {\rho }}}^{2}} - {{{\dot {\varphi }}}^{2}})(\mu - 1)g{\kern 1pt} '(\beta ) + \\ \, + \dot {\rho }\dot {\varphi }(({{\mu }^{2}} - 2\mu )g(\beta ) - g{\kern 1pt} ''(\beta ))){{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\frac{\mu }{2} - 2}}}, \\ \end{gathered} $

$\begin{gathered} {{H}_{{22}}} = \frac{{{{\partial }^{2}}S}}{{\partial {{{\dot {\varphi }}}^{2}}}} = (2\dot {\varphi }\dot {\rho }(\mu - 1)g{\kern 1pt} '(\beta ) + \\ \, + \mu ({{{\dot {\rho }}}^{2}} + {{{\dot {\varphi }}}^{2}}(\mu - 1))g(\beta ) + g{\kern 1pt} ''(\beta ){{{\dot {\rho }}}^{2}}){{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\frac{\mu }{2} - 2}}}, \\ \end{gathered} $

а сам гессиан

(12)

$\begin{gathered} {\text{det}}{\mathbf{H}} = {{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\mu - 2}}}(\mu - 1)({{g}^{2}}(\beta ){{\mu }^{2}} + \\ \, + g(\beta )g{\kern 1pt} ''(\beta )\mu - g{\kern 1pt} {{'}^{2}}(\beta )(\mu - 1)). \\ \end{gathered} $

Следующая теорема дает достаточное условие оптимальности траектории, претендующей на решение задачи.

Теорема 2. Предположим, что выполнены условия теоремы 1, лемм 2 и 5, и detH > 0 для всех β. Тогда экстремальная траектория, удовлетворяющая (6), доставляет функционалу (4) сильный минимум.

Таким образом, положительность детерминанта матрицы Гессе гарантирует оптимальность логарифмической спирали как решения задачи. Теорема 2 позволяет для произвольной индикатрисы g(β) однозначно ответить на вопрос оптимальности траектории (8) как решения задачи. Действительно, знак гессиана зависит от знака третьего сомножителя в (12), который при заданном μ зависит только от вида g(β). В случае, когда достаточные условия не выполнены, искомая оптимальная траектория будет иметь более сложный вид и будет составлена из нескольких логарифмических спиралей.

В более общем случае можно рассматривать движение объекта с многообразия на многообразие, выводы относительно вида траекторий останутся справедливыми.

4. ПРИМЕР

Рассмотрим пример для частного случая μ = 2, что может соответствовать распространению первичного акустического сигнала в однородной водной среде. Пусть индикатриса излучения объекта имеет такой вид:

$g\left( \beta \right) = {{K}_{1}} + {{K}_{2}}{\text{co}}{{{\text{s}}}^{2}}\beta .$

Коэффициенты K₁ и K₂ строго положительны и определяют характер излучения и нормализованы, т.е. ${{K}_{1}} + {{K}_{2}} = 1$. Индикатриса излучения такого вида проиллюстрирована на рис. 2 для ${{K}_{1}}$ = 0.25, K₂ = = 0.75. Обратимся к лемме 5 и вычислим гессиан

${\text{det}}{\mathbf{H}} = 4{{K}_{1}}\left( {{{K}_{1}} + {{K}_{2}}} \right) = 4{{K}_{1}}.$

Очевидно, что гессиан строго положителен, тогда, согласно теореме 2, логарифмическая спираль (8) является оптимальной траекторией с минимальным риском при движении между двумя точками на плоскости. Проверим это утверждение с помощью вариации функционала (4):

$\begin{gathered} \delta R = 2\dot {\rho }\delta \rho {\text{|}}_{0}^{T} + \dot {\varphi }\delta \varphi {\text{|}}_{0}^{T} - 2\int\limits_0^T {(\ddot {\rho }\delta \rho + \ddot {\varphi }\delta \varphi )\,dt} + \\ + \,\int\limits_0^T {(\delta {{\rho }^{2}} + {{K}_{1}}\delta {{\varphi }^{2}})dt = \int\limits_0^T {(\delta {{\rho }^{2}} + {{K}_{1}}\delta {{\varphi }^{2}})} } \,dt, \\ \end{gathered} $

где δρ, δφ – вариации координат, которые являются достаточно гладкими функциями времени. Первое и второе слагаемые равны нулю в силу фиксированных краевых условий для вариаций, третье слагаемое зануляется из-за выполнения уравнений Эйлера–Лагранжа на экстремальной траектории, следствием из которых является (6). Осталась только взвешенная сумма квадратов, которая, очевидно, положительна. Таким образом, любая вариация траектории (логарифмической спирали) увеличивает значение функционала риска, что доказывает ее оптимальность. По лемме 4 значение риска на этой траектории равно

$R{\text{*}} = \frac{1}{T}\left( {{\text{l}}{{{\text{n}}}^{2}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}} + K_{1}^{2}{{{\left( {{{\varphi }_{B}} - {{\varphi }_{A}}} \right)}}^{2}}} \right)$

и зависит только от краевых условий.

Список литературы

Zabarankin M., Uryasev S., Pardalos P. Optimal Risk Path Algorithms Cooperative Control and Optimization // Eds. R. Murphey, P. Pardalos. Dordrecht: Kluwer Acad. 2002. V. 66. P. 271–303.
Галяев А.А. О функционале обнаружения при движении объекта в конфликтной среде // АиТ. 2010. № 4. С. 100–105.
Сысоев Л.П. Критерий вероятности обнаружения на траектории в задаче управления движением объекта в конфликтной среде // Пробл. управл. 2010. № 6. С. 64–70.
Галяев А.А., Маслов Е.П. Оптимизация закона уклонения подвижного объекта от обнаружения при наличии ограничений // АиТ. 2012. № 6. С. 73–88.
Sidhu H., Mercer G., Sexton M. Optimal trajectories in a threat environment // Journal of Battlefield technology. 2006. V. 9. № 3. P. 33–39.
Panda M., Das B., Subudhi B., et al. A Comprehensive Review of Path Planning Algorithms for Autonomous Underwater Vehicles // Int. J. Autom. Comput. 2020. https://doi.org/10.1007/s11633-019-1204-9
Galyaev A.A., Dobrovidov A.V., Lysenko P.V., Shaikin M.E., Yakhno V.P. Path Planning in Threat Environment for UUV with Non-Uniform Radiation Pattern // Sensors. 2020. V. 20. P. 2076.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал